Factors Influencing Pile Friction Bearing Capacity: Proposing a Novel Procedure Based on Gradient Boosted Tree Technique
Abstract
:1. Introduction
2. Methods and Material
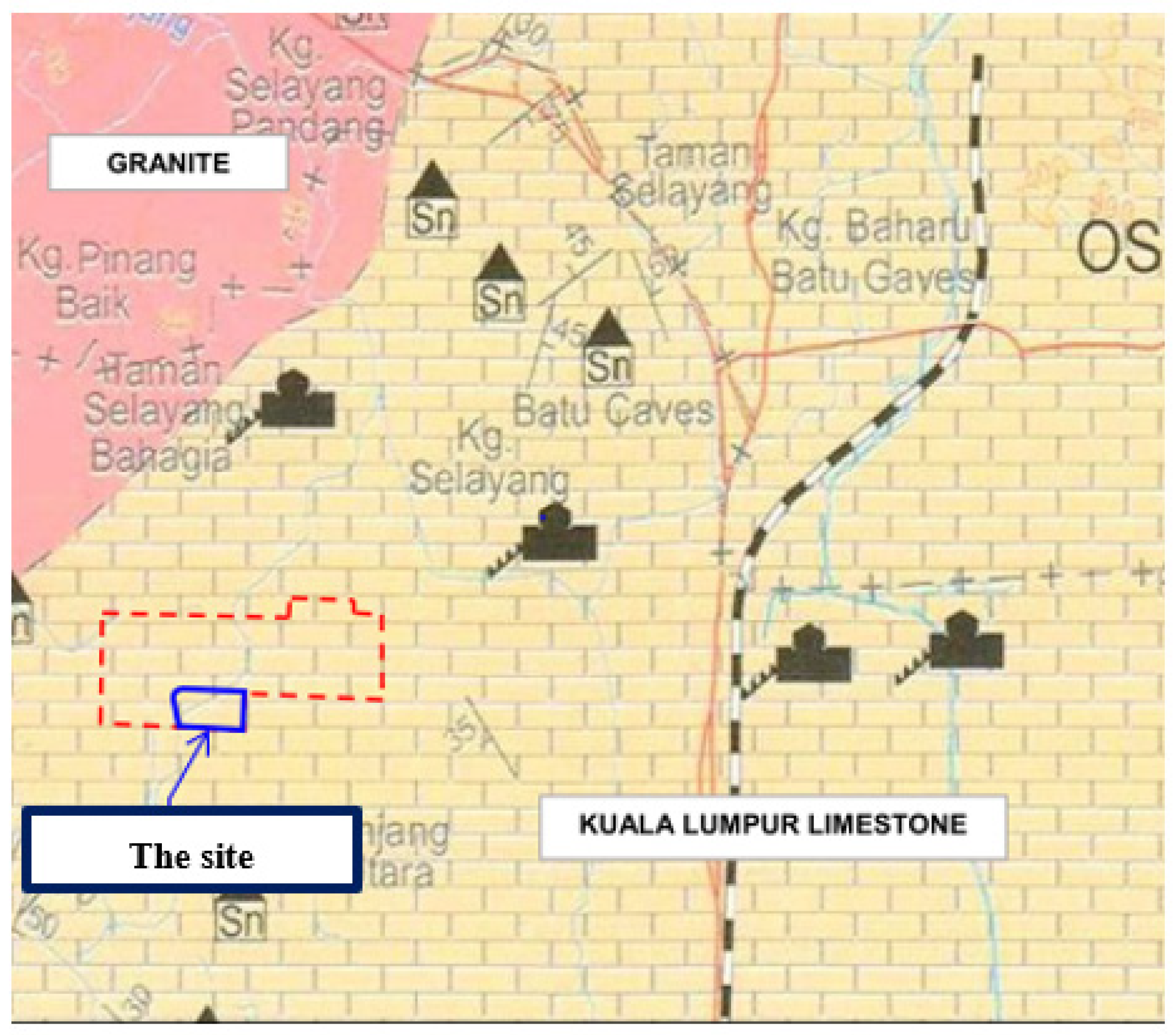
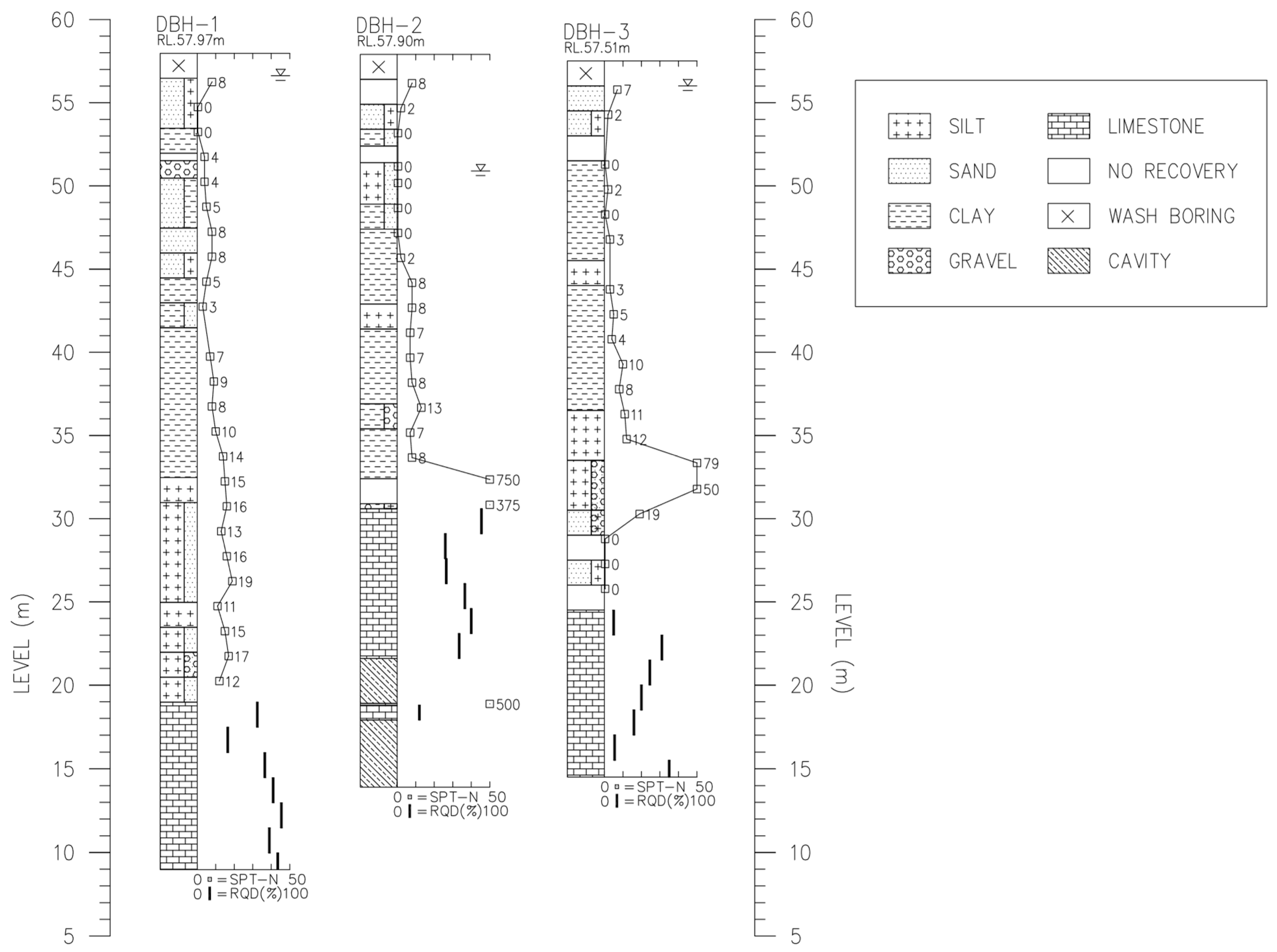
2.1. Case Study and Established Database
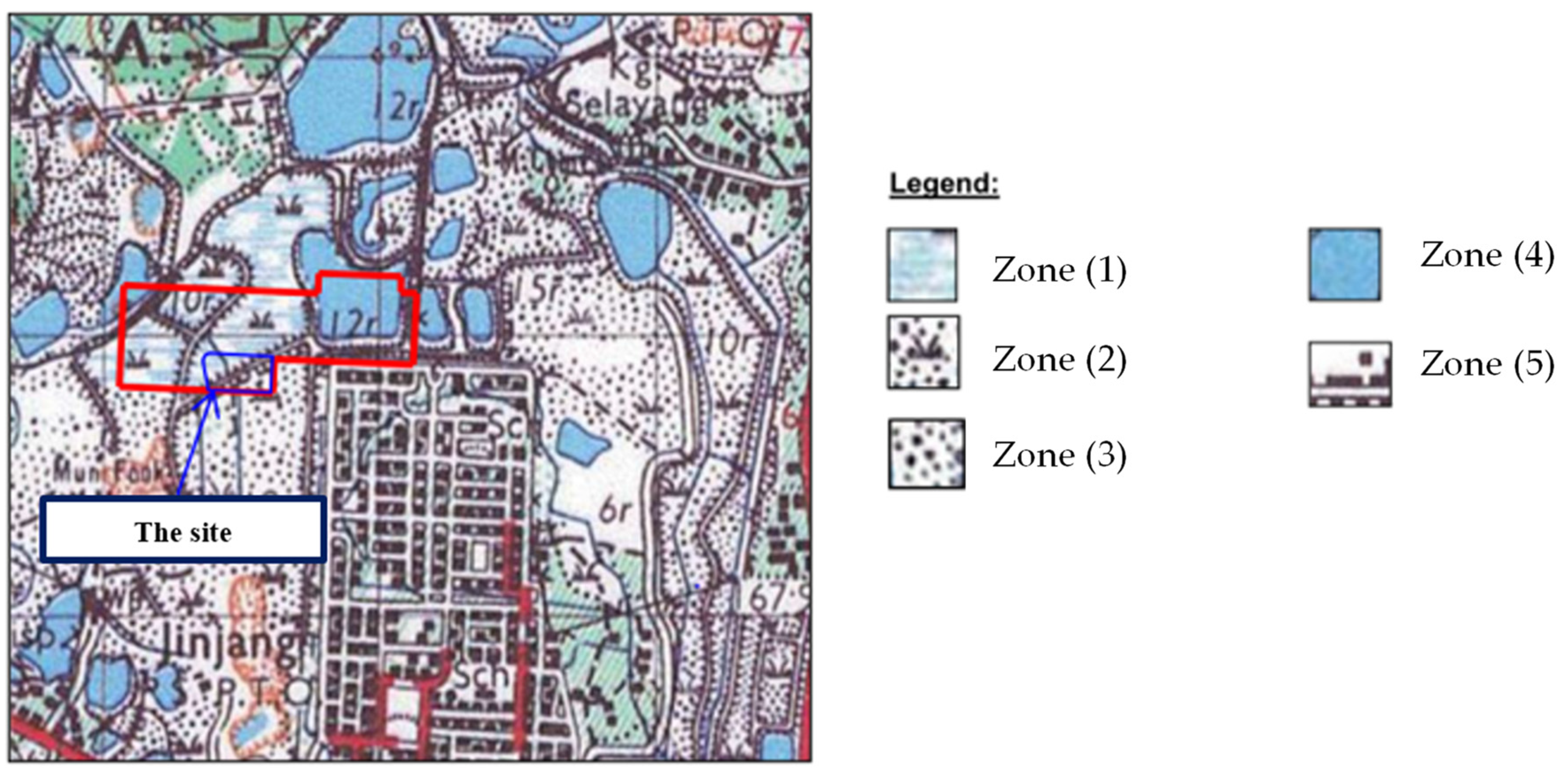
- Zone (1): Fresh water (Swamps)—The region is continuously or seasonally submerged by freshwater and commonly seen in the lower sections of rivers and near freshwater.
- Zone (2): Vegetation—The region is covered by plants.
- Zone (3): Mining Land—The region that used for the extraction of valuable minerals.
- Zone (4): Pond and Lake—The region that comprise of freshwater and living creatures.
- Zone (5): Building—The area covered by building.
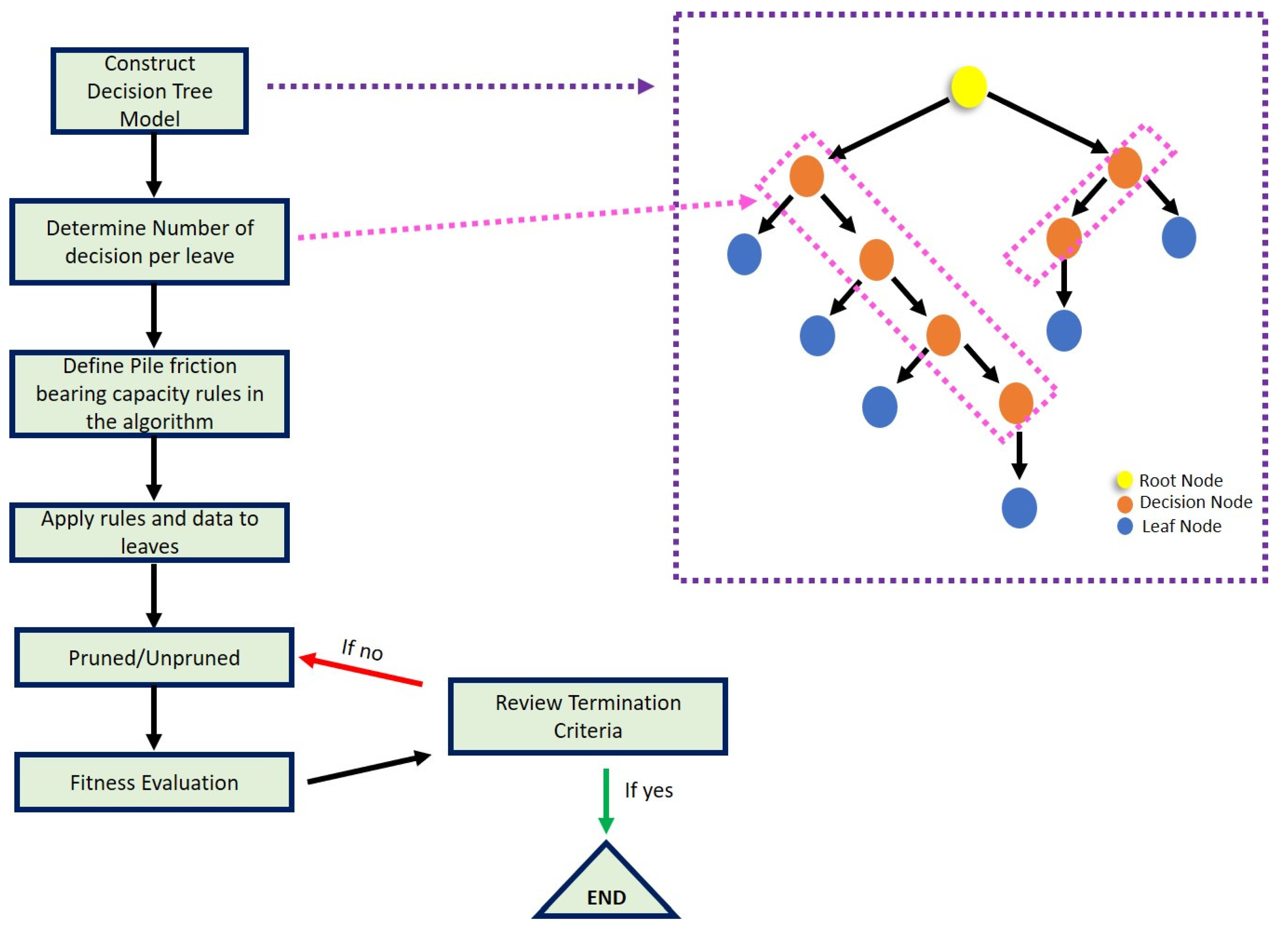
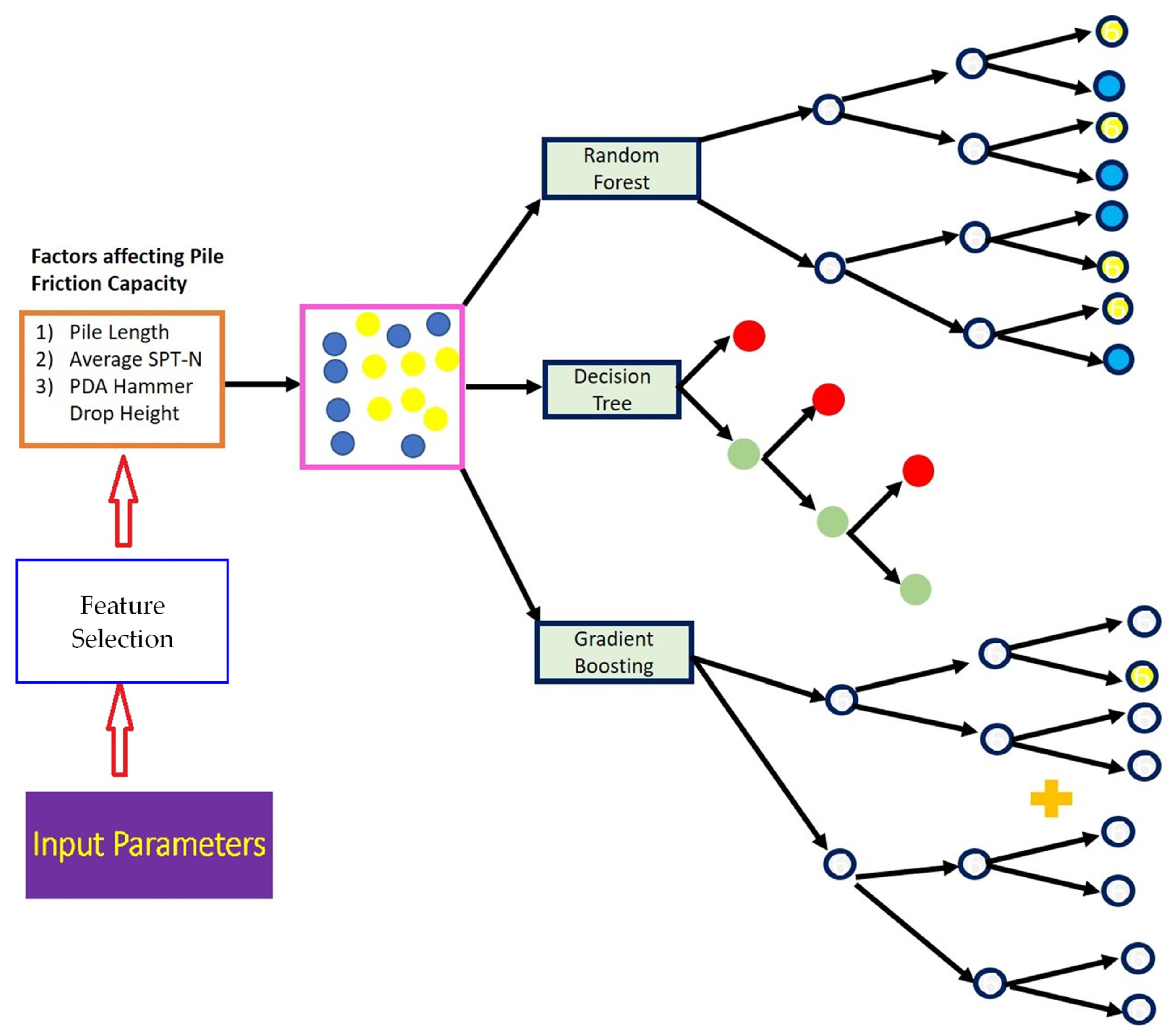
2.2. Decision Tree (DT)
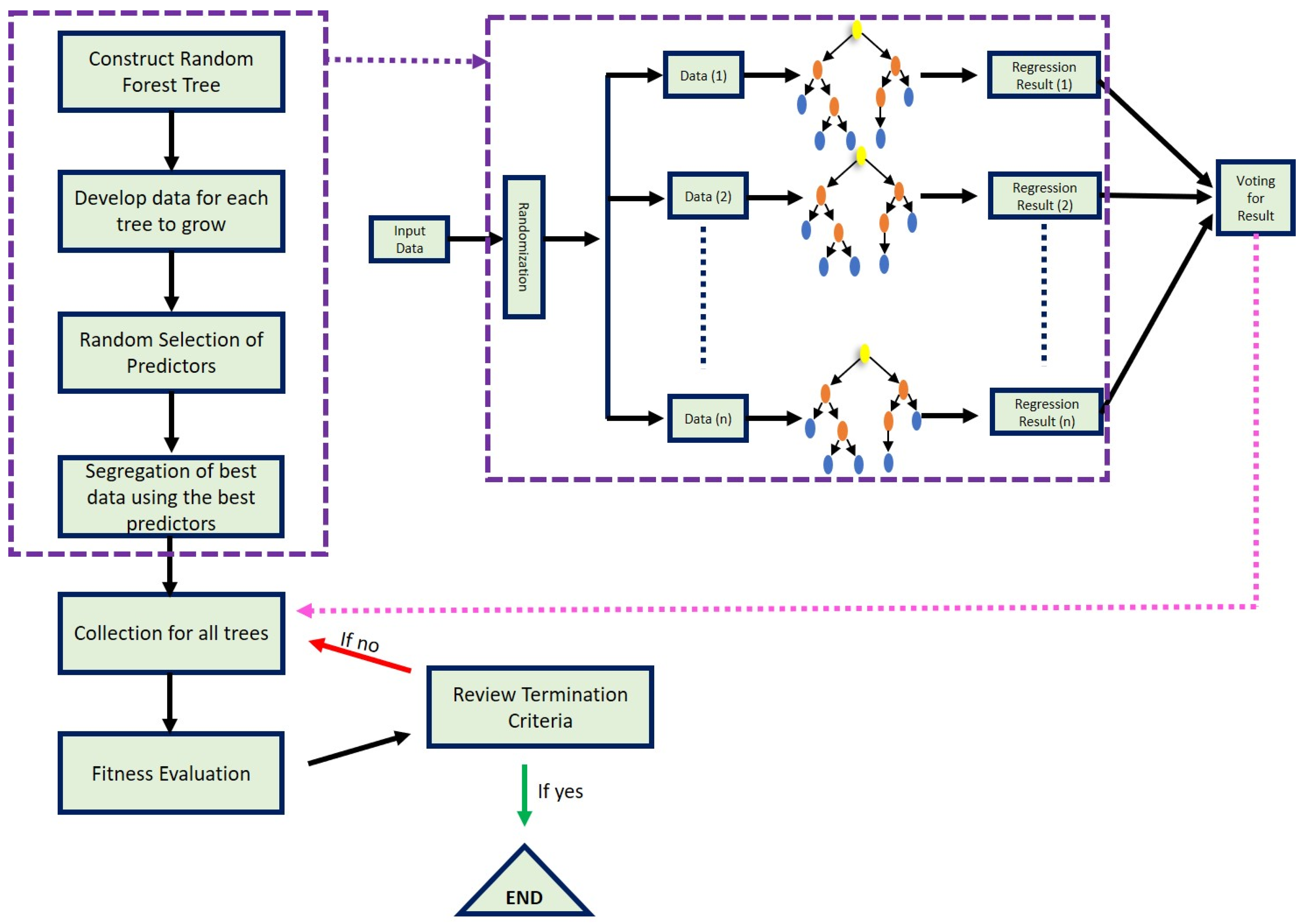
2.3. Random Forest (RF)
- Automatically provide estimation of missing value.
- Weight data to balance the errors found in imbalanced data.
- Determine the crucial variables by estimation for classification.
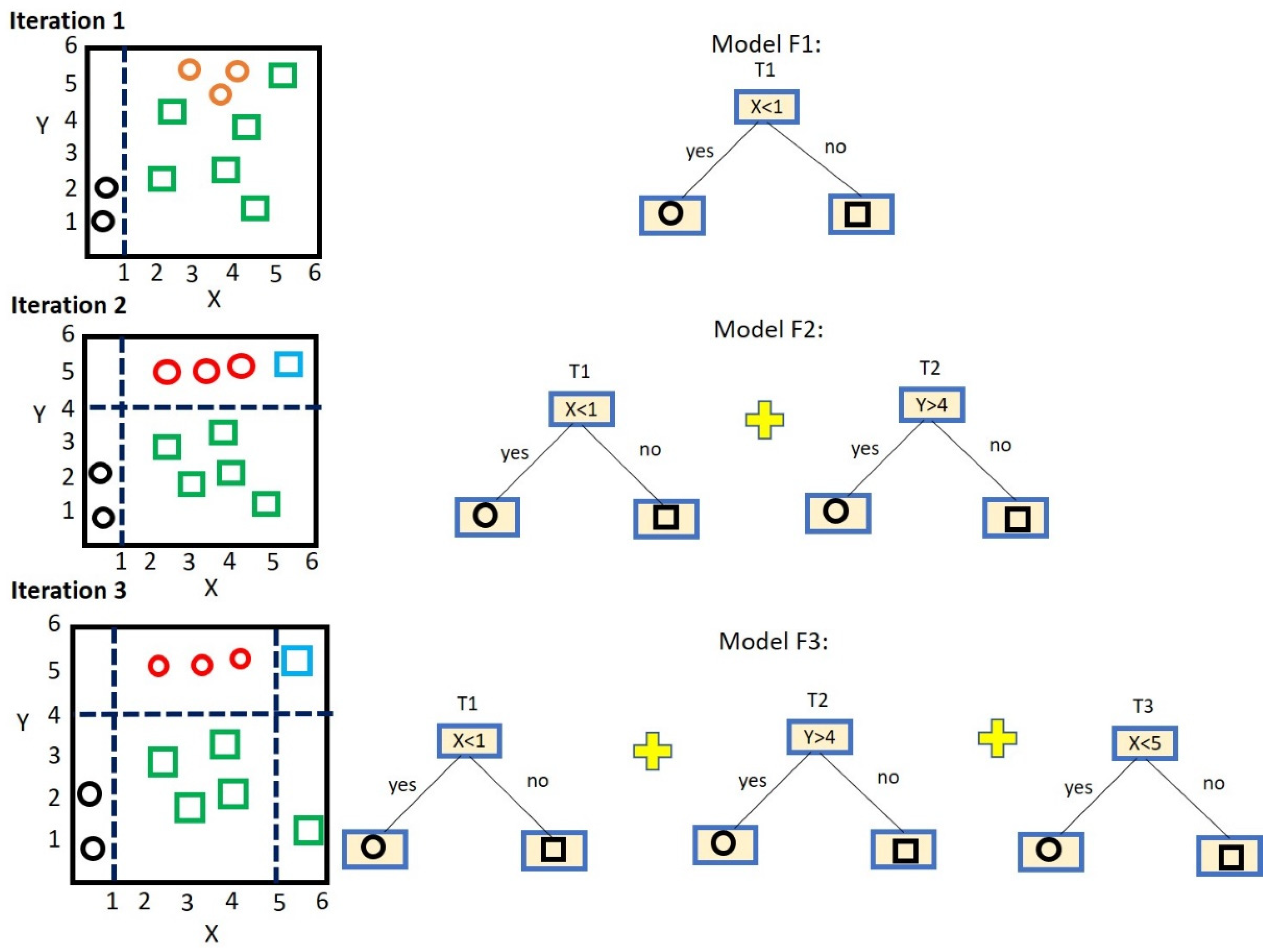
2.4. Gradient Boosted Tree (GBT)
- A constant value is begun in the model to lower down the loss function.
- During the iteration of training process, the residual value of the model is estimated from the negative gradient of the loss function.
- The current residual value is fit by newly trained regression tree.
- The combination of final regression with past models and residual is updated.
- When the maximum number of iterations set by the user is achieved, the iteration in the algorithm is ceased.
2.5. Performance Indices
2.6. Study Steps
3. Input Selection
3.1. Correlation
3.2. Supervised Feature Selection
4. Modeling and Results
5. Discussion
6. Optimum Parameters Based on Simulation Model
7. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Viggiani, C.; Mandolini, A.; Russo, G. Piles and Pile Foundations; Spon Press: London, UK, 2012; p. 278. ISBN 1498725538. [Google Scholar]
- Torshizi, M.F.; Saitoh, M.; Álamo, G.M.; Goit, C.S.; Padrón, L.A. Influence of pile radius on the pile head kinematic bending strains of end-bearing pile groups. Soil Dyn. Earthq. Eng. 2018, 105, 184–203. [Google Scholar] [CrossRef]
- Ma, Y.; Deng, N. Deep foundations. Substruct. Des. 2014, 239, 18. [Google Scholar]
- Vesic, A.S. Design of Pile Foundations. National Cooperative Highway Research Program Synthesis of Practice no. 42; Transportation Research Board: Washington, DC, USA, 1977; p. 3248. [Google Scholar]
- Helwany, S. Applied Soil Mechanics with ABAQUS Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007; ISBN 0471791075. [Google Scholar]
- Liu, Y.J.; Liang, S.H.; Wu, J.W.; Fu, N. Prediction method of vertical ultimate bearing capacity of single pile based on support vector machine. Adv. Mater. Res. 2011, 168–170, 2278–2282. [Google Scholar] [CrossRef]
- Shah, D.L.; Shroff, A.V. Soil Mechanics and Geotechnical Engineering; CRC Press: Boca Raton, FL, USA, 2003; ISBN 9058092356. [Google Scholar]
- Momeni, E.; Nazir, R.; Armaghani, D.J.; Maizir, H. Application of artificial neural network for predicting shaft and tip resistances of concrete piles. Earth Sci. Res. J. 2015, 19, 85–93. [Google Scholar] [CrossRef]
- Brinkgreve, R.B.J.; Engin, E. Validation of geotechnical finite element analysis. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013; Volume 2, pp. 677–682. [Google Scholar]
- Nawari, N.O.; Liang, R.; Nusairat, J. Artificial intelligence techniques for the design and analysis of deep foundations. Electron. J. Geotech. Eng. 1999, 4, 1–21. [Google Scholar]
- Wardani, S.P.R.; Surjandari, N.S.; Jajaputra, A.A. Analysis of ultimate bearing capacity of single pile using the artificial neural networks approach: A case study. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013; pp. 837–840. [Google Scholar]
- Jianbin, Z.; Jiewen, T.; Yongqiang, S. An ANN model for predicting level ultimate bearing capacity of PHC pipe pile. In Earth and Space 2010: Engineering, Science, Construction, and Operations in Challenging Environments; ASCE: Reston VA, USA, 2010; pp. 3168–3176. [Google Scholar]
- Suman, S. Prediction of Pile Capacity Parameters Using Functional Networks and Multivariate Adaptive Regression Splines. Doctoral Dissertation, Department of Civil Engineering National Institue of Technology Rourkela, Odisha, India, 2015. [Google Scholar]
- Doherty, P.; Gavin, K. The shaft capacity of displacement piles in clay: A state of the art review. Geotech. Geol. Eng. 2011, 29, 389–410. [Google Scholar] [CrossRef]
- Shahin, M.A. Artificial intelligence in geotechnical engineering: Applications, modeling aspects, and future directions. In Metaheuristics in Water, Geotechnical and Transport Engineering; Elsevier: Amsterdam, The Netherlands, 2013; p. 169204. [Google Scholar]
- Momeni, E.; Maizir, H.; Gofar, N.; Nazir, R. Comparative study on prediction of axial bearing capacity of driven piles in granular materials. J. Teknol. 2013, 61, 15–20. [Google Scholar] [CrossRef] [Green Version]
- Bazaraa, A.R.; Kurkur, M.M. N-values used to predict settlements of piles in Egypt. In Proceedings of the Use of In Situ Tests in Geotechnical Engineering, Virginia, VA, USA, 23–25 June 1986; pp. 462–474. [Google Scholar]
- Décourt, L. Prediction of the bearing capacity of piles based exclusively on N values of the SPT. In Penetration Testing; Routledge: Oxfordshire, UK, 2021; pp. 29–34. [Google Scholar]
- Lopes, F.R.; Laprovitera, H. On the prediction of the bearing capacity of bored piles from dynamic penetration tests. In Proceedings of the International Geotechnical Seminar on Deep Foundations on Bored and Auger Piles, Ghent, Belgium, 1–7 June 1988; pp. 537–540. [Google Scholar]
- Meyerhof, G.G. Penetration tests and bearing capacity of cohesionless soils. J. Soil Mech. Found. Div. 1956, 82, 861–866. [Google Scholar] [CrossRef]
- Shioi, Y.; Fukui, J. Application of N-value to design of foundations in Japan. In Penetration Testing; Routledge: Oxfordshire, UK, 2021; pp. 159–164. [Google Scholar]
- Aoki, N.; Velloso, D.A. An approximate method to estimate the bearing capacity of piles. In Proceedings of the 5th Pan-American Conf. of Soil Mechanics and Foundation Engineering, Bueno Aires, Argentina, 17–22 November 1975; International Society of Soil Mechanics and Geotechnical Engineering Buenos. Volume 1, pp. 367–376. [Google Scholar]
- Reese, L.C.; O’Neill, M.W. New design method for drilled shafts from common soil and rock tests. In Foundation Engineering: Current Principles and Practices; ASCE: Reston, VA, USA, 1989; pp. 1026–1039. [Google Scholar]
- Robert, Y. A few comments on pile design. Can. Geotech. J. 1997, 34, 560–567. [Google Scholar] [CrossRef]
- Randolph, M.F. Science and empiricism in pile foundation design. Géotechnique 2003, 53, 847–875. [Google Scholar] [CrossRef]
- Momeni, E.; Nazir, R.; Armaghani, D.J.; Maizir, H. Prediction of pile bearing capacity using a hybrid genetic algorithm-based ANN. Measurement 2014, 57, 122–131. [Google Scholar] [CrossRef]
- Harandizadeh, H.; Armaghani, D.J.; Khari, M. A new development of ANFIS–GMDH optimized by PSO to predict pile bearing capacity based on experimental datasets. Eng. Comput. 2021, 37, 685–700. [Google Scholar] [CrossRef]
- Chen, W.; Sarir, P.; Bui, X.-N.; Nguyen, H.; Tahir, M.M.; Armaghani, D.J. Neuro-genetic, neuro-imperialism and genetic programing models in predicting ultimate bearing capacity of pile. Eng. Comput. 2020, 36, 1101–1115. [Google Scholar] [CrossRef]
- Lee, I.-M.; Lee, J.-H. Prediction of pile bearing capacity using artificial neural networks. Comput. Geotech. 1996, 18, 189–200. [Google Scholar] [CrossRef]
- Likins, G.E.; Rausche, F. Correlation of CAPWAP with static load tests. In Proceedings of the Seventh International Conference on the Application of Stresswave Theory to Piles, Petaling Jaya, Malaysia, August 2004; pp. 153–165. [Google Scholar]
- Moayedi, H.; Armaghani, D.J. Optimizing an ANN model with ICA for estimating bearing capacity of driven pile in cohesionless soil. Eng. Comput. 2018, 34, 347–356. [Google Scholar] [CrossRef]
- Jahed Armaghani, D.; Shoib, R.S.N.S.B.R.; Faizi, K.; Rashid, A.S.A. Developing a hybrid PSO–ANN model for estimating the ultimate bearing capacity of rock-socketed piles. Neural Comput. Appl. 2017, 28, 391–405. [Google Scholar] [CrossRef]
- Huang, J.; Asteris, P.G.; Pasha, S.M.K.; Mohammed, A.S.; Hasanipanah, M. A new auto-tuning model for predicting the rock fragmentation: A cat swarm optimization algorithm. Eng. Comput. 2020. Available online: https://link.springer.com/article/10.1007/s00366-020-01207-4 (accessed on 24 October 2021). [CrossRef]
- Chen, H.; Asteris, P.G.; Jahed Armaghani, D.; Gordan, B.; Pham, B.T. Assessing Dynamic Conditions of the Retaining Wall: Developing Two Hybrid Intelligent Models. Appl. Sci. 2019, 9, 1042. [Google Scholar] [CrossRef] [Green Version]
- Parsajoo, M.; Armaghani, D.J.; Mohammed, A.S.; Khari, M.; Jahandari, S. Tensile strength prediction of rock material using non-destructive tests: A comparative intelligent study. Transp. Geotech. 2021, 31, 100652. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Hajihassani, M.; Mohamad, E.T.; Marto, A.; Noorani, S.A. Blasting-induced flyrock and ground vibration prediction through an expert artificial neural network based on particle swarm optimization. Arab. J. Geosci. 2014, 7, 5383–5396. [Google Scholar] [CrossRef]
- Xie, C.; Nguyen, H.; Choi, Y.; Armaghani, D.J. Optimized functional linked neural network for predicting diaphragm wall deflection induced by braced excavations in clays. Geosci. Front. 2021, 101313. [Google Scholar] [CrossRef]
- Apostolopoulou, M.; Asteris, P.G.; Armaghani, D.J.; Douvika, M.G.; Lourenço, P.B.; Cavaleri, L.; Bakolas, A.; Moropoulou, A. Mapping and holistic design of natural hydraulic lime mortars. Cem. Concr. Res. 2020, 136, 106167. [Google Scholar] [CrossRef]
- Asteris, P.G.; Kolovos, K.G. Self-compacting concrete strength prediction using surrogate models. Neural Comput. Appl. 2019, 31, 409–424. [Google Scholar] [CrossRef]
- Khandelwal, M.; Mahdiyar, A.; Armaghani, D.J.; Singh, T.N.; Fahimifar, A.; Faradonbeh, R.S. An expert system based on hybrid ICA-ANN technique to estimate macerals contents of Indian coals. Environ. Earth Sci. 2017, 76, 399. [Google Scholar] [CrossRef]
- Khandelwal, M.; Singh, T.N. Prediction of blast induced air overpressure in opencast mine. Noise Vib. Worldw. 2005, 36, 7–16. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Harandizadeh, H.; Momeni, E. Load carrying capacity assessment of thin-walled foundations: An ANFIS–PNN model optimized by genetic algorithm. Eng. Comput. 2021. Available online: https://link.springer.com/article/10.1007/s00366-021-01380-0 (accessed on 24 October 2021).
- Gajurel, A.; Chittoori, B.; Mukherjee, P.S.; Sadegh, M. Machine learning methods to map stabilizer effectiveness based on common soil properties. Transp. Geotech. 2021, 27, 100506. [Google Scholar] [CrossRef]
- Jahed Armaghani, D.; Asteris, P.G.; Askarian, B.; Hasanipanah, M.; Tarinejad, R.; Huynh, V. Van Examining Hybrid and Single SVM Models with Different Kernels to Predict Rock Brittleness. Sustainability 2020, 12, 2229. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, A.S.; Asteris, P.G.; Koopialipoor, M.; Alexakis, D.E.; Lemonis, M.E.; Armaghani, D.J. Stacking Ensemble Tree Models to Predict Energy Performance in Residential Buildings. Sustainability 2021, 13, 8298. [Google Scholar] [CrossRef]
- Hajihassani, M.; Jahed Armaghani, D.; Kalatehjari, R. Applications of Particle Swarm Optimization in Geotechnical Engineering: A Comprehensive Review. Geotech. Geol. Eng. 2018, 36, 705–722. [Google Scholar] [CrossRef]
- Harandizadeh, H.; Toufigh, M.M.; Toufigh, V. Application of improved ANFIS approaches to estimate bearing capacity of piles. Soft Comput. 2019, 23, 9537–9549. [Google Scholar] [CrossRef]
- Mayerhof, G.G. Bearing capacity and settlemtn of pile foundations. J. Geotech. Geoenviron. Eng. 1976, 102, 196–228. [Google Scholar]
- Armaghani, D.J.; Faradonbeh, R.S.; Rezaei, H.; Rashid, A.S.A.; Amnieh, H.B. Settlement prediction of the rock-socketed piles through a new technique based on gene expression programming. Neural Comput. Appl. 2016, 29, 1115–1125. [Google Scholar] [CrossRef]
- Shahin, M.A. Intelligent computing for modeling axial capacity of pile foundations. Can. Geotech. J. 2010, 47, 230–243. [Google Scholar] [CrossRef] [Green Version]
- Goh, A.T.C. Back-propagation neural networks for modeling complex systems. Artif. Intell. Eng. 1995, 9, 143–151. [Google Scholar] [CrossRef]
- Pal, M. Modelling pile capacity using generalised regression neural network. In Proceedings of the Indian Geotechnical Conference, Kochi, India, 15–17 December 2011. [Google Scholar]
- Alkroosh, I.; Nikraz, H. Predicting axial capacity of driven piles in cohesive soils using intelligent computing. Eng. Appl. Artif. Intell. 2012, 25, 618–627. [Google Scholar] [CrossRef]
- Alavi, A.H.; Aminian, P.; Gandomi, A.H.; Esmaeili, M.A. Genetic-based modeling of uplift capacity of suction caissons. Expert Syst. Appl. 2011, 38, 12608–12618. [Google Scholar] [CrossRef]
- Momeni, E.; Dowlatshahi, M.B.; Omidinasab, F.; Maizir, H.; Armaghani, D.J. Gaussian Process Regression Technique to Estimate the Pile Bearing Capacity. Arab. J. Sci. Eng. 2020, 45, 8255–8267. [Google Scholar] [CrossRef]
- Goh, A.T.C. Nonlinear modelling in geotechnical engineering using neural networks. Trans. Inst. Eng. Aust. Civ. Eng. 1994, 36, 293–297. [Google Scholar]
- Goh, A.T.C. Pile driving records reanalyzed using neural networks. J. Geotech. Eng. 1996, 122, 492–495. [Google Scholar] [CrossRef]
- Kiefa, M.A.A. General regression neural networks for driven piles in cohesionless soils. J. Geotech. Geoenvironmental Eng. 1998, 124, 1177–1185. [Google Scholar] [CrossRef]
- Das, S.K.; Basudhar, P.K. Undrained lateral load capacity of piles in clay using artificial neural network. Comput. Geotech. 2006, 33, 454–459. [Google Scholar] [CrossRef]
- Pal, M.; Deswal, S. Modeling pile capacity using support vector machines and generalized regression neural network. J. Geotech. Geoenvironmental Eng. 2008, 134, 1021–1024. [Google Scholar] [CrossRef]
- Pal, M.; Deswal, S. Modelling pile capacity using Gaussian process regression. Comput. Geotech. 2010, 37, 942–947. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. A new multi-gene genetic programming approach to nonlinear system modeling. Part I: Materials and structural engineering problems. Neural Comput. Appl. 2012, 21, 171–187. [Google Scholar] [CrossRef]
- Kordjazi, A.; Nejad, F.P.; Jaksa, M.B. Prediction of ultimate axial load-carrying capacity of piles using a support vector machine based on CPT data. Comput. Geotech. 2014, 55, 91–102. [Google Scholar] [CrossRef]
- Ghorbani, B.; Sadrossadat, E.; Bazaz, J.B.; Oskooei, P.R. Numerical ANFIS-based formulation for prediction of the ultimate axial load bearing capacity of piles through CPT data. Geotech. Geol. Eng. 2018, 36, 2057–2076. [Google Scholar] [CrossRef]
- Dehghanbanadaki, A.; Khari, M.; Amiri, S.T.; Armaghani, D.J. Estimation of ultimate bearing capacity of driven piles in c-φ soil using MLP-GWO and ANFIS-GWO models: A comparative study. Soft Comput. 2020, 25, 4103–4119. [Google Scholar] [CrossRef]
- Pham, T.A.; Ly, H.-B.; Tran, V.Q.; Van Giap, L.; Vu, H.-L.T.; Duong, H.-A.T. Prediction of pile axial bearing capacity using artificial neural network and random forest. Appl. Sci. 2020, 10, 1871. [Google Scholar] [CrossRef] [Green Version]
- Zabidi, H.; De Freitas, M.H. Re-evaluation of rock core logging for the prediction of preferred orientations of karst in the Kuala Lumpur Limestone Formation. Eng. Geol. 2011, 117, 159–169. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Fridline, M.M.; Roke, D.A. Decision tree approach for soil liquefaction assessment. Sci. World J. 2013, 2013, 346285. [Google Scholar] [CrossRef] [Green Version]
- Ramesh Murlidhar, B.; Yazdani Bejarbaneh, B.; Jahed Armaghani, D.; Mohammed, A.S.; Mohamad, E.T. Application of Tree-Based Predictive Models to Forecast Air Overpressure Induced by Mine Blasting. Nat. Resour. Res. 2021, 30, 1865–1887. [Google Scholar] [CrossRef]
- Tiryaki, B. Predicting intact rock strength for mechanical excavation using multivariate statistics, artificial neural networks, and regression trees. Eng. Geol. 2008, 99, 51–60. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Faradonbeh, R.S.; Amnieh, H.B.; Armaghani, D.J.; Monjezi, M. Forecasting blast-induced ground vibration developing a CART model. Eng. Comput. 2017, 33, 307–316. [Google Scholar] [CrossRef]
- Khalilia, M.; Chakraborty, S.; Popescu, M. Predicting Disease Risks from Highly Imbalanced Data Using Random Forest; Springer Link: New York, NY, USA, 2011. [Google Scholar]
- Aghaabbasi, M.; Shekari, Z.A.; Shah, M.Z.; Olakunle, O.; Armaghani, D.J.; Moeinaddini, M. Predicting the use frequency of ride-sourcing by off-campus university students through random forest and Bayesian network techniques. Transp. Res. Part A Policy Pract. 2020, 136, 262–281. [Google Scholar] [CrossRef]
- Kardani, N.; Zhou, A.; Nazem, M.; Shen, S.-L. Estimation of bearing capacity of piles in cohesionless soil using optimised machine learning approaches. Geotech. Geol. Eng. 2020, 38, 2271–2291. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Zhu, S.; Armaghani, D.J.; Khandelwal, M.; Mohamad, E.T. Estimation of the TBM advance rate under hard rock conditions using XGBoost and Bayesian optimization. Undergr. Space 2021, 6, 506–515. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.N.; Choi, Y.; Lee, C.W.; Armaghani, D.J. A Novel Combination of Whale Optimization Algorithm and Support Vector Machine with Different Kernel Functions for Prediction of Blasting-Induced Fly-Rock in Quarry Mines. Nat. Resour. Res. 2021, 30, 191–207. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Armaghani, D.J.; Zhang, W.; Li, C.; Zhu, S.; Tarinejad, R. Predicting TBM penetration rate in hard rock condition: A comparative study among six XGB-based metaheuristic techniques. Geosci. Front. 2021, 12, 101091. [Google Scholar] [CrossRef]
- Raschka, S. Model Evaluation, Model Selection, and Algorithm Selection in Machine Learning. arXiv 2018, arXiv:1811.12808. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Xu, H.; Zhou, J.; Asteris, G.P.; Jahed Armaghani, D.; Tahir, M.M. Supervised Machine Learning Techniques to the Prediction of Tunnel Boring Machine Penetration Rate. Appl. Sci. 2019, 9, 3715. [Google Scholar] [CrossRef] [Green Version]
- Harandizadeh, H.; Armaghani, D.J.; Mohamad, E.T. Development of fuzzy-GMDH model optimized by GSA to predict rock tensile strength based on experimental datasets. Neural Comput. Appl. 2020, 32, 14047–14067. [Google Scholar] [CrossRef]
- Kardani, N.; Bardhan, A.; Samui, P.; Nazem, M.; Zhou, A.; Armaghani, D.J. A novel technique based on the improved firefly algorithm coupled with extreme learning machine (ELM-IFF) for predicting the thermal conductivity of soil. Eng. Comput. 2021. Available online: https://link.springer.com/article/10.1007/s00366-021-01329-3 (accessed on 24 October 2021). [CrossRef]
- Armaghani, D.J.; Yagiz, S.; Mohamad, E.T.; Zhou, J. Prediction of TBM performance in fresh through weathered granite using empirical and statistical approaches. Tunn. Undergr. Space Technol. 2021, 118, 104183. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Mohamad, E.T.; Momeni, E.; Narayanasamy, M.S. An adaptive neuro-fuzzy inference system for predicting unconfined compressive strength and Young’s modulus: A study on Main Range granite. Bull. Eng. Geol. Environ. 2015, 74, 1301–1319. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Harandizadeh, H.; Momeni, E.; Maizir, H.; Zhou, J. An optimized system of GMDH-ANFIS predictive model by ICA for estimating pile bearing capacity. Artif. Intell. Rev. 2021. Available online: https://link.springer.com/article/10.1007/s10462-021-10065-5 (accessed on 24 October 2021). [CrossRef]

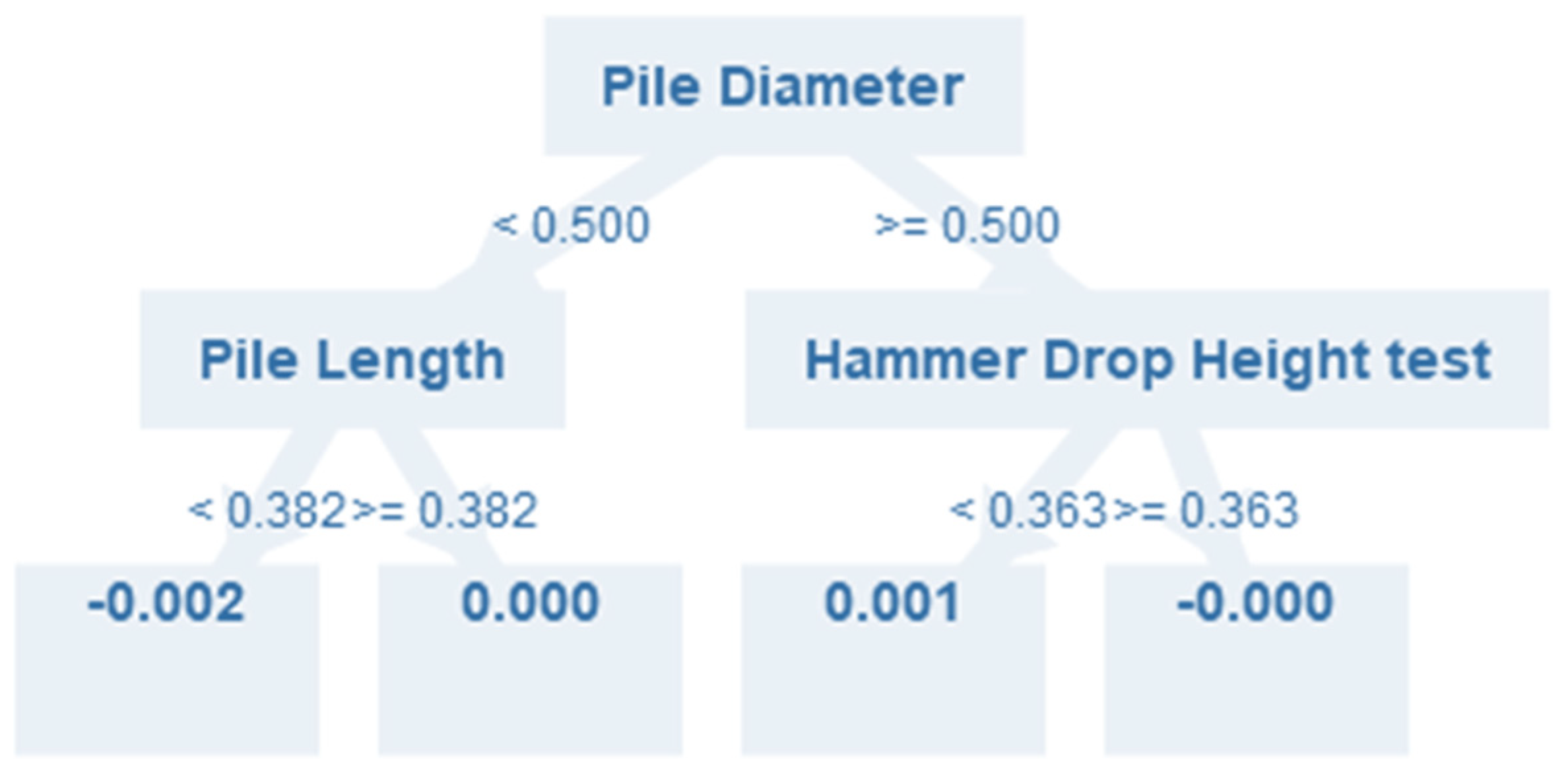
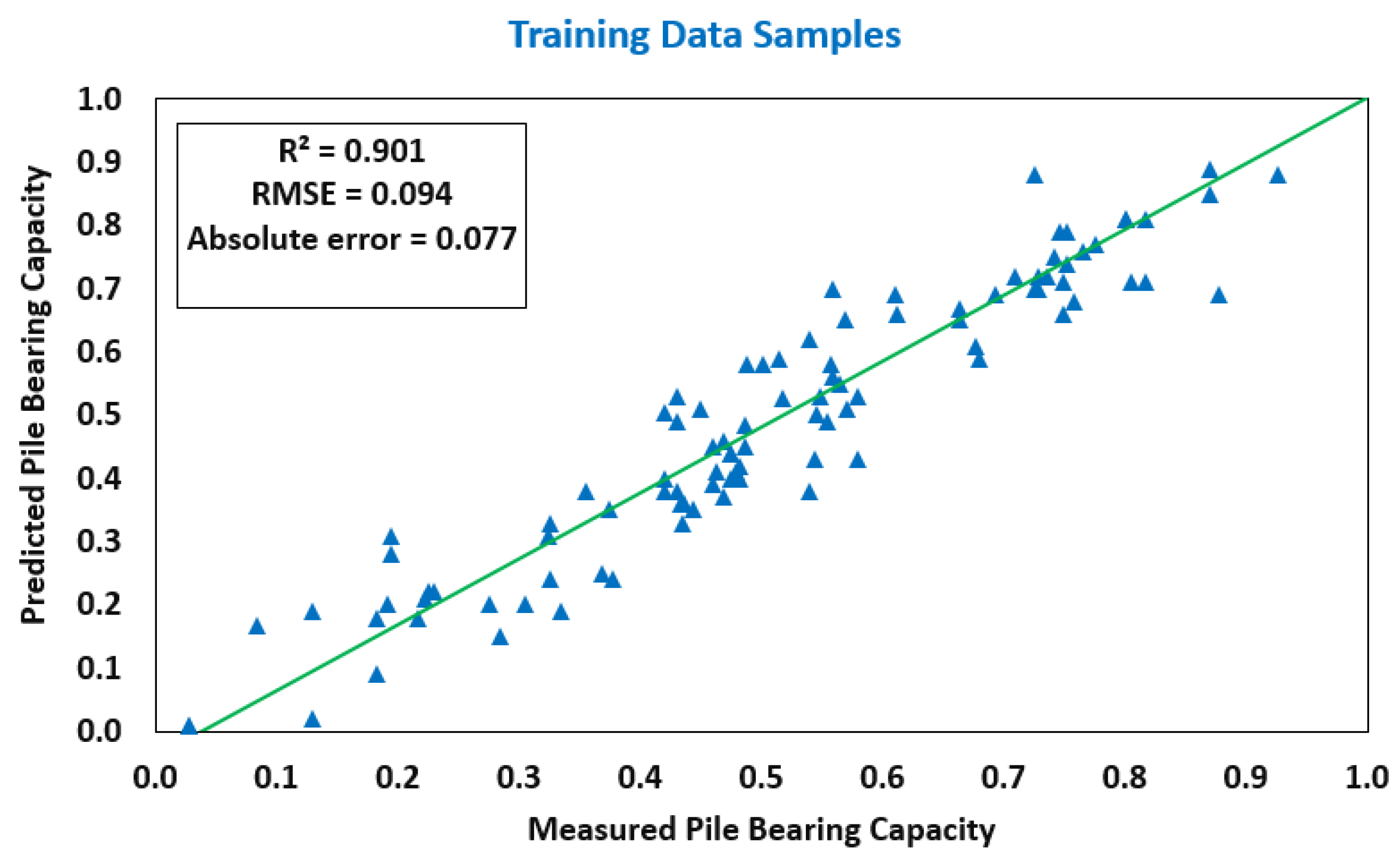
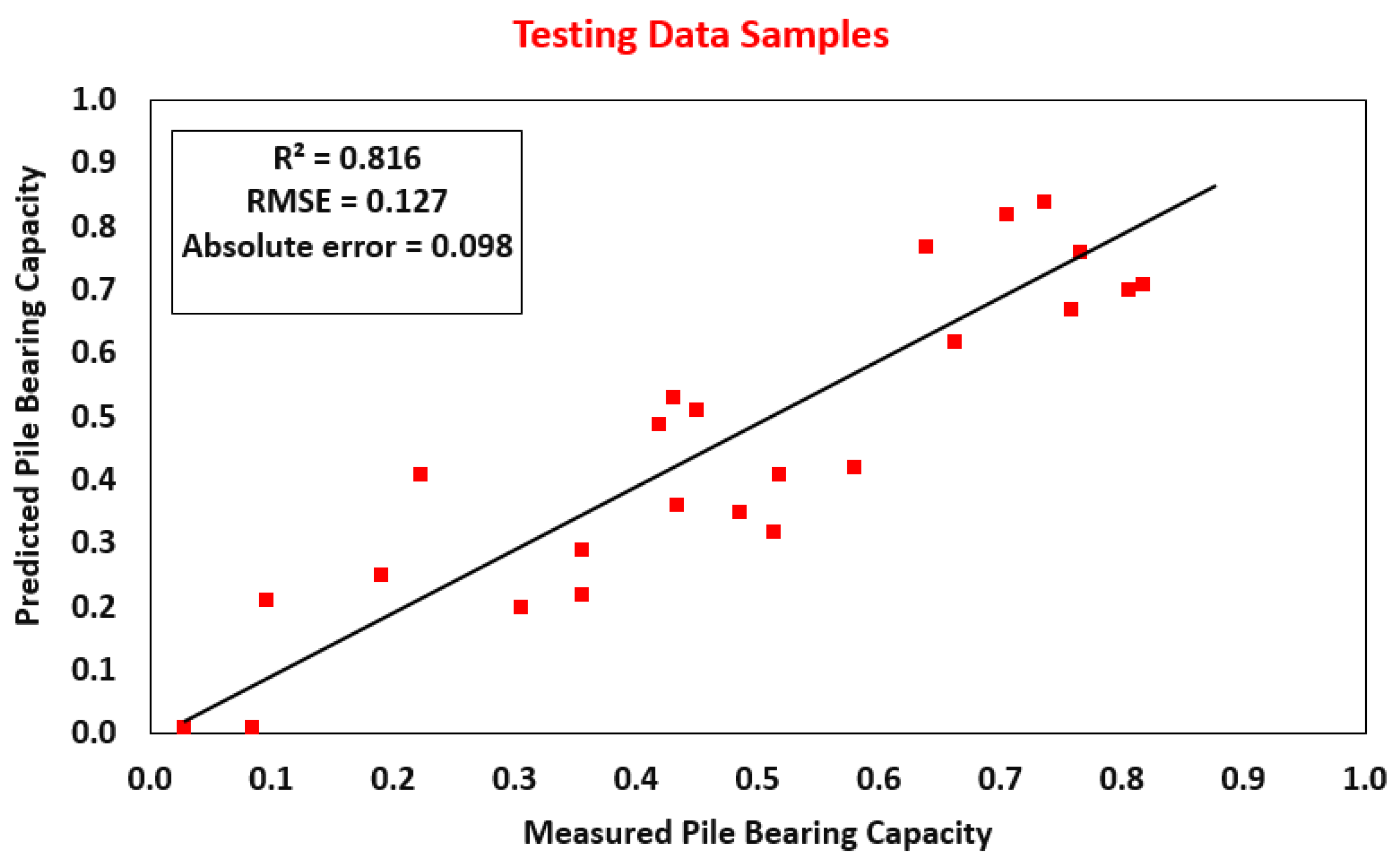
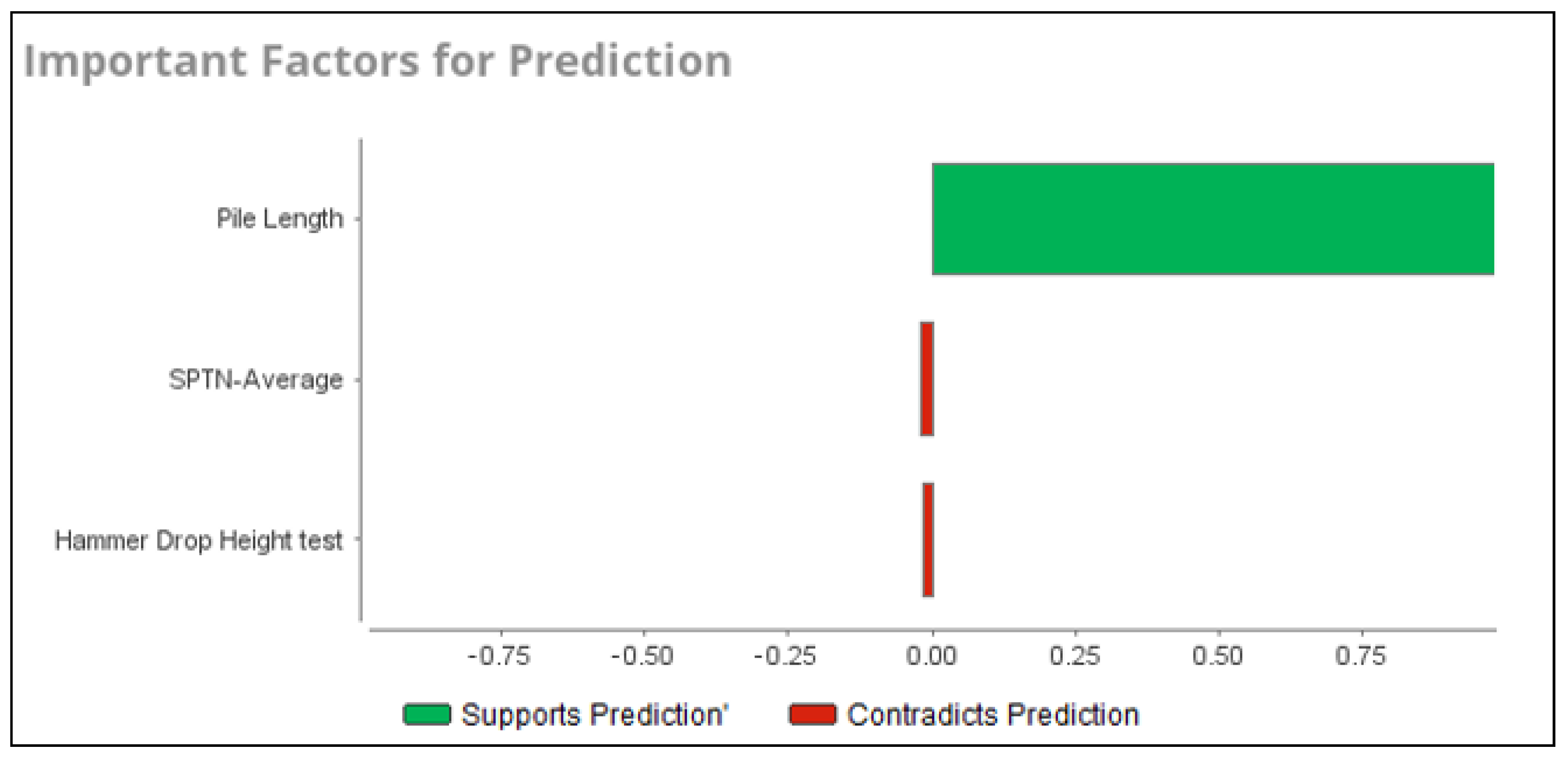
| No | References | Equation | ns (kPa) | Type of Installation Pile |
|---|---|---|---|---|
| 1 | Bazaraa and Kurkur [17] | qs = 0.67 N if D ≤ 0.5 m. | 0.67 if D ≤ 0.5 m, 1.34 for the other D values (where D is pile diameter in m) | Bored |
| else | ||||
| qs = 1.34 N | ||||
| 2 | Decourt [18] | qs =10 (N/3+1) | - | Bored |
| 3 | Lopes and Laprovitera [19] | qs = 1.62 N | 1.62 in sand | Bored |
| qs = 1.94 N | 1.94 in silty sand | |||
| 4 | Meyerhof [20] | qs = 1 N | 1 | Bored |
| qs = 2 N | 2 | Driven | ||
| 5 | Shioi and Fukui [21] | qs = 1 N | 1 | Bored |
| qs = 2 N | 2 | Driven | ||
| 6 | Aoki and Veloso [22] | qs = 2 N | 2.00 in sand | Bored |
| qs = 2.28 N | 2.28 in silty sand | |||
| 7 | Reese and O’Neill [23] | qs = 3.3 N | 3.3 | Bored |
| 8 | Robert [24] | qs = 1.9 N | 1.90 | Bored |
| 1.90 | Driven |
| No | Reference | Input | Model | Soil Type | Datasets | Performance |
|---|---|---|---|---|---|---|
| 1 | Goh [56] and Goh [51] | Pile length and diameter, effective overburden stress and undrained shear strength | ANN | Clay | 65 driven piles (timber and steel) | R = 0.956 |
| 2 | Lee and Lee [29] | Model pile load test: penetration depth ratio, mean normal stress of calibration chamber, number of hammer blows In-situ pile load test: penetration depth ratio, average SPT-N value with the pile shaft depth and close to the end of pile, pile set, final penetration depth/blow, hammer energy | ANN | Sand | Model pile load test: 28 steel tube In-situ pile load test: 24 piles | Maximum error of prediction < 25% |
| 3 | Goh [57] | Pile elastic modulus, pile length and cross sectional area, weight of pile, hammer drop height and weight, pile set and type of hammer | ANN | Sand | 116 piles (timber precast concrete and steel) | R = 0.965 |
| 4 | Kiefa [58] | Soil shear resistance encompassing the pile shaft, soil shear resistance at the tip of pile, effective overburden stress, pile length and pile area | GRNN | Sand | 59 load tests on different type of driven pile | R2 = 0.912 |
| 5 | Das and Basudhar [59] | Pile diameter, pile length, eccentricity of load and undrained shear strength | MFPNN | Clay | 38 short and rigid piles | R = 0.947 |
| 6 | Pal and Deswal [60] | Force, velocity multiplied by impedance, hollow pipes piles diameter, wall thickness, and pile depth | SVM and GRNN | - | 105 pre-stressed precast spun piles | R SVM = 0.964 GRNN = 0.977 |
| 7 | Pal and Deswal [61] | Pile diameter, pile length, eccentricity of load and undrained shear strength | GPR | Non-cohesive soil | 94 load tests piles (timber, precast concrete and steel piles) | R = 0.950 |
| 8 | Alavi et al. [54] | Pile length/pile diameter, lateral force point of application distance/pile length, chain force angle with the horizontal, undrained shear strength at pile tip, and soil permeability | LGP | All soil types | 62 suction caissons | R2 = 0.994 |
| 9 | Gandomi et al. [62] | Pile diameter and length, eccentricity of load, and pile tip undrained shear strength | Multi-Gene GP | Clay | 38 short and rigid piles | R = 0.985 |
| 10 | Alkroosh and Nikraz [53] | Pile diameter and length, CPT pile tip resistance, cone sleeve friction along pile length, CPT resistance along pile shaft, elastic modulus of pile and type of pile | GEP | Non-cohesive soil | 25 driven piles (concrete and steel) | R = 0.94 |
| 11 | Kordjazi et al. [63] | Cross section area of the tip, perimeter of pile, embedded pile length, average cone tip resistance, average cone sleeve friction, and average cone tip resistance below the pile tip | Different SVM kernels | Sands, clays and silts | 108 pile tests | R = range from 0.966–0.982 |
| 12 | Momeni et al. [26] | Pile set, pile length and cross-sectional area, hammer drop height and weight | GA-ANN | - | 50 pre-cast concrete piles | R2 = 0.990 |
| 13 | Ghorbani et al. [64] | Area of the pile at tip, unit shaft resistance of the soil, average of cone tip resistance for shaft and tip, and average of sleeve friction value along the pile embedded length | ANFIS | All soil types | 108 concrete, steel and composite piles | R = 0.96 |
| 14 | Harandizadeh et al. [27] | Pile length, cross-section shape and material, cone tip resistance and sleeve friction of cone | ANFIS-GMDH-PSO | Sand, silty sand, clay, sandy clay, and silty clay | 41 Concrete and 31 Steel piles | R = 0.96 |
| 15 | Dehghanbanadaki et al. [65] | Pile area, pile length, flap number, average soil cohesion and friction angle, average soil specific weight and average pile-soil friction angle | ANFIS-GWO | - | 100 steel and concrete driven piles | R = 0.930 |
| 16 | Momeni et al. [55] | Pile length and diameter, pile set, ram weight, and hammer drop height | GPR | - | 296 precast driven piles | R2 = 0.81 |
| 17 | Pham et al. [66] | Pile diameter, pile tip segment length, second pile segment length, pile top segment length, natural ground elevation, pile top elevation, guide pile segment sop driving elevation, pile tip elevation, and average SPT | RF and ANN | - | 2314 reinforced concrete piles | R2 RF = 0.861 ANN = 0.811 |
| Parameter | Unit | Range |
|---|---|---|
| Pile Length | m | 18.5–47 |
| Hammer Drop Height | m | 0.55–1.1 |
| Pile Diameter | mm | 400–450 |
| Hammer Weight | Kg | 7000 |
| SPT-N Average | - | 4–17 |
| Pile Friction Bearing Capacity | kN | 2028–4844 |
| Attributes | Hammer Drop Height Test | Pile Diameter | Pile Length | Shaft Friction | SPT-N Average |
|---|---|---|---|---|---|
| Hammer Drop Height Test | 1 | 0.358 | 0.504 | 0.476 | −0.025 |
| Pile Diameter | 0.358 | 1 | 0.103 | 0.436 | 0.207 |
| Pile Length | 0.504 | 0.103 | 1 | 0.794 | −0.030 |
| Shaft Friction | 0.476 | 0.436 | 0.794 | 1 | 0.036 |
| SPT-N Average | −0.025 | 0.207 | −0.030 | 0.036 | 1 |
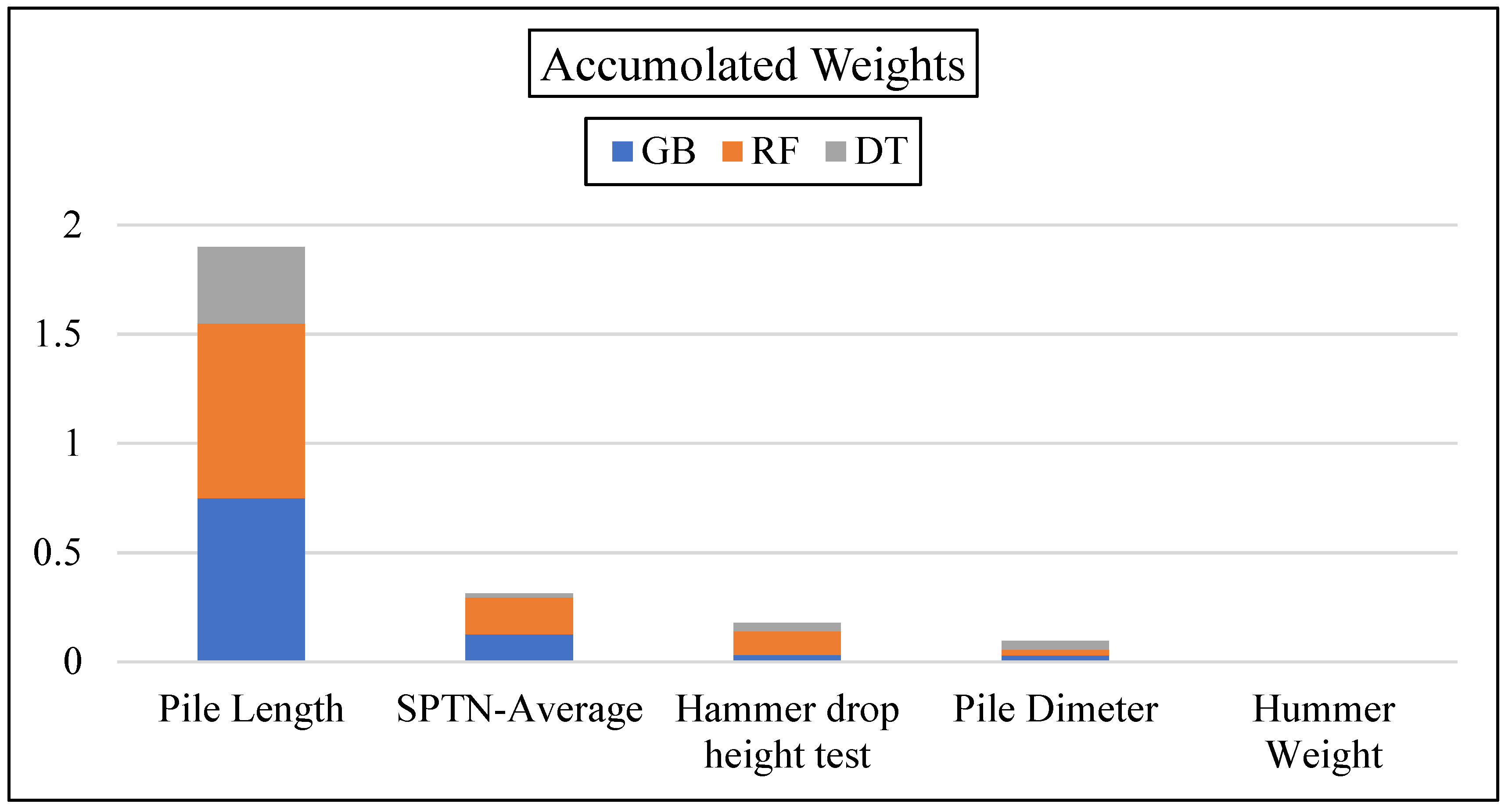
| GB | RF | DT | |||
|---|---|---|---|---|---|
| Attribute | Weight | Attribute | Weight | Attribute | Weight |
| Pile Length | 0.75 | Pile Length | 0.80 | Pile Length | 0.35 |
| SPT-N Average | 0.125 | SPT-N Average | 0.17 | Pile Dimeter | 0.04 |
| Hammer drop height test | 0.031 | Hammer drop height test | 0.11 | Hammer drop height test | 0.037 |
| Pile Dimeter | 0.030 | Pile Dimeter | 0.025 | SPT-N Average | 0.018 |
| Hammer Weight | 0.00 | Hammer Weight | 0.00 | Hammer Weight | 0.00 |
| Technique | Train | Test | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | Absolute Error | R2 | RMSE | Absolute Error | |
| GBT | 0.911 | 0.073 | 0.052 | 0.841 | 0.089 | 0.098 |
| RF | 0.892 | 0.082 | 0.073 | 0.813 | 0.071 | 0.100 |
| DT | 0.861 | 0.135 | 0.121 | 0.773 | 0.121 | 0.167 |
| Technique | Train | Test | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | Absolute Error | R2 | RMSE | Absolute Error | |
| GBT | 0.901 | 0.094 | 0.077 | 0.816 | 0.127 | 0.098 |
| RF | 0.881 | 0.095 | 0.081 | 0.761 | 0.081 | 0.100 |
| DT | 0.853 | 0.170 | 0.152 | 0.712 | 0.130 | 0.167 |
| Attribute | Weight |
|---|---|
| Pile Length | 0.81 |
| SPT-N Average | 0.21 |
| Hammer drop height | 0.075 |
| GBT Model No. | No. of Trees | Maximal Depth | Learning Rate | Error Rate |
|---|---|---|---|---|
| 1 | 30 | 2.0 | 0.001 | 0.2891 |
| 2 | 90 | 2.0 | 0.001 | 0.2814 |
| 3 | 150 | 2.0 | 0.001 | 0.2745 |
| 4 | 30 | 4.0 | 0.001 | 0.2891 |
| 5 | 90 | 4.0 | 0.001 | 0.2814 |
| 6 | 150 | 4.0 | 0.001 | 0.2745 |
| 7 | 30 | 7.0 | 0.001 | 0.2891 |
| 8 | 90 | 7.0 | 0.001 | 0.2814 |
| 9 | 150 | 7.0 | 0.001 | 0.2745 |
| 10 | 30 | 2.0 | 0.01 | 0.2597 |
| 11 | 90 | 2.0 | 0.01 | 0.2366 |
| 12 | 150 | 2.0 | 0.01 | 0.2189 |
| 13 | 30 | 4.0 | 0.01 | 0.2597 |
| 14 | 90 | 4.0 | 0.01 | 0.2370 |
| 15 | 150 | 4.0 | 0.01 | 0.2209 |
| 16 | 30 | 7.0 | 0.01 | 0.2597 |
| 17 | 90 | 7.0 | 0.01 | 0.2370 |
| 18 | 150 | 7.0 | 0.01 | 0.2209 |
| 19 | 30 | 2.0 | 0.1 | 0.1986 |
| 20 | 90 | 2.0 | 0.1 | 0.1889 |
| 21 | 150 | 2.0 | 0.1 | 0.1953 |
| 22 | 30 | 4.0 | 0.1 | 0.1985 |
| 23 | 90 | 4.0 | 0.1 | 0.1912 |
| 24 | 150 | 4.0 | 0.1 | 0.1955 |
| 25 | 30 | 7.0 | 0.1 | 0.1985 |
| 26 | 90 | 7.0 | 0.1 | 0.1912 |
| 27 | 150 | 7.0 | 0.1 | 0.1955 |
| Attribute | Optimum Value (Normalized) | Optimum Value (Actual) | Maximum Pile Capacity |
|---|---|---|---|
| Pile Length | 0.90 | 44 | 4844 |
| Hammer Drop Height | 0.419 | 1.1 | |
| SPT-N Average | 0.702 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huat, C.Y.; Moosavi, S.M.H.; Mohammed, A.S.; Armaghani, D.J.; Ulrikh, D.V.; Monjezi, M.; Hin Lai, S. Factors Influencing Pile Friction Bearing Capacity: Proposing a Novel Procedure Based on Gradient Boosted Tree Technique. Sustainability 2021, 13, 11862. https://doi.org/10.3390/su132111862
Huat CY, Moosavi SMH, Mohammed AS, Armaghani DJ, Ulrikh DV, Monjezi M, Hin Lai S. Factors Influencing Pile Friction Bearing Capacity: Proposing a Novel Procedure Based on Gradient Boosted Tree Technique. Sustainability. 2021; 13(21):11862. https://doi.org/10.3390/su132111862
Chicago/Turabian StyleHuat, Chia Yu, Seyed Mohammad Hossein Moosavi, Ahmed Salih Mohammed, Danial Jahed Armaghani, Dmitrii Vladimirovich Ulrikh, Masoud Monjezi, and Sai Hin Lai. 2021. "Factors Influencing Pile Friction Bearing Capacity: Proposing a Novel Procedure Based on Gradient Boosted Tree Technique" Sustainability 13, no. 21: 11862. https://doi.org/10.3390/su132111862
APA StyleHuat, C. Y., Moosavi, S. M. H., Mohammed, A. S., Armaghani, D. J., Ulrikh, D. V., Monjezi, M., & Hin Lai, S. (2021). Factors Influencing Pile Friction Bearing Capacity: Proposing a Novel Procedure Based on Gradient Boosted Tree Technique. Sustainability, 13(21), 11862. https://doi.org/10.3390/su132111862










