Abstract
As an important way to reduce emission, forestry carbon sink (FCS) has not been implemented effectively. Therefore, this paper aims to analyze the effectiveness and mechanism of applying blockchain technology in FCS projects by utilizing the differential game model. A Stackelberg differential game model between forest farmers and emission-controlled enterprises (ECEs) is developed to analyze the optimal emission reduction efforts and the optimal trajectory of forest farmers and ECEs before and after introducing blockchain technology. It is found that: (1) At the initial stage of the utilization of blockchain technology, if blockchain technology takes a leading role in stabilizing carbon prices, the ECEs prefer to purchase FCS instead of reducing emissions by their own technology. On the contrary, if blockchain technology takes a leading role in stimulating the vitality of the carbon trading market, ECEs tend to use emission abatement technology to meet the carbon quote requirements. (2) In the later stage, the incentive and stabilizing effects of blockchain technology on carbon prices tend to be balanced, and the emission reduction efforts of ECEs are lower than the efforts before applying blockchain technology. (3) The application of blockchain technology increases forest farmers’ willingness to reduce emissions because of its effection of cost reduction and efficiency improvement. Meanwhile, blockchain technology reduces abatement costs by influencing carbon prices. Therefore, blockchain technology improves forest farmers’ emission reduction efforts on the whole.
1. Introduction
The annual report released by the United Nations in 2019 pointed out that the world needs to take more emission reduction measures to achieve carbon neutrality. The international organization attaches great importance to the role of forestry carbon sink (FCS) in tackling climate change. More and more countries have included FCS in the carbon market system and identified FCS projects that produce FCS in the form of legal provisions. In 2001, the 7th Conference of the Parties (COP7) to the United Nations Framework Convention on Climate Change reached the Marrakesh Agreement and agreed to use afforestation and reforestation projects as CDM in the forestry sector; In 2007, COP13 accepted the Bali Road Map, agreeing to Reduced Emissions from Deforestation and Degradation (REDD) as a qualified FCS project; In 2009, COP15 reached the Copenhagen Agreement, based on REDD, agreed to Reducing Emissions from Deforestation and forest Degradation, as well as the sustainable management of forests and the conservation and enhancement of forest carbon stocks (REDD+) as a qualified FCS project. In December 2015, the United Nations Climate Conference included forestry as a separate clause in the newly reached Paris Agreement, clearly stipulating that after 2020, countries should take actions to protect and enhance FCS, and continue to encourage developing countries to implement REDD+ [1]. Compared with other emission reduction measures, FCS projects have more advantages in terms of economic, social, and ecological benefits [2] FCS projects not only provide forest farmers profit and employment opportunities but also provide emission reduction channels for enterprises to control emissions [3,4].
However, the development of FCS projects is not ideal [5]. In the carbon trading market, emission-controlled enterprises (ECEs) are important participants and demanders of FCS. ECEs will respond flexibly to FCS based on the principle of profit maximization. On the one hand, the main reason why forestry accounts for less than one percent of carbon trading projects is the high project cost. FCS products need to go through six stages: design, verification, filing, implementation and monitoring, emission reduction verification, and emission reduction issuance. The complicated process makes forest farmers bear higher costs [6]. In addition, the long forest growth cycle increases the uncertainty of carbon sink output and harms the enthusiasm of forest farmers to participate in FCS severely. On the other hand, the long development cycle and complicated processes of FCS products result in increased likelihood of fraud because of opaque transaction information [7]. Those characteristics not only affect the ECEs’ acceptance of prices of carbon sink but also lead to instability of carbon trading prices.
An increase in the supply of FCS will stimulate the vitality of the carbon trading market. The demand side will decide the optimal emission reduction plan while weighing its emission reduction capabilities. Conversely, the increase in demand will have an incentive effect on the supply side. In this process, the information asymmetry caused by the imperfect FCS market and the high cost and low output caused by the characteristics of FCS has hindered the development of FCS projects significantly. At present, the research on FCS mostly stays on the supply side [8,9,10] and less on the demand side. In addition, the research related to FCS demand carries out theoretical analysis from the aspects of influencing factors [11] and demand mechanism [12], emphasizing risk measurement [6] and government incentives [13,14].
Blockchain is an emerging distributed ledger technology. Its smart contract and decentralized features [15] can lower the operating threshold of FCS projects effectively, and provide a safe, transparent and trustworthy trading environment for both parties to the transaction. The blockchain consensus mechanism and secure data interaction provide a new development idea for promoting FCS transactions.
Most of the research on blockchain technology in carbon trading focuses on optimizing the application logic [16,17] and application scenarios of the carbon emissions trading process [18], reflecting the influence of blockchain on emission reduction model [19], trading market [20] and price [21]. Moreover, most of the research aims to integrate the blockchain with the power [22] and construction [23,24] industries. For FCS, a high-cost emission reduction project, existing studies do not consider the ability of smart contract technology to act on carbon sink suppliers and the specific manifestations of decentralization characteristics on carbon sink transaction prices. Therefore, it is important to study the management mechanism of blockchain technology applied to FCS projects.
In the promotion of FCS projects, forest farmers and ECEs can have different objectives and strategies. There is a dynamic game process between them. Forest farmers’ decisions affect the stable supply of FCS directly. The purpose of forest farmers to provide FCS is to obtain carbon sink revenues. ECEs can achieve the national carbon quotas in two ways: improving their technology to reduce emissions and purchasing FCS. The purpose of ECEs is to get the maximum profit. In this process, the information asymmetry caused by the imperfect carbon sink market and the characteristics of FCS project make it difficult for the system to achieve the desired balance of supply and demand. Blockchain technology can solve problems effectively and improve the enthusiasm of both sides of supply and demand. The game model is widely used in the study of competitive strategy [25,26], which is also applicable to the analysis of each subject’s strategy in FCS [27,28]. Therefore, taking FCS trading as the research object, this paper constructs a Stackelberg differential game model between forest farmers and ECEs to explore the mechanism of blockchain technology to optimize FCS trading by assuming that carbon sink transaction prices fluctuate randomly.
The rest of the paper is organized as follows. First, the problem is described and basic assumptions are presented in Section 2. Then, Stackelberg differential game models before and after applying blockchain technology are constructed and solved in Section 3. The main results are discussed in Section 4. After that, numerical examples are presented in Section 5 to verify the theoretical results. Finally, Section 6 concludes the paper.
2. Problem Description and Basic Assumptions
2.1. Problem Description
FCS projects have multiple subjects, complex processes, long cycles, and opaque transactions. These characteristics lead to high development costs for FCS projects and harm the enthusiasm of forest farmers severely [10]. High investment costs and low output efficiency are important constraints for the development of FCS projects [2]. The “cross-subject interaction” feature of the blockchain can set the complex and coherent FCS as a “smart contract” to realize electronic interaction between multiple related subjects, which can reduce costs and improve operations efficiency [29].
The long cycle and complicated process of FCS projects may cause problems such as fraud and opaque transactions at various process nodes. In the carbon trading market, it is necessary to ensure the authenticity and transparency of carbon emissions data [29]. However, relying on central servers for carbon trading cannot guarantee data security, which affects the ECEs’ tolerance of the price of FCS seriously. In the blockchain carbon trading mode, the information distributed on the data chain is maintained jointly by all participating entities, and each authorized user has the right to require historical information about carbon trading and carbon emissions, which not only realizes collective supervision of data but also enhances information transparency and the difficulty of information fraud [16]. In addition, with the help of the proof-of-work mechanism of blockchain technology, the relevant reward and punishment mechanism is designed technically, which improves the ECE’s tolerance of FCS and flattens the price fluctuations [20].
There are two main entities involved in FCS trading: forest farmers and ECEs. First, forest farmers increase output of FCS by improving management capabilities and other methods. Second, ECEs choose to apply technology to reduce emissions or purchase FCS based on their emission reduction capabilities, such as initial carbon allowances, low-carbon technology research and development costs. This process can be modeled as a Stackelberg differential game between forest farmers and ECEs. In the first stage, forest farmers decide their efforts level of emission reduction. In the second stage, ECEs decide their efforts level of emission reduction.
2.2. Assumptions and Model Parameters
Differential game is used commonly to construct emission reduction models [27,28]. According to the structure of differential game and the FCS trading process, we make the following assumptions.
(1) The management ability of forest farmers will have an impact on the number of FCS. The lower management level of forest farmers will lead to overdensity or oversparseness of forests, poor quality of forests, and diseases of insect pests and forest fires caused by inadequate supervision. Sufficient expected income can ensure the full investment of forest farmers to improve their management level. Therefore, forest farmers need to weigh cost and income to achieve optimal efficiency. Reference to the convexity assumption of cost [30], assume that the forest farmers’ emission reduction cost is a convex function of forest farmers’ emission reduction efforts.
where is the forest farmer’s abatement cost function; is the forest farmer’s emission reduction efforts; is the forest farmer’s abatement cost coefficient which reflects the impact of forest farmers’ emission reduction input level changes on the cost.
(2) The rate of FCS is related to its age closely [31]. Usually, the forest age is divided into young, middle-aged, near-mature, mature, and over-mature. Young and middle-aged forests have relatively fast carbon sequestration rates, while near-mature, mature, and over-mature forests have balanced carbon absorption and release due to the decline in growth rates [32]. The relationship between forest carbon density and forest age can be expressed by a logistic growth curve [33,34]. The evolution law of FCS can be described as
where Q is the final carbon sink that the forest can provide based on its own growth law; r is the growth factor of carbon sinks per unit time; c is a constant; and t is the growth time of trees. The differential equation expression of Equation (2) is
(3) Assuming that the carbon sink price x at time t is a random variable in the , the probability density function of x is , the mean is , and the variance is . The increase in the mean of the price random variable x is used to describe the incentive effect of the blockchain on the carbon sink market, and the decrease in the variance indicates the promotion of the blockchain in stabilizing the carbon price. The price after applying blockchain technology is assumed to be
where , ; and are the incentive coefficients of blockchain technology in stabilizing market prices and stimulating the vitality of the carbon trading market. Obviously, the mean of is , and the variance is .
(4) FCS is affected mainly by internal and external factors. The internal factors are the number of carbon sinks based on the growth of forest trees [34]. The external factors mainly include forest farmers’ scientific tending of forest trees and supervision abilities [35]. Hence, the FCS at time t can be denoted as
where is the influence coefficient of forest farmers’ emission reduction efforts on FCS, and is the influence coefficient of random factors on FCS. Equation (5) reflects the role of three influencing factors of carbon sink growth. The first is the emission reduction efforts of forest farmers, the second is forest growth, and the third is other uncertain factors.
(5) The demand of ECEs on FCS is related mainly to the initial carbon allowance and CCER [36,37]. Generally, the CCER is less than the carbon quota. Hence, the demand of ECEs on FCS is the difference between the carbon allowance and CCER. That is,
where the of ECEs is related to its emission reduction efforts . In addition, ECEs choose emission reduction strategies based on supply of FCS in the market [38]. When the quantity of FCS increases, the willingness of ECEs to achieve carbon allowances through the purchase of FCS increases. Then, the differential state expression of is
where is the influence coefficient of ECEs’ emission reduction efforts on ; is the influence coefficient of FCS on ; is the influence coefficient produced by random factors.
Similarly, assume that the technical abatement cost of ECEs is a convex function of emission reduction efforts.
where is the abatement cost coefficient of ECEs, which reflects the degree of impact of the emission reduction efforts of ECEs on the cost.
(6) The government will subsidize the costs of implementing FCS projects to encourage forest farmers participating in FCS projects. Assume that the subsidy ratio is and . That is, the government shares the forest farmers’ cost. In addition, the government will adopt special funds and other incentive measures to mobilize the enthusiasm of ECEs to reduce emissions. Assuming that the subsidy ratio is and , it will share the abatement costs of ECEs.
(7) The forest farmers and ECEs seek to maximize their benefits during the time interval . Assume that forest farmers and ECEs have the same positive discount rate and the daily operating income of ECEs is . The main felling and thinning of forest trees are not considered.
For simplicity, the time unit t will be omitted in the following text. Based on the above assumptions, related symbols and definitions are further described as follows:
: the quantity of FCS at time t;
: the emission reduction of ECEs at time t (CCER);
: forest farmers’ emission reduction efforts at time t;
: ECEs’ emission reduction efforts at time t;
: the quantity required for FCS at time t;
: forest farmers’ abatement costs at time t;
: ECEs’ abatement costs at time t;
Q: the final carbon sink that the forest can provide based on its own growth law;
r: FCS unit time growth factor (self-growth);
: operating return of ECEs;
: initial carbon allowances of ECEs;
: the influence coefficient of forest farmers’ emission reduction efforts on FCS;
: the influence coefficient of ECEs’ emission reduction efforts on emission reduction;
: the abatement cost coefficient of forest farmers;
: the abatement cost coefficient of ECEs;
: coefficient of government subsidies for forest farmers’ emission reduction;
: coefficient of government subsidies for ECEs’ emission reduction;
x: the price of FCS;
: the influence coefficient of FCS on emission reduction of ECEs;
: the influence coefficient of random factors on FCS;
: the influence coefficient of random factors on emission reduction of ECEs;
: discount factor;
: the extent to which blockchain technology plays a role in stabilizing carbon prices;
: the extent to which blockchain technology plays a role in stimulating the vitality of the carbon trading market.
3. The Model and the Solutions
3.1. Before Applying Blockchain Technology
Forest farmers’ income from carbon sink trading is . Abatement cost is . Hence, the expected return of forest farmers is
where is the expected price of FCS.
ECEs purchase FCS after considering the economic feasibility of technical emission reduction. The cost of purchasing FCS is . The technical emission reduction cost of ECEs is . Hence, the expected return of ECEs is
In the next, according to the Stackelberg differential game analysis framework, we solve the optimal strategy of forest farmers and ECEs.
First, the optimal decision-making model of ECEs is as follows:
From model (11), the Hamilton–Jacobi–Bellman (HJB) equation of ECEs’ optimal return is
It can be found that Equation (12) is a concave function of S. Therefore, the global optimal solution exists. The first-order condition of S is
Second, the optimal decision-making model of forest farmers are as follows:
From model (14), the HJB equation of the forest farmer’s optimal return is
Based the first-order condition of F, we can get
According to the structure of Equations (18) and (19), we assume that
where and are the undetermined coefficients. Substitute the partial derivatives of E and K in Equations (18)–(), respectively. Comparing Equations (18) and (19) with the coefficients of the similar terms on both sides of the equation, we can obtain
Then, by substituting Equation (24) into Equation (13), the optimal emission reduction efforts of ECEs is
Substituting Equation (25) into Equation (17), the optimal emission reduction efforts of forest farmers is
3.2. After Applying Blockchain Technology
The forest farmers’ abatement cost coefficient is , ; the influence coefficient of forest farmers’ emission reduction efforts on FCS is and .
The HJB equation of ECEs’ optimal return is
where is the expected price of FCS after applying blockchain technology.
The HJB equation of the forest farmer’s optimal return is
The first-order condition of F is
According to the structure of Equations (35) and (36), assume:
where and are the undetermined coefficient. Substitute the partial derivatives of E and K in Equations (37) and (38) into Equations (35) and (36), respectively. Comparing Equations (35) and (36) with the coefficients of the similar terms on both sides of the equation, we can obtain
Substituting Equation (42) into Equation (34), the optimal emission reduction efforts of forest farmers is
The optimal trajectory of FCS is
The optimal trajectory of the emission reduction of ECEs is
4. Discussions and Management Implications
4.1. Discussion
In order to show the role of blockchain technology in FCS trading, we compared the emission reduction efforts of forest farmers and ECEs before and after the introduction of blockchain technology.
(1) According to Equations (26) and (43), S is proportional to x. Therefore, if the price of FCS increases, ECEs tend to reduce emissions by technology. Contrarily, if the price of FCS decreases, due to the high cost of emission reduction technology, ECEs tend to purchase FCS.
At the initial stage of the utilization of blockchain technology, it needs to be integrated with the market effectively, and through continuous adjustments to adapt to the law of market development [39]. Comparing S before and after the introduction of blockchain technology:
The necessary condition for is , and , that is
Hence, the lower is, , , and then . This indicates a smaller price fluctuation range. That is, is large, and is easier to achieve. The Equation (48) is established. Therefore, when blockchain technology plays a leading role in stabilizing carbon sink prices, ECEs are more inclined to purchase FCS to meet carbon quota requirements, and S will decrease.
The necessary condition for is , and , that is
When and are larger, Equation (49) is easier to hold. The larger the , the greater the deviation of P from , which means that the price fluctuation range is larger, and is larger. That is, when blockchain technology plays a leading role in stimulating carbon trading market, ECEs are more inclined to achieve carbon quota requirements through their emission reduction technology, and S increases.
In the later stage of the utilization of blockchain technology, the incentive and stabilizing effects of blockchain technology on carbon prices tend to balance [39], and the role of blockchain technology will be analyzed in the numerical example.
(2) According to Equations (27) and (44), F is inversely proportional to , which confirms that the current high investment cost of FCS is a restrictive factor in the development of the project. This inhibits the enthusiasm of forest farmers. Furthermore, and x are proportional to F, which shows that the higher the efficiency of converting efforts into income, the more willing forest farmers are to participate in FCS projects. In addition, is proportion to F. Therefore, the higher the government’s cost–sharing ratio, the more it can provide incentives for forest farmers.
Comparing Equations (27) and (44), we can find that the impact of blockchain on F is reflected in the price, cost, and output efficiency. Driven by the blockchain, the government only needs to share a small proportion of the cost to obtain better emission reduction effects than before, which reduces the government’s economic burden.
The impact of blockchain on carbon prices is the effect of blockchain on the carbon trading market. The specific mechanism of the two effects will be analyzed in the numerical example.
4.2. Management Implications
Based on the above discussion, we propose the following actions.
(1) The government should regulate policies on carbon quota and subsidies dynamically.
The government’s policy should be adjusted dynamically according to the different growth stages of the forest. Implementing emission reduction commitments has become an important way for China to contribute to the construction of global ecological civilization. Factors such as national economic development, land prices, timber prices, and international carbon sink prices will all have an impact on the supply of FCS [13,31]. In addition, the quantity of FCS has shown an S-shaped growth. Before the turning point of the curve, the annual increment of FCS will increase. At this stage, the government should increase carbon allowances and encourage ECEs to purchase FCS appropriately. After the turning point of the curve, the government should reduce carbon allowances appropriately. In this way, blockchain technology will reduce more effectively the cost of forest farmers participating in FCS. Therefore, the government should reduce the proportion of emission reduction subsidies to forest farmers.
(2) The key to forest farmers’ decision-making is the government carbon quota distribution policy.
As the main suppliers of FCS, forest farmers are driven by profits to participate in FCS projects. Forest farmers’ decision-making depends on multiple factors, such as farmers’ own factors, social policy factors, risks, and time preferences [6,12]. Among them, project costs and market demand are two key factors affecting forest farmers’ participation in FCS. The market demand is mainly related to the national carbon allowances and carbon sink prices. After applying blockchain technology, carbon allowances is the key point that forest farmers need to consider. Therefore, forest farmers should share information with the government to formulate a reasonable carbon quota.
(3) The key to ECEs’ decision making is the application stage of blockchain technology and the predictive ability of FCS.
The decision making of ECEs needs to consider the application stage of blockchain technology. In the early stage of the introduction of blockchain technology, ECEs need to pay special attention to market changes and adjust emission reduction measures in time. In the later stage of the introduction of blockchain technology, ECEs need to plan emission reduction measures in advance based on the characteristics of the forest growth cycle to obtain the greatest benefits.
5. A Numerical Example
In this section, we assign values to relevant parameters in the transactions between forest farmers and ECEs to verify the results of the above models.
5.1. Changes in S before and after Applying the Blockchain Technology
Assume , , , , , , , . The results are shown in Figure 1.
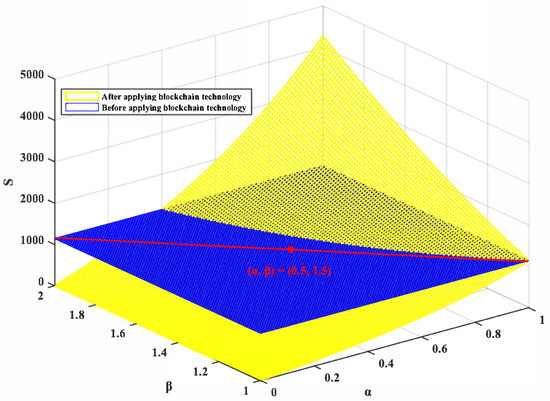
Figure 1.
The influence of x on S.
From the area of the horizontal plane in Figure 1, it can be seen that blockchain technology reduces the willingness of ECEs to reduce emissions through technology by stabilizing carbon prices and stimulating the vitality of the carbon trading market. Only when and are larger, the amount of stimuli for the carbon trading market by blockchain technology is far greater than the degree of stable carbon prices. In this situation, carbon prices tends to be unstable and high. ECEs are more willing to use their technology to reduce emissions to meet the carbon quota requirements, and emission reduction efforts S will increase.
At the initial stage of the utilization of blockchain technology, it needs to be integrated with the market effectively, and through continuous adjustments to adapt to the law of market development. If blockchain technology takes stabilizing carbon prices as the leading role, the willingness of ECEs to purchase FCS increases, and the willingness of technology to reduce emissions decreases. The emission reduction efforts of ECEs will be lower than the level before the introduction of blockchain technology. If blockchain technology takes the leading role in stimulating the carbon trading market, the price of carbon trading is relatively high, and ECEs will tend to achieve carbon quota requirements through their technology to reduce emissions. In the later stage of the utilization of blockchain technology, the incentive and stabilizing effects of blockchain technology on carbon prices tend to balance, , and the emission reduction efforts of ECEs are lower than the efforts before the applying blockchain technology.
5.2. The Relationship between S and ,
From Equations (26) and (43), we can find that the emission reduction efforts of ECEs are related to abatement cost , emission reduction efficiency , and price x. Assume that and after the introduction of blockchain technology. , , . The results are shown in Figure 2.
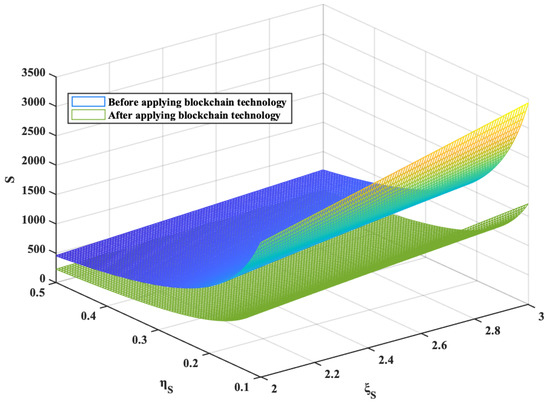
Figure 2.
The influence of S, and .
From Figure 2, it can be seen that the cost generated by the emission reduction behavior of ECEs suppresses its emission reduction behavior. The greater the emission reduction efficiency, the higher the emission reduction investment efficiency of ECEs. This encourages emission reduction behaviors of ECEs. Blockchain technology has stabilized carbon prices and stimulated the vitality of the carbon trading market, so that ECEs tend to purchase FCS while maximizing their profits and reducing the willingness of ECEs to reduce emissions through their technology.
5.3. Changes in F before and after Applying the Blockchain Technology
Forest farmers’ emission reduction efforts are related to the abatement cost, the efficiency of forest farmers’ input into carbon sinks, and government subsidies. Blockchain technology reduces FCS operating costs and improves output efficiency through smart contract technology. That is, and are changed. Assume that before using blockchain technology, , , after using blockchain technology, , . The discount rate , the influence coefficient of random factors , the government subsidy coefficient , , . The results are shown in Figure 3.
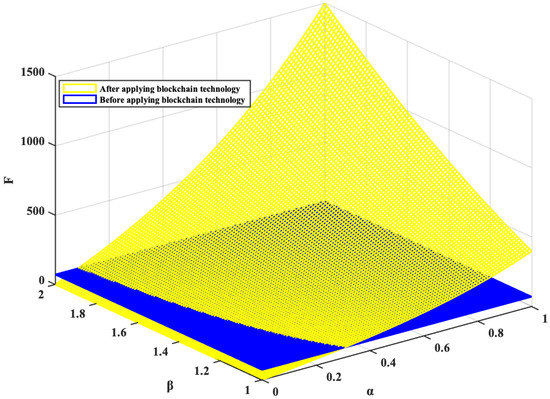
Figure 3.
Changes in F before and after applying the blockchain technology.
As shown in Figure 3, blockchain technology greatly encourages forest farmers to reduce emissions by reducing the costs of FCS project. This improves output efficiency, stabilizes carbon prices, and stimulates the vitality of the carbon trading market. When the influence of blockchain technology on stabilizing carbon prices is dominant and the price is low, forest farmers will be less motivated to reduce emissions, and F will be lower than before the introduction of blockchain technology. If the price is stable at a high level, the market demand will decrease. At this point, forest farmers will reduce their input based on maximizing benefits, and F will decrease. In reality, such a situation does not exist. In addition, according to the principle of supply and demand, the market will adjust prices spontaneously. Under normal circumstances, the (, ) will fluctuate within a small range of .
To be more clear, we decompose the effect of blockchain technology on the FCS project and carbon trading market. The results are shown in Figure 4.
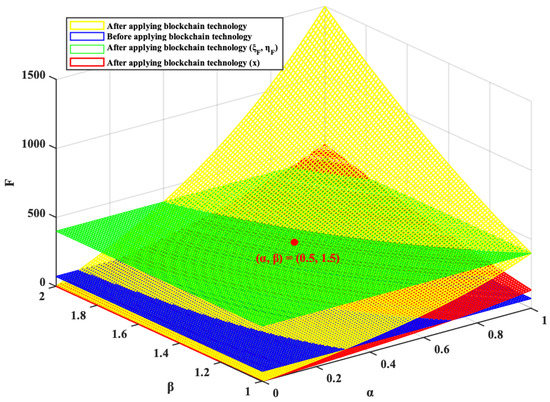
Figure 4.
An exploded view of the role of blockchain technology.
Blockchain technology optimizes the project by reducing costs and improving output efficiency and increasing forest farmers’ willingness to reduce emissions. Thus, the effect is greater than the impact of adjusting prices. When the carbon price is stable at a low level, forest farmers will reduce input and avoid additional expenditures to maximize benefits.
When the carbon trading market reaches a stable state through its evolution, , forest farmers make appropriate adjustments to the scale of input by predicting returns. When the blockchain technology only acts on the project, the forest farmers’ emission reduction efforts is reduced to avoid unnecessary expenditures. However, forest farmers’ optimal emission reduction efforts are still higher than before using blockchain technology, which has encouraged forest farmers to reduce emissions.
Therefore, blockchain technology mainly affects F from two aspects: (1) reducing costs and improving output efficiency, and then, increasing forest farmers’ willingness to reduce emissions; (2) stabilizing carbon prices and stimulating the vitality of the carbon trading market. Forest farmers make a more accurate forecast of the future benefits, then adjust the investment ratio to maximize its benefits appropriately.
5.4. The Optimal Trajectory for FCS and ECEs’ Emission Reductions before and after Applying Blockchain Technology
Assume that is ten thousand million tons and is one thousand tons. Before the introduction of blockchain technology, , , after using blockchain technology, , . The discount rate , the influence coefficient of random factors , . The final amount of carbon sinks that forests can provide Q is 1 million tons, the carbon sink unit time growth factor , and the government’s emission reduction compensation coefficient , , . The results are shown in Figure 5.
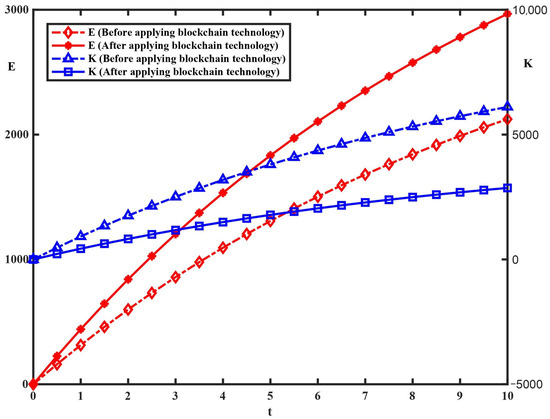
Figure 5.
The optimal trajectory for FCS and ECEs’ emission reductions before and after applying blockchain technology.
From Figure 5, it can be seen that blockchain technology improves the evolution trajectory of FCS and reduces the willingness of ECEs to reduce emissions through carbon abatement technology. In addition, the greater the growth rate of FCS, the lower the growth rate of technological emission reductions of ECEs.
Summarize the functional mechanism of blockchain technology in the above four aspects, as shown in Figure 6.
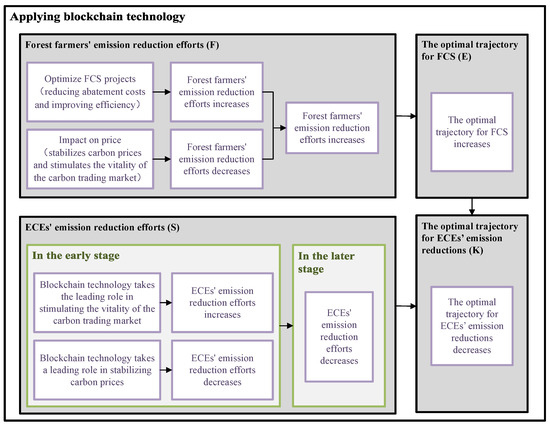
Figure 6.
Mechanism of applying blockchain technology to optimize FCS profits.
6. Conclusions
This paper makes a game analysis on FCS trading. By introducing blockchain technology, we find the following main conclusions.
(1) The emission reduction efforts of ECEs are affected mainly by FCS prices, abatement costs, and government subsidies. ECEs choose emission reduction methods with the goal of economic maximization. (1) At the initial stage of the utilization of blockchain technology, if blockchain technology takes stabilizing carbon prices as the leading role, the willingness of ECEs to purchase FCS will increase and the willingness of technology to reduce emissions will decrease. The emission reduction efforts of ECEs will be lower than the level before applying blockchain technology. If blockchain technology takes the leading role in stimulating the carbon trading market, the price of carbon trading is relatively high, and ECEs will tend to achieve carbon quota requirements through their technology to reduce emissions. The emission reduction efforts of ECEs will be higher than the level before applying blockchain technology. (2) In the later stage of the utilization of blockchain technology, the incentive and stabilizing effects of blockchain technology on carbon prices tend to balance, and the emission reduction efforts of ECEs are lower than the efforts before applying blockchain technology.
(2) Blockchain technology affects forest farmers’ emission reduction efforts in two aspects. (1) Optimizing FCS projects from the inside. Blockchain technology reduces costs and improves output efficiency, then increases forest farmers’ willingness to reduce emissions; (2) Adjusting the price of carbon sinks. In the later stage of the utilization of blockchain technology, forest farmers make a more accurate forecast of the future profit, and then adjust the investment ratio to maximize its benefits appropriately because the application of blockchain technology stabilizes carbon prices and stimulates the vitality of the carbon trading market. To sum up, applying blockchain technology encourages forest farmers’ emission reduction efforts, and the effect of blockchain technology on the optimization of FCS projects is higher than the effect of adjusting carbon prices.
(3) Blockchain technology optimizes the trajectory for FCS and ECEs’ emission reductions. Blockchain technology increases FCS. The emission reductions of ECEs follow changes in FCS. Blockchain affects the emission reductions of ECEs by changing the price and quantity of FCS. The greater the growth rate of FCS, the lower the growth rate of technological emission reductions of ECEs.
Author Contributions
Conceptualization, R.S. and D.H.; methodology, R.S. and D.H.; software, R.S. and L.T.; validation, R.S. and D.H.; formal analysis, R.S.; data curation, R.S and D.H.; writing—original draft preparation, R.S and L.T.; writing—review and editing, D.H. and J.Y.; visualization, R.S.; supervision, J.Y. and D.H. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Special public welfare project of the Ministry of Natural Resources (201211003).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Y.; Li, F.; Li, Y. A Study of the Forestry-Based Carbon Sink Market and the Development of Forestry-Based Carbon Sink Trading in Hainan under the Background of Carbon Neutrality. J. Hainan Norm. Univ. 2021, 39, 35–43. [Google Scholar]
- Song, Y.; Peng, H. Strategies of Forestry Carbon Sink under Forest Insurance and Subsidies. Sustainability 2019, 11, 4067. [Google Scholar] [CrossRef] [Green Version]
- Cornelis, V.K.G.; Maria, N.; Kimpton, B. Can carbon accounting promote economic development in forest-dependent, indigenous communities? For. Policy Econ. 2019, 100, 68–74. [Google Scholar]
- Ojha, H.; Maraseni, T.; Nightingale, A.; Bhattarai, B.; Khatri, D. Rescuing forests from the carbon trap. For. Policy Econ. 2019, 101, 15–18. [Google Scholar] [CrossRef]
- Keren, C.; Qiyuan, C.; Nan, Z.; Yinan, L.; Changyong, L.; Yuanfei, L. Forest carbon sink evaluation—An important contribution for carbon neutrality. IOP Conf. Ser. Earth Environ. Sci. 2021, 811, 012009. [Google Scholar]
- Jin, T.; Gao, Q.; Cao, X.; Wu, W. Research on risk measurement and impact of forestry carbon sink project. Issues For. Econ. 2021, 41, 304–310. [Google Scholar]
- Du, X.; Liang, K.; Li, D. Reward and penalty model of carbon emission reduction and carbon trading matching model for power industry based on blockchain technology. Autom. Electr. Power Syst. 2020, 44, 29–35. [Google Scholar]
- Chuang, T.J.; Yen, T.M. Public views on the value of forests in relation to forestation projects—A case study in central Taiwan. For. Policy Econ. 2017, 78, 173–179. [Google Scholar] [CrossRef]
- White, A.E.; Lutz, D.A.; Howarth, R.B.; Soto, J.R. Small-scale forestry and carbon offset markets: An empirical study of Vermont Current Use forest landowner willingness to accept carbon credit programs. PLoS ONE 2018, 13, e0201967. [Google Scholar] [CrossRef]
- Khanal, P.N.; Grebner, D.L.; Straka, T.J.; Adams, D.C. Obstacles to participation in carbon sequestration for nonindustrial private forest landowners in the southern United States: A diffusion of innovations perspective. For. Policy Econ. 2019, 100, 95–101. [Google Scholar] [CrossRef]
- Zou, Y.; Li, J.; Qi, Y.; Guan, J. Demand willingness and influencing factors of emission control enterprises for forest carbon sink in the context of carbon trade: Based on the theory of planned behavior. Sci. Silvae Sin. 2020, 56, 162–172. [Google Scholar]
- Zhang, Y.; Qi, H.; Xu, X.; Long, F. Research on the policy combination effect of the demand response of the forestry carbon sink market. Issues For. Econ. 2021, 41, 311–319. [Google Scholar]
- Lin, B.; Ge, J. Does institutional freedom matter for global forest carbon sinks in the face of economic development disparity? China Econ. Rev. 2021, 65, 101563. [Google Scholar] [CrossRef]
- Tsai, W. Forest resource management and its climate-change mitigation policies in Taiwan. Climate 2020, 9, 3. [Google Scholar] [CrossRef]
- Jiang, S.; Lu, Y.L.Q.; Hong, Y.; Guan, D.; Xiong, Y.; Wang, S. Policy assessments for the carbon emission flows and sustainability of Bitcoin blockchain operation in China. Econ. Pap. J. Appl. Econ. Policy 2021, 12, 1938–1947. [Google Scholar]
- Pop, C.; Cioara, T.; Antal, M.; Anghel, I.; Ioan Salomie, M.B. Blockchain based decentralized management of demand response programs in smart energy grids. Sensors 2018, 18, 162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khaqqi, K.N.; Sikorski, J.J.; Hadinoto, K.; Kraft, M. Incorporating seller/buyer reputation-based system in blockchain-enabled emission trading application. Appl. Energy 2018, 209, 8–19. [Google Scholar] [CrossRef]
- Hua, W.; Jiang, J.; Sun, H.; Wu, J. A blockchain based peer-to-peer trading framework integrating energy and carbon markets. Appl. Energy 2020, 279, 115539. [Google Scholar] [CrossRef]
- Wang, M. Blockchain technology and its role in enhancing supply chain integration capability and reducing carbon emission: A conceptual framework. Sustainability 2020, 12, 10550. [Google Scholar] [CrossRef]
- Hartmann, S.; Thomas, S. Applying blockchain to the Australian carbon market. Econ. Pap. 2020, 39, 133–151. [Google Scholar] [CrossRef]
- Liu, T. Research on the impact of blockchain technology on carbon trading price mechanism. Price Theory Pract. 2020, 54–57. [Google Scholar]
- Ji, B.; Chang, L.; Chen, Z.; Liu, Y.; Zhu, D.; Zhu, L. Blockchain technology based design and application of market mechanism for power carbon emission allowance trading. Autom. Electr. Power Syst. 2021, 45, 1–10. [Google Scholar]
- Rodrigo, M.N.N.; Perera, S.; Senaratne, S.; Jin, X. Potential application of blockchain technology for embodied carbon estimating in construction supply chains. Buildings 2020, 10, 140. [Google Scholar] [CrossRef]
- Woo, J.; Fatima, R.; Kibert, C.J.; Newman, R.E.; Tian, Y.; Srinivasan, R.S. Applying blockchain technology for building energy performance measurement, reporting, and verification (MRV) and the carbon credit market: A review of the literature. Build. Environ. 2021, 205, 108199. [Google Scholar] [CrossRef]
- Sadik-Zada, E.R. An Ode to ODA against all Odds? A Novel Game-Theoretical and Empirical Reappraisal of the Terrorism-Aid Nexus. Atl. Econ. J. 2021, 49, 221–240. [Google Scholar] [CrossRef]
- Sadik-Zada, E.R. Distributional Bargaining and the Speed of Structural Change in the Petroleum Exporting Labor Surplus Economies. Eur. J. Dev. Res. 2020, 32, 51–98. [Google Scholar] [CrossRef]
- Wang, D.; Wang, T. Dynamic Optimization of Cooperation on Carbon Emission Reduction and Promotion in Supply Chain Under Government Subsidy. J. Syst. Manag. 2021, 30, 14–27. [Google Scholar]
- Wang, M.; Liu, Y.; Shi, W.; Li, M.; Zhong, C. Research on technology remote synergic sharing strategy of low carbon under the ETS in China. Syst.-Eng.-Theory Pract. 2019, 39, 1419–1434. [Google Scholar]
- Hou, B. Discussion on the Risks of Forestry Asset Securitization from the Perspective of Block Chain. China For. Econ. 2021, 130–134. [Google Scholar] [CrossRef]
- Caulkins, J.P.; Feichtinger, G.; Grass, D.; Hartl, R.F.; Kort, P.M.; Seidl, A. Interaction of pricing, advertising and experience quality: A dynamic analysis. Eur. J. Oper. Res. 2017, 256, 877–885. [Google Scholar] [CrossRef]
- Gundersen, P.; Thybring, E.E.; Nord-Larsen, T.; Vesterdal, L.; Nadelhoffer, K.J.; Johannsen, V.K. Old-growth forest carbon sinks overestimated. Nature 2021, 591, 21–23. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, X.; Fu, C.; Yu, G.; Liu., Z. Estimation of carbon sequestration potential of forest biomass in China based on National Forest Resources Inventory. Acta Ecol. Sin. 2019, 39, 4002–4010. [Google Scholar]
- Li, Q.; Zhu, J.; Feng, Y.; Xiao, W. Carbon storage and carbon sequestration potential of the forest in China. Clim. Chang. Res. 2018, 14, 287–294. [Google Scholar]
- Ren, J.; Xia, J. Prediction of Forest Carbon Sink Potential in Heilongjiang Province: The Carbon Density-Age Relationship-Based Approach. Res. Environ. Sci. 2017, 30, 552–558. [Google Scholar]
- Yang, F.; Jiang, Y.; Paudel, K.P. Farmers’ Willingness to Participate in Forest Management for Carbon Sequestration on the Sloping Land Conservation Program in China. Sci. Total Environ. 2021, 23, 244–261. [Google Scholar]
- Du, W.; Li, M. Assessing the impact of environmental regulation on pollution abatement and collaborative emissions reduction: Micro-evidence from Chinese industrial enterprises. Environ. Impact Assess. Rev. 2020, 82, 106382. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, Z.; Yang, L. Carbon emission reduction decisions in the retail-/dual-channel supply chain with consumers’ preference. J. Clean. Prod. 2017, 141, 852–867. [Google Scholar] [CrossRef]
- Qiu, L.; Zeng, W.; Shashi, K.; Wang, S. The role of social capital in rural households’ perceptions toward the benefits of forest carbon sequestration projects: Evidence from a rural household survey in Sichuan and Yunnan provinces, China. Land 2021, 10, 91. [Google Scholar] [CrossRef]
- Gleim, M.R.; Stevens, J.L. Blockchain: A game changer for marketers? Mark. Lett. 2021, 32, 123–128. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).