1. Introduction
A growing amount of literature has surged in recent months on the novel coronavirus COVID-19. SARS-CoV-2 may lead in severe cases to acute respiratory distress (Mehta et al., 2020) and has been classified as the latest worldwide pandemic, with an unprecedented impact on the health sector [
1], global economy [
2,
3], and epidemiology [
4,
5]. With the first cases identified in late 2019 at an epicenter in Wuhan, China, it has spread at an alarming rate throughout the rest of the world. A new epicenter was identified early March 2020 in Italy [
6], with incidence rising exponentially worldwide, reaching a total of 6,140,934 cases as of 2 June 2020 according to the WHO dashboard [
7]. The number of cases in China has subsided since early March, with China preparing to ease the drastic containment measures taken months earlier [
8]. The spread of the virus itself, particularly with the global nature of transmission of the disease and the new epicenters generated throughout, has created an upsurge in literature as well as planning structures to address this global concern. It is expected that the virus will be controlled. Not since the great depression have the impacts on key economic drivers and regional effects been this significant. It is expected that a paradigm shift will occur, impacting (1) education (Wang et al., 2020), (2) geographies of proximity [
9], (3) urban agglomeration, and (4) the liveability of cities [
10]. With the incremental impacts on commercial activity and the retail sector, and the rise of technological integration for remote work, the virus will, with a growing amount of certainty, reshape the world that we have known since the beginning of the millennia, in an unpreceded fashion that applies to all sectors worldwide [
11].
Significant amounts of data have been reported at a global level, allowing a more consistent understanding of the spread of COVID-19 throughout the world. [
12,
13]. At local level, however, only a few, often unorganized sources exist where information is shared. In the case of Canada, no federal initiative exists that informs on the exact locations of cases. While this issue raises a series of privacy concerns, such an initiative would provide a vital information pool for the general public and governance. The importance of locational information of COVID-19 sets a framework for further epidemiological analysis of transmission characteristics. Understanding the social, environmental, and economic determinants that have rarely been studied today for this pandemic will permit the creation of an explanatory model that directly enables mitigation and spatial decision support. Furthered by the iteration of environmental and geodemographic data, the interactions between the surrounding landscape and environment can be shaped, constituting a crucial link to public health [
5].
In the case of COVID-19, no precedent studies exist that provide a thorough spatial analysis. A significant number of studies have assessed regional impacts on epidemiological factors at a spatial scale. These studies combine several spatially explicit methods in the field of health geography. The understanding of spatial distribution is of utmost importance for understanding environmental and social determinants, and, in particular, the role of their spatial interactions with the population and the correlation of disease spread within the Euclidean confinement of set spatial boundaries of geographical interaction [
14]. Socio-economic characteristics are intrinsically geographical and permit calculations between geographical administrative boundaries, where unique features relating to socio-economic indicators exist [
15]. Recognizing the relationship of geography with socio-economic variables and the spread of COVID-19 will allow for precise quantitative analytics found using geostatistics and spatial analytical methods, where simple mapping does not relay a clear picture [
16]. By assembling the available data using employing geocomputation techniques, significant advances to mitigate the spread of the disease can be made [
17]. With regard to the characteristics of spatial data in relation to geography in particular this would allow for tackling pandemic impacts at both a regional and global scale in various ways, for example through:
The monitoring of the containment of spread using proximity characteristics and distance relationships,
The study of disease interactions with key demographic drivers and spatial containment strategies,
The integration of land use typologies within the spread of the virus to offer insights into which types of land use configuration justify particular policies and measures.
In this sense, the combination of spatial analytical techniques with landscape metrics may have an additional role in the containment and monitoring of COVID-19, while offering, through spatial clustering as well as spatial profiling, a combined approach for landscape research to support policies and governance interactions, mitigating the spread of the novel coronavirus at the neighborhood level. This paper sets the stage for local-level analysis of COVID-19 by means of spatial analysis and geodemographics. Further to this section, the second section explores the study area of Toronto, where the data have been made available recently at the neighborhood level.
Section 3 presents the data and the integrated methodology, and
Section 4 explores the results and paves the way to offer a robust spatial model that identifies determinants for COVID-19 in large cities such as Toronto.
Section 5 offers concluding remarks on the necessary integration of local-level analysis towards mitigation and efficient planning for current and future pandemics through geographical information.
2. Study Area
On 2 June 2020 Canada reported a total of 91,351 cases and a total of 7305 deaths due to COVID-19. According to the provincial website, Ontario presently holds a total of 28,263 cases and as of 4 June 2020, 90% of all COVID-19 cases were located in Ontario and Quebec. The city of Toronto represents the densest urban core in the province, and also is one of the most densely populated regions in North America. At the regional level, known as the Greater Toronto Area, it has four additional municipalities: York, Peel, Halton, and Durham. The region itself extends from its core at 43°38′33″ N, 79°23′14″ W and has a total population of over six million inhabitants. Its population density is significantly higher than Ontario’s average, with a total population density of 850 inhabitants per km2. Given its population density, this region is at particular risk of an excess of COVID-19 cases. The public transportation network extending in all directions is served by the municipal transportation system, and the vast majority of transport users within the Greater Toronto Area are commuters using either the GO Transit or the Toronto Transit Commission (TTC) systems by means of trains, buses, and streetcars in the city core.
Toronto’s economic growth has been at the forefront of North American economic growth. Its retail and commercial sectors have grown markedly in the last decade due to economic prosperity and demographic changes. The region has a diversified ethnic and cultural legacy. This cultural diversity has given rise to new economic opportunities, contributing to the municipal prosperity and the ongoing growth of commercial activity in the Greater Toronto Area. Still, there is growing concern as commercial activity has been put on hold since the end of March 2020. Furthermore, as a consequence of this growth, the region has suffered significant urban sprawl [
18]. There is a growing risk of pollution as population density increases in the neighboring areas within the perimeter of the city of Toronto. Although this sprawl is still far from reaching Ontario’s greenbelt, it must be considered and monitored by decision-makers and stakeholders. With rapid urbanization and the significant growth of real estate prices in the last decade, the city of Toronto shows a stark amount of economic heterogeneity. It is where geographical clusters of poverty are evident in some neighborhoods throughout the city. The asymmetry between wealth and poverty throughout the city has led to escalating issues that directly affect health, planning, social justice, transportation efficiency, and economic activity [
19]. These are crucial aspects that may inadvertently impact the distribution of COVID-19 cases and should be systematically assessed.
3. Data and Methods
3.1. Data Gathering and Processing
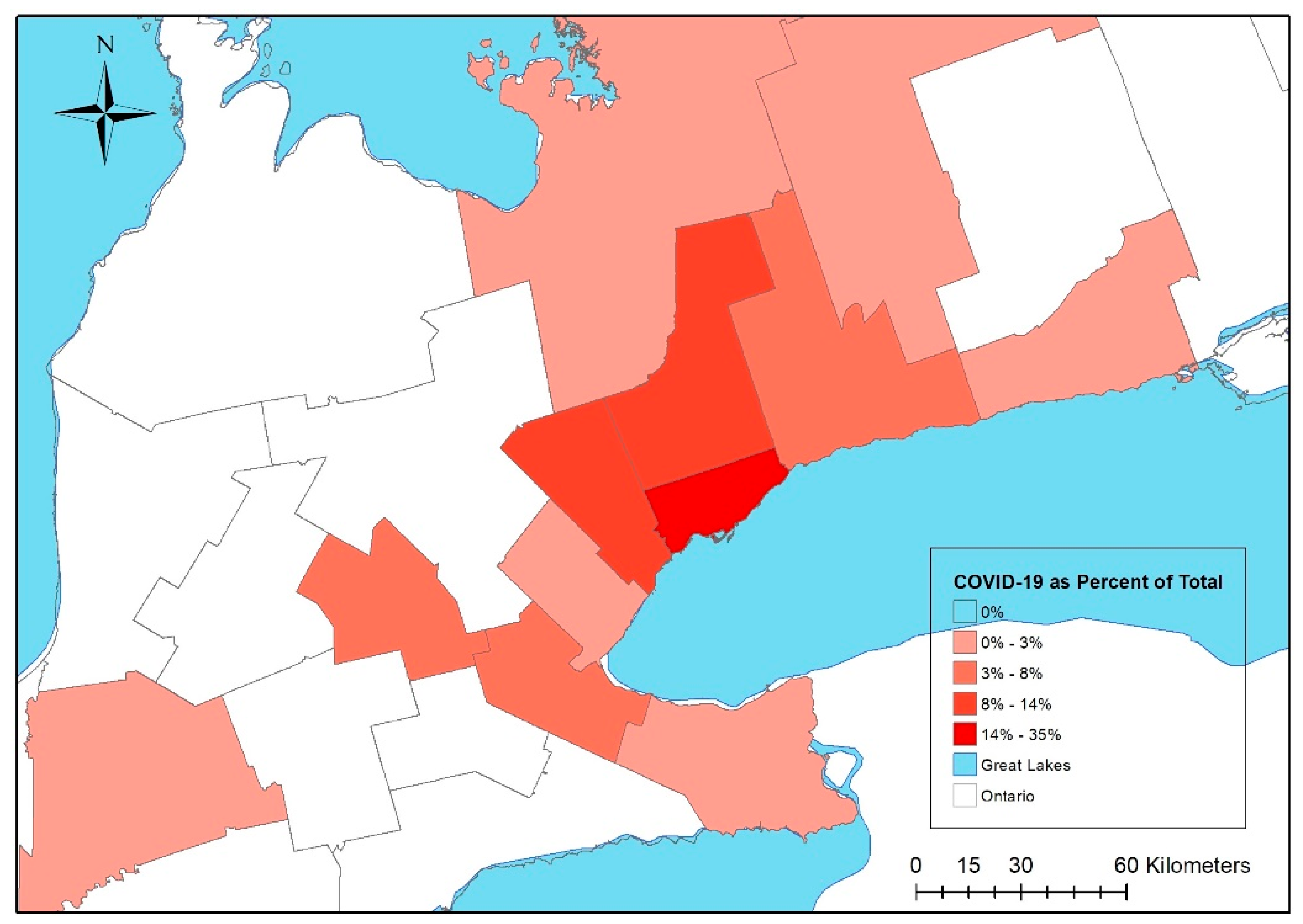
The recent release of information on COVID-19 cases for the city of Toronto has allowed us to conduct a spatial-exploratory approach at the neighborhood level. Each health unit comprising the Greater Golden Horseshoe shares daily information on COVID-19 cases within its health unit website. A first step consisted of understanding the geospatial morphology of COVID-19 cases. The cases were downloaded for 8 April 2020. In total, 2346 cases were compiled within southern Ontario’s health unit network boundary. Of these, 2086 were considered as part of the Greater Golden Horseshoe, while the remaining 260 cases, belonging to the Middlesex-London Health Unit and City of Ottawa Health Unit, were excluded. Two topological considerations were taken into account with respect to the administrative boundaries of the counties of Simcoe and the Kawartha Lakes Division, for which the health unit boundaries differ from those of its northern limit, holding a larger spatial radius than the municipal extent. The figure below (
Figure 1) shows the distribution of cases per health unit as of 8 April 2020. A radial distribution is clear, stemming from the City of Toronto and reaching outwards towards the Greater Toronto Area.
This picture, however, can only be realistically interpreted in function of the prevalent population density, as distribution of population is a key vector of potential transmission. As such, COVID-19 density was calculated accounting for population density and COVID-19 cases as follows (Equation (1)):
where the density of COVID-19 cases
COVd corresponds to the number of cases of COVID-19 in the administrative boundary
COVn per population
p, considering the area
A in km
2. This allowed for a more thorough and integrative analysis of the spatial distribution of COVID-19 cases, establishing the preliminary finding throughout the province of Ontario which suggested a strong spatial clustering of COVID-19 cases throughout the province. These initial findings allowed for the confirmation of the importance of further exploration at a spatial level for the city of Toronto and served as a validation of the preliminary hypothesis, where spatial autocorrelation at a global level for southern Ontario tested positive. The recent availability at city level released on 28 May 2020 allowed for a spatial exploration of the neighborhood level of the identified cases, which share the following characteristics relating to general epidemic dynamics for the city of Toronto (
Table 1):
Some relevant preliminary findings reported by the city suggest that the 50–59-year age group had the highest percentage of cases, with an incidence of 15.8%. The gender distribution further shows that the majority of cases occurred in females (54%), with male cases representing 44% of the total. A majority of the cases (53%) resulted from close contact with a case, while 23.9% were related to community spread. Both close contact and community spread may be seen as geographically deterministic, and thus require further inspection at the spatial level (
Figure 2).
3.2. Socio-Economic Data
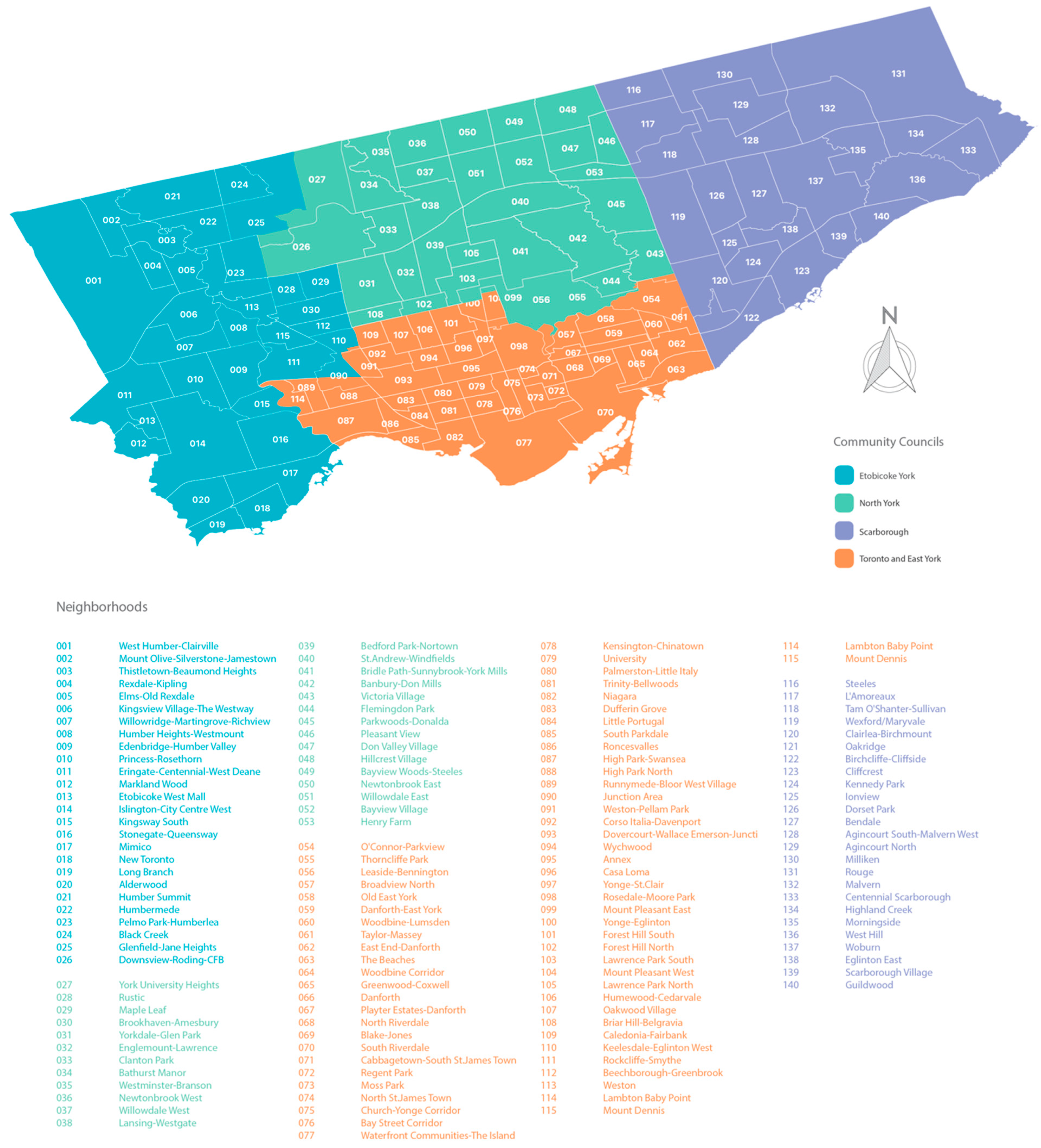
Wellbeing Toronto (WT) data were used to assess critical variables at the neighborhood level for Toronto. WT corresponds to an integrative and open approach for visualization of Toronto’s 140 neighborhoods [
20]. As an open data concept, it hosts a significant amount of data over three reference periods (2008, 2011, and 2014), with crucial variables encouraging citizen participation, government accountability, and data transparency (
Figure 3).
For health analytics, these are vital requisites for successful policy implementation. The table below shows the variables that were selected from the WT portal (
Table 2).
3.3. Modifiable Areal Unit Problem and COVID-19 Data
Performing an assessment at highest resolution is of utmost importance and has generated a debate within ongoing spatially explicit studies concerning COVID-19. Often resulting in false conclusions, bias relates to the key dimensions assessed by [
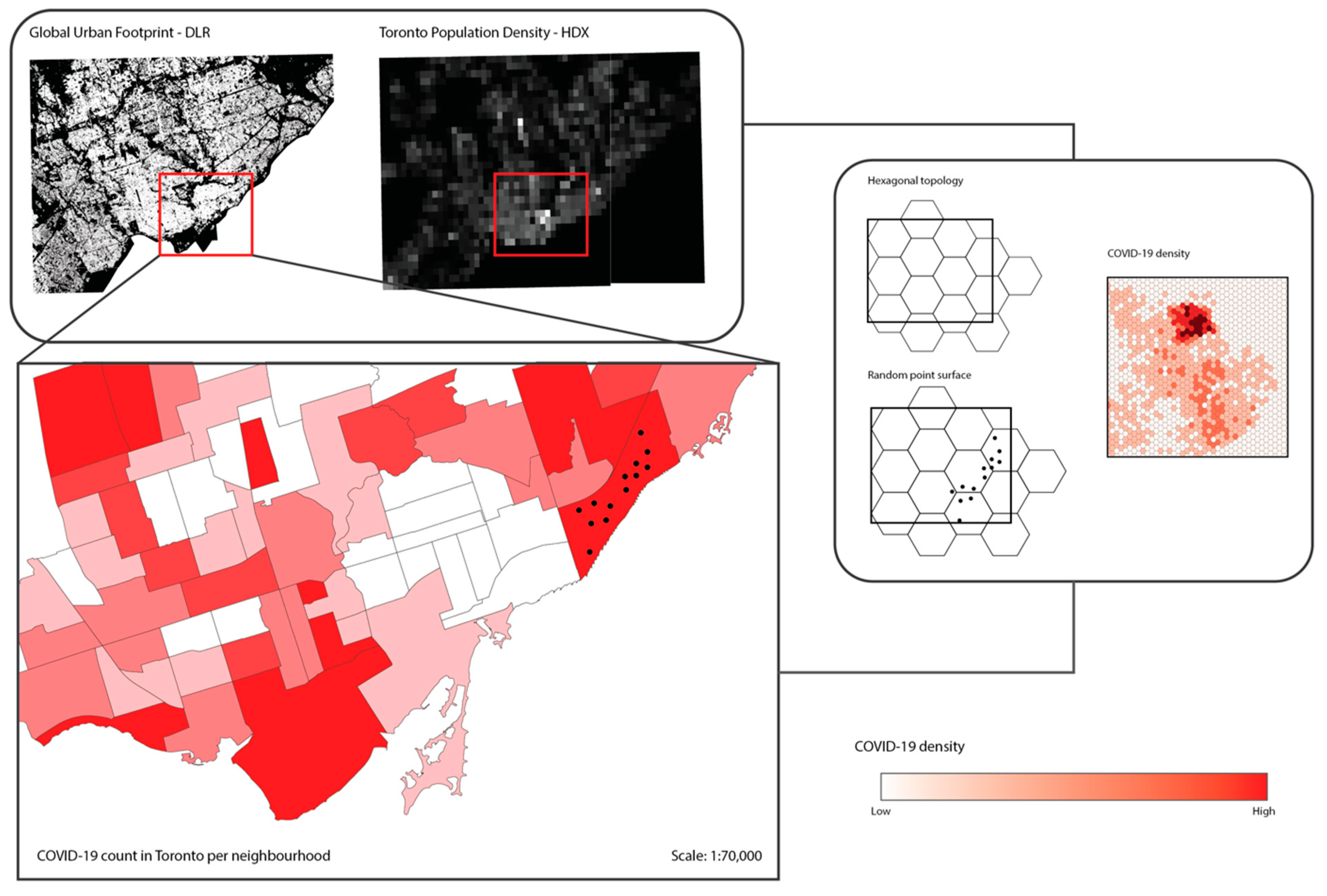
21]. Rather than expecting limitations of the modifiable areal unit problem (MAUP), it is thus important to attempt solutions that through zonal interpolation generate a higher accuracy of population density so as to allow a better assessment at a spatial scale. This was performed by combining urban footprint data from the German Space Agency with Humanitarian Data Exchange (HDX) data for population density.
The Global Urban Footprint (GUF) data consists of a pixel-based classification approach using TerraSAR-X data as well as with an object-based classification approach using multitemporal optical Landsat data [
22]. The authors adopted the available data from 1975 with a geometric resolution of 59 m (multispectral scanner), from 1990 with a resolution of 28.5 m (thematic scanner), and from the year 2000 with a resolution of 15 m (enhanced thematic mapper). The algorithm is based on a temporal backwards-oriented hierarchical approach as presented in [
23,
24,
25].
The Humanitarian Data Exchange (HDX) data for population density in Canada at a 1-km spatial resolution were extracted for the Toronto boundary. Both layers were combined and normalized within a hexagonal bin topology of 100-m hexagons. The usage of both GUF and HXD data allows for data replicability for other regions throughout the world as a high spatial resolution performance indicator, creating a density surface and thus avoiding the restrictions of the MAUP while allowing the assessment of eminent health issues [
26]. This allowed for a local zonal interpolation with a significantly better performance than traditional neighborhood analysis (
Figure 4).
3.4. Methods
3.4.1. Global Spatial Autocorrelation
Global spatial autocorrelation was tested employing a Moran’s I index per injury category (Moran). This statistic was conducted to test the null hypothesis (Ho) relating to the absence of spatial clustering of COVID-19 in Toronto (α = 0.05) (Equation (2)):
where w
ij corresponds to a binary weight matrix defined with the weight of one, given a contiguity of adjacency for any value that holds as w
ij = 1 and any value without adjacency as w
ij = 0. The product of the distance is defined as x
i for any location i in the distance in relation to its mean. This holds as a statistic for assessing the entire spatial distribution of adjacency formed for the city of Toronto. The null hypothesis was rejected in all categories, suggesting a high spatial autocorrelation for all the COVID-19 categories in Toronto.
3.4.2. Local Spatial Autocorrelation
The Local
statistic was calculated by first determining the injury density [
27,
28]. While several approaches allow for spatial density estimation, we considered that the importance of neighborhood demographics should hold. Thus, the neighborhood injury density resulted from a ratio where density corresponded to the number of COVID-19 cases found in a neighborhood with respect to the total population count of the neighborhood. While greater spatial detail could have helped the accuracy of the assessment, one should note that the objective is related to the potential of participatory interaction of injury with available open data. In this sense, neighborhoods are the ideal geographic boundary for governance and city planning.
This approach allowed for a seamless definition of injury density at a spatial level and calculation of the statistic to determine the locational aggregation of injury hotspots and coldspots [
29]. The calculation of the local
statistic is as follows (Equation (3)):
where w
ij is the spatial weight matrix following a 1-km distance (d), and w
ij (d) is assumed as 1. The maps show densities of injury patient residences as hot spots and cold spots, with red representing the highest concentrations of injury and blue the lowest. The selection of regional socio-demographic characteristics for this analysis was guided by previous research and availability of Wellbeing Toronto data.
3.4.3. Regression Framework
A backward stepwise regression was conducted to create an optimum selection of neighborhood variables [
13,
30]. This stepwise regression approach allowed for the use of a full list of available neighborhood variables for the city Toronto and the integration of a step elimination process so as to offer a reduced model with enhanced explanatory performance. This minimized the possible issue of multicollinearity, thus avoiding any issues resulting from overfitting. This allowed for a successful preliminary selection of variables that were applied to three distinct regressions frameworks: (1) the spatial lag model, (2) the spatial error model as well as a non-spatial model to compare performance, and (3) the ordinary least squares model [
31]. The spatial lag model (SL) (Equation (3)) understands spatial dependency by the addition of a dependent variable that defines the spatial attribute.
where
I represents an identity matrix, and the
N(0,
I) indicates that the errors follow a normal distribution with mean equal to zero and constant variance. When
ρ is zero, the lag-dependent term is canceled out, leaving the model under the ordinary least squares (OLS) form. When
ρ is not zero, it means that spatial dependency exists, and that non-random spatial observable interactions are present [
32]. As for the spatial error model (Equation (4)), the spatial dependency
ξ is accounted within the error term
ϵ, assuming the errors of the model as spatially correlated.
4. Results
4.1. Spatial Autocorrelation
4.1.1. Global Spatial Autocorrelation
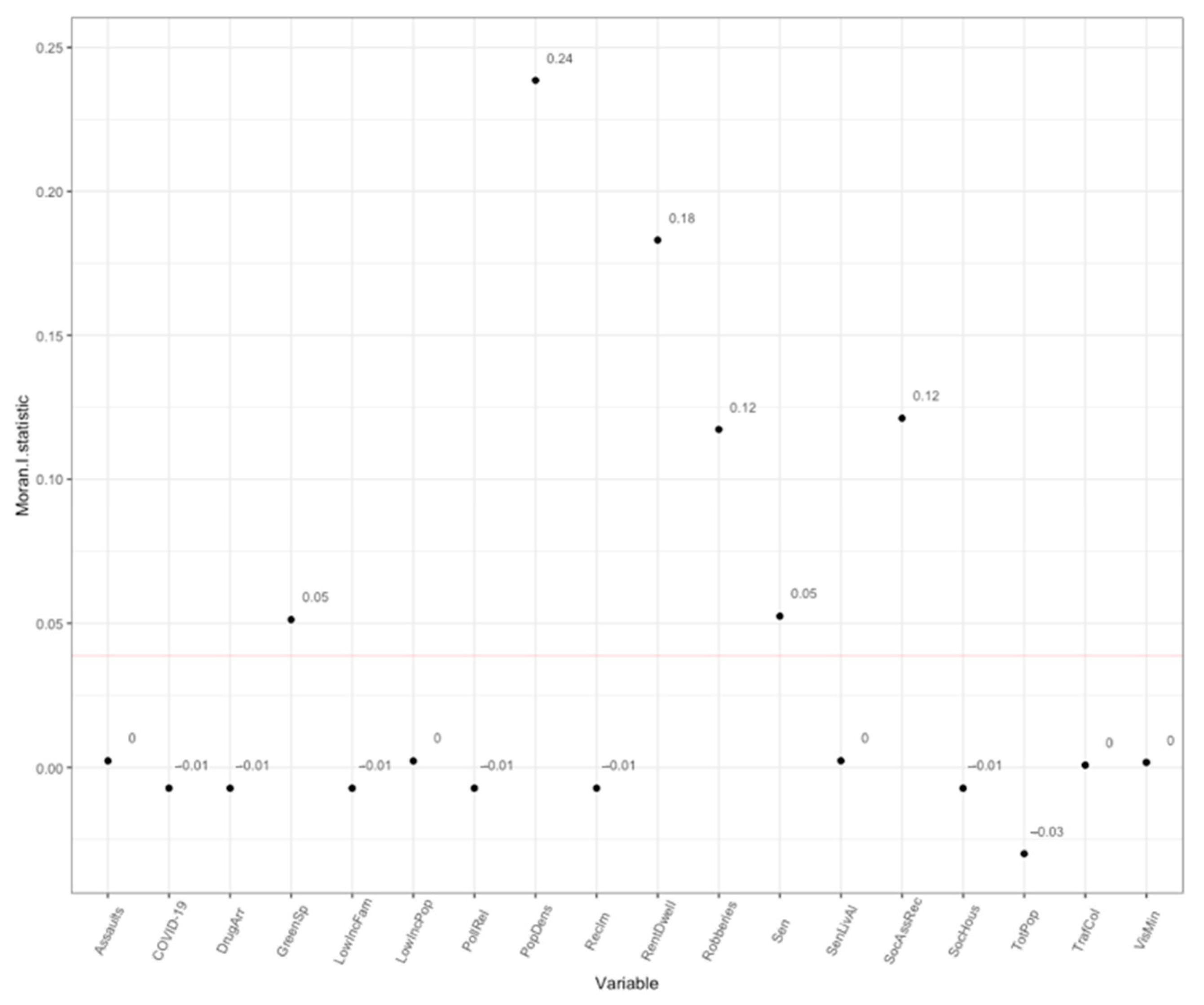
Testing for spatial autocorrelation through Moran’s I statistic provides evidence that there is significant spatial autocorrelation for COVID-19 within Toronto. Despite regional differences in the dynamics of cases, the spatial patterns of the residences of those assessed cases were found to be highly spatially autocorrelated (
p < 0.01), with a Moran’s I result of 0.417. This suggested a high spatial clustering that justified further local exploration and confirmed that the cases of SARS-CoV-2 in Toronto were significantly spatially related. Further testing of global spatial autocorrelation was performed for all the variables studied (
Figure 5).
The p-value for all variables was significantly high. Of particular interest was the finding that spatial autocorrelation of COVID-19 cases was very high, with a similar value to variables known to have very strong geographically explicit clustering, such as crime and population density. This in itself is a remarkable conclusion with regard to the spatially explicit nature of COVID-19 throughout cities, suggesting the presence of clearly definable hotspots throughout the city. Further inspection of local spatial autocorrelation will be paved by the promising results from global spatial autocorrelation in the following section.
4.1.2. Local Spatial Autocorrelation
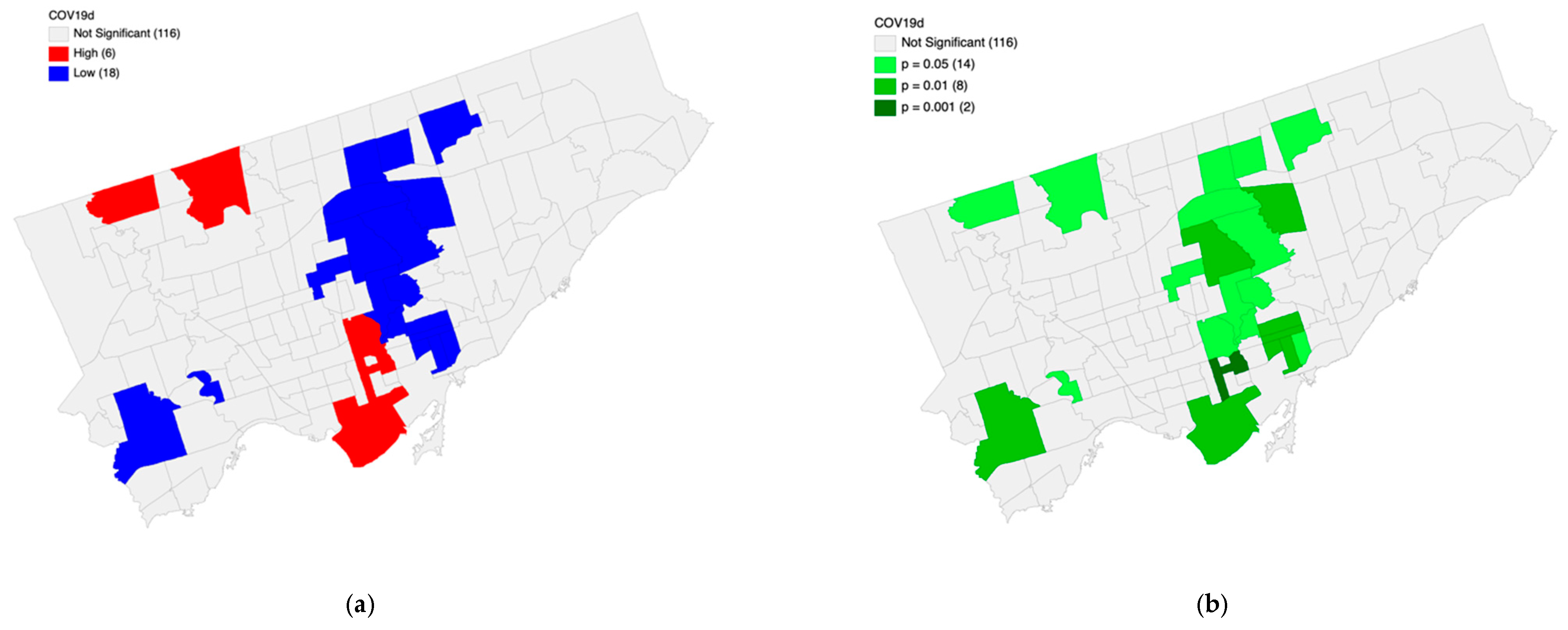
The calculation of Local allowed for the exploration of spatial distributions of hotspots and their significance levels for the categories of COVID-19 cases. A weight matrix was generated of queen contiguity type of order 1 for the 140 neighborhoods, with a minimum number of neighbors 3 and a maximum number of neighbors of 11. The mean and median neighbors corresponded to 5.96 and 6.00, respectively, and a total percentage of non-zero values of 4.26% was found.
The most intriguing aspect of these distributions, besides the clear evidence of hotspots and coldspots, was the unique spatial profile of COVID-19 (
Figure 6a,b). Red represents “hotspots”, or areas with high injury density, and blue represents cold spots or areas of low or no clustering of COVID-19 cases. Six high-clustering areas were found of which several with high significance, suggesting a clear spatial proxy in certain neighborhoods such as: York University Heights, Humber Summit, Waterfront communities, Cabbagetown-South St. James Town, and Rosedale-Moore Park.
Further inspection at the neighborhood level (
https://www.toronto.ca/city-government/data-research-maps/neighbourhoods-communities/neighbourhood-profiles/) paved a clear picture of the demographic profile within these communities. Several critical findings were noted within the comparison of the general city of Toronto profile and the characteristics of the communities within the neighborhoods. There was a stark contrast with regard to median household income, where the average salary was on average 22% higher in the rest of the city. With respect to poverty (Market Basket Measure), a disparity of 4% by comparison was also suggested. The greatest difference reported was with regard to the utilization of public transportation and the incidence of longer than 1-h commutes within the identified hotspots. Furthermore, there were significantly fewer individuals with education to bachelor’s degree-level and above in the identified neighborhoods. Most of the identified neighborhoods had a higher number of immigrants and a significant number of children between the ages of 0 and 14. Four silos of geodemographic characteristics were identified based on these findings: (1) transportation, (2) education, (3) income, and (4) social vulnerability. Overall, it is possible to note that these neighborhoods are of concern with regard to social injustice, where the key drivers are linked to lower education, presence of unemployment, and families with young children. It is crucial that decision-making connects with these communities efficiently so as to mitigate such disparities.
4.2. Statistical Analysis
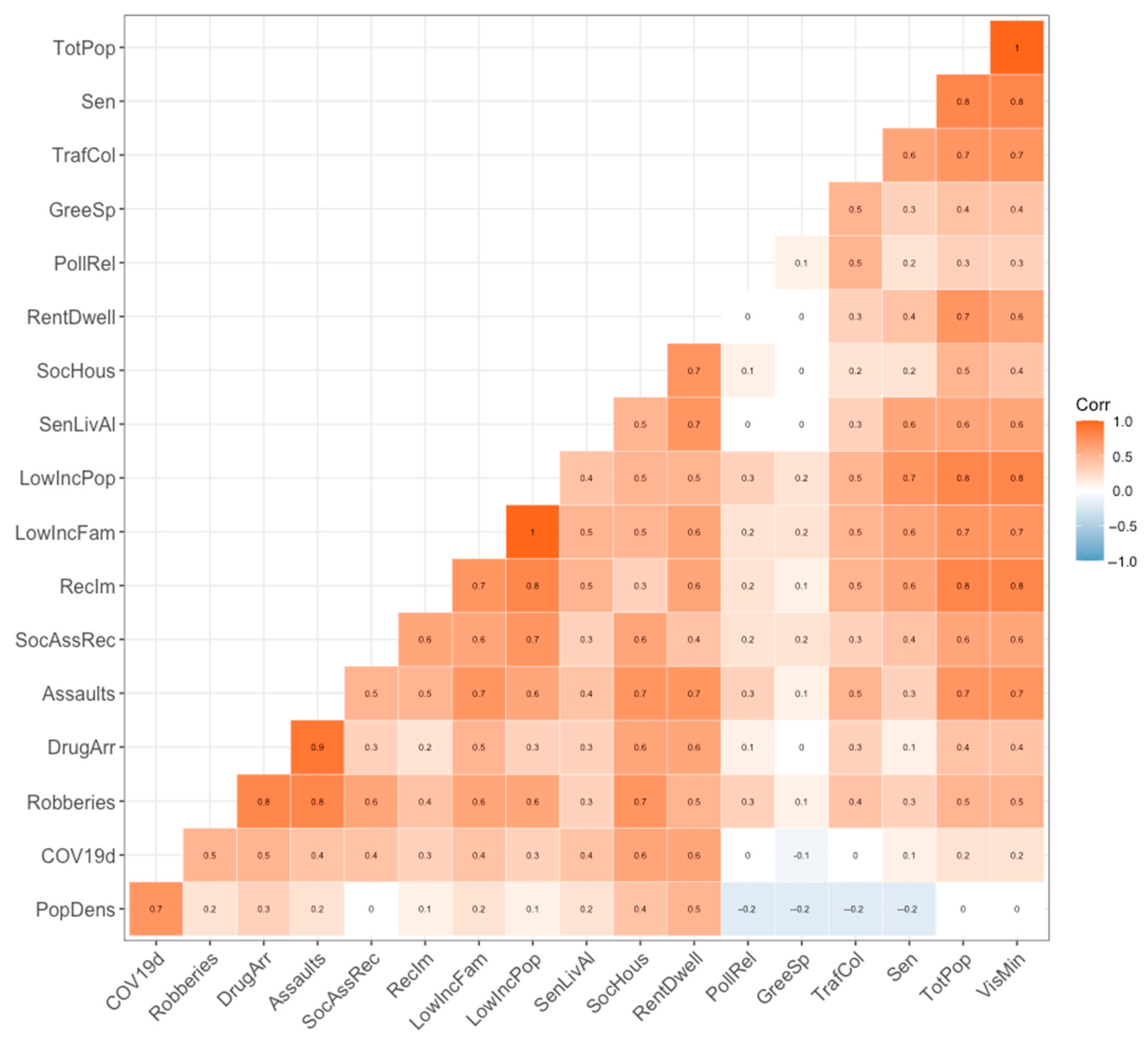
A Pearson correlation matrix was performed to test the correlation of all variables (
Figure 7). This allowed for an initial assessment of correlation between variables. Of particular interest were the correlations found between COVID-19 density, later explored through the regression framework.
Regression Results
The table below (
Table 3) shows the result of the OLS regression performed through backward stepwise regression:
In all cases the model registered a similar
R2 with limited improvement through spatial regression techniques. This suggests that the data available at Wellbeing Toronto may well support decision-making in neighborhoods and community participation for injury analysis and integration without the need to incur into demanding spatial analytics from a statistical standpoint. Of particular interest was the error model, which held a performance of
, performing slightly better than the OLS and Lag models. Data in the Wellbeing Toronto portal had a remarkable explanatory value (
Table 4).
The spatial regression outperformed the ordinary least squares, albeit with unsubstantial improvement. It became evident that several important strategic conclusions may be drawn based on the modeled relations of spatial attributes throughout COVID-19 cases. The spatial relations are intrinsic to the adequate spatial interpretation of localized COVID-19 data. Indeed, there should be different policies and preparedness integration within the city’s public health decisions. The models can in all cases be explained by the following:
- (1)
Vulnerable demographics: Three key groups were identified with regard to vulnerability to COVID-19: Young families with children, those with low income, and social assistance recipients.
- (2)
Social injustice: Low-income families and areas of higher crime that host social housing were of particular concern for COVID-19 transmission.
- (3)
Population density: Neighborhoods with high population density and a significant urban footprint, likely brought from high-rises, show a paramount relation to COVID-19.
Within the increasingly complex demographic and socio-economic interactions of growing urban metropolises, adequate spatial planning has become a vital instrument to support public policy through the consideration of geographically explicit mechanisms that respond to epidemiological concerns. Linking spatial planning with governance and public policy has resulted in significant advances in public health, transportation, commercial activity, and the livability of cities. Most of these vectors of optimization will profoundly impact the cities of the future, particularly with regard to the somewhat heterogeneous profiles at the spatial level regarding wealth, environmental justice, and deprivation in large North American cities such as Toronto. The combination socio-economic analysis and territorial knowledge furthers a clear understanding of the impacts of COVID-19. It has become evident through the establishment of geographically weighted topologies that:
- (1)
There is clear dimension of space that has to be considered within cities.
- (2)
These spatial dimensions may have public policy interactions through the demands of neighborhoods.
- (3)
The neighborhood-scale is an essential aspect for consideration in public policy instruments.
This article’s centerpiece has focused on deprived individuals within the city of Toronto who have a higher likelihood of contracting COVID-19. Indeed, it is the public awareness of these neighborhoods and the overarching understanding of spatial equity that need to be addressed in the larger framework of COVID-19 policy. Open data and the incremental potential of smart cities that pave the way to entail future spatial structures efficiently will become paramount tools for a more robust vision to avoid and mitigate the risk of pandemics in future [
33].
5. Conclusions
Recent advances in geocomputational methods, as well as spatial analysis, have resulted in new techniques that better enable the understanding of spatial characteristics of cities and regions [
34]. It is of utmost importance to understand regional patterns of epidemiological concern in order to better optimize public health efficiency in rapidly changing regions [
35] (Vaz, 2020). In this sense, geocomputational methods, when combined with extensive spatially explicit data, allow for significant contributions towards the regional understanding of epidemiological dynamics. Supported by data availability, open data at the city level may have a profound impact on the assessment and resulting community and policy intervention strategies for neighborhoods. The application of geocomputational techniques to COVID-19 at the local level has allowed us to perceive the pattern of the spread of cases and define that trends are not spatially random but very spatially dependent, with particular demographics.
The unprecedented consequences of COVID-19 with respect to the livability and the projection of future sustainability of cities are of concern. Never in recent history has humankind faced such a challenge, with global efforts being undertaken at an international scale. With these unprecedented changes, it is expected that the status quo of the current socio-economic model will drastically change, particularly in cities that have witnessed unprecedented economic growth in the last decade. It is these cities with the most significant growth that are remarkably less prepared to deal with the spread of COVID-19.
The pluralistic nature of driving forces for cases also depends mostly on governance and how policymakers reconsider the distribution of wealth, livability, and social injustice. Indeed, cities must reinvent their positions as economic drivers and economic hubs of the 21st century. This is evident in cities such as Toronto, where health determinants such as income and social status, education, employment or working conditions, social and physical environments, and personal health practices play an intrinsic role in mitigation and response to future pandemics.
This study is the first of its kind to study to demonstrate that the spatial distributions of residence locations are similar regardless of the mechanism of spread at the local level of COVID-19. This finding was consistently seen in the choice of selected variables, despite marked differences in size, economy, and cultural composition. Finally, the most resounding conclusion is that a tailor-made prevention strategy must be used for COVID-19, addressing local foci that respond to the specificities of neighborhoods and types of cases to guarantee a successful mechanism of spatial decision support and efficient prevention of spread at the local level.
While a lack of consensus on the role of spatial interpretation has paved the landscape for COVID-19 analytics, no consensus exists on interpreting spatial findings in assessing the outbreaks throughout cities. The complexity of COVID-19 has led to a substantial amount of speculation, where the notion of spatial decision systems has either had an absolutist, relational, or relativistic perspective. In terms of ontology, this is mostly a result of the different fields that have focused on understanding the epidemiological reasoning of this pandemic specifically. Indeed, it might be argued that neighborhood studies create a biased picture of COVID-19 outbreaks in absolutist terms.
This is indeed a shortcoming of pluralistic studies that assess geographical patterns over the place [
36]. However, coining the importance of creating an absolutist understanding of geographies enables the potential for community awareness and intervention, which are usually limited when concerning the highly confidential data of the individual patient and mobility studies. The concept of relational space hosts the specificities of place that best captures the essence of a vision that allows an assessment of cities and creates an integrative approach to planning communities through public policy participation and engagement.
In this sense, the analysis of COVID-19 becomes one of spatial community engagement in addition to considering interaction of public policy with spatial decision systems. These aspects lay the groundwork for sustainable solutions considering the spatial allocation of asymmetries through geographical space and the potential of harnessing the power of neighborhood decisions and information strategies.