Artificial Intelligence and Bio-Inspired Soft Computing-Based Maximum Power Plant Tracking for a Solar Photovoltaic System under Non-Uniform Solar Irradiance Shading Conditions—A Review
Abstract
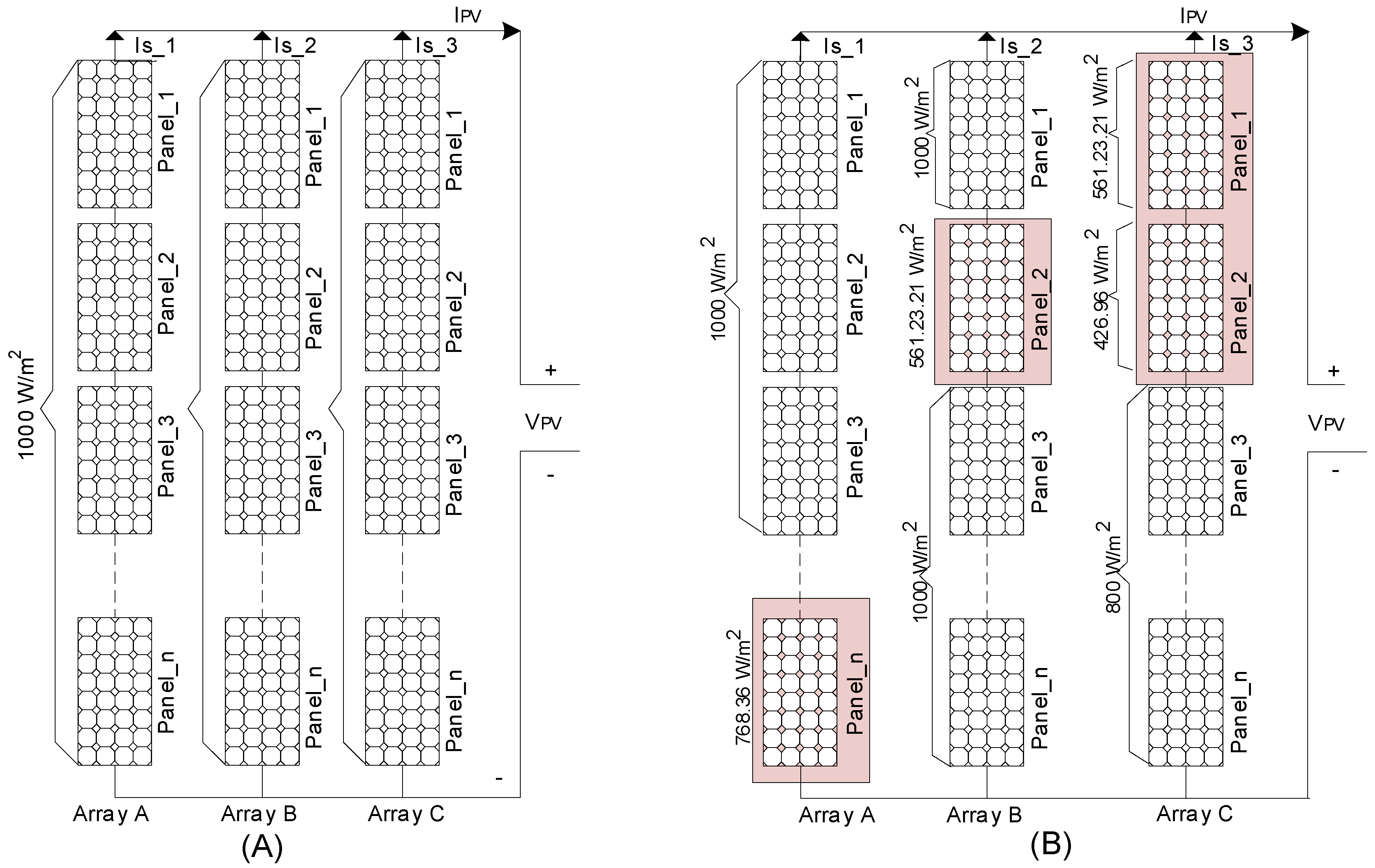
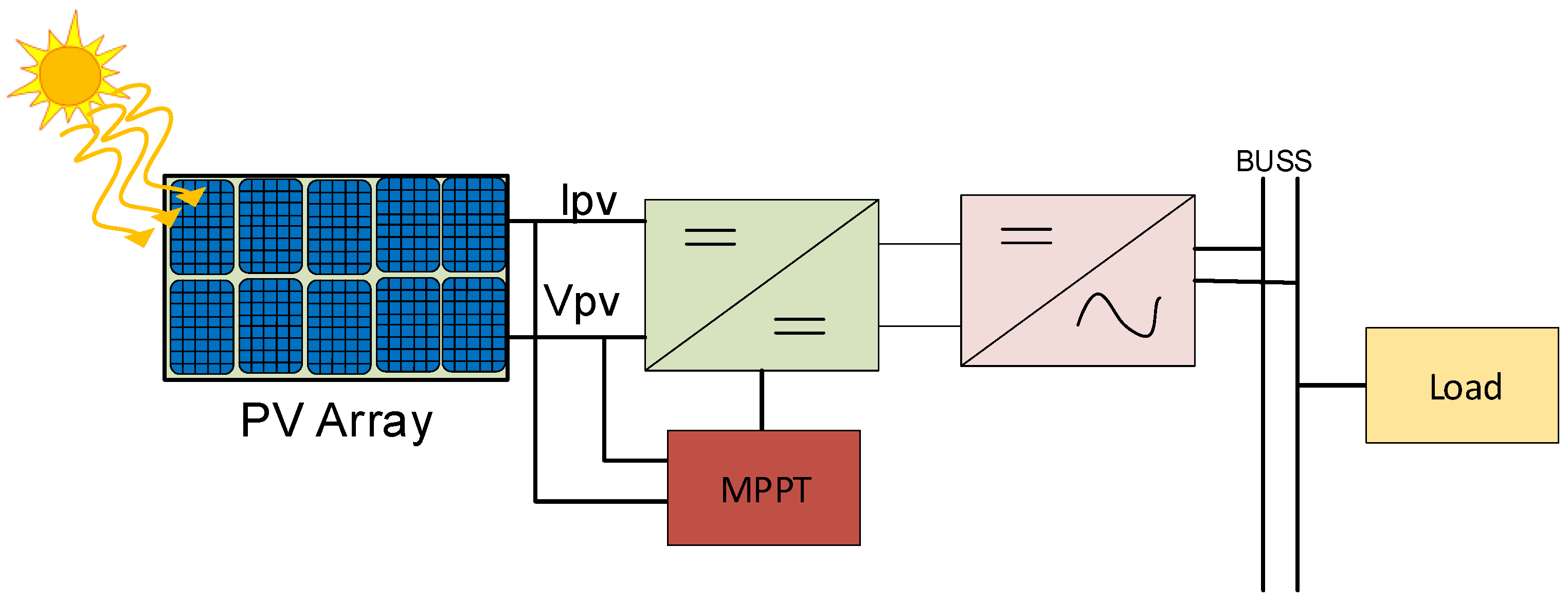
:1. Introduction
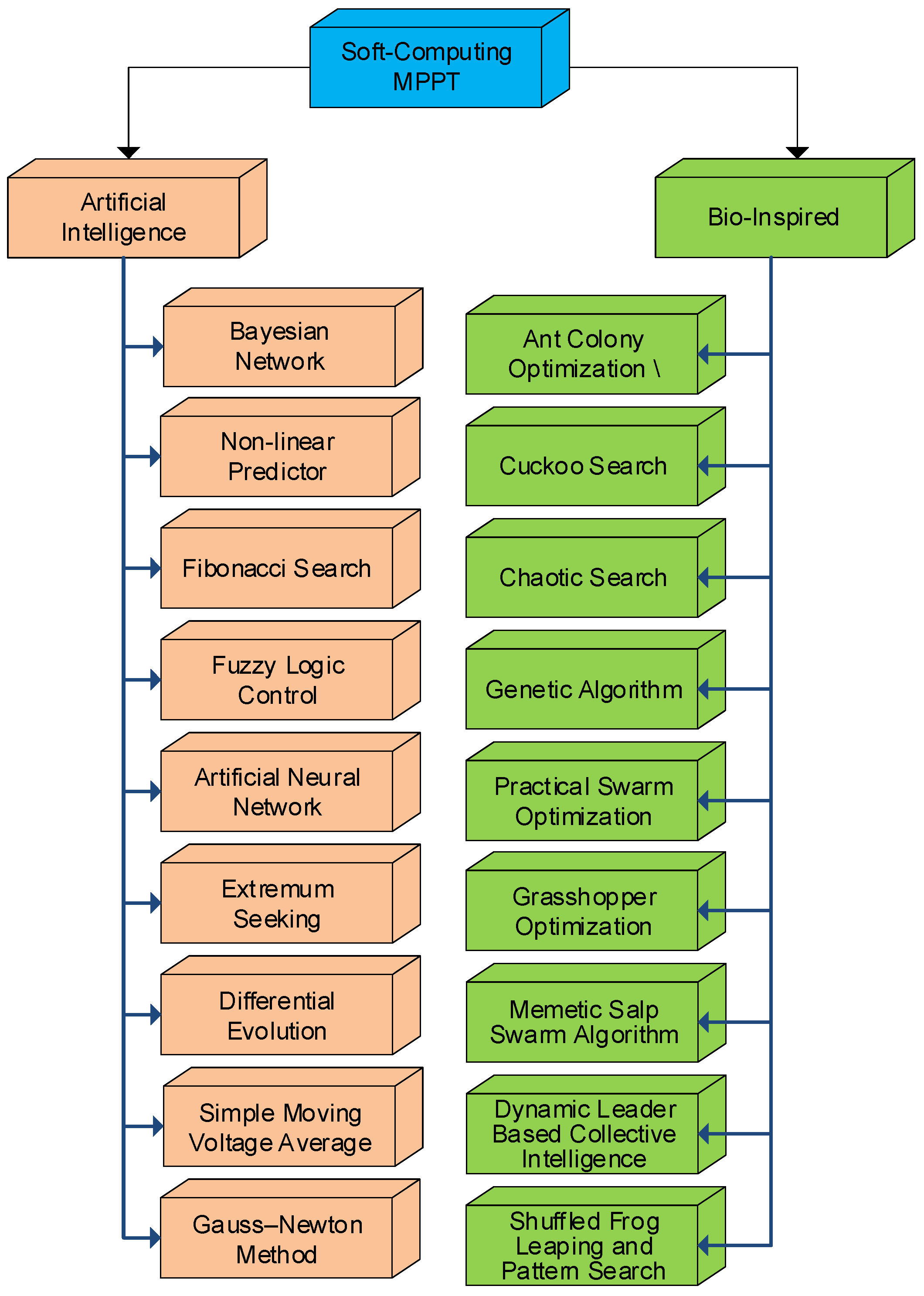
2. Soft Computing (SC)-Based MPP Tracking
2.1. Artificial Intelligence (AI)-Based SC-MPPT Methods
2.2. Bio-Inspired (BI)-Based SC-MPPT Methods
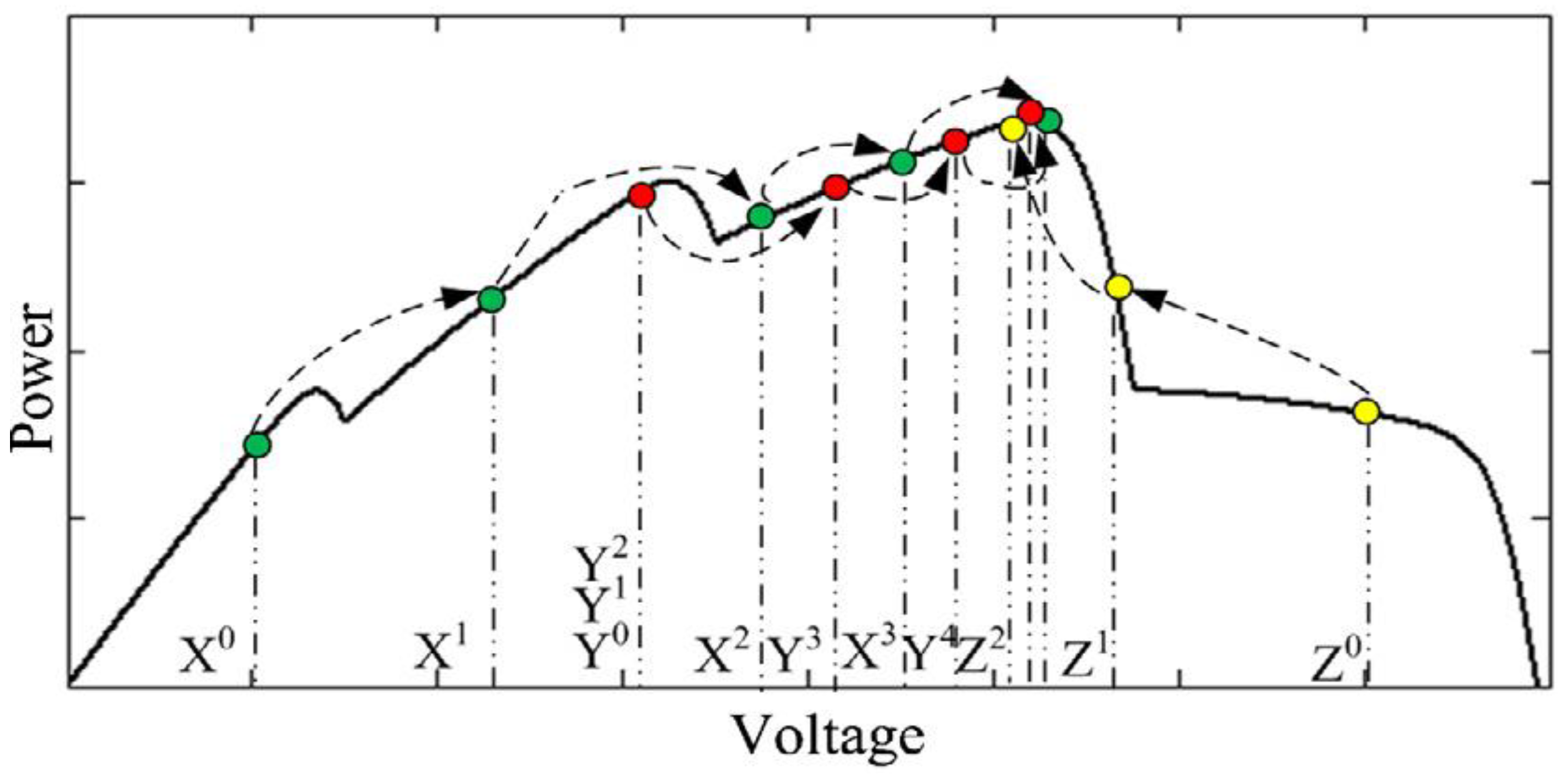
2.3. Generalized Processes of SCMPPT
2.3.1. Initialization
2.3.2. Reproduction
2.3.3. Selection
2.3.4. Stopping Criterion
- (a)
- Generation of a predefined number of iterations (). With this criterion, the algorithm is halted after reaching a certain number of iterations, which is defined at the onset of the SC algorithm.
- (b)
- Convergence of the population. This particular condition halts the algorithm when the value difference between the maximum and minimum values of the members of the generation is within a certain acceptable value.
- (c)
- Finest fitness threshold. When the value of (), also known as the objective function, becomes lower than the predefined value of (), this condition kicks in and stops the algorithm.
- (d)
- Fitness convergence. When the difference in the objective function () between the maximum and minimum becomes lower than a predefined recommended tolerance values for all members of the population.
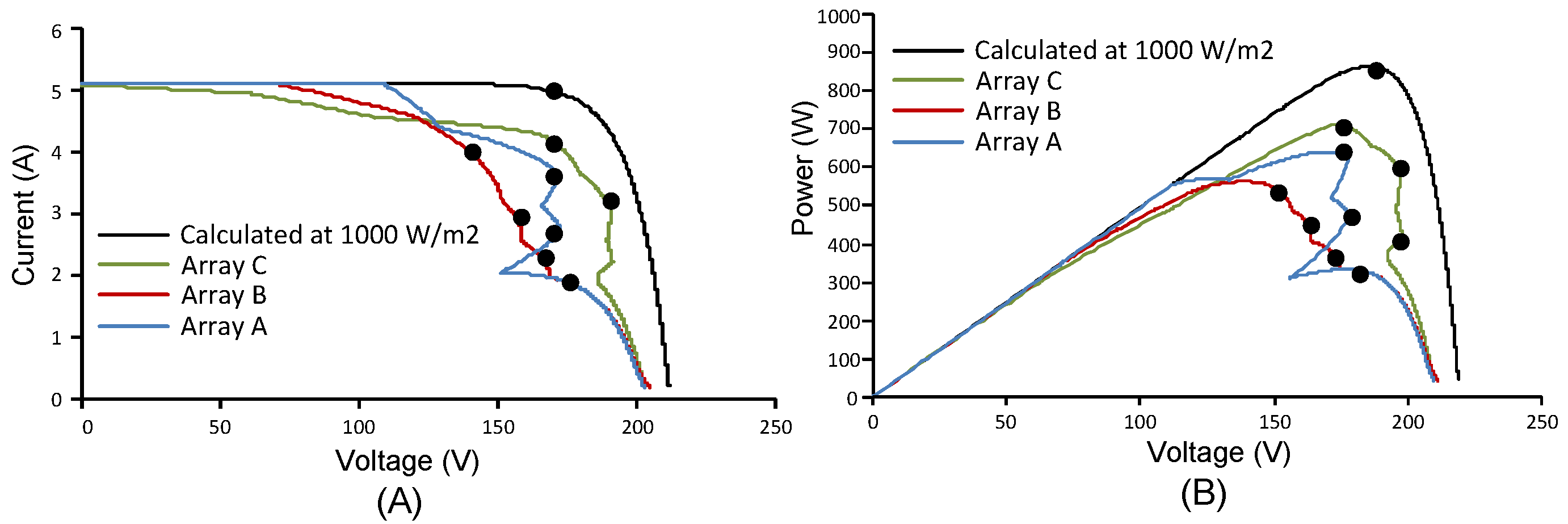
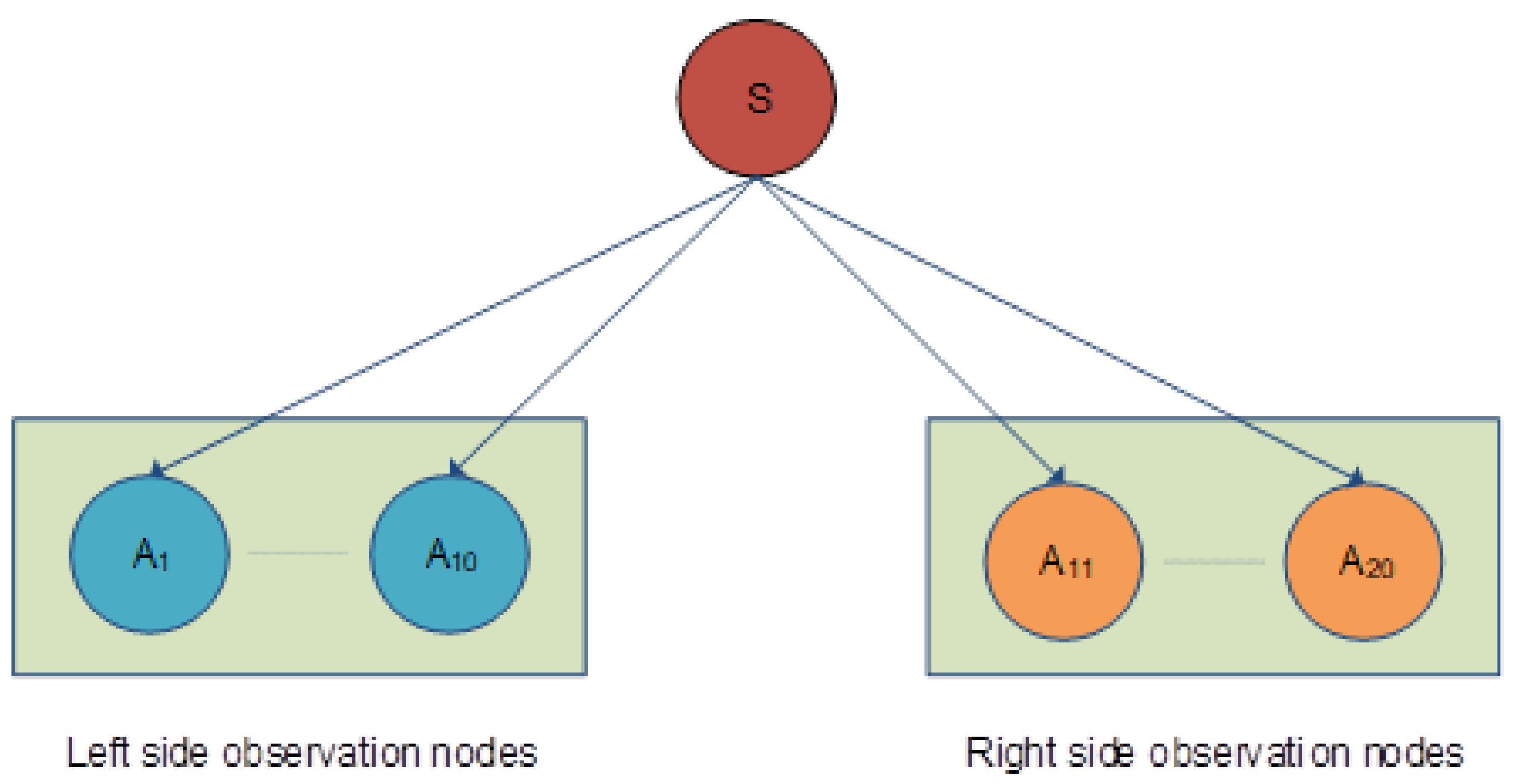
2.4. Bayesian Network Method (BN)
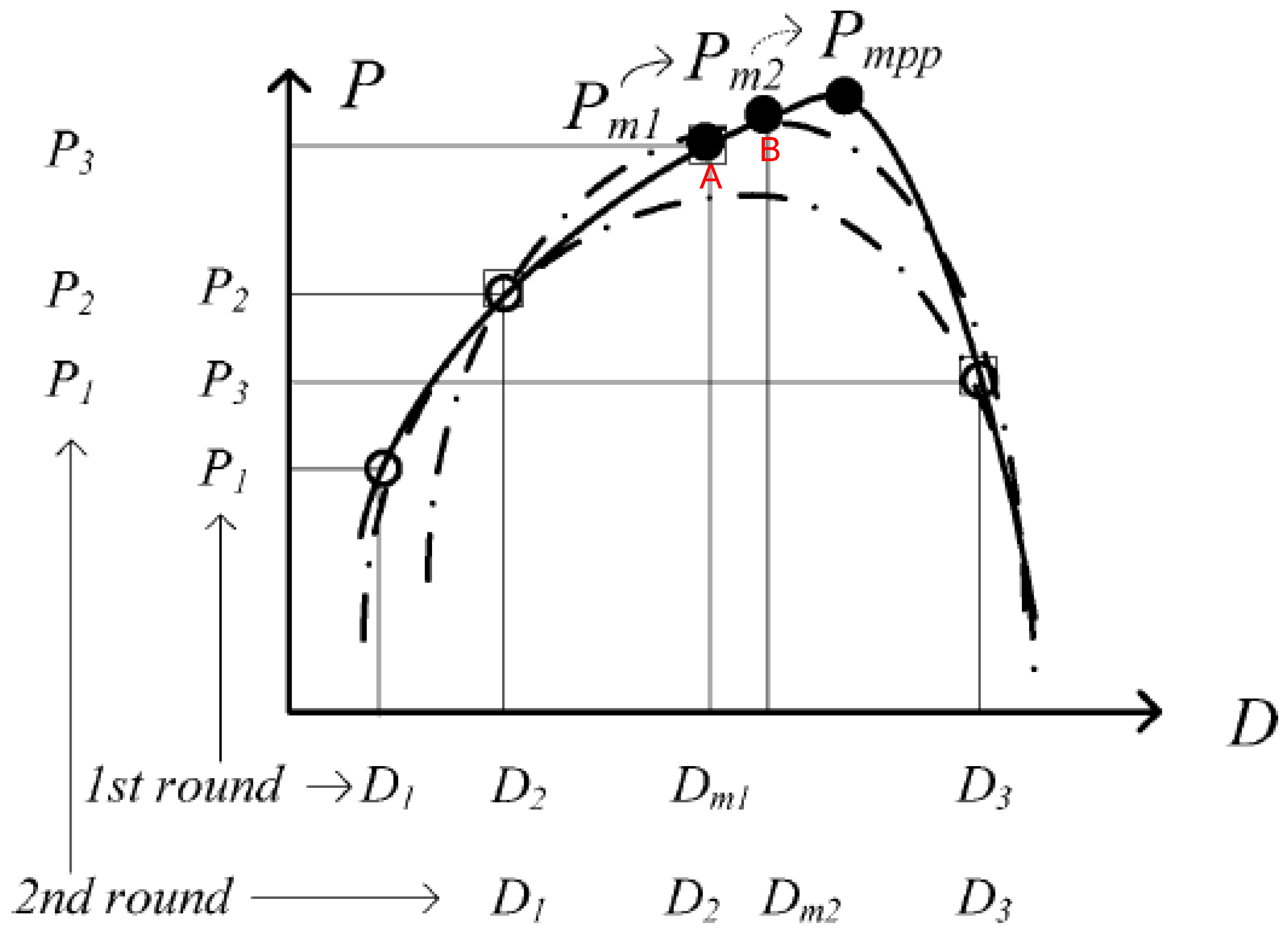
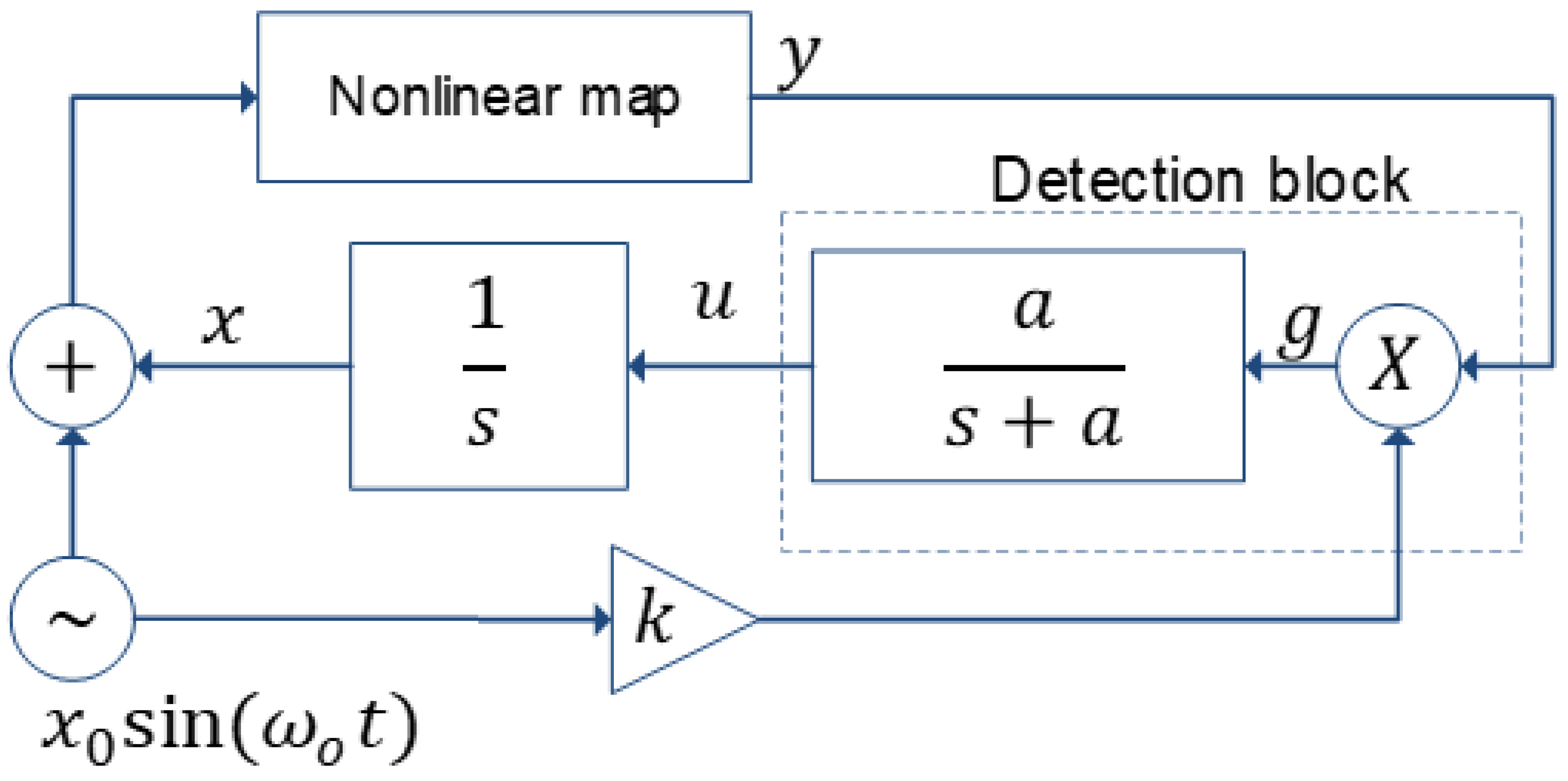
2.5. Non Linear Predictor Method (NLP)
2.6. Ant Colony Optimization Method (ACO)
2.7. Cuckoo Search Method (CS)
2.8. Fibonacci Search Method (FS)
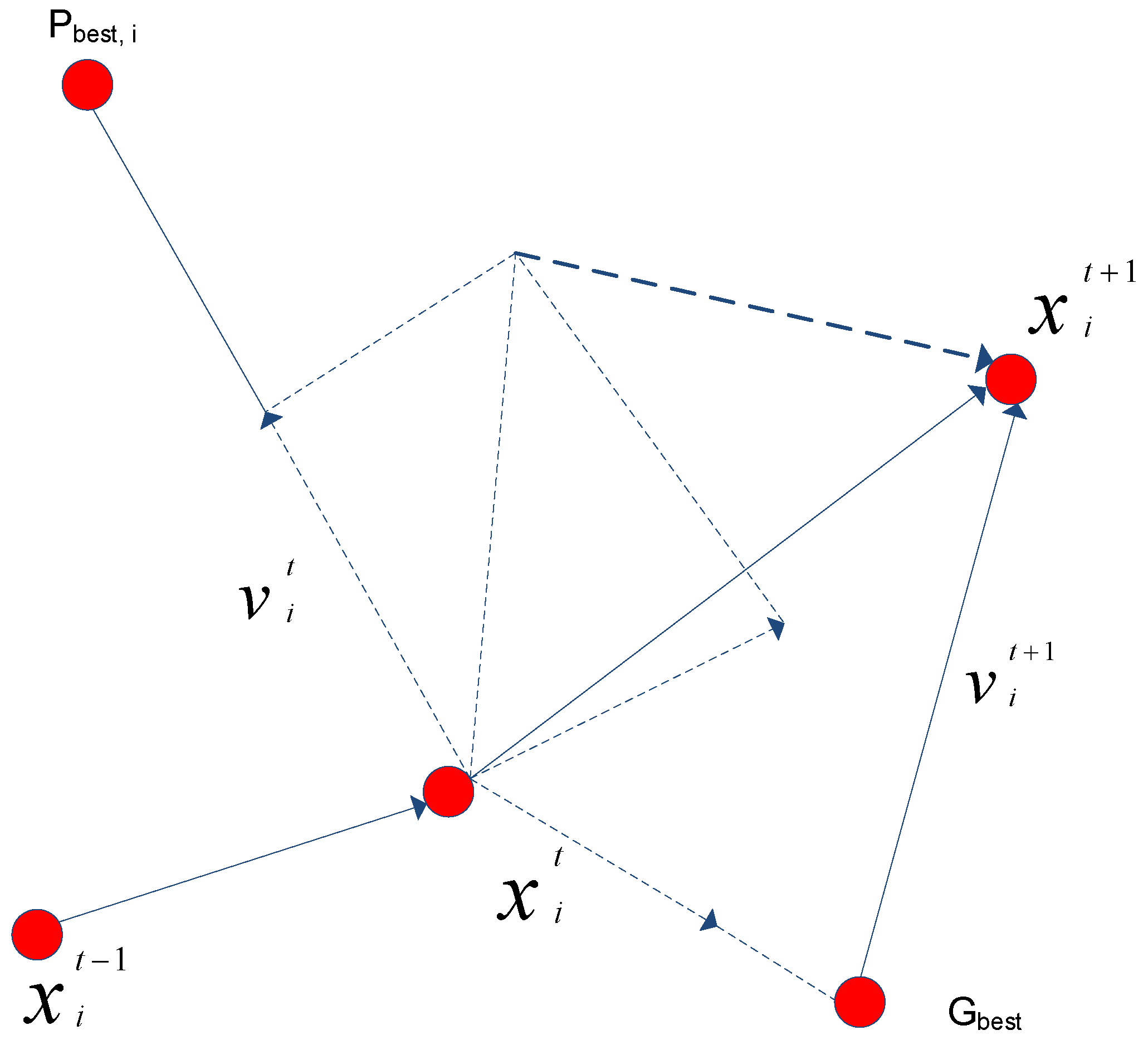
2.9. Particle Swarm Optimization Method (PSO)
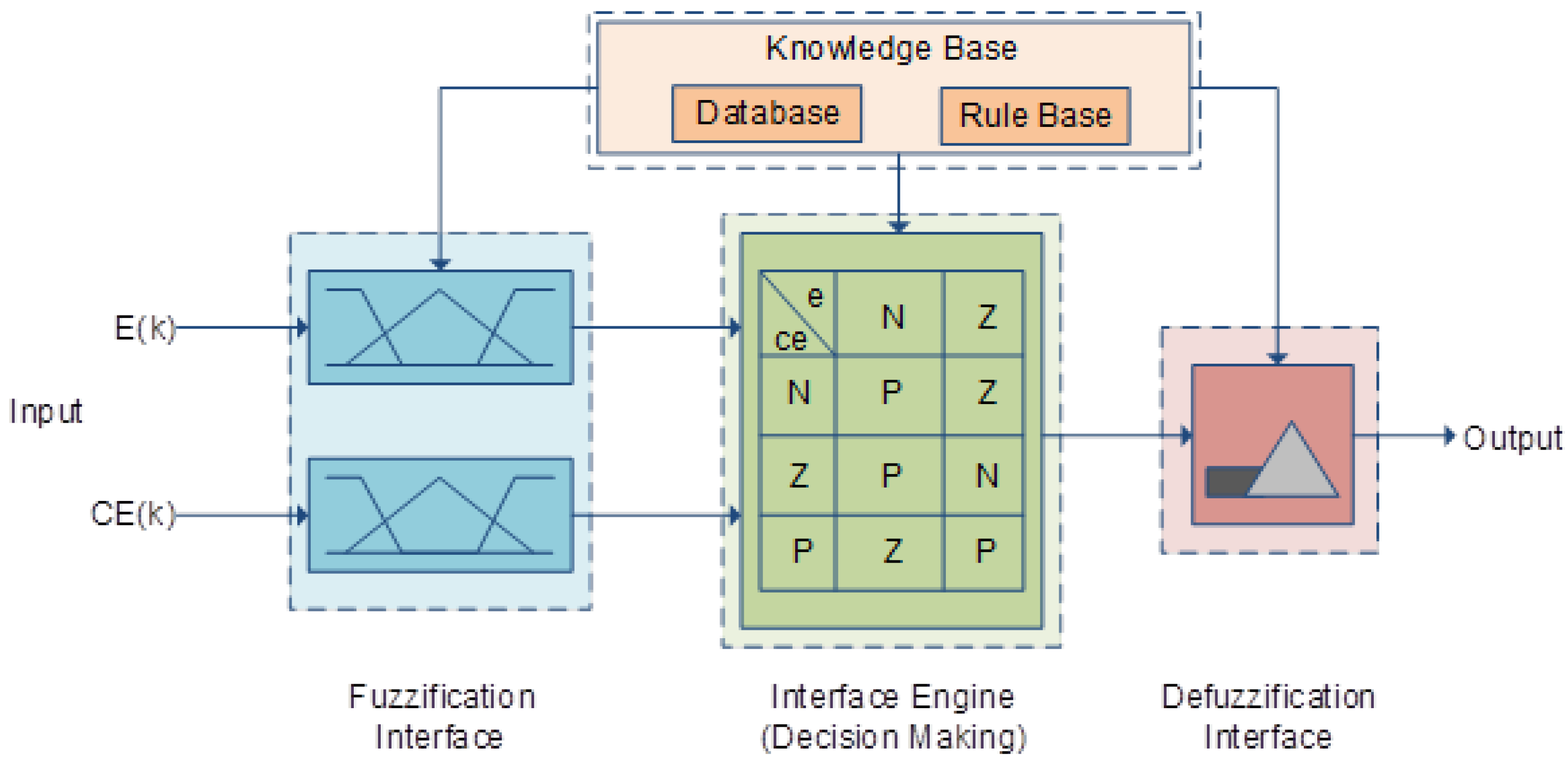
2.10. Fuzzy Logic Control Method (FLC)
- (a)
- The fuzzification block; this block converts the elements of the system from numerical values to binary values that are either 1 or 0.
- (b)
- The knowledge base block; the function of this block is to contain the controlling regulations and the data bank of the linguistic explanations set by the developer.
- (c)
- The inference engine block, which takes the fuzzified values from the fuzzification block and applies the regulations from the knowledge block to make decisions on what elements satisfy the regulations, which are passed to the next block.
- (d)
- The defuzzification block, which transfers the values that satisfied the inference engine from binary values into a defuzzified control action.
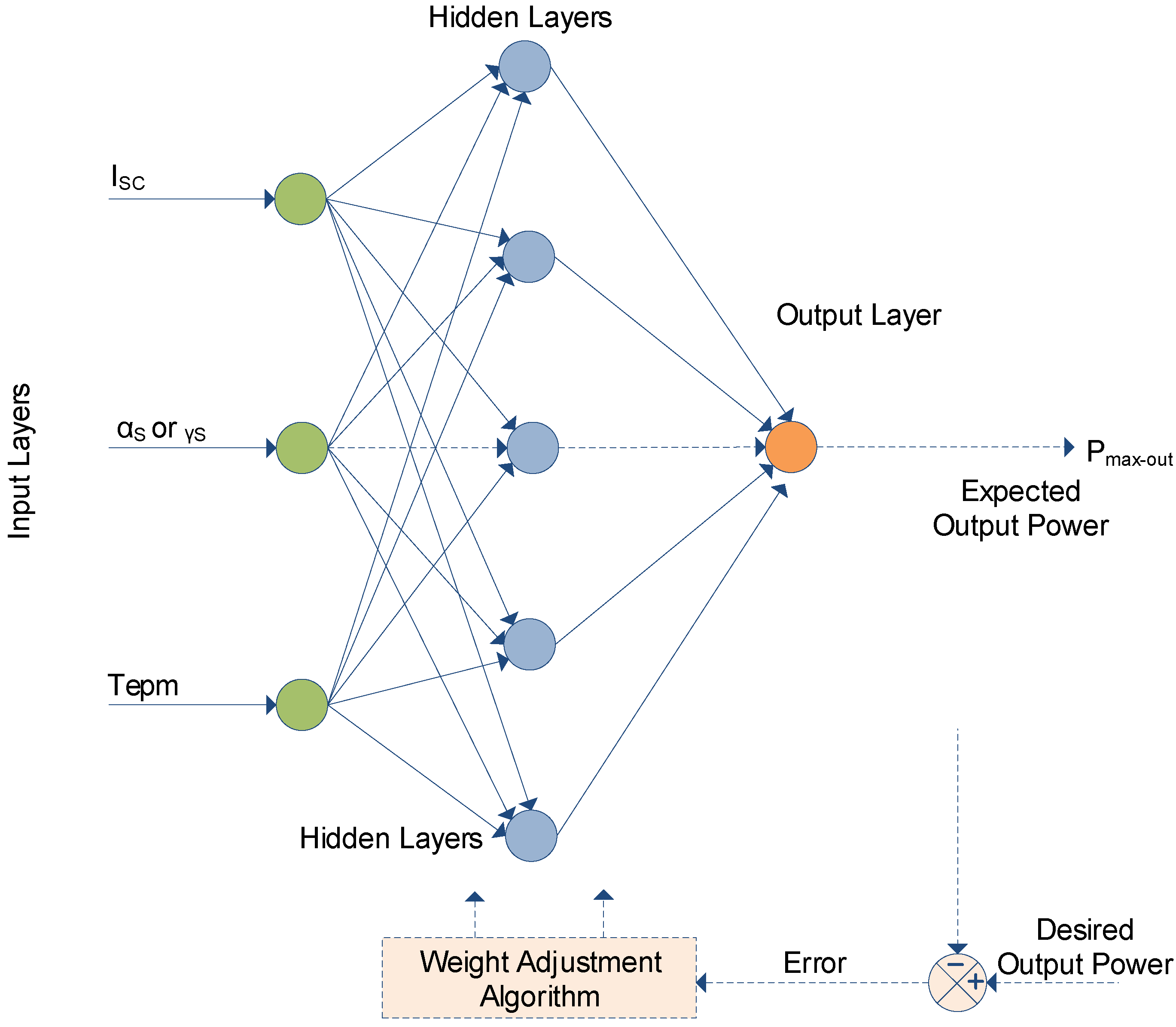
2.11. Artificial Neural Network Method (ANN)
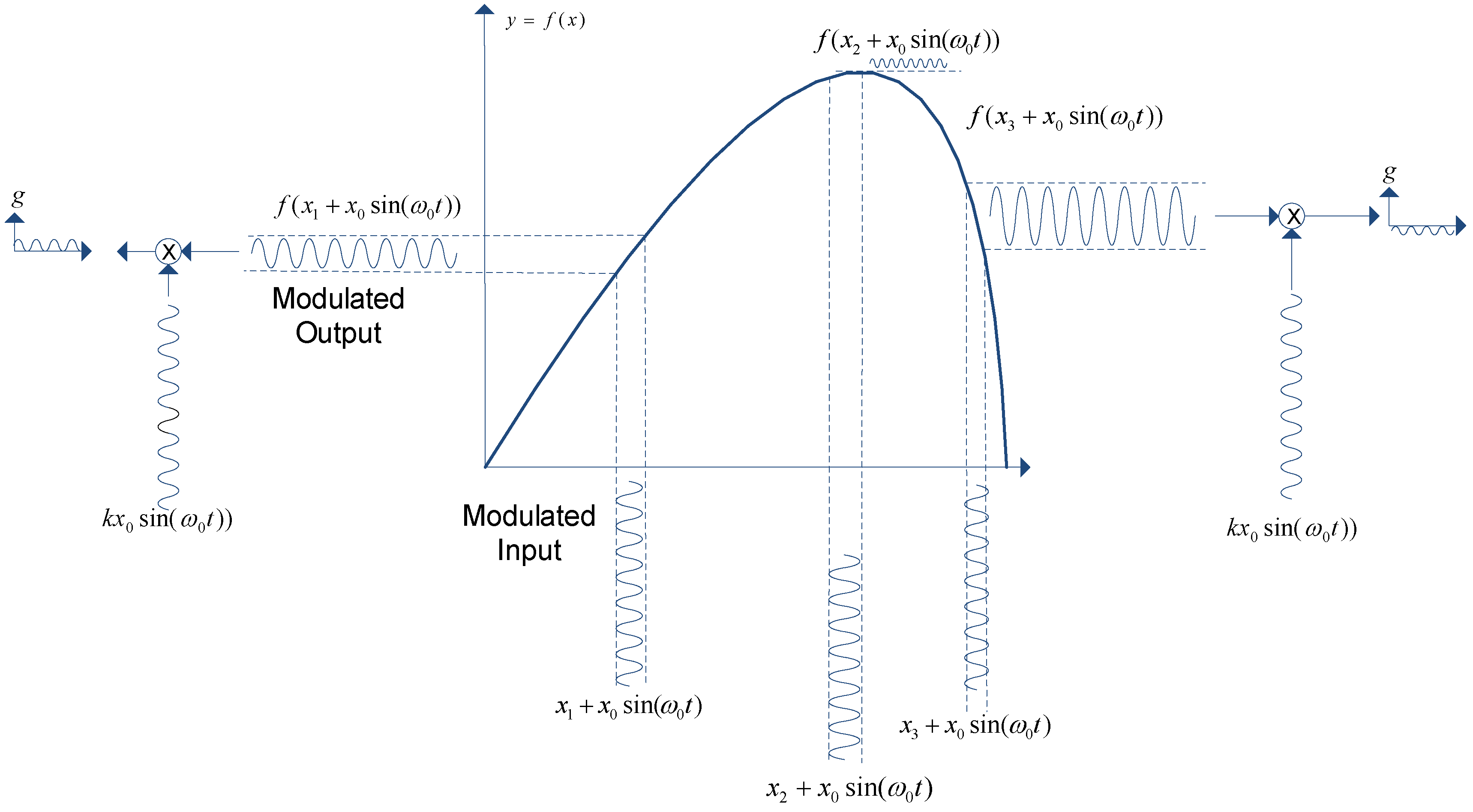
2.12. Extremum Seeking Method (ES)
2.13. Chaotic Search Method (CS)
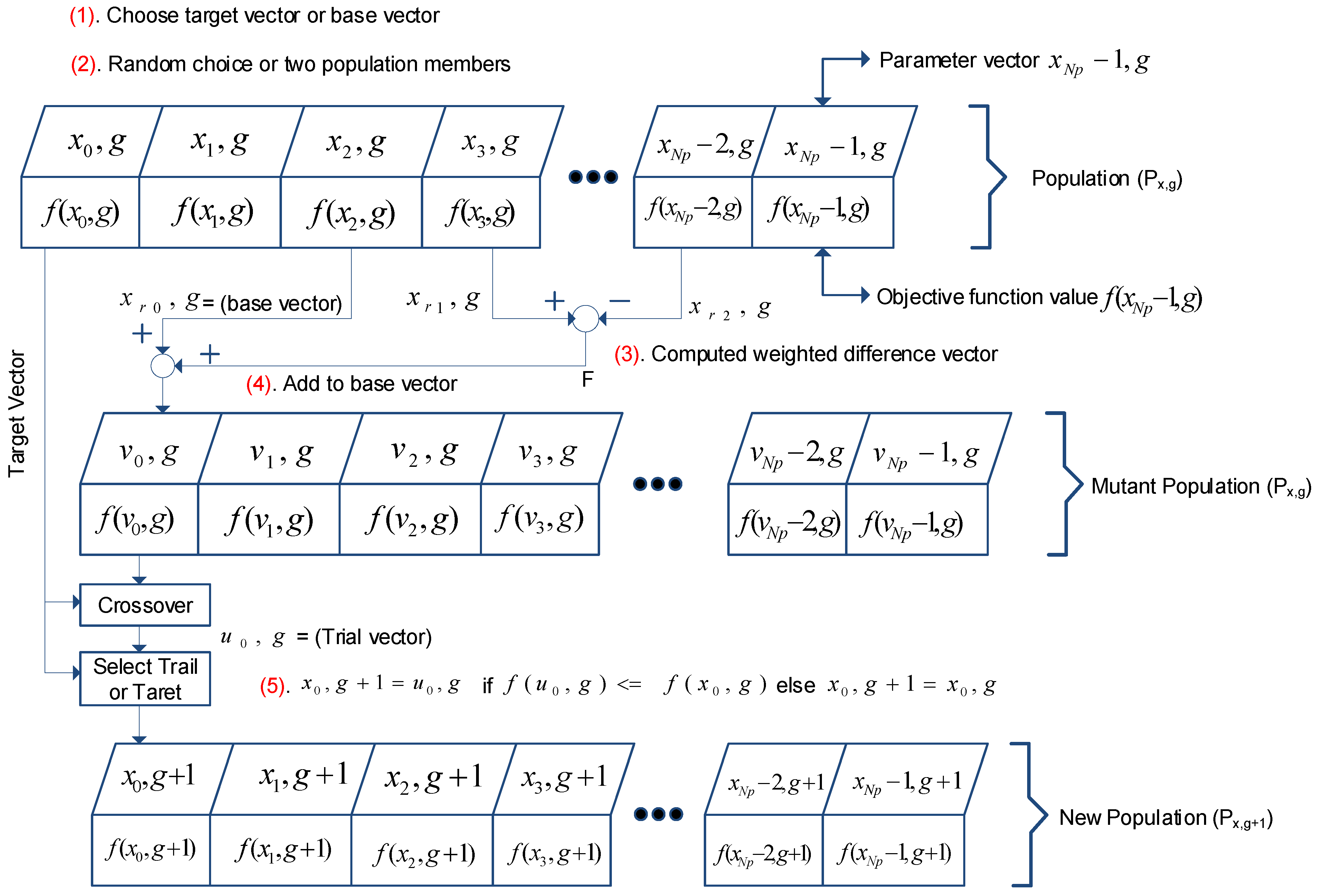
2.14. Differential Evolution Method (DE)
2.15. Genetic Algorithm Method (GA)
- (a)
- Selection, where genotypes are picked from the current population to be passed directly onto the next generation based on their fitness level to the PV equation.
- (b)
- Crossover, where new genotypes are produced by choosing some characteristics from the first and second generation and combining them.
- (c)
- Mutation, where new genes are produced to maintain chromosome diversity in produced generations to reach stochastic variability in the gene pool.
2.16. Simple Moving Voltage Average Method (SMVA)
2.17. Gauss–Newton Method (GN)
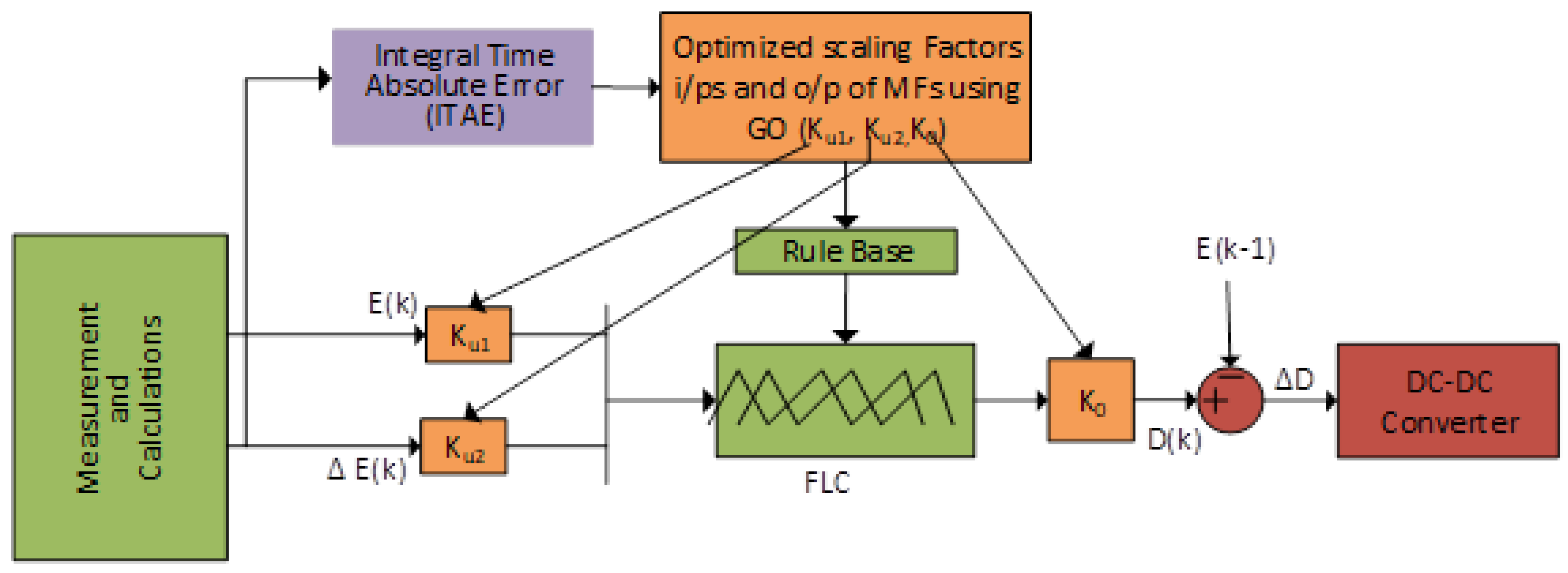
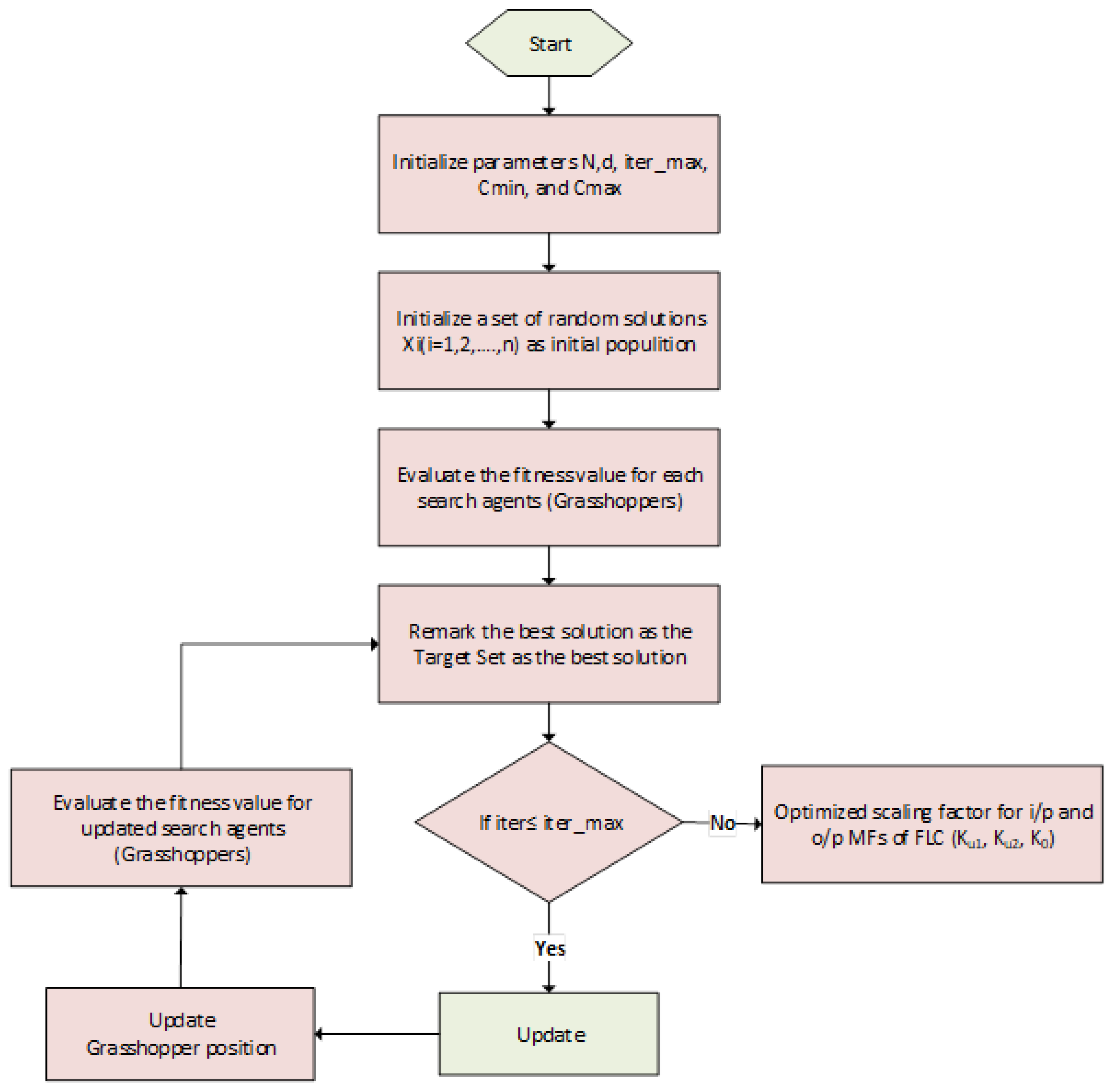
2.18. Grasshopper-Optimized Fuzzy Logic Method (GOFL)
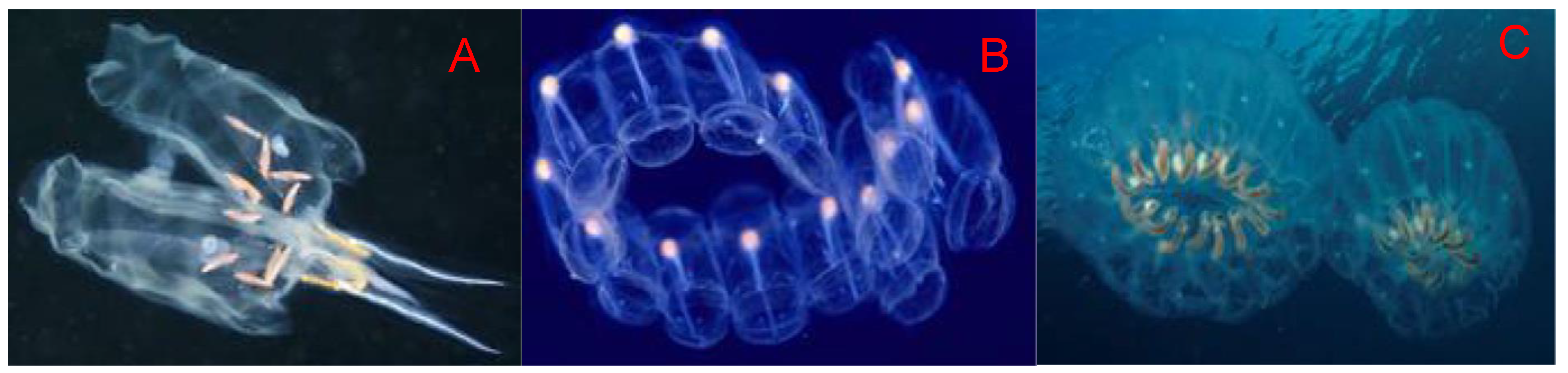
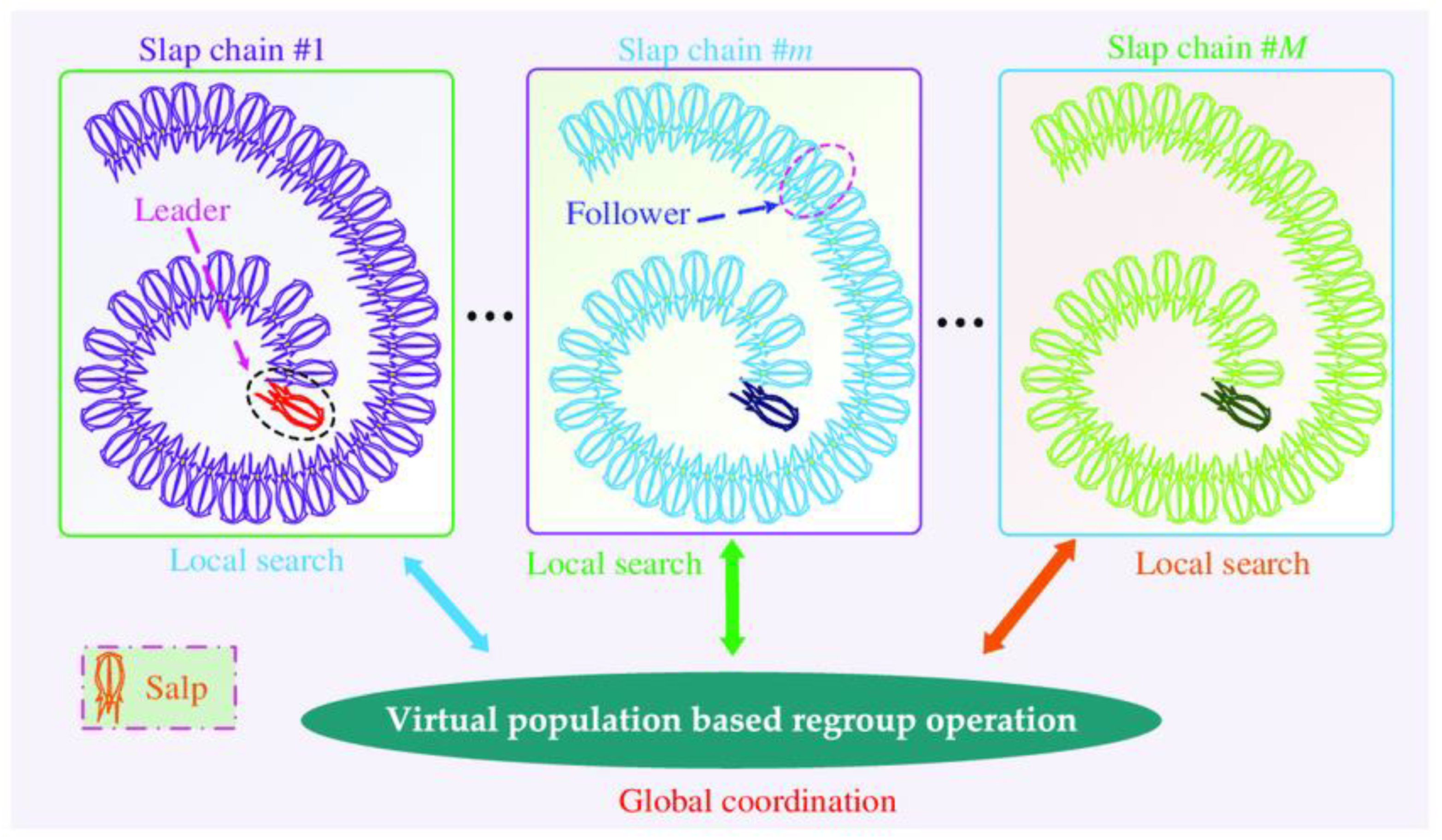
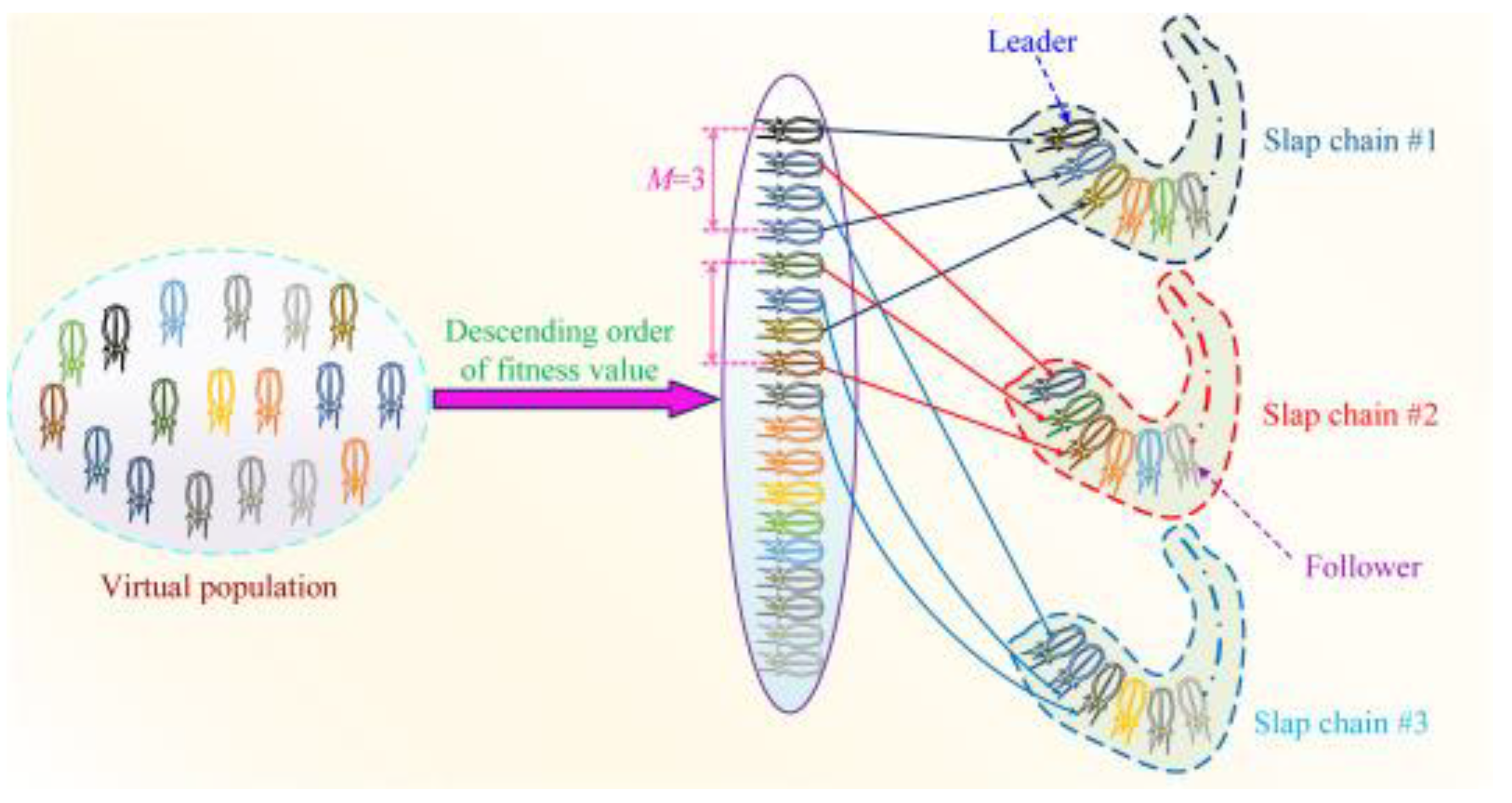
2.19. Memetic Salp Swarm Algorithm (MSSA)
2.20. Dynamic Leader-Based Collective Intelligence (DLCI)
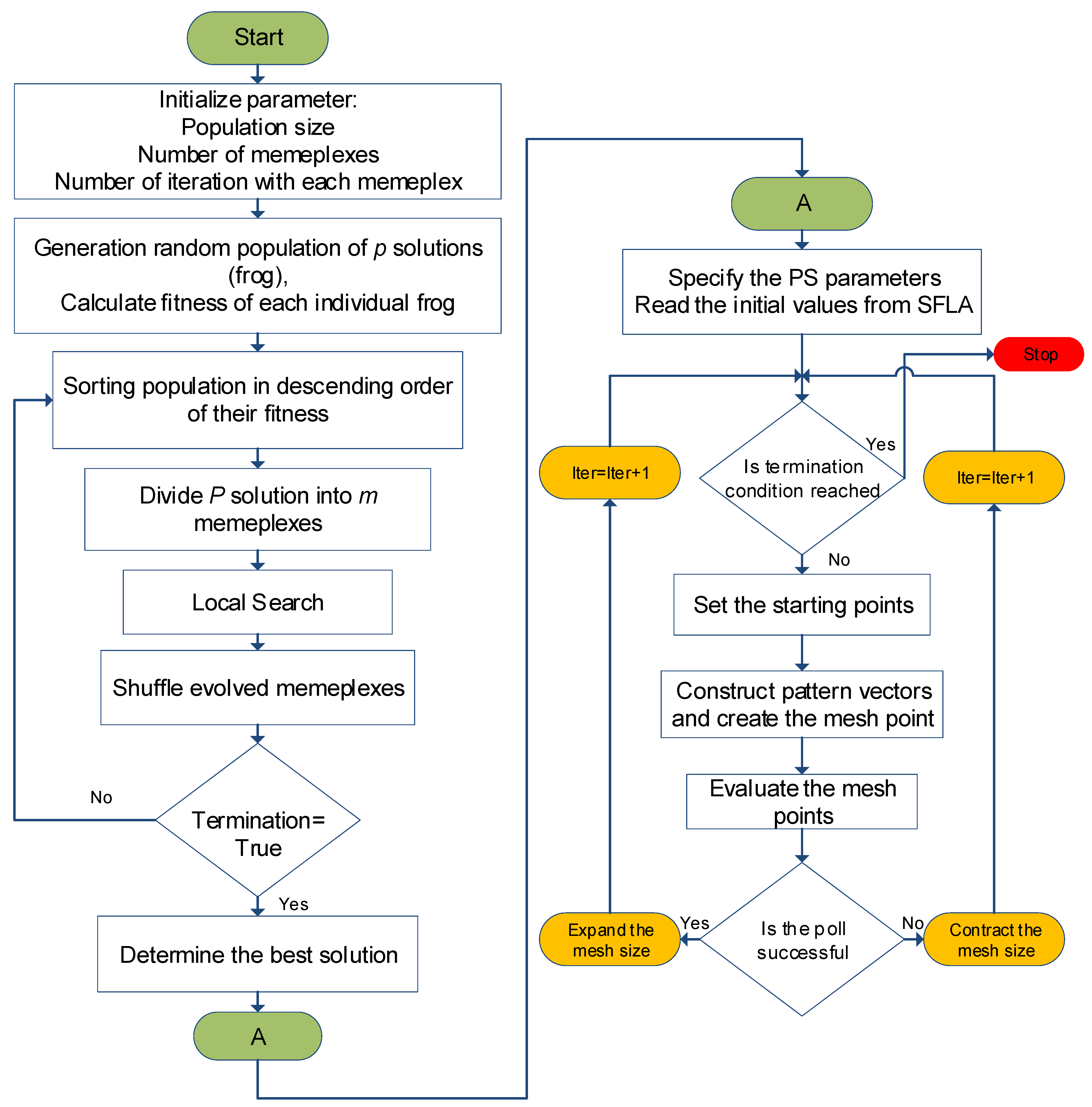
2.21. Shuffled Frog Leaping and Pattern Search (HSFL–PS)
Comparative Analysis
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ali, A.; Almutairi, K.; Padmanaban, S.; Tirth, V.; Algarni, S.; Irshad, K.; Islam, S.; Zahir, H.; Shafiullah; Malik, M.Z. Investigation of MPPT Techniques Under Uniform and Non-Uniform Solar Irradiation Condition–A Retrospection. IEEE Access 2020, 8, 127368–127392. [Google Scholar] [CrossRef]
- Ali, A.; Almutairi, K.; Malik, M.Z.; Irshad, K.; Tirth, V.; Algarni, S.; Zahir, H.; Islam, S.; Shafiullah; Shukla, N.K. Review of Online and Soft Computing Maximum Power Point Tracking Techniques under Non-Uniform Solar Irradiation Conditions. Energies 2020, 13, 3256. [Google Scholar] [CrossRef]
- Marañón-Ledesma, H.; Tomasgard, A. Analyzing Demand Response in a Dynamic Capacity Expansion Model for the European Power Market. Energies 2019, 12, 2976. [Google Scholar] [CrossRef] [Green Version]
- Verma, D.; Nema, S.; Shandilya, A.; Dash, S.K. Maximum power point tracking (MPPT) techniques: Recapitulation in solar photovoltaic systems. Renew. Sustain. Energy Rev. 2016, 54, 1018–1034. [Google Scholar] [CrossRef]
- Tantiwechwuttikul, R.; Yarime, M.; Ito, K. Solar Photovoltaic Market Adoption: Dilemma of Technological Exploitation vs Technological Exploration. In BT-Technologies and Eco-Innovation Towards Sustainability II: Eco Design Assessment and Management; Hu, A.H., Matsumoto, M., Kuo, C.T., Smith, S., Eds.; Springer: Singapore, 2019; pp. 215–227. [Google Scholar]
- Ustun, T.S.; Ozansoy, C.; Zayegh, A. Recent developments in microgrids and example cases around the world—A review. Renew. Sustain. Energy Rev. 2011, 15, 4030–4041. [Google Scholar] [CrossRef]
- Romankiewicz, J.; Marnay, C.; Zhou, N.; Qu, M. Lessons from international experience for China’s microgrid demon-stration program. Energy Policy 2014, 67, 198–208. [Google Scholar] [CrossRef]
- Bódis, K.; Kougias, I.; Taylor, N.; Jäger-Waldau, A. Solar Photovoltaic Electricity Generation: A Lifeline for the European Coal Regions in Transition. Sustainability 2019, 11, 3703. [Google Scholar] [CrossRef] [Green Version]
- Amjad, A.; Wuhua, L.; Xiangning, H. Simple Moving Voltage Average Incremental Conductance MPPT Technique with Direct Control Method under Nonuniform Solar Irradiance Conditions. Int. J. Photoenergy 2015, 2015, 479178. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M.Z.; Rahim, N.A.; Selvaraj, J.A. Recent progress and development on power DC-DC converter topology, control, design and applications: A review. Renew. Sustain. Energy Rev. 2018, 81, 205–230. [Google Scholar] [CrossRef]
- Reisi, A.R.; Moradi, M.H.; Jamasb, S. Classification and comparison of maximum power point tracking tech-niques for photovoltaic system: A review. Renew. Sustain. Energy Rev. 2013, 19, 433–443. [Google Scholar] [CrossRef]
- Subudhi, B.; Pradhan, R. A Comparative Study on Maximum Power Point Tracking Techniques for Photovoltaic Power Systems. IEEE Trans. Sustain. Energy 2012, 4, 89–98. [Google Scholar] [CrossRef]
- Andrean, V.; Chang, C.P.; Lian, L.K. A Review and New Problems Discovery of Four Simple Decentralized Maximum Power Point Tracking Algorithms—Perturb and Observe, Incremental Conductance, Golden Section Search, and Newton’s Quadratic Interpolation. Energies 2018, 11, 2966. [Google Scholar] [CrossRef] [Green Version]
- Koutroulis, F.B.E. Overview of Maximum Power Point Tracking Techniques for Photovoltaic Energy Production Systems. Electr. Power Components Syst. 2015, 43, 1329–1351. [Google Scholar] [CrossRef]
- Ahmad, R.; Murtaza, A.F.; Sher, H. Power tracking techniques for efficient operation of photovoltaic array in solar applications –A review. Renew. Sustain. Energy Rev. 2018, 101, 82–102. [Google Scholar] [CrossRef]
- Belhachat, F.; Larbes, C. Comprehensive review on global maximum power point tracking techniques for PV systems subjected to partial shading conditions. Sol. Energy 2019, 183, 476–500. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z. A review of maximum power point tracking techniques of PV system for uniform insolation and partial shading condition. Renew. Sustain. Energy Rev. 2013, 19, 475–488. [Google Scholar] [CrossRef]
- Bastidas-Rodriguez, J.D.; Franco, E.; Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G. Maximum power point tracking architectures for photovoltaic systems in mismatching conditions: A review. IET Power Electron. 2014, 7, 1396–1413. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Chen, J.-H.; Huang, J.-W. A review of maximum power point tracking techniques for use in partially shaded conditions. Renew. Sustain. Energy Rev. 2015, 41, 436–453. [Google Scholar] [CrossRef]
- Salam, Z.; Ahmed, J.; Merugu, B.S. The application of soft computing methods for MPPT of PV system: A technological and status review. Appl. Energy 2013, 107, 135–148. [Google Scholar] [CrossRef]
- Liu, L.; Meng, X.; Liu, C. A review of maximum power point tracking methods of PV power system at uniform and partial shading. Renew. Sustain. Energy Rev. 2016, 53, 1500–1507. [Google Scholar] [CrossRef]
- Ramli, M.A.; Twaha, S.; Ishaque, K.; Al-Turki, Y.A. A review on maximum power point tracking for photovoltaic systems with and without shading conditions. Renew. Sustain. Energy Rev. 2017, 67, 144–159. [Google Scholar] [CrossRef]
- Li, G.; Jin, Y.; Akram, M.W.; Chen, X.; Ji, J. Application of bio-inspired algorithms in maximum power point tracking for PV systems under partial shading conditions–A review. Renew. Sustain. Energy Rev. 2018, 81, 840–873. [Google Scholar] [CrossRef]
- Jiang, L.L.; Srivatsan, R.; Maskell, D.L. Computational intelligence techniques for maximum power point tracking in PV systems: A review. Renew. Sustain. Energy Rev. 2018, 85, 14–45. [Google Scholar] [CrossRef]
- Hussan, R.; Sarwar, A. Maximum Power Point Tracking Techniques under Partial Shading Condition-A Review. In Proceedings of the 2018 2nd IEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 22–24 October 2018; pp. 293–298. [Google Scholar] [CrossRef]
- Dash, S.K.; Nema, S.; Nema, R.K.; Verma, D. A comprehensive assessment of maximum power point tracking techniques under uniform and non-uniform irradiance and its impact on photovoltaic systems: A review. J. Renew. Sustain. Energy 2015, 7, 063113. [Google Scholar] [CrossRef]
- Kumar, B.; Jha, S.K.; Kumar, T. Review of maximum power point tracking techniques for photovoltaic arrays working under uniform/non-uniform insolation level. Int. J. Renew. Energy Technol. 2018, 9, 439–452. [Google Scholar] [CrossRef]
- Syafaruddin, S. Review of Maximum Power Point Tracking Control of Photovoltaic Systems in Case of Uniform & Non-uniform Irradiance Conditions. In Proceedings of the Proceeding International Conference on Science and Engineering, Yogyakarta, Indonesia, 12 September 2017; Volume 1, p. xv. [Google Scholar] [CrossRef]
- Keyrouz, F.; Hamad, M.; Georges, S. Bayesian fusion for maximum power output in hybrid wind-solar systems. In Proceedings of the 2012 3rd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aalborg, Denmark, 25–28 June 2012; pp. 393–397. [Google Scholar]
- Priyanka, G.; Dash, S.K. A Detailed Review on Intelligent Maximum Power Point Tracking Algorithms. In Proceedings of the 2020 2nd International Conference on Innovative Mechanisms for Industry Applications (ICIMIA), Bangalore, India, 5–7 March 2020; pp. 47–53. [Google Scholar]
- Gauvain, J.-L.; Lee, C.-H. Maximum a posteriori estimation for multivariate Gaussian mixture observations of Markov chains. IEEE Trans. Speech Audio Process. 1994, 2, 291–298. [Google Scholar] [CrossRef]
- Specht, D.F. Probabilistic neural networks. Neural Netw. 1990, 3, 109–118. [Google Scholar] [CrossRef]
- Keyrouz, F.; Georges, S. Efficient multidimensional Maximum Power Point Tracking using Bayesian fusion. In Proceedings of the 2011 2nd International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 15–17 November 2011; pp. 1–5. [Google Scholar]
- Ali, H.G.; Arbos, R.V.; Herrera, J.; Tobón, A.; Peláez-Restrepo, J. Non-Linear Sliding Mode Controller for Photovoltaic Panels with Maximum Power Point Tracking. Processes 2020, 8, 108. [Google Scholar] [CrossRef] [Green Version]
- Pai, F.-S.; Chao, R.-M.; Ko, S.H.; Lee, T.-S. Performance Evaluation of Parabolic Prediction to Maximum Power Point Tracking for PV Array. IEEE Trans. Sustain. Energy 2010, 2, 60–68. [Google Scholar] [CrossRef]
- Pai, F.-S.; Chao, R.-M. A New Algorithm to Photovoltaic Power Point Tracking Problems with Quadratic Maximization. IEEE Trans. Energy Convers. 2009, 25, 262–264. [Google Scholar] [CrossRef]
- Jiang, L.L.; Maskell, D.L.; Patra, J. A novel ant colony optimization-based maximum power point tracking for photovoltaic systems under partially shaded conditions. Energy Build. 2013, 58, 227–236. [Google Scholar] [CrossRef]
- Sundareswaran, K.; Vigneshkumar, V.; Sankar, P.; Simon, S.P.; Nayak, P.S.R.; Palani, S. Development of an Improved P&O Algorithm Assisted Through a Colony of Foraging Ants for MPPT in PV System. IEEE Trans. Ind. Informatics 2015, 12, 187–200. [Google Scholar] [CrossRef]
- Nivetha, V.; Gowri, G.V. Maximum power point tracking of photovoltaic system using ant colony and particle swam optimization algorithms. In Proceedings of the 2nd International Conference on Electronics and Communication Systems (ICECS), Coimbatore, India, 26–27 February 2015; pp. 948–952. [Google Scholar] [CrossRef]
- Emerson, N.; Srinivasan, S. Integrating hybrid power source into islanded microgrid using ant colony optimization. In Proceedings of the International Conference on Advanced Computing and Communication Systems, Coimbatore, India, 5–7 January 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Jiang, L.L.; Maskell, D.L. A uniform implementation scheme for evolutionary optimization algorithms and the ex-perimental implementation of an ACO based MPPT for PV systems under partial shading. In Proceedings of the IEEE Symposium on Computational Intelligence Applications in Smart Grid (CIASG), Orlando, FL, USA, 9–12 December 2014; pp. 1–8. [Google Scholar]
- Besheer, A.H.; Adly, M. Ant colony system based PI maximum power point tracking for stand alone photovoltaic system. In Proceedings of the IEEE International Conference on Industrial Technology, Athens, Greece, 19–21 March 2012; pp. 693–698. [Google Scholar] [CrossRef]
- Adly, M.; Besheer, A.H. An optimized fuzzy maximum power point tracker for stand alone photovoltaic systems: Ant colony approach. In Proceedings of the 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012; pp. 113–119. [Google Scholar] [CrossRef]
- Krishnan, G.S.; Satheesh, G.; Kinattingal, S.S.; Simon, S.P.; Nayak, P.S.R. MPPT in PV systems using ant colony optimisation with dwindling population. IET Renew. Power Gener. 2020, 14, 1105–1112. [Google Scholar] [CrossRef]
- Nguyen, T.; Vo, D.N.; Truong, A.V. Cuckoo search algorithm for short-term hydrothermal scheduling. Appl. Energy 2014, 132, 276–287. [Google Scholar] [CrossRef]
- Basha, C.H.H.; Bansal, V.; Rani, C.; Brisilla, R.M.; Odofin, S. Development of Cuckoo Search MPPT Algorithm for Partially Shaded Solar PV SEPIC Converter BT-Soft Computing for Problem Solving. In Soft Computing for Problem Solving; Springer: Singapore, 2020; pp. 727–736. [Google Scholar]
- Yang, X.; Deb, S. Cuckoo Search via Lévy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Yang, X.-S.; Deb, S. Multiobjective cuckoo search for design optimization. Comput. Oper. Res. 2013, 40, 1616–1624. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A critical evaluation on maximum power point tracking methods for partial shading in PV systems. Renew. Sustain. Energy Rev. 2015, 47, 933–953. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
- Miyatake, M.; Inada, T.; Hiratsuka, I.; Zhao, H.; Otsuka, H.; Nakano, M. Control characteristics of a fibonac-ci-search-based maximum power point tracker when a photovoltaic array is partially shaded. In Proceedings of the 4th International Power Electronics and Motion Control Conference (IPEMC), Xi’an, China, 14–16 August 2004; pp. 816–821. [Google Scholar]
- Ramaprabha, R.; Mathur, B.; Ravi, A.; Aventhika, S. Modified Fibonacci Search Based MPPT Scheme for SPVA Under Partial Shaded Conditions. In Proceedings of the 2010 3rd International Conference on Emerging Trends in Engineering and Technology, Goa, India, 19–21 November 2010; pp. 379–384. [Google Scholar]
- Khan, S.U.; Yang, S.; Wang, L.; Liu, L. A Modified Particle Swarm Optimization Algorithm for Global Optimizations of Inverse Problems. IEEE Trans. Magn. 2015, 52, 1–4. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, S.; Huang, J.; Liang, W. A Particle Swarm Optimization-Based Maximum Power Point Tracking Algo-rithm for PV Systems Operating Under Partially Shaded Conditions. IEEE Trans. Energy Convers. 2012, 27, 1027–1035. [Google Scholar] [CrossRef]
- Takano, H.; Asano, H.; Gupta, N. Application Example of Particle Swarm Optimization on Operation Scheduling of Microgrids BT-Frontier Applications of Nature Inspired Computation. Khosravy, M., Gupta, N., Patel, N., Senjyu, T., Eds.; Springer: Singapore, 2020; pp. 215–239. [Google Scholar]
- Khare, A.; Rangnekar, S. A review of particle swarm optimization and its applications in Solar Photovoltaic system. Appl. Soft Comput. 2013, 13, 2997–3006. [Google Scholar] [CrossRef]
- Alajmi, B.N.F.M.T.; Ahmed, K.H.; Finney, S.J.; Williams, B.W. Fuzzy-Logic-Control Approach of a Modified Hill-Climbing Method for Maximum Power Point in Microgrid Standalone Photovoltaic System. IEEE Trans. Power Electron. 2010, 26, 1022–1030. [Google Scholar] [CrossRef]
- Patcharaprakiti, N.; Premrudeepreechacharn, S. Maximum power point tracking using adaptive fuzzy logic control for grid-connected photovoltaic system. Renew. Energy 2003, 30, 1771–1788. [Google Scholar] [CrossRef]
- Syafaruddin; Karatepe, E.; Hiyama, T. Artificial neural network-polar coordinated fuzzy controller based maximum power point tracking control under partially shaded conditions. IET Renew. Power Gener. 2009, 3, 239–253. [Google Scholar] [CrossRef]
- Algazar, M.M.; Al-Monier, H.; El-Halim, H.A.; Salem, M.E.E.K. Maximum power point tracking using fuzzy logic control. Int. J. Electr. Power Energy Syst. 2012, 39, 21–28. [Google Scholar] [CrossRef]
- Larbes, C.; Cheikh, S.M.A.; Obeidi, T.; Zerguerras, A. Genetic algorithms optimized fuzzy logic control for the max-imum power point tracking in photovoltaic system. Renew. Energy 2009, 34, 2093–2100. [Google Scholar] [CrossRef]
- Ramaprabha, R.; Gothandaraman, V.; Kanimozhi, K.; Divya, R.; Mathur, B.L. Maximum power point tracking using GA-optimized artificial neural network for Solar PV system. In Proceedings of the 1st International Conference on Electrical Energy Systems, Chennai, India, 3–5 January 2011; pp. 264–268. [Google Scholar] [CrossRef]
- Mellit, A.; Benghanem, M.; Kalogirou, S. Modeling and simulation of a stand-alone photovoltaic system using an adaptive artificial neural network: Proposition for a new sizing procedure. Renew. Energy 2007, 32, 285–313. [Google Scholar] [CrossRef]
- Punitha, K.; Devaraj, D.; Sakthivel, S. Artificial neural network based modified incremental conductance algorithm for maximum power point tracking in photovoltaic system under partial shading conditions. Energy 2013, 62, 330–340. [Google Scholar] [CrossRef]
- Veerachary, M.; Senjyu, T.; Uezato, K. Neural-network-based maximum-power-point tracking of coupled-inductor interleaved-boost-converter-supplied pv system using fuzzy controller. IEEE Trans. Ind. Electron. 2003, 50, 749–758. [Google Scholar] [CrossRef] [Green Version]
- Khaitan, S.K.K.; Gopalakrishnan, K.; Kalogirou, S. (Eds.) Soft Computing in Green and Renewable Energy Systems; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Leyva, R.; Olalla, C.; Zazo, H.; Cabal, C.; Cid-Pastor, A.; Queinnec, I.; Alonso, C. MPPT Based on Sinusoidal Extremum-Seeking Control in PV Generation. Int. J. Photoenergy 2012, 2012, 672765. [Google Scholar] [CrossRef]
- Brunton, S.L.; Rowley, C.W.; Kulkarni, S.R.; Clarkson, C. Maximum Power Point Tracking for Photovoltaic Optimi-zation Using Ripple-Based Extremum Seeking Control. IEEE Trans. Power Electron. 2010, 25, 2531–2540. [Google Scholar] [CrossRef]
- Heydari-Doostabad, H.; Keypour, R.; Khalghani, M.R.; Khooban, M.H. A new approach in MPPT for photovoltaic array based on Extremum Seeking Control under uniform and non-uniform irradiances. Sol. Energy 2013, 94, 28–36. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, Y.; Guo, K.; Jia, F. New Approach for MPPT Control of Photovoltaic System with Mutative-Scale Du-al-Carrier Chaotic Search. IEEE Trans. Power Electron. 2011, 26, 1038–1048. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, Y.; Liu, Q.; Wu, J. Maximum power point tracking (MPPT) control of a photovoltaic system based on dual carrier chaotic search. J. Control. Theory Appl. 2012, 10, 244–250. [Google Scholar] [CrossRef]
- Taheri, H.; Salam, Z.; Ishaque, K.; Syafaruddin. A novel Maximum Power Point tracking control of photovoltaic system under partial and rapidly fluctuating shadow conditions using Differential Evolution. In Proceedings of the IEEE Symposium on Industrial Electronics and Applications (ISIEA), Penang, Malaysia, 3–5 October 2010; pp. 82–87. [Google Scholar] [CrossRef]
- da Costa, W.T.; Fardin, J.F.; Simonetti, D.S.L.; Neto, L.D.V.B.M. Identification of photovoltaic model parameters by Differential Evolution. In Proceedings of the 2010 IEEE International Conference on Industrial Technology, Via del Mar, Chile, 14–17 March 2010; pp. 931–936. [Google Scholar] [CrossRef]
- Kulaksız, A.A.; Akkaya, R. A genetic algorithm optimized ANN-based MPPT algorithm for a stand-alone PV system with induction motor drive. Sol. Energy 2012, 86, 2366–2375. [Google Scholar] [CrossRef]
- Liu, L.; Liu, C. A Novel Combined Particle Swarm Optimization and Genetic Algorithm MPPT Control Method for Multiple Photovoltaic Arrays at Partial Shading. J. Energy Resour. Technol. 2012, 135, 012002. [Google Scholar] [CrossRef]
- Ali, A.; Wang, Y.; Li, W.; He, X. Implementation of simple moving voltage average technique with direct control in-cremental conductance method to optimize the efficiency of DC microgrid. In Proceedings of the International Conference on Emerging Technologies (ICET), Peshawar, Pakistan, 19–20 December 2015; pp. 1–5. [Google Scholar]
- Ali, A.; Li, W.; He, X. Performance Analysis of Incremental Conductance MPPT with Simple Moving Voltage Average Method for Distributed PV System. Open Electr. Electron. Eng. J. 2016, 10, 118–128. [Google Scholar] [CrossRef] [Green Version]
- Stanimirović, P.S.; Petković, M.D. Improved GNN Models for Constant Matrix Inversion. Neural Process. Lett. 2019, 50, 321–339. [Google Scholar] [CrossRef]
- Shmilovitz, D. On the control of photovoltaic maximum power point tracker via output parameters. IEE Proc. Electr. Power Appl. 2005, 152, 239–248. [Google Scholar] [CrossRef] [Green Version]
- Uoya, M.; Koizumi, H. A Calculation Method of Photovoltaic Array’s Operating Point for MPPT Evaluation Based on One-Dimensional Newton–Raphson Method. IEEE Trans. Ind. Appl. 2014, 51, 567–575. [Google Scholar] [CrossRef]
- Yu, M.Q. Parameter Identification of Photovoltaic Cell Model Based on Perturbation and Observation and Modified Gauss-Newton Method. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018. [Google Scholar] [CrossRef]
- Bhukya, L.; Nandiraju, S. A novel photovoltaic maximum power point tracking technique based on grasshopper op-timized fuzzy logic approach. Int. J. Hydrog. Energy 2020, 45, 9416–9427. [Google Scholar] [CrossRef]
- Yang, B.; Zhong, L.; Zhang, X.; Shu, H.; Yu, T.; Li, H.; Jiang, L.; Sun, L. Novel bio-inspired memetic salp swarm algorithm and application to MPPT for PV systems considering partial shading condition. J. Clean. Prod. 2019, 215, 1203–1222. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Zhang, X.; Li, H.; Shu, H.; Sang, Y.; Jiang, L. Dynamic leader based collective intelligence for maximum power point tracking of PV systems affected by partial shading condition. Energy Convers. Manag. 2018, 179, 286–303. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Jiang, M.; Ghahremani, M.; Dadfar, S.; Chi, H.; Abdallah, Y.N.; Furukawa, N. A novel combinatorial hybrid SFL–PS algorithm based neural network with perturb and observe for the MPPT controller of a hybrid PV-storage system. Control. Eng. Pr. 2021, 114, 104880. [Google Scholar] [CrossRef]



| AI- and BI-Based Soft Computing Methods | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MPTT Technique | Dependency on PV Array | Sensor Type | MPP Tracking Speed | MPP Tracking Accuracy | Efficiency | Circuitry Type | Application | ||||
| T | I | V | D | A | Grid Connected | Stand Alone | |||||
| AI-Based SC-MPPT Techniques | |||||||||||
| Bayesian Network | × | × | √ | √ | M | Me | H | √ | √ | √ | √ |
| Nonlinear Predictor | × | × | √ | √ | F | H | H | √ | √ | √ | √ |
| Fibonacci Search | × | × | √ | √ | F | M | M | √ | × | × | √ |
| Fuzzy Logic Control | √ | × | √ | √ | F | M | H | √ | × | × | √ |
| Artificial Neural Network | √ | √ | √ | √ | F | M | H | √ | × | × | √ |
| Extremum Seeking | × | × | √ | F | M | M | √ | × | × | √ | |
| Differential Evolution | × | × | √ | √ | F | M | H | √ | × | × | √ |
| Simple Moving Voltage Average | √ | × | √ | F | H | H | √ | √ | × | √ | |
| Gauss–Newton | × | × | √ | √ | F | H | H | √ | × | × | √ |
| BI-Based SC-MPPT Techniques | |||||||||||
| Ant Colony Optimization | √ | √ | √ | √ | F | M | H | √ | × | × | √ |
| Cuckoo Search | × | × | √ | VF | H | H | √ | × | × | √ | |
| Chaotic Search | × | × | √ | √ | F | M | M | √ | × | × | √ |
| Genetic Algorithm | × | × | √ | √ | F | M | H | √ | × | × | √ |
| Practical Swarm Optimization | × | × | √ | √ | F | M | H | √ | × | × | √ |
| Grasshopper | × | × | √ | √ | F | H | H | √ | × | × | √ |
| Memetic Salp Swarm Algorithm | × | × | √ | √ | VF | H | H | √ | × | × | √ |
| Dynamic Leader-based Collective Intelligence | × | × | √ | √ | VF | H | H | √ | × | × | √ |
| Shuffled Frog Leaping and Pattern Search | × | × | √ | √ | VF | H | H | √ | × | × | √ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, A.; Irshad, K.; Khan, M.F.; Hossain, M.M.; Al-Duais, I.N.A.; Malik, M.Z. Artificial Intelligence and Bio-Inspired Soft Computing-Based Maximum Power Plant Tracking for a Solar Photovoltaic System under Non-Uniform Solar Irradiance Shading Conditions—A Review. Sustainability 2021, 13, 10575. https://doi.org/10.3390/su131910575
Ali A, Irshad K, Khan MF, Hossain MM, Al-Duais INA, Malik MZ. Artificial Intelligence and Bio-Inspired Soft Computing-Based Maximum Power Plant Tracking for a Solar Photovoltaic System under Non-Uniform Solar Irradiance Shading Conditions—A Review. Sustainability. 2021; 13(19):10575. https://doi.org/10.3390/su131910575
Chicago/Turabian StyleAli, Amjad, Kashif Irshad, Mohammad Farhan Khan, Md Moinul Hossain, Ibrahim N. A. Al-Duais, and Muhammad Zeeshan Malik. 2021. "Artificial Intelligence and Bio-Inspired Soft Computing-Based Maximum Power Plant Tracking for a Solar Photovoltaic System under Non-Uniform Solar Irradiance Shading Conditions—A Review" Sustainability 13, no. 19: 10575. https://doi.org/10.3390/su131910575
APA StyleAli, A., Irshad, K., Khan, M. F., Hossain, M. M., Al-Duais, I. N. A., & Malik, M. Z. (2021). Artificial Intelligence and Bio-Inspired Soft Computing-Based Maximum Power Plant Tracking for a Solar Photovoltaic System under Non-Uniform Solar Irradiance Shading Conditions—A Review. Sustainability, 13(19), 10575. https://doi.org/10.3390/su131910575