Many-Objective Hybrid Optimization Method for Impeller Profile Design of Low Specific Speed Centrifugal Pump in District Energy Systems
Abstract
:1. Introduction
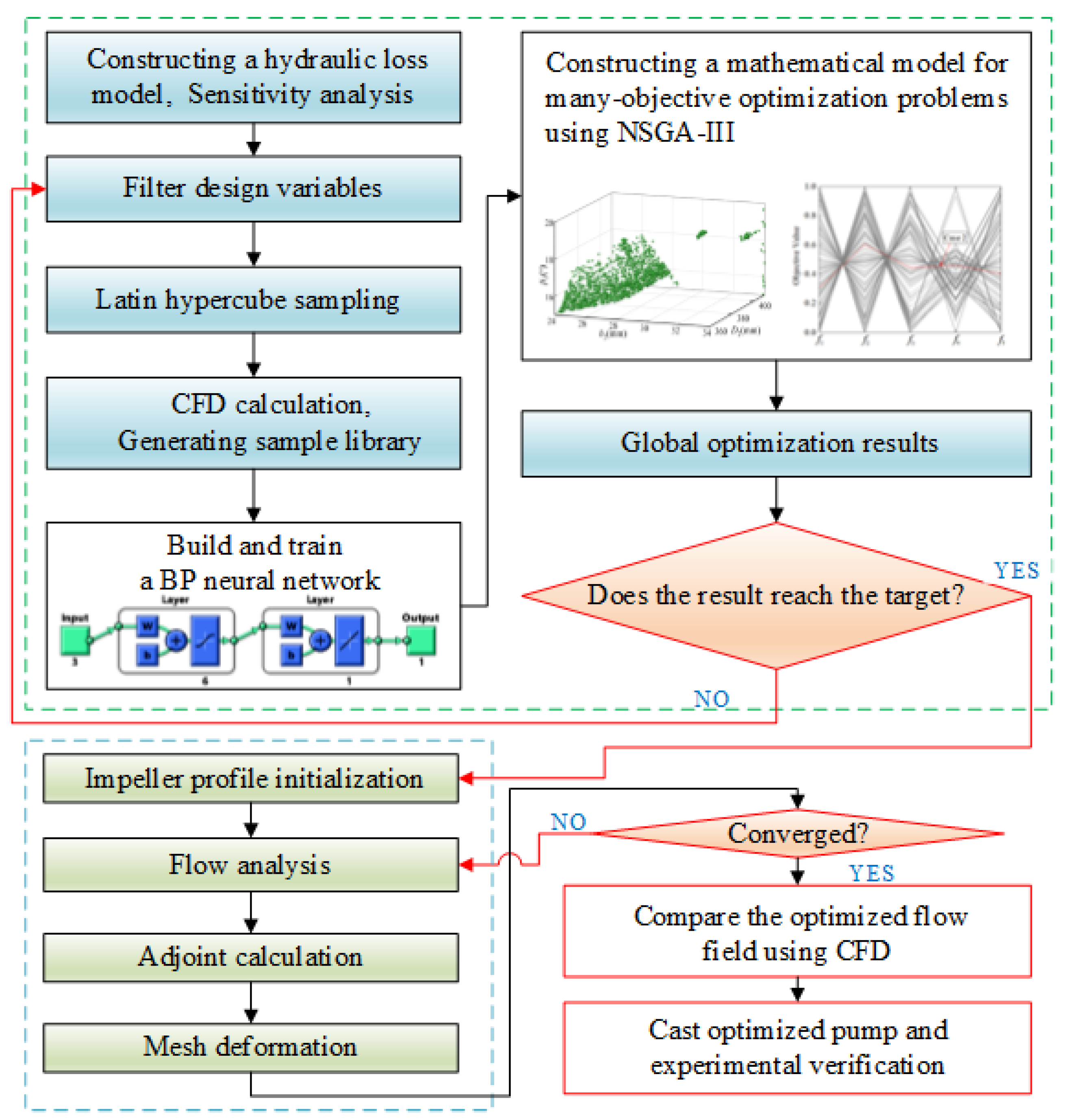
2. Model Description
2.1. Sensitivity Analysis
2.2. Latin Hypercube Sampling
2.3. Surrogate Model
2.4. The Global Optimization Using NSGA-III
2.5. The Gradient-Based Optimization Using Adjoint Method
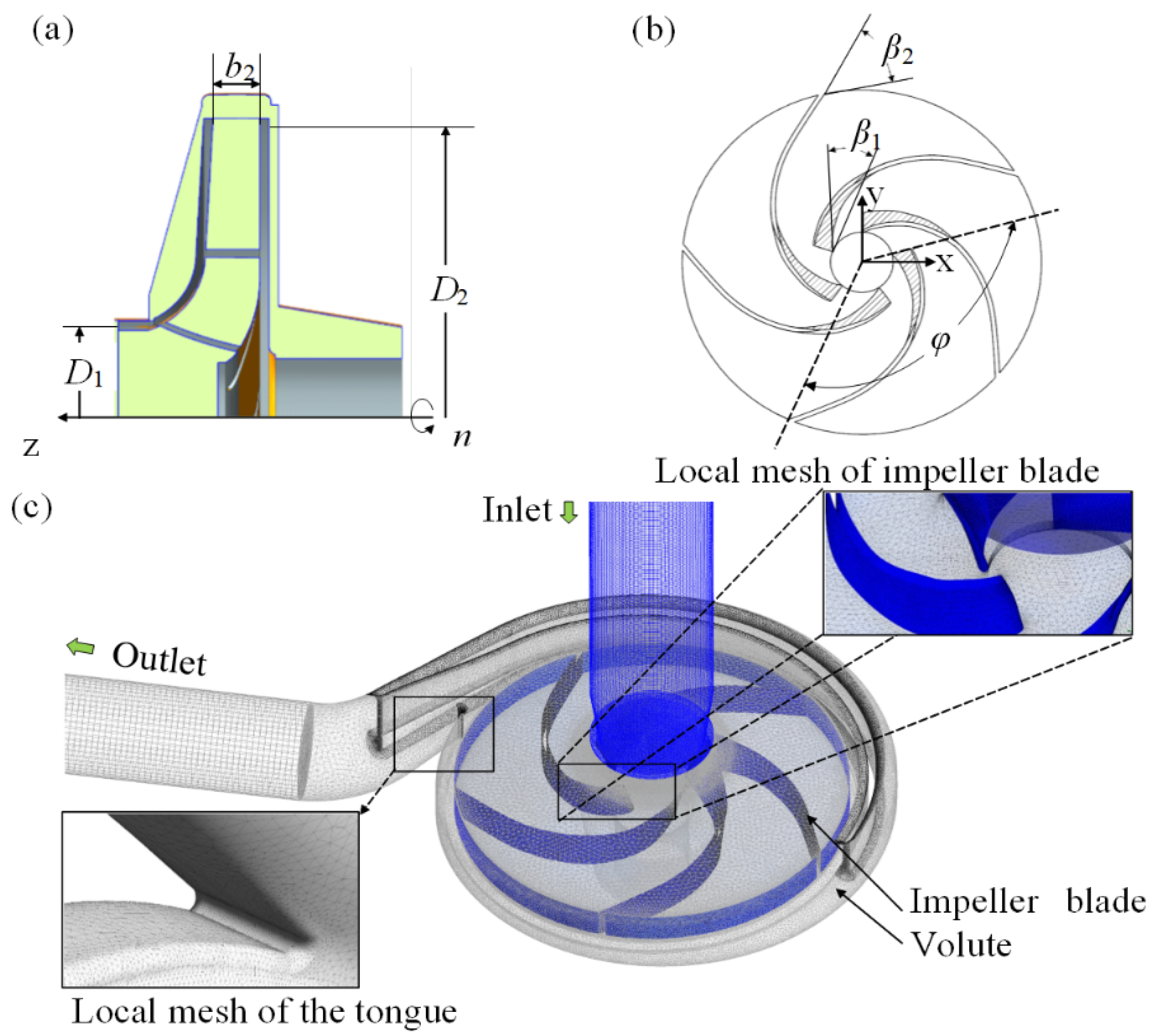
3. Numerical Methods and Test Equipment
3.1. Numerical Methods
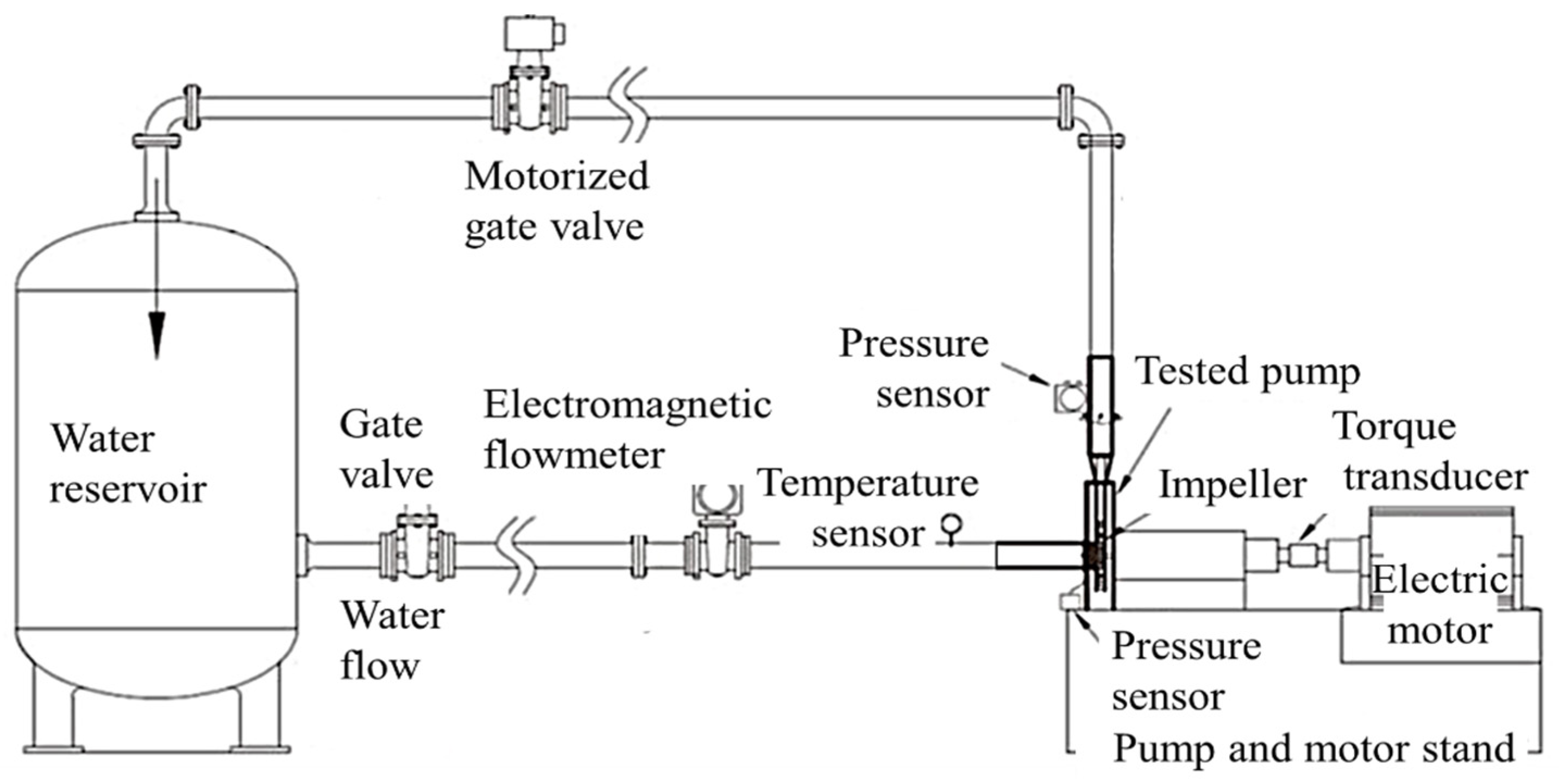
3.2. Test Setup to Validate Numerical Method
4. Results and Discussion
4.1. DVs and Objective Functions
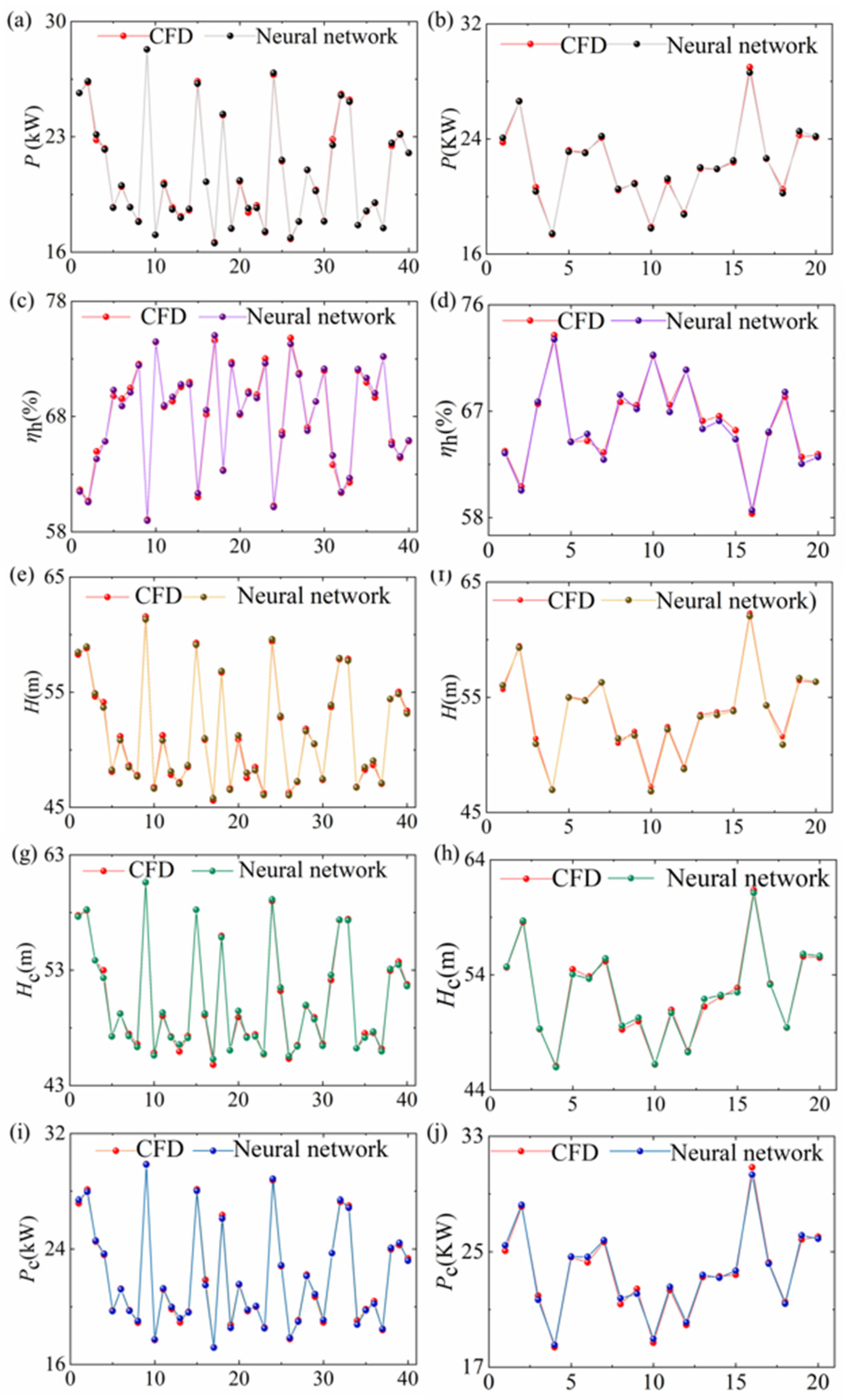
4.2. BPNN Model Verification
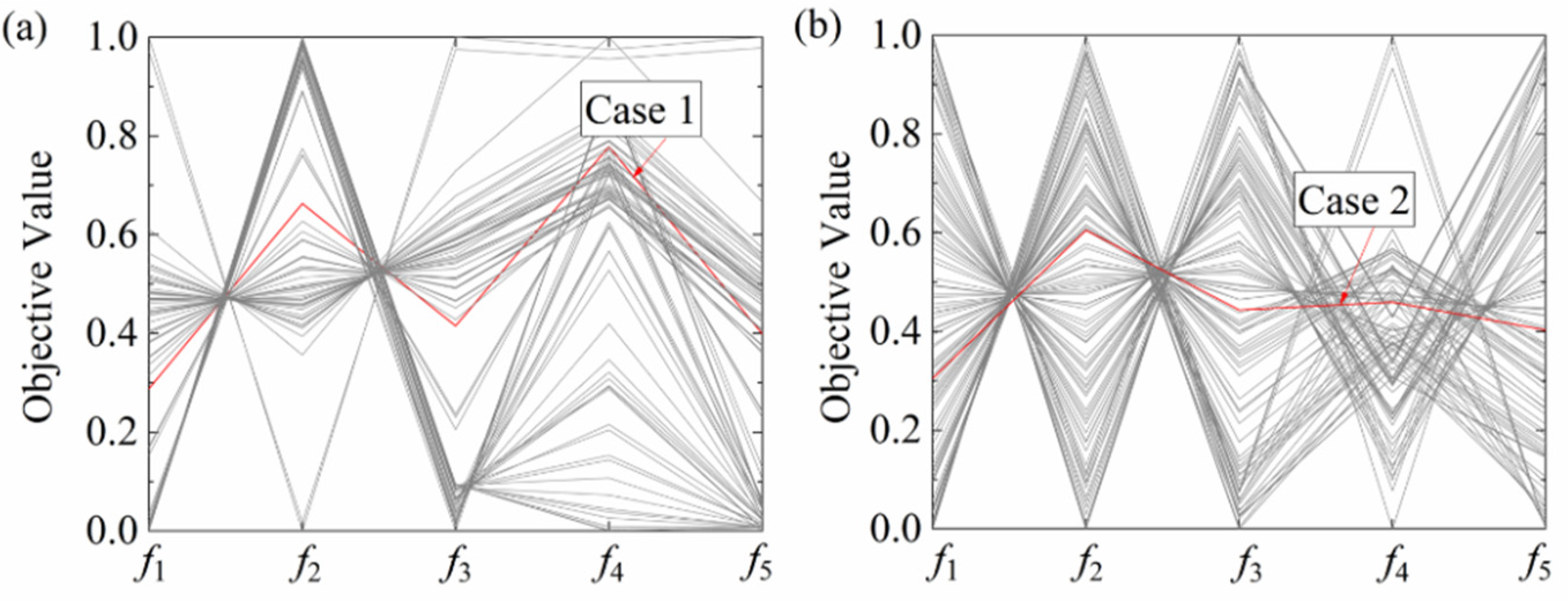
4.3. Result of Optimization
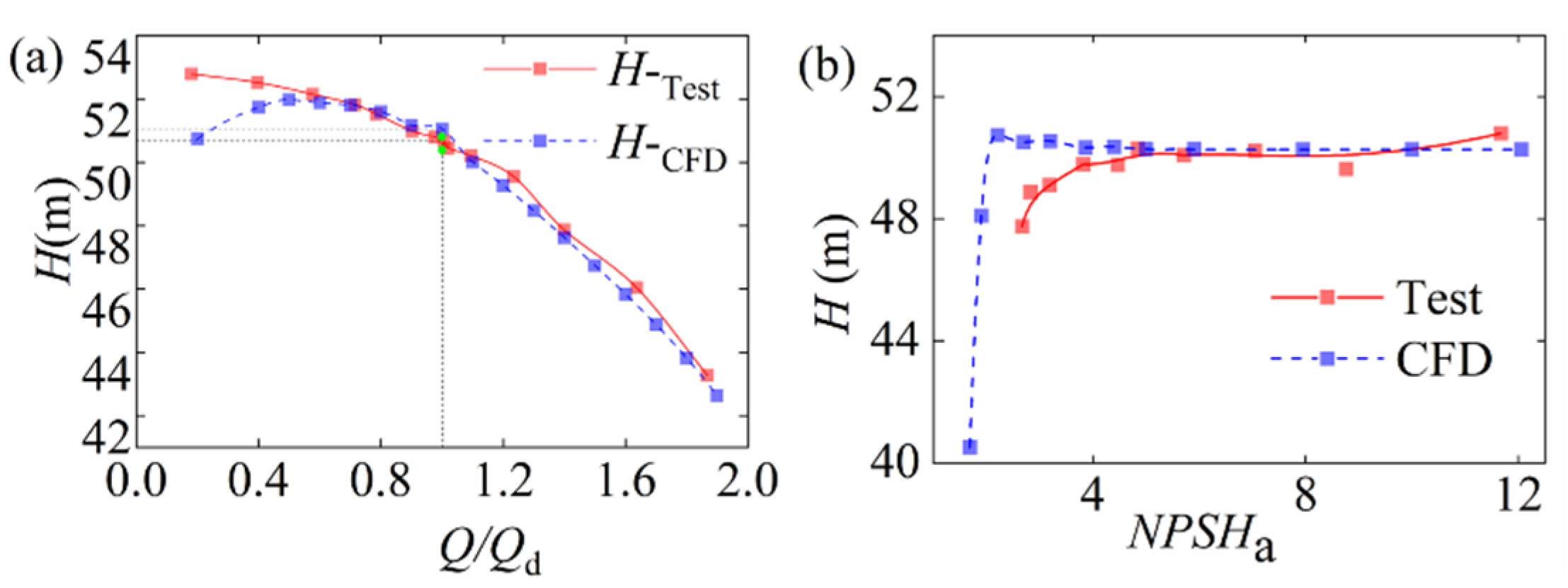
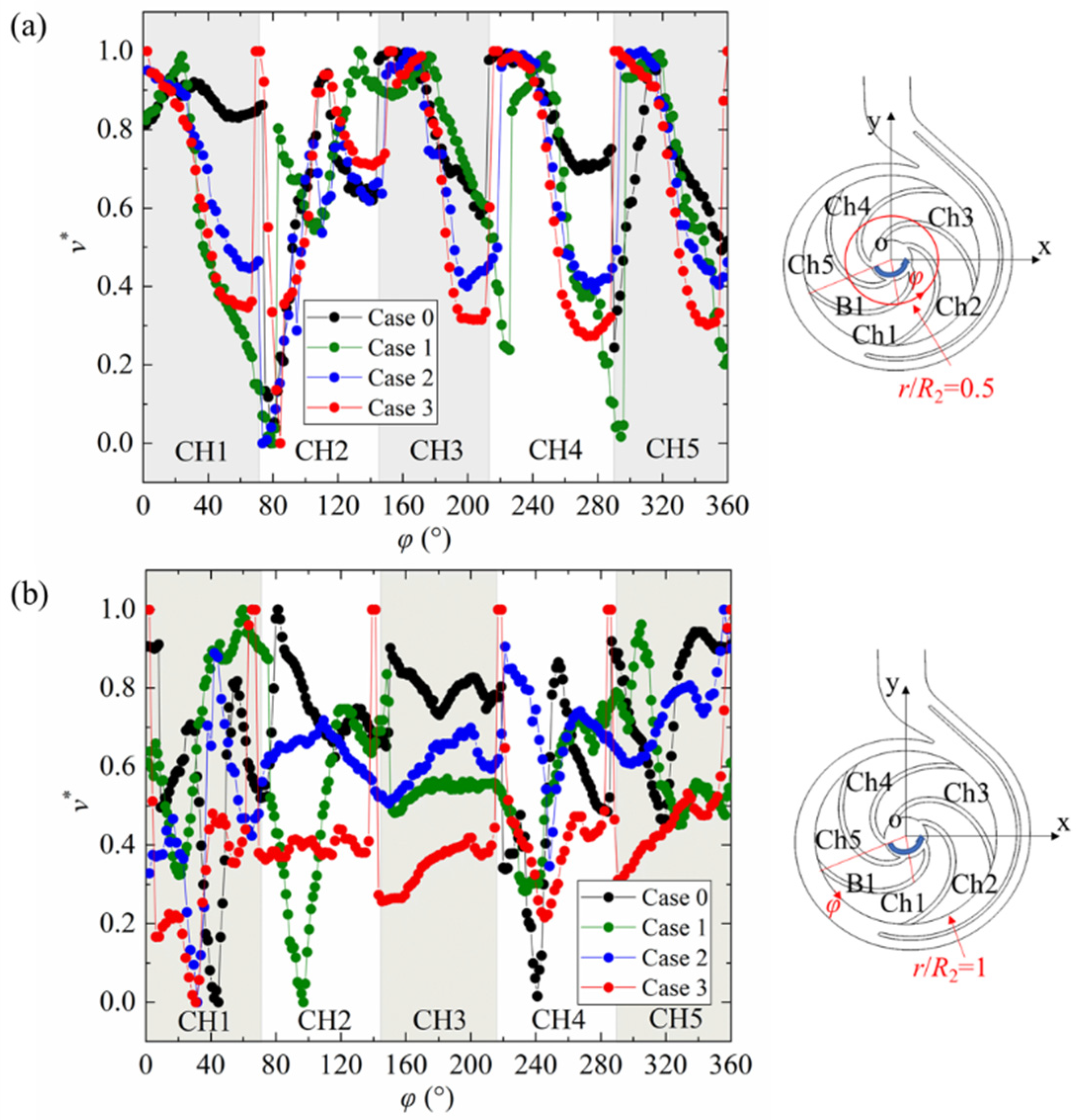
4.4. Hydraulic Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Paredes-Sanchez, B.M.; Paredes, J.P.; Caparrini, N.; Rivo-Lopez, E. Analysis of District Heating and Cooling Energy Systems in Spain: Resources, Technology and Management. Sustainability 2021, 13, 5442. [Google Scholar] [CrossRef]
- Sarbu, I.; Valea, E.S. Energy Savings Potential for Pumping Water in District Heating Stations. Sustainability 2015, 7, 5705–5719. [Google Scholar] [CrossRef] [Green Version]
- Pei, J.; Wang, W.J.; Yuan, S.Q.; Zhang, J.F. Optimization on the Impeller of a Low-specific-speed Centrifugal Pump for Hydraulic Performance Improvement. Chin. J. Mech. Eng. 2016, 29, 992–1002. [Google Scholar] [CrossRef]
- Zhang, R.H.; Chen, X.B.; Luo, J.Q. Knowledge Mining of Low Specific Speed Centrifugal Pump Impeller Based on Proper Orthogonal Decomposition Method. J. Therm. Sci. 2020, 30, 840–848. [Google Scholar] [CrossRef]
- Zhao, A.; Lai, Z.N.; Wu, P.; Cao, L.L.; Wu, D.Z. Multi-objective optimization of a low specific speed centrifugal pump using an evolutionary algorithm. Eng. Optim. 2016, 48, 1251–1274. [Google Scholar] [CrossRef]
- Kaya, D.; Yagmur, E.A.; Yigit, K.S.; Kilic, F.C.; Eren, A.S.; Celik, C. Energy efficiency in pumps. Energy Convers. Manag. 2008, 49, 1662–1673. [Google Scholar] [CrossRef]
- Derakhshan, S.; Pourmahdavi, M.; Abdolahnejad, E.; Reihani, A.; Ojaghi, A. Numerical shape optimization of a centrifugal pump impeller using artificial bee colony algorithm. Comput. Fluids 2013, 81, 145–151. [Google Scholar] [CrossRef]
- Wang, W.J.; Li, Y.P.; Osman, M.K.; Yuan, S.Q.; Zhang, B.Y.; Liu, J. Multi-Condition Optimization of Cavitation Performance on a Double-Suction Centrifugal Pump Based on ANN and NSGA-II. Processes 2020, 8, 1124. [Google Scholar] [CrossRef]
- Safikhani, H.; Khalkhali, A.; Farajpoor, M. Pareto Based Multi-Objective Optimization of Centrifugal Pumps Using CFD, Neural Networks and Genetic Algorithms. Eng. Appl. Comput. Fluid Mech. 2011, 5, 37–48. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Xiao, R.F. Multiobjective Optimization Design of a Pump–Turbine Impeller Based on an Inverse Design Using a Combination Optimization Strategy. J. Fluids Eng. 2014, 136. [Google Scholar] [CrossRef]
- Wang, W.J.; Osman, M.K.; Pei, J.; Gan, X.C.; Yin, T.Y. Artificial Neural Networks Approach for a Multi-Objective Cavitation Optimization Design in a Double-Suction Centrifugal Pump. Processes 2019, 7, 246. [Google Scholar] [CrossRef] [Green Version]
- Derakhshan, S.; Bashiri, M. Investigation of an efficient shape optimization procedure for centrifugal pump impeller using eagle strategy algorithm and ANN (case study: Slurry flow). Struct. Multidiscip. Optim. 2018, 58, 459–473. [Google Scholar] [CrossRef]
- Liu, X.W.; Li, H.C.; Shi, X.X.; Fu, J.F. Application of biharmonic equation in impeller profile optimization design of an aero-centrifugal pump. Eng Comput. 2019, 36, 1764–1795. [Google Scholar] [CrossRef]
- Wang, X.D.; Hirsch, C.; Kang, S.; Lacor, C. Multi-objective optimization of turbomachinery using improved NSGA-II and approximation model. Comput. Methods Appl. Mech. Eng. 2011, 200, 883–895. [Google Scholar] [CrossRef]
- Pei, J.; Wang, W.J.; Yuan, S.Q. Multi-point optimization on meridional shape of a centrifugal pump impeller for performance improvement. J. Mech. Sci. Technol. 2016, 30, 4949–4960. [Google Scholar] [CrossRef]
- Benturki, M.; Dizene, R.; Ghenaiet, A. Multi-Objective Optimization of Two-Stage Centrifugal Pump using NSGA-II Algorithm. J. Appl. Fluid Mech. 2018, 11, 929–943. [Google Scholar] [CrossRef]
- Tong, S.G.; Zhao, H.; Liu, H.Q.; Tong, Z.M.; Yu, Y.; Tang, N.; Wu, W.J.; Li, J.f.; Cong, F.Y.; Zhang, H. Optimization calculation method for efficiency of multistage split case centrifugal pump. J. ZheJiang Univ. (Eng. Sci.) 2019, 53, 988–996. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. Ieee T Evol. Comput 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Verstraete, T.; Mueller, L. Adjoint-Based Multi-Point and Multi-Objective Optimization of a Turbocharger Radial Turbine. Int. J. Turbomach. Propuls. Power 2019, 4, 10. [Google Scholar] [CrossRef] [Green Version]
- Namgoong, H.; Crossley, W.; Lyrintzis, A. Global Optimization Issues for Transonic Airfoil Design. Aiaa/Issmo Symp. Multidiscip. Anal. Optim. 2013. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Zhu, T. A new hydraulic regulation method on district heating system with distributed variable-speed pumps. Energy Convers. Manag. 2017, 147, 174–189. [Google Scholar] [CrossRef]
- Kuosa, M.; Kontu, K.; Mäkilä, T.; Lampinen, M.; Lahdelma, R. Static study of traditional and ring networks and the use of mass flow control in district heating applications. Appl. Therm. Eng. 2013, 54, 450–459. [Google Scholar] [CrossRef]
- Zhang, J.J. Development of Performance Prediction Software for Low Specific Speed Centrifugal Pump. Water Sav. Irrig. 2009, 46–49. [Google Scholar] [CrossRef]
- Siddique, M.H.; Afzal, A.; Samad, A. Design Optimization of the Centrifugal Pumps via Low Fidelity Models. Math. Probl. Eng. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Jameson, A. Aerodynamic design via control theory. J. Sci. Comput. 1988, 3, 233–260. [Google Scholar] [CrossRef] [Green Version]
- Callejo, A.; Bauchau, O.A.; Diskin, B. Adjoint method for the sensitivity analysis of composite beam cross-sections. Comput Struct 2019, 213, 100–111. [Google Scholar] [CrossRef]
- Li, Y.; Tong, Z. Development of real-time adaptive model-free extremum seeking control for CFD-simulated indoor thermal environment. Sustain. Cities Soc. 2021, 5, 103166. [Google Scholar] [CrossRef]
- Shim, H.S.; Afzal, A.; Kim, K.Y.; Jeong, H.S. Three-objective optimization of a centrifugal pump with double volute to minimize radial thrust at off-design conditions. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 598–615. [Google Scholar] [CrossRef]
- Li, W.; Agarwal, R.K.; Zhou, L.; Li, E.; Ji, L. Effect of Tip Clearance on Rotating Stall in a Mixed-Flow Pump. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019. [Google Scholar]
- Chen, Z.; Jiang, Y.; Tong, Z.; Tong, S.; Tan, J. Fatigue Analysis of Spherical Contact Subjected to Cyclic Elastic-Plastic Normal Loading. ASME J. Tribol. 2021, 143, 074502. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, Y.; Tong, Z.; Tong, S. Residual Stress Distribution Design for Gear Surfaces Based on Genetic Algorithm Optimization. Materials 2021, 14, 366. [Google Scholar] [CrossRef]
- Tong, Z.; Xin, J.; Tong, S.; Yang, Z.; Zhao, J.; Mao, J. Internal flow structure, fault detection, and performance optimization of centrifugal pumps. J. Zhejiang Univ. Sci. A 2020, 21, 85–117. [Google Scholar] [CrossRef]
- Tong, Z.; Cheng, Z.; Tong, S. A review on the development of compressed air energy storage in China: Technical and economic challenges to commercialization. Renew. Sustain. Energy Rev. 2021, 135, 110178. [Google Scholar] [CrossRef]
- Tong, Z.; Cheng, Z.; Tong, S. Preliminary Design of Multistage Radial Turbines Based on Rotor Loss Characteristics under Variable Operating Conditions. Energies 2019, 12, 2550. [Google Scholar] [CrossRef] [Green Version]
- Tong, Z.; Chen, Y.; Tong, S.; Yu, Y.; Li, J. Multi-objective optimization design of low specific speed centrifugal pump based on NSGA-III algorithm. China Mech. Eng. 2019, 1–9. [Google Scholar] [CrossRef]
- Zhang, Q.; Tong, Z.; Tong, S.; Cheng, Z. Research on water and heat management in the cold start process of proton exchange membrane fuel cell with expanded graphite bipolar plate. Energy Convers. Manag. 2021, 233. [Google Scholar] [CrossRef]
- Ding, H.; Visser, F.C.; Jiang, Y. A Practical Approach To Speed up Npshr Prediction of Centrifugal Pumps Using Cfd Cavitation Model. In Fluids Engineering Division Summer Meeting; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 505–514. [Google Scholar]
- Technical Specifications for Centrifugal Pumps—Class II (ISO 5199:2002). Available online: https://www.sis.se/api/document/preview/32285/ (accessed on 4 September 2021).




| Reference | Design Variables | Optimization Objectives | Method | Optimization Algorithm |
|---|---|---|---|---|
| Safikhani et al. [9] | Leadingedge angle, trailing edge angle, and stagger angle | Efficiency and net positive suction head required (NPSHr) | CFD | MOGA |
| Yang and Xiao. [10] | Impeller high-pressure and low-pressure side diameter, impeller low-pressure side hub diameter, impeller high-pressure side exit width | Hydraulic efficiency in differient mass flow rate | CFD and Experiment | MOGA |
| Wang et al. [11] | Hub inlet angle, hub exit angle, hub wrap angle, leading-edge wrap angle at hub, shroud inlet angle, shroud exit angle, shroud wrap angle, and the leading edge wrap angle at the shroud | Efficiency and NPSHr | CFD and Experiment | MOGA |
| Derakhshan et al. [7] | Hub diameter, suction diameter, impeller diameter, impeller width, inlet, and outlet blade angles | Efficiency and total pressure difference | CFD and Experiment | ABC |
| Derakhshan and M. Bashiri. [12] | Hub diameter, suction diameter, impeller diameter, impeller width, and inlet and outlet blade angles | Efficiency and total pressure difference | CFD and Experiment | ES |
| Liu et al. [13] | Hub streamline and shroud streamline | Hydraulic efficiency | CFD and Experiment | AFSA |
| Wang et al. [14] | Four angles for the sweep and lean | Efficiencies at two working points and total pressure ratio | CFD | NSGA-II |
| Zhao et al. [5] | Blade outlet angle, blade inlet angle, splitter offset angle, impeller meridional section | Anti-cavitation ability and the hydraulic efficiency | CFD and Experiment | NSGA-II |
| Pei et al. [15] | The shroud radius, the hub radius, the shroud angle, and the hub angle | Hydraulic efficiency in differient mass flow rate | CFD and Experiment | NSGA-II |
| Benturki et al. [16] | Leading and trailing edge blade angles, impeller blade thickness, wrap angles | Head, hydraulic efficiency, and NPSHr | CFD and Experiment | NSGA-II |
| Tong et al. [17] | Impeller outlet diameter, impeller outlet width, and impeller exit angle | Head, and hydraulic efficiency | CFD | NSGA-II |
| Profile Parameter | Value |
|---|---|
| Impeller inlet diameter D1 (mm) | 112 |
| Impeller outlet diameter D2 (mm) | 400 |
| Impeller inlet angle β1 (°) | 16.54 |
| Impeller outlet angle β2 (°) | 42 |
| Impeller outlet width b2 (mm) | 30 |
| Blade wrap angle φ (°) | 130 |
| Number of the impeller blades Z | 5 |
| The Main Profile Parameters | Range |
|---|---|
| D1 (mm) | [80, 120] |
| D2 (mm) | [360, 410] |
| β1 (°) | [15, 45] |
| β2 (°) | [15, 45] |
| b2 (mm) | [24, 34] |
| Z | [3, 7] |
| Profile Parameters | SH | Sηh | SP |
|---|---|---|---|
| D1 | 0.00924 | 0.00924 | 0.02 |
| D2 | 2.33447 | 0.04835 | 2.28391 |
| β1 | 0.02503 | 0.01503 | 0.01 |
| β2 | 0.24553 | 0.09565 | 0.15017 |
| b2 | 0.0793 | 0.04237 | 0.12178 |
| Z | 0.03537 | 0.04157 | 0.03985 |
| Scheme | b2 (mm) | D2 (mm) | β2 (°) | H (m) | ηh (%) | P (KW) | ΔH (%) | Pc (KW) | |
|---|---|---|---|---|---|---|---|---|---|
| Case 0 | Original | 30 | 400 | 42 | 50.64 | 66.01 | 20.9 | 3.1 | 22.4 |
| Case 1 | NSGA-II | 28.85 | 387.1 | 16.8 | 51.66 | 69.86 | 20.1 | 3 | 22.0 |
| Case 2 | NSGA- III | 25.16 | 383.2 | 16.1 | 51.58 | 70.34 | 20.0 | 2.9 | 21.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, Z.; Xin, J.; Ling, C. Many-Objective Hybrid Optimization Method for Impeller Profile Design of Low Specific Speed Centrifugal Pump in District Energy Systems. Sustainability 2021, 13, 10537. https://doi.org/10.3390/su131910537
Tong Z, Xin J, Ling C. Many-Objective Hybrid Optimization Method for Impeller Profile Design of Low Specific Speed Centrifugal Pump in District Energy Systems. Sustainability. 2021; 13(19):10537. https://doi.org/10.3390/su131910537
Chicago/Turabian StyleTong, Zheming, Jiage Xin, and Chengzhen Ling. 2021. "Many-Objective Hybrid Optimization Method for Impeller Profile Design of Low Specific Speed Centrifugal Pump in District Energy Systems" Sustainability 13, no. 19: 10537. https://doi.org/10.3390/su131910537
APA StyleTong, Z., Xin, J., & Ling, C. (2021). Many-Objective Hybrid Optimization Method for Impeller Profile Design of Low Specific Speed Centrifugal Pump in District Energy Systems. Sustainability, 13(19), 10537. https://doi.org/10.3390/su131910537






