Abstract
In this article, we propose an application of humanitarian logistics theory to build a supportive framework for economic reactivation and pandemic management based on province vulnerability against COVID-19. The main research question is which factors are related to COVID-19 mortality between Peruvian provinces? We conduct a spatial regression analysis to explore which factors determine the differences in COVID-19 cumulative mortality rates for 189 Peruvian provinces up to December 2020. The most vulnerable provinces are characterized by having low outcomes of long-run poverty and high population density. Low poverty means high economic activity, which leads to more deaths due to COVID-19. There is a lack of supply in the set of relief goods defined as Pandemic Response and Recovery Supportive Goods and Services (PRRSGS). These goods must be delivered in order to mitigate the risk associated with COVID-19. A supportive framework for economic reactivation can be built based on regression results and a delivery strategy can be discussed according to the spatial patterns that we found for mortality rates.
1. Introduction
Since 2020, the novel coronavirus has caused changes in the livelihoods of the people and the nature of work. These changes motivated a set of public policies that aims to reactivate economies while minimizing the total number of contagions to reduce mortality rates. For a case study of Peru, the government adopted a preventive framework including early lockdowns, curfews, prolonged mobility restrictions between regions, and prohibitions to agglomeration in closed spaces [1,2,3,4,5]. After these lockdowns, a set of subsidiary policies for the population and companies [1,2,6], and macroeconomic policies oriented toward reactivate consumption and production were implemented in order to mitigate the impacts of COVID-19 [7].
The COVID-19 pandemic had an impact both on the people directly affected by the virus, who used a lot of resources in their recovery, and on those indirectly affected, who suffered from the scarcity of income sources due to the short-run contractions of the economy, which includes the livelihoods of healthy people affected by lockdowns. Recent literature aimed to generate evidence on the direct and indirect impacts of COVID-19 on variables such as macroeconomic consumption, investment, production, microeconomic poverty, health, and labor, among others [8,9,10]. This branch of COVID-19 literature proposed policies oriented toward mitigating the impacts of COVID-19 such as the optimal duration of quarantines and labor-oriented policies, among others. However, what is missing in the general COVID-19 literature is a humanitarian logistics perspective, which is important because it aims to reduce human suffering in the context of a pandemic [11,12,13] and allows us to build a supportive framework for economic reactivation based on vulnerability assessment and disaster management principles [14].
Another branch of COVID-19 literature explores the factors affecting the rates of contagions or mortality by COVID-19 [15,16]. This branch uses statistical modeling and supporting machine learning methodologies in order to determine the relationship between a set of observable factors and the COVID-19 mortality rates [17,18]. This literature contributes to the empirical evidence using vulnerability assessment, while most of the COVID-19 related literature is based on calibrated methodologies. Empirical methodologies still represent a gap in the COVID-19 literature.
This work focuses on supporting economic reactivation and pandemic management in the post-lockdown context. A humanitarian logistics supportive framework is built based on provinces’ vulnerability against COVID-19 [14]. This vulnerability according to the literature review could be directly related to economic activity [15,16,17], socio-demographic characteristics [18,19,20], the population’s health [21,22,23], and health system performance [24,25,26,27]. The vulnerability against COVID-19 is directly related to the mortality rates, which is the variable of interest in this study since mortality focuses on symptomatic population, and it represents a better proxy for the demand for relief goods. The main research question is which factors are related to COVID-19 mortality between Peruvian provinces? Additionally, with this information, how can a supportive framework be implemented for underpinning the economic reactivation? We conduct a regression analysis to explore which factors determine the differences in COVID-19 cumulative mortality rates for 189 Peruvian provinces up to December 2020. In order to contribute to the empirical literature, in this work, we also test the significance of the spatial interaction effects of the COVID-19 vulnerability drivers extracted from the literature [15,16,24]. From a theoretical perspective, there are several reasons to suspect that these vulnerability drivers have spatial interaction effects, as socioeconomic variables such as wealth or employment tend to have spatial spillovers [28,29] and these could be correlated with COVID-19 mortality. Controlling these spatial effects helps reduce the bias on the coefficients, so a post-estimation analysis is more reliable. This is an important step because model predictions and vulnerability assessments are used as the basis of our supportive framework for economic reactivation.
After the regression analysis, we use the results to build support for economic reactivation, which is based on the delivery of essential goods and services to face the pandemic. The type of goods is drawn from literature and is defined as Pandemic Response and Recovery Supportive Goods and Services (PRRSGS). We classify the demand for these essential supplies according to quartiles low, medium, high, and very high demand, and this classification is used to assess economic reactivation based on the level of vulnerability. For the case of seven provinces with zero deaths, we use an elastic-net regression (ENR) to forecast their demand classification. This methodology covers the four phases of humanitarian logistics: risk mitigation, preparedness, response, and recovery [30]. Risk mitigation can be achieved by implementing policies based on the vulnerability drivers (seen in regression analysis), and disaster preparedness policies can be developed for the zero-death provinces, where there has been no infection yet. Response and recovery policies require defining PRRSGS and tracing a delivery strategy based on demand estimation.
The main contribution of this work is methodological, as a humanitarian logistics perspective is missing in COVID-19 literature. This is in the form of a proposal of an alternative framework for economic reactivation and pandemic management, which includes supportive policies that prioritize the vulnerable. This work also contributes to the empirical literature with the estimation of spatial dependence models; a statistical modeling approach [31]; and ENR, a conventional supervised machine learning technique. To the best of our knowledge, both applications are missing in the empirical literature.
The remainder of this study is structured as follows. Section 2 presents the relevant literature and the theoretical framework. Section 3 describes the data collection procedures and the data processing methods to estimate provinces’ vulnerability to COVID-19 and the demand for PRRSGS. Section 4 outlines the main results and discusses the hypothesis. Section 5 addresses the implications of our results for policymakers. Finally, Section 6 presents the conclusions and recommendations for future research.
2. Literature Review
First, in this literature review, we show how humanitarian logistics serves disaster management, specifically in the case of a pandemic, considered as a type of disaster. Second, we review some work in which the sets of determinants for the cases and number of deaths resulting from COVID-19 are analyzed. Third, vulnerability to COVID-19 mortality is defined based on those factors, and a contribution to the definition of vulnerability based on the effects of spatial interaction is established.
2.1. A Humanitarian Logistics Framework for Pandemic Assessment
The problem can be defined as follows: there are different outcomes of COVID-19 deaths between Peruvian provinces that are caused by a set of explanative factors; the main goal of this paper is to find the determinants of COVID-19 mortality rates for Peruvian provinces in order to guide disaster response and recovery at the national level. However, the number deaths due to COVID-19 deaths is in a strong relationship with the number of infections—causally, infection leads to mortality—but focusing our attention on the mortality rates is how we can assess the severity of a pandemic and guide response and recovery.
Governments around the world are applying social policies oriented toward mitigating the direct and indirect impacts of COVID-19 as an economic catastrophe [32,33]. Direct impacts include people infected by COVID-19, as they have to expend time and resources for their recovery. Indirect impacts arise from the changes in the operations, with the economies contracting themselves as a consequence of the pandemic; therefore, consumption, production, and thus the livelihoods of people are affected [8,34]. Human suffering rises [12] because, in most economies, supply could not respond to rising demands regarding health care services (hospitalization and intensive care units), key health care goods (oxygen and automatic respirators), and social aid (because with lockdowns, unemployment causes hunger and raises the incidence of poverty). All of the aforementioned lead to an increase in deprivation costs that need to be mitigated [12]. In this work, the concept of deprivation costs is emphasized.
The central aim of the humanitarian logistics discipline is to minimize the deprivation costs or the lack of essential goods to survive the aftermath of a disaster [11,12,13]. Then, four phases of disaster management are followed: risk mitigation, preparedness, response, and recovery [30]. This discipline also tries to prioritize cases where the costs of deprivation are the highest or where help is required immediately [35]. For our case, this happens when a community faces high COVID-19 mortality because mortality is a consequence of the scarcity of essential goods and services, and of essential supplies, in general, to recover from COVID-19 symptoms.
A logistics-based humanitarian framework is especially useful for pandemic outbreaks management due to the need to improve demand response and to prioritize vulnerable populations. However, for the Peruvian case, policymakers are not considering the implementation of this framework [1]. Instead, the government adopted a preventive framework, including early closures, curfews, prolonged restrictions on mobility between regions, and prohibitions on crowding in closed spaces [2,3,4,5]. Given the restrictive nature of the first measures, it is counterintuitive that Peru is one of the most affected countries by COVID-19 due to its number of cases and deaths.
Furthermore, the humanitarian logistics conceptual framework allows us to identify and prioritize a vulnerable population based on the level of deprivation costs, which are specially related to higher COVID-19 mortality rates. Higher mortality rates can be explained by high economic activity indicators such as employment or internal mobility. Especially in informal economies, the working population cannot work from home and all of people who maintain face-to-face interactions with other people are especially vulnerable [24]. COVID-19 deaths are more likely if a set of vulnerability characteristics are met by provinces (see Section 2.3 for more details). It is worth mentioning that we emphasize the demand for an analysis on the deaths rather than the contagions because we want to avoid the asymptomatic population and prioritize the resolution of human suffering.
The pandemic response and recovery framework that was applied in Peru until the end of 2020 included a set of subsidiary policies for the population and companies [3,4,6], and macroeconomic policies oriented toward reactivate consumption and production [7]. In addition to this, the humanitarian logistics proposal for response and recovery phases while economic reactivation is carried out is a supportive framework aimed at reactivating the economy by mitigating the impacts of COVID-19 (based on the idea that maintaining low mortality rates is required to carry out economic reactivation). This framework is based on the estimation of the demand for a set of PRRSGSs at the provincial level, which is based on province vulnerability, so that supply can respond to the demand. In Table 1, we list the PRRSGS and consider the goods from [36,37]:

Table 1.
Pandemic recovery supportive goods and services.
The responding supply has a significant impact on the deprivation costs and serves to mitigate injuries for the response phase and to accelerate the transition to a business-as-usual scheme regarding the recovery phase. In zero-contagion/death provinces, estimating its possible demand serves preparedness policies regarding the COVID-19 pandemic.
2.2. Previous Works on Determinants of COVID-19 Cases and Deaths
Since the beginning of the pandemic outbreak, a large amount of literature has been published. One branch explores the determinants of COVID-19 cases [15,16,17,18,19,20,21] and of deaths due to COVID-19 [22,23]. Ref. [15] found age, disability, language, race, and employment to be the determinants of COVID-19 cases for the United States. [16] discussed the importance of a disadvantaged socioeconomic position on COVID-19 disease and mortality, concluding that high-quality data on socioeconomic characteristics are needed to generate more evidence about this relationship. For Ceará, a state of Brazil, [17] found that the number of intensive care beds has spatial patterns, but they do not coincide with the ones for COVID-19 cases. Ref. [18] concluded that socioeconomic status is essential to staying healthy in the context of a pandemic; thus, poverty may lead to more contagions in the US. Ref. [19] found that per capita income, average household size, population density, and minority composition are significant predictors of COVID-19 cases in nursing homes in the US. Ref. [20] found that, in the US, states with little tolerance for deviance from enforced rules saw faster early epidemic growth and that population density is a significant predictor for COVID-19 cases. Ref. [21] focused on the significance of geographical factors, finding population density and topographic altitude as predictors of COVID-19 cases. Ref. [22] showed that pulmonary embolism was the main determinant of excess out-of-hospital deaths during COVID-19 in Paris, France. Finally, ref. [23] found that population density, the proportion of elderly residents, and percent population tested are key predictors for both COVID-19 cases and deaths.
Another branch of literature has suggested the adoption of data-driven machine learning (ML)-based frameworks for pandemic assessment, these frameworks focused on the estimation of the expected number of COVID-19 cases or deaths [24,25,26,27] and on prioritizing humanitarian operations for the vulnerable. However, the better/worse performance of ML methods concerning traditionally applied statistical analysis is still being discussed. Among the applied ML methods, some authors [24,25,26] applied unsupervised cluster-analysis algorithms, allowing them to explore the agglomeration patterns in the data to recover categories that explain the differences between reported COVID-19 cases or deaths. Inherent Risk of Contagion [24] was applied for municipalities, and a country-level cluster analysis was applied by [25]. Supervised approaches were discussed in [26] and [27], which are useful for making short-term forecasts of the number of COVID-19 cases or deaths. Supervised approaches included Random Forest (RF), Gradient Boosted Machine (GBM) [26], Linear Regression (LR), Support Vector Machine (SVM), Least Absolute Shrinkage and Selection Operator (LASSO), and Exponential Smoothing (ES) [27] for the country-level number of COVID-19 cases or deaths. According to the results, unsupervised approaches outperformed supervised ones. Among the most important predictors, economic activity, size of the population, the prevalence of chronic illness, and environmental pollution remained.
Spatial modeling applied to COVID-19 outcomes has been performed with scarce literature. Ref. [38,39] applied spatial modeling, finding that there are significant spatial interaction effects that reduce bias in the analysis of COVID-19 determinants. At this point, our paper contributes to the empirical literature. Spatial modeling is a special case of statistical modeling literature, and we want to test for significative spatial interaction effects between COVID-19 mortality and vulnerability drivers.
2.3. COVID-19 Pandemic in Peru: A Brief Review
The Peruvian response to the pandemic was an early lockdown with a set of prohibitions and mobility restrictions. There are several ways in which the pandemic affected Peruvians’ livelihoods, mental health, and information technology development, among others [40,41,42]. According to [40], Peru reached a milestone of more than 1200 deaths per one million of inhabitants by February 2021. Possible explanations for these poor outcomes are the overwhelmed and fragmented public health system, gaps in the infrastructure, a lack of specialized personnel, and deficient leadership of political authorities. Following [41], there was an info-demic composed of excessive and unfounded information that hindered an appropriate public health response and harmed the mental health of the population. However, the authors argue that Peru could control the info-demic due the introduction of prison sentences to discourage creating and sharing fake news. Finally, following [42], there were good advances in digitalization that were caused by the pandemic; nevertheless, more efforts are needed to implement telemedicine and to offer access to the internet to achieve high-quality telemedicine to all vulnerable groups in Peru.
2.4. Vulnerability Sources of Peruvian Provinces Regarding COVID-19 Pandemic
A spatial dependence econometric model (SDM) is proposed to investigate the factors affecting the number of COVID-19 cases and deaths in 189 Peruvian provinces. This regression model allows us to test for spatial interaction effects while we conduct a regression analysis on COVID-19 vulnerability drivers. This model is used to estimate the demand for PRRSGS based on COVID-19 mortality rates. If spatial interaction effects are significant, the predictions of the demand is less biased compared with the case of a simple linear model. The spatial analysis contributes to the planning of PRRSGS distribution among the provinces at the country level. If there are strong COVID-19 mortality rate spatial patterns, it is possible to study the patterns and to use the information to trace a delivery strategy for PRRSGS.
Based on the concept of deprivation costs [12] and on the literature of social determinants of health [43,44,45,46], we can theoretically build up a definition of vulnerability at the province level, which serves to motivate the SDMs and to define the expected signs of the effects of the variables. Our goal is to test the theoretical framework for vulnerability against COVID-19; thus, some of the propositions can be empirically rejected by the evidence. This definition has seven blocks that are built using previous literature that explores COVID-19 determinants [15,16,17,18,19,20,21], ML applications [24,25,26,27], and social determinants [43,44,45,46]. This definition also contains the main hypothesis that is tested in this paper.
It is important to notice that, for some groups of variables, we could have two opposite effects according to the relationship of the variable with poverty, which is the main social determinant of health: a poverty condition causes more vulnerability to COVID-19 mortality due to the scarcity of resources to face illness, malnutrition, and other vulnerability conditions. Poverty in this paper is considered a variable that has a negative relationship with mortality rates, even if it could be positively associated with vulnerability. The reason behind this consideration is that low poverty is a proxy for high demand for help, as provinces with high economic activity tend to have more cases. This argument is defended by the machine learning literature [47], and we acknowledge that it is opposite to the social determinants argument.
Assuming that empirical poverty is negatively associated with COVID-19 mortality, the example of health insurance makes the interpretations more complex: a good coverage of health insurance may lead to lower mortality rates, but this implies high economic activity so it may lead to higher mortality rates at the same time. The literature that assesses social determinants of health has a different perspective of the effects of the following definition blocks. For this literature, poverty is a condition that exacerbates COVID-19 deaths, and all other factors related to poverty such as educational level, black skin color, low income, and bad system performance, among other variables [43,44,45,46]. In this paper, we expect a negative relationship because the context contains the data when pandemic was in its first stage, and thus, it is plausible that the relationship between COVID-19 and poverty is negative for the case of Peru. The following section contains the definition blocks and the perspective bridging theories from machine learning applications and social determinants of health:
- First: a province is vulnerable in the post-lockdown context if it has a lower incidence of poverty, unemployment, and other indicators of bad economic performance. Economic activity, which is inversely related to poverty, requires internal mobility and interpersonal interaction [47]. This does not mean that we should give less importance to poor provinces, even if they might have a lower demand for PRRSGS. The optimal policy must give the latter equal weight in the humanitarian objective function. We argue that this proposition is valid if we measure long-run poverty from households, and short-run measures may not prove this relationship.
- Second: provinces that have more proportion of the vulnerable population in terms of age (the older); sex (the males); skin color (black); and chronic diseases such as hypertension, diabetes, and obesity, among others. Deprivation costs are higher for people with a higher probability of dying due to COVID-19, including people with the aforementioned characteristics [43,44,45] reach the same signs of effects for the case of USA). Two types of overcrowding measures are accounted for regarding vulnerability: overcrowding in households and overcrowding in cities (proxied by population density). Provinces with higher overcrowding in households may have worse COVID-19 outcomes [44]. We expect the same for provinces with higher overcrowding in cities. Poverty is generally negatively associated with overcrowding in cities but positively associated with overcrowding in households [45].
- Third: A short-run households’ income drastically reduced and then slowly recovered, so there is a shortage in the available resources to battle the contagion, which cannot be covered. In the absence of high coverage of health insurance, this would lead to a greater number of deaths. However, we acknowledge that, in order to obtain high health insurance coverage, provinces must work, so the economic activity must be high for provinces with high health insurance coverage, and thus, this could lead to higher mortality rates. In consequence, we face two possible effects of health insurance: whether health insurance coverage positively or negatively affects the number of deaths due to COVID-19 is an empirical question.
- Fourth: health system performance indicators play a key role in the determination of COVID-19 outcomes, especially when the COVID-19 cases exceed the capacity of hospitals and other health facilities. Provinces where the health system performs bad are more vulnerable and likely to have a greater number of deaths [24]. However, as economic activity is a condition for good health system performance, the final effect is theoretically ambiguous [45]. Whether the effect is finally positive or negative regarding COVID-19 deaths is also an empirical question.
- Fifth: the COVID-19 outcome of a province regarding mortality rates may be affected by neighboring provinces with a high incidence of COVID-19 deaths. These are called endogenous interaction effects.
- Sixth: considering previous exploratory works on determinants of COVID-19 cases and deaths, and the previous vulnerability definition block, there is no reason not to suspect that the COVID-19 outcome in a province is affected by the exogenous outcomes of neighboring provinces (i.e., poverty, demographics, health systems, etc.). These are called exogenous interaction effects.
- Seventh: after considering all of the information above, it is possible that the spatial dependence model still has a residual that represents all of the variability of COVID-19 outcomes that could not be explained by the predictors. In this residual, there may be correlated effects, as is pointed out by [48], where the COVID-19 outcomes of a province are affected by unobserved similar characteristics of their neighbors.
The following Table 2 shows the final expected signs for groups of variables:

Table 2.
Expected signs for variables.
Empirically, we test blocks fifth, sixth, and seventh, and we estimate seven models to visualize the different types of spatial interaction effects. These models or specifications passed a model selection phase where we selected the one that better fits and matches the data.
The main contribution of the framework proposed in this paper to the literature is that it configures pandemic management in the function of vulnerability regarding COVID-19 mortality, arguing that higher deprivation costs are found where there are greater mortality rates. Our proposal tries to build a supportive framework for economic reactivation-based on-demand assessment. This framework supports the policymakers in optimizing the available resources and improves the disaster management policies.
3. Materials and Methods
This section presents the data collection and data processing methods. First, the construction of variables is explained. Second, the spatial regression models are defined. Third, the model selection phase as well as the metrics used for model selection are explained. Fourth, the methodology for the assessment of demand is defined.
Two different software were used in this study: STATA 16 for spatial regression models and Python 3.6 for ENR and demand forecasting. Additionally, we used QGIS software for mapping of COVID-19 mortality rates.
3.1. Data Collection Methods
For this paper, the data listed in Table 2 were collected from different open-access sources such as Ministerio de Salud (MINSA by its Spanish acronym), the XII Population, VII Household, and III Indigenous Communities Census carried out in 2017, the Encuesta Demográfica y de Salud Familiar (ENDES by its Spanish acronym), the Encuesta Nacional a Hogares (ENAHO by its Spanish acronym), and the Sistema Nacional de Defunciones (SINADEF by its Spanish acronym). We rescaled the data at the province level to obtain indicators about poverty; employment; education; demographic characteristics; the prevalence of chronic illness such as diabetes, hypertension, and obesity; health insurance; and health system performance indicators. The number of COVID-19 deaths was recovered from the MINSA (2020) database (from 6 March 2020 to 12 December 2020). The deaths are reported by familiars and confirmed by autopsy. The quality of these data in representing the real differences between provinces is not the best; however, we show that the data are reliable for the analysis when interpreting the empirical results. Table 3 describes all of the variables included in this study.

Table 3.
Description of variables.
3.2. Data Processing Methods
The SDM to be used has to be selected from a family of cross sectional spatial dependence models described in [48,49]. This family of models arises from different ways in which spatial patterns can affect a dependent variable outcome: the endogenous interaction effects, the exogenous interaction effects, and the correlated effects. There are a total of seven models, including the single ordinary least squares model (OLS), which is a sub-case with none of the effects listed above (these models are estimated in the literature for spatial dependence models application). From the most general aspect to the particular one, these models are defined as follows:
In Equations (1)–(7), represents a vector of observations on the dependent variable, which is the number of deaths by COVID-19. First, on the right side, is a matrix of observations for the exogenous variables of the model and is the vector of parameters related to the exogenous regressors. Second, is the matrix of spatially lagged exogenous variables pre-multiplied by the vector of parameters associated with these spatially lagged variables (to account for exogenous interaction effects). Third, represents the spatially lagged dependent variable, with the scalar (called the autoregressive parameter) pre-multiplying the term, which is a vector of observations on the spatially lagged dependent variable (to account for endogenous interaction effects). Finally, is an error, which can be correlated with its spatial lag as it is represented by Equations (1), (2), (4), and (6), and is a scalar parameter that accounts for the spatial correlation of the error term. Finally, is the idiosyncratic stochastic error, which is assumed to be white noise that captures all of the remaining variability of the dependent variable and is uncorrelated with other variables in the model.
The W matrix represents a spatial weighting matrix that is important to test if the spatial interaction effects are significant. This matrix provides information about the spatial units that, in this work, are the provinces. A spatial weights matrix, formally, is a positive symmetric matrix for which the weights named define the spatial relations among locations and, therefore, determine the spatial autocorrelation statistics [50].
The following Equation (8) has been used for defining spatial weight matrix W:
where .
Nevertheless, there are several ways of defining W matrix; we list three of them that are based on Euclidian distance: Queen’s criteria (contiguity), Gabriel criteria, and K-nearest neighbors’ criteria [38,39]. We based our selection of W on the maximization of the value of the Moran Statistic that is estimated with a W definition [39]. The Moran Statistic is a measure of spatial autocorrelation that lies in the interval [−1,1], but its significance determines the level of observable spatial autocorrelation among a variable. We found that Queen’s criteria maximize the significance of Moran statistic, and thus, this is the optimal way to define the W matrix. We focus on the spatial patterns that can be measured with the data.
Equations (1)–(7) are estimated with maximum-likelihood methods assuming that . This implies that the distribution of COVID-19 mortality is normal. The parameters are obtained, maximizing the following Equation (9):
where and errors are obtained from the reduced form of models from (1) to (7). The terms and can appear or disappear in the expression according to the model formulation. Definition of errors and the abovementioned terms changes according to the model; for example, if we estimate Equation (6), which is the spatial error model, the errors will be with and we only maintain the term in the likelihood equation. Equation (9) is known as the unconcentrated log-likelihood function and is discussed in Lee (2004).
A disadvantage of SDMs is that they do not support out-of-sample predictions, which is the case for the seven provinces. Data are available for 189 provinces out of a total of 196 provinces in Peru. The missing provinces are considered as contributing zero cases or deaths. However, this hypothesis is questionable because, in some of these provinces, there are high indicators of economic activity (for example, Cañete with a value of 38.60 in the composite poverty index, which reflects low poverty below the average of 56.81). Therefore, for an estimation of the provinces with missing data, we use ENR, a machine learning tool that comes as close as possible to linear models of spatial dependency. The following Equation (10) shows the parameter estimation method and the objective function for ENR:
where is the parameter for the term associated with LASSO and to the Tikhonov regularization associated with ridge regression. The parameters can take any value from zero to infinity, and they measure the weight of the penalization for irrelevant or correlated regressors, respectively [51]. The method sacrifices bias to get a lower variance estimator that has been proven to outperform low bias over-fitted estimators in the context of out-of-sample predictions. The selection of and penalization size and the ratio are made by repeated k-fold cross-validation (with ), maximizing the out-of-sample predictive power measured with mean absolute error.
In order to qualitatively estimate the demand of PRRSGS, Equations (1)–(7) are estimated; then, we selected the model that better fits the data based upon the following metrics [51] (the less-biased model, considering only the 189 nonzero provinces that were part of the estimation of Equations (1)–(7)):
This information is complemented with ENR outcomes; this model does not pass for model selection phase, but it passes through repeated k-fold cross-validation to maximize its predictive power.
3.3. Demand Assessment
Once the model selection phase is carried out, the one that better fitted the data was used to make predictions. Within the sample, predictions were used as proxies for the demand of PRRSGS and out-of-sample predictions used with ENR tool are employed as forecasts of demand for provinces that have zero contagions or deaths (Equation (10)). The data are visualized spatially, and we report the results for the best models.
Demand is assessed by quartiles of the number of predicted COVID-19 mortality rates. This implies that the demand assessment is based on vulnerability as the predicted mortality rates are a function of a set of vulnerability drives listed in Section 2.3. We can distinguish four groups. This categorization of demand helps to trace a delivery strategy and to identify vulnerability patterns in the space, as mortality is ranked from low to very high categories:
- : Low demand
- : Medium demand
- : High demand
- : Very high demand
In the end, every province has an established demand, so that a distribution strategy for the 196 provinces can be discussed. In the Results and Discussion section, we focus on spatial insights and their contribution to the humanitarian logistics framework. In managerial and research implications, we summarize and discuss the main results, and their utility at the moment of tracing a humanitarian logistics supportive framework strategy for pandemic management.
The methodology first does a regression analysis using the SDM in Equations (1)–(7) and (10); then, it passes the model selection phase using Equations (11)–(16). After the model selection phase, we use the best SDM specification to predict the level of demand of PRRSGS, and for provinces with zero deaths, we use estimates from Equation (10) to forecast demand. Finally, with the post estimation results and demand quartile classification, we discuss a delivery strategy at the national level using provinces as the unit of analysis.
4. Results
The COVID-19 mortality rates have been log-transformed to draw a normal distribution for it. Figure 1 shows a box plot with a swarm plot and a kernel density of the log-transformed mortality rates.
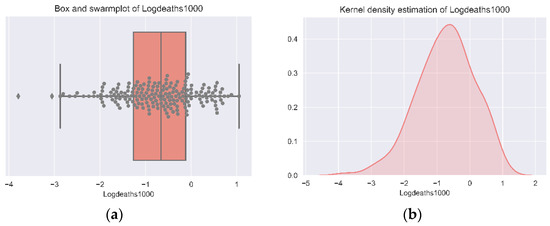
Figure 1.
Distribution plots of Logdeaths1000. (a) Boxplot of Logdeaths1000. (b) Kernel density plot of Logdeaths1000. Authors’ own elaboration.
We observe that, on average, provinces face less than one death per 1000 inhabitants. This is consistent with the mortality rates from international estimations for COVID-19. Although the mortality rates are low, they can vary a lot, and this is why it is important to understand the factors behind those differences. For this purpose, we propose a set of variables listed in Table 3 in the previous section. Figure 2 shows a plot of the correlation matrix between the variables that explain the differences between COVID-19 mortality rates.
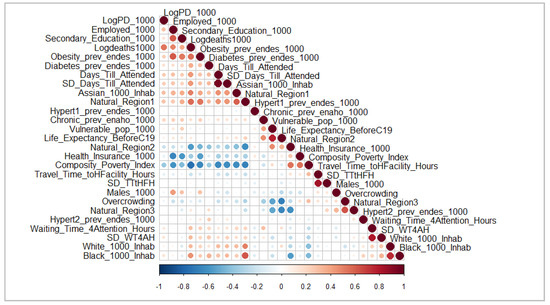
Figure 2.
Correlation matrix of variables. Authors’ own elaboration.
In Figure 2, blue circles represent the negative correlation and red ones represent the positive correlation. The size and transparency of the circles represent the magnitude of the correlation between the variables. The mortality rates (Logdeaths1000) are, on the one hand, negatively related to belonging to the highlands region (Natural_Region2), health insurance (Health_Insurance_1000), and poverty (Composite_Poverty_Index). On the other hand, they are positively related to belonging to the coastal region (Natural_Region1), presence of Asian population (Assian_1000_Inhab), presence of Black population (Black_1000_Inhab), the average days until a patient is attended (Days_Till_Attended), the inequity of the days for medical attention (SD_Days_Till_Attended), the average waiting time for attention in a health facility (Waiting_Time_4Attention_Hours), the inequity of waiting time for attention (SD_WT4AH), the prevalence of diabetes (Diabetes_prev_endes_1000), and the log population density (LogPD_1000).
The long-run poverty (Composite_Poverty_Index) variable is related to many other variables in the model. It is negatively related to the log population density (LogPD_1000), employment (Employed_1000), human capital with secondary education (Secondary_Education_1000), log of mortality rates (Logdeaths1000), obesity prevalence (Obesity_prev_endes_1000), the average days until a patient is attended in a health facility (Days_Till_Attended), the inequity in time for patient attention (SD_Days_Till_Attended), the Asian population (Assian_1000_Inhab), and the belonging to the coastal region (Natural_Region1), and it is positively related to belonging to highlands region (Natural_Region2) and being health insured (Health_Insurance_1000). According to these correlations, poor provinces are those with a low population density, employment, human capital, obesity prevalence, bad performance of health system, and low health insurance coverage.
This correlation could lead to a possible multicollinearity problem. Nevertheless, the mean-variance inflation factor across all variables after an OLS estimation is 4.96, which reflects low multicollinearity. The following Table 4 shows the descriptive statistics for all the variables considered in the paper:

Table 4.
Descriptive statistics.
After running an OLS regression, we test for spatial dependence in the residuals using a contiguity spatial weighting matrix using the residuals. The Moran’s standard deviates statistic is 5.0581, with the lowest p-value between other spatial weighting matrices (see Table 5 for results with other spatial weighting matrices), rejecting the null hypothesis that states that the errors are independently and identically distributed with 99% of confidence and a p-value of 0.000, favoring the hypothesis of spatially correlated errors.

Table 5.
Moran’s standard deviate statistic and significance (p-values).
We proceed with the results of the SDMs, in Table 6, we summarize the main ones that contribute to model selection. We select the one with a lower bias for in-sample predictions. For out-of-sample prediction, we use an ENR, which minimizes the variance, sacrificing some bias to obtain lower variance predictions.

Table 6.
Models for COVID-19 deaths (per 1000 inhabitants).
First, the variables used in OLS regression produced a McFadden pseudo-R² of 0.52 and an R² of 0.74. These results support the hypothesis of the positive relationship between vulnerability to COVID-19 and the mortality rates. Even though the lowest AIC and BIC outcomes are for the and , they have a higher bias than OLS, as they have 0.275 and 0.273 outcomes in RMSE, respectively, versus 0.269. Furthermore, RMSE is reduced in to 0.267. This means that is the best candidate for the model that better fits the data. Although , , and are equivalent in McFadden pseudo-R², R², and RMSE, we must consider that the spatial dependence in residuals is strongly significant, so instead of basing the model selection decision on AIC BIC, it is better to select the model with higher significance on spatial terms; this is measured by the Wald Test for significance of spatial terms. In consequence, the best model that better fits the data is the .
We consider the possibility that residuals vary in a non-random way. Specifically, we believe that the dataset suffers from heteroscedasticity. In order to test it, we used the OLS model residuals. The Breusch–Pagan test chi-squared statistic, subject to one degree of freedom, is 16.69, which rejects the null hypothesis of homoscedasticity with 99% of confidence and a p-value of 0.000. The following Figure 3 plots the mortality rates versus the predictions of the model; it confirms the presence of heteroscedasticity:
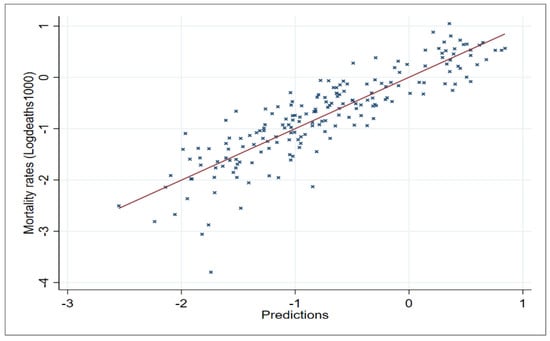
Figure 3.
Linear fit plot of real mortality rates versus predictions. Authors’ own elaboration.
We observed that provinces with lower mortality rates have a higher variance in the residuals than other provinces. Furthermore, the variance for other provinces seemed to be constant. For this reason, we report robust standard errors for the individual significance of coefficients in the model. The following Table 7 shows the regression results:

Table 7.
Regression results (coefficients).
The results can be summarized as follows:
Poverty (Composite_Poverty_Index): there is a strong negative relationship between long-run poverty and COVID-19 mortality rates. While economic reactivation is carried out, provinces that had a high level of economic activity, which is related to lower poverty and is captured in the index, are especially vulnerable to COVID-19 mortality. After the short-run shock, the economy tends to return to its long-run level; this is the main reason for the sign of this effect. Poor provinces are vulnerable to the indirect effects of a pandemic: unemployment and shortage in available resources, among others. This insight favors the proposal of an implementation of a reactivation framework rather than a lockdown: provinces are returning to their long-run level economic activity, and this must be reintroduced safely. There is no evidence that poverty produces exogenous interaction effects on mortality rates.
Overcrowding in cities or population density (LogPD_1000): there is a strong positive relationship between population density and COVID-19 mortality rates. Higher mortality is found in provinces with higher population density. In low population density provinces or rural provinces, the health system may be inexistent, but since the data used for this analysis represent the initial period of COVID-19 with limited spread between provinces, we do not observe the effects of bad health system performance, but instead, we observe the effect of population density or overcrowding in cities where infection spread earlier. According to empirical results, poor provinces are less overcrowded in cities (negative correlation of −0.50) but more overcrowded in households (correlation of 0.30). The effect of population density is on the same line as the effect of poverty: those provinces that are rich and have high population density (since both attributes are correlated) are more vulnerable to COVID-19 deaths. There is marginal evidence that population density produces positive exogenous interaction effects on mortality: increases in population density, in neighboring provinces, can lead to higher mortality rates, but the significance of this effect is not sufficient to reject the hypothesis of no effect at all. Future deeper research is needed to better explain this relationship.
Overcrowding in households (overcrowding) is intuitive in that there is a strong positive relationship between overcrowding in households and COVID-19 mortality rates. Overcrowding is a serious issue in less developed countries, and it is a consequence of the informal settlement and bad birth control policies, among other factors. Mortality is magnified by the fact that more individuals live in a household than normal given the number of bedrooms. In order to improve pandemic management, the government should minimize the contagion not only outside but also inside the household. Nevertheless, there is strong evidence that overcrowding produces negative exogenous interaction effects on mortality: increases in overcrowding, even in neighboring provinces, lead to lower mortality rates on a province. The indirect effect and the direct effect are counteracted, but the indirect effect is greater than the direct effect (see Table 4). The final effect of an increase in the proportion of overcrowded households is a small decrease in mortality rates. Policymakers should consider that an increase in overcrowding in households may lead to lower mortality rates, even though the size of the effect is small. This is another reason why poor provinces, which are more overcrowded in households, have lower mortality rates.
Population ethnic composition (White_1000_Inhab and Black_1000_Inhab) produces significant effects on mortality rates. These effects are spatial interaction effects. An increase in the white population in neighboring provinces would lead to higher mortality rates in a province; on the other hand, an increase in the black population in neighboring provinces leads to lower mortality rates in a province. These effects are contrary to the effects of ethnic groups found by [46] for the US. It is interesting to acknowledge that a white population has a higher probability of dying according to the results of the model for the case of Peru. We reject the hypothesis of positive effects in favor of negative effects for skin color and null effect of other variables.
ENR validates the effects for poverty, population density, overcrowding, vulnerable population, health insurance, white population, black population, hypertension2 (second way of measuring diagnosed hypertension), obesity, and inequity in health. However, the size of the effect for the vulnerable population, health insurance, white population, black population, hypertension2, obesity, and inequity in health is relatively small (i.e., 0.001 < effect < 0.01). These results prove the robustness of the . The following Table 8 shows the direct and indirect (from spatial spillovers) impacts predicted by the model:

Table 8.
Direct, indirect, and total effects predicted after .
First, keeping the remaining variables constant, the effect of an increase in one unit of Composite_Poverty_Index produces a significant direct decrease of 0.029% deaths per 1000 inhabitants, and the same increase in neighboring provinces produces an insignificant increase of 0.008% deaths per 1000 inhabitants. The total effect is a significant decrease of 0.021 in the deaths per 1000 inhabitants. Second, an increase of 1% in logPD_1000, is related to a direct increase of 0.079% in deaths per 1000 inhabitants, and an insignificant indirect increase of 0.038%. The total effect is insignificant. Third, an increase of one percentage unit in overcrowding would lead to a positive direct effect of 0.019% in deaths per 1000 inhabitants, and a negative indirect effect of 0.031%. Both effects are statistically significant, and the total effect is insignificant. After reviewing the marginal effects, it is clear that provinces vulnerable to COVID-19 mortality are those with higher economic activity, high population density, and a high proportion of overcrowded households. Most of the indirect effects are insignificant except for overcrowding. However, overcrowding’s direct and indirect effects are counteracted, and then, policies linked to this variable may not produce the desired impact. We recommend that future research should evaluate the impact of overcrowding in households on mortality rates.
The following provinces listed in Table 9 have zero reported deaths (if there were zero COVID-19 cases, the deaths were replaced by zero):

Table 9.
Province forecast of deaths.
The ENR regression model was cross-validated using a repeated k-fold algorithm, it resulted in parameters and . It predicts demand based on vulnerability characteristics against COVID-19 mortality. The predictions vary from 0.20 to 1.28 deaths per 1000 inhabitants. Additionally, we have prediction categories from low to very high demand. According to their observable characteristics, it is not very likely that these provinces have zero deaths, as is reported on the dataset. In Figure 4, we plot the spatial distribution of the mortality rates. In the first panel, we show the real mortality rates; in the second, the rates predicted by , and in the third panel, we show the predictions for ENR model. We observe that the predictions of are higher in the north. We have high demand predictions in the coastal and jungle regions. In the highlands, the predominant category is high, and in central-south highlands, medium demand is predominant. Low demand is present in the south and central-north highlands.
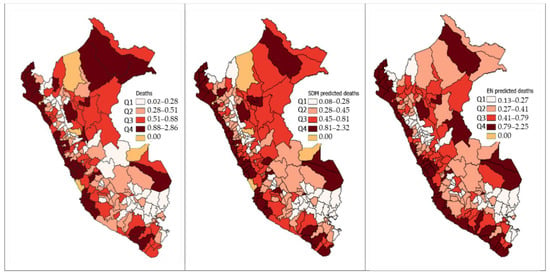
Figure 4.
Number of deaths mapped by COVID-19 (per 1000 inhabitants) versus the predictions. First panel shows the actual mortality rates. Second panel shows the predicted mortality rates by SDM (1,1,1). Third panel shows the forecasts of ENR. Authors’ own elaboration.
The government should deliver to very high demand provinces first; furthermore, the central warehouses for PRRSGS must be located in coastal provinces and jungle provinces with very high-demand categories. The second echelon of the delivery could be from very high-demand provinces to high-, medium-, and low-demand ones. The number of warehouses depends on the number of spatial clusters of very high-demand points. Across the coastal region, delivery must use the main road to reach all very high-demand provinces and, then, in a second echelon, reach the other provinces. In the second echelon, the delivery must be from coastal to highlands and from jungle to highlands. The low-demand provinces must be provided with PRRSGS at the end so that we can prioritize medium- and high-demand provinces. To follow this delivery strategy, policymakers should consider the predictions of the model complemented by the predictions of the ENR model. This must be performed in order to overcome data limitations and to establish a delivery strategy for PRRSGS. As pandemic outbreak evolves, more and more supplies will be needed, so establishing a national-level delivery strategy is very important for successful pandemic management. In Figure 4, we also observe spatial clusters in the coastal and jungle regions. The delivery of PRRSGS must be made first in the clusters of high COVID-19 mortality, and then, the supplies must be delivered to the medium-and low-demand quartiles, according to the spatial distribution. If we consider the forecasts of demand present in the third panel of Figure 4, we also find that, in coastal and jungle regions, we have spatial clusters with high COVID-19 mortality.
5. Discussion
Based on the results of this work, we summarize the managerial and research implications:
The highly vulnerable provinces are those with lower poverty, good economic performance, and high urban population density (Population density: total population divided by total urban area for each province). Economic activity is related to population density and agglomeration, and provinces that maintain a certain level of economic activity tend to have higher mortality rates; that is the reason why we need a supporting framework for economic reactivation. High economic activity provinces suffer from a lack of supply for PRRSGS; that is the reason why we have found this effect.
In order to mitigate risks, decision-makers must pay attention to economic performance, population density, and household overcrowding. High mortality should be expected in highly vulnerable provinces with the previously defined characteristics; thus, risk mitigation policies must consider these vulnerability drivers. Population overcrowding in households was a significant predictor, but its direct effect is counteracted by its indirect spatial spillover effect, so more research is needed to clarify its impact on COVID-19 mortality.
There are significant spatial patterns in COVID-19 mortality rates (based on Moran’s statistic’s significance). This allowed us to trace a delivery strategy based on spatial clusters. We must, first, deliver to very high-demand provinces; second, deliver PRRSGS to neighboring high-demand provinces; and third, deliver to medium- and low-demand provinces. This delivery is from the high-demand points to the low- and medium-demand points. Policymakers should treat forecasts as complementary information and include the zero-death provinces into the general delivery strategy.
The forecasts are made based on province-level observable characteristics and suggest that we can follow the same strategy of delivery from coastal and jungle regions to highlands.
Pandemic preparedness, response, and recovery success depend on the methodology used to estimate the demand. This methodology guarantees that we can used vulnerability to COVID-19 mortality as a proxy for demand. Deprivation costs are high where there is high mortality against COVID-19, so we propose that a demand assessment must follow this criterion.
6. Conclusions
In this paper, we argued that a supportive framework for economic reactivation can be built based on vulnerability against COVID-19 mortality. This vulnerability arises from deprivation costs that are high as a consequence of the pandemic. Following this idea, we decided to estimate SDMs, where the dependent variable was the mortality rates for COVID-19 at the provincial level. This regression model helped to understand, first, the difference between mortality rates as the difference in vulnerability against COVID-19. The rest of the methodological steps included a model selection and post-estimation analysis that helped to find the best model and to use their predictions to trace a delivery strategy for PRRSGS. The demand for PRRSGS was proxied by the predicted COVID-19 mortality rates, which determined vulnerability against COVID-19 mortality.
The principal result for the regression analysis is that , the more general SDM, is the one that better fits the data, suggesting that there are statistically significant endogenous, exogenous, and correlated spatial interaction effects. This means that mortality rates exhibit spatial patterns. Two branches of literature were analyzed: the prediction-oriented machine learning literature and the social determinants of health literature. The evidence favors the hypotheses related to the machine learning literature for the early stages of the pandemic. Poverty, population density, and overcrowding remained the main predictors. However, overcrowding’s direct and indirect (spatial spillovers) effects are counteracted, so further research is needed to clarify the relationship between overcrowding and mortality rates. Provinces are inevitably returning to their long-run level of economic activity, and high mortality rates exist because there is scarcity in essential supplies that are needed to save lives regarding infection with COVID-19. Population density is positively related to mortality rates, so for provinces with high population density (overcrowding in cities), policymakers should expect higher mortality rates, and thus, the delivery of PRRSGS must be prioritized. The rest of the vulnerability drivers related to demographics, health insurance, and health system performance were not significant, and thus, empirically, we reject the hypotheses regarding these variables.
The hypothesis of provinces’ vulnerability to natural disasters (and all of its blocks) is partially accepted; there are important sources of vulnerability based on poverty, population density, and overcrowding in households. It is important to notice that poverty interacts with other variables theoretically and empirically, and in this case, it helps to define the effect of population density and overcrowding in households. Poor provinces are more overcrowded in households but less overcrowded in cities; they also have lower mortality rates, which means that overcrowding in households is negatively correlated with mortality rates. Overcrowding in cities or population density is positively correlated with COVID-19 mortality. These correlations include spatial interactions, which were important at the moment when the final effect on the mortality rates is determined. Regarding age, sex, skin-color, chronic disease prevalence, obesity, and health system performance, we have not arrived at statistically significant results, and thus, we cannot reject the null hypothesis of no relationship between mortality rates and these variables.
This paper contributes empirical methodologies, and statistical (spatial regression) and machine learning (ENR)-related methods applied to the field of humanitarian logistics. The evidence provided by this paper mean new insights for a specific case, and spatial interaction effects represent new mechanisms through which vulnerability drivers affect COVID-19 mortality. There is an increasing demand of empirical methodologies in this field because they help to integrate academia with practitioners. Consequently, the novelty in this paper regarding similar papers on the field is the application of humanitarian logistics principles to a data-driven analysis, using the insights obtained to build a framework for economic reactivation based on an analysis of the demand and identifying the goods needed for the delivery of humanitarian aid.
The economy must be reactivated considering humanitarian logistics principles, which requires an assessment of the demand for humanitarian aid, considering COVID-19 mortality as the main proxy for this demand. The applied methodology shows that data-driven techniques are especially useful in improving disaster management techniques and decision-making. This methodology can be replicated with other cases to optimize the policies for pandemic response and recovery phases. However, future research is still needed to overcome the limitations of data and to validate these first exploratory results. Further research in the field should be encouraged in order to link practitioners with academia; this can be performed by using empirical methods in humanitarian logistics research. This paper contributes to the empirical literature, but research in the field should be further expanded in order to overcome the limitations and other related studies.
Author Contributions
Conceptualization, R.R.-R., R.Q., I.d.B.J. and M.C.; methodology, R.Q., R.R.-R. and A.L.; software, R.Q.; validation, R.R.-R., A.L. and R.Q.; formal analysis, R.Q., R.R.-R. and A.L.; investigation, I.d.B.J., M.C. and R.Q.; resources, R.R.-R., I.d.B.J. and M.C.; data curation, R.Q.; writing—original draft preparation, R.Q., I.d.B.J. and M.C.; writing—review and editing, A.L., I.d.B.J., M.C., R.R.-R. and R.Q.; visualization, R.R.-R. and A.L. supervision, M.C.; project administration, M.C.; funding acquisition, M.C., R.R.-R. and I.d.B.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Vicerrectorado de Investigación (VRI) y Centro de Investigación de la Universidad del Pacífico (CIUP), Universidad Nacional Abierta y a Distancia and the Coordination for the Improvement of Higher Education Personnel-Brazil (CAPES), Procad Defesa 88887.387760/2019-00.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data as well as software program used to perform the estimation is attached in the following link: https://github.com/renatoquiliche/COVID19-socsi (accessed on 20 December 2020).
Conflicts of Interest
Authors declare no conflicts of interest.
References
- Presidencia del Consejo de Ministros. Decreto Supremo que precisa los alcances del artículo 8 del Decreto Supremo N 044-2020-PCM, que declara el estado de emergencia nacional por las graves circunstancias que afectan la vida de la nación a consecuencia del brote del COVID-19. In Decreto Supremo N° 045-2020-PCM; El Peruano: Lima, Peru, 2020. [Google Scholar]
- Presidencia del Consejo de Ministros. Decreto Supremo que modifica el Decreto Supremo N° 116-2020-PCM, Decreto Supremo que establece las medidas que debe seguir la ciudadanía en la nueva convivencia social y prorroga el Estado de Emergencia Nacional por las graves circunstancias que afectan la vida de la Nación a consecuencia del COVID-19, modificado por los Decretos Supremos N° 129-2020-PCM, N° 135-2020-PCM, N° 139-2020-PCM, N° 146-2020-PCM, N° 151-2020- PCM, N° 156-2020-PCM, N° 162-2020-PCM y N° 165-2020-PCM. In Decreto Supremo N° 170-2020-PCM; El Peruano: Lima, Peru, 2020. [Google Scholar]
- Poder Ejecutivo. Decreto de urgencia que establece el retiro extraordinario del fondo de pensiones en el sistema privado de pensiones como medida para mitigar efectos económicos del aislamiento social obligatorio y otras medidas. In Decreto de Urgencia N° 034-2020; El Peruano: Lima, Peru, 2020. [Google Scholar]
- Poder Ejecutivo. Decreto de urgencia que establece medidas para reducir el impacto en la economía peruana, de las disposiciones de prevención establecidas en la declaratoria de estado de emergencia nacional ante los riesgos de propagación del COVID-19. In Decreto de Urgencia N° 033-2020; El Peruano: Lima, Peru, 2020. [Google Scholar]
- Ministerio del Interior. Aprueban protocolo para la implementación de las medidas que garanticen el ejercicio excepcional del derecho a la libertad de tránsito en el marco del Estado de Emergencia Nacional declarado mediante D.S. N° 044-2020-PCM. In Resolución Ministerial N° 304-2020-IN; El Peruano: Lima, Peru, 2020. [Google Scholar]
- Ministerio de Economía y Finanzas. Aprueban el Reglamento Operativo del Fondo de Apoyo Empresarial a la MYPE (FAE-MYPE). In Resolución Ministerial N° 124-2020-EF/15; El Peruano: Lima, Peru, 2020. [Google Scholar]
- Montoro, C.; Pérez, F.; Herrada, R. Medidas del BCRP Frente a la Pandemia del Nuevo Coronavirus. Rev. Moneda 2020, 182, 10–18. [Google Scholar]
- Brodeur, A.; Gray, D.; Islam, A.; Bhuiyan, S. A Literature Review of the Economics of Covid-19. IZA Discussion Paper No. 13411. 2020. Available online: https://ssrn.com/abstract=3636640 (accessed on 20 December 2020).
- Acemoglu, D.; Chernozhukov, V.; Werning, I.; Whinsnton, M.D. A Multi-Risk SIR Model with Optimally Targeted Lockdown Working Paper No. 27102; Working Paper Series; National Bureau of Economic Research: Cambridge, MA, USA, 2020. [Google Scholar] [CrossRef]
- Béland, L.-P.; Brodeur, A.; Mikola, D.; Wright, T. The Short-Term Economic Consequences of Covid-19: Occupation Tasks and Mental Health in Canada; Social Science Research Network: New York, NY, USA, 2020; Available online: https://papers.ssrn.com/abstract=3602430 (accessed on 20 December 2020).
- Overstreet, R.E.; Hall, D.J.; Hanna, J.B.; Rainer, R.K. Research in humanitarian logistics. J. Humanit. Logist. Supply Chain Manag. 2011, 1, 114–131. [Google Scholar] [CrossRef]
- Holguín-Veras, J.; Pérez, N.; Jaller, M.; Van Wassenhove, L.N.; Aros-Vera, F. On the appropriate objective function for post-disaster humanitarian logistics models. J. Oper. Manag. 2013, 31, 262–280. [Google Scholar] [CrossRef]
- Leiras, A.; Junior, I.D.B.; Peres, E.Q.; Bertazzo, T.R.; Yoshizaki, H.T.Y. Literature review of humanitarian logistics research: Trends and challenges. J. Humanit. Logist. Supply Chain Manag. 2014, 4, 95–130. [Google Scholar] [CrossRef]
- Renteria, R.; Chong, M.; de Brito Junior, I.; Luna, A.; Quiliche, R. An entropy-based approach for disaster risk assessment and humanitarian logistics operations planning in Colombia. J. Humanit. Logist. Supply Chain Manag. 2021, 11, 428–456. [Google Scholar] [CrossRef]
- Andersen, L.M.; Harden, S.R.; Sugg, M.M.; Runkle, J.D.; Lundquist, T.E. Analyzing the spatial determinants of local Covid-19 transmission in the United States. Sci. Total Environ. 2021, 754, 142396. [Google Scholar] [CrossRef]
- Khalatbari-Soltani, S.; Cumming, R.G.; Delpierre, C.; Kelly-Irving, M. Importance of collecting data on socioeconomic determinants from the early stage of the COVID-19 outbreak onwards. J. Epidemiol. Community Health 2020, 74, 620–623. [Google Scholar] [CrossRef] [PubMed]
- Pedrosa, N.L.; de Albuquerque, N.L.S. Spatial analysis of COVID-19 cases and intensive care beds in the state of Ceará, Brazil. Cienc. Saude Coletiva 2020, 25, 2461–2468. [Google Scholar] [CrossRef]
- Rollston, R.; Galea, S. COVID-19 and the Social Determinants of Health. Am. J. Health Promot. 2020, 34, 687–689. [Google Scholar] [CrossRef]
- Sugg, M.M.; Spaulding, T.J.; Lane, S.J.; Runkle, J.D.; Harden, S.R.; Hege, A.; Iyer, L.S. Mapping community-level determinants of COVID-19 transmission in nursing homes: A multi-scale approach. Sci. Total Environ. 2020, 752, 141946. [Google Scholar] [CrossRef]
- White, E.R.; Hébert-Dufresne, L. State-level variation of initial COVID-19 dynamics in the United States. PLoS ONE 2020, 15, e0240648. [Google Scholar] [CrossRef]
- Gupta, A.; Banerjee, S.; Das, S. Significance of geographical factors to the COVID-19 outbreak in India. Model. Earth Syst. Environ. 2020, 6, 2645–2653. [Google Scholar] [CrossRef]
- Benzakoun, J.; Hmeydia, G.; Delabarde, T.; Hamza, L.; Meder, J.; Ludes, B.; Mebazaa, A. Excess out-of-hospital deaths during the COVID -19 outbreak: Evidence of pulmonary embolism as a main determinant. Eur. J. Heart Fail. 2020, 22, 1046–1047. [Google Scholar] [CrossRef]
- Zhang, C.H.; Schwartz, G.G. Spatial Disparities in Coronavirus Incidence and Mortality in the United States: An Ecological Analysis as of May 2020. J. Rural. Health 2020, 36, 433–445. [Google Scholar] [CrossRef]
- Bruno, G.; Wemole, R.; Ronsivalle, G.B.; Foresti, L.; Poledda, G. A Prototype Model of Georeferencing the Inherent Risk of Contagion from COVID-19; ResearchGate preprint: Rome, Italy, 2020. [Google Scholar] [CrossRef]
- Carrillo-Larco, R.M.; Castillo-Cara, M. Using country-level variables to classify countries according to the number of confirmed COVID-19 cases: An unsupervised machine learning approach. Wellcome Open Res. 2020, 5, 56. [Google Scholar] [CrossRef]
- Chakraborti, S.; Maiti, A.; Pramanik, S.; Sannigrahi, S.; Pilla, F.; Banerjee, A.; Das, D.N. Evaluating the plausible application of advanced machine learnings in exploring determinant factors of present pandemic: A case for continent specific COVID-19 analysis. Sci. Total Environ. 2021, 765, 142723. [Google Scholar] [CrossRef]
- Rustam, F.; Reshi, A.A.; Mehmood, A.; Ullah, S.; On, B.-W.; Aslam, W.; Choi, G.S. COVID-19 Future Forecasting Using Supervised Machine Learning Models. IEEE Access 2020, 8, 101489–101499. [Google Scholar] [CrossRef]
- Crandall, M.S.; Weber, B.A. Local Social and Economic Conditions, Spatial Concentrations of Poverty, and Poverty Dynamics. Am. J. Agric. Econ. 2004, 86, 1276–1281. [Google Scholar] [CrossRef] [Green Version]
- Wardhana, D.; Ihle, R.; Heijman, W. Agro-clusters and Rural Poverty: A Spatial Perspective for West Java. Bull. Indones. Econ. Stud. 2017, 53, 161–186. [Google Scholar] [CrossRef]
- Alexander, D.E. Principles of Emergency Planning and Management; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Smith, C.D.; Mennis, J. Incorporating Geographic Information Science and Technology in Response to the COVID-19 Pandemic. Prev. Chronic Dis. 2020, 17, 246. [Google Scholar] [CrossRef] [PubMed]
- Zeckhauser, R. The economics of catastrophes. J. Risk Uncertain. 1996, 12, 113–140. [Google Scholar] [CrossRef]
- Pindyck, R.S.; Wang, N. The Economic and Policy Consequences of Catastrophes. Am. Econ. J. Econ. Policy 2013, 5, 306–339. [Google Scholar] [CrossRef] [Green Version]
- Yoshizaki, H.; de Brito Junior, I.; Hino, C.; Aguiar, L.; Pinheiro, M. Relationship between Panic Buying and Per Capita Income during COVID-19. Sustainability 2020, 12, 9968. [Google Scholar] [CrossRef]
- Gutjahr, W.J.; Fischer, S. Equity and deprivation costs in humanitarian logistics. Eur. J. Oper. Res. 2018, 270, 185–197. [Google Scholar] [CrossRef]
- Alibaba. COVID-19 Outbreak Hospital Response Strategy; Zhejiang University School of Medicine: Hangzhou, China, 2020. [Google Scholar]
- Alibaba. Handbook of COVID-19 Prevention and Treatment; Zhejiang University School of Medicine: Hangzhou, China, 2020. [Google Scholar]
- Guliyev, H. Determining the spatial effects of COVID-19 using the spatial panel data model. Spat. Stat. 2020, 38, 100443. [Google Scholar] [CrossRef]
- Sun, F.; Matthews, S.A.; Yang, T.-C.; Hu, M.-H. A spatial analysis of the COVID-19 period prevalence in U.S. counties through 28 June 2020: Where geography matters? Ann. Epidemiol. 2020, 52, 54–59.e1. [Google Scholar] [CrossRef]
- Schwalb, A.; Seas, C. The COVID-19 Pandemic in Peru: What Went Wrong? Am. J. Trop. Med. Hyg. 2021, 104, 1176–1178. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Risco, A.; Mejia, C.R.; Delgado-Zegarra, J.; Del-Aguila-Arcentales, S.; Arce-Esquivel, A.A.; Valladares-Garrido, M.J.; Del Portal, M.R.; Villegas, L.F.; Curioso, W.H.; Sekar, M.C.; et al. The Peru Approach against the COVID-19 Infodemic: Insights and Strategies. Am. J. Trop. Med. Hyg. 2020, 103, 583–586. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Risco, A.; Del-Aguila-Arcentales, S.; Yáñez, J.A. Telemedicine in Peru as a Result of the COVID-19 Pandemic: Perspective from a Country with Limited Internet Access. Am. J. Trop. Med. Hyg. 2021, 105, 6–11. [Google Scholar] [CrossRef]
- Turner-Musa, J.; Ajayi, O.; Kemp, L. Examining Social Determinants of Health, Stigma, and COVID-19 Disparities. Health Care 2020, 8, 168. [Google Scholar] [CrossRef]
- Burström, B.; Tao, W. Social determinants of health and inequalities in COVID-19. Eur. J. Public Health 2020, 30, 617–618. [Google Scholar] [CrossRef] [PubMed]
- Fielding-Miller, R.K.; Sundaram, M.E.; Brouwer, K. Social determinants of COVID-19 mortality at the county level. PLoS ONE 2020, 15, e0240151. [Google Scholar] [CrossRef] [PubMed]
- Thakur, N.; Lovinsky-Desir, S.; Bime, C.; Wisnivesky, J.P.; Celedón, J.C. The Structural and Social Determinants of the Racial/Ethnic Disparities in the U.S. COVID-19 Pandemic. What’s Our Role? Am. J. Respir. Crit. Care Med. 2020, 202, 943–949. [Google Scholar] [CrossRef] [PubMed]
- Engle, S.; Stromme, J.; Zhou, A. Staying at Home: Mobility Effects of COVID-19; SSRN: New York, NY, USA, 2020. [Google Scholar]
- Elhorst, J.P. Applied Spatial Econometrics: Raising the Bar. Spat. Econ. Anal. 2010, 5, 9–28. [Google Scholar] [CrossRef]
- Kelejian, H.H.; Prucha, I.R. A Generalized Moments Estimator for the Autoregressive Parameter in a Spatial Model. Int. Econ. Rev. 1999, 40, 509–533. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Lin, H. Spatial Weights Matrix. In Encyclopedia of GIS; Springer: Berlin/Heidelberg, Germany, 2008; p. 1113. [Google Scholar] [CrossRef]
- O. Ogutu, J.; Schulz-Streeck, T.; Piepho, H.-P. Genomic selection using regularized linear regression models: Ridge regression, lasso, elastic net and their extensions. BMC Proc. 2012, 6, S10. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).