Abstract
The growing demand for electrical energy and the impact of global warming leads to a paradigm shift in the power sector. This has led to the increased usage of renewable energy sources. Due to the intermittent nature of the renewable sources of energy, devices capable of storing electrical energy are required to increase its reliability. The most common means of storing electrical energy is battery systems. Battery usage is increasing in the modern days, since all mobile systems such as electric vehicles, smart phones, laptops, etc., rely on the energy stored within the device to operate. The increased penetration rate of the battery system requires accurate modelling of charging profiles to optimise performance. This paper presents an extensive study of various battery models such as electrochemical models, mathematical models, circuit-oriented models and combined models for different types of batteries. It also discusses the advantages and drawbacks of these types of modelling. With AI emerging and accelerating all over the world, there is a scope for researchers to explore its application in multiple fields. Hence, this work discusses the application of several machine learning and meta heuristic algorithms for battery management systems. This work details the charging and discharging characteristics using the black box and grey box techniques for modelling the lithium-ion battery. The approaches, advantages and disadvantages of black box and grey box type battery modelling are analysed. In addition, analysis has been carried out for extracting parameters of a lithium-ion battery model using evolutionary algorithms.
1. Introduction
The lifetime of any battery depends on its physical properties. The aging of battery cells is also nonlinear. A battery’s lifetime cannot be extended by minimising the power consumption at a particular point. Rather, it depends on the way the power is consumed, as well as current extraction patterns and current levels. Moreover, continuous drawing of high current inhibits the residual capacity [1]. Battery Management system (BMS) are essential to ensure the safe, fail-safe and efficient operation of batteries.
The main function of battery management systems is ensuring the safe operation of a battery, controlling a battery’s charge and discharge process, cell balancing, over temperature protection and estimating the state-of-charge (SoC) by measuring voltage, current and temperature. BMS monitors the conditions and state of the battery such as SoC, state-of-health (SoH), Depth of Discharge (DoD) and operating temperature [2,3]. However, these states are to be inferred from the state estimators that depend on the battery model. Therefore, the modelling of a battery becomes an important role in studying, estimating or predicting the real-time operation of the battery.
1.1. Significance of Battery Modelling
The mathematical modelling of a battery is significant because of the following reasons:
- (i)
- Development of efficient BMS.
- (ii)
- Key in the improvement of charging/discharging techniques and the enhancement of battery capacity.
- (iii)
- Need to capture the influence of power consumption on the battery.
- (iv)
- To prevent serious damage to batteries from overcharging or over-discharging.
- (v)
- Faster and safer way to study battery behaviour under different operating conditions.
- (vi)
- Identifying the operating limits that achieve best lifetime for specific applications.
1.2. Contributions of the Proposed Study
This paper examines numerous battery models for various types of batteries, including electrochemical models, mathematical models, circuit-oriented models and combination models. There is a lot of scope for researchers to investigate the deployment of Artificial Intelligence in a variety of disciplines as it emerges around the world and makes laborious tasks easier. As a result, the applications of numerous machine learning and meta-heuristic methods for battery management systems are discussed in this paper. Furthermore, using evolutionary algorithms, a study was conducted to extract parameters from a lithium-ion battery model.
2. Types of Battery Modelling
A wide variety of battery models have been developed with differing complexities which can be useful in various application areas [4,5,6,7,8,9,10]. According to the degree of physical insight, battery models can be differentiated into three levels, viz., white box model (e.g., electrochemical model), grey box model (e.g., circuit-oriented model) and black box model (e.g., artificial neural network (ANN) model) [11]. An important factor in the modelling of a battery is the estimation of battery parameters. Different modelling strategies for extracting the battery parameters are electrochemical, mathematical, circuit-oriented and data-driven [12,13].
The average lifetime of a battery is determined from its degradation capacity from its initial value. In particular, if the batteries are employed for electric vehicle applications, the lifetime of the battery is reduced due to acceleration and braking, which requires ten times more power than the required average power. To overcome this drawback, it is advised not only to improve the required specific energy but also to model a battery using optimisation techniques to improve efficiency and reliability. The average battery efficiencies of cells such as Li-ion and LiFePO4 are 92% and 95%, respectively [14]. The Depth of Discharge for both type of cells is 80%. The modelling of any battery affects the efficiency of the battery to a great extent.
2.1. Electrochemical Modelling of a Battery
Battery chemistry can be extensively described by electrochemical modelling, thus making these models precise. They rely on electrochemical reactions that take place in the electrodes and the electrolyte deployed. Various chemical reactions that happen inside the battery can be depicted using a set of non-linear differential equations [2]. The difficulty of identifying the physical parameters of the fundamental electrochemical-based Doyle–Fuller–Newman (DFN) battery model was studied by Joel C. Forman [15]. Doyle, Fuller and Newman proposed a Pseudo-Two-Dimensional (P2D) model and addressed complex mechanisms using a group of partial differential equations and algebraic equations [16,17,18]. Meng showed that the Single Particle Model (SPM) is simpler than the P2D model as it uses fewer parameters [19], but its use is restricted to low current densities.
The dynamic working of a battery can be expressed in terms of the electrochemical principles that it works on. This method of representation is known as electrochemical battery modelling, whereby the effect of the various electrochemical reactions taking place in the cell on the cell potential are written in the form of a set of partial differential equations. This involves the combining of electrochemical mechanisms and electrical principles to obtain suitable and efficient models that describe a system. These models are known to be advantageous as they are a true representation of what occurs in the cell and are known to be very accurate. Most of the current models relate mass transfer phenomena (such as solid diffusion) and current laws (Ohms law). Another approach is to couple thermal equations to the electrochemical equations. However, without any simplification, models of this complexity can only be solved using powerful computational tools and methods such as Computational Fluid Dynamics (CFD) frameworks. Thermal coupled models have recently been developed that are suited to evaluate the model functioning in Indian tropical climatic conditions [20]. Control-oriented thermal-electrochemical modelling and validation of large-size prismatic lithium batteries have also been recently conducted for commercial applications [21].
One of the first uses of electrochemical modelling was in dealing with nonlinear systems. Nonlinear systems often involve partial differential equations with various unknown variables and become hard to solve. Thus, in an attempt to gain clarity, electrochemical principles were incorporated and the number of variables in the formed partial derivate was seen to reduce, making this method appreciable in solving nonlinear battery modelling systems. DC nonlinear battery behaviour has been expressed in electrochemical battery modelling methods right from the late 1990s. The research involved realising the voltage-source SPICE model, which implements the electrochemical equations using behavioural sources and integrates the short-term linear impedance behaviour, with the long-term nonlinear DC resistance behaviour [22].
Let us take the case of a lithium-ion battery. One of the most commonly used batteries, their performance is greatly influenced by various factors. In order to simulate and predict the battery effectively, it is important to use reasonable model of lithium-ion battery. This model must be able to factor in the various parameters that affect its working, which are ultimately dependent on the electrochemical working and characteristics of the battery. Thus, electrochemical models have been used as all the parameters used in these models have a clear physical measurable significance. This battery has been represented by three models, namely the P2D model, SP model and extended SP model. P2D model can describe the internal and external characteristics of lithium-ion battery at the same time. Proposed by J. Newman, M. Doyle and T.F. Fuller, this model deals with the behaviour of lithium ions in the process of charging and discharging and describes the behaviour of lithium ions in detail. It is mainly used in the electrode analysis of LiCoO2 material. However, this model is characterised by partial differential equations and nonlinear algebra, with many iterations.
In order to simplify calculations, the SP model was developed for the condition of low-rate charge and discharge. This model makes the assumption of even distribution and concentration of lithium ions in the liquid phase everywhere in the battery and also assumes that the electric potential of the solid phase is constant in the electrode. Compared with the P2D model, the SP model has fewer solving equations, fewer parameters and higher solving efficiency. However, this oversimplification reduced the accuracy of the model. In order to deal with these shortcomings, an extended SP model was developed, in which liquid phase diffusion and heterogenous reactions were considered. While the SP model simplifies the P2D model by virtually eliminating the partial differential equations that deal with liquid phase diffusion and also simultaneously reduces the electrode to a single particle of consideration, the extended SP model further simplifies the electrode into a single active particle but no longer directly solves the partial differential equation by iteration, but uses curve fitting or approximate solution to process the partial differential equation. Although the complexity of the model has increased by this process in the computation of an extended SP model, the actual computational efficiency has not decreased too much due to the avoidance of iterative solving [23].
Though there are numerous electrochemical models available and developed, it is almost recommended to study the battery and come up with an accurate model that is able to describe the system in depth. An example of developing an electrochemical model has been explained by a recent research discussed further on. A novel composite battery model can easily be made using various known electrochemical battery models. For the composite battery model developed by [24], the State of Charge of the battery was considered as a state variable in the system, denoting the number of the state vectors present in the system. The output voltage of the battery was expressed as . The composite model is built based on three different electrochemical models as follows:
Shepherd model:
Unnewehr universal model:
Nernst model:
In order to frame Equations (1)–(3), the reactions occurring at the anode and cathode of the battery and the electrolyte ion transfer process are considered and these empirical simplified equations were evaluated, instead of the conventional partial differential equation formation strategy [24]. The electrochemical models of Equations (1)–(3) reflect the relationship between the terminal voltage and the SoC (). R is the internal resistance (Ohmic resistance) and changes with the charging/discharging state of the battery (Rik). K1/ from Equation (1) and K2· from Equation (2) reflect the polarisation resistances of the battery [24]. K3·ln () and K4·ln (1 − ) from Equation (3) represent the influence of the internal temperature and material activity during the electrochemical reaction of the battery, respectively [24]. Combining these equations, the model developed is as follows:
While the above equation is used to describe the state equation based on the composite battery mode, the output voltage was expressed as:
where K0 was used to describe the Open Circuit Voltage (OCV) voltage of the battery, which was not accounted for in Equations (1)–(3) [24]. This shows that the mere adding up of known models would not be possible in the framing of these models, and experimental data are needed. With the help of the data that are derived, a relevant model is developed. The importance of empirical formulation of these models is thus stressed in this example.
Electrochemical models have also been used in the battery modelling of electric vehicles. A specialised set of differential equations are used to work on these models, which are based on diffusion, as discussed earlier. Ref. [25] describes various types of electrochemical modelling that are currently carried out in electric vehicles. The study also explained the ways to compute these equations using various numerical techniques. The conventional analytic method is used to find an exact solution using Eigen function series expansion or Laplace transform methodologies and solve the partial differentials described earlier. Two approximation models have been developed, namely Pade’s approximation model and the integral approximation model. Pade’s approximation model is used to expand the infinitely differentiable hyperbolic functions in a power series at the origin. The integral method forms a distribution across the cell for the distributed variable of interest and converts the partial differential equations into ordinary differentiation equations, thus making them easier to compute. The finite element method involves approximating the response over subdomains and then developing transfer functions or state-space equations for the nodal dynamics. A subset of this analysis in which convergence is not guaranteed but simplicity is achieved is the finite differential method. The Ritz method of evaluation works over domains such as Fourier series with sinusoidal functions. These are just few of the many techniques that can be used.
Summarising, there is no doubt that good electrochemical battery models serve as some of the most accurate among battery models, due to the very fact that they can mathematically explain key behaviours of a battery at the microscopic scale based on the basis of chemical reactions occurring inside the battery in the liquid phase and in the electrode. Considering accuracy as the most important aspect of modelling, these models are excellent and can be used to complement experimental data for evaluation of other models. One advantage of electrochemical models over real data is that internal states are fully observable, allowing ‘virtual measurements’ of quantities that cannot be measured in practice. They are able to even record the changes caused by temperature changes. As these temperature changes result in different responses from an electrochemical perspective, these models can account for fluctuations and changes in temperature [26].
Although these electrochemical models have high precision, the highly detailed description presents complex model structures which are tedious to configure and have low-speed operation. A set of partial differential equations are required to depict the ion diffusion phenomena, mass and charge balance, ion distribution and temperature effects and hence, these models become too complicated. Analytical solutions do not exist for such models and parameter identification is very challenging in this type of approach. Thus, their suitability for real time battery management in hybrid electric vehicles is not promising [27]. Some researchers have simplified and proposed a series of simplified models in order to improve practicality at the risk of model accuracy [15,28].
2.2. Mathematical Modelling of a Battery
Based on the Shepherd discharge model, mathematical models are mainly developed to predict system-level behaviour. Empirical equations or math-based stochastic models are used in mathematical models, which only evaluate the charge recovery effect and ignores all other factors. The number of equations is reduced and simplified compared to the electrochemical model [29]. These models monitor the non-linear relationship between the real-time operation of the battery and the discharge rate without considering the recovery effect [7,30]. The use of mathematical models is very low, because the relation with the parameters of the model and I-V characteristics is not sufficient [16].
Shepherd discharge model, modified Shepherd discharge model and linear regression are the common strategies used to extract the battery parameters. However, they are able to represent only the pulse discharge. Many typical mathematical battery models are regarded to function only for specific applications and produce results with 5–20% error [6].
2.3. Circuit-Oriented Modelling of a Battery
The aforementioned mathematical and electrochemical models are based on the high-level representation of the battery with analytic expressions based on physical laws. Consequently, these models are computationally complex and tailored to predict only individual behavioural aspects of the battery [31]. Circuit-Oriented Models (COM) are electrical equivalent models. Shuhui presented a comparison between COM and a mathematical model [6]. It is found that the performance of a Shepherd mathematical model derived from solving a system of equations or a regression technique varies for different battery types and is affected by a predefined function. So, it results in a badly deteriorated performance for the extracted battery model. Of all the battery models, COM are most suitable to represent the features of the battery [6,32]. There have been primarily five subclasses of COM: simple models, Thevenin-based models, impedance-based models, runtime-based models and combined models [33].
Simple models are resistance models that use an ideal voltage source and an internal resistance to represent the battery and they do not take into account charging/discharging rates, SoC and nonlinear effects. There is another impedance model called war burg impedance model in which the parameters are determined using a complicated Electrochemical Impedance Spectroscopy (EIS) method. Here, each component of the circuit is related to an electrochemical process of the battery and thus provides a good description of its internal behaviour. Since the complex impedance elements cannot be easily approximated by RC elements, the conversion of these models from the frequency domain to the time domain becomes complex. Therefore, the capability of these models to match the complex transient features of the battery is also limited. In addition, these models work only at fixed SoC values [31].
The runtime-based models use coupled electrical networks and look-up tables to determine SoC, battery runtime, cell voltage and thermal characteristics. They simulate the battery lifetime and voltage during the continuous current discharge process with reasonable accuracy, but they could not present good results when simulating variable current discharges due to their low precision modelling of transient battery characteristics. These models are substantially complex and inaccurate in predicting battery characteristics [24].
Thevenin subclass models provide the transient responses of the battery using resistor–capacitor (RC) networks [11,31], and these models are usually able to capture two time-dependent effects, depletion and recovery. They mimic the transient and steady-state behaviour of the battery. SoC is determined using the coulomb counting procedure or extended Kalman filter [34,35]. Circuit parameters are obtained by either (a) the battery’s time response using pulse discharge test, (b) by looking at the instantaneous voltage drop, the time constants of the charge depletion and recovery regions and the current, (c) the least square method, etc. [31]. The precise estimation of internal battery parameters is a difficult task, according to the literature, due to nonlinear effects. For parameter identification, an approach that compares the battery model simulation to the actual battery response using an objective function is used [12]. Multi-swarm particle swarm optimisation [36] and genetic algorithm (GA) [7] are used with an objective function to match several battery models to the same experimental data.
2.4. Combined Modelling of a Battery
The subclass of the combined model consists of the combination of different electrical models in order to combine the best attributes of each model, such as the correct prediction of the battery lifetime, steady-state and transient responses and accurate estimation of the SoC. One example is the Chen and Rincon-Mora model applied for the mathematical modelling of lithium polymer (LiPo) battery lifetime [36,37]. This model is capable of capturing the electrical and dynamic characteristics of the battery such as open circuit voltage, usable capacity and transient response. M. F. B. Binelo et al. combined coulomb counting and circuit-oriented model-based methods to estimate circuit parameters [33]. These different battery modelling techniques are useful in extracting battery parameters.
3. Battery Modelling Using Black Box Modelling Data-Driven Techniques
Many soft computing and optimisation techniques have been developed for battery parameter estimation. These techniques are called data-driven approaches which include (a) fuzzy-based estimation, (b) fuzzy-based neural network, (c) artificial neural network, (d) bio-inspired algorithm, (e) support vector machine, etc.
Since the default capabilities required for performing machine learning (ML) algorithms are generally included in BMS, ML techniques for modelling charging/discharging profiles are promising. Large amounts of data storage and robust data analytic tools are essential for ML model implementation. ML techniques are adaptable to any changes in the system and need minimum resources. Modelling is a fairly simple process that can be carried out based on the amount of information given. Modelling the charging/discharging profiles of battery systems can be performed using various machine learning tasks such as pattern recognition, clustering and classification. For predicting the charging and discharging behaviour of any battery system, models based on an artificial neural network and ML techniques other than ANN are also employed.
Machine learning outperforms traditional methods when it comes to predicting battery parameters due to its ability to deal with nonlinearity. By implementing a learning model, a general machine learning system for monitoring battery conditions can simulate the nonlinear relationship between input and output variables. The model’s input variables can be a variety of elements that affect battery performance, while the model’s output variables include battery state characteristics including SOC, remaining useful life (RUL) and capacity.
This framework consists of three steps: data pre-processing, training and estimation.
- The first phase is sample construction, after which the selected data are cleaned, normalised and transformed before being extracted and selected as samples for a machine learning algorithm. The data are then split into training and test sets. The second phase is to construct the model, which includes the “core” algorithms after which machine learning takes place. Support vector machine (SVM), support vector regression, artificial neural network, Bayesian principles, recurrent neural network and various optimisation algorithms such as genetic algorithms and simulated annealing methods are among the most widely used machine learning algorithms. The information gathered from the samples is preserved in a machine-readable manner for the following phase.
- Phase 2 involves using training and validation sets to find the best model.
- The third stage is model evaluation, which applies the knowledge gained in the previous step. SOC, RUL, etc., are estimated and the performance of the estimation models is evaluated using the estimation models determined in the previous phase. Root mean square error, absolute error and other metrics are commonly employed for model evaluation.
4. Battery Parameters Extraction Techniques Using Black Box Modelling Data-Driven Approach
Empirical modelling is a popular method for calculating charging and discharging profiles of battery systems in the literature. ML-based models, on the other hand, allow exceptional flexibility and need little resources for implementation in the case of battery systems used for renewable integration and other grid-related applications.
The proposed machine learning models are suitable for determining the charging profiles of battery systems. The model’s input variables are various factors that affect battery performance, while the model’s output variables are parameters of battery states such as SoC, SoH, RUL and Capacity. SoC is a metric for predicting electric vehicles’ (EV) remaining range and determining a safe management strategy to avoid overcharging and discharging the batteries. In practical applications, it is very difficult to estimate SOC accurately because of imprecise initial SoC and heavy calculation.
4.1. Estimation of SoC Using Black Box Modelling Data-Driven Approach
With the development of artificial intelligence, data-based methods have been proposed in recent years to estimate SoC. Cai et al. (2003) developed an Adaptive Neuro-Fuzzy Inference System (ANFIS) to estimate SoC [38]. The discharging current, discharging time, battery terminal voltage and the ratio R are all input variables in the ANFIS, and they were obtained using three different correlation analysis techniques: linear correlation analysis (LCA), nonparametric correlation analysis (NCA) and partial correlation analysis (PCA). For SoC estimation, Lee et al. (2007) presented a machine learning system using learning controllers, fuzzy neural networks and cerebellar model articulation controller networks [39]. Voltage and discharge efficiency are used as the input variables for this system.
Other methods used to estimate SoC include support vector machine [40,41,42], neural network with an extended Kalman filter (EKF) [43,44], support vector machine (SVM) optimised by particle swarm optimisation [45], optimised SVM [46], multi-layered [47] perceptron neural network, fuzzy least square support vector machine [48], time-delayed neural network [49], Levenberg–Marquardt (L-M) algorithm optimised multi-hidden-layer wavelet neural network (WNN) [50], back propagation neural network [51,52], feed-forward artificial neural network [53] and recurrent neural network with gated recurrent unit [54].
Cai et al. (2003) developed an adaptive neuro-fuzzy inference system (ANFIS) to estimate SoC [38]. The mean squared error is 4.8819 × 10−5 and the maximum of absolute values of absolute error is not more than 4.44%. Hansen et al. (2005) investigated the use of SVM to estimate the SoC of a large-scale lithium-ion-polymer (LiP) battery pack [40]. When the optimal SVM is tested with US06, the driving cycle is provided by US and the RMSE (root mean square error) obtained is 5.76%.
Lee et al. proposed a machine learning system for SoC estimation and it has good average prediction error under 6% in the whole battery lifecycle. Charkhgard presents a method for modelling and estimation of SoC for lithium-ion (Li-Ion) batteries using neural networks (NNs) and the extended Kalman filter (EKF) [43]. Neural networks find the model needed in the state-space equations of the EKF, where the state variables are the battery terminal voltage at the previous sample and the SoC at the present sample. The inputs are the battery voltage at the sampling time (k − 1), the estimated SoC at the sampling time k and the battery terminal current at the sampling time k. NNs find an approximation of the battery terminal voltage at the sampling time k. The RMSE error between the actual SoC and the estimated one is equal to 2%.
Chen et al. (2011) investigated the online dynamic SoC estimation using a combination of Kalman filter and a neural network [44]. The input vectors are I(k), V(k), ΔI(k), ΔV(k), T(k) and SoC(k − 1), where I, V and T represent current, voltage and temperature, respectively, and ΔI(k) = (I(k) − I(k − 1)), ΔV(k) = (V(k) − V(k − 1)), and SoC(k − 1) is the estimate of SoC at k − 1 by EKF. The experimental tests showed that the proposed NN–EKF method gave SoC estimation with the error less than 1%. Anton et al. (2013) estimated the State of Charge (SoC) of a high-capacity lithium iron manganese phosphate (LiFeMnPO4) battery cell from an experimental dataset using SVM approach [41]. The SVM SoC estimator maintains a high level of accuracy better than 6% of overall ranges of operation. A hybrid radial basis function neural network method to estimate the SoC of lithium ferro phosphate (LFP) battery was proposed [55] in 2013. The orthogonal least squares algorithm determines the optimal structure of the RBF neural network and adaptive genetic algorithm is used to tune the parameters of the RBF neural network. Average absolute percentage error is 0.021 for the RBF neural network-based method.
Guo et al. (2014) proposed an SVM optimised by particle swarm optimisation (PSO) to improve SoC estimation accuracy. The inputs taken are voltage, discharge current, impedance and temperature. Prediction error values are smaller between +1.3% and −1.3% [45]. Hu et al. (2014) proposed an SoC estimation based on an optimised SVM for regression with a double search optimisation process [46]. The developed method was tested by simulation experiments in the ADVISOR, with a comparison of the estimations based on ANN. They used eight common cycle conditions (ARTERIAL, NYCCOM, UDDSHDV, COMMUTER, WVUINTER, 5PEAK, CSHVR, CBD14) in ADVISOR. Features considered are current out of the battery, module temperature of the Energy Storage System (ESS), available power out of the ESS, requested power out of ESS, actual power loss for the ESS, heat removed from battery by cooling air and the average temperature of the cooling air.
Toha et al. (2014) devised a multi-layered perceptron neural network (MLPNN) and Elman recurrent neural network (ERNN) to find SoC. The percentage accuracy achieved was 96.68% and 97.51% using MLPNN and ERNN, respectively [47]. Sheng et al. (2015) proposed an SoC estimation method based on the fuzzy least square support vector machine [48].
H. Chaoui et al. uses the multi-layer perceptron structure with back-propagation learning rule to achieve a more precise value of SoH and SoC. It was tested using a lithium ion and was found to evaluate the required parameters with minimal error caused because of hysteresis, aging and temperature. Moreover, this modelling does not require any prerequisite knowledge of battery parameters [49]. B. Xia et al. proposed the L-M algorithm-based WNN for intelligently estimating the values of SoC. In this literature, Samsung ICR-18650-22P lithium-ion batteries were used for testing the algorithm’s efficacy. It was concluded that this algorithm gave a better solution set when compared with BPNN and EKF [50].
Dang et al. (2016) proposed the OCV-based method for SoC estimation by using the dual neural network fusion battery model [56]. Tong et al. (2016) proposed a new architecture for SoC estimation using a load-classifying neural network and yielded a 3.8% average estimation error [57]. Ampere hour counting with current correction and the dual adaptive extended Kalman filter algorithms are combined to estimate model parameters and State of Charge. Least squares support vector machine is implemented to predict the available capacity [42]. Five feature vectors made of temperature, two impedance parameters, voltage change and present voltage are used. A 2% maximum error of predicted capacity is obtained. Meng et al. (2016) proposed an algorithm based on adaptive unscented Kalman filters (AUKF) and least-square support vector machines (LSSVM).
Chaoui et al. (2017) proposed SoC and SoH estimation based on the input time-delayed neural network (ITDNN) that accounts for both aging and temperature effects. This technique used the multi-layer perceptron structure with the back propagation (BP) learning rule to adjust the intra-neuron connecting weights to yield accurate results [42]. Back propagation neural network (BPNN) is proposed to reduce the SoC estimation error significantly [44]. An algorithm based on the adaptive extended Kalman filtering algorithm for lithium-ion power battery SoC estimation is introduced [58].
Xia et al. (2018) proposed the Levenberg–Marquardt (L-M) algorithm optimised multi-hidden-layer WNN for SoC estimation. Particle swarm optimisation (PSO) algorithm is used to optimise L-M based three-layer WNN (LMWNN) for SoC estimation problem [43]. Furthermore, it was validated that L-M-based multi-hidden-layer WNN (LMMWNN) has better performance than LMWNN. Under a single driving cycle, such as the New European Driving Cycle (NEDC), the mean absolute error of PLMMWNN was decreased to 0.6% and the maximum absolute error to 5%. A novel hybrid method by fusion of back propagation neural network and improved the ampere hour counting method is proposed for SoC estimation of lithium-ion battery [45]. Five input eigen values (nodes) of the neural network selected are voltage, current, surface temperature of battery, measurement time and number of cycles. Maximum absolute errors of SoC estimation are confined to an error band of ±2.0% at different aging cycles.
A feed-forward artificial neural network (ANN) has been used to estimate SoC of calendar-aged lithium-ion pouch cells. The ANN achieved a root mean square error (RMSE) of 1.17% over discharge data and 1.81% over charge data, confirming the ability of the network to capture input-output dependency [53]. Li et al. (2019) introduced an SoC estimation approach for lithium-ion batteries using a recurrent neural network with gated recurrent unit, where observable variables such as voltage, current and temperature are directly mapped to SoC estimation. The proposed method is evaluated on two public data sets of vehicle drive cycles and another high-rate pulse discharge condition dataset with mean absolute errors (MAEs) of 0.86%, 1.75% and 1.05%, respectively [54].
4.2. Estimation of SoH Using Black Box Modelling Data-Driven Approach
The data-driven technique has become the favoured approach for SoH estimation due to advancements in computation units such as graphical processing units (GPUs) and enhanced learning algorithms. Because understanding electrochemical events occurring inside the battery is not required, ANN is an excellent method for estimating battery SoH. In particular, fuzzy logic (FL), support vector regression, probabilistic neural network, advanced sparse Bayesian predictive modelling (SBPM), recurrent neural network, support vector machine, multilayer perceptron, artificial neural network and recurrent neural network are some of the few data-driven approaches used for battery SoH estimation. Effective forecast of SoH aids in avoiding inconveniences or dangerous events caused by a sudden battery failure. You et al. (2017) estimated SoH using recurrent neural networks [59].
Zenati et al. (2010) combined impedance measurements and fuzzy logic to evaluate SoC/SoH [60]. Lin et al. (2013) used a probabilistic neural network (PNN) to estimate the state of health (SoH) of Li-ion batteries [61]. The accurate prediction of SoH helps to avoid inconveniences or fatal accidents from the sudden malfunction of the battery. The results show that the average error of the prediction is 0.28% and the standard deviation is 1.15%. You et al. (2017) estimated SoH using recurrent neural network with the average error lower than 0.0765 Ah (2.46%) over all of their experimental data [59]. Weng et al. (2013) proposed a battery SoH monitoring scheme based on partially charging data. The use of support vector regression (SVR) is shown to provide the most consistent identification results with moderate computational load. Results show that the SVR model built upon the data from one single cell is able to predict the capacity fading of seven other cells within a 1% error bound [62].
Advanced sparse Bayesian predictive modelling (SBPM) methodology is employed to capture the underlying correspondence between the capacity loss and sample entropy [63] (2016). The result shows that the estimator is accurate, and the average error is less than 1.2% at each temperature. A nonlinear autoregressive with exogenous inputs (NARX) architecture of the dynamically driven recurrent network (DDRN) is designed for both SoC and SoH estimation [64].
The support vector machine (SVM) with radial basis function (RBF) as kernel function is applied for SoH estimation [65]. Feng et al. (2019) proposed a machine learning-based algorithm for the online SoH estimation of a Li-ion battery [66]. A predictive diagnosis model used in the algorithm is established based on support vector machine (SVM). The algorithm functions by comparing partial charging curves with the stored SVMs. Similarity factor is defined, after comparison, to quantify the SoH of the data under evaluation. The algorithm estimates the battery SoH with less than 2% error for 80% of all the cases and less than 3% error for 95% of all the cases.
Kim et al. (2018) introduced a practical SoH classification scheme based on multilayer perceptron (MLP). SoH is estimated with high accuracy of less than 0.3% in trained SoH section and additionally, the SoH of untrained section is also estimated with high accuracy of less than 1.5% [67]. Venugopal et al. (2019) proposed a unique SoH estimation approach, using an independently recurrent neural network (IndRNN). Experimental results indicate that the IndRNN-based model is able to predict a battery’s SoH accurately with RMSE reduced to 1.33% and mean absolute error (MAE) reduced to 1.14%. The maximum error (MAX) produced by the IndRNN throughout the testing process is 2.5943%, which is well below the acceptable SoH error range of ±5% for EVs.
The idea of ensemble learning is considered, and by generating differential data samples and synthesising the output of a series of base learners, a good learning performance is achieved [54]. Furthermore, grey relational analysis is used for feature correlation analysis. Ensemble learning provides more accurate and stable SoH prediction. In the data setB0005, MAS, MSE and RMSE of ensemble learning predictive results are 0.47%, 5.68 × 10−3% and 0.75%, in the data set B0006, they are 0.76%, 1.5 × 10−2% and 1.23%, in the data set B0007, they are 0.65%, 9.5 × 10−3% and 0.97%, and for data set B0034, they are 1.32%, 8.06 × 10−2% and 2.84%, respectively.
4.3. Estimation of RUL Using Black Box Modelling Data-Driven Approach
Another parameter, namely, battery remaining useful life (RUL) estimation, facilitates the design of a reliable battery system. Several data-driven approaches are available to predict RUL including support vector machine [68], support vector regression [69], optimised relevance vector-machine algorithm [70,71], feed forward neural network [72], autoencoder with deep neural network [73] and long short-term memory recurrent neural network [74].
Nuhic et al. (2013), for the estimation of SoH and RUL, combined SVM with a new method for training and testing data processing based on load collectives [68]. In Patil et al. (2015), support vector regression (SVR) is used to predict the accurate RUL if the battery is close to the end of life (EoL). This model has a RMSE of 0.357% with 95% over and under estimation error of 7.87% and 10.75% [69].
Liu et al. (2015) presented an optimised relevance vector machine algorithm to improve the accuracy and the stability of RUL estimation and to present the uncertainty of RUL estimation [70]. The framework carries out raw HI extraction, transformation, correlation analysis and verification and evaluation to achieve health indicators (HI) enhancement. In particular, the Box Cox transformation is adopted to improve the correlation between the extracted HI and the battery’s actual degradation state. To estimate the battery’s RUL using the enhanced HI, an optimised relevance vector-machine algorithm is utilised, which is performed in a flexible and agile way.
Wu (2016) used a feed forward neural network (FNN) to calculate the RUL through sampled voltage data. The mean absolute error and mean square error of the proposed method in the prediction of the RUL were 29.4218 and 1.6184 × 103, respectively, in about (2000) cycles [72]. Yang (2016) proposed an ensemble-based relevance vector machine (RVM) learning algorithm to predict the RUL of degraded lithium-ion batteries. The study also demonstrated that the hybrid prognostic approach using the selective kernel ensemble-based RVM learning algorithm outperformed the hybrid prognostic approaches using the single kernel-based RVM learning algorithm and the ensemble all-based RVM learning algorithm [71].
Ren et al. (2018) introduced an integrated deep learning approach for RUL prediction of lithium-ion battery by integrating auto encoder with deep neural network (DNN). The results show that RMSE is 6.6% and the accuracy rate is 93.34% [73]. Zhang et al. (2018) employed the long short-term memory (LSTM) recurrent neural network (RNN) to learn the long-term dependencies among the degraded capacities of lithium-ion batteries. The LSTM RNN is adaptively optimised using the resilient mean square back-propagation method, and a dropout technique is used to address the overfitting problem. A Monte Carlo simulation is combined to generate a probabilistic RUL prediction. Capacity fitting error for dropout, L1 regularisation and L2 regularisation are 6.6 × 10−3, 5.7 × 10−3 and 1.4 × 10−2, respectively [74].
Park et al. (2020) proposed novel RUL prediction techniques based on long short-term memory (LSTM) [69]. Unlike the traditional LSTM prediction that matches the input layer with the output layer as a one-to-one structure, a many-to-one structure is used for various input types and to substantially reduce the number of parameters for better generalisation. The experimental results show that the proposed single-channel LSTM model improves the mean absolute percentage error (MAPE) by 39.2% compared to the baseline LSTM model. Furthermore, the proposed multi-channel LSTM model significantly improves the mean absolute percentage error (MAPE) by 63.7% compared to the baseline. The proposed model achieves 0.47% to .88% of MAPE while the state-of-the-art baseline LSTM shows 0.6% to.45% of MAPE.
4.4. Estimation of Capacity Using Black Box Modelling Data-Driven Approach
Wang et al. (2018) introduced quantum computing theory into the classical machine learning technique, an integrated quantum particle swarm optimisation-based support vector regression estimation framework, as well as its application to characterise the relationship between extracted feature and battery remaining capacity [75]. Li et al. (2018) proposed random forest regression for battery capacity estimation. Experimental results show that the proposed technique is able to evaluate the health states of different batteries under varied cycling conditions with a root mean square error of less than 1.3% [76].
Choi et al. (2019) proposed a capacity estimation framework for lithium-ion battery based on multi-channel machine learning techniques using FNN, convolutional neural network (CNN) and LSTM. Results show that the proposed multi-channel technique based on voltage, current and temperature profiles outperforms the conventional method that uses only voltage profile by up to 25–58% in terms of mean absolute percentage error [77].
Shen et al. (2018, 2019) used a deep convolutional neural network (DCNN) to estimate the capacity of a battery cell and concluded that the DCNN model with five convolutional layers produced a slightly lower RMSE as compared to models with any other number of convolutional layers [78,79].
Apart from ML approaches, methods such as fitting based on least squares [36], subspace identification, multiple linear regression and curve fitting approaches [1,11] are employed for determining the charging profiles of BS. Since these models contain continuous time differential equations whose states are not directly measurable, the analytical methods for identifying the model parameters are not applicable.
The machine learning models proposed in the literature are suitable for determining the charging profiles of battery systems (BS) [75,76,77,80,81,82,83,84,85,86]. The data set applied for carrying out the research is listed in Table 1. The different types of battery systems for which the performance analysis carried out by different researchers are listed in Table 1.

Table 1.
Data set for black box modelling.
5. Battery Parameters Extraction Techniques Using Grey Box Modelling Data-Driven Approach
Bio-inspired algorithms have also been extensively researched in recent years owing to their versatility and ease of implementation [87]. To model a battery, the internal circuit parameters need to be estimated. Estimation of these parameters is difficult due to their non-linear behaviour. The battery modelling (BM) problem is a constrained, multi-dimensional, mixed variable, non-convex, non-linear optimisation problem. Many bio-inspired techniques have been successfully employed to estimate the battery parameters [9,16,89,90]. When bio-inspired algorithms are implemented for COM to extract parameters in real time [9], then they are called grey box models. BM stands as a complex iterative procedure, and such complex associated BM analytical calculations are not handled accurately by the derivative-based methods and thus, the optimal solution is not guaranteed by the analytical methods. Apart from the deterministic methods, derivative free soft computing techniques such as GA are needed for the parameter identification to identify the optimal values for the polynomial coefficients of battery parameters of RC model [9]. This type of method is generally called bionic intelligent optimisation algorithms. Compared to all other methods, this technique has obvious advantages in accuracy and reliability, and it has become a popular method for parameter identification [91].
To understand the performance characteristics at varied charge/discharge rates, a thorough COM is discussed, and the polynomial coefficients were optimised using GA [90], so that the output of the model best matches the measurement. Bio-inspired algorithms used to optimise parameters of the electrical circuit model were verified for different drive cycles and the results show that better accuracy is achieved with an error rate of less than 1% in comparison with the conventional parameterisation procedure, which is based on the visual analysis of pulsed discharge curves [14,33]. The level of accuracy obtained with this procedure is comparable to other black box-type models that simply fit input to output behaviour without any physical analogy, such as ANN.
The battery modelling problem is also treated as a bi-objective optimisation problem in most of the recent research. Two objectives such as discharging terminal voltage and surface temperature are minimised using non-dominated sorting GA (NSGA) for lithium-ion batteries. Identified parameters of the P2D electro chemical model can indicate battery internal characteristics accurately, but the charging scenario, ageing mechanism and COM are not analysed. A multi-objective optimisation approach is also applied for COM parameter identification treating charge/discharge data at different currents [92,93,94,95,96].
COM results so far demonstrated in all the above-mentioned existing evolutionary algorithm-based literatures of grey box modelling present the characteristics of different battery types, focusing only on meeting the objectives. However, the values of internal parameters and effects of temperature are not yet studied and attempted to be maintained in the standard range of values. Hence, by addressing the various research gaps identified in the existing literature, this proposed work applies a recent evolutionary algorithm to build (a) a first order and second order circuit-oriented battery model with parameters identified for different charging and discharging rates and (b) a capacity fade model with higher precision order COM developed for estimating remaining useful life, including the effect of temperature effects.
5.1. Modelling of Circuit Oriented Model for Grey Box Modelling
An accurate and simple circuit-oriented battery model (COM) has to be established to describe the static as well as dynamic characteristics of the battery. This model monitors the battery behaviour and its parameters. The general approach for modelling involves development of COM and validation of models.
Various Thevenin forms of COMs such as first order, second order [96] and third order are shown in Figure 1. Rincorn Mora applied a simple electrical model to capture the dynamic battery characteristics from open circuit voltage and current. However, when the internal battery parameters such as resistance, capacitance and open circuit voltage are studied completely with the SoC from the extracted mode, it is found that this simplified model dealt in this work is intuitive and ignored self-discharge effects [37].
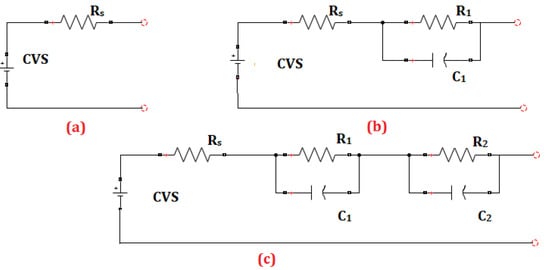
Figure 1.
Electrical circuit model with (a) one resistance, (b) one resistance and one RC network, and (c) one resistance and two RC networks.
Direct measurement EMF method is used to determine the state of charge of NiMH batteries for electric cars by employing first and second order equivalent circuit models. Results show that the precision of the second order model is higher than the first order model [78]. A systematic comparative study of various equivalent circuit models, i.e., twelve lumped COMs, was conducted for parameter optimisations [75]. On model comparison, it is suggested to prefer a lower order RC battery model, since other n-order RC models [32] are found expensive, complex and more susceptible to uncertainties [15]. Battery models that are accurate and simple are preferred.
In Figure 1, RS is the total resistance of the two electrodes, electrolytes and contacts. The transient behaviour of the battery is characterised using R1, R2, C1 and C2. Two RC networks having the time constants τ1 = R1 × C1 and τ2 = R2 × C2 (in the order of seconds and minutes, respectively) are used to depict the internal charge distribution of the battery. Constant voltage source (CVS) represents for the battery’s internal voltage source, which is modelled as the battery’s open circuit voltage (OCV) characteristics. CVS and OCV have been demonstrated to differ experimentally based on the amount of current.
5.2. Development of Thevenin’s COM Model
A first order COM shown in Figure 1b, which is simpler, convenient and ensures fast computation, is preferred in this section for discussion [89]. The Li-ion battery model considered here for parameter extraction utilises the features of both Thevenin’s electrical circuit and analytical modelling techniques. Under all static and dynamic states, the internal voltage CVS (V0) is realised as a second-order polynomial function of SoC to accurately replicate the terminal properties while maintaining the model’s simplicity.
In the Figure 2 model, the circuit parameters are derived for different charge/discharge rates. The calculated terminal voltage values are compared with the measured battery terminal voltage values provided by manufacturers to verify the accuracy obtained from this model. The mathematical representation of battery parameters R1, R2, C1 and V0 under constant current charging/discharging conditions are represented with polynomial equations as a function of charge rate (Cr) SoC for charging scenario and discharge rate (Dr) DoD for discharging scenario. The behaviour of Cr and Dr features is exponentially growing and reducing with regards to Cr and Dr, as shown in Figure 3. As a result, utilising a polynomial equation with an exponential function is the ideal way to express the battery charge and discharge rate characteristics [9].
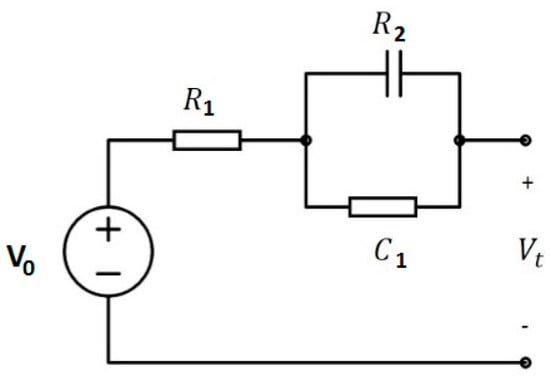
Figure 2.
First order battery model [Reprinted with permission from [98] CC BY 4.0].
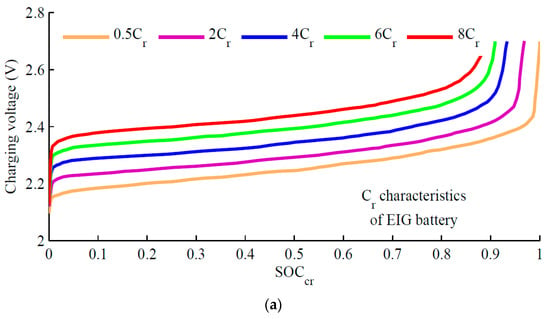
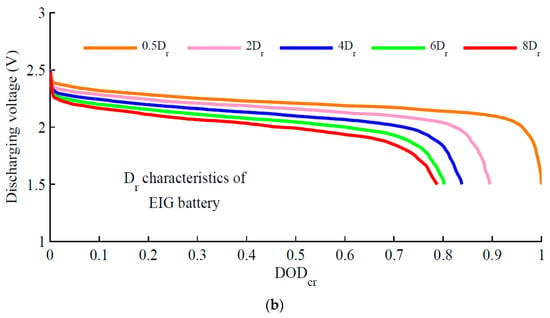
Figure 3.
(a) Charging characteristics of EIG battery from manufacturer’s catalogue for first order model in Figure 2. (b) Discharging characteristics of EIG battery from manufacturer’s catalogue [Reprinted with permission from [98] CC BY 4.0].
5.3. Representation of SoC and DoD Using Polynomial Equations
V0 is defined as the voltage between the terminals of battery in open circuit condition. SoCcr, DoDcr, Cr, Dr, temperature and cycle number are all multi-variable functions in the battery. The parameters V0 and R1 in series with parallel R2C combination are used to determine the effective capacity, instantaneous voltage drop and self-discharge energy. The model’s R2C network is comparable to Thevenin’s transient response model. The exponential nature of the battery parameters R1, R2, V0 and C is approximated by polynomial functions. The general polynomial equations for the parameters are given in Equations (6)–(9) [9].
In the above set of equations, R1, R2, C and V0 are represented in terms of polynomial equations and there are 31 coefficients (from a1 to a31) in total. The following section explains the comprehensive extraction process for finding these polynomial coefficients. The charging process parameters are generated by substituting x and y with Cr and SOCcr, whereas the discharging process parameters are derived by replacing Dr and (1 − DoDcr). Here, (1 − DODcr) is chosen for discharging voltage as V0 decreases with increase in DODcr.
5.4. Battery Terminal Voltage Calculations
The battery terminal voltage is calculated with various charging/discharging rates using the polynomial coefficients that were found at specified charge/discharge rates. Therefore, under the constant current, the battery terminal voltage for charging (Vbc) and discharging scenario (Vbd) with respect to time is as given [88]. Calculating battery terminal voltage for charging or discharging at various Cr and Dr is performed using equations. The battery’s terminal charge or discharge voltage (Vcjc or Vdjc) varies depending on the battery’s capacity, SOCcr/DODcr levels and Cr/Dr. The parameters of the non-linear Vcjc/Vdjc relationship are also expressed in terms of polynomial equations, where i and j signify the ith and jth determined charging and discharging voltage values, respectively. As a result, Equations (10) and (11) yield the battery terminal voltage for charging and discharging scenarios with regard to time when the current is constant (6) [9,97,98].
where Qr is the remaining capacity of the battery and tc, Ic, td and Id are charge time, charge current, discharge time and discharge current, respectively. Thus, Equations (10) and (11) accurately represent the behaviour of any battery type, if the parameters are well defined. These equations capture the non-linear behaviour of the battery which depends on the actual battery charge/discharge voltage.
5.5. Charge/Discharge Rate and SoC Calculations Using Grey Box Modelling
The amount of charge stored or extracted can be determined using the charge or discharge rate algorithm. The Cr and SOCcr of the battery vary depending on the present condition of the battery. The user-defined Cr limit (Clmt) and initial battery SoC (SOCini) have also been taken into consideration. The and of the battery can be expressed as given below [9,97,98].
The required calculations are performed by taking into consideration the current status of the battery. To regulate the charge current of the battery, the minimum of charge rate based on Clmt and is chosen by the algorithm. A similar type of control algorithm is used for discharging scenarios. The SOCcr and DODcr are calculated from Equations (14) and (15) [9,97,98].
where SOCini is the initial SOC of the battery; SOCmax and DODmax are the maximum user-defined SOC and DOD limits. The non-linear behaviour of the battery is identified using the polynomial equations mentioned above. It has a unique dependence on the charge/discharge voltage. The actual behaviour of the battery is represented using this model and accurate results are obtained from it. The parameters are easily detectable in this model, and are made to compare with different types of battery manufacturers’ data [99,100,101,102].
5.6. Parameter Extraction of the Grey Box Modelling Using Bio-Inspired Algorithms
The advantages of the application of an evolutionary algorithm for optimisation are as follows.
- (a)
- The purpose of using an evolutionary algorithm for a battery parameter extraction problem lies in the fact that it requires only manufacturers Cr and Dr characteristics and gives consistent polynomial coefficients of the battery model during relatively fewer iterations.
- (b)
- Evolutionary algorithms are more flexible in extracting the battery parameters with any initial values, while other numerical methods are incapable of obtaining satisfactory solutions.
- (c)
- The algorithm is easy to understand and is optimised using the fitness function.
- (d)
- With optimising capability, the algorithm steers the fitness function to be more representative and yields an accurate solution set even if the initial values are far from the solutions.
The objective of the optimisation process is to find the values of polynomial coefficients of parameter equations, which produce a Voltage-SOC characteristic that best fits the characteristic curve obtained from the manufacture’s battery data. GA was the first meta-heuristic optimisation algorithm proposed by Holland et al. in 1988 based on Darwin’s principle of natural selection. GA is a suitable algorithm for the parameter’s extraction of this model in terms of its complexity and the large number of its parameters [102,103,104,105]. GA imitates the process of biological evolution, including selection, crossover and mutation based on the principle that good individuals survive and breed good individuals [86]. The algorithm initiates by creating the random set of chromosomes/solutions, each solution being a vector of polynomial co-efficient (a1 − a31) in the search space. The next requirement after generation of the random solution set is the measure of the quality/fitness of the solution set. This can be achieved by establishing a fitness function value for the entire population.
The fitness function for optimisation is calculated as the difference between measured ( or ) and the calculated terminal voltage ( or ) for the charging or discharging case and is determined as given in Equation (16) [9,97,98].
The algorithm now selects the chromosomes that participate as parents for the next process (crossover and mutation), based on the fitness of each solution. The chromosomes that have a good fitness obtain a better chance to be selected. After that, the chromosomes selected play the role of parents and undergo crossover to produce offsprings (new solutions). In the mutation process, the children generated after crossover in the previous step are randomly subjected to a change of some characters. Next, the new solution set is checked for fitness and the solution set is updated. Finally, the optimality condition is checked to know whether the solution set has reached the best fitness. If it is not reached, the solution set becomes the parent for the next iteration and the optimisation iterative process continues until (the optimal values for 31 variables) the fitness is optimised from the search space. Similar steps are followed to extract the parameters with needed changes based on the adopted bio-inspired algorithm [105,106,107,108].
6. Discussion
This study starts with the review of electrochemical modelling of a battery. Three different electrochemical models and their output equations were discussed. Even though they are accurate and precise among various battery models, their highly detailed descriptions make them very laborious to configure. Moreover, they have very low-speed operation, thus making them unsuitable for applications in electric vehicles. Parameter extraction is difficult in this type of modelling. The modelling technique that follows is mathematical modelling, which is used primarily to depict system-level behaviour. However, their usage is very low owing to the insufficient relation between the parameters and the I-V characteristics of the model. An electric equivalent model, called the circuit-oriented model, was found to be the most suitable model as it addresses various issues that were found in the previously discussed models.
While dealing with battery parameters, there exists an issue of non-linearity. In this scenario, machine learning algorithms were found to be more efficient than traditional algorithms because of their ability to process non-linear data. Thus, a detailed study on black box and the grey box data-driven techniques to estimate SoC, SoH, RUL and capacity was provided along with discussions of various literatures and their contribution. Lastly, the process of parameter extraction of a circuit-oriented model was depicted using a grey box data-driven technique. The equations mentioned show the non-linear behaviour of various parameters. Moreover, these parameters are easily detectable, thus making evolutionary algorithms and ML-based algorithms more efficient. The various parameters of battery estimation for different types of batteries with machine learning algorithms discussed in the literature are summarised in the following Table 2.

Table 2.
Batteries with extracted parameters using different machine learning algorithms discussed in literature.
7. Conclusions
This paper presents a brief survey on literature in the area of battery modelling. It unfolds the need for battery modelling, its significance and different modes and approaches for battery modelling. Different models such as electrochemical models, mathematical models, circuit-oriented models and combined models are studied and their advantages and drawbacks are compared. For the circuit-oriented battery model, the impact of modelling using data-driven techniques such as the grey box technique and the black box technique has been explained with the procedure. In the grey box battery modelling data-driven approach, the extraction of battery parameters such as resistance, capacitance and voltage are detailed using evolutionary algorithms and in black box modelling, the procedure is explicated with polynomial regression in python environment. It is necessary to choose a reliable battery model and a modelling technique to achieve the desired results. Nowadays, with the burgeoning of renewable energy systems and electric vehicles to reduce environmental problems, batteries have become important devices and it is necessary to optimise various parameters governing them using suitable algorithms. Thus, the paper offers a detailed survey on battery modelling and provides a simple, recent and effective direction for researchers in the relevant area.
Funding
Deanship of Scientific Research at King Khalid University, Saudi Arabia, Grant No: R.G.P.1/82/42.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia, for funding this work through Research Group Program under Grant No: R.G.P.1/82/42.
Conflicts of Interest
Not Applicable.
Nomenclature
| BMS | Battery Management System |
| SoC | State of Charge |
| SoH | State of Health |
| DoD | Depth of Discharge |
| ANN | Artificial Neural Network |
| DFN | Doyle-Fuller-Newman |
| SPM | Single Particle Model |
| CFD | Computational Fluid Dynamics |
| P2D | Pseudo-Two-Dimensional |
| LiCoO2 | Lithium Cobalt Oxide |
| xk | Number of State Vectors in the system |
| x | State variable depicting the SoC of the Battery |
| yk | Output Voltage of the Battery |
| E0 | Output Voltage |
| R | Internal Resistance (Ohmic Resistance) |
| ik | Current Flowing through the resistance |
| V0 | Open Circuit Voltage of the Battery |
| RC | Resistor-Capacitor |
| EKF | Extended Kalman filter |
| OCV | Open Circuit Voltage |
| COM | Circuit Oriented Model |
| EIS | Electrochemical Impedance Spectroscopy |
| GA | Genetic Algorithm |
| ML | Machine Learning |
| WNN | Wavelet Neural Network |
| GPU | Graphical processing units |
| FL | Fuzzy logic |
| SBPM | Sparse Bayesian Predictive Modelling |
| PNN | Probabilistic neural network |
| SVR | Support vector regression |
| RVM | Relevance vector machine |
| LSTM | Long Short-Term Memory |
| MAPE | Mean Absolute Percentage Error |
| CNN | Convolutional Neural Network |
| DCCN | Deep Convolutional Neural Network |
| SOCcr | State of Charge |
| DODcr | Depth of Discharge |
| Vbc | Battery’s Terminal Voltage for Charging |
| Li-Ion | Lithium-ion |
| Current charging rate | |
| SOCini | Initial SoC of the Battery |
| Ic | Charging Current |
| NSGA | Non-Dominated Sorting GA |
| RUL | Remaining useful life |
| SVM | Support Vector Machine |
| ANFIS | Adaptive Neuro Fuzzy Inference System |
| LCA | Linear Correlation Analysis |
| EV | Electric Vehicle |
| LiFeMnPO4 | Lithium Iron Manganese Phosphate |
| RBF | Radial Basis Function |
| ESS | Energy Storage System |
| BM | Battery Modelling |
| MLPNN | Multi layered Perception Neural Network |
| ERNN | Elman Recurrent Neural Network |
| LM | Levenberg-Marquardt |
| AUKF | Adaptive Unscented Kalman Filter |
| LSSVM | Least-square support vector machines |
| ITDNN | input time-delayed neural network |
| BPNN | Back propagation Neural Network |
| L-MA | Levenberg-Marquardt Algorithm |
| LiP | Lithium-ion-polymer |
| LFP | Lithium Ferro Phosphate |
| PSO | Particle Swarm Optimisation |
| NEDC | National European Driving Cycle |
| GRU | Gated Recurrent Unit |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| NN | Neural Network |
| FNN | Feed Forward Neural Network |
| DDRN | Dynamically driven recurrent network |
| IndRNN | Independently recurrent neural network |
| HI | Health Indicator |
| EoL | End of Life |
| CVS | Constant Voltage Source |
| τ1 | Time constant in the order of minutes |
| τ2 | Time constant in the order of seconds |
| Cr | Charge Rate |
| Dr | Discharge Rate |
| Vcjc | Battery’s Terminal Charge Voltage |
| Vdjc | Battery’s Terminal Discharge Voltage |
| Vbd | Battery’s Terminal Voltage for Discharging |
| LMWNN | L-M-based three-layer Wavelet Neural Network |
| LMMWNN | L-M-based Multi hidden layer Wavelet Neural Network |
| DODini | Initial DOD of the Battery |
| Id | Discharging Current |
| RNN | Recurrent Neural Network |
References
- Chaudhari, K.; Kandasamy, N.K.; Kanamarlapudi, R.K.; Gooi, H.B.; Ukil, A. Modeling of charging profiles for stationary battery systems using curve fitting approach. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 2777–2781. [Google Scholar]
- Moura, S.J.; Chaturvedi, N.A.; Krstić, M. Adaptive partial differential equation observer for battery state-of-charge/state-of-health estimation via an electrochemical model. J. Dyn. Syst. Meas. Control 2014, 136, 11. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Grandjean, T.R.B.; McGordon, A.; Jennings, P.A. Structural identifiability of equivalent circuit models for Li-ion batteries. Energies 2017, 10, 90. [Google Scholar] [CrossRef] [Green Version]
- Jongerden, M.R.; Haverkort, B.R.H.M. Battery Modelling; University of Twente, Faculty of Mathematical Sciences: Enschede, The Netherlands, 2008; ISBN 1381-3625. [Google Scholar]
- Li, S.; Ke, B. Study of battery modeling using mathematical and circuit oriented approaches. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar]
- El Ghossein, N.; Salameh, J.P.; Karami, N.; El Hassan, M.; Najjar, M.B. Survey on electrical modeling methods applied on different battery types. In Proceedings of the 2015 Third International Conference on Technological Advances in Electrical, Electronics and Computer Engineering (TAEECE), Beirut, Lebanon, 29 April–1 May 2015; pp. 39–44. [Google Scholar]
- Timmermans, J.-M.; Nikolian, A.; De Hoog, J.; Gopalakrishnan, R.; Goutam, S.; Omar, N.; Coosemans, T.; Van Mierlo, J.; Warnecke, A.; Sauer, D.U.; et al. Batteries 2020—Lithium-ion battery first and second life ageing, validated battery models, lifetime modelling and ageing assessment of thermal parameters. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–8 September 2016; pp. 1–23. [Google Scholar]
- Thirugnanam, K.; TP, E.R.J.; Singh, M.; Kumar, P. Mathematical modeling of Li-ion battery using genetic algorithm approach for V2G applications. IEEE Trans. Energy Convers. 2014, 29, 332–343. [Google Scholar]
- Muenzel, V.; de Hoog, J.; Brazil, M.; Vishwanath, A.; Kalyanaraman, S. A multi-factor battery cycle life prediction methodology for optimal battery management. In Proceedings of the 2015 ACM Sixth International Conference on Future Energy Systems, Bangalore, India, 14–17 July 2015; pp. 57–66. [Google Scholar]
- Yu, Y.; Narayan, N.; Vega-Garita, V.; Popovic-Gerber, J.; Qin, Z.; Wagemaker, M.; Bauer, P.; Zeman, M. Constructing accurate equivalent electrical circuit models of lithium iron phosphate and lead–acid battery cells for solar home system applications. Energies 2018, 11, 2305. [Google Scholar] [CrossRef] [Green Version]
- Seaman, A.; Dao, T.-S.; McPhee, J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation. J. Power Source 2014, 256, 410–423. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.; Khare, N.; Chaturvedi, P.K. A Comprehensive Review on Li-ion Battery Ageing Estimation Techniques for Green Energy Vehicles. Int. J. Eng. Sci. Res. Technol. 2017, 6, 22–39. [Google Scholar]
- Zsiborács, H.; Hegedűsné Baranyai, N.; Vincze, A.; Háber, I.; Pintér, G. Economic and technical aspects of flexible storage photovoltaic systems in europe. Energies 2018, 11, 1445. [Google Scholar] [CrossRef] [Green Version]
- Forman, J.C.; Bashash, S.; Stein, J.L.; Fathy, H.K. Reduction of an electrochemistry-based li-ion battery model via quasi-linearization and pade approximation. J. Electrochem. Soc. 2010, 158, A93. [Google Scholar] [CrossRef]
- Kroeze, R.C.; Krein, P.T. Electrical battery model for use in dynamic electric vehicle simulations. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–16 June 2008; pp. 1336–1342. [Google Scholar]
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and optimization of the dual lithium ion insertion cell. J. Electrochem. Soc. 1994, 141, 1. [Google Scholar] [CrossRef] [Green Version]
- Fuller, T.F.; Doyle, M.; Newman, J. Relaxation phenomena in lithium-ion-insertion cells. J. Electrochem. Soc. 1994, 141, 982. [Google Scholar] [CrossRef] [Green Version]
- Guo, M.; Sikha, G.; White, R.E. Single-particle model for a lithium-ion cell: Thermal behavior. J. Electrochem. Soc. 2010, 158, A122. [Google Scholar] [CrossRef]
- Shrimali, H.; Patel, P.; Patel, R.; Ray, A.; Mukhopadhyay, I. Electrochemical-thermal modelling of commercially available cylindrical lithium-ion cells for the tropical climate of India. Mater. Today Proc. 2021, 46. [Google Scholar]
- Li, D.; Yang, L.; Li, C. Control-oriented thermal-electrochemical modeling and validation of large size prismatic lithium battery for commercial applications. Energy 2021, 214, 119057. [Google Scholar] [CrossRef]
- Glass, M.C. Battery electrochemical nonlinear/dynamic SPICE model. In Proceedings of the IECEC 96, 31st Intersociety Energy Conversion Engineering Conference, Washington, DC, USA, 11–16 August 1996; Volume 1, pp. 292–297. [Google Scholar]
- Zhou, J.; Xing, B.; Wang, C. A review of lithium ion batteries electrochemical models for electric vehicles. In Proceedings of the E3S Web of Conferences, EDP Sciences, Jeju Island, Korea, 7–9 August 2020; Volume 185, p. 4001. [Google Scholar]
- Ding, N.; Prasad, K.; Lie, T.T.; Cui, J. State of charge estimation of a composite lithium-based battery model based on an improved extended kalman filter algorithm. Inventions 2019, 4, 66. [Google Scholar] [CrossRef] [Green Version]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, M. A review on electric vehicle battery modelling: From Lithium-ion toward Lithium–Sulphur. Renew. Sustain. Energy Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef] [Green Version]
- Fan, G.; Li, X.; Zhang, R. Global Sensitivity Analysis on Temperature-Dependent Parameters of A Reduced-Order Electrochemical Model And Robust State-of-Charge Estimation at Different Temperatures. Energy 2021, 223, 120024. [Google Scholar] [CrossRef]
- Hu, M.; Li, Y.; Li, S.; Fu, C.; Qin, D.; Li, Z. Lithium-ion battery modeling and parameter identification based on fractional theory. Energy 2018, 165, 153–163. [Google Scholar] [CrossRef]
- Cai, L.; White, R.E. An efficient electrochemical–thermal model for a lithium-ion cell by using the proper orthogonal decomposition method. J. Electrochem. Soc. 2010, 157, A1188. [Google Scholar] [CrossRef]
- Hu, T.; Zanchi, B.; Zhao, J. Simple analytical method for determining parameters of discharging batteries. IEEE Trans. Energy Convers. 2011, 26, 787–798. [Google Scholar] [CrossRef]
- Gao, L.; Liu, S.; Dougal, R.A. Dynamic lithium-ion battery model for system simulation. IEEE Trans. Compon. Packag. Technol. 2002, 25, 495–505. [Google Scholar]
- Saxena, S.; Raman, S.R.; Saritha, B.; John, V. A novel approach for electrical circuit modeling of Li-ion battery for predicting the steady-state and dynamic I–V characteristics. Sādhanā 2016, 41, 479–487. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Kroeze, R.C.; Krein, P.T. Multi-timescale parametric electrical battery model for use in dynamic electric vehicle simulations. IEEE Trans. Transp. Electrif. 2016, 2, 432–442. [Google Scholar] [CrossRef]
- De Binelo, M.F.B.; Sausen, A.T.Z.R.; Sausen, P.S.; Binelo, M.O. Mathematical modeling and parameter estimation of battery lifetime using a combined electrical model and a genetic algorithm. TEMA 2019, 20, 149–167. [Google Scholar] [CrossRef]
- Cheng, K.W.E.; Divakar, B.P.; Wu, H.; Ding, K.; Ho, H.F. Battery-management system (BMS) and SOC development for electrical vehicles. IEEE Trans. Veh. Technol. 2010, 60, 76–88. [Google Scholar] [CrossRef]
- Rahmoun, A.; Biechl, H. Modelling of Li-ion batteries using equivalent circuit diagrams. Prz. Elektrotechniczny 2012, 88, 152–156. [Google Scholar]
- Sangwan, V.; Sharma, A.; Kumar, R.; Rathore, A.K. Equivalent circuit model parameters estimation of li-ion battery: C-rate, soc and temperature effects. In Proceedings of the 2016 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Kerala, India, 11–17 December 2016; pp. 1–6. [Google Scholar]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and IV performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Cai, C.H.; Du, D.; Liu, Z.Y. Battery state-of-charge (SOC) estimation using adaptive neuro-fuzzy inference system (ANFIS). In Proceedings of the 12th IEEE International Conference on Fuzzy Systems, FUZZ’03, St. Louis, MO, USA, 25–28 May 2003; Volume 2, pp. 1068–1073. [Google Scholar]
- Lee, D.-T.; Shiah, S.-J.; Lee, C.-M.; Wang, Y.-C. State-of-charge estimation for electric scooters by using learning mechanisms. IEEE Trans. Veh. Technol. 2007, 56, 544–556. [Google Scholar] [CrossRef]
- Hansen, T.; Wang, C.-J. Support vector based battery state of charge estimator. J. Power Source 2005, 141, 351–358. [Google Scholar] [CrossRef]
- Anton, J.C.A.; Nieto, P.J.G.; Viejo, C.B.; Vilán, J.A.V. Support vector machines used to estimate the battery state of charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Deng, Z.; Yang, L.; Cai, Y.; Deng, H.; Sun, L. Online available capacity prediction and state of charge estimation based on advanced data-driven algorithms for lithium iron phosphate battery. Energy 2016, 112, 469–480. [Google Scholar] [CrossRef]
- Charkhgard, M.; Farrokhi, M. State-of-charge estimation for lithium-ion batteries using neural networks and EKF. IEEE Trans. Ind. Electron. 2010, 57, 4178–4187. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, S.; Masrur, M.A.; Murphey, Y.L. Battery state of charge estimation based on a combined model of Extended Kalman Filter and neural networks. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 2156–2163. [Google Scholar]
- Guo, G.F.; Shui, L.; Wu, X.L.; Cao, B.G. Soc estimation for li-ion battery using svm based on particle swarm optimization. In Advanced Materials Research; Trans Tech Publications Ltd.: Bäch, Switzerland, 2014; Volume 1051, pp. 1004–1008. [Google Scholar]
- Hu, J.N.; Hu, J.J.; Lin, H.B.; Li, X.P.; Jiang, C.L.; Qiu, X.H.; Li, W.S. State-of-charge estimation for battery management system using optimized support vector machine for regression. J. Power Source 2014, 269, 682–693. [Google Scholar] [CrossRef]
- Toha, S.F.; Faezaa, N.H.; Azubair, N.A.M.; Hanis, N.; Hassan, M.; Ibrahim, B.S.K. Lithium Iron Phosphate Intelligent SOC Prediction for Efficient Electric Vehicle. In Advanced Materials Research; Trans Tech Publications Ltd.: Bäch, Switzerland, 2014; Volume 875, pp. 1613–1618. [Google Scholar]
- Sheng, H.; Xiao, J. Electric vehicle state of charge estimation: Nonlinear correlation and fuzzy support vector machine. J. Power Source 2015, 281, 131–137. [Google Scholar] [CrossRef]
- Chaoui, H.; Ibe-Ekeocha, C.C.; Gualous, H. Aging prediction and state of charge estimation of a LiFePO4 battery using input time-delayed neural networks. Electr. Power Syst. Res. 2017, 146, 189–197. [Google Scholar] [CrossRef]
- Xia, B.; Cui, D.; Sun, Z.; Lao, Z.; Zhang, R.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. State of charge estimation of lithium-ion batteries using optimized Levenberg-Marquardt wavelet neural network. Energy 2018, 153, 694–705. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, Z.; Huang, L. SoC estimation of Lithium battery based on improved BP neural network. Energy Procedia 2017, 105, 4153–4158. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, X.; Zhang, X. Modeling of back-propagation neural network based state-of-charge estimation for lithium-ion batteries with consideration of capacity attenuation. Adv. Electr. Comput. Eng. 2019, 19, 3–10. [Google Scholar] [CrossRef]
- Kashkooli, A.G.; Fathiannasab, H.; Mao, Z.; Chen, Z. Application of artificial intelligence to state-of-charge and state-of-health estimation of calendar-aged lithium-ion pouch cells. J. Electrochem. Soc. 2019, 166, A605. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Xiao, F.; Fan, Y. An approach to state of charge estimation of lithium-ion batteries based on recurrent neural networks with gated recurrent unit. Energies 2019, 12, 1592. [Google Scholar] [CrossRef] [Green Version]
- Chang, W.-Y. Estimation of the state of charge for a LFP battery using a hybrid method that combines a RBF neural network, an OLS algorithm and AGA. Int. J. Electr. Power Energy Syst. 2013, 53, 603–611. [Google Scholar] [CrossRef]
- Dang, X.; Yan, L.; Xu, K.; Wu, X.; Jiang, H.; Sun, H. Open-circuit voltage-based state of charge estimation of lithium-ion battery using dual neural network fusion battery model. Electrochim. Acta 2016, 188, 356–366. [Google Scholar] [CrossRef]
- Tong, S.; Lacap, J.H.; Park, J.W. Battery state of charge estimation using a load-classifying neural network. J. Energy Storage 2016, 7, 236–243. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, Z.; Huang, L. SoC estimation of lithium battery based on AEKF algorithm. Energy Procedia 2017, 105, 4146–4152. [Google Scholar] [CrossRef]
- You, G.-W.; Park, S.; Oh, D. Diagnosis of electric vehicle batteries using recurrent neural networks. IEEE Trans. Ind. Electron. 2017, 64, 4885–4893. [Google Scholar] [CrossRef]
- Zenati, A.; Desprez, P.; Razik, H. Estimation of the SOC and the SOH of li-ion batteries, by combining impedance measurements with the fuzzy logic inference. In Proceedings of the IECON 2010-36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 1773–1778. [Google Scholar]
- Lin, H.-T.; Liang, T.-J.; Chen, S.-M. Estimation of battery state of health using probabilistic neural network. IEEE Trans. Ind. Inform. 2012, 9, 679–685. [Google Scholar] [CrossRef]
- Weng, C.; Cui, Y.; Sun, J.; Peng, H. On-board state of health monitoring of lithium-ion batteries using incremental capacity analysis with support vector regression. J. Power Source 2013, 235, 36–44. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, J.; Cao, D.; Egardt, B. Battery health prognosis for electric vehicles using sample entropy and sparse Bayesian predictive modeling. IEEE Trans. Ind. Electron. 2015, 63, 2645–2656. [Google Scholar] [CrossRef]
- Chaoui, H.; Ibe-Ekeocha, C.C. State of charge and state of health estimation for lithium batteries using recurrent neural networks. IEEE Trans. Veh. Technol. 2017, 66, 8773–8783. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, M.; Shu, X.; Xiao, R.; Shen, J. Online state of health estimation for lithium-ion batteries based on support vector machine. Appl. Sci. 2018, 8, 925. [Google Scholar] [CrossRef] [Green Version]
- Feng, X.; Weng, C.; He, X.; Han, X.; Lu, L.; Ren, D.; Ouyang, M. Online state-of-health estimation for Li-ion battery using partial charging segment based on support vector machine. IEEE Trans. Veh. Technol. 2019, 68, 8583–8592. [Google Scholar] [CrossRef]
- Kim, J.; Yu, J.; Kim, M.; Kim, K.; Han, S. Estimation of Li-ion battery state of health based on multilayer perceptron: As an EV application. IFAC-PapersOnLine 2018, 51, 392–397. [Google Scholar] [CrossRef]
- Nuhic, A.; Terzimehic, T.; Soczka-Guth, T.; Buchholz, M.; Dietmayer, K. Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods. J. Power Source 2013, 239, 680–688. [Google Scholar] [CrossRef]
- Patil, M.A.; Tagade, P.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Yeo, T.; Doo, S. A novel multistage Support Vector Machine based approach for Li ion battery remaining useful life estimation. Appl. Energy 2015, 159, 285–297. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, J.; Liao, H.; Peng, Y.; Peng, X. A health indicator extraction and optimization framework for lithium-ion battery degradation modeling and prognostics. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 915–928. [Google Scholar]
- Yang, W.-A.; Xiao, M.; Zhou, W.; Guo, Y.; Liao, W. A hybrid prognostic approach for remaining useful life prediction of lithium-ion batteries. Shock Vib. 2016, 2016, 3838765. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Zhang, C.; Chen, Z. An online method for lithium-ion battery remaining useful life estimation using importance sampling and neural networks. Appl. Energy 2016, 173, 134–140. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, L.; Hong, S.; Zhao, S.; Wang, H.; Zhang, L. Remaining useful life prediction for lithium-ion battery: A deep learning approach. IEEE Access 2018, 6, 50587–50598. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, S.; Guo, J.; Qin, T. Remaining capacity estimation of lithium-ion batteries based on the constant voltage charging profile. PLoS ONE 2018, 13, e0200169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.-W.; Van den Bossche, P.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Choi, Y.; Ryu, S.; Park, K.; Kim, H. Machine learning-based lithium-ion battery capacity estimation exploiting multi-channel charging profiles. IEEE Access 2019, 7, 75143–75152. [Google Scholar] [CrossRef]
- Shen, S.; Sadoughi, M.; Hu, C. Online estimation of lithium-ion battery capacity using transfer learning. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Seogwipo-si, Korea, 5–8 May 2019; pp. 1–4. [Google Scholar]
- Shen, S.; Sadoughi, M.; Chen, X.; Hong, M.; Hu, C. A deep learning method for online capacity estimation of lithium-ion batteries. J. Energy Storage 2019, 25, 100817. [Google Scholar] [CrossRef]
- Lin, C.; Xing, J.; Tang, A. Lithium-ion battery state of charge/state of health estimation using SMO for EVs. Energy Procedia 2017, 105, 4383–4388. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Liu, Z. A LSTM-RNN method for the lithuim-ion battery remaining useful life prediction. In Proceedings of the 2017 Prognostics and System Health Management Conference (PHM-Harbin), Harbin, China, 9–12 July 2017; pp. 1–4. [Google Scholar]
- Meng, J.; Luo, G.; Gao, F. Lithium polymer battery state-of-charge estimation based on adaptive unscented Kalman filter and support vector machine. IEEE Trans. Power Electron. 2015, 31, 2226–2238. [Google Scholar] [CrossRef]
- Junping, W.; Quanshi, C.; Binggang, C. Support vector machine based battery model for electric vehicles. Energy Convers. Manag. 2006, 47, 858–864. [Google Scholar] [CrossRef]
- Panahi, D.; Deilami, S.; Masoum, M.A.S.; Islam, S.M. Forecasting plug-in electric vehicles load profile using artificial neural networks. In Proceedings of the 2015 Australasian Universities Power Engineering Conference (AUPEC), Wollongong, Australia, 27–30 September 2015; pp. 1–6. [Google Scholar]
- Kandasamy, N.K.; Badrinarayanan, R.; Kanamarlapudi, V.R.K.; Tseng, K.J.; Soong, B.-H. Performance Analysis of Machine-Learning Approaches for Modeling the Charging/Discharging Profiles of Stationary Battery Systems with Non-Uniform Cell Aging. Batteries 2017, 3, 18. [Google Scholar] [CrossRef] [Green Version]
- Klass, V.; Behm, M.; Lindbergh, G. Capturing lithium-ion battery dynamics with support vector machine-based battery model. J. Power Source 2015, 298, 92–101. [Google Scholar] [CrossRef]
- Kai, H.; Yong-Fang, G.; Zhi-Gang, L.; Hsiung-Cheng, L.; Ling-Ling, L. Development of Accurate Lithium-Ion Battery Model Based on Adaptive Random Disturbance PSO Algorithm. Math. Probl. Eng. 2018, 2018, 13. [Google Scholar] [CrossRef]
- Park, K.; Choi, Y.; Choi, W.J.; Ryu, H.-Y.; Kim, H. LSTM-based battery remaining useful life prediction with multi-channel charging profiles. IEEE Access 2020, 8, 20786–20798. [Google Scholar] [CrossRef]
- Zhang, L.; Chang, H.; Xu, R. Equal-width partitioning roulette wheel selection in genetic algorithm. In Proceedings of the 2012 Conference on Technologies and Applications of Artificial Intelligence, Tainan, Taiwan, 16–18 November 2012; pp. 62–67. [Google Scholar]
- Kumar, P.; Bauer, P. Parameter extraction of battery models using multiobjective optimization genetic algorithms. In Proceedings of the 14th International Power Electronics and Motion Control Conference EPE-PEMC 2010, Ohrid, Macedonia, 6–8 September 2010; pp. T9-106–T9-110. [Google Scholar]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Source 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Brand, J.; Zhang, Z.; Agarwal, R.K. Extraction of battery parameters of the equivalent circuit model using a multi-objective genetic algorithm. J. Power Source 2014, 247, 729–737. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, L.; Hinds, G.; Lyu, C.; Zheng, J.; Li, J. Multi-objective optimization of lithium-ion battery model using genetic algorithm approach. J. Power Source 2014, 270, 367–378. [Google Scholar] [CrossRef]
- Shen, J.; He, Y.; Ma, Z. Simultaneous model selection and parameter estimation for lithium-ion batteries: A sequential MINLP solution approach. AIChE J. 2016, 62, 78–89. [Google Scholar] [CrossRef]
- Sun, X.; Ji, J.; Ren, B.; Xie, C.; Yan, D. Adaptive forgetting factor recursive least square algorithm for online identification of equivalent circuit model parameters of a lithium-ion battery. Energies 2019, 12, 2242. [Google Scholar] [CrossRef] [Green Version]
- Wu, G.; Zhu, C.; CC, C. Comparison of the first order and the second order equivalent circuit model applied in state of charge estimation for battery used in electric vehicles. J. Asian Electr. Veh. 2010, 8, 1357–1362. [Google Scholar] [CrossRef] [Green Version]
- Tamilselvi, S.; Karuppiah, N. Capacity Fade Modeling of Li-Ion Battery using Evolutionary Algorithm. In Proceedings of the E3S Web of Conferences, EDP Sciences, Hyderabad, India, 14–16 February 2019; Volume 87, p. 1026. [Google Scholar]
- Tamilselvi, S.; Karuppiah, N.; Muthubalaji, S. Design of an efficient battery model using evolutionary algorithms. Period. Eng. Nat. Sci. 2018, 6, 265–282. [Google Scholar] [CrossRef] [Green Version]
- Jilte, R.; Afzal, A.; Panchal, S. A novel battery thermal management system using nano-enhanced phase change materials. Energy 2021, 219, 119564. [Google Scholar] [CrossRef]
- Afzal, A.; Samee, A.D.M.; Jilte, R.D.; Islam, T.; Manokar, A.M.; Abdul, K. Battery thermal management: An optimization study of parallelized conjugate numerical analysis using Cuckoo search and Artificial bee colony algorithm. Int. J. Heat Mass Transf. 2021, 166, 120798. [Google Scholar] [CrossRef]
- Afzal, A.; Mokashi, I.; Khan, S.A.; Abdullah, N.A.; Azami, M.H. Optimization and analysis of maximum temperature in a battery pack affected by low to high Prandtl number coolants using response surface methodology and particle swarm optimization algorithm. Numer. Heat Transf. Part A Appl. 2020, 79, 1–30. [Google Scholar] [CrossRef]
- Mokashi, I.; Afzal, A.; Khan, S.A.; Abdullah, N.A.; Bin Azami, M.H.; Jilte, R.D.; Samuel, O.D. Nusselt number analysis from a battery pack cooled by different fluids and multiple back-propagation modelling using feed-forward networks. Int. J. Therm. Sci. 2021, 161, 106738. [Google Scholar] [CrossRef]
- Asif, H.F.; Mohammed, A.A.D.; Manzoore, S.; Soudagar, E.M.; Akram, N. Optimization of Thermal and Structural Design in Lithium-ion Batteries to Obtain Energy Efficient Battery Thermal Management System (BTMS): A Critical Review; Springer: Berlin/Heidelberg, Germany, 2021; ISBN 0123456789. [Google Scholar]
- Afzal, A.; Ramis, M.K. Multi-objective optimization of thermal performance in battery system using genetic and particle swarm algorithm combined with fuzzy logics. J. Energy Storage 2020, 32, 101815. [Google Scholar] [CrossRef]
- Mokashi, I.; Khan, S.A.; Abdullah, N.A.; Azami, M.H.; Afzal, A. Maximum temperature analysis in a Li-ion battery pack cooled by different fluids. J. Therm. Anal. Calorim. 2020, 141, 1–17. [Google Scholar] [CrossRef]
- Afzal, A.; Mohammed Samee, A.D.; Abdul Razak, R.K.; Ramis, M.K. Effect of spacing on thermal performance characteristics of Li-ion battery cells. J. Therm. Anal. Calorim. 2019, 135, 1797–1811. [Google Scholar] [CrossRef]
- Jilte, R.; Afzal, A.; Islam, M.T.; Manokar, A.M. Hybrid cooling of cylindrical battery with liquid channels in phase change material. Int. J. Energy Res. 2021, 45, 11065–11083. [Google Scholar] [CrossRef]
- Afzal, A.; Razak, A.; Jilte, R.D.; Ibrahim, M.; Kumar, R.; Mujtaba, M.A.; Alshahrani, S.; Saleel, C.A. Thermal modelling and characteristic evaluation of electric vehicle battery system. Case Stud. Therm. Eng. 2021, 26, 101058. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).