Household Vulnerability to Food Insecurity and the Regional Food Insecurity Gap in Kenya

Abstract

Food insecurity remains a vital concern in Kenya. Vulnerable members of the population, such as children, the elderly, marginalised ethnic minorities, and low-income households, are disproportionately affected by food insecurity. Following the pioneering work of Sen, which examined exposure to food insecurity at a household level using his “entitlement approach”, this paper estimates households’ vulnerability to food insecurity. In turn, the outcome variable is decomposed in order to explain the food insecurity gap between households classified as “marginalised” and “non-marginalised”. We applied the Oaxaca-Blinder decomposition method to examine vulnerability to food insecurity and, in particular, contributions of observed differences in socio-demographic characteristics (endowments) or differences in the returns to these characteristics, which, in our context, is associated with poor public services and infrastructure in the vicinity of the household. The results indicated that differences in vulnerability to food insecurity were mainly attributable to observed differences in socio-demographic characteristics such as education, age, and household income. Therefore, policies seeking to attain equity by investment into targeted household characteristics in terms of access to food and other productive resources could effectively combat food insecurity. For example, policymakers could develop programs for household inclusiveness using education and social protection programs, including insurance schemes against risk of endowment loss.

1. Introduction

Food insecurity is on the rise in sub-Saharan Africa due to low productivity and adverse agri-ecological factors [1,2,3]. The Food Security Information Network (FSIN) [4] reports that 49 countries are at risk of famine. Kenya is one of these countries, where the vulnerable, namely children, elderly, marginalised ethnic minorities, and low-income households, are disproportionately affected by food insecurity [5]. The situation is the worst in the north and north-eastern regions of the country [6]. A food insecurity mapping study by [6] showed that regional differences could be attributed to either ecological or socio-political drivers. However, there has not been a study that was able to systematically pinpoint these regional differences in food security status and, therefore, inform the design of targeted food security policies [7]; thus, this was one of the aims of this paper.

This paper is also concerned with how vulnerable households’ social characteristics relate to marginalisation and exclusion [8]. Several studies concerning food insecurity, e.g., [8,9,10,11], linked household vulnerability to two specific issues: (1) an exposure to a hazard (or shock), and (2) an ability to cope with the shock; or, in other words, the susceptibility of a household to threats to their livelihood. Sen’s [1] entitlement approach provides a useful framework for understanding the sources of hunger and vulnerabilities to hunger. Building on Sen’s entitlement approach, this study aimed to model and study households that suffer from a lack of food entitlement, which makes individuals more susceptible to hunger and can become a source of hunger [10].

Vulnerability, in this context, is the risk that a household’s entitlement will fail to safeguard it against food insecurity associated with shocks such dislocation, or other losses [9,12]. A household’s food entitlement is said to consist of the food that the household can access through production, exchange, or any possible means permissible under the law [13]. When households are able to generate a surplus in food, the excess resources are diverted into assets, which can be exchanged in the future (either for food or money) in the event that the household faces an environmental, social, or economic shock [14]. Swift’s analysis also indicated that a household’s vulnerability to food insecurity is linked to immediate entitlements and the lack of household capital assets.

This paper studied Kenyan households, particularly those in the North and North-Eastern Development Initiative (NEDI) counties of Kenya, that are often vulnerable to food insecurity and have reportedly been excluded from social and economic growth [15,16]. These households are often considered marginalised, specifically owing to their geographical remoteness and ecological disadvantages. They have poor road networks and do not have access to sufficient electricity for household or industrial use. The availability of essential services, quality water, sanitation, and security, which is vital for economic growth, is limited for these areas [15,16]. To study the differences in regional food insecurity, we followed the 2010 Kenyan Constitution Guidance and report by the Commission on Revenue Allocation (CRA) [16] that categorised areas according to their economic conditions. According to CRA [16], fourteen of the forty-seven counties were considered marginalised, while the rest were considered non-marginalised.

Using data from the Kenyan Demographic and Health Survey [17] on a sample of 17,409 households, a two-stage empirical estimation strategy was employed. The first step estimated the severity of food insecurity using the zero-inflated Poisson and negative binomial (ZIP and ZINB) regression models. The ZIP model captures both food insecure households and those at risk of food insecurity. It is of particular importance that policies target both those that are currently food insecure and those inclined to be food insecure. This study set out to show that households can use their endowment set, or good regional returns to any given endowment, to cope during periods of short-term food insecurity.

The second step estimated the regional differences in food insecurity between households from marginalised and non-marginalised areas. To explain these differences, this study adopts the Blinder-Oaxaca decomposition method [18,19]. The overall mean difference in the outcome variable can be separated into a part that is due to differences in observable characteristics (or an explained effect) and a part that is due to regional differences in coefficients of observable characteristics (or an unexplained effect) [20,21]. While the former may provide economic justification for group differences, the latter is often attributed to discrimination [21,22]. In our context, it is the unobserved regional differences in public infrastructures. Sinning [23] proposed a non-linear Blinder–Oaxaca decomposition method for count data, which was subsequently used in this study. In comparison to other estimation strategies, such as the quantile regression and the exogenous switching treatment regression, the non-linear Blinder-Oaxaca (B-O) decomposition model was found to be better aligned with the aims of this study, namely the aim of estimating the food insecurity gap. The other main factor considered in its selection was the nature of the key indicator rCSI (reduced coping strategies index), which appeared to be over dispersed, with 69% zeros and a non-normal distribution, hence the use of zero-inflated negative binomial (ZINB), fitted into the non-linear Blinder-Oaxaca (B-O) decomposition model. The decomposition models can assist in identifying the reason behind regional disparities in food insecurity status.

Investigating the underlying factors that account for the regional disparities in food insecurity in Kenya is a high priority for policymakers. This knowledge may assist in designing effective policies that enhance regional equity to food security [24,25]. For example, if regional differences are mainly due to observed characteristics, such as the education level of the household head and the household’s composition [7,23], policies that advance the household’s education level and composition could be expected to reduce the differences in resource accessibility between households from areas classed as “marginalized” and “non-marginalised”. On the other hand, if regional differences are due to unobserved inherent regional bias, then policies that encourage regional access to resources could be a more effective alternative.

In summary, the approach of the paper is informed by studies from different areas of the literature. Sen’s [1] entitlement approach is used to frame the sources of vulnerabilities to hunger and, thus, food insecurity; Mabuza et al. [26] informed our investigation of the factors associated with the employment of food insecurity coping strategies by households in different regions; Sinning’s [23] non-linear Blinder–Oaxaca decomposition method assisted us in identifying the reasons behind regional disparities in food insecurity status; and Kassie et al. [27] aided our analysis of the food insecurity gap in Kenya, with an emphasis on the regional differences and inequalities in food security. Thus, the paper was able to address the following research questions:

• What is the status of food insecurity, and which factors are associated with food insecurity in Kenya?
• What differences exist in terms of food insecurity between households from areas classed as “marginalized” and “non-marginalised”?
• What are the factors that can explain the differences identified?

2. Materials and Methods

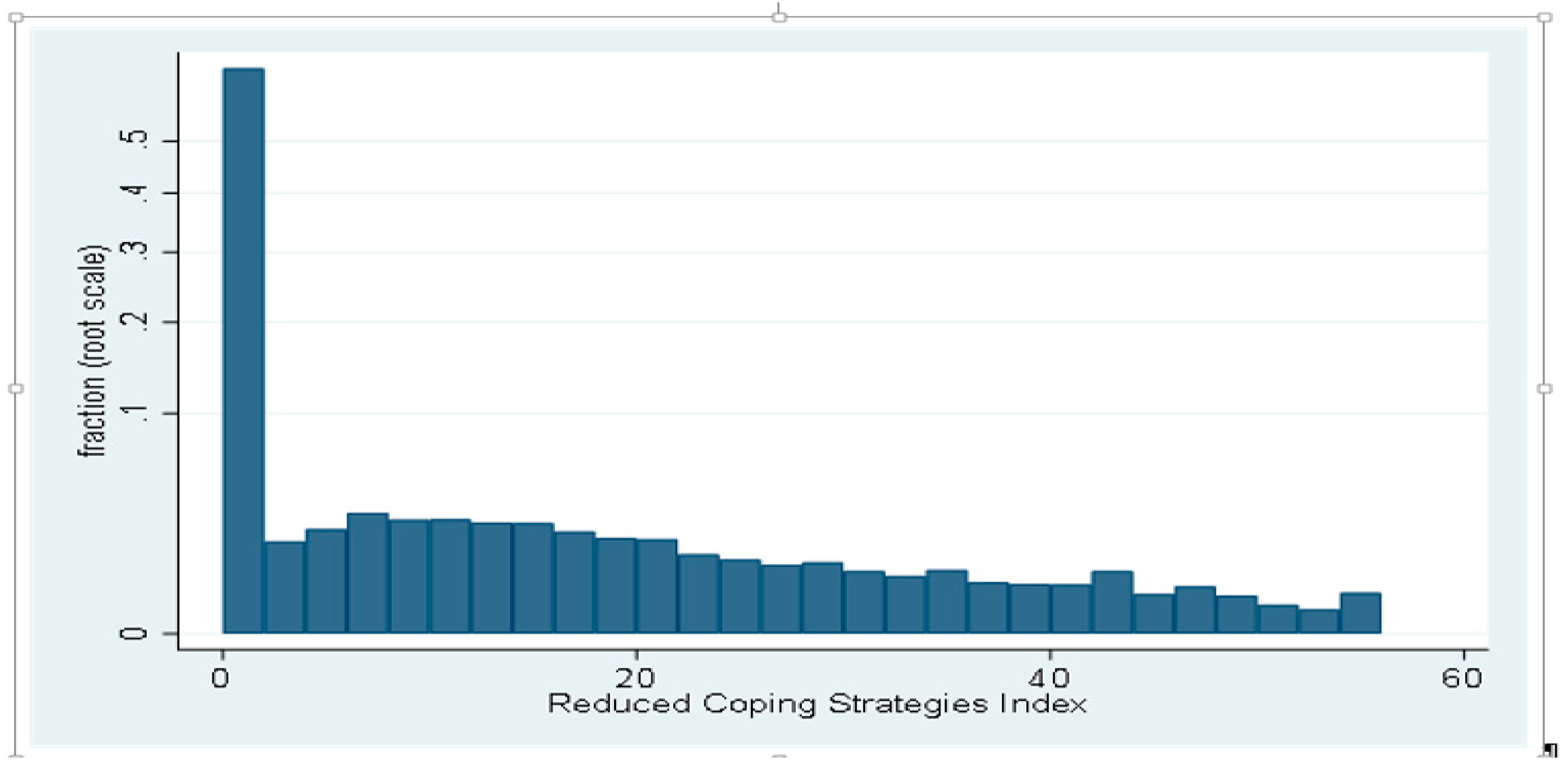
2.1. Coping Strategy Index

The coping strategy index (CSI), built around a behavioural approach to food security analysis [28], is a tool that measures what people do when they cannot access enough food. The CSI is an index based on a series of questions about how households manage to cope with a shortfall in food for consumption in terms of the occurrence, quantity, sufficiency, and frequency of consumption, such as the need to beg or borrow to procure food, reduce meal frequency or portions, or consume seed stocks [28,29]. However, according to Pinstrup-Andersen [30], there is a downside to this approach and it may not give an accurate picture of the food security status among households. For instance, the study claimed that the use of such questions in a survey may run a moral risk if respondents anticipated that their answers would influence whether they could access government support, especially where the questions were administered to severely food insecure households to assess the general status of household food insecurity. This argument may be valid for the majority of poor households, however, [28,29,31] suggested that valuable information can indeed be drawn from the coping strategy questions to measure food insecurity.

The CSI was originally developed for Uganda, Ghana, and Kenya, but it has since been used more widely to capture the nature of the behavioural response to food insecurity in various contexts [28]. The CSI tool relies on counting coping strategies that are not equal in severity. Different strategies are “weighted"”multiplied by a weight that reflects their severity—before being added together. The simplest procedure for doing this is to group the strategies according to similar levels of severity and assign a weight to each group. The individual behaviours identified and enumerated are likely to be specific to that context, and both the behaviours themselves, along with the relative severity of individual behaviours, vary significantly from location to location. There are two different types of CSI indices that can be created through the routine collection of CSI data: the original “context-specific” CSI and the comparative “reduced” CSI (rCSI). The original CSI was developed as a context-specific indicator, while the comparative rCSI was designed to compare food security across different contexts, thus reflecting localised conditions. The original CSI has value in identifying the most vulnerable households for household targeting purposes. It is not very useful, however, for geographic targeting purposes unless the areas being compared are very similar [28].

These behaviours are recurrent across different contexts, suggesting that rCSI would permit a broader comparative analysis and, as such, the rCSI was chosen for this study. It uses the five most common strategies that can be employed by any household in any location in response to food shortages with standardised weights [28,32]. The strategies are a sub-set of the original CSI (about 12 to 15 coping strategies) modified to a simplified rCSI, which contains a standard list of five coping strategies [31]. However, critics argue that the rCSI is less valuable in identifying the most vulnerable households in a given location because it contains less information about particularly extreme behaviours that could result from increased food insecurity levels [28,29]. As a result, it was recommended that a full range of context-specific behaviours be collected. However, Maxwell and Caldwell [31] demonstrated that rCSI reflected food insecurity nearly as well as the original CSI and can thus be used as a food security measure across different contexts and geographic locations. Regardless of this, the present study was not limited and is still very useful in comparing incidences and severity across geographical targets as it measures the same sets of behaviours.

Typically, food-insecure households employ four types of consumption coping strategies. Firstly, households may change their diet by, for example, switching their food consumption from preferred foods to cheaper, less preferred substitutions. Secondly, the household may attempt to increase its food supplies using short-term strategies that are not sustainable over a long period. Typical examples include borrowing or purchasing on credit, and more extreme measures involve begging. Thirdly, if the available food is still inadequate to meet the household’s needs, households can reduce the number of people they have to feed by sending some of them elsewhere (for instance, sending children to a neighbour’s house when those neighbours are eating). Fourthly, and most commonly, households can attempt to manage the shortfall by rationing the household’s food (cutting portion sizes or the number of meals, favouring certain household members over other members, or skipping whole days without eating). These behaviours indicate a problem in household food security, but not necessarily problems of the same severity. A household in which no one eats for an entire day is more food insecure than one in which individuals have switched from consuming rice to ugali (made from maize flour). This research sought to measure the frequency of these coping behaviours (how often is the coping strategy used) and the severity of the strategy (what degree of food insecurity do they suggest). Information on frequency and severity was then combined into a single score—the reduced coping strategies index (rCSI)—as an indicator of the household’s food insecurity status.

The coping strategies described (c) comprise the set C (c ∈ C). First, a binary response was recorded, wherein households were asked a “yes” or “no” question, which enquired as to whether or not there were any days in the seven preceding the survey in which their household did not have food or enough money to buy food, thus categorising them into food insecure or food secure (0 = food secure; 1 = food insecure). Then, for those deemed to be food insecure, the survey asked for the number of days in the past week (a seven-day recall period) that a household engaged in each coping mechanism listed, and then multiplied those days by a weight: $w_c$. The following weights (in parenthesis) were used on the five standard coping strategies: eating less-preferred foods (1.0), borrowing food or money from friends or relatives (2.0), limiting portions at mealtimes (1.0), limiting adult intake (3.0), and reducing the number of meals per day (1.0). The higher the weight, the more severe a strategy was perceived. This meant that limiting adult intake was considered more severe than reducing the number of meals per day. This approach followed the studies of Maxwell [33] and Maxwell and Caldwell [31]. The rCSI was calculated as follows:

$$\mathrm{rCSI} ={\sum }_c^C{w}_c*day{s}_c,$$

where rCSI is the weighted sum of days engaged in each coping strategy, c, $day{s}_c$ is the number of days a household engaged in a given coping strategy over the past week, and $w_c$ is the assigned severity weight. A household with an rCSI of 10 may eat less preferred foods or limit portions at mealtimes. A household with an rCSI of 40 may do this every day, while also reducing the number of meals per day, borrowing food or money from friends or relatives, and occasionally limiting adult intake. A higher rCSI score thus indicated higher levels of food insecurity and, therefore, less personal well-being. Findings from our data showed that the minimum possible rCSI score (among households reporting any of the lists of coping strategies) was 7.0, and the maximum possible score was 56.0. Those households that did not report a lack of food or money to purchase food were recorded with an rCSI = 0. The rCSI score, therefore, ranged between 0 and 56.

The distribution of the rCSI, as shown in Figure 1, is not normal. Therefore, in this study, the rCSI was modelled as a count data variable because the variable values could be separated into a countable number of distinct groups. Therefore, because the rCSI was a distinctly countable variable, and not normally distributed, it was appropriate to use it in a count regression model [34]. Research has found that the best way to assess the frequency of coping strategies is not to count the number of times a household has used them, but to ask a household respondent for a rough indication of the relative frequency of their use over the previous month. Precise recall is often difficult over a long period of time, but asking for the relative frequency provides adequate information. There are various ways that a relative frequency count can work. The questions used in this study asked roughly what proportion of the days of a week people relied on various coping strategies due to a lack of food or money to buy food. The distribution of rCSI was characterised by a large number of zero counts (69%) and a long right tail (31%), which meant there was an excess of zeros.

The best solution for the “excess zeros” problem was to separate participants into two alternate populations, wherein those who produced structural zeros could be identified and eliminated from the data set (i.e., 69% in our data), while those who had counts higher than zero were retained (i.e., the 31%). If information identifying those households deemed to be structural zeros was not available, or if the interest of the research was in the full population including food secure households, then zero-inflated Poisson models or zero-inflated negative binomial models could be used [32,35]. These models account for the fact that the traditional application of Poisson does not address the possibility of over-dispersion. Such a violation of the assumption of normal Poisson distribution may yield either an overestimation or an underestimation of the results [36,37]. In this study, we were interested in the 31% of households that had experienced lack of food or money within the seven days preceding the survey and, as a result, used coping strategies to sustain their livelihood.

2.2. Regression Models with Count Outcome

Count variables share certain properties: (a) their values are always integers or whole numbers; (b) their lowest possible value is zero, so they can never be negative; and (c) they frequently appear to be positively skewed, with most values being low and relatively fewer high [34,38]. However, some count variables have a considerable number of zero values. This typically occurs when the variable is often derived from negative events, as there will often be a stack of zeros in the data, indicating that many people have never engaged in the behaviour and that very few observations exhibit the behaviour (e.g., abuse or drug use) [34].

The discrete nature of a non-negative count dependent variable, and the shape of its distribution, demand the use of appropriate estimators. For instance, the least squares regression would not guarantee that predicted values are non-negative [39]. Therefore, the generalised linear model (GLM) can directly handle the distribution of the count variables. Count variables need to be modelled differently from either continuous or dichotomous variables [38]. Nelder and McCullagh [36] described a class of GLM that extended linear regression to permit non-normal stochastic and non-linear systematic components. GLMs encompass a broad and empirically useful range of specifications that include linear regression, logistic and probit models, and Poisson models. All GLMs require two components: a proper specification of residuals’ distribution and a function to link the outcome and the linear combination of the predictor variables [34]. In this section, four common types of GLM for count data are discussed briefly—Poisson, negative binomial, zero-inflated Poisson (ZIP), and zero-inflated negative binomial (ZINB)—in order to justify the model choice for the study. Each of these is designed for a different type of count variable distribution.

The most common type of distribution for count variables is the Poisson distribution. The Poisson distribution is used because it is a probability distribution designed for non-negative integers. It is defined by a single parameter, λ, which estimates both the mean and variance of the distribution, thereby completely controlling the distribution’s shape. When λ is close to zero, the distribution is positively skewed, but, as λ increases, the distribution becomes less skewed and appears closer to a normal distribution. The major differences between a Poisson regression and its typical regression counterpart are twofold [34]. Firstly, the Poisson regression model assumes that the residuals follow a Poisson distribution rather than a normal distribution. Secondly, predictor variables are linked to the outcome via a natural log transformation [38] similar to that of logistic regression [37].

The log transformation guarantees that the regression model’s predicted values are never negative. For a simple Poisson regression, the model is:

$$\begin{gathered} \underbrace{\ln \left({\mathsf{\lambda }}_i\right)={ \mu }_i}=\underbrace{a+b{X}_i}, \\ \mathrm{Predicted} \mathrm{count}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{Structural} \\ (\mathrm{Transformed} \mathrm{by} \mathrm{Link})\hspace{1em}\hspace{1em}\left(\mathrm{Original}\right) \end{gathered}$$

(1)

where X is a predictor variable, i represents a group of observations with the same value of X. Respectively, a and b are the intercept and slope, and μ_i is the expected value of the outcome variable for all respondents whose value of X is X_i. As the mean of a Poisson distribution is λ and the link function for a Poisson regression is the natural log, Equation (1) shows that the mean of the regression equation, μ_i, equals ln(λ_i). To return the outcome variable to its original count scale requires the transformation of the structural part of Equation (1) by the inverse of the link function. The inverse of the natural log function is the exponent function:

$$\begin{gathered} \underbrace{{\lambda }_i=\exp \left({ \mu }_i\right)}=\underbrace{\exp \left(a+b{X}_i\right)}. \\ \mathrm{Predicted} \mathrm{count}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{Structural} \\ \hspace{1em}\hspace{1em}\hspace{1em}\left(\mathrm{Original}\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(\mathrm{Transformed} \mathrm{by} \mathrm{Inverse} \mathrm{Link}) \end{gathered}$$

(2)

The Poisson distribution assumes that the mean and variance of the variable are equal [34]. However, count variables tend not to support this assumption, especially when there are more zeros or more high values than expected. This is called over-dispersion and it results in a variable’s variance (v) being much larger than its mean (λ). Over-dispersion can be incorporated into the GLM regression by estimating the amount of extra variation. One way of doing this is to use a negative binomial (NB) distribution for the residuals. The NB distribution model variance is:

$$\upsilon =\mathsf{\lambda }+\frac{{\lambda }^2}{\mathsf{\theta }}.$$

(3)

Here, θ is an over-dispersion parameter [35]. Another way is to use zero-inflated models: zero-inflated Poisson (ZIP) regression [40] and zero-inflated negative binomial (ZINB) regression [41]. These are a class of regression models that can account for excess zeros in the data [34,40]. In some cases, it is common for many of the respondents to never have exhibited the behaviour for outcomes that are mainly negative. ZIP and ZINB regressions directly model the excessive number of zeros in the outcome variable by fitting a mixture of zeros and continuously distributed non-zero values. The outcome variable’s distribution is approximated by mixing two models and two distributions, and, thus, the resulting zero-inflated models produce two sets of coefficients [34,40]. It is assumed that the zero values for the mixed-distribution model are true zeros, not proxies for zero, negative, or missing values caused by left censoring or truncation. Therefore, if the dependent variable has no true zeros then sample selection models, such as the Tobit model [42] and Heckman’s selection model [43,44], would potentially be more appropriate.

The first model examines whether or not the behaviour has occurred using logistic regression. Unlike usual methods, in which a typical logistic regression predicts a behaviour’s occurrence, ZIP and ZINB models’ logistic regression predicts a lack of occurrence (i.e., it predicts the zeros vs. the non-zeros). The second model examines how frequently the behaviour has occurred, using either a Poisson or NB regression. In this study, the logistic part predicted households that had never engaged in the behaviour (i.e., those that have never used coping strategies because they were food secure), while the other part predicted the frequency of behaviour occurrence (i.e., the frequency at which households used coping strategies because they were food insecure) using Poisson or NB. Some studies estimated both parts simultaneously, adjusting the mean and the variance of the Poisson or NB model in an attempt to eliminate the likelihood that some of the zero observations were, in fact, structural zeros [45]. Consequently, this study’s approach (ZIP and ZINB) provided a convenient interpretation of the populations that are food insecure and are at risk vs. those not at risk. The models were compared against each other, using the tests appropriate for each comparison. The results showed that the ZIP and ZINB were preferred. The two models were compared using the BIC and AIC. The model with the lowest BIC and AIC was the most preferred, which, in this case, was ZINB model as it fit the data. This result was used later in the decomposition analysis. However, both ZIP and ZINB were used in the initial analysis when predicting the households engaging in coping strategies. The results on the model comparisons are available from the authors. The excess zeros consisted of those who were never food insecure during the study and, thus, did not require coping strategies (therefore, they were not at risk). While the count were those who were food insecure and had to use coping strategies, as well as those that had not used them during the week of the survey, but are likely to do so in the future (those at risk of being insecure).

For count data, the regression model uses maximum likelihood (ML) to estimate the parameters. ML seeks to find values for the regression coefficients that have the highest probability of producing the observed data [34]. ML usually requires an iterative set of procedures to identify the parameter estimates, which can be problematic with models that use many predictor variables or small sample sizes. If the ML estimation procedure converges, it means that it has found a unique set of values for each parameter, the combination of which has returned the highest likelihood value of all parameter values examined [34,39]. Therefore, it will return parameter estimates, standard errors, and the ML value. This likelihood value, or transformations of it, is used to compare the fit of competing models. These regression models may be difficult to interpret because of the log link function [34], which places the regression coefficients on the natural log scale. Exponentiation of the regression coefficients places the predicted values for the outcome on its original scale, Equation (2), but this does not completely solve the interpretation problem. To aid in interpreting ZIP and ZINB models’ coefficients, ref. [39] recommended a common way of interpreting logistic regression models via the exponentiation of the coefficients, which places the coefficients in an odds-ratio scale. An alternative approach is to use the inverse logit function to transform the resulting regression model, which places the outcome on the probability scale [34].

2.3. The Non-Linear Blinder–Oaxaca Decomposition

To analyse differences in the food insecurity severity between households in marginalised and non-marginalised areas, an extension of the Blinder–Oaxaca framework [18,19], the non-linear decomposing model of Sinning [23], was employed. The Blinder-Oaxaca decomposition divides the gap in the outcome between the two groups into two parts: a part that is explained by the gap in the level of the observed determinants, such as income or education, and a part that is explained by the gap in the effect of the determinants on the outcome variable [46]. This method is concerned with answering questions regarding how much of the food insecurity gap between households in marginalised and non-marginalised areas is attributable to higher education amongst the marginalised; or how much is due to the fact that non-marginalised households may have increased access to better resources. For instance, rural children could be less healthy not only because they visit health care providers less frequently, but also because health care providers in rural regions are less effective [25].

This study uses a technique developed by [23,47,48], which extends the Blinder–Oaxaca decomposition to non-linear models. The Blinder–Oaxaca model was originally designed for decomposing disparities in a continuous dependent variable. It is a technique that was used predominantly in literature concerning labour economics to study gaps in wages and employment, mostly across ethnic and gender groups [49,50]. Recently, this method has been applied in health and nutrition economics literature [23,46]. Although Blinder-Oaxaca decompositions have been a mainstay of empirical research on discrimination, they can, in principle, be applied to explain differences in any continuous outcome across any two groups.

Assuming that households in marginalised areas are more severely food insecure in comparison to non-marginalised areas, this can be formalised as in [23]:

$$\Delta =\left[E_{{\beta }_N}\left(Y^N| X^N\right)-E_{{\beta }_N}\left(Y^M| X^M\right)\right]+\left[E_{{\beta }_N}\left(Y^M|X^M\right)-E_{{\beta }_M}\left(Y^M|X^M\right)\right]$$

(4)

Here, $\beta$ denotes the vector of regression coefficients. The counterfactual term $\Delta$ is the food insecurity gap between households in marginalised (M) and non-marginalised (N) areas. Marginalised households are most vulnerable to food insecurity and live specifically in geographically marginalised arid and semi-arid areas [15,16]. For this study, we designated 14 out of 47 counties as marginalised following the National Commission on Revenue Allocation [16].

$$E_{{\beta }_N}\left(Y^M| X^M\right)$$

(5)

Equation (5) approximates the imagined food insecurity status evaluated by multiplying the marginalised covariates with non-marginalised coefficient estimates. In this way, the first part of Equation (4),$E_{{\beta }_N}\left(Y^N| X^N\right)-E_{{\beta }_N}\left(Y^M| X^M\right)$, explains the food insecurity gap attributed to observed characteristics (differences in covariate values), while the second part,$[E_{{\beta }_N}\left(Y^M| X^M\right)-E_{{\beta }_M}\left(Y^M| X^M\right)]$, alternatively explains the gap attributed to unobserved mechanisms (differences in coefficient estimates). Through this procedure, we could distinguish the relative explanatory powers of the observed characteristics and unobserved mechanisms in food insecurity disparities. The bootstrap method was applied to derive standard errors in the components of the decomposition equation. The command calculated different variants of the decomposition equation, but did not separate the contributions of single variables, which is a limitation of the non-linear decomposition.

In this study, the outcome variable to be decomposed was the rCSI, which is a proxy for severity of food insecurity. The appropriate regression specification for the study was the ZINB model. The data consisted of an outcome variable and a set of explanatory variables, which were selected based on a careful review of scholarly literature on key determinants that can best reflect household food consumption behaviour during shortages. The choice of variables was made in the context of the entitlement approach ([1], which assesses those household assets that can be used to counter vulnerability to food insecurity. Households with fewer or no assets have a higher likelihood of being vulnerable and, subsequently, food insecure [33]. Thus, the selected explanatory variables were ownership of livestock, land for agricultural production, receipt of cash transfers, household size, wealth index, and characteristics of household head in terms of age, gender, and education. Previous studies have used this information to assess the economic status and disparities across households, e.g., [25,51].

2.4. Data

The research questions outlined in preceding sections are addressed using data from the 2014 Kenya Demographic and Health Survey (KDHS), obtained from the Kenya National Bureau of Statistics (KNBS). The KNBS serves as the implementing agency of the World Bank Demographic and Health survey program (DHS) by guiding the overall survey planning, development of survey tools, training of personnel, data collection, processing, analysis, and dissemination of the results [17]. The survey’s primary purpose is to provide valuable data for monitoring and evaluating population food security and health status in Kenya. The KDHS is conducted every five years, and the data collection was undertaken from May 2014 to October 2014.

The 2014 KDHS was drawn from the Fifth National Sample Survey and Evaluation Programme (NASSEP V), a household-based master sampling frame created and maintained by the KNBS. This is a frame that KNBS currently uses to conduct household-based surveys throughout Kenya. Development of the frame began in 2012, and it contains a total of 5360 clusters split into four equal sub-samples. These clusters were drawn with a stratified probability, proportional to size-sampling methodology, from 96,251 enumeration areas (EAs) in the 2009 Kenya Population and Housing Census (KNBS, 2014).

The 2014 KDHS used two sub-samples of the NASSEP V frame that were developed in 2013. Approximately half of the clusters in these two sub-samples were updated between November 2013 and September 2014. Kenya consists of 47 counties that serve as devolved units of administration, created in the new constitution of 2010. During the development of the NASSEP V, each of the 47 counties was stratified into urban and rural strata. As the counties of Nairobi and Mombasa have only urban areas, the resulting total was 92 sampling strata. The sample consisted of 40,300 households from 1612 clusters spread across the country, with 995 clusters in rural areas and 617 in urban areas. Samples were selected independently in each sampling stratum, using a two-stage sample design. The 1612 enumeration areas (EAs) were selected with equal probability from the NASSEP V frame in the first stage. The households from listing operations served as the sampling frame for the second stage of selection, in which 25 households were selected from each cluster. The interviewers visited only the pre-selected households, and no replacement of the pre-selected households was allowed during data collection.

There are three versions of the questionnaire used in the survey: the “household questionnaire” targeting the head of the household; the “women’s questionnaire” for female respondents aged between 15 and 49; and the “men’s questionnaire” for male respondents aged 15 to 54 years. The household questionnaire and the women’s questionnaire were administered in all households, while the men’s questionnaire was administered in every other household. Some basic information was collected on the characteristics of each person listed, including age, sex, education, and relationship to the head of the household. The household questionnaire also collected information on characteristics of the household’s dwelling unit, such as the source of water, type of toilet facilities, materials used for the floor and roof of the house, and ownership of various durable goods. A total of 39,679 households were selected for the sample, of which 36,812 were found to be occupied at the time of the fieldwork. Of these households, 36,430 were successfully interviewed. Due to the non-proportional allocation of the sampling strata and the fixed sample size per cluster, the survey was not self-weighting. Therefore, the resulting data was weighted to be representative at a national, regional, and county level.

Household respondents in the 2014 KDHS were asked if there were any days in the seven days preceding the survey when their household did not have food or enough money to buy food. Respondents who answered “yes” to the question were asked to indicate how many days in that week their household had to rely on less preferred foods, rely on borrowed foods, reduce the number of meals, reduce the size of meals, or reduce what adults ate in order for small children to eat. The answers to this question reflect a series of behaviours in a household dealing with a shortfall in food availability. These were formulated into numeric frequency scores, reflecting the frequency and perceived severity of the adopted coping behaviours. Households that did not need to employ any coping strategy would record a score of zero. Therefore, a high score could be assumed to reflect a greater reliance on coping strategies, suggesting a relatively high level of food insecurity. From the formulated frequency scores, the reduced coping strategy index (rCSI) was calculated.

3. Results and Discussion

3.1. Descriptive Statistics

Summary statistics for the households that were fully interviewed are presented in

Table 1. Summary of descriptive statistics.

Variable	Description	Whole Sample	Non-Marginalised	Marginalised	Statistical Difference
(rCSI)	Reduced Coping Strategy Index	5.35	5.03	7.39	2.364 ***
Livestock	Ownership of any livestock (dummy)	0.64	0.64	0.68	0.038 ***
Agricultural land	Ownership of any agricultural land (dummy)	0.66	0.68	0.48	−0.201 ***
Cash transfer	Receiving any cash transfer or assistance (dummy)	0.03	0.02	0.06	0.033 ***
Household size	Total number of people (continuous)	3.94	3.82	4.7	0.880 ***
Wajir	Regions of residency Wajir (dummy)	0.01	0	0.05	0.048 ***
Turkana	Regions of residency Tukana (dummy)	0.01	0	0.09	0.087 ***
Mandera	Regions of residency Mandera (dummy)	0.01	0	0.04	0.044***
Marsabit	Regions of residency Marsabit (dummy)	0.01	0	0.05	0.029 ***
Samburu	Regions of residency Samburu (dummy)	0.00	0	0.03	0.030 ***
West Pokot	Regions of residency West Pokot(dummy)	0.01	0	0.07	0.065 ***
Tana River	Regions of residency Tana River (dummy)	0.01	0	0.04	0.042 ***
Narok	Regions of residency Narok (dummy)	0.02	0	0.15	0.151 ***
Kwale	Regions of residency Kwale (dummy)	0.02	0	0.14	0.143 ***
Garissa	Regions of residency Garissa (dummy)	0.01	0	0.05	0.054 ***
Kilifi	Regions of residency Kilifi (dummy)	0.03	0	0.2	0.199 ***
Taita Taveta	Regions of residency Taita Taveta (dummy)	0.01	0	0.06	0.061 ***
Isiolo	Regions of residency Isiolo (dummy)	0.00	0	0.03	0.025 ***
Lamu	Regions of residency Lamu (dummy)	0.00	0	0.02	0.021 ***
Other Counties	Regions of residency other counties (dummy)	0.85	1	0	−1.000 ***
Wealth index	Wealth index (continuous)	3.18	3.35	2.14	−1.202 ***
Education	Household head’s highest level of education (continuous)	1.40	1.48	0.87	−0.617 ***
Female head	Household head is female (dummy)	0.34	0.33	0.39	0.068 ***
Age of head	Age of household head (continuous)	42.84	42.87	42.69	−0.178
Age of head2	Age of household head squared (continuous)	2087.07	2088.87	2075.58	−13.292
N	Number of observations	17,409	12,743	4663	17,406

Notes: *** p < 0.001.

. The sample composition is as follows: whole sample (n = 17,409 households), which were categorised into two different groups: marginalised (n = 4663 households) and non-marginalised (n = 12,746 households). The last column in Table 1 represents the difference in mean tests of each variable between the two groups.

Wealth is determined by scoring households based on a set of characteristics, including access to electricity and ownership of various consumer goods. Households are then ranked from lowest score to highest score. This list is then separated into five equal pieces (or quintiles), each representing 20% of the population. Therefore, those in the highest quintiles may not be “rich”, but they are of a higher socio-economic status than 80% of Kenya.

The average rCSI is 5.35, with a standard deviation of 10.51 for the whole sample; for households in marginalised areas the mean was 7.39, while for those in non-marginalised areas it was 5.03. The raw data of our dependent variable was thus over-dispersed. Importantly, the observed differences in characteristics between households from marginalised and non-marginalised areas were all statistically significant at 1%. For example, the households in marginalised areas possessed a lower mean average of agricultural land compared to non-marginalised households: 48% vs. 68%. Consistent with this fact, we also observed that households were poorer in the marginalised areas, with a wealth index mean of 2.14 compared to 3.35 for non-marginalised households. Unsurprisingly, the differences in education followed the same pattern as wealth.

Table 2. Distribution of food insecurity by type of area.

	Non-Marginalised	Marginalised	Total
Food secure	0.70	0.63	0.68
Food insecure	0.30	0.37	0.32

shows the distribution of household’s food insecurity status across marginalised and non-marginalised areas. Of the total sample, 32% were food insecure, and in the marginalised areas, 37% were food insecure as compared to 30% in the non-marginalised areas.

3.2. Estimation Results

The estimation results were presented in two sets of analysis. Firstly, the determinants of utilising food insecurity coping strategies was analysed, which focused on food-insecure households and those at risk of being food insecure. The second set of analysis provided an estimation of the underlying factors that accounted for the regional disparities in food insecurity status of households in marginalised and non-marginalised areas. The subsequent sections present the findings and discuss them in detail.

3.2.1. Determinants of Using Food Insecurity Coping Strategies

The empirical analysis looked into the determinants of utilising various coping strategies, indicating the severity food insecurity. The higher the rCSI index, the more food insecure a household is. The rCSI was approximated by the Poisson (count) distribution in our ZIP and ZINB models. The estimation results are reported in

Table 3. Estimates for households engaging in coping strategies from ZIP and ZINB models.

		ZIP				ZINB
Variables	b	t-Test	%stdX	eb	b	t-Test	%stdX	eb
Count r CSI
Livestock	−0.0877 **	−3.18	−4.1	0.916 **	−0.0984 ***	−3.37	−4.6	0.906 ***
Agricultural land	−0.146 ***	−4.84	−6.7	0.864 ***	−0.154 ***	−4.76	−7	0.858 ***
Cash transfer	0.110 *	2.16	1.8	1.116 *	0.103	1.95	1.7	1.109
Household size	0.0454 ***	10.09	11.5	1.046 ***	0.0498 ***	10.01	12.7	1.051 ***
Wajir	−0.396 ***	−4.87	−3.1	0.673 ***	−0.403 ***	−4.89	−3.2	0.668 ***
Turkana	0.354 ***	6.88	3.9	1.424 ***	0.361 ***	7.05	4	1.435 ***
Mandera	−0.704 ***	−9.69	−5.3	0.495 ***	−0.725 ***	−9.71	−5.4	0.484 ***
Marsabit	0.159 **	2.43	1	1.172 **	0.146 *	2.19	0.9	1.157 *
Samburu	−0.0256	−0.44	−0.2	0.975	−0.0245	−0.42	−0.2	0.976
West Pokot	0.0419	0.64	0.4	1.043	0.0474	0.72	0.4	1.049
Tana River	−0.160 **	−2.70	−1.2	0.852 **	−0.168 **	−2.68	−1.2	0.845 **
Narok	−0.0336	−0.48	−0.5	0.967	−0.032	−0.44	−0.5	0.968
Kwale	−0.204 **	−2.52	−2.8	0.816 **	−0.220 **	−2.80	−3	0.802 **
Garissa	−0.503 ***	−6.68	−4.2	0.605 ***	−0.490 ***	−6.25	−4.1	0.613 ***
Kilifi	−0.351 ***	−3.77	−5.5	0.704 ***	−0.359 ***	−3.41	−5.7	0.698 ***
Taita Taveta	−0.0105	−0.14	−0.1	0.99	−0.00918	−0.12	−0.1	0.991
Isiolo	−0.168 **	−2.67	−1	0.846 **	−0.165 *	−2.55	−1	0.848 *
Lamu	−0.335 ***	−3.47	−1.8	0.715 ***	−0.310 **	−3.06	−1.6	0.734 **
Wealth index	−0.0691 ***	−5.59	−9.3	0.933 ***	−0.0717 ***	−5.65	−9.6	0.931 ***
Education	−0.0821 ***	−4.11	−7	0.921 ***	−0.0901 ***	−4.12	−7.7	0.914 ***
Female head	0.0348	1.47	1.7	1.035	0.0359	1.43	1.7	1.037
Age_hh	0.0076 *	2.14	12.8	1.008 *	0.0086 *	2.22	14.7	1.009 *
Age_hh2 (×10−2)	−0.0059	−1.75	−8.9	1.006	−0. 0067	−1.83	−10	1.006
Constant	2.845 ***	30.15			2.815 ***	27.24
Logistic
Livestock	0.339 ***	5.72	17.7	1.404 ***	0.338 ***	5.68	17.6	1.403 ***
Agricultural land	0.200 **	3.19	10	1.222 **	0.197 **	3.13	9.8	1.218 **
Cash transfer	−0.300 **	−2.74	−4.9	0.741 **	−0.300 **	−2.73	−4.9	0.741 **
Household size	−0.0837 ***	−8.18	−18.2	0.920 ***	−0.0828 ***	−8.05	−18	0.921 ***
Wajir	0.165	0.86	1.3	1.18	0.153	0.79	1.2	1.165
Turkana	−1.431 ***	−4.55	−14.3	0.239 ***	−1.433 ***	−4.52	−14.3	0.238 ***
Mandera	1.358 ***	8.19	11	3.887 ***	1.342 ***	8.05	10.9	3.829 ***
Marsabit	−0.628 ***	−4.35	−4	0.534 ***	−0.631 ***	−4.36	−4	0.532 ***
Samburu	−0.15	−1.02	−0.9	0.861	−0.153	−1.03	−1	0.858
West Pokot	0.593 ***	3.92	5.7	1.810 ***	0.596 ***	3.92	5.7	1.815 ***
Tana River	0.505 **	3.13	3.8	1.657 **	0.502 **	3.1	3.8	1.653 **
Narok	0.507 **	3.26	7.5	1.660 **	0.507 **	3.25	7.5	1.660 **
Kwale	0.759 ***	4.49	11	2.135 ***	0.756 ***	4.44	10.9	2.129 ***
Garissa	1.376 ***	7.83	12.5	3.961 ***	1.369 ***	7.76	12.4	3.933 ***
Kilifi	1.006 ***	6.08	17.7	2.734 ***	0.999 ***	5.99	17.6	2.715 ***
Taita Taveta	0.235	1.53	2.2	1.265	0.236	1.53	2.2	1.266
Isiolo	0.299	1.79	1.8	1.348	0.295	1.76	1.7	1.343
Lamu	0.791 ***	4.83	4.3	2.206 ***	0.785 ***	4.77	4.3	2.192 ***
Wealth index	0.465 ***	21.58	92.5	1.592 ***	0.465 ***	21.52	92.5	1.592 ***
Education	0.247 ***	6.87	24.4	1.280 ***	0.245 ***	6.8	24.2	1.278 ***
Female head	−0.203 ***	−4.18	−9.1	0.817 ***	−0.202 ***	−4.16	−9.1	0.817 ***
Age hh	−0.025 **	−3.07	−32.7	0.975 **	−0.025 **	−3.03	−32.5	0.976 **
Age hh2 (×10−2)	0.019 *	2.44	35.2	1.019 *	0.019 *	2.41	34.9	1.019 *
Constant	−0.223	−1.17			−0.239	−1.24
lnalpha					−0.880 ***	−29.75		0.415 ***
N	17,342			17,342	17,342			17,342
McFadden (adj)	0.0841				0.049
aic0	8.07 × 1010				5.81 × 1010
bic	8.07 × 1010				5.81 × 1010

Notes: b = Coefficients; e^b = exponentiated coefficients; %StdX = % change in expected count for a SD increase in X/% change in odds for a SD increase in X; * p < 0.05, ** p < 0.01, and *** p < 0.001. Number of observations = 17,342. This is the number of observations for which all of the response and predictor variables were present. Non-zero observations = 5998. This is the number of observations for which the response variable was not equal to zero. Zero observations = 11,344. This is the number of observations for which the response variable was equal to zero.

.

The analysis could be narrowed down to the effect of household entitlements (using endowments) on household food insecurity status. That is, the role of household’s assets when it came to supporting household members during a period in which there was either a shortage of food or a lack of money to pay for food. Socio-economic, demographic, and geographical attributes are important factors for household entitlements as they can contribute to household food security. A mixture of continuous and categorical predictor variables were used. There were two sets of coefficients for each of the ZIP and ZINB models related to the logistic and count portions of the models, respectively. The distribution of the outcome could then be modelled in terms of two parameters: π, the probability of “always zero = logistic portion”, and μ, the mean number of coping strategies for those not in the “always zero group = count portion”. A natural way to introduce covariates is to model the log of the probability of π always being zero and the log of the mean μ for those not in the always zero class.

The interpretation of the results was trickier than with typical regression models because of the log-link function [31], which placed the regression coefficients on the natural log scale. Therefore, while exponentiating the regression coefficients places the predicted values for the outcome on its original scale (Equation (2)), this does not entirely solve the problem of interpretation. Hence, to interpret the effect of the individual predictors, Atkins and Gallop (2007) recommended either the use of the coefficient, the percentage change in SD increase (%stdX), or the exponentials (e^b). For this analysis, the percentage change/difference in SD increase was used. The estimation resulted, as shown in Table 3, is in two parts: count and logistic portions. The top half of the table shows the predicted continuous frequency of the use of coping strategies by households in the “not always zero” group, while the output in the bottom half of the table shows the predicted dichotomous outcome of group membership (i.e., “not always zero” vs. “always zero” groups). This study was mainly concerned with the upper section (the count portion)–the households that use coping strategies because they are regarded as food insecure. As reported by their binary response (“yes” or “no”) when asked if there were any days in the seven days preceding the survey in which they did not have food or enough money to buy food (0 = no (food-secure); 1 = yes (food-insecure)). The bottom section (the “always zero” group) will also be discussed to provide some elaboration on the food secure group of the population.

Results displayed under %stdX represent percentage changes in the expected count for a SD increase in X. The standardised percentage effects reveal the relative impacts of the predictors on the outcome variable (rCSI). For example, in our data, we found a 4.1% decrease in the expected coping strategies value for one SD increase in livestock ownership for the ZIP model and 4.6% for the ZINB model, while all other factors remain constant. A one standard deviation (SD) increase in the explanatory variable is the same as a unit increase in the standardised version used in regression, and the effect on the outcome variable being reported is just the marginal effect or elasticity of that standardised explanatory variable. The “fully standardised coefficient” is also known as beta coefficients. Likewise, one SD increase in agricultural land owned gave a 6.7% ZIP decrease and a 7.0% ZINP decrease in the expected coping strategies value, while all other factors remain constant. Generally, owning livestock and agricultural land, higher wealth index and education all negatively affected a household’s frequency in using coping strategies, although the impacts varied. On the other hand, the age of the household head and household size both had a positive effect on a household’s frequency of using coping strategies.

The output on the bottom half represented the “always-zero” group. Those households that were food secure and were, therefore, not using coping strategies. Next, the results considering the ZIP model are discussed; very similar results were obtained from the ZINB model. The effect of a one SD change in wealth index (92.5%) had an almost four-fold larger impact than a one SD change in education (24.4%) in the same (positive) direction. Cash transfer, female-headed households, household size, and Turkana as the location, all had a negative impact on whether the household remained in the “always zero” group (having never used coping strategies); the age of the household head had a non-linear U-shape effect. This meant that households with female and younger heads had higher odds of being food insecure. On the other hand, higher wealth index, more education, and ownership of agricultural land and livestock all increased the likelihood of never using coping strategies, thus increasing the odds of households being food secure.

3.2.2. Food Insecurity Gap

Some of the households studied are located in marginalised areas, such as the Turkana and Marsabit counties. Findings from the preceding section show that households in these counties used more coping strategies when compared to households located in other counties. Several counties included in the model are frequently food insecure and often dependent on food aid, including Turkana and Marsabit counties, which are the worst off. For example, the level of stunting in children under five, which is an indicator of chronic malnutrition, is highest in the counties of Turkana and Marsabit (as well as Mandera), which also have the highest levels of poverty in the country. These findings are consistent with the Food Security Information Network [4] report, which states that food insecurity is always persistent in Turkana and Marsabit. These counties are mainly represented by arid and semi-arid lands and have a population of about 10 million, with over 60% of the people living below the poverty line [52]. They usually have scant savings and few other sources of income to cushion them from external shocks.

Next, we conduct a decomposition analysis of the food insecurity gap by means of a non-linear Blinder-Oaxaca model.

Table 4. Estimates for households engaging in coping strategies from ZINB model (marginalised vs. non-marginalised areas).

	Marginalised		Non-Marginalised
	Count	Logistic	Count	Logistic
Livestock	−0.932	1.316 *	−0.905 **	1.407 ***
	(1.25)	(2.29)	(2.95)	(5.13)
Agricultural land	−0.909 *	1.808 ***	−0.839 ***	1.179 *
	(2.02)	(6.00)	(4.59)	(2.30)
Cash transfer	1.293 ***	−0.527 ***	1.095	−0.727 *
	(4.33)	(3.93)	(1.30)	(2.41)
Household size	1.014	1.003	1.055 ***	−0.908 ***
	(1.63)	(0.17)	(9.33)	(8.22)
Wealth index	−0.922 **	1.467 ***	−0.926 ***	1.626 ***
	(2.90)	(8.18)	(5.51)	(20.57)
Education	−0.874 ***	1.241 **	−0.918 ***	1.290 ***
	(3.55)	(3.00)	(3.45)	(6.45)
Female hh head	1.163 **	−0.856	1.026	−0.802 ***
	(3.20)	(1.60)	(0.91)	(4.07)
Age hh	1.016 *	−0.956 **	1.008	−0.977 *
	(2.15)	(2.68)	(1.74)	(2.54)
Age hh2 (×10−2)	−1.000 *	1.000 *	−1.000	1.000 *
	(2.16)	(2.40)	(1.31)	(2.01)
Lnalpha	−0.427 ***		−0.427 ***
	(16.90)		(25.86)
Wald chi2	100.69		188.93
Prob > chi2	0.0000		0.0000
No observations	4632		12,710

Notes: * p < 0.05, ** p < 0.01, and *** p < 0.001.

reports the differences in coefficients between food-insecure households in marginalised and non- marginalised areas. The criteria used in separating the marginalised from non-marginalised households includes their location in a marginalised or non-marginalised county, as identified by the Commission on Revenue Allocation (CRA) in Kenya. Fourteen counties were identified as marginalised out of the total forty-seven counties using the county development index (CDI): a composite index constructed from indicators measuring the state of health, education, infrastructure, and poverty in a county. CDI is complemented by two other sources of information: expert analysis on historical and legislative discrimination and the CRA’s county marginalisation survey results. The fourteen marginalised counties are: Turkana, Mandera, Wajir, Marsabit, Samburu, West Pokot, Tana River, Narok, Kwale, Garissa, Kilifi, Taita Taveta, Isiolo, and Lamu [16].

There are observable, albeit relatively small, differences in coefficients by household type. For instance, the odds of households being in the “not always zero” group decreased by 0.922 for marginalised households and by 0.926 for non-marginalised ones considering the effect of the wealth index, while other factors remained constant. Such differences in magnitude and significance level can be observed for the majority of income- and asset-related variables used to predict a households’ food insecurity status.

The decomposition results, presented in

Table 5. Summary of decomposition results (marginalised vs. non-marginalised households).

Results	Coefficient	p-Value	Percentage Change
Characteristics differential (explained)	3.82 (0.28)	0.000	153.85%
Coefficient differential (unexplained)	−1.50 (0.19)	0.000	−53.85%
Outcome mean differential	2.31 (0.29)		100%

Notes: standard error in parentheses.

, indicate that most of the differences in food insecurity between marginalised and non-marginalised households are due to variation in observable household characteristics, rather than differences in the estimated coefficients, which would be associated with structural regional disparities. These findings are indeed significant from a policy perspective and not surprising given the relatively small coefficient differences between marginalised and non-marginalised samples reported in Table 4. Furthermore, in Table 3, the coefficients of the majority of the counties classified by the CRA as marginalised were often equally or more favourable to food security (i.e., with lower rCSI) compared to the reference group of non-marginalised counties. Indeed, only two (Turkana and Marsabit) out of the fourteen marginalised counties were observed to be systematically unfavourable to food security conditions.

Table 5 shows that 154% of the food insecurity differential could be explained by differences in observable household characteristics and −54% by differences in estimated coefficients. This implied there would be no differences in food insecurity status between households in marginalised and non-marginalised areas if they had the same socio-economic characteristics. Clearly, households in marginalised areas are disadvantaged in terms of observable characteristics, and there is no inherent food insecurity structural bias against those households in marginalised areas with regards to accessing food. In fact, the negative “discrimination” coefficient could be interpreted as positive discrimination of marginalised areas, which could be associated with the various location-specific support programmes in place. Therefore, this study supports the notion that structural (regional) disparities do not reduce food access for marginalised households, but rather a lack of investment in individual household characteristics do.

4. Conclusions

This paper explored the determinants of using coping strategies, as an indicator for the severity of food insecurity, amongst Kenyan households during periods of food unavailability and inaccessibility. We also analysed the food insecurity gap, while estimating inequalities between households from areas classed as “marginalized” and “non-marginalised”. The empirical analysis was carried out via the following steps. First, we estimated the reduced coping strategies index (rCSI) of each household to show the frequency at which coping strategies were utilised. The rCSI counts and weighs coping behaviours at the household level. The zero-inflated Poisson (ZIP) and zero-inflated negative binomial (ZINB) models were then employed to explain the household’s frequency of engagement in coping behaviours during shortages as an indicator of household food insecurity. Next, we applied the Blinder-Oaxaca decomposition method to decompose the (outcome variable) difference in the household rCSI between areas classed as “marginalized” and “non-marginalised” into covariate and coefficient effects. This allowed for the examination of whether differences in vulnerability to food insecurity were attributable to observed differences in socio-demographic characteristics or instead due to “discrimination” or different household returns and access to structural regional amenities, such as poor public health infrastructure.

The study’s results indicated that a household’s resilience to food insecurity during shortages largely depended on a household’s resourcefulness and assets, which drive the household level of entitlement. For example, poor populations are less resilient to environmental stress and disasters, as they rely heavily on the natural environment. They lack the capacity and the resources required to recover from disasters or shocks. In addition, the ongoing climate crisis is likely to significantly impact food insecure and poor populations due to limited access to water resources, healthcare, and public infrastructure services.

The Blinder-Oaxaca decomposition was employed to identify and quantify how these factors contributed to a measured food insecurity gap, thus investigating the drivers of regional differences in food insecurity. The importance of regional balance is a critical element in the fight against food insecurity in Kenya. This study investigated the severity of food insecurity, the differences in food insecurity status, and the extent to which observable or unobservable characteristics can explain regional differences. The study findings indicate a significant disparity in access to economic resources between households from areas classed as marginalised and non-marginalised. The results suggest that marginalised households could be as equally well off as non-marginalised households given the same endowment and entitlement levels, such as livestock, agricultural land, incomes, and the same demographics. This implies that deliberate social protection programs that target equity in these dimensions could effectively combat food insecurity outcomes and vulnerability. Offering social protection against risks and adversity, including social insurance and social transfer payments to support and enable the poor and vulnerable, could greatly enhance the ability of marginalised households to achieve sustainable food security in the face of adverse shocks. This would aid Kenya in achieving the targets of the UN Sustainable Development Goals 1.3 to 1.5. In addition, global funds have the potential to underwrite the roll out of comprehensive social protection systems [53].