Household Vulnerability to Food Insecurity and the Regional Food Insecurity Gap in Kenya
Abstract
:1. Introduction
- What is the status of food insecurity, and which factors are associated with food insecurity in Kenya?
- What differences exist in terms of food insecurity between households from areas classed as “marginalized” and “non-marginalised”?
- What are the factors that can explain the differences identified?
2. Materials and Methods
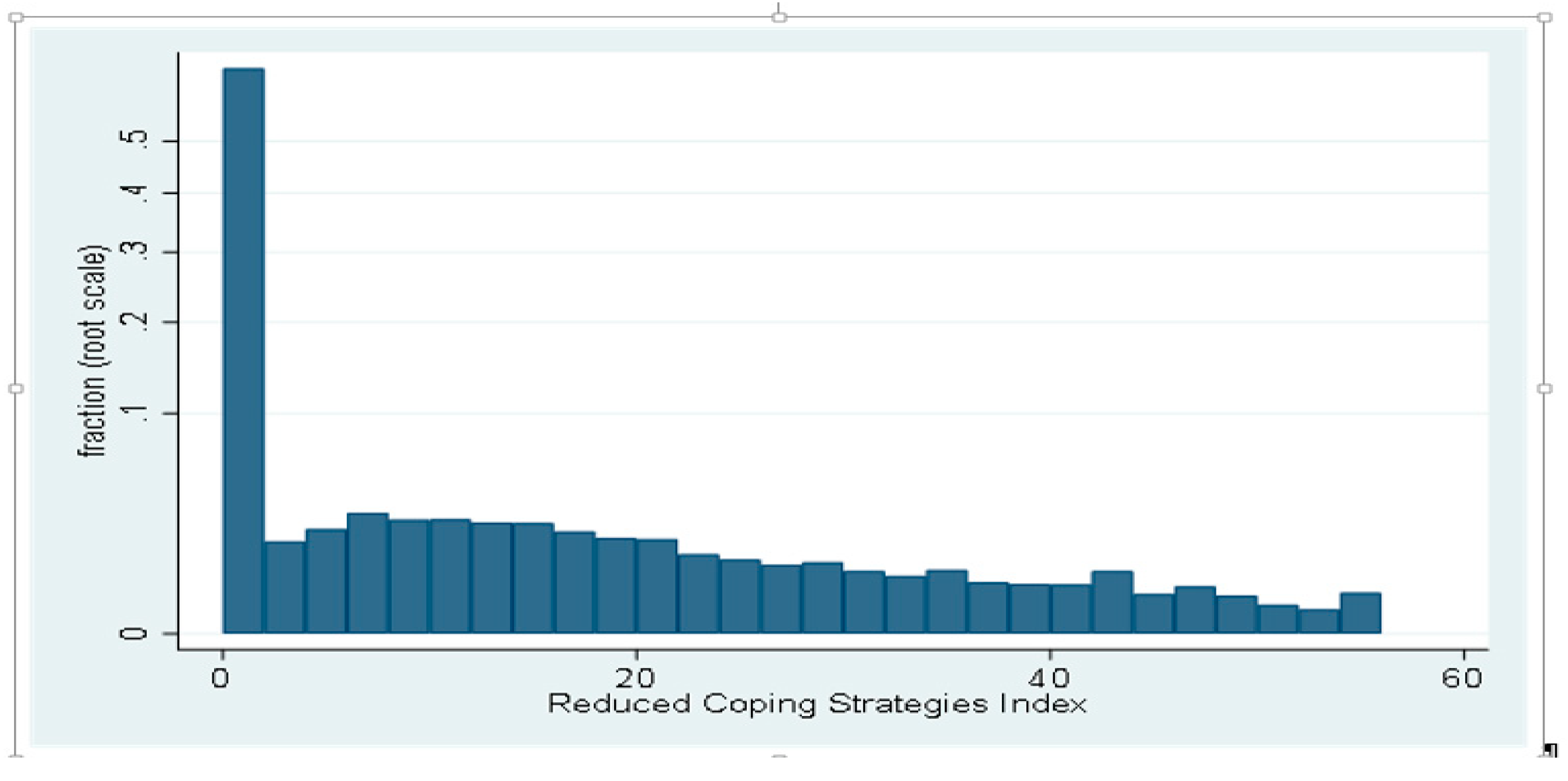
2.1. Coping Strategy Index
2.2. Regression Models with Count Outcome
2.3. The Non-Linear Blinder–Oaxaca Decomposition
2.4. Data
3. Results and Discussion
3.1. Descriptive Statistics
3.2. Estimation Results
3.2.1. Determinants of Using Food Insecurity Coping Strategies
3.2.2. Food Insecurity Gap
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sen, A. Poverty and Entitlements; Oxford University Press: Oxford, UK, 1983; ISBN 978-0-19-159690-2. [Google Scholar]
- FAO; WFP; IFAD. The State of Food Insecurity in the World 2012. Economic Growth Is Necessary but Not Sufficient to Accelerate Reduction of Hunger and Malnutrition; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2012; p. 65. [Google Scholar]
- The Impact of Disasters and Crises on Agriculture and Food Security: 2021; FAO: Roma, Italy, 2021; ISBN 978-92-5-134071-4.
- Food Security Information Network (FSIN). Global Report on Food Crises 2018; World Food Programme (WFP): Rome, Italy, 2018. [Google Scholar]
- Sibhatu, K.T.; Krishna, V.V.; Qaim, M. Production Diversity and Dietary Diversity in Smallholder Farm Households. Proc. Natl. Acad. Sci. USA 2015, 112, 10657–10662. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ehrensperger, A.; Kiteme, B.; Grimm, O. Spatial Analysis of Food Insecurity Drivers and Potential Impacts of Biofuels Cultivation: A Contribution to Sustainable Regional Development and National Biofuel Policies in Kenya, IFSA Symposium; BORIS: Aarhus, Denmark, 2012. [Google Scholar] [CrossRef]
- Sinyolo, S.A.; Sinyolo, S.; Mudhara, M.; Ndinda, C. Gender Differences in Water Access and Household Welfare among Smallholder Irrigators in Msinga Local Municipality, South Africa. J. Int. Women’s Stud. 2018, 19, 20. [Google Scholar]
- Raleigh, C. Political Marginalization, Climate Change, and Conflict in African Sahel States. Int. Stud. Rev. 2010, 12, 69–86. [Google Scholar] [CrossRef]
- Neil Adger, W. Social Vulnerability to Climate Change and Extremes in Coastal Vietnam. World Dev. 1999, 27, 249–269. [Google Scholar] [CrossRef]
- Devereux, S. Sen’s Entitlement Approach: Critiques and Counter-Critiques. Oxf. Dev. Stud. 2001, 29, 245–263. [Google Scholar] [CrossRef]
- Ansah, I.G.K.; Gardebroek, C.; Ihle, R. Resilience and Household Food Security: A Review of Concepts, Methodological Approaches and Empirical Evidence. Food Secur. 2019, 11, 1187–1203. [Google Scholar] [CrossRef] [Green Version]
- Seaman, J.A.; Sawdon, G.E.; Acidri, J.; Petty, C. The Household Economy Approach. Managing the Impact of Climate Change on Poverty and Food Security in Developing Countries. Clim. Risk Manag. 2014, 4–5, 59–68. [Google Scholar] [CrossRef] [Green Version]
- Drèze, J.; Sen, A. Hunger and Public Action; Wider Studies in Development Economics; Reprint; Oxford University Press: Oxford, UK, 2002; ISBN 978-0-19-828365-2. [Google Scholar]
- Swift, J. Why Are Rural People Vulnerable to Famine? IDS Bull. 1989, 20, 8–15. [Google Scholar] [CrossRef] [Green Version]
- Overseas Development Institute. Leaving No One behind in the Roads Sector. An SDG Stocktake in Kenya; Overseas Development Institute (ODI): London, UK, 2016. [Google Scholar]
- Commission on Revenue allocation (CRA). Policy on the Criteria for Identifying Marginalised Areas and Sharing of the Equalisation Fund; Commission on Revenue Allocation: Nairobi, Kenya, 2013. [Google Scholar]
- Kenya National Bureau of Statistics (KNBS); Demographic and Health Survey (DHS). 2014 Kenya Demographic and Health Survey; Kenya National Bureau of Statistics (KNBS): Nairobi, Kenya, 2014. [Google Scholar]
- Blinder, A.S. Wage Discrimination: Reduced Form and Structural Estimates. J. Hum. Resour. 1973, 8, 436. [Google Scholar] [CrossRef]
- Oaxaca, R. Male-Female Wage Differentials in Urban Labor Markets. Int. Econ. Rev. 1973, 14, 693. [Google Scholar] [CrossRef]
- Jann, B. The Blinder–Oaxaca Decomposition for Linear Regression Models. Stata J. Promot. Commun. Stat. Stata 2008, 8, 453–479. [Google Scholar] [CrossRef] [Green Version]
- Schwiebert, J. A Detailed Decomposition for Nonlinear Econometric Models. J. Econ. Inequal. 2015, 13, 53–67. [Google Scholar] [CrossRef]
- Weichselbaumer, D.; Winter-Ebmer, R. A Meta-Analysis of the International Gender Wage Gap: Meta-Analysis of the International Wage Gap. J. Econ. Surv. 2005, 19, 479–511. [Google Scholar] [CrossRef]
- Sinning, M.; Hahn, M.; Bauer, T.K. The Blinder–Oaxaca Decomposition for Nonlinear Regression Models. Stata J. Promot. Commun. Stat. Stata 2008, 8, 480–492. [Google Scholar] [CrossRef] [Green Version]
- Alinovi, L.; D’Errico, M.; Mane, E.; Romano, D. Livelihoods Strategies and Household Resilience to Food Insecurity: An Empirical Analysis to Kenya; European Report on Development: Dakar, Senegal, 2010. [Google Scholar]
- Sharaf, M.F.; Rashad, A.S. Regional Inequalities in Child Malnutrition in Egypt, Jordan, and Yemen: A Blinder-Oaxaca Decomposition Analysis. Health Econ. Rev. 2016, 6, 23. [Google Scholar] [CrossRef] [Green Version]
- Mabuza, M.L.; Ortmann, G.F.; Wale, E. Frequency and Extent of Employing Food Insecurity Coping Strategies among Rural Households: Determinants and Implications for Policy Using Evidence from Swaziland. Food Secur. 2016, 8, 255–269. [Google Scholar] [CrossRef]
- Kassie, M.; Ndiritu, S.W.; Stage, J. What Determines Gender Inequality in Household Food Security in Kenya? Application of Exogenous Switching Treatment Regression. World Dev. 2014, 56, 153–171. [Google Scholar] [CrossRef]
- Maxwell, D.; Caldwell, R.; Langworthy, M. Measuring Food Insecurity: Can an Indicator Based on Localized Coping Behaviors Be Used to Compare across Contexts? Food Policy 2008, 33, 533–540. [Google Scholar] [CrossRef]
- Maxwell, D.; Ahiadeke, C.; Levin, C.; Armar-Klemesu, M.; Zakariah, S.; Lamptey, G.M. Alternative Food-Security Indicators: Revisiting the Frequency and Severity of ‘coping Strategies’. Food Policy 1999, 24, 411–429. [Google Scholar] [CrossRef]
- Pinstrup-Andersen, P. Food Security: Definition and Measurement. Food Secur. 2009, 1, 5–7. [Google Scholar] [CrossRef]
- Caldwell, R. Caldwell, Richard The Coping Strategies Index Field Methods Manual, 2nd ed.; Cooperative for Assistance and Relief Everywhere, Inc. (CARE): Northeast Atlanta, GA, USA, 2008. [Google Scholar]
- Leroy, J.L.; Ruel, M.; Frongillo, E.A.; Harris, J.; Ballard, T.J. Measuring the Food Access Dimension of Food Security: A Critical Review and Mapping of Indicators. Food Nutr. Bull. 2015, 36, 167–195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maxwell, D.G. Measuring Food Insecurity: The Frequency and Severity of “Coping Strategies”. Food Policy 1996, 21, 291–303. [Google Scholar] [CrossRef] [Green Version]
- Beaujean, A.A.; Grant, M.B. Tutorial on Using Regression Models with Count Outcomes Using R. Pract. Assess. Res. Eval. 2016, 21, 2. [Google Scholar] [CrossRef]
- Ver Hoef, J.M.; Boveng, P.L. Boveng Quasi-Poisson vs. Negative Binomial Regression: How Should We Model Overdispersed Count Data? Ecology 2007, 88, 2766–2772. [Google Scholar]
- McCullagh, J.A.P. Nelder FRS Generalized Linear Models, 2nd ed.; Chapman and Hall: London, UK, 1983; ISBN 978-0-203-75373-6. [Google Scholar]
- Hosmer, D.W.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression, 3rd ed.; Wiley Series in Probability and Statistics; Wiley: New York, NY, USA, 2013; Volume 398, ISBN 978-0-470-58247-3. [Google Scholar]
- Colin Cameron, A.; Pravin, K. Regression Analysis of Count Data; Trivedi-Google Books; Cambridge University: Cambridge, UK, 2013. [Google Scholar]
- Atkins, D.C.; Gallop, R.J. Rethinking How Family Researchers Model Infrequent Outcomes: A Tutorial on Count Regression and Zero-Inflated Models. J. Fam. Psychol. 2007, 21, 726–735. [Google Scholar] [CrossRef]
- Lambert, D. Zero-Inflated Poisson Regression, with an Application to Defects in Manufacturing. Technometrics 1992, 34, 1. [Google Scholar] [CrossRef]
- Greene, W.H. Accounting for Excess Zeros and Sample Selection in Poisson and Negative Binomial Regression Models; NYU Work. Pap. No EC-94-10 1994; Springer Nature: Cham, Switzerland, 2014. [Google Scholar]
- Tobin, J. Estimation of Relationships for Limited Dependent Variables. Econometrica 1958, 26, 24. [Google Scholar] [CrossRef] [Green Version]
- Heckman, J. Shadow Prices, Market Wages, and Labor Supply. Econometrica 1974, 42, 679. [Google Scholar] [CrossRef]
- Heckman, J.J. The Common Structure of Statistical Models of Truncation, Sample Selection and Limited Dependent Variables and a Simple Estimator for Such Models. Ann. Econ. Soc. Meas. 1976, 5, 475–492. [Google Scholar]
- Coxe, S.; West, S.G.; Aiken, L.S. The Analysis of Count Data: A Gentle Introduction to Poisson Regression and Its Alternatives. J. Pers. Assess. 2009, 91, 121–136. [Google Scholar] [CrossRef] [PubMed]
- Ciaian, P.; Cupák, A.; Pokrivčák, J.; Rizov, M. Food Consumption and Diet Quality Choices of Roma in Romania: A Counterfactual Analysis. Food Secur. 2018, 10, 437–456. [Google Scholar] [CrossRef] [Green Version]
- Fairlie, R.W. The Absence of the African-American Owned Business: An Analysis of the Dynamics of Self-Employment. J. Labor Econ. 1999, 17, 80–108. [Google Scholar] [CrossRef] [Green Version]
- Fairlie, R.W. An Extension of the Blinder-Oaxaca Decomposition Technique to Logit and Probit Models. J. Econ. Soc. Meas. 2005, 30, 305–316. [Google Scholar] [CrossRef] [Green Version]
- Drydakis, N. Roma Women in Athenian Firms: Do They Face Wage Bias? Ethn. Racial Stud. 2012, 35, 2054–2074. [Google Scholar] [CrossRef] [Green Version]
- Croucher, R.; Ramakrishnan, S.; Rizov, M.; Benzinger, D. Perceptions of Employability among London’s Low-Paid: ‘Self-Determination’ or Ethnicity? Econ. Ind. Democr. 2018, 39, 109–130. [Google Scholar] [CrossRef] [Green Version]
- Firestone, R.; Punpuing, S.; Peterson, K.E.; Acevedo-Garcia, D.; Gortmaker, S.L. Child Overweight and Undernutrition in Thailand: Is There an Urban Effect? Soc. Sci. Med. 2011, 72, 1420–1428. [Google Scholar] [CrossRef] [PubMed]
- Kiome, R. Food Security in Kenya; Ministry of Agriculture, Kenya: Nairobi, Kenya, 2009; p. 31. [Google Scholar]
- Murphy, S.; Walsh, P.P. Social Protection Beyond the Bottom Billion. Available online: https://www.esr.ie/article/view/140 (accessed on 1 July 2021).
| Variable | Description | Whole Sample | Non-Marginalised | Marginalised | Statistical Difference |
|---|---|---|---|---|---|
| (rCSI) | Reduced Coping Strategy Index | 5.35 | 5.03 | 7.39 | 2.364 *** |
| Livestock | Ownership of any livestock (dummy) | 0.64 | 0.64 | 0.68 | 0.038 *** |
| Agricultural land | Ownership of any agricultural land (dummy) | 0.66 | 0.68 | 0.48 | −0.201 *** |
| Cash transfer | Receiving any cash transfer or assistance (dummy) | 0.03 | 0.02 | 0.06 | 0.033 *** |
| Household size | Total number of people (continuous) | 3.94 | 3.82 | 4.7 | 0.880 *** |
| Wajir | Regions of residency Wajir (dummy) | 0.01 | 0 | 0.05 | 0.048 *** |
| Turkana | Regions of residency Tukana (dummy) | 0.01 | 0 | 0.09 | 0.087 *** |
| Mandera | Regions of residency Mandera (dummy) | 0.01 | 0 | 0.04 | 0.044*** |
| Marsabit | Regions of residency Marsabit (dummy) | 0.01 | 0 | 0.05 | 0.029 *** |
| Samburu | Regions of residency Samburu (dummy) | 0.00 | 0 | 0.03 | 0.030 *** |
| West Pokot | Regions of residency West Pokot(dummy) | 0.01 | 0 | 0.07 | 0.065 *** |
| Tana River | Regions of residency Tana River (dummy) | 0.01 | 0 | 0.04 | 0.042 *** |
| Narok | Regions of residency Narok (dummy) | 0.02 | 0 | 0.15 | 0.151 *** |
| Kwale | Regions of residency Kwale (dummy) | 0.02 | 0 | 0.14 | 0.143 *** |
| Garissa | Regions of residency Garissa (dummy) | 0.01 | 0 | 0.05 | 0.054 *** |
| Kilifi | Regions of residency Kilifi (dummy) | 0.03 | 0 | 0.2 | 0.199 *** |
| Taita Taveta | Regions of residency Taita Taveta (dummy) | 0.01 | 0 | 0.06 | 0.061 *** |
| Isiolo | Regions of residency Isiolo (dummy) | 0.00 | 0 | 0.03 | 0.025 *** |
| Lamu | Regions of residency Lamu (dummy) | 0.00 | 0 | 0.02 | 0.021 *** |
| Other Counties | Regions of residency other counties (dummy) | 0.85 | 1 | 0 | −1.000 *** |
| Wealth index | Wealth index (continuous) | 3.18 | 3.35 | 2.14 | −1.202 *** |
| Education | Household head’s highest level of education (continuous) | 1.40 | 1.48 | 0.87 | −0.617 *** |
| Female head | Household head is female (dummy) | 0.34 | 0.33 | 0.39 | 0.068 *** |
| Age of head | Age of household head (continuous) | 42.84 | 42.87 | 42.69 | −0.178 |
| Age of head2 | Age of household head squared (continuous) | 2087.07 | 2088.87 | 2075.58 | −13.292 |
| N | Number of observations | 17,409 | 12,743 | 4663 | 17,406 |
| Non-Marginalised | Marginalised | Total | |
|---|---|---|---|
| Food secure | 0.70 | 0.63 | 0.68 |
| Food insecure | 0.30 | 0.37 | 0.32 |
| ZIP | ZINB | |||||||
|---|---|---|---|---|---|---|---|---|
| Variables | b | t-Test | %stdX | eb | b | t-Test | %stdX | eb |
| Count r CSI | ||||||||
| Livestock | −0.0877 ** | −3.18 | −4.1 | 0.916 ** | −0.0984 *** | −3.37 | −4.6 | 0.906 *** |
| Agricultural land | −0.146 *** | −4.84 | −6.7 | 0.864 *** | −0.154 *** | −4.76 | −7 | 0.858 *** |
| Cash transfer | 0.110 * | 2.16 | 1.8 | 1.116 * | 0.103 | 1.95 | 1.7 | 1.109 |
| Household size | 0.0454 *** | 10.09 | 11.5 | 1.046 *** | 0.0498 *** | 10.01 | 12.7 | 1.051 *** |
| Wajir | −0.396 *** | −4.87 | −3.1 | 0.673 *** | −0.403 *** | −4.89 | −3.2 | 0.668 *** |
| Turkana | 0.354 *** | 6.88 | 3.9 | 1.424 *** | 0.361 *** | 7.05 | 4 | 1.435 *** |
| Mandera | −0.704 *** | −9.69 | −5.3 | 0.495 *** | −0.725 *** | −9.71 | −5.4 | 0.484 *** |
| Marsabit | 0.159 ** | 2.43 | 1 | 1.172 ** | 0.146 * | 2.19 | 0.9 | 1.157 * |
| Samburu | −0.0256 | −0.44 | −0.2 | 0.975 | −0.0245 | −0.42 | −0.2 | 0.976 |
| West Pokot | 0.0419 | 0.64 | 0.4 | 1.043 | 0.0474 | 0.72 | 0.4 | 1.049 |
| Tana River | −0.160 ** | −2.70 | −1.2 | 0.852 ** | −0.168 ** | −2.68 | −1.2 | 0.845 ** |
| Narok | −0.0336 | −0.48 | −0.5 | 0.967 | −0.032 | −0.44 | −0.5 | 0.968 |
| Kwale | −0.204 ** | −2.52 | −2.8 | 0.816 ** | −0.220 ** | −2.80 | −3 | 0.802 ** |
| Garissa | −0.503 *** | −6.68 | −4.2 | 0.605 *** | −0.490 *** | −6.25 | −4.1 | 0.613 *** |
| Kilifi | −0.351 *** | −3.77 | −5.5 | 0.704 *** | −0.359 *** | −3.41 | −5.7 | 0.698 *** |
| Taita Taveta | −0.0105 | −0.14 | −0.1 | 0.99 | −0.00918 | −0.12 | −0.1 | 0.991 |
| Isiolo | −0.168 ** | −2.67 | −1 | 0.846 ** | −0.165 * | −2.55 | −1 | 0.848 * |
| Lamu | −0.335 *** | −3.47 | −1.8 | 0.715 *** | −0.310 ** | −3.06 | −1.6 | 0.734 ** |
| Wealth index | −0.0691 *** | −5.59 | −9.3 | 0.933 *** | −0.0717 *** | −5.65 | −9.6 | 0.931 *** |
| Education | −0.0821 *** | −4.11 | −7 | 0.921 *** | −0.0901 *** | −4.12 | −7.7 | 0.914 *** |
| Female head | 0.0348 | 1.47 | 1.7 | 1.035 | 0.0359 | 1.43 | 1.7 | 1.037 |
| Age_hh | 0.0076 * | 2.14 | 12.8 | 1.008 * | 0.0086 * | 2.22 | 14.7 | 1.009 * |
| Age_hh2 (×10−2) | −0.0059 | −1.75 | −8.9 | 1.006 | −0. 0067 | −1.83 | −10 | 1.006 |
| Constant | 2.845 *** | 30.15 | 2.815 *** | 27.24 | ||||
| Logistic | ||||||||
| Livestock | 0.339 *** | 5.72 | 17.7 | 1.404 *** | 0.338 *** | 5.68 | 17.6 | 1.403 *** |
| Agricultural land | 0.200 ** | 3.19 | 10 | 1.222 ** | 0.197 ** | 3.13 | 9.8 | 1.218 ** |
| Cash transfer | −0.300 ** | −2.74 | −4.9 | 0.741 ** | −0.300 ** | −2.73 | −4.9 | 0.741 ** |
| Household size | −0.0837 *** | −8.18 | −18.2 | 0.920 *** | −0.0828 *** | −8.05 | −18 | 0.921 *** |
| Wajir | 0.165 | 0.86 | 1.3 | 1.18 | 0.153 | 0.79 | 1.2 | 1.165 |
| Turkana | −1.431 *** | −4.55 | −14.3 | 0.239 *** | −1.433 *** | −4.52 | −14.3 | 0.238 *** |
| Mandera | 1.358 *** | 8.19 | 11 | 3.887 *** | 1.342 *** | 8.05 | 10.9 | 3.829 *** |
| Marsabit | −0.628 *** | −4.35 | −4 | 0.534 *** | −0.631 *** | −4.36 | −4 | 0.532 *** |
| Samburu | −0.15 | −1.02 | −0.9 | 0.861 | −0.153 | −1.03 | −1 | 0.858 |
| West Pokot | 0.593 *** | 3.92 | 5.7 | 1.810 *** | 0.596 *** | 3.92 | 5.7 | 1.815 *** |
| Tana River | 0.505 ** | 3.13 | 3.8 | 1.657 ** | 0.502 ** | 3.1 | 3.8 | 1.653 ** |
| Narok | 0.507 ** | 3.26 | 7.5 | 1.660 ** | 0.507 ** | 3.25 | 7.5 | 1.660 ** |
| Kwale | 0.759 *** | 4.49 | 11 | 2.135 *** | 0.756 *** | 4.44 | 10.9 | 2.129 *** |
| Garissa | 1.376 *** | 7.83 | 12.5 | 3.961 *** | 1.369 *** | 7.76 | 12.4 | 3.933 *** |
| Kilifi | 1.006 *** | 6.08 | 17.7 | 2.734 *** | 0.999 *** | 5.99 | 17.6 | 2.715 *** |
| Taita Taveta | 0.235 | 1.53 | 2.2 | 1.265 | 0.236 | 1.53 | 2.2 | 1.266 |
| Isiolo | 0.299 | 1.79 | 1.8 | 1.348 | 0.295 | 1.76 | 1.7 | 1.343 |
| Lamu | 0.791 *** | 4.83 | 4.3 | 2.206 *** | 0.785 *** | 4.77 | 4.3 | 2.192 *** |
| Wealth index | 0.465 *** | 21.58 | 92.5 | 1.592 *** | 0.465 *** | 21.52 | 92.5 | 1.592 *** |
| Education | 0.247 *** | 6.87 | 24.4 | 1.280 *** | 0.245 *** | 6.8 | 24.2 | 1.278 *** |
| Female head | −0.203 *** | −4.18 | −9.1 | 0.817 *** | −0.202 *** | −4.16 | −9.1 | 0.817 *** |
| Age hh | −0.025 ** | −3.07 | −32.7 | 0.975 ** | −0.025 ** | −3.03 | −32.5 | 0.976 ** |
| Age hh2 (×10−2) | 0.019 * | 2.44 | 35.2 | 1.019 * | 0.019 * | 2.41 | 34.9 | 1.019 * |
| Constant | −0.223 | −1.17 | −0.239 | −1.24 | ||||
| lnalpha | −0.880 *** | −29.75 | 0.415 *** | |||||
| N | 17,342 | 17,342 | 17,342 | 17,342 | ||||
| McFadden (adj) | 0.0841 | 0.049 | ||||||
| aic0 | 8.07 × 1010 | 5.81 × 1010 | ||||||
| bic | 8.07 × 1010 | 5.81 × 1010 |
| Marginalised | Non-Marginalised | |||
|---|---|---|---|---|
| Count | Logistic | Count | Logistic | |
| Livestock | −0.932 | 1.316 * | −0.905 ** | 1.407 *** |
| (1.25) | (2.29) | (2.95) | (5.13) | |
| Agricultural land | −0.909 * | 1.808 *** | −0.839 *** | 1.179 * |
| (2.02) | (6.00) | (4.59) | (2.30) | |
| Cash transfer | 1.293 *** | −0.527 *** | 1.095 | −0.727 * |
| (4.33) | (3.93) | (1.30) | (2.41) | |
| Household size | 1.014 | 1.003 | 1.055 *** | −0.908 *** |
| (1.63) | (0.17) | (9.33) | (8.22) | |
| Wealth index | −0.922 ** | 1.467 *** | −0.926 *** | 1.626 *** |
| (2.90) | (8.18) | (5.51) | (20.57) | |
| Education | −0.874 *** | 1.241 ** | −0.918 *** | 1.290 *** |
| (3.55) | (3.00) | (3.45) | (6.45) | |
| Female hh head | 1.163 ** | −0.856 | 1.026 | −0.802 *** |
| (3.20) | (1.60) | (0.91) | (4.07) | |
| Age hh | 1.016 * | −0.956 ** | 1.008 | −0.977 * |
| (2.15) | (2.68) | (1.74) | (2.54) | |
| Age hh2 (×10−2) | −1.000 * | 1.000 * | −1.000 | 1.000 * |
| (2.16) | (2.40) | (1.31) | (2.01) | |
| Lnalpha | −0.427 *** | −0.427 *** | ||
| (16.90) | (25.86) | |||
| Wald chi2 | 100.69 | 188.93 | ||
| Prob > chi2 | 0.0000 | 0.0000 | ||
| No observations | 4632 | 12,710 | ||
| Results | Coefficient | p-Value | Percentage Change |
|---|---|---|---|
| Characteristics differential (explained) | 3.82 (0.28) | 0.000 | 153.85% |
| Coefficient differential (unexplained) | −1.50 (0.19) | 0.000 | −53.85% |
| Outcome mean differential | 2.31 (0.29) | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korir, L.; Rizov, M.; Ruto, E.; Walsh, P.P. Household Vulnerability to Food Insecurity and the Regional Food Insecurity Gap in Kenya. Sustainability 2021, 13, 9022. https://doi.org/10.3390/su13169022
Korir L, Rizov M, Ruto E, Walsh PP. Household Vulnerability to Food Insecurity and the Regional Food Insecurity Gap in Kenya. Sustainability. 2021; 13(16):9022. https://doi.org/10.3390/su13169022
Chicago/Turabian StyleKorir, Lilian, Marian Rizov, Eric Ruto, and Patrick Paul Walsh. 2021. "Household Vulnerability to Food Insecurity and the Regional Food Insecurity Gap in Kenya" Sustainability 13, no. 16: 9022. https://doi.org/10.3390/su13169022
APA StyleKorir, L., Rizov, M., Ruto, E., & Walsh, P. P. (2021). Household Vulnerability to Food Insecurity and the Regional Food Insecurity Gap in Kenya. Sustainability, 13(16), 9022. https://doi.org/10.3390/su13169022






