Modelling Faecal Sludge Dewatering Processes in Drying Beds Based on the Results from Tete, Mozambique
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Development
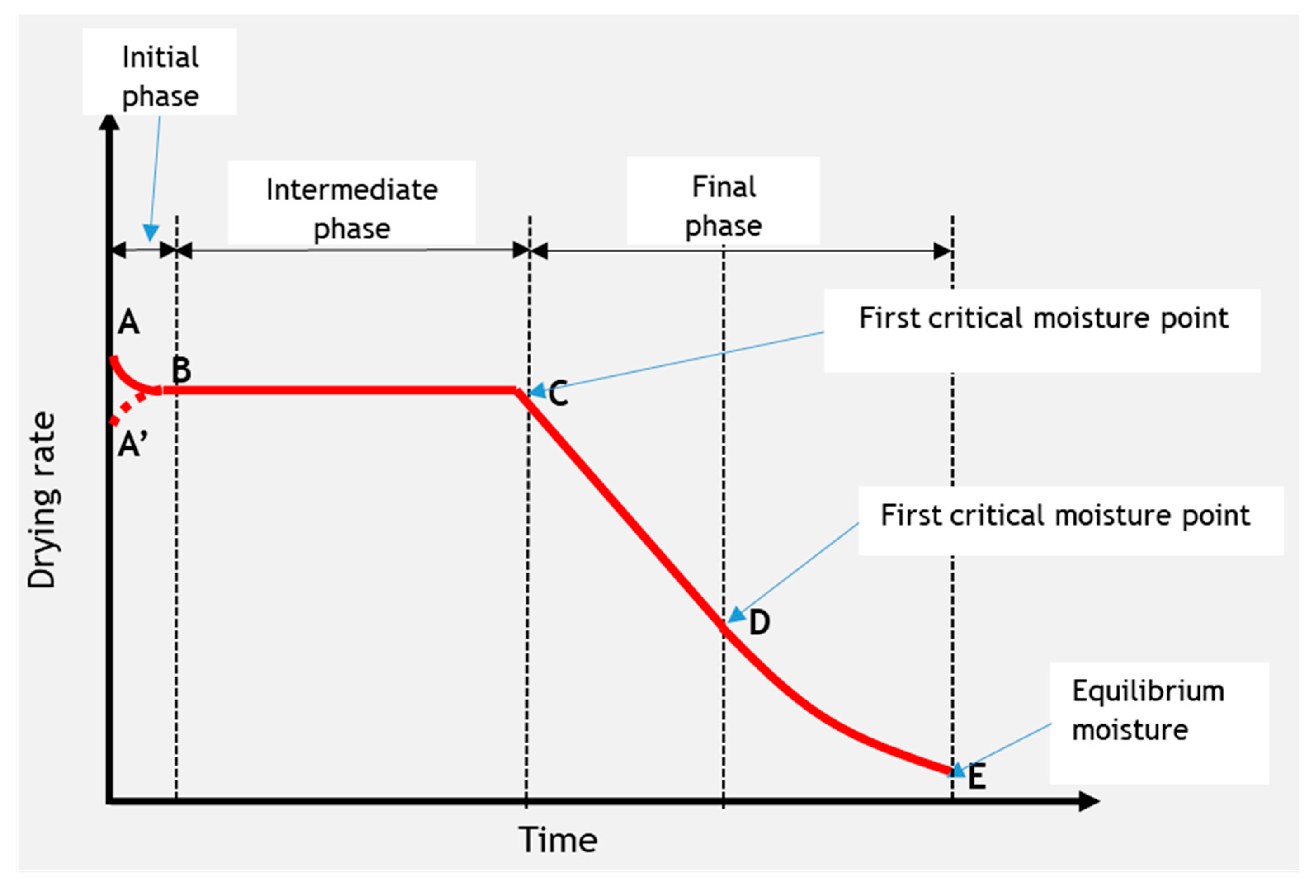
2.1.1. Theoretical Overview of the Sludge Dewatering Processes of Drying Beds
Drainage Process
Evaporation
2.1.2. Model Scope and Key Assumptions
- Sludge is considered heterogeneous, with solid and fluid phases. The water mass in the sludge is present in free, interstitial, adsorbed and intracellular fractions.
- Air is considered to be an ideal gas with a constant composition that flows perpendicularly to the SDB with a certain temperature (), wind speed () and relative humidity ().
- Drying beds are subject to atmospheric pressure and temperature.
- During SDB loading, the influence of the settling velocity on the drainage process is neglectable.
- Sludge solids are deposited over the entire surface of the filter medium, forming a homogeneous porous layer with a constant permeability.
- The effect of biochemical transformations that may occur throughout the dewatering process is neglected both in the sludge and inside the filter medium.
- Drainage processes start after the cake is formed, corresponding with the intermediate phase.
- The energy available for the drainage is constant.
- The mass of solids remains constant as evaporation occurs.
- Evaporation occurs from the interfacial area of the sludge layer, neglecting the transfer of mass and energy through the side walls and through the bottom of the drying beds.
2.1.3. Mathematical Formulation of the Sludge Dewatering Process
Initial Water Mass
Precipitated Water Mass
Drained Water Mass
Evaporated Water Mass
- (a)
- turbulent regime (; ):
- (b)
- laminar regime (; ):
2.2. Pilot Facility
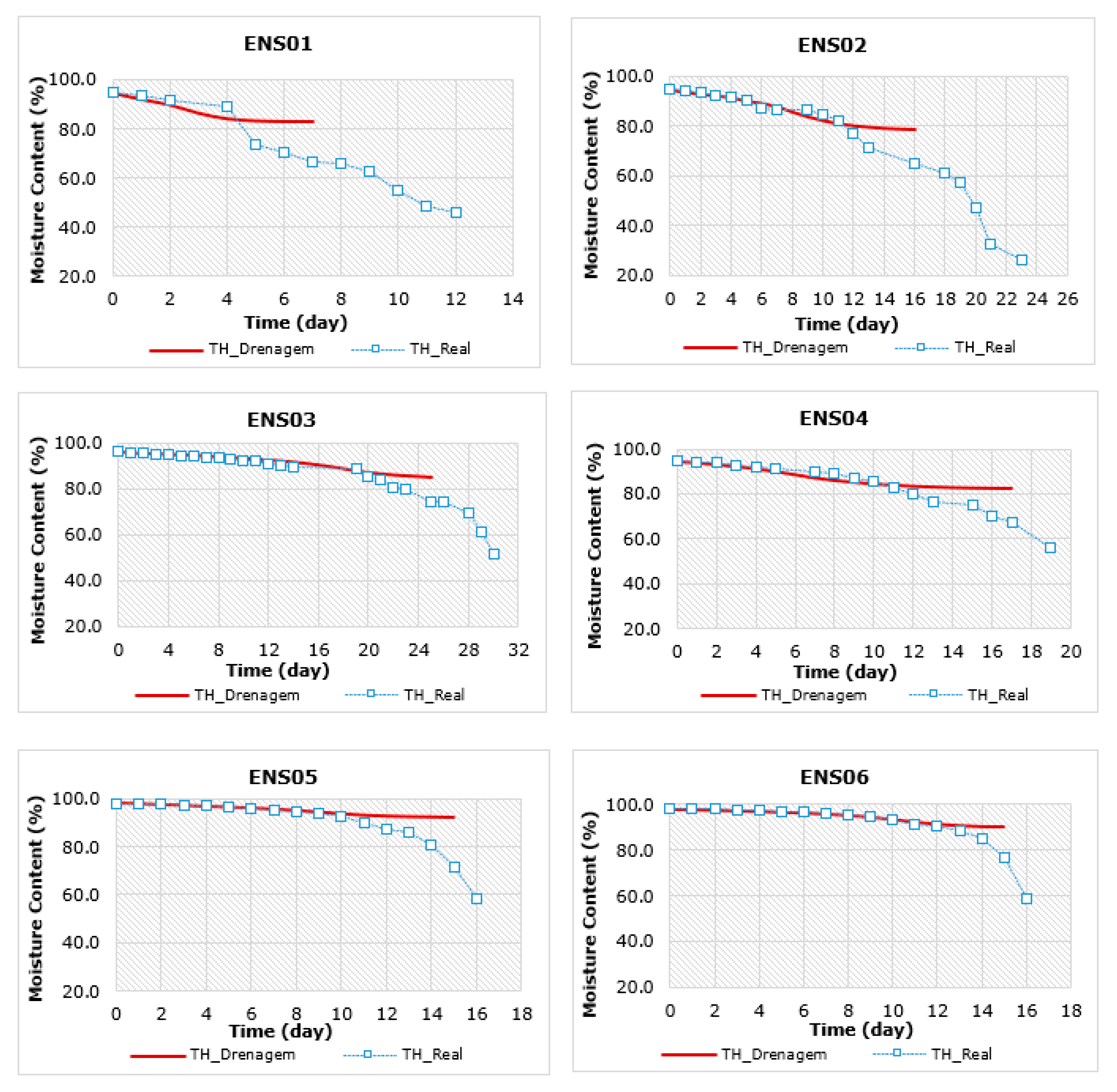
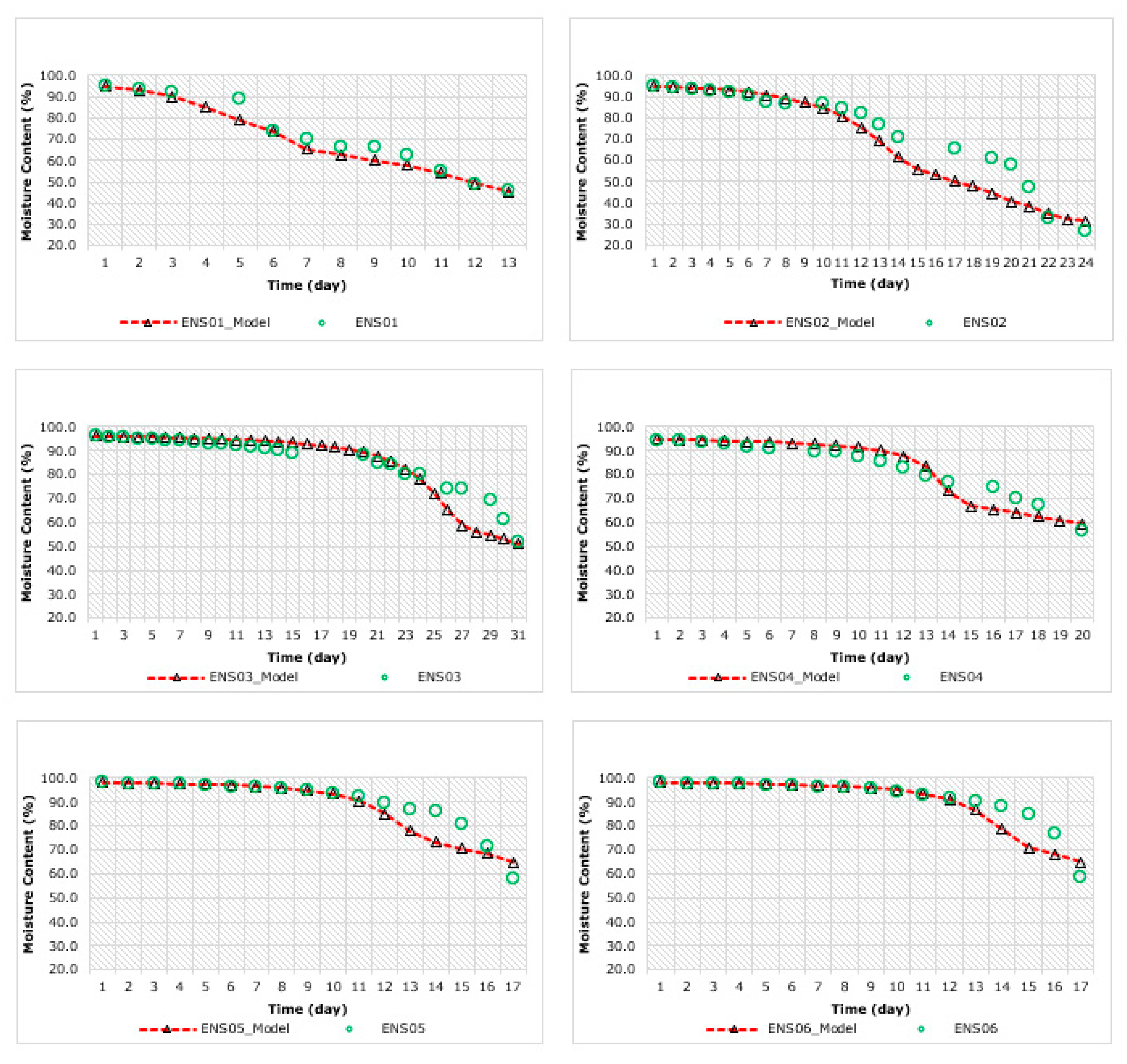
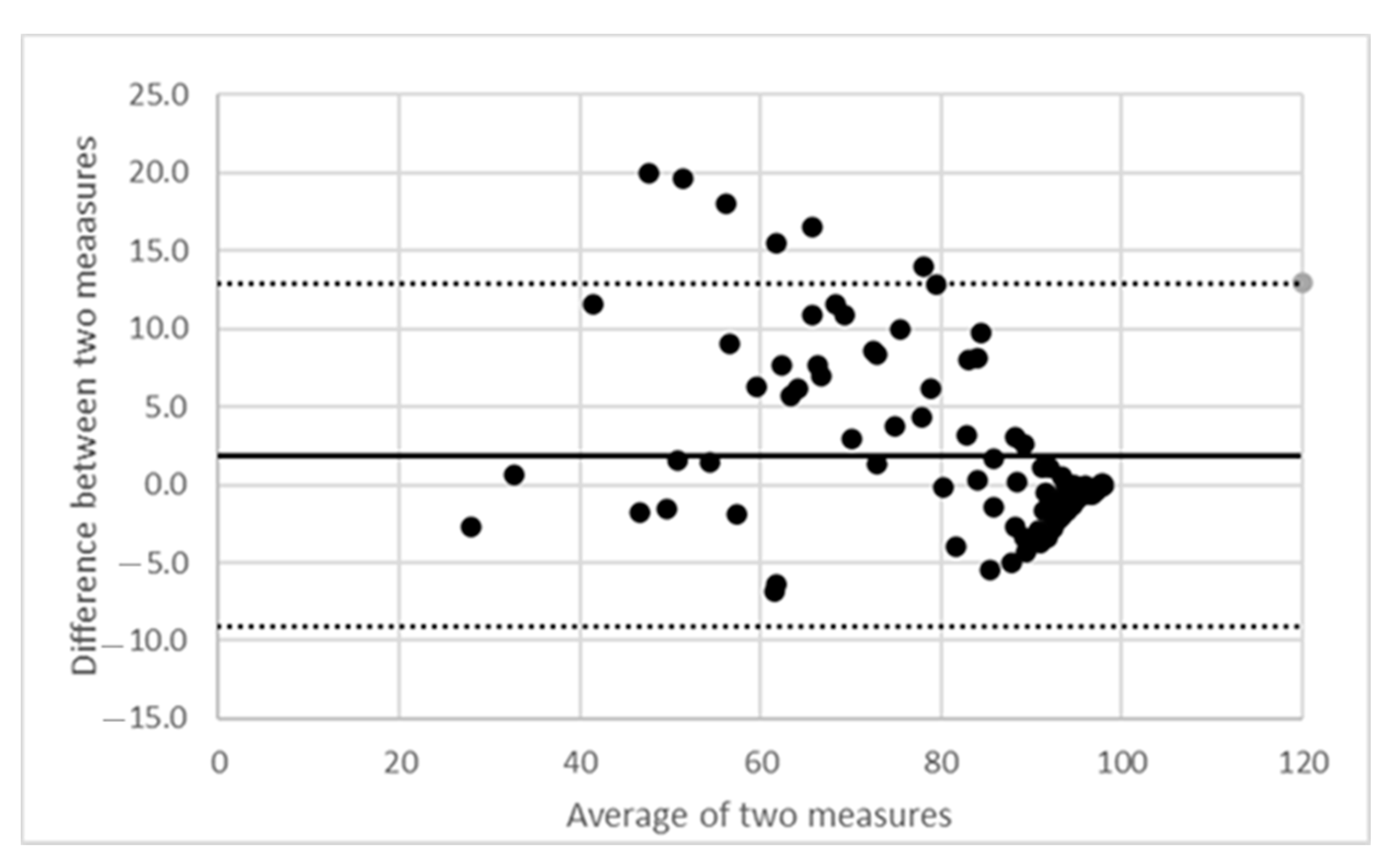
3. Experimental Results
4. Discussion of the Experimental Results
4.1. Sludge Field Capacity
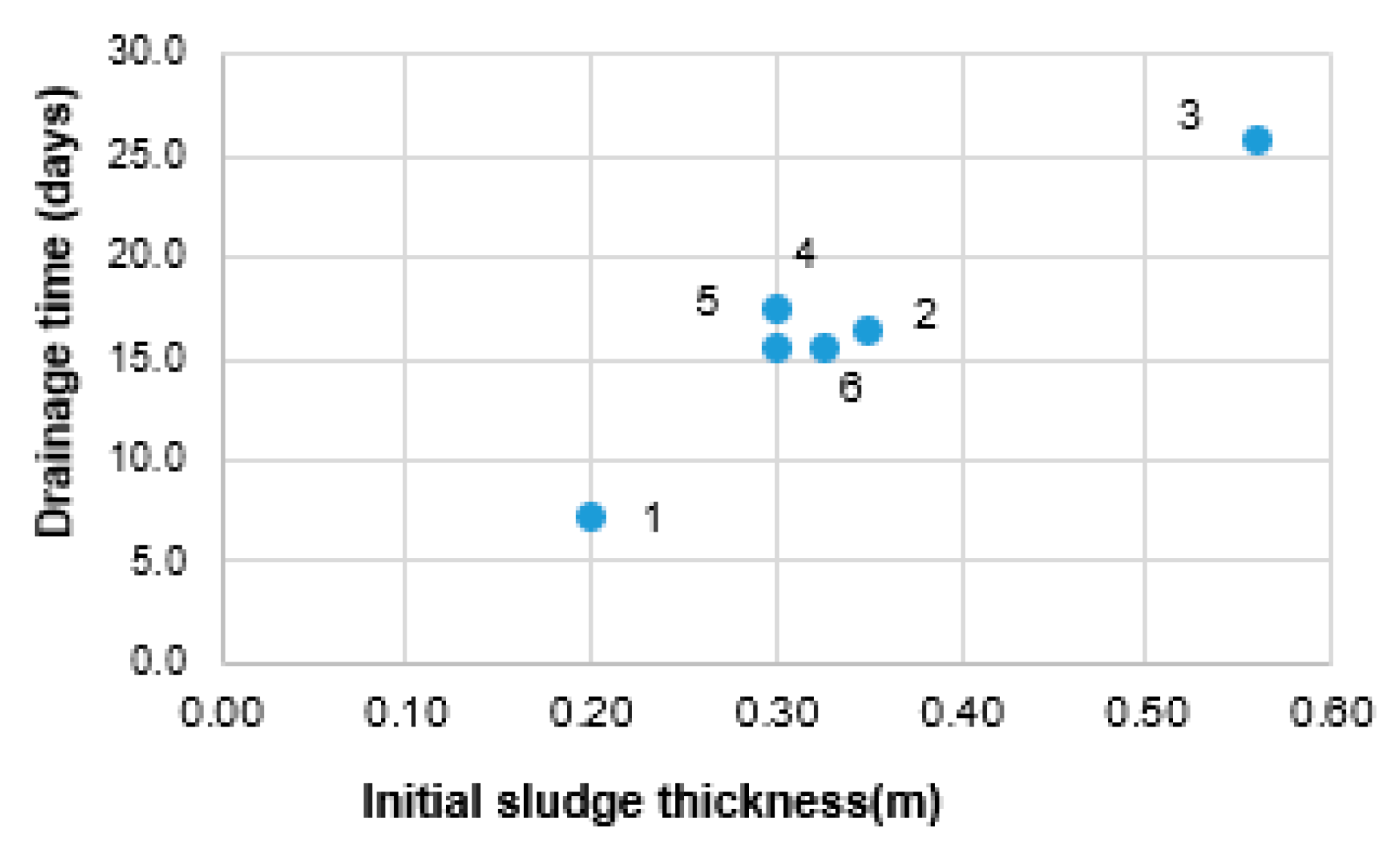
4.2. Total Drainage Time
4.3. Filter Medium Resistance
4.4. Cake Specific Resistance
4.5. Mass Transfer Coefficient
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Strande, L.; Brdjanovic, D. Faecal Sludge Management—Systems Approach for Implementation and Operation; IWA Publishing: London, UK, 2014. [Google Scholar]
- Tilley, E.; Lüthi, C.; Morel, A.; Zurbrügg, C.; Schertenleib, R.E. Compendium of Sanitation Systems and Technologies; Eawag: Dübendorf, Switzerland, 2009. [Google Scholar]
- Montangero, A.; Strauss, M.; Ingallinella, A.M.; Koottatep, T.; Larmie, S.A. Cuando Los Tanques Septicos Estan Llenos—El Desafio Del ManeJo Y Tratamiento De Lodos Fecales. In Congreso Argentino de Saneamento y Medio Ambiente; AIDIS: Mendoza, Argentina, 2000; p. 14. [Google Scholar]
- Van Haandel, A.; Marais, G. O Comportamento Do Sistema de Lodo Ativado Teoria e Aplicações Para Projeto E Operação; Epgraf: Campina Grande, Brazil, 1999. [Google Scholar]
- Soares, S.R.A.; Matos, Z.M.D.; Bernardes, R.S. Modelagem do processo de desidratação de lodo anaeróbio em leitos de secagem simulados. Rev. Bras. Eng. Agrícola Ambient. 2001, 5, 313–319. [Google Scholar] [CrossRef]
- Flaga, A. Sludge drying. In Proceedings of the Polish-Swedish Seminars Integration and Optimisation of Urban Sanitation Systems, Cracow, Poland, 23–25 March 2005; pp. 73–82. [Google Scholar]
- Lo, K.M. Digital Computer Simulation of Water and Wastewater Sludge Dewatering on Sand Beds. Ph.D. Thesis, Environmental Engineering, Department of Civil Engineering, University of Massachusetts, Amherst, MA, USA, 1971. [Google Scholar]
- Melo, A.S.D. Contribuição Para o Dimensionamento de Leitos de Secagem de Lodo. Master’s Thesis, Civil and Environmental Engineering, Department of Technology and Natural Resources Center, Universidade Federal de Campina Grande, Campina Grande, Brazil, 2006. [Google Scholar]
- Gharaibeh, A.; Sivakumar, M.; Hagare, D. Mathematical model to predict solids content of water treatment residuals during drying. J. Environ. Eng. 2007, 133, 165–172. [Google Scholar] [CrossRef][Green Version]
- Christensen, M.L.; Dominiak, D.M.; Nielsen, P.H.; Sedin, M.; Keiding, K. Gravitational drainage of compressible organic materials. Am. Inst. Chem. Eng. J. 2010, 56, 3099–3108. [Google Scholar] [CrossRef]
- Font, R.; Gomez-Rico, M.F.; Fullana, A. Skin effect in the heat and mass transfer model for sewage sludge drying. Sep. Purif. Technol. 2011, 77, 146–161. [Google Scholar] [CrossRef]
- Obianyo, J.; Agunwamba, J. Modeling of Evaporation Losses in Sewage Sludge Drying Bed. Niger. J. Technol. 2015, 34, 890. [Google Scholar] [CrossRef]
- Kavoosi, A. Iinvestigating the Fundamental Parameters of Cake Filtration Using a Gravity Column Device. Master’s Thesis, Chemical Engineering and Applied Chemistry, University of Toronto, Toronto, ON, Canada, 2014. [Google Scholar]
- Barua, A. Experimental Study of Filter Cake Cracking During Deliquoring. Ph.D. Thesis, Department of Chemical Engineering end Chemical Technology, Imperial College of Science, Technology and Medicine, London, UK, 2014. [Google Scholar]
- Dominiak, D.; Christensen, M.; Keiding, K.; Nielsen, P.H. Gravity drainage of activated sludge: New experimental method and considerations of settling velocity, specific cake resistance and cake compressibility. Water Res. 2011, 45, 1941–1950. [Google Scholar] [CrossRef] [PubMed]
- Ficza, I. Mathematical model of solar drying of sewage sludge. Master’s Thesis, Faculty of Mechanical Engineering, Institute of Mathematics, Brno University of Technology, Brno, Czech Republic, 2010. [Google Scholar]
- Azevedo, E.G.; Alves, A.M. Engenharia de Processos de Separação, 2nd ed.; IST Press: Lisboa, Portugal, 2013. [Google Scholar]
- Bergman, T.; Lavine, A.; Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ferranti, E.M. Desidratação de Lodos de Estação de Tratamento de Água. Master’s Thesis, Instituto de Pesquisas Hidráulicas, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil, 2015. [Google Scholar]
- Korczak-Niedzielska, M.; Gromiec, M.J. Suszienieosadowsciekowych, Materialy VII Konf.Nauk-Techn.nt. In Osadysciekowe w Praktyce Pod Red. J.B. Bienna; Wydawnictwo Politechniki Czestochoskiej: Czestochowa, Poland, 1998. [Google Scholar]
- Dominiak, D.M.; Christensen, M.; Keiding, K.; Nielsen, P.H. Sludge quality aspects of reed bed drainage. Water Res. 2011, 45, 6453–6460. [Google Scholar] [CrossRef]
- Kavanagh, B.V. The Dewatering of Activated Sludge: Measurement of Specific Resistance to Filtration and Capillary Suction Time. Wat. Pollut. 1980, 3, 388–398. [Google Scholar]
- Berktay, A. Properties of Sludge Produced from the Pressurized Wastewater Treatment Process. J. Eng. Environ. Sci. 1998, 22, 377–385. [Google Scholar]
- Kim, M.J. The Effect of Sludge Retention Time: On Dewaterabuity of Activated Sludge. Master’s Thesis, Department of Chemical Engineering e Applied Chemistry, University of Toronto, Toronto, ON, Canada, 2001. [Google Scholar]
- Marrero, T.R.; Mason, E.A. Gaseous Diffusion Coefficients. J. Phys. Chem. Ref. Data 1972, 1, 3. [Google Scholar] [CrossRef]
- VDI Gesellschaft. VDI Heat Atlas, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Moiambo, O. Simulação Hidráulica da Desidratação de Lamas Fecais, Baseada em Estudos de Caso em Portugal e Moçambique. Ph.D. Thesis, Instituto Superior Técnico, Universidade de Lisboa, Lisbon, Portugal, 2018. [Google Scholar]
- Van Haandel, A.; Lettinga, G. Tratamento Anaeróbio de Esgotos: Um Manual Para Regiões de Clima Quente; Epgraf: Campina Grande, Brazil, 1994. [Google Scholar]




| Period | Cycle | SDB Ident. | Test Ident | Sludge Source | Initial Sludge Depth (m) |
|---|---|---|---|---|---|
| 9 May 2017 to 7 June 2017 | 1st | LS01 LS02 LS03 | ENS01 ENS02 ENS03 | ST01 ST01 ST01 + PT01 | 0.20 0.35 0.56 |
| 22 June 2017 to 10 July 2017 | 2nd | LS01 | ENS04 | ST02 | 0.30 |
| 1 August 2017 to 17 August 2017 | 3rd | LS01 LS03 | ENS05 ENS06 | ST03 ST03 + PT01 | 0.30 0.32 |
| Variable | ENS01 | ENS02 | ENS03 | ENS04 | ENS05 | ENS06 |
|---|---|---|---|---|---|---|
| Sludge type | ST | ST | ST + PT | ST | ST | ST + PT |
| Loading date | 9 May 2017 | 9 May 2017 | 9 May 2017 | 22 June 2017 | 1 August 2017 | 1 August 2017 |
| Conductivity (µS/cm) | 1528 | 1528 | 1959 | 908 | 3790 | 2740 |
| Average sludge temperature (°C) | 28.8 | 28.8 | 28.5 | 27.2 | 28.0 | 23.5 |
| pH | 7.8 | 7.8 | 7.5 | 6.8 | 7.6 | 8.0 |
| Initial solid content (%) | 5.2 | 5.2 | 4.0 | 5.4 | 2.0 | 2.0 |
| Air average temperature (°C) | 26.3 | 26.2 | 26.0 | 24.1 | 24.5 | 24.5 |
| Air average humidity (%) | 63 | 62 | 62 | 66 | 64 | 64 |
| Maximum solar insolation (hours/day) | 7 | 8 | 8 | 8 | 8 | 8 |
| Average wind speed (km/h) | 14 | 13 | 13 | 11 | 10 | 10 |
| Parameter | Unit | Determined Values |
|---|---|---|
| Mass transfer coefficient () | kg/s/m2 | 0.007–0.013 |
| Cake specific resistance ) | m/kg | 2.3–6.6 × 1010 |
| ENS01 | ENS02 | ENS03 | ENS04 | ENS05 | ENS06 | Global | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp. | Model | Exp. | Model | Exp. | Model | Exp. | Model | Exp. | Model | Exp. | Model | Exp. | Model | |
| Mean | 71.5 | 69.7 | 74.9 | 66.8 | 85.9 | 84.0 | 83.4 | 82.0 | 90.0 | 88.4 | 91.3 | 89.9 | 83.4 | 81.5 |
| SD | 17.5 | 17.2 | 21.0 | 24.9 | 11.7 | 15.7 | 11.1 | 14.5 | 10.9 | 12.0 | 10.2 | 11.4 | 15.4 | 18.1 |
| Var | 304.6 | 295.5 | 442.8 | 619.3 | 137.8 | 245.9 | 122.3 | 211.2 | 119.1 | 143.8 | 103.1 | 130.4 | 237.4 | 328.6 |
| n | 12 | 13 | 19 | 24 | 25 | 31 | 17 | 20 | 17 | 17 | 17 | 17 | 107 | 107 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moiambo, O.; Mutevuie, R.; Ferreira, F.; Matos, J. Modelling Faecal Sludge Dewatering Processes in Drying Beds Based on the Results from Tete, Mozambique. Sustainability 2021, 13, 8981. https://doi.org/10.3390/su13168981
Moiambo O, Mutevuie R, Ferreira F, Matos J. Modelling Faecal Sludge Dewatering Processes in Drying Beds Based on the Results from Tete, Mozambique. Sustainability. 2021; 13(16):8981. https://doi.org/10.3390/su13168981
Chicago/Turabian StyleMoiambo, Osvaldo, Raúl Mutevuie, Filipa Ferreira, and José Matos. 2021. "Modelling Faecal Sludge Dewatering Processes in Drying Beds Based on the Results from Tete, Mozambique" Sustainability 13, no. 16: 8981. https://doi.org/10.3390/su13168981
APA StyleMoiambo, O., Mutevuie, R., Ferreira, F., & Matos, J. (2021). Modelling Faecal Sludge Dewatering Processes in Drying Beds Based on the Results from Tete, Mozambique. Sustainability, 13(16), 8981. https://doi.org/10.3390/su13168981








