A Machine Learning Approach to Determine Airport Asphalt Concrete Layer Moduli Using Heavy Weight Deflectometer Data
Abstract
:1. Introduction
2. Experimental Campaign
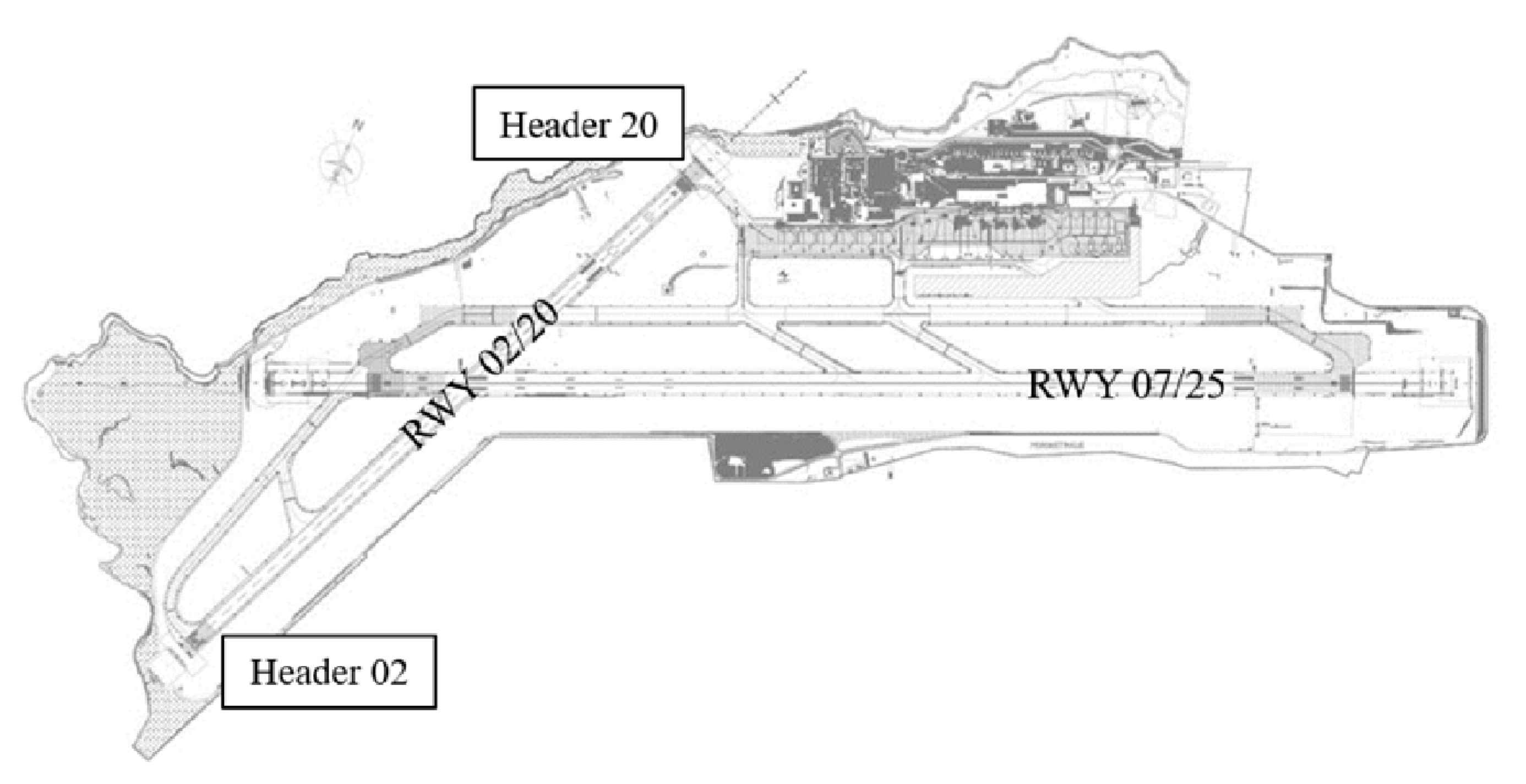
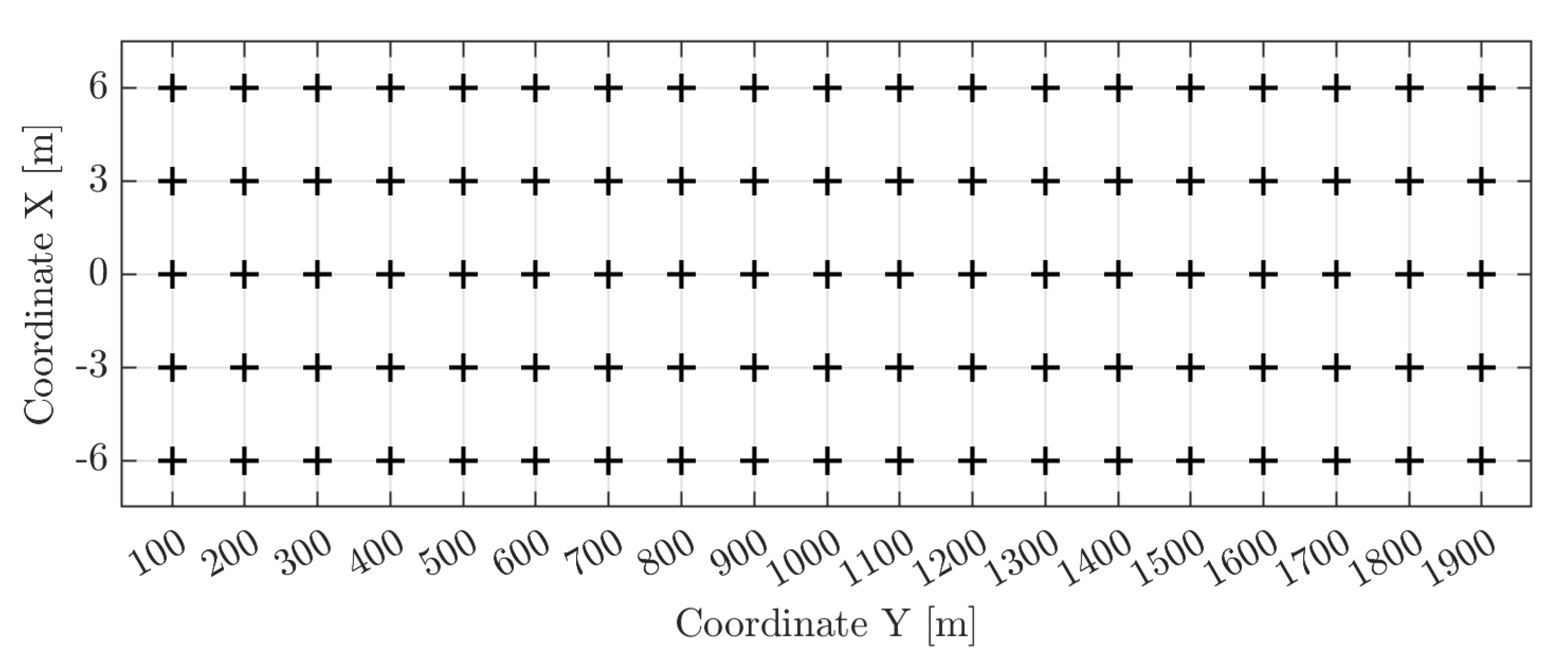
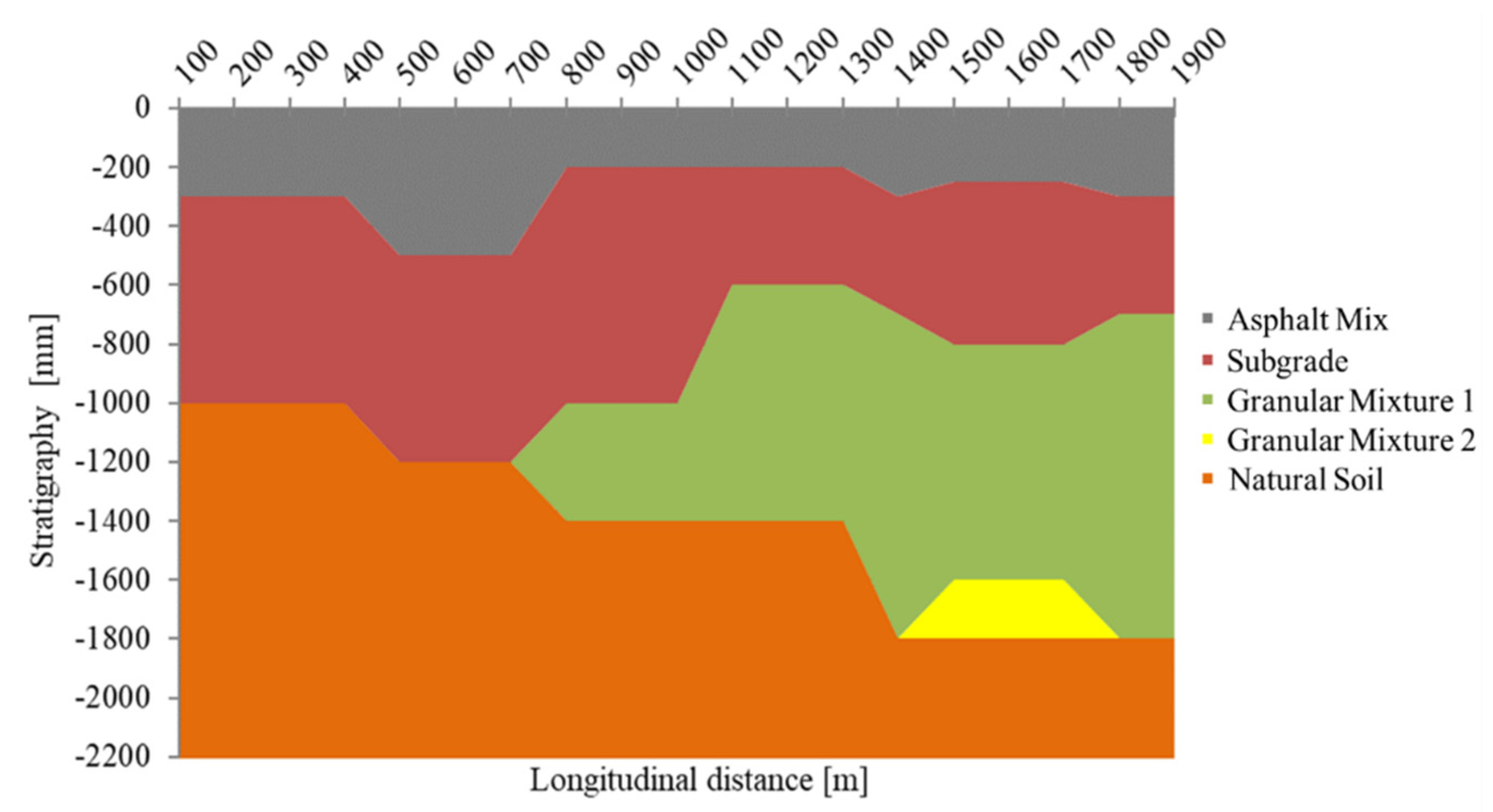
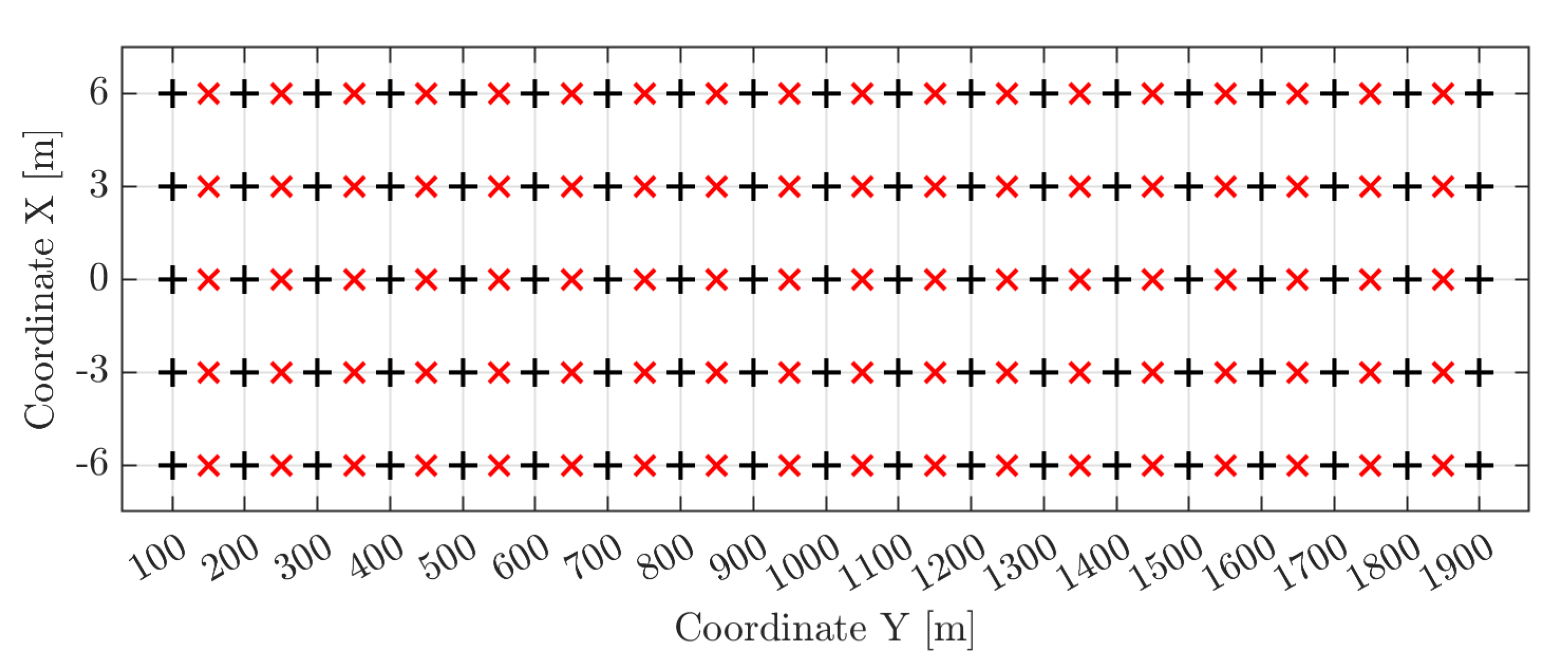
2.1. In Situ Investigation
2.2. Deflection Basin Parameters
- Surface curvature index (SCI) which provides information on changes in the near-surface layer’s relative strength.
- Deflection ratio (DR) which takes into account the type and quality of materials by relating them to the ratio of two deflections.
- Area under deflection basin curve (AREA) which relates the stiffness of the pavement structure to a shape factor. In fact, it is the partial area under the deflection basin curve normalized with respect to using Simpson’s rule [48].
2.3. Backcalculation Process
3. Theory and Calculation
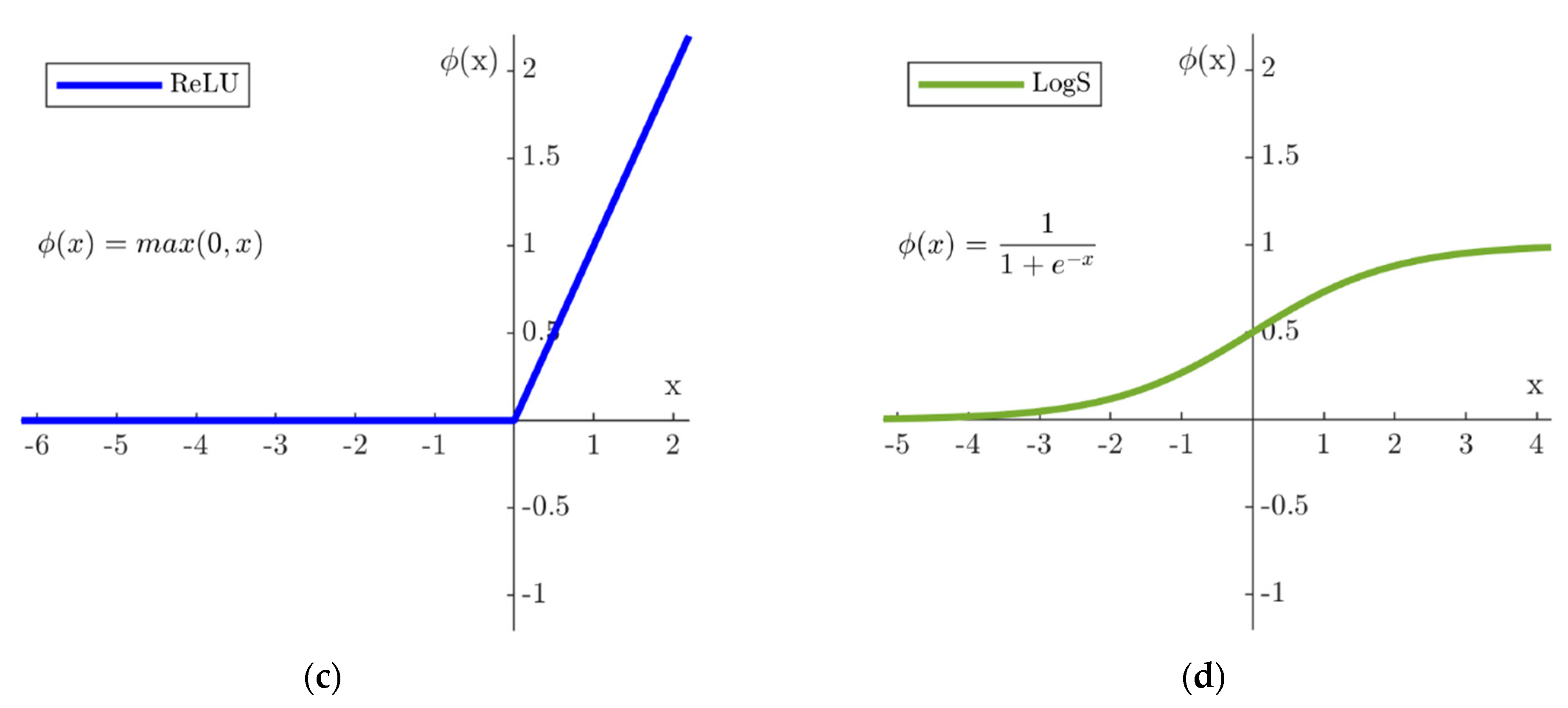
3.1. Neural Modeling
3.2. Bayesian Regularization
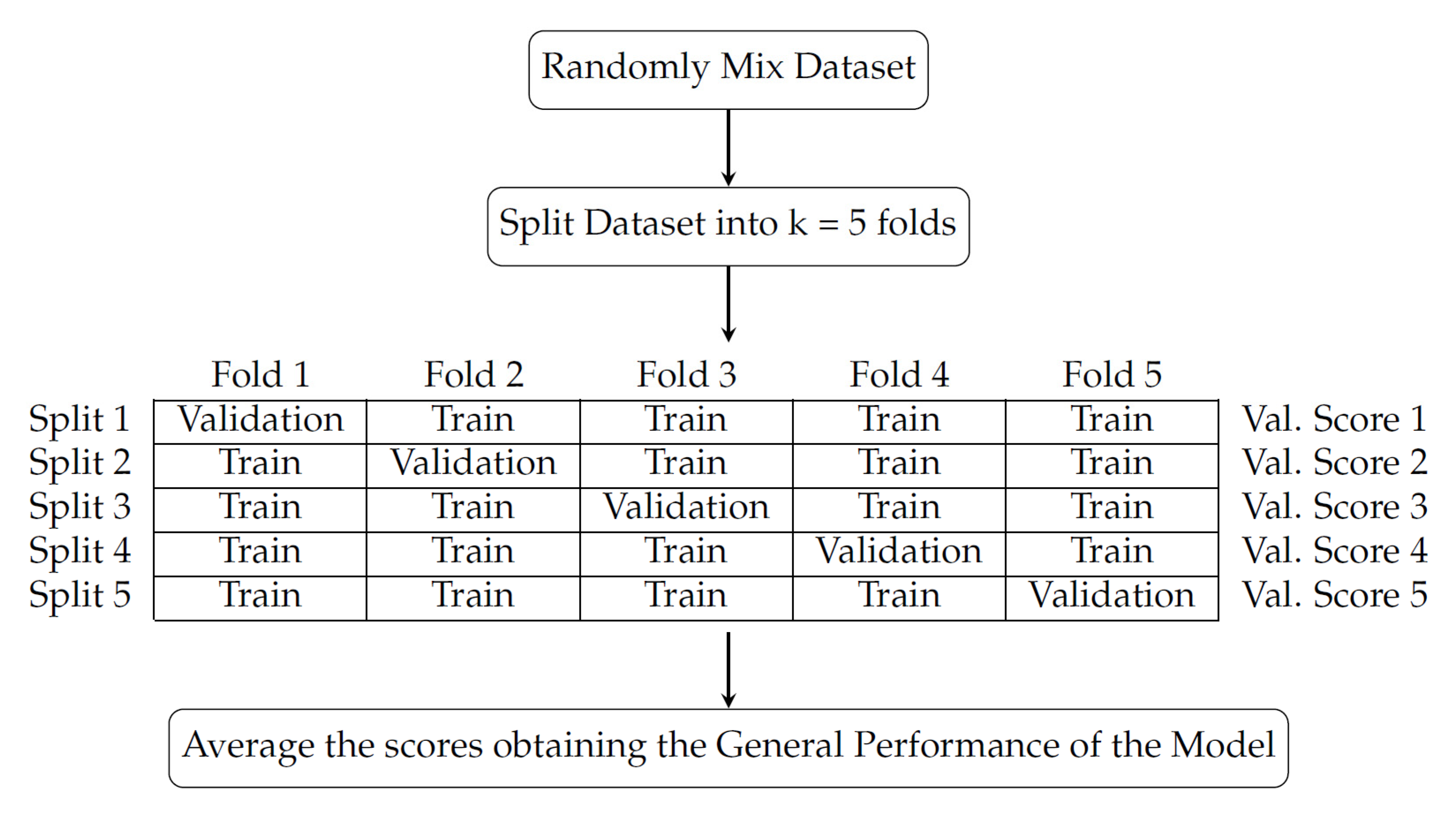
3.3. K-Fold Cross-Validation
3.4. Data Augmentation
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moteff, J.; Parfomak, P. Critical Infrastructure and Key Assets: Definition and Identification; Library of Congress Washington DC Congressional Research Service: Washington, DC, USA, 2004. [Google Scholar]
- Schweikert, A.; Chinowsky, P.; Espinet, X.; Tarbert, M. Climate change and infrastructure impacts: Comparing the impact on roads in ten countries through 2100. Procedia Eng. 2014, 78, 306–316. [Google Scholar] [CrossRef] [Green Version]
- Makovšek, D.; Tominc, P.; Logožar, K. A cost performance analysis of transport infrastructure construction in Slovenia. Transportation 2012, 39, 197–214. [Google Scholar] [CrossRef]
- Navneet, G.; Guo, E.; McQueen, R. Operational Life of Airport Pavements; Federal Aviation Administration: Washington, DC, USA, 2004. [Google Scholar]
- Ashtiani, A.Z.; Murrell, S.; Brill, D.R. Machine Learning Approach to Identifying Key Environmental Factors for Airfield Asphalt Pavement Performance. In Airfield and Highway Pavements 2021, Virtual Conference, 8–10 June 2021; American Society of Civil Engineers: Reston, VA, USA, 2021; pp. 328–337. [Google Scholar]
- Carlucci, F.; Cirà, A.; Coccorese, P. Measuring and explaining airport efficiency and sustainability: Evidence from Italy. Sustainability 2018, 10, 400. [Google Scholar] [CrossRef] [Green Version]
- Rix, G.J.; Baker, N.C.; Jacobs, L.J.; Vanegas, J.; Zureick, A.H. Infrastructure assessment, rehabilitation, and reconstruction. In Proceedings of the Frontiers in Education 1995 25th Annual Conference. Engineering Education for the 21st Century, Atlanta, GA, USA, 1–4 November 1995; IEEE: New York, NY, USA, 1995; Volume 2, pp. 4c1–11. [Google Scholar]
- Zou, L.; Yi, L.; Sato, M. On the use of lateral wave for the interlayer debonding detecting in an asphalt airport pavement using a multistatic GPR system. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4215–4224. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; He, X.; Peeta, S.; Weiss, W.J. Internal curing for concrete bridge decks: Integration of a social cost analysis in evaluation of long-term benefit. Transp. Res. Rec. 2016, 2577, 25–34. [Google Scholar] [CrossRef]
- Haas, R.; Hudson, W.R.; Zaniewski, J.P. Modern Pavement Management; Krieger Publishing Company: Melbourne, FL, USA, 1994. [Google Scholar]
- Zheng, M.; Chen, W.; Ding, X.; Zhang, W.; Yu, S. Comprehensive life cycle environmental assessment of preventive maintenance techniques for asphalt pavement. Sustainability 2021, 13, 4887. [Google Scholar] [CrossRef]
- De Souza, N.M.; De Almeida Filho, A.T. A systematic airport runway maintenance and inspection policy based on a delay time modeling approach. Autom. Constr. 2020, 110, 103039. [Google Scholar] [CrossRef]
- Chern, S.G.; Lee, Y.S.; Hu, R.F.; Chang, Y.J. A research combines nondestructive testing and a neuro-fuzzy system for evaluating rigid pavement failure potential. J. Mar. Sci. Technol. 2005, 13, 133–147. [Google Scholar]
- Huang, Y.H. Pavement Analysis and Design; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Hoffman, M. Comparative study of selected nondestructive testing devices. Transp. Res. Rec. 1982, 852, 32–41. [Google Scholar]
- ASTM. ASTM D4695. Standard Test Method for Deflections with A Falling Weight-Type Impulse Load Device; ASTM: West Conshohocken, PA, USA, 1996. [Google Scholar]
- ASTM. ASTM D5340. Standard Test Method for Airport Pavement Condition Index Survey; ASTM: West Conshohocken, PA, USA, 1996. [Google Scholar]
- ASTM. ASTM D4695-96. Standard Guide for General Pavement Deflection Measurement; ASTM: West Conshohocken, PA, USA, 1996. [Google Scholar]
- Sebaaly, B.E.; Mamlouk, M.S.; Davies, T.G. Dynamic analysis of falling weight deflectometer data. Transp. Res. Rec. 1986, 1070, 63–68. [Google Scholar]
- Bush III, A.J.; Alexander, D.R. Pavement evaluation using deflection basin measurements and layered theory. Transp. Res. Rec. 1985, 1022, 16–29. [Google Scholar]
- Chang, D.W.; Kang, Y.V.; Roesset, J.M.; Stokoe, K. Effect of depth to bedrock on deflection basins obtained with Dynaflect and falling weight deflectometer tests. Transp. Res. Rec. 1992, 1355, 8–16. [Google Scholar]
- Ullidtz, P.; Coetzee, N. Analytical procedures in nondestructive testing pavement evaluation. Transp. Res. Rec. 1995, 1482, 61–66. [Google Scholar]
- Weil, G.J. Non-destructive testing of bridge, highway and airport pavements. In Proceedings of the Fourth International Conference of Ground Penetrating Radar, Rovaniemi, Finland, 8–13 June 1992; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 1992; pp. 259–266. [Google Scholar]
- Gopalakrishnan, K. Instantaneous pavement condition evaluation using non-destructive neuro-evolutionary approach. Struct. Infrastruct. Eng. 2012, 8, 857–872. [Google Scholar] [CrossRef]
- FAA. USDOT Advisory Circular 150/5370-11B. Use of Nondestructive Testing in the Evaluation of Airport Pavements; FAA: Washington, DC, USA, 2011. [Google Scholar]
- Talvik, O.; Aavik, A. Use of FWD deflection basin parameters (SCI, BDI, BCI) for pavement condition assessment. Transformation 2009, 7, 260. [Google Scholar] [CrossRef]
- Gopalakrishnan, K.; Thompson, M.R. Use of nondestructive test deflection data for predicting airport pavement performance. J. Transp. Eng. 2007, 133, 389–395. [Google Scholar] [CrossRef]
- Goktepe, A.B.; Agar, E.; Lav, A.H. Advances in backcalculating the mechanical properties of flexible pavements. Adv. Eng. Softw. 2006, 37, 421–431. [Google Scholar] [CrossRef]
- Burmister, D.M. The general theory of stresses and displacements in layered soil systems. III. J. Appl. Phys. 1945, 16, 296–302. [Google Scholar] [CrossRef]
- Ullidtz, P. Will Nonlinear Backcalculation Help? In Nondestructive Testing of Pavements and Backcalculation of Moduli; American Society for Testing and Materials: West Conshohocken, PA, USA, 2000; pp. 14–22. [Google Scholar]
- Lytton, R.L. Backcalculation of layer moduli, state of the art. In Nondestructive Testing of Pavements and Backcalculation of Moduli; ASTM International: West Conshohocken, PA, USA, 1989; pp. 7–38. [Google Scholar]
- Uzan, J. Advanced backcalculation techniques. In Nondestructive Testing of Pavements and Backcalculation of Moduli: Second Volume; ASTM International: West Conshohocken, PA, USA, 1994; pp. 3–37. [Google Scholar]
- Siddharthan, R.; Norris, G.M.; Epps, J.A. Use of FWD data for pavement material characterization and performance. J. Transp. Eng. 1991, 117, 660–678. [Google Scholar] [CrossRef]
- Goel, A.; Das, A. Nondestructive testing of asphalt pavements for structural condition evaluation: A state of the art. Nondestruct. Test. Eval. 2008, 23, 121–140. [Google Scholar] [CrossRef]
- Scimemi, G.F.; Turetta, T.; Celauro, C. Backcalculation of airport pavement moduli and thickness using the Lévy Ant Colony Optimization Algorithm. Constr. Build. Mater. 2016, 119, 288–295. [Google Scholar] [CrossRef]
- Lei, T.; Claudel, C. Inertial Measurement Units-based probe vehicles: Path reconstruction and map matching. In Proceedings of the 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: New York, NY, USA, 2018; pp. 2899–2904. [Google Scholar]
- Adeli, H. Neural networks in civil engineering: 1989–2000. Comput. Aided Civ. Infrastruct. Eng. 2001, 16, 126–142. [Google Scholar] [CrossRef]
- Li, M.; Wang, H. Development of ANN-GA program for backcalculation of pavement moduli under FWD testing with viscoelastic and nonlinear parameters. Int. J. Pavement Eng. 2019, 20, 490–498. [Google Scholar] [CrossRef]
- Gopalakrishnan, K.; Ceylan, H.; Guclu, A. Airfield pavement deterioration assessment using stress-dependent neural network models. Struct. Infrastruct. Eng. 2009, 5, 487–496. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Xie, P.; Ji, R.; Gagnon, J. Prediction of airfield pavement responses from surface deflections: Comparison between the traditional backcalculation approach and the ANN model. Road Mater. Pavement Des. 2020, 1–16. [Google Scholar] [CrossRef]
- Justo-Silva, R.; Ferreira, A.; Flintsch, G. Review on machine learning techniques for developing pavement performance prediction models. Sustainability 2021, 13, 5248. [Google Scholar] [CrossRef]
- Crovetti, J.A.; Shahin, M.; Touma, B.E. Comparison of two falling weight deflectometer devices, Dynatest 8000 and KUAB 2M-FWD. In Nondestructive Testing of Pavements and Backcalculation of Moduli; ASTM International: West Conshohocken, PA, USA, 1989. [Google Scholar]
- Claessen, A.; Valkering, C.; Ditmarsch, R. Pavement evaluation with the falling weight deflectometer. Assoc. Asph. Paving Technol. Proc. 1976, 45, 122–157. [Google Scholar]
- Chen, D.H.; Bilyeu, J.; Scullion, T.; Lin, D.F.; Zhou, F. Forensic evaluation of premature failures of Texas specific pavement study-1 sections. J. Perform. Constr. Facil. 2003, 17, 67–74. [Google Scholar] [CrossRef]
- ICAO. Annex 14: Aerodromes, Volume I–Aerodrome Design and Operations, 7th ed.; ICAO: Montréal, QC, Canada, 2016. [Google Scholar]
- Hossain, A.; Zaniewski, J.P. Characterization of falling weight deflectometer deflection basin. Transp. Res. Rec. 1991, 1293, 1–11. [Google Scholar]
- Xu, B.; Ranjithan, S.R.; Kim, Y.R. New relationships between falling weight deflectometer deflections and asphalt pavement layer condition indicators. Transp. Res. Rec. 2002, 1806, 48–56. [Google Scholar] [CrossRef]
- Gopalakrishnan, K.; Thompson, M.R. Use of deflection basin parameters to characterize structural degradation of airport flexible pavements. In Advances in Pavement Engineering; ASCE Library: Austin, TX, USA, 2005; pp. 1–15. [Google Scholar]
- Hill, H.J. Early Life Study of the FA409 Full-Depth Asphalt Concrete Pavement Sections. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Urbana-Champaign, IL, USA, 1988. [Google Scholar]
- Thompson, M.; Garg, N. Mechanistic-Empirical Evaluation of the Mn/ROAD Low Volume Road Test Sections; Project IHR-535; University of Illinois at Urbana-Champaign: Urbana-Champaign, IL, USA, 1997. [Google Scholar]
- Battiato, G.; Ame, E.; Wagner, T. Description and implementation of RO.MA. for urban road and highway network maintenance. In Proceedings of the 3rd International Conference on Managing Pavement, San Antonio, TX, USA, 22–26 May 1994. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Otuoze, S.H.; Hunt, D.V.L.; Jefferson, I. Neural network approach to modelling transport system resilience for major cities: Case studies of Lagos and Kano (Nigeria). Sustainability 2021, 13, 1371. [Google Scholar] [CrossRef]
- Demuth, H.B.; Beale, M.H.; De Jesús, O.; Hagan, M.T. Neural Network Design, 2nd ed.; Martin Hagan: Boston, MA, USA, 2014; Chapter 11; pp. 4–7. [Google Scholar]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network Toolbox. User’s Guide; MathWorks: Natick, MA, USA, 2010. [Google Scholar]
- Da Silva, I.N.; Spatti, D.H.; Flauzino, R.A.; Liboni, L.H.B.; dos Reis Alves, S.F. Artificial neural network architectures and training processes. In Artificial Neural Networks; Springer: Cham, Switzerland, 2017; pp. 21–28. [Google Scholar]
- Baldo, N.; Manthos, E.; Pasetto, M. Analysis of the mechanical behaviour of asphalt concretes using artificial neural networks. Adv. Civ. Eng. 2018, 2018, 1650945. [Google Scholar] [CrossRef] [Green Version]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representation by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Padhi, S.; Millstein, T.; Nori, A.; Sharma, R. Overfitting in synthesis: Theory and practice. In Proceedings of the International Conference on Computer Aided Verification, New York, NY, USA, 15–18 July 2019; Springer: Cham, Switzerland, 2019; pp. 315–334. [Google Scholar]
- Tikhonov, A.N. On the solution of ill-posed problems and the method of regularization. In Doklady Akademii Nauk; Russian Academy of Sciences: Moscow, Russia, 1963; pp. 501–504. [Google Scholar]
- MacKay, D.J. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; Chapter 5; pp. 175–201. [Google Scholar]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity analysis of k-fold cross validation in prediction error estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 569–575. [Google Scholar] [CrossRef]
- Jung, Y. Multiple prediction K-fold cross-validation for model selection. J. Nonparametr. Stat. 2018, 30, 197–215. [Google Scholar] [CrossRef]
- Baldo, N.; Manthos, E.; Miani, M. Stiffness modulus and marshall parameters of hot mix asphalts: Laboratory data modeling by artificial neural networks characterized by cross-validation. Appl. Sci. 2019, 9, 3502. [Google Scholar] [CrossRef] [Green Version]
- Li, J. A critical review of spatial predictive modeling process in environmental sciences with reproducible examples in R. Appl. Sci. 2019, 9, 2048. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, M.; Johnson, J. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; Chapter 4; pp. 61–92. [Google Scholar]
- Lunardi, A. Interpolation Theory; Edizioni della Normale: Pisa, Italy, 2018. [Google Scholar]
- Oh, C.; Han, S.; Jeong, J. Time-series data augmentation based on interpolation. Procedia Comput. Sci. 2020, 175, 64–71. [Google Scholar] [CrossRef]
- Akima, H. A new method of interpolation and smooth curve fitting based on local procedures. J. ACM 1970, 17, 589–602. [Google Scholar] [CrossRef]
- Akima, H. A method of bivariate interpolation and smooth surface fitting based on local procedures. Commun. ACM 1974, 17, 18–20. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Tang, T.; Guo, Y.; Zhou, X.; Labi, S.; Zhu, S. Understanding electric bike riders’ intention to violate traffic rules and accident proneness in China. Travel Behav. Soc. 2021, 23, 25–38. [Google Scholar] [CrossRef]





| Inputs | Output | Activation Fun. | Best Architecture | |||
|---|---|---|---|---|---|---|
| δ0, HS, X, Y | ELU | 4-12-1 | 0.9673 | 0.0682 | 0.9231 | |
| ReLU | 4-27-1 | 0.9408 | 0.1309 | 0.8627 | ||
| TanH | 4-25-1 | 0.9780 | 0.0494 | 0.9477 | ||
| LogS | 4-22-1 | 0.9772 | 0.0474 | 0.9461 |
| Inputs | Output | Activation Fun. | Best Architecture | |||
|---|---|---|---|---|---|---|
| δ0, δ2, δ3, δ4, δ5, HS, X, Y | ELU | 8-27-1 | 0.9805 | 0.0423 | 0.9368 | |
| ReLU | 8-3-1 | 0.9455 | 0.1217 | 0.8277 | ||
| TanH | 8-9-1 | 0.9806 | 0.0437 | 0.9370 | ||
| LogS | 8-13-1 | 0.9844 | 0.0370 | 0.9493 |
| Inputs | Output | Activation Fun. | Best Architecture | |||
|---|---|---|---|---|---|---|
| SCI1, SCI2, SCI3, DR, AUPP, AREA, HS, X, Y | ELU | 9-18-1 | 0.9804 | 0.0501 | 0.9303 | |
| ReLU | 9-14-1 | 0.9555 | 0.0963 | 0.8441 | ||
| TanH | 9-26-1 | 0.9807 | 0.0439 | 0.9312 | ||
| LogS | 9-23-1 | 0.9864 | 0.0321 | 0.9516 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baldo, N.; Miani, M.; Rondinella, F.; Celauro, C. A Machine Learning Approach to Determine Airport Asphalt Concrete Layer Moduli Using Heavy Weight Deflectometer Data. Sustainability 2021, 13, 8831. https://doi.org/10.3390/su13168831
Baldo N, Miani M, Rondinella F, Celauro C. A Machine Learning Approach to Determine Airport Asphalt Concrete Layer Moduli Using Heavy Weight Deflectometer Data. Sustainability. 2021; 13(16):8831. https://doi.org/10.3390/su13168831
Chicago/Turabian StyleBaldo, Nicola, Matteo Miani, Fabio Rondinella, and Clara Celauro. 2021. "A Machine Learning Approach to Determine Airport Asphalt Concrete Layer Moduli Using Heavy Weight Deflectometer Data" Sustainability 13, no. 16: 8831. https://doi.org/10.3390/su13168831
APA StyleBaldo, N., Miani, M., Rondinella, F., & Celauro, C. (2021). A Machine Learning Approach to Determine Airport Asphalt Concrete Layer Moduli Using Heavy Weight Deflectometer Data. Sustainability, 13(16), 8831. https://doi.org/10.3390/su13168831









