Setting Up a Flipped Classroom Design to Reduce Student Academic Procrastination
Abstract
1. Introduction
Academic Procrastination
2. Methodology
2.1. Objective
2.2. Participants
Information Collection Tools
3. Data Analysis and Results
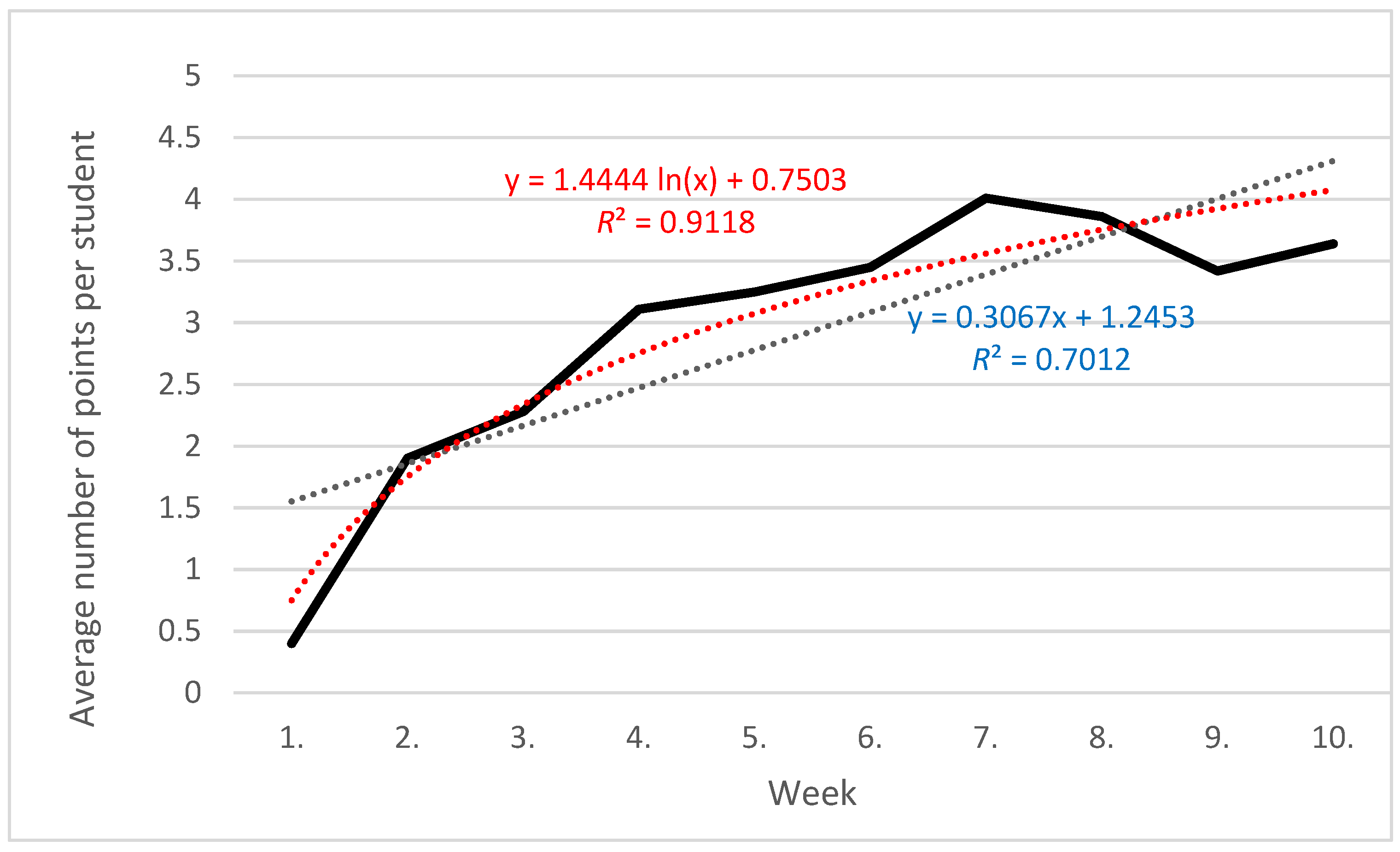
3.1. Activities Outside the Classroom
3.2. Students’ Activity in the Classroom
3.3. Knowledge Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hussin, A.A. Education 4.0 made simple: Ideas for teaching. Int. J. Educ. Lit. Stud. 2018, 6, 92–98. [Google Scholar] [CrossRef]
- Porter, W.W.; Graham, C.R.; Spring, K.A.; Welch, K.R. Blended learning in higher education: Institutional adoption and implementation. Comput. Educ. 2014, 75, 185–195. [Google Scholar] [CrossRef]
- Garrison, D.R.; Kanuka, H. Blended learning: Uncovering its transformative potential in higher education. Internet High. Educ. 2004, 7, 95–105. [Google Scholar] [CrossRef]
- Lage, M.J.; Platt, G.J.; Treglia, M. Inverting the classroom: A gateway to creating an inclusive learning environment. J. Econ. Educ. 2000, 31, 30–43. [Google Scholar] [CrossRef]
- Kontrova, L.; Lengyelfalusy, T.; Lengyelfalusyova, D. A statistical analysis of the effectiveness of selected methods in the teaching of mathematics. Commun. Sci. Lett. Univ. Zilina 2012, 14, 55–60. [Google Scholar]
- Lage, M.J.; Platt, G. The internet and the inverted classroom. J. Econ. Educ. 2000, 31, 11. [Google Scholar] [CrossRef]
- Bergmann, J.; Sams, A. Remixing chemistry class: Two Colorado teachers make vodcasts of their lectures to free up class time for hands-on activities. Learn. Lead. Technol. 2009, 36, 22–27. [Google Scholar]
- Barkley, E.F.; Major, C.H. Student Engagement Techniques: A Handbook for College Faculty; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Coates, H. Student Engagement in Campus-Based and Online Education: University Connections; Routledge: Philadelphia, PA, USA, 2006. [Google Scholar]
- Chuang, H.H.; Weng, C.Y.; Chen, C.H. Which students benefit most from a flipped classroom approach to language learning? Br. J. Educ. Technol. 2018, 49, 56–68. [Google Scholar] [CrossRef]
- Lightner, C.A.; Lightner-Laws, C.A. A blended model: Simultaneously teaching a quantitative course traditionally, online, and remotely. Interact. Learn. Environ. 2016, 24, 224–238. [Google Scholar] [CrossRef]
- Çakıroğlu, Ü.; Öztürk, M. Flipped classroom with problem-based activities: Exploring self-regulated learning in a programming language course. J. Educ. Technol. Soc. 2017, 20, 337–349. [Google Scholar]
- AlJarrah, A.; Thomas, M.K.; Shehab, M. Investigating temporal access in a flipped classroom: Procrastination persists. Int. J. Educ. Technol. High. Educ. 2018, 15, 1–18. [Google Scholar] [CrossRef]
- Broadbent, J. Comparing online and blended learner’s self-regulated learning strategies and academic performance. Internet High. Educ. 2017, 33, 24–32. [Google Scholar] [CrossRef]
- Maycock, K.W.; Lambert, J.; Bane, D. Flipping learning not just content: A 4-year action research study investigating the appropriate level of flipped learning. J. Comput. Assist. Learn. 2018, 34, 661–672. [Google Scholar] [CrossRef]
- Sun, J.C.Y.; Wu, Y.T.; Lee, W.I. The effect of the flipped classroom approach to OpenCourseWare instruction on students’ self-regulation. Br. J. Educ. Technol. 2017, 48, 713–729. [Google Scholar] [CrossRef]
- van Eerde, W.; Klingsieck, K.B. Overcoming procrastination? A meta-analysis of intervention studies. Educ. Res. Rev. 2018, 25, 73–85. [Google Scholar] [CrossRef]
- Pychyl, T.A.; Flett, G.L. Procrastination and self-regulatory failure: An introduction to the special issue. J. Ration. Cogn. Ther. 2012, 30, 203–212. [Google Scholar] [CrossRef]
- Stead, R.; Shanahan, M.J.; Neufeld, R.W. “I’ll go to therapy, eventually”: Procrastination, stress and mental health. Personal. Individ. Differ. 2010, 49, 175–180. [Google Scholar] [CrossRef]
- Klingsieck, K.B.; Grund, A.; Schmid, S.; Fries, S. Why students procrastinate: A qualitative approach. J. Coll. Stud. Dev. 2013, 54, 397–412. [Google Scholar] [CrossRef]
- Kim, K.R.; Seo, E.H. The relationship between procrastination and academic performance: A meta-analysis. Personal. Individ. Differ. 2015, 82, 26–33. [Google Scholar] [CrossRef]
- Wäschle, K.; Allgaier, A.; Lachner, A.; Fink, S.; Nückles, M. Procrastination and self-efficacy: Tracing vicious and virtuous circles in self-regulated learning. Learn. Instr. 2014, 29, 103–114. [Google Scholar] [CrossRef]
- Simpson, W.K.; Pychyl, T.A. In search of the arousal procrastinator: Investigating the relation between procrastination, arousal-based personality traits and beliefs about procrastination motivations. Personal. Individ. Differ. 2009, 47, 906–911. [Google Scholar] [CrossRef]
- Steel, P. The nature of procrastination: A meta-analytic and theoretical review of quintessential self-regulatory failure. Psychol. Bull. 2007, 133, 65. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, J.R. Procrastination as self-regulation failure of performance: Effects of cognitive load, self-awareness, and time limits on ‘working best under pressure’. Eur. J. Personal. 2001, 15, 391–406. [Google Scholar] [CrossRef]
- Steel, P. Arousal, avoidant and decisional procrastinators: Do they exist? Personal. Individ. Differ. 2010, 48, 926–934. [Google Scholar] [CrossRef]
- Grunschel, C.; Patrzek, J.; Fries, S. Exploring reasons and consequences of academic procrastination: An interview study. Eur. J. Psychol. Educ. 2013, 28, 841–861. [Google Scholar] [CrossRef]
- Akçayır, G.; Akçayır, M. The flipped classroom: A review of its advantages and challenges. Comput. Educ. 2018, 126, 334–345. [Google Scholar] [CrossRef]
- Akinsola, M.K.; Tella, A.; Tella, A. Correlates of academic procrastination and mathematics achievement of university undergraduate students. Eurasia J. Math. Sci. Technol. Educ. 2007, 3, 363–370. [Google Scholar] [CrossRef]
- Asri, D.N.; Setyosari, P.; Hitipeuw, I.; Chusniyah, T. The influence of project-based learning strategy and self-regulated learning on academic procrastination of junior high school students’ mathematics learning. Am. J. Educ. Res. 2017, 5, 88–96. [Google Scholar] [CrossRef][Green Version]
- Henschel, S.; Roick, T. Relationships of mathematics performance, control and value beliefs with cognitive and affective math anxiety. Learn. Individ. Differ. 2017, 55, 97–107. [Google Scholar] [CrossRef]
- Asikhia, O.A. Academic Procrastination in Mathematics: Causes, Dangers and Implications of Counselling for Effective Learning. Int. Educ. Stud. 2010, 3, 205–210. [Google Scholar] [CrossRef]
- Solomon, L.J.; Rothblum, E.D. Academic procrastination: Frequency and cognitive-behavioral correlates. J. Couns. Psychol. 1984, 31, 503. [Google Scholar] [CrossRef]
- O’Flaherty, J.; Phillips, C. The use of flipped classrooms in higher education: A scoping review. Internet High. Educ. 2015, 25, 85–95. [Google Scholar] [CrossRef]
- Bishop, J.L.; Verleger, M.A. The flipped classroom: A survey of the research. In Proceedings of the 120th ASEE Annual Conference & Exposition, American Society for Engineering Education, Atlanta, GA, USA, 23–26 June 2013. [Google Scholar]
- Pluta, W.J.; Richards, B.F.; Mutnick, A. PBL and beyond: Trends in collaborative learning. Teach. Learn. Med. 2013, 25, S9–S16. [Google Scholar] [CrossRef] [PubMed]
- Wilson, P. Promoting Positive Attitudes. Mathematics Teaching Incorporating Micromath. 2008. Available online: http://eric.ed.gov/?q=promoting+positive+attitudes&id+EJ815090 (accessed on 1 May 2008).
- Reed, H.C.; Drijvers, P.; Kirschner, P.A. Effects of attitudes and behaviours on learning mathematics with computer tools. Comput. Educ. 2010, 55, 1–15. [Google Scholar] [CrossRef]
- Zappe, S.; Leicht, R.; Messner, J.; Litzinger, T.; Lee, H.W. “Flipping” the classroom to explore active learning in a large undergraduate course. In Proceedings of the ASEE Annual Conference and Exposition, American Society for Engineering Education, Austin, GA, USA, 14–17 June 2009. [Google Scholar]
- Perrin, C.J.; Miller, N.; Haberlin, A.T.; Ivy, J.W.; Meindl, J.N.; Neef, N.A. Measuring and reducing college students’procrastination. J. Appl. Behav. Anal. 2011, 44, 463–474. [Google Scholar] [CrossRef]
- Glomann, L.; Hager, V.; Lukas, C.A.; Berking, M. Patient-centered design of an e-mental health app. In International Conference on Applied Human Factors and Ergonomics; Springer: Cham, Switzerland, 2018; pp. 264–271. [Google Scholar]
- Lukas, C.A.; Berking, M. Reducing procrastination using a smartphone-based treatment program: A randomized controlled pilot study. Internet Interv. 2018, 12, 83–90. [Google Scholar] [CrossRef]
- Akçayır, M.; Dündar, H.; Akçayır, G. What makes you a digital native? Is it enough to be born after 1980? Comput. Hum. Behav. 2016, 60, 435–440. [Google Scholar] [CrossRef]
- Chen, L.; Chen, T.L.; Chen, N.S. Students’ perspectives of using cooperative learning in a flipped statistics classroom. Australas. J. Educ. Technol. 2015, 31, 621–640. [Google Scholar] [CrossRef]
- Stuart, A. A test for homogeneity of the marginal distributions in a two-way classification. Biometrika 1955, 42, 412–416. [Google Scholar] [CrossRef]
- Maxwell, A.E. Comparing the classification of subjects by two independent judges. Br. J. Psychiatry 1970, 116, 651–655. [Google Scholar] [CrossRef]
- McNemar, Q. Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 1947, 12, 153–157. [Google Scholar] [CrossRef] [PubMed]
- Mason, G.S.; Shuman, T.R.; Cook, K.E. Comparing the effectiveness of an inverted classroom to a traditional classroom in an upper-division engineering course. IEEE Trans. Educ. 2013, 56, 430–435. [Google Scholar] [CrossRef]
- Young, T.P.; Bailey, C.J.; Guptill, M.; Thorp, A.W.; Thomas, T.L. The flipped classroom: A modality for mixed asynchronous and synchronous learning in a residency program. West. J. Emerg. Med. 2014, 15, 938. [Google Scholar] [CrossRef] [PubMed]
- Tuckman, B.W. Using tests as an incentive to motivate procrastinators to study. J. Exp. Educ. 1998, 66, 141–147. [Google Scholar] [CrossRef]
- Cooper, K.M.; Liddle, S.; Dascalu, S. Experiences Using Defect Checklists in Software Engineering Education. In Proceedings of the ISCA 18th International Conference on Computer Applications in Industry and Engineering, Honolulu, HI, USA, 9–11 November 2005; pp. 402–409. [Google Scholar]
- Lidu, E.Z.F.; Laň, S.S.; Chu, C.H.; Júna, S.M. Web-besede peer review: The learner as both adapter and reviewer. IEEE Trans. Educ. 2001, 44, 246–251. [Google Scholar]
- Toto, R.; Nguyen, H. Flipping the work design in an industrial engineering course. In Proceedings of the 2009 39th IEEE Frontiers in Education Conference, San Antonio, TX, USA, 18–21 October 2009; pp. 1–4. [Google Scholar]
- Gonda, D.; Ďuriš, V.; Pavlovičová, G.; Tirpáková, A. Analysis of factors influencing students’ Access to mathematics education in the form of MOOC. Mathematics 2020, 8, 1229. [Google Scholar] [CrossRef]
- De Grazia, J.L.; Falconer, J.L.; Nicodemus, G.; Medlin, W. Incorporating screencasts into chemical engineering courses. In Proceedings of the 119th ASEE Annual Conference & Exposition, San Antonio, TX, USA, 10–13 June 2012; American Society for Engineering Education: San Antonio, TX, USA; pp. 25–762. [Google Scholar]
- Sappington, J.; Kinsey, K.; Munsayac, K. Two studies of reading compliance among college students. Teach. Psychol. 2002, 29, 272–274. [Google Scholar] [CrossRef]
- Vermetten, Y.J.; Vermunt, J.D.; Lodewijks, H.G. A longitudinal perspective on learning strategies in higher education: Different viewpoints towards development. Br. J. Educ. Psychol. 1999, 69, 221–242. [Google Scholar] [CrossRef]
- Boyle, E.A.; Duffy, T.; Dunleavy, K. Learning styles and academic outcome: The validity and utilityof Vermunt´s inventory of learning styles in a Brittish higher education setting. Br. J. Educ. Psychol. 2003, 73, 267–290. [Google Scholar] [CrossRef]
- Bryson, C.; Hand, L. The role of engagement in inspiring teaching and learning. Innov. Educ. Teach. Int. 2007, 44, 349–362. [Google Scholar] [CrossRef]
- Hockings, C.; Cooke, S.; Yamashita, H.; McGinty, S.; Bowl, M. Switched off? A study of disengagement among computing students at two universities. Res. Pap. Educ. 2008, 23, 191–201. [Google Scholar] [CrossRef]
- Blackwell, L.S.; Trzesniewski, K.H.; Dweck, C.S. Implicit theories of intelligence predict achievement across an adolescent transition: A longitudinal study and an intervention. Child Dev. 2007, 78, 246–263. [Google Scholar] [CrossRef]
- Tice, D.M.; Baumeister, R.F. Longitudinal study of procrastination, performance, stress, and health: The costs and benefits of dawdling. Psychol. Sci. 1997, 8, 454–458. [Google Scholar] [CrossRef]
- Aharony, N.; Bar-Ilan, J. Students’ perceptions on MOOCs: An exploratory study. Interdiscip. J. E-Ski. Life Long Learn. 2016, 12, 145–162. [Google Scholar] [CrossRef]





. | … … … | . | ||
| … | 1 |
. | … … … | . | ||
| … | n |
| Before | After | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | Sum | |
| 1 | 7 | 0 | 0 | 0 | 0 | 7 |
| 2 | 19 | 5 | 2 | 0 | 0 | 26 |
| 3 | 12 | 19 | 5 | 0 | 0 | 35 |
| 4 | 2 | 19 | 7 | 0 | 0 | 28 |
| 5 | 0 | 0 | 0 | 2 | 2 | 5 |
| Sum | 40 | 42 | 14 | 2 | 2 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonda, D.; Pavlovičová, G.; Tirpáková, A.; Ďuriš, V. Setting Up a Flipped Classroom Design to Reduce Student Academic Procrastination. Sustainability 2021, 13, 8668. https://doi.org/10.3390/su13158668
Gonda D, Pavlovičová G, Tirpáková A, Ďuriš V. Setting Up a Flipped Classroom Design to Reduce Student Academic Procrastination. Sustainability. 2021; 13(15):8668. https://doi.org/10.3390/su13158668
Chicago/Turabian StyleGonda, Dalibor, Gabriela Pavlovičová, Anna Tirpáková, and Viliam Ďuriš. 2021. "Setting Up a Flipped Classroom Design to Reduce Student Academic Procrastination" Sustainability 13, no. 15: 8668. https://doi.org/10.3390/su13158668
APA StyleGonda, D., Pavlovičová, G., Tirpáková, A., & Ďuriš, V. (2021). Setting Up a Flipped Classroom Design to Reduce Student Academic Procrastination. Sustainability, 13(15), 8668. https://doi.org/10.3390/su13158668








