Service Evaluation of Electric Vehicle Charging Station: An Application of Improved Matter-Element Extension Method

Abstract

To reach the targets of carbon peaking and neutral, China needs to develop electric vehicles extensively. The service level of electric vehicle charging stations (EVCSs) notably decides the promotion of electric vehicles. Given the current unsatisfactory service performance of charging stations, this paper established a multi-criteria evaluation system for the electric vehicle charging stations. We conducted a survey in 2020 by distributing questionnaires to experts and charging station users. Firstly, from the perspective of the subject and object of charging station service, the evaluation system of 16 indexes for operator service and customer service was constructed. Secondly, the order relation method and entropy weight method were used to determine the subjective weight and objective weight of the indexes, respectively. It was concluded that charging price and parking cost have a great influence on the service evaluation. Then, a comprehensive evaluation model based on the improved matter-element extension method was established to appraise three charging stations in Beijing. Sensitive analysis and comparative analysis were implemented to further demonstrate the effectiveness and stability of the proposed evaluation method. Finally, the evaluation results provided implications for improving the charging service performance.

1. Introduction

Traditional fuel vehicles have led to the depletion of petroleum resources and the emission of a large number of gases, causing serious pollution to the environment [1,2], while the development of electric vehicles (EVs) is an important solution for alleviating the energy crisis and environmental pollution [3] and also an indispensable measure to promote the sustainable development of the automobile industry [4]. To promote the extension of electric vehicles, many countries have implemented a variety of financial and non-financial incentives to stimulate the purchase and use of electric vehicles [5]. According to the latest report from the International Energy Agency (IEA), the global sales of electric vehicles in 2020 exceeded 3.24 million, up by 43% on a year-on-year basis; among which, China’s sales accounted for 40.1% of the global total sales.

As one of the infrastructures for the electric vehicle industry, the electric vehicle charging station is an important guarantee for the large-scale promotion of electric vehicles [6], because convenient and efficient electric charging service can heighten consumers’ purchase intention [7]. Since 2015, China’s incentive policies for charging infrastructure have been issued frequently. Driven by the market and supported by the government, more and more charging stations are being built and operating in many cities [8,9,10]. The increase in electric vehicle ownership in China creates a bright outlook for the charging pile market [11]. In December 2018, the Central Economic Work Conference put forward the concept of new infrastructure, taking charging piles of EVs as one of the major fields. Since then, major enterprises have invested heavily and announced to enter the field of charging piles. The number of public charging stations in China has reached 558,000 by June 2020, up to 86% than that in 2018.

With the continuous acceleration of charging station construction, the scarcity of charging piles has been alleviated, but the dilemma of poor user experience challenges the EVs industry [12,13]. At present, the charging station urgently requires operators to improve the charging station service quality [14]. It helps to improve user’s experience and arouse consumer’s fervor for EVs. In return, it also stimulates direct investment and promote a strong industry-pull effect and industry aggregation. The EVs likely marks the beginning of the transformation and upgrading of the automobile industry and green transportation [15].

Considering the full life cycle of charging stations, previous studies focus on the planning, site selection, and commercial model of EVCSs, while fewer scholars discuss the operation service topic. This paper aims to present a charging service appraisal framework for the EVCS operators, which upfolds the literature review from three fields including research topics, service indicators, and evaluation method. Especially, the matter-element extension method applied in this paper is highlighted.

The site selection optimization and evaluation of charging stations and the primary task for charging station planning and construction [16]; the quality of site selection will directly affect the operation of charging stations in the future. References [16,17,18] established the evaluation indicator system of charging station site selection, employing a comprehensive evaluation method to determine the optimal site. In addition, some scholars focused on optimizing the layout [19] and size [20] of charging stations. For example, Reference [21] summarized the main influence factors of charging stations’ layout, and Reference [22] applied the genetic algorithm to solve the problem of charging stations’ size optimization. In terms of charging station capacity configuration [23], References [24,25,26] constructed the capacity configuration model based on the intelligent algorithm to solve the optimal configuration scheme.

Improving the service quality of charging stations is an important way to promote the sustainable development of the electric vehicle industry. The evaluation of the service level of charging stations is very important for the safe operation of charging stations; Helmus et al. provided key performance indicators for electric vehicle charging stations [27], which provided a reference for follow-up scholars to study the service evaluation of charging stations. Zenginis et al. indicated that a fast-charging station with a high service level can increase the penetration of electric vehicles [28]. Zhang et al. used the improved TOPSIS model to evaluate the performance of three public charging stations in Beijing from five aspects of planning rationality, operation efficiency, service capacity, charging safety, and sustainable development [29]. Li et al. employed the Analytic Hierarchy Process (AHP) and the entropy weight method to calculate the subject and object weight and then used the fuzzy comprehensive evaluation method to assess charging stations’ performance [30]. Nan et al. assessed four fast-charging networks of a city using the fuzzy comprehensive evaluation method [31]. Zhang et al. evaluated the operational service of electric vehicle charging stations from the perspectives of charging stations’ operational level, the quality of customer service, the impact on the transportation network, and power distribution network [32]. In general, scholars evaluated the operational level and service quality of charging stations from different perspectives, which provided the direction for government and operators to improve charging stations.

In general, Multi-Criteria Decision-Making (MCDM) problems contain multiple conflicting criteria under uncertain conditions. MCDM theory is widely used in many fields, the most common methods of which are Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS), Preference Ranking Organization Method for Enrichment Evaluations (PROMETHEE), and Visekriterijumska Optimizacija I Kompromisno Resenje (VIKOR). De et al. developed a risk evaluation model based on the Intuitionistic Fuzzy Analytic Hierarchy Process and assessed the credit risk rating of power retail companies in China [33]. Solangi et al. employed the Fuzzy TOPSIS method to rank 13 energy strategies in Pakistan for achieving sustainable energy planning [34]. Erbaş et al. proposed a multi-objective criteria decision method based on GIS, and used the Fuzzy AHP and TOPSIS method to solve the location of electric vehicle charging stations [35]. Wang et al. put forward an extended MCDM model and used Fuzzy AHP, Data Envelopment Analysis (DEA), and TOPSIS to determine the optimal site from 46 alternatives [36]. Barbosa et al. employed AHP and PROMETHEE to evaluate the performance of distribution utilities [37]. Xu et al. applied the VIKOR method to assess the service performance of three electric vehicle sharing programs in Beijing [38]. However, Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS), PROMETHEE, and VIKOR are the methods based on the rank distance with complex calculation process.

The matter-element extension method is considered a practical and superior method to solve MCDM problems. Therefore, this paper employed an improved matter-element extension model to assess the service level of electric vehicle charging stations. Tan et al. used ideal matter-element extension and grey cluster model to evaluate the site selection of wind farms from the perspectives of economy, society, and environment [39]. Dong et al. applied an improved matter-element extension cloud model to evaluate the operation of the electricity market in Y province in May 2019 [40]. Guo et al. employed an improved matter-element extension model to evaluate the business risk of China power retail companies, which provides a reference for risk management and sustainable development of companies [41]. Bu et al. introduced an evaluation method combining entropy weight method and matter-element extension model to comprehensively evaluate the service quality of power supply companies, which further improves the market competitiveness of power supply companies [42].

This paper aims to propose an EV charging station service evaluation model based on improved matter-element extension. The innovations of this paper are as follows: (1) the service evaluation index system of the electric vehicle charging stations is developed and expanded considering operators providing charging services and users enjoying charging services, to provide insights for the better planning and operation of charging stations; and (2) this paper presents a new case that applies the improved matter-element extension model to evaluate the service level of charging stations.

The rest of the paper is organized as follows: Section 2 constructs the service evaluation index system including charging station operator and EV user. Section 3 introduces the appraisal method. In Section 4, three charging stations in Beijing are selected for empirical analysis, and sensitivity analysis of indicators and comparative analysis of evaluation methods are carried out. Section 5 concludes the paper and puts forward some implications.

2. Evaluation Index System

Given the uneven service level of current charging stations, to improve the service quality of charging stations and the satisfaction of electric vehicle users, this paper establishes a service evaluation index system for electric vehicle charging stations. To assess EVCSs comprehensively, an evaluation index system should be constructed. The charging stations’ operators aim at improving their service level and realizing sustainable development. Based on a large number of literature review of charging stations and questionnaire results analysis, coupled with the basic construction principle of the evaluation index system, we determined the electric vehicle charging station’s evaluation indexes. The first-level index and the second-level index were determined by the following procedures. Firstly, 30 experts were selected, including 10 professors in the field of charging stations, 10 operation managers of EVCS, and 10 electric vehicle users who have over five years’ experience. Then, after referring to relevant literature and reports, an initial index system was established by experts. Finally, we designed a questionnaire table delivered to the experts. After analyzing the results of questionnaire survey, a final evaluation index system was obtained. See Appendix A for the specific contents of the questionnaire. According to the results of Reference [29], service capacity and operational efficiency are the top two criteria; therefore, we construct the first-level index from the view of operator and customer correspondingly. The index system includes two first-level indexes and 16 s-level indexes. The specific description of index type and index value type is shown in

Table 1. Evaluation index system of the electric vehicle charging station.

Goal	First-Level Index	Second-Level Index	Index Type	Value Type
Service level of electric vehicle charging station	Operational service level (OS)	Average service distance C1	C	Crisp
		Ratio of fast charging piles C2	B	Crisp
		Average utilization C3	B	Crisp
		Average turnover rate C4	B	Crisp
		Average failure rate C5	C	Crisp
		Charging safety C6	B	Language variable
		Illegal occupancy rate of fuel vehicles C7	C	Crisp
		Additional value service C8	B	Language variable
	Customer service level (CS)	Average charging time C9	C	Crisp
		Charging price C10	C	Interval number
		Service fee C11	C	Crisp
		Parking cost per hour C12	C	Crisp
		Trading convenience C13	B	Language variable
		Data-push accuracy C14	B	Crisp
		Feedback processing speed C15	B	Language variable
		User Satisfaction C16	B	Language variable

Note: B: Benefit indicator; C: Cost indicator.

.

2.1. Operational Service Level

This first-level index describes the operational state of the charging station, which mainly indicates the operational level and assesses the operational effect to develop corresponding indexes.

Average service distance (C1) refers to the average value of the maximum charging travel distance of EVs served by charging stations, which reflects the optimization of the layout of the charging stations. The calculation process is shown in Equation (1).

$$L_S=\frac{1}{n}{\displaystyle \sum _{i=1}^n\max (l_{ij}})$$

(1)

where $l_{ij}$ is the distance between the $i_{th}$ charging pile and the $j_{th}$ user and $\max (l_{ij})$ is the furthest distance of the user to the charging pile of the $i_{th}$ charging pile.

The ratio of fast charging piles (C2) represents the proportion of the number of fast charging piles to the number of all charging piles in the charging station [29], which reflects the scale and advanced degree of charging stations. It is calculated as follows:

$$\phi =\frac{n_F}{n}$$

(2)

where $n_F$ is the number of fast charging piles and $n$ is the total number of charging piles.

Average utilization (C3) equals the rate of charging time to the total use time of the per charging station [31], which reflects the use efficiency. The calculation process is shown in Equation (3), where the utilization ${\eta }_{S,i}$ of the $i_{th}$ charging pile is calculated using Equation (4).

$${\eta }_S=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\eta }_{S,i}}$$

(3)

$${\eta }_{S,i}=\frac{t_{S,i}}{t}$$

(4)

where $t_{S,i}$ is the actual working time of the $i_{th}$ charging pile and $t$ is the total operating time.

Average turnover rate (C4) is the average use frequency per charging station, which represents the use intensity of the charging station.

Average failure rate (C5) denotes the ratio of the time when the charging station is not in operation to the total operating time. It is the stability of the charging device in a certain period. The calculation process is shown in Equation (5), where the failure rate of the $i_{th}$ charging pile is calculated using Equation (6).

$${\eta }_F=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\eta }_{F,i}}$$

(5)

$${\eta }_{F,i}=\frac{t_{F,i}}{t}$$

(6)

where ${\eta }_{F,i}$ is the failure rate of the $i_{th}$ charging pile and $t_{F,i}$ is the failure time of the $i_{th}$ charging pile.

Charging safety (C6) refers to the charging equipment and other auxiliary systems to maintain a reliable state during the charging process. It can reflect the quality of the relevant charging devices.

Illegal occupancy rate of fuel vehicles (C7) is the ratio of the number of sites occupied by fuel vehicles to the number of all charging sites in each charging station [32]. It denotes the operating management level of the charging station.

Additional value service (C8) involves the additional service provided to users except for basic charging service, which includes route planning, malfunction repair, and electricity bill payment, etc.

2.2. Customer Service Level

This first-level index is the capability that charging stations provide an efficient and stable experience to the user, which assesses the service quality that the charging station provides the user with charging service and constructs relevant indexes.

Average charging time (C9) refers to the meantime that the electric vehicle charges to 100% [31]; the charging time can measure the efficiency of the charging station in providing services to users. The calculation process is shown in Equation (7).

$$T_{\alpha }=\frac{1}{C}{\displaystyle \sum _{j=1}^C{T}_j}$$

(7)

where $C$ is the number of users with charging needs and $T_j$ is the charging time of the $j_{th}$ user.

Charging price (C10) is the cost per kilowatt-hour to charge an electric vehicle.

Service fee (C11) refers to the service charge that the operator has to charge in addition to the charging price.

Parking cost per hour (C12) reflects the fee paid by users to occupy space for charging electric vehicles.

Trading convenience (C13) represents the payment methods that users can choose when paying charging fees. The more payment methods they can choose, the more convenient the transaction is.

Data-push accuracy (C14) refers to the accuracy of real-time information provided by the APP supporting EV charging [29], which represents the intelligence of supporting services of charging stations.

Feedback processing speed (C15) refers to the description of the speed at which operators process the charging station status feedback from EV users [29].

User satisfaction (C16) represents the satisfaction of EV users with the service provided by charging stations, including the service attitude of employees and complaint handling, etc.

3. Methodology and Data Process

The matter-element extension model is based on both matter-element theory and extension set theory [39,40,41,42]. By establishing classical domain, node domain, and evaluation grade, the correlation degree of each evaluation grade corresponding to the matter element is calculated according to the original data collected, and the grade of the evaluation object is determined accordingly. The improved matter-element extension evaluation model applied in this paper overcomes the limitations of the traditional matter-element extension model by normalizing the classical domain and the matter-element to be evaluated and replacing the maximum membership principle with the closeness criterion [43].

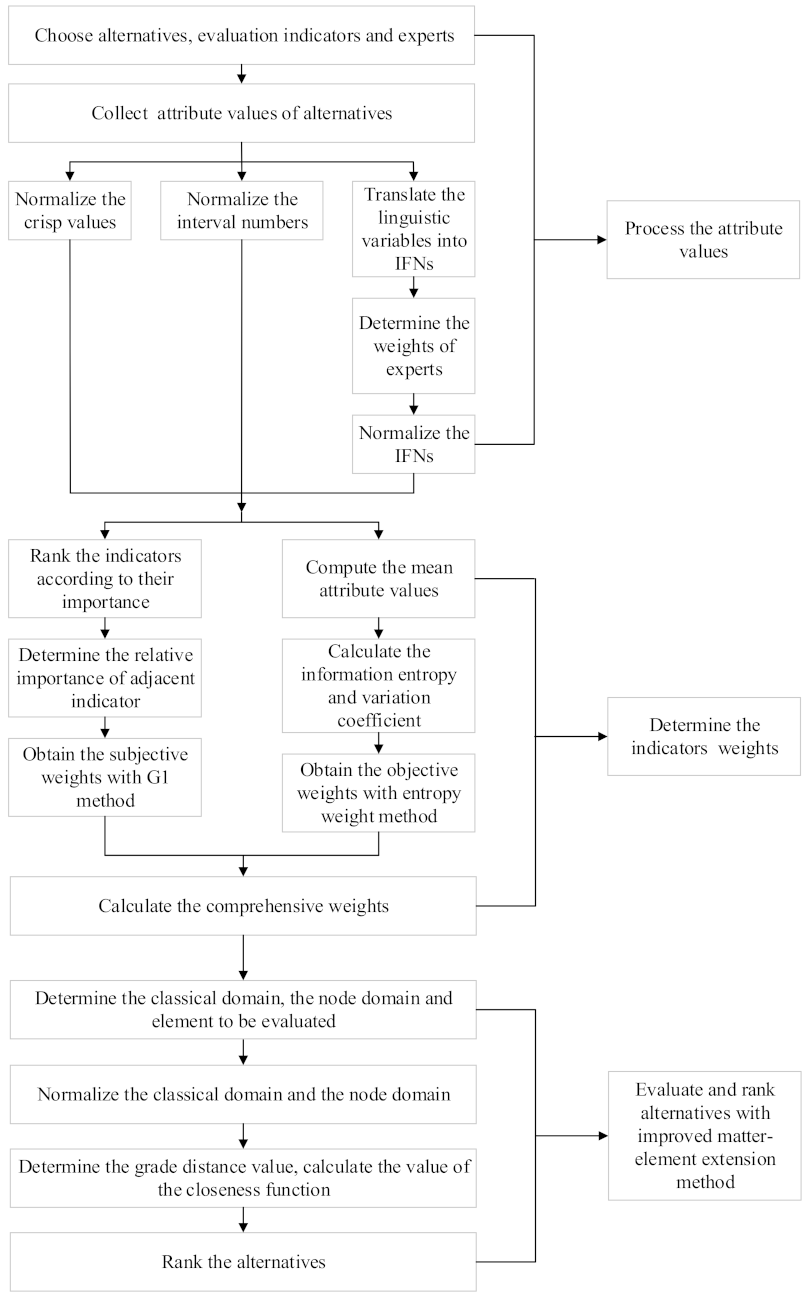
The EVCS service evaluation process is shown in Figure 1. The first step is to screen the charging stations and evaluation indexes, as well as four experts. Secondly, original data of the second-level index of the charging stations and corresponding standardization methods should be addressed according to different types of indicators. Then, considering the difference of experts’ attention to the indexes, the order relation method is used to calculate its subjective weight; the entropy weight method is used to determine the objective weight of the original data based on the second-level index The weighting method group can calculate the comprehensive weight value of each index. Finally, the improved matter-element extension model is employed to evaluate charging stations’ service level and make a rank to find some significant conclusions.

3.1. Preliminary Knowledge

Definition 1.

Suppose that$R^L$and$R^U$are two real numbers as well as satisfying$R^L\le R^U$, then$[R^L,R^U]$is defined as an interval number expressed as$\tilde{r}$ [38].

Definition 2.

Let$\tilde{a}=[a^L,a^U]$and$\tilde{b}=[b^L,b^U]$ be two interval numbers [38], and the distance between them is calculated as Equation (8).

$$d(a,b)=\sqrt{\frac{1}{2}[{(a^L-b^L)}^2+{(a^U-b^U)}^2}$$

(8)

Definition 3.

Suppose that$X$is the universe of discourse and the intuitionistic fuzzy set (IFS) on$X$is defined as$A=\left\{x,{\mu }_A(x),{\nu }_A(x)\left|x\in X\right.\right\}$ [38].

Where ${\mu }_A(x)$ and ${\nu }_A(x)$ are the membership and non-membership degrees expressed as ${\mu }_A:X\to [0,1],x\in X\to {\mu }_A(x)\in [0,1]$ and ${\nu }_A:X\to [0,1],x\in X\to {\nu }_A(x)\in [0,1]$ which satisfy $0\le {\mu }_A(x)+{\nu }_A(x)\le 1$ for $x\in X$, respectively.

Definition 4.

The hesitancy degree of$x\in X$belonging to$A$is expressed as${\pi }_A(x)=1-{\mu }_A(x)-{\nu }_A(x)$which satisfies$0\le {\pi }_A(x)\le 1$ [38].

Definition 5.

In particular,$\alpha =({\mu }_{\alpha },{\nu }_{\alpha },{\pi }_{\alpha })$is called an intuitionistic fuzzy number (IFN) which satisfies${\mu }_{\alpha }\in [0,1]$,${\nu }_{\alpha }\in [0,1]$, and${\mu }_{\alpha }+{\nu }_{\alpha }\le 1$ [38].

Definition 6.

Suppose that$\alpha =({\mu }_{\alpha },{\nu }_{\alpha },{\pi }_{\alpha })$and$\beta =({\mu }_{\beta },{\nu }_{\beta },{\pi }_{\beta })$ are two IFNs and the distance between them is defined as Equation (9).

$$d=\sqrt{\frac{1}{2}[{({\mu }_{\alpha }-{\mu }_{\beta })}^2+{({\nu }_{\alpha }-{\nu }_{\beta })}^2+{({\pi }_{\alpha }-{\pi }_{\beta })}^2]}$$

(9)

3.2. Methods to Determine Index Weight

3.2.1. Order Relation Method

To reduce the complexity of calculation, the order relation method is used to determine the subjective weight. The order relation method is a typical method to determine the subjective weight without considering the index data [29]. Compared to the AHP method, it does not need to establish a judgment matrix and carry out a consistency test. The specific steps to evaluate the service level of charging stations by using the order relation method are as follows:

(1)

Rank the indexes according to their importance. For the index set $C=\left\{C_1,\dots ,C_j,\dots ,C_n\right\}$, the only order relation can be determined.

(2)

Determine the relative importance $r_j={\omega }_{j-1}/{\omega }_j$ of adjacent indexes $C_{j-1}$ and $C_j$ according to

Table 2. The value of relative importance of indicators.

${\mathit{r}}_{\mathit{j}}$	Description
1.0	$C_{j-1}$ is the same important as $C_j$
1.2	$C_{j-1}$ is slightly more important than $C_j$
1.4	$C_{j-1}$ is more important than $C_j$
1.6	$C_{j-1}$ is strongly more important than $C_j$
1.8	$C_{j-1}$ is extremely important than $C_j$

.

(3)

Calculate the subjective weights of indexes by Equations (10) and (11).

$${\omega }_{sn}={(1+{\displaystyle \sum _{i=2}^n{\displaystyle \prod _{j=i}^n{r}_j}})}^{-1}$$

(10)

$${\omega }_{sj}={\displaystyle \prod _{k=j+1}^n{r}_k{\omega }_{sn}}$$

(11)

For the problems which need multiple experts to evaluate, according to Equation (12), the final weights should be determined according to the calculation results and the weights of several experts.

$${\omega }_{sj}={\displaystyle \sum _{s=1}^p{\omega }_{sj}^s{\lambda }_s}$$

(12)

where ${\omega }_{sj}^s$ is the subjective weight determined by the $s_{th}$ expert and ${\lambda }_s$ is the weight of the $s_{th}$ expert.

3.2.2. Entropy Weight Method

The entropy weight method, as an objective weighting method, can determine the fluctuation among indexes and use the variation degree of indexes to determine the weight of each evaluation index [38]. It can highlight the partial differences among indexes. The basic principle to determine the weight coefficient is that according to the different degrees of the observed value of the same index in different evaluation objects, the importance of the index in the system is determined. When a certain index has a great difference among different evaluation objects, it indicates that the comparative effect of the index is greater and the corresponding weight coefficient is larger. On the contrary, the weight coefficient is smaller by using the entropy weight method. Suppose the observed value of the $j_{th}$ index of the $i_{th}$ evaluation object is $r_{ij}$; the value of $i$ is 1,2,3; and the value of $j$ is 1–16. The steps of determining crisp indexes’ weight are as follows:

(1)

Calculate the ratio of the observed value of evaluation index $C_j$ to the sum of indexes of all evaluation objects:

$$p_{ij}=\frac{r_{ij}}{{\displaystyle \sum _{i=1}^n{r}_{ij}}}$$

(13)

(2)

Calculate the entropy of the $j_{th}$ index, where $0\le e_j\le 1$.

$$e_j=-\frac{1}{\ln n}{\displaystyle \sum _{i=1}^n{p}_{ij}\ln p_{ij}}$$

(14)

(3)

Calculate the divergence coefficient of the evaluation index $C_j$.

$$g_j=1-e_j$$

(15)

(4)

Determine the weight coefficient of the index.

$${\omega }_{oj}=\frac{g_j}{{\displaystyle \sum _{j=1}^n{g}_j}}$$

(16)

where ${\omega }_{oj}$ is the objective weight coefficient of each index in the evaluation system, and the sum of all indexes is 1.

For the objective weight determining of interval numbers and IFNs, the steps are as follows:

(1)

Calculate the mean value of normalized index value by Equation (17).

$$\begin{array}{l}{\tilde{f}}_j=(f_{1j}\oplus \dots \oplus f_{ij}\oplus \dots \oplus f_{mj})/m\\ =\left\{\begin{array}{l}[\frac{1}{m}{\displaystyle \sum _{i=1}^m{f}_{ij}^L},\frac{1}{m}{\displaystyle \sum _{i=1}^m{f}_{ij}^U}],C_j\in C^1\\ \left(1-{\displaystyle \prod _{i=1}^m(1-{\mu }_{ij}}{)}^{1/m},{\displaystyle \prod _{i=1}^m{({\nu }_{ij})}^{1/m}},{\displaystyle \prod _{i=1}^m(1-{\mu }_{ij}}{)}^{1/m}-{\displaystyle \prod _{i=1}^m{({\nu }_{ij})}^{1/m}}\right),C_j\in C^2\end{array}\right.\end{array}$$

(17)

(2)

Where $C^1$ represents the set of interval numbers, $C^2$ represents the set of IFNs.

(3)

Calculate the information entropy of the $j_{th}$ index using Equation (18).

$$h_j=-K{\displaystyle \sum _{i=1}^m{f}_{ij}^{\prime }\ln f_{ij}^{\prime }}$$

(18)

(4)

Where $f_{ij}^{\prime }=d(f_{ij},{\tilde{f}}_j)/{\displaystyle \sum _{i=1}^{m}d(f_{ij},{\tilde{f}}_j)}(i=1,2,\dots ,m;j=1,2,\dots ,n),K=1/\ln \mathrm{m}$.

(5)

Calculate the variation coefficient by Equation (19).

$$b_j=1-h_j$$

(19)

(6)

Calculate the objective weight of the index using Equation (20).

$${\omega }_{oj}=\frac{b_j}{{\displaystyle \sum _{j=1}^n{b}_j}}$$

(20)

3.3. The Comprehensive Evaluation Based on Improved Matter-Element Extension Method

This paper supposes that there are $m$ evaluation objects $A_i(i=1,2,\cdots ,m)$ and $n$ evaluation indexes $C_j(j=1,2,\cdots ,n)$ [38]. After defining evaluation objects and indexes, the initial data of each charging station are collected and sorted. Table 1 shows that the EVCS service evaluation index system can be divided into quantitative and qualitative indexes, among which the quantitative indexes can be further divided into crisp value and interval numbers.

By normalizing the initial data of indexes, the influence of the index dimension can be eliminated, and the evaluation results can be more accurate. This paper employed different standardized methods to deal with the initial data. Three different types of indexes data normalized process are described as follows [38].

(1)

Crisp value

According to different properties of quantitative indexes, it can be divided into benefit indicator and cost indicator.

Benefit indicator means the greater the value of the metric, the better, while the cost indicator means the smaller the value of the metric, the better. For the benefit indicator, the normalized process is given using Equation (21).

$$f_{ij}=\frac{r_{ij}-\min \{r_{ij}\}}{\underset{1\le i\le n}{\max }\{r_{ij}\}-\underset{1\le i\le n}{\min }\{r_{ij}\}}$$

(21)

For the cost indicator, the normalized process is expressed as Equation (22).

$$f_{ij}=\frac{\max \{r_{ij}\}-r_{ij}}{\underset{1\le i\le n}{\max }\{r_{ij}\}-\underset{1\le i\le n}{\min }\{r_{ij}\}}$$

(22)

(2)

Interval numbers

Since the values of some indicators change over time, they fluctuate within a certain range and are denoted by interval numbers [44]. If the index value is presented by interval numbers, then the index value should be normalized. For the benefit indicator, the normalized process is presented as Equation (23).

$$f_{ij}=\left[\frac{r_{ij}^L}{{\displaystyle \sum _{i=1}^n{r}_{ij}^U}},\frac{r_{ij}^U}{{\displaystyle \sum _{i=1}^n{r}_{ij}^L}}\right]$$

(23)

For the cost indicator, the normalized process is denoted as Equation (24).

$$f_{ij}=\left[\frac{1/r_{ij}^U}{{\displaystyle \sum _{i=1}^n(1/r_{ij}^L)}},\frac{1/r_{ij}^L}{{\displaystyle \sum _{i=1}^n(1/r_{ij}^U)}}\right]$$

(24)

(3)

Linguistic variable

For the initial data collecting of qualitative indexes, we invite $p$ experts $E_s(s=1,2,\cdots ,p)$ to assess. For indexes that cannot be described by real values, four experts score the metrics. The IFS method mentioned in Section 3.1 is employed to process the linguistic variables quantitatively [38].

Step 1 Quantify the qualitative indexes by intuitionistic fuzzy set.

In this paper, qualitative descriptions are given by four experts according to their experience, and the linguistic variable conversion rules are quantified by IFNs [37] shown in

Table 3. The conversion rules of linguistic variables provided by experts.

Linguistic Variables	Corresponding IFNs
Extremely poor (EP)	(0.05,0.95,0.00)
Very poor (VP)	(0.15,0.80,0.05)
Poor (P)	(0.25,0.65,0.10)
Medium poor (MP)	(0.35,0.55,0.10)
Medium (M)	(0.50,0.40,0.10)
Medium good (MG)	(0.65,0.25,0.10)
Good (G)	(0.75,0.15,0.10)
Very good (VG)	(0.85,0.10,0.05)
Extremely good (EG)	(0.95,0.05,0.00)

.

Step 2 Determine the experts’ weights.

The experts’ weights are denoted as $\lambda =({\lambda }_1,\cdots ,{\lambda }_s,\cdots ,{\lambda }_p)$. The calculation process is shown as Equations (25) and (26).

$$b_s(\pi )=-\frac{1}{({\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{\pi }_{ij}^s)\ln ({\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m{\pi }_{ij}^s)}}}}}$$

(25)

$${\lambda }_s=\frac{b_s(\pi )}{{\displaystyle \sum _{s=1}^p{b}_s(\pi )}}$$

(26)

Step 3 Integrate the value given by experts.

Assume that $r_{ij}^s=({\mu }_{ij}^s,{\nu }_{ij}^s,{\pi }_{ij}^s)$ is the IFN of evaluation object $A_i$ concerning evaluation index $C_j$ given by the expert $E_s$. The integrated value is calculated by Equation (27).

$$\begin{array}{l}{f}_{ij}={\lambda }_1{r}_{ij}^1\oplus {\lambda }_2{r}_{ij}^2\oplus \cdots \oplus {\lambda }_s{r}_{ij}^s\oplus \cdots \oplus {\lambda }_p{r}_{ij}^p\\ =(1-{\displaystyle \prod _{s=1}^p{(1-{\mu }_{ij}^s)}^{{\lambda }_s}},{\displaystyle \prod _{s=1}^p{({\nu }_{ij}^s)}^{{\lambda }_s}},{\displaystyle \prod _{s=1}^p{(1-{\mu }_{ij}^s)}^{{\lambda }_s}}-{\displaystyle \prod _{s=1}^p{({\nu }_{ij}^s)}^{{\lambda }_s}})\end{array}$$

(27)

According to the G1 method and entropy weight method mentioned in Section 3.2, the subjective weight and objective weight of each index are calculated to lay a foundation for future comprehensive evaluation.

To achieve a scientific and reasonable evaluation of EVCS, the improved matter-element extension method was introduced to build a comprehensive evaluation framework. The matter-element extension model can reduce the subjectivity of evaluation results and divide the grade of evaluation objects [43]. In this paper, firstly, the EVCS service level is divided into different grades. Secondly, the classical domain of indexes and the node domain are determined according to the collected data of three charging stations to obtain the matter element to be evaluated. Then, the classical domain and the matter element are normalized. Ultimately, the grade distance value and the closeness function value are computed, which is the proof to rank the EVCS service level. The basic steps of the improved matter-element extension method are as follows:

(1)

Determine the classical domain, node domain, and matter element to be evaluated.

$$R_q=(P_q,C_i,V_{iq})=\left[\begin{array}{ccc}\begin{array}{l}{P}_q\\ \\ \\ \end{array}& \begin{array}{c}{c}_1\\ \begin{array}{l}{c}_2\\ ⋮\end{array}\\ c_n\end{array}& \begin{array}{l}{v}_{1q}\\ v_{2q}\\ ⋮\\ v_{nq}\end{array}\end{array}\right]=\left[\begin{array}{ccc}\begin{array}{l}{P}_q\\ \\ \\ \end{array}& \begin{array}{c}{c}_1\\ \begin{array}{l}{c}_2\\ ⋮\end{array}\\ c_n\end{array}& \begin{array}{l}〈a_{1q},b_{1q}〉\\ 〈a_{2q},b_{2q}〉\\ ⋮\\ 〈a_{nq},b_{nq}〉\end{array}\end{array}\right]$$

(28)

$$R_s=(P,C_i,V_{si})=\left[\begin{array}{ccc}\begin{array}{l}P\\ \\ \\ \end{array}& \begin{array}{c}{c}_1\\ \begin{array}{l}{c}_2\\ ⋮\end{array}\\ c_n\end{array}& \begin{array}{l}{v}_{s1}\\ v_{s2}\\ ⋮\\ v_{sn}\end{array}\end{array}\right]=\left[\begin{array}{ccc}\begin{array}{l}P\\ \\ \\ \end{array}& \begin{array}{c}{c}_1\\ \begin{array}{l}{c}_2\\ ⋮\end{array}\\ c_n\end{array}& \begin{array}{l}〈a_{s1},b_{s1}〉\\ 〈a_{s2},b_{s2}〉\\ ⋮\\ 〈a_{sn},b_{sn}〉\end{array}\end{array}\right]$$

(29)

where $R_q$ is the classical domain; $P_q$ is the $q_{th}$ evaluation grade; $c_1,c_2,\dots ,c_n$ is $n$ indexes of $P_q$; $v_{1q},v_{2q},\dots ,v_{nq}$ is the value range of $P_q$ for $c_1,c_2,\dots ,c_n$; $R_s$ is node domain, $P$ is all grades of evaluation objects; and $v_{s1},v_{s2},\dots ,v_{sn}$ is the value range of $P$ for $c_1,c_2,\dots c_n$.

• The classical domain of quantitative indexes in the evaluation system can be obtained by searching References [29,31,32], and the qualitative indexes’ classical domain is determined by experts using a 10-point scoring method.
• Determine the matter elements to be evaluated $R_{A0}$, $R_{B0}$, and $R_{C0}$

(2)

Normalizing process

When the collected data of evaluation indexes exceeds the range of node domain, its corresponding correlation function value cannot be calculated, and then the matter-element model should be improved, that is, to normalize the classical domain and the matter-element to be evaluated. Thereinto, the normalization of the matter element to be evaluated takes charging station A as an example.

$$R_q^{\prime }=(P_q,C_i,V_{iq}^{\prime })=\left[\begin{array}{ccc}\begin{array}{l}{P}_q\\ \\ \\ \\ \\ \\ \end{array}& \begin{array}{c}\begin{array}{l}{c}_1\\ \end{array}\\ \begin{array}{l}{c}_2\\ \\ ⋮\end{array}\\ \begin{array}{l}{c}_n\\ \end{array}\end{array}& \begin{array}{l}〈\frac{a_{1q}}{b_{s1}},\frac{b_{1q}}{b_{s1}}〉\\ 〈\frac{a_{2q}}{b_{s2}},\frac{b_{2q}}{b_{s2}}〉\\ ⋮\\ 〈\frac{a_{nq}}{b_{sn}},\frac{b_{nq}}{b_{sn}}〉\end{array}\end{array}\right]$$

(30)

$$R_{A0}^{\prime }=\left[\begin{array}{ccc}\begin{array}{l}{P}_{A0}\\ \\ \\ \end{array}& \begin{array}{c}{c}_1\\ \begin{array}{l}{c}_2\\ ⋮\end{array}\\ c_n\end{array}& \begin{array}{l}{v}_1/b_{s1}\\ v_2/b_{s2}\\ \begin{array}{ccc}& ⋮& \end{array}\\ v_n/b_{sn}\end{array}\end{array}\right]$$

(31)

where $R_q^{\prime }$ is the classical domain after being normalized and $R_{A0}^{\prime }$ is charging station A after being normalized.

(3)

Compute the grade distance value $D_q({\nu }_j^{\prime })$

Employ the G1 method and entropy weight method to determine the comprehensive weights and compute the grade distance value $D_q({\nu }_j^{\prime })$ of evaluation objects by Equation (32).

$$D_q({\nu }_j^{\prime })=\left|{\nu }_j^{\prime }-\frac{a_{jq}^{\prime }+b_{jq}^{\prime }}{2}\right|-\frac{(b_{jq}^{\prime }-a_{jq}^{\prime })}{2}$$

(32)

(4)

Build the closeness function and calculate the value of the closeness function.

Reference [43] for a review of the matter-element corresponds to the closeness formula of grade is given by Equation (33).

$$N_q(p_0)=1-\frac{1}{n(n+1)}{\displaystyle \sum _{j=1}^n{D}_q({\nu }_j^{\prime }){\omega }_j}$$

(33)

(5)

Rank the evaluation objects.

From $N_{q^{\prime }}(p_0)=max\left\{N_q(p_0)\right\}$ we can know that the matter element to be evaluated belongs to $q^{\prime }$ grade.

$${\overline{N}}_q(p_0)=\frac{N_q(p_0)-\underset{q}{\min }{N}_q(p_0)}{\underset{q}{\max }{N}_q(p_0)-\underset{q}{\min }{N}_q(p_0)}$$

(34)

$$q^{*}=\frac{{\displaystyle \sum _{q=1}^{m}q{\overline{N}}_q(p_0)}}{{\displaystyle \sum _{q=1}^m{\overline{N}}_q(p_0)}}$$

(35)

where ${\overline{N}}_q(p_0)$ is the closeness function value after normalizing and $q^{*}$ is the grade variable eigenvalue of the matter element to be evaluated. The value of $q^{*}$ can determine which grade the matter element to be evaluated is closer to.

3.4. Data Process

The basic data of three charging stations were collected, such as the number of fast charging piles, charging price and service fee, etc. For the qualitative indexes, we designed a survey questionnaire for experts to score.

3.4.1. General Situation of Charging Stations

We selected three similarly sized EVCSs in Beijing as evaluation samples, of which the charging station information is from State Grid, Star Charge, and TELD. For convenience, we marked them with A, B, and C, respectively.

Table 4. Basic information of three EVCSs.

	A	B	C
Operating time	8 h	24 h	24 h
Mean service distance	4.60 km	5.24 km	4.89 km
number of fast charging piles	20 fast-charging piles	12 fast-charging piles and 4 slow	6 fast-charging piles and 9 slow
Average utilization	21.36%	43.52%	56.17%
Average turnover	1.61	3.28	4.23
Mean failure rate	7.14%	5.63%	3.78%
Charging safety	High safety performance	General safety performance	Equipped with non-electric plugs
Illegal occupancy rate of fuel vehicles	15.42%	12.57%	4.26%
Value-added services	Route planning, pay electricity bills, and non-inductive parking	Route planning and malfunction repair	Route planning
Average charging time	1.9 h	3.4 h	4.7 h
Charging price	[0.3483, 0.9276]	[0.4558, 1.4982]	[0.8058, 1.3782]
Service fee	0.8	0.6	0.44
Parking fee	2 yuan/h	1 yuan/h	5 yuan/h
Trading convenience	Pay by charging card, QR code and APP	Pay by APP	Pay by APP, WeChat and AliPay
Accuracy of information push	97%	100%	95%
Feedback processing speed	Within ten hours	Within six hours	Within one day
Customer satisfaction	Charging facilities and environment are general	Good environment, fast charging speed, convenient parking	Adequate charging facilities

Note: compiled by the author based on public information.

describes the relative operation data of charging stations.

3.4.2. The Initial Data of EVCS Evaluation Indexes

According to Table 3, to determine the initial value of the second-level indexes, the value of quantitative indexes collected are represented by value, and for qualitative indexes, their initial data are denoted as code in conversion rules. The final results are shown in

Table 5. Initial indexes value of three EVCSs.

		A				B				C
		E1	E2	E3	E4	E1	E2	E3	E4	E1	E2	E3	E4
OS	C1	4.60				5.24				4.89
	C2	100%				75%				40%
	C3	21.36%				43.52%				56.17%
	C4	1.61				3.28				4.23
	C5	7.14%				5.63%				3.78%
	C6	G	VG	VG	G	G	G	MG	G	VG	G	VG	VG
	C7	15.42%				12.57%				4.26%
	C8	VG	VG	G	VG	G	G	VG	VG	G	MG	MG	G
CS	C9	1.9				3.4				4.7
	C10	[0.3483, 0.9276]				[0.4558, 1.4982]				[0.8058, 1.3782]
	C11	0.8				0.6				0.44
	C12	2				1				5
	C13	G	MG	MG	G	M	MP	MP	M	VG	EG	EG	VG
	C14	97%				100%				95%
	C15	G	G	MG	G	VG	VG	EG	VG	MG	MG	MG	M
	C16	G	MG	G	MG	G	VG	G	MG	G	G	VG	MG

.

4. Empirical Analysis

In this section, three charging stations in Beijing were selected to assess their charging service level. Secondly, standardized data are obtained after processing the original data; the comprehensive weight of each index is determined by combining subjective and objective weight tools. Then, an improved matter-element extension model is employed to evaluate the EVCS service level. Finally, sensitivity analysis of indexes and comparative analysis of evaluation methods are used to explain the influence of index weight change on the evaluation result [29].

4.1. Normalizing Initial Data

Firstly, according to Equations (21)–(24), the crisp value index and interval index are normalized. The four experts invited are from different practitioners in the field of EVCS, respectively. E1 is an operator manager of EVCS; E2 is a university professor who specializes in EVCS; E3 is an office worker of city manager committee in Beijing; and E4 is an electric vehicle owner with over three years’ using experience of EVCS. According to Equations (25) and (26), we can get experts’ weights expressed as $\lambda =(0.1421,0.2216,0.4624,0.1738)$.

Then, according to Table 5, experts’ weights and Equation (27), the normalized value of qualitative indexes is determined, as shown in

Table 6. Normalized indexes’ value.

		A				B				C
		E1	E2	E3	E4	E1	E2	E3	E4	E1	E2	E3	E4
OS	C1	1.0000				0.0000				0.5469
	C2	1.0000				0.5833				0.0000
	C3	0.0000				0.6366				1.0000
	C4	0.0000				0.6374				1.0000
	C5	0.0000				0.4494				1.0000
	C6	(0.8237, 0.1137, 0.0626)				(0.7079, 0.1900, 0.1021)				(0.8320, 0.1094, 0.0586)
	C7	0.0000				0.2554				1.0000
	C8	(0.8100, 0.1206, 0.0693)				(0.8194, 0.1159, 0.0647)				(0.6853, 0.2127, 0.1020)
CS	C9	1.0000				0.4643				0.0000
	C10	[0.1710, 1.1619]				[0.1058, 0.8878]				[0.1151, 0.5022]
	C11	0.0000				0.5556				1.0000
	C12	0.7500				1.0000				0.0000
	C13	(0.6853, 0.2127, 0.1020)				(0.4017, 0.4974, 0.1009)				(0.9293, 0.0622, 0.0085)
	C14	0.4000				1.0000				0.0000
	C15	(0.7079, 0.1900, 0.1021)				(0.9097, 0.0726, 0.0177)				(0.6276, 0.2713, 0.1011)
	C16	(0.7144, 0.1836, 0.1020)				(0.7633, 0.1498, 0.0868)				(0.7907, 0.1359, 0.0734)

.

4.2. Results of the Index Weights

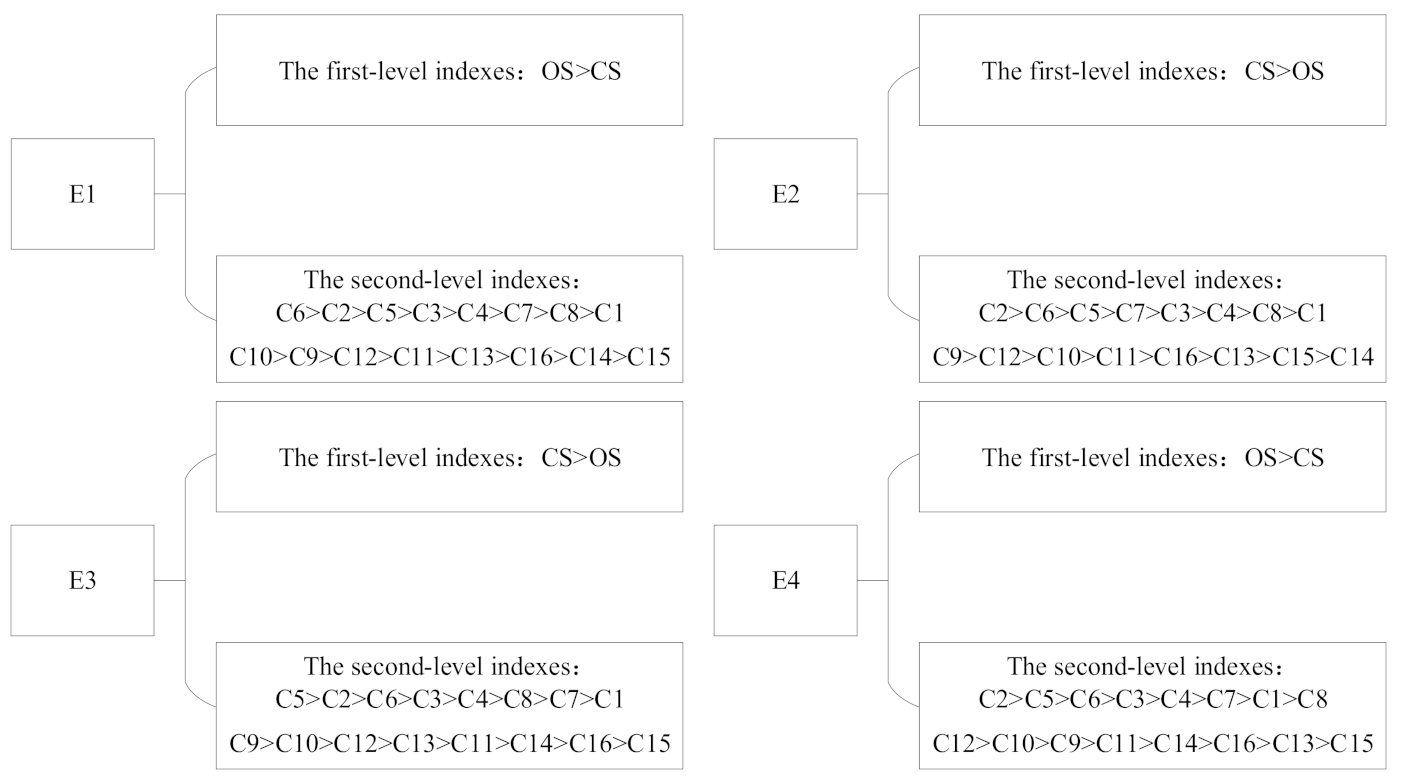
The important degree order of first-level indexes and second-level indexes given by four experts’ weights is shown in Figure 2.

According to the normalized value of indexes and important degree order, the weights of the first-level and second-level indexes and comprehensive weights can be obtained as shown in

Table 7. The weights of indexes.

The First-Level Indexes	Weight	The Second-Level Indexes	Subjective Weight	Objective Weight	Comprehensive Weight	Ranking
OS	0.4731	C1	0.0999	0.0009	0.0477	13
		C2	0.0833	0.0411	0.0599	7
		C3	0.0759	0.0452	0.0585	8
		C4	0.0595	0.0451	0.0507	12
		C5	0.0556	0.0210	0.0368	14
		C6	0.0509	0.0776	0.0629	6
		C7	0.0417	0.0733	0.0564	9
		C8	0.0331	0.0786	0.0551	10
CS	0.5269	C9	0.1144	0.0405	0.0805	5
		C10	0.0926	0.1417	0.1197	1
		C11	0.0787	0.0191	0.0510	11
		C12	0.0604	0.1308	0.0972	2
		C13	0.0509	0.1218	0.0877	3
		C14	0.0430	0.0002	0.0227	16
		C15	0.0329	0.0280	0.0314	15
		C16	0.0271	0.1351	0.0818	4

.

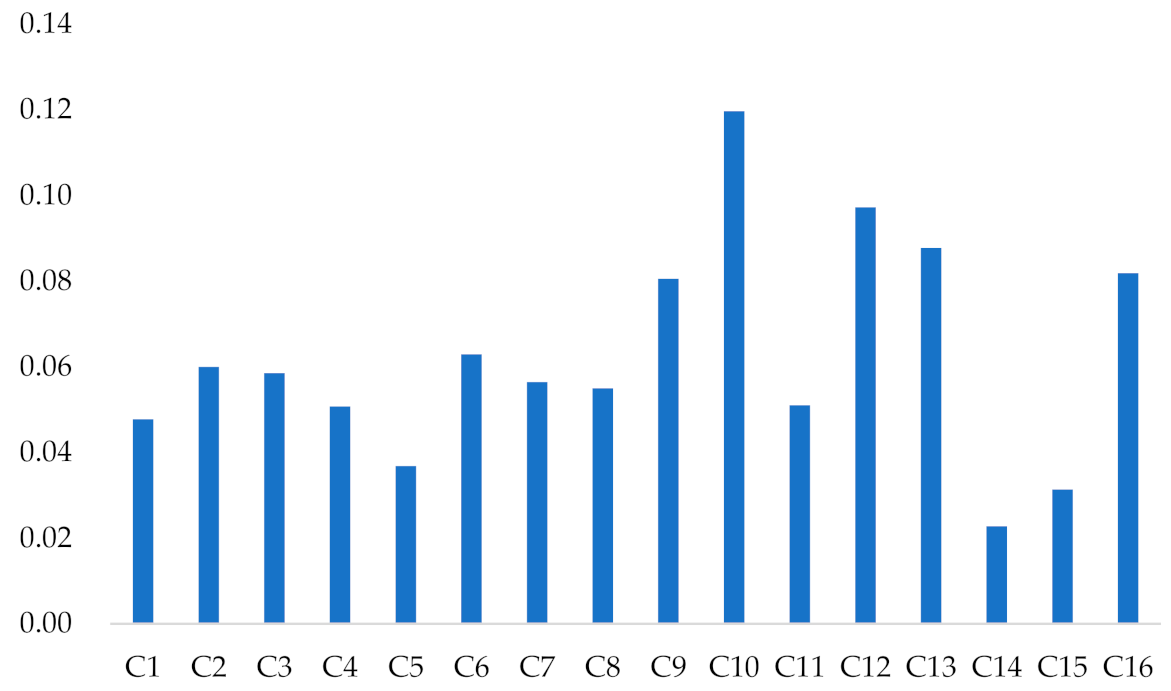
We can summarize the weights of indexes and get the second-level indexes’ weight graph as shown in Figure 3. This graph can reflect the second-level indexes’ weights intuitively.

According to Figure 3, Charging price (C10), Parking cost (C12), and Trading convenience (C13) are the top three metrics affecting the service level most. Previous studies draw the conclusion that average charging fee and utilization are two important factors [29], and Reference [32] found that the number of fast charging piles and annual profit were the two most influential factors. Thus, we can find the similarity of their results that charging price or annual profit is the most important factor in charging station evaluation, due to these factors being related to the benefit of charging stations. Therefore, the government should issue relevant subsidy policies, which can not only ensure the overall benefit of charging station operators and stimulate their investment in charging stations further but also make electric vehicle users have a high degree of satisfaction.

4.3. EVCS Service Appraisal

Referring to Reference [43] the grade dividing standard on power quality, this paper supposes that the charging level of EVCS is divided into $q$ grades. Given the current operation situation of EVCS in Beijing, we divide it into five grades: Excellent, Good, Medium, Qualified, and Unqualified.

(1)

Determine the classical domain, node domain and matter element to be evaluated.

• The classical domain and node domain corresponding to grades of indexes are shown in

  Table 8. Classical domain and node domain of indexes.

  Number	Grades					Node Domain
  	Excellent	Good	Medium	Qualified	Unqualified
  C1	(0.3)	(3, 4)	(4, 4.5)	(4.5, 5)	(5, 6)	(0.6)
  C2	(80%, 100%)	(60%, 80%)	(40%, 60%)	(20%, 40%)	(0, 20%)	(0, 100%)
  C3	(40%, 50%)	(30%, 40%)	(20%, 30%)	(10%, 20%)	(0, 10%)	(0, 50%)
  C4	(4, 5)	(3, 4)	(2, 3)	(1, 2)	(0, 1)	(0, 5)
  C5	(0,4%)	(4%, 8%)	(8%, 12%)	(12%, 16%)	(16%, 20%)	(0, 20%)
  C6	(9, 10)	(8, 9)	(7, 8)	(6, 7)	(0, 6)	(0, 10)
  C7	(0, 3%)	(3%, 6%)	(6%, 9%)	(9%, 12%)	(12%, 15%)	(0, 15%)
  C8	(9, 10)	(8, 9)	(7, 8)	(6, 7)	(0, 6)	(0, 10)
  C9	(1, 2)	(2, 3)	(3, 4)	(4, 5)	(5, 6)	(1, 6)
  C10	(0.4, 0.6)	(0.6, 0.8)	(0.8, 1.0)	(1.0, 1.2)	(1.2, 1.4)	(0.4, 1.4)
  C11	(0.25, 0.45)	(0.45, 0.65)	(0.65, 0.85)	(0.85, 1.05)	(1.05, 1.25)	(0.25, 1.25)
  C12	(0, 1.5)	(1.5, 3)	(3, 4.5)	(4.5, 6)	(6, 7.5)	(0, 7.5)
  C13	(9, 10)	(8, 9)	(7, 8)	(6, 7)	(0, 6)	(0, 10)
  C14	(98%, 100%)	(96%, 98%)	(94%, 96%)	(92%, 94%)	(90%, 92%)	(90%, 100%)
  C15	(9, 10)	(8, 9)	(7, 8)	(6, 7)	(0, 6)	(0, 10)
  C16	(9, 10)	(8, 9)	(7, 8)	(6, 7)	(0, 6)	(0, 10)

  .

The classical domain and node domain of indexes are determined by referring to relative literatures and research.

• $R_{A0}$, $R_{B0}$ and $R_{C0}$ are established according to the collected data as shown in

  Table 9. Initial value of elements to be evaluated.

  Number	${\mathit{R}}_{\mathit{A}0}$	${\mathit{R}}_{\mathit{B}0}$	${\mathit{R}}_{\mathit{C}0}$
  C1	4.60	5.24	4.89
  C2	100%	75%	40%
  C3	21.36%	43.52%	56.17%
  C4	1.61	3.28	4.23
  C5	7.14%	5.63%	3.78%
  C6	8.237	7.079	8.320
  C7	15.42%	12.57%	4.26%
  C8	8.100	8.194	6.853
  C9	1.9	3.4	4.7
  C10	0.638	0.977	1.092
  C11	0.8	0.6	0.44
  C12	2	1	5
  C13	6.853	4.017	9.293
  C14	97%	100%	95%
  C15	7.079	9.097	6.276
  C16	7.144	7.633	7.907

  Note: The data are collected by looking into the charging stations’ operation situations.

  .

(2)

Normalizing process

We can see that the actual value of the index $C_3$ and $C_7$ is beyond the scope of node domain according to (1); therefore, they should be normalized. The normalized result of the classical domain and elements to be evaluated is shown in

Table 10. The normalized result of the classical domain.

Number	Grade
	Excellent	Good	Medium	Qualified	Unqualified
C1	(0, 0.5)	(0.5, 0.667)	(0.667, 0.75)	(0.75, 0.833)	(0.833, 1)
C2	(0.8, 1)	(0.6, 0.8)	(0.4, 0.6)	(0.2, 0.4)	(0, 0.2)
C3	(0.8, 1)	(0.6, 0.8)	(0.4, 0.6)	(0.2, 0.4)	(0, 0.2)
C4	(0.7, 1)	(0.4, 0.7)	(0.2, 0.4)	(0.1, 0.2)	(0, 0.1)
C5	(0, 0.2)	(0.2, 0.4)	(0.4, 0.6)	(0.6, 0.8)	(0.8,1)
C6	(0.9, 1)	(0.8, 0.9)	(0.7, 0.8)	(0.6, 0.7)	(0, 0.6)
C7	(0, 0.2)	(0.2, 0.4)	(0.4, 0.6)	(0.6, 0.8)	(0.8, 1)
C8	(0.9, 1)	(0.8, 0.9)	(0.7, 0.8)	(0.6, 0.7)	(0, 0.6)
C9	(0.167, 0.333)	(0.333, 0.5)	(0.5, 0.667)	(0.667, 0.833)	(0.833, 1)
C10	(0.286, 0.429)	(0.429, 0.571)	(0.571, 0.714)	(0.714, 0.857)	(0.857, 1)
C11	(0.2, 0.36)	(0.36, 0.52)	(0.52, 0.68)	(0.68, 0.84)	(0.84, 1)
C12	(0, 0.2)	(0.2, 0.4)	(0.4, 0.6)	(0.6, 0.8)	(0.8, 1)
C13	(0.9, 1)	(0.8, 0.9)	(0.7, 0.8)	(0.6, 0.7)	(0, 0.6)
C14	(0.98, 1)	(0.96, 0.98)	(0.94, 0.96)	(0.92, 0.94)	(0.90, 0.92)
C15	(0.9, 1)	(0.8, 0.9)	(0.7, 0.8)	(0.6, 0.7)	(0, 0.6)
C16	(0.9, 1)	(0.8, 0.9)	(0.7, 0.8)	(0.6, 0.7)	(0, 0.6)

and

Table 11. The normalized result of elements to be evaluated.

Number	${\mathit{R}}_{\mathit{A}0}^{\prime }$	${\mathit{R}}_{\mathit{B}0}^{\prime }$	${\mathit{R}}_{\mathit{C}0}^{\prime }$
C1	0.7667	0.8733	0.815
C2	1	0.75	0.4
C3	0.4272	0.8704	1.1234
C4	0.322	0.656	0.846
C5	0.357	0.2815	0.189
C6	0.8237	0.7079	0.832
C7	1.028	0.838	0.284
C8	0.81	0.8194	0.6853
C9	0.3167	0.5667	0.7833
C10	0.4557	0.6979	0.78
C11	0.64	0.48	0.352
C12	0.2667	0.1333	0.6667
C13	0.6853	0.4017	0.9293
C14	0.97	1	0.95
C15	0.7079	0.9097	0.6276
C16	0.7144	0.7633	0.7907

Note: The normalized method is the same as that of the classical domain.

.

To facilitate the subsequent calculation convenient, we normalized the classical domain to make their values located in interval (0, 1).

(3)

Compute the grade distance value $D_q({\nu }_j^{\prime })$

The grade distance value of EVCS is shown in the Appendix B in detail.

(4)

Build the closeness function and calculate the value of the closeness function.

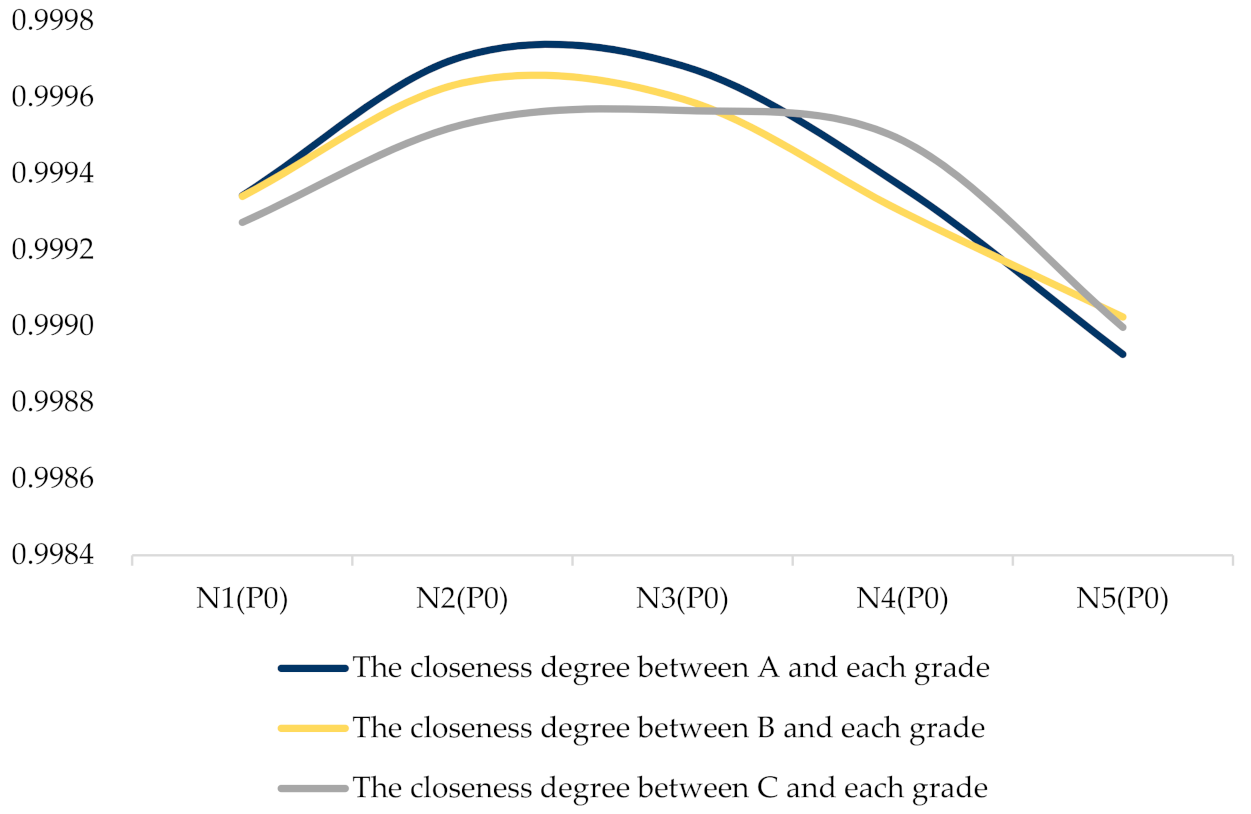
The closeness between EVCS and each grade is shown in Figure 4.

This figure illustrates the closeness degree between charging stations and each grade. We can conclude that charging stations A and B are similar with each other, while charging station C performs a little worse than A and B. More details are discussed in next section.

(5)

Rank the evaluation objects.

Through the closeness degree between elements to be evaluated $R_{A0}$, $R_{B0}$, $R_{C0}$, and each grade, we can judge that $N_2(P_{A0})=\max \{N_q(P_{A0})\}=0.999706$, $N_2(P_{B0})=\max \{N_q(P_{B0})\}=0.999637$, $N_3(P_{C0})=\max \{N_q(P_{C0})\}=0.999565$, $q=1,2,3,4,5$.

According to the maximum of $N_q(P_0)$, the corresponding grade is EVCS’s ranking result. We can know that the grade of A and B is good, and the grade of C is medium. Since the grade of A and B is the same, to distinguish which grade they are closer to, we calculate the grade variable eigenvalue according to Equations (34) and (35). The results are as follows:

$$\begin{array}{l}{\overline{N}}_q(P_{A0})=\{0.5344,1.0000,0.9695,0.5621,0.0000\}\\ {\overline{N}}_q(P_{B0})=\{0.5150,1.0000,0.9319,0.4494,0.0000\}\\ {\overline{N}}_q(P_{C0})=\{0.4838,0.9349,1.0000,0.8606,0.0000\}\end{array}$$

(36)

$$q_{A*}=2.5086,q_{B*}=2.4543,q_{C*}=2.6823$$

(37)

The calculation results are summarized and sorted to get the final evaluation results as shown in

Table 12. The evaluation result of EVCS service level.

	The Closeness Degree	The Grade of Service Level	The Eigenvalue	Ranking
A	0.999,701	Good	2.5086	2
B	0.999,637	Good	2.4543	1
C	0.999,560	Medium	2.6823	3

. Through the eigenvalue to rank the same grade, the smaller the grade variable eigenvalue is, the better the evaluation result is. Therefore, it can be concluded from the table that the ranking result of EVCS is B > A > C.

4.4. Discussion

4.4.1. Comparative Analysis

In this section, the comparative analysis of different evaluation methods is implemented. The common methods including VIKOR and TOPSIS are used. VIKOR method is a compromise ranking method based on positive and negative ideal points [38], which is based on the integration function of measurable ideal solution distance to make a rank. TOPSIS method is to rank by checking the distance between the optimal and worst solution [29]. If the evaluation object is closest to the optimal solution, it means the best or the worst. The appraisal value of using VIKOR and TOPSIS methods is shown in

Table 13. The value $S_i$, $R_i$, $Q_i$, $d_i^{PIS}$, $d_i^{NIS}$, and $D_i$ of EVCSs.

	VIKOR			TOPSIS
	${\mathit{S}}_{\mathit{i}}$	${\mathit{R}}_{\mathit{i}}$	${\mathit{Q}}_{\mathit{i}}$	${\mathit{d}}_{\mathit{i}}^{\mathit{P}\mathit{I}\mathit{S}}$	${\mathit{d}}_{\mathit{i}}^{\mathit{N}\mathit{I}\mathit{S}}$	${\mathit{D}}_{\mathit{i}}$
A	0.4413	0.0818	0.0703	0.3680	0.4334	0.5408
B	0.5397	0.1197	0	0.3577	0.4438	0.5537
C	0.4252	0.0972	0.2032	0.3471	0.3572	0.5072

.

The results of the comparative analysis are shown in

Table 14. The ranking results of three MCDM methods.

	Improved Matter-Element Extension	Ranking	VIKOR	Ranking	TOPSIS	Ranking
A	2.5086	2	0.0707	2	0.5408	2
B	2.4543	1	0	1	0.5537	1
C	2.6823	3	0.2032	3	0.5072	3

. Compared to VIKOR and TOPSIS method, the improved matter-element extension method can divide the grades of EVCS service level firstly and then rank the evaluation objects. While the VIKOR method only ranks by the scores of evaluation objects, the TOPSIS method ranks according to the relative closeness coefficient. It can be seen that the ranking result of the three methods is the same, and this means the proposed method can get a relatively robust and reliable result.

In the comparative analysis, the disadvantage of TOPSIS method is that it depends on the establishment of decision matrix, and when the establishment of decision matrix is not accurate, the result is affected. Compared to TOPSIS method, VIKOR method compensates the defects of TOPSIS method, which does not consider the distance between alternative scheme and the positive and negative ideal solution. Both of them cannot always make the highest-ranked scheme close to the ideal the most. Therefore, this paper employs the improved matter-element extension method to evaluate the service of charging stations. The purpose of the comparative analysis is to illustrate the stability of the proposed method.

4.4.2. Sensitive Analysis

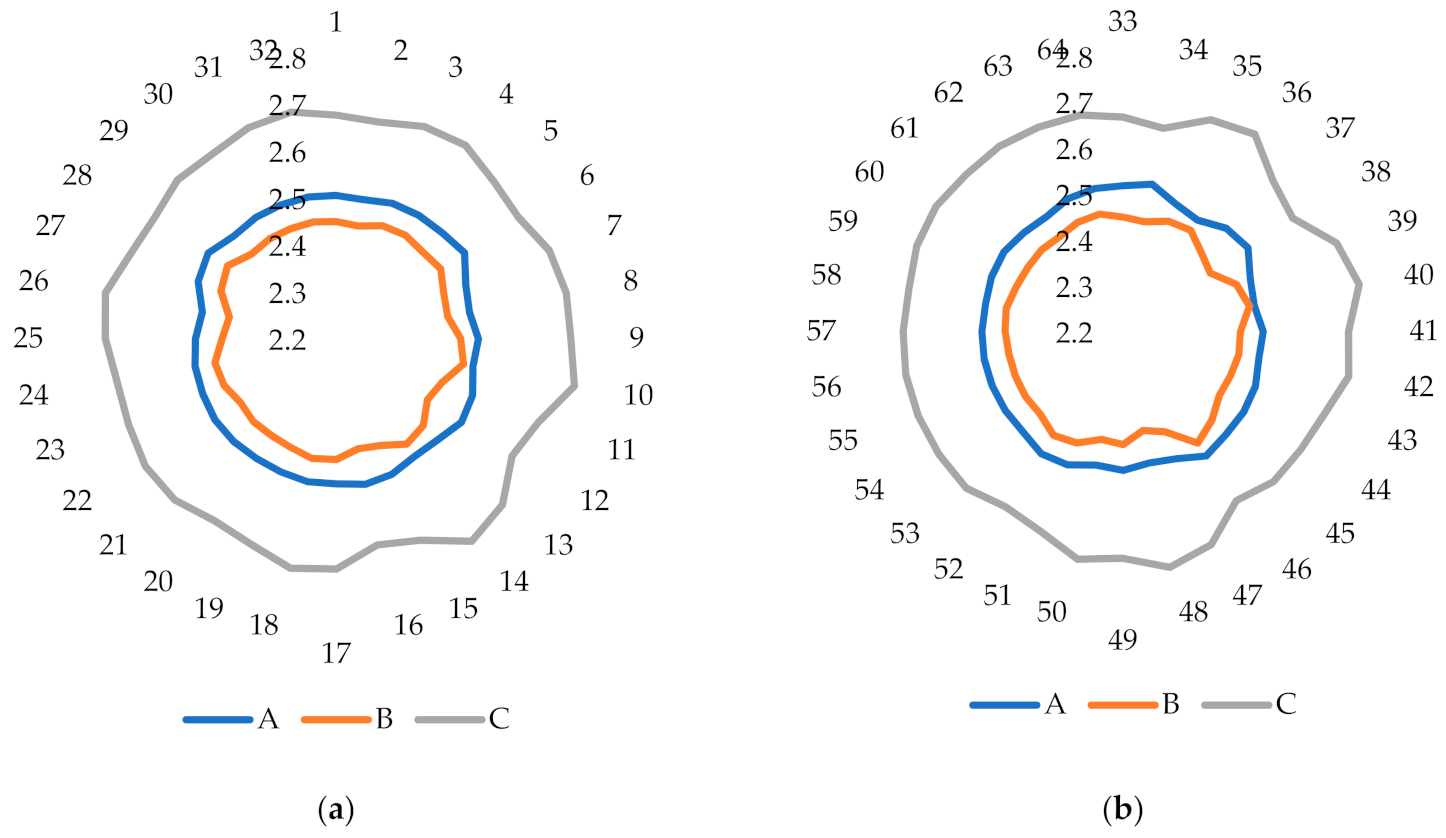
In this section, we employ sensitive analysis to verify the influence of the indexes’ weight change on three charging stations’ service. We increase or decrease initial index weights by 10% and 20%, respectively, and then recalculate the closeness degree between three charging stations and different grades [38]. Therefore, each index has four new experiments. When the $j_{th}$ index increases or decreases by 10% or 20%, because the sum of weights is 1, and then other weights should change correspondingly. Supposing the initial weight ${\omega }_j$ changes into ${\omega }_j^{\prime }=\epsilon {\omega }_j$ (thereinto, $\epsilon$ equals 80%, 90%, 110%, and 120%), other weights change into ${\omega }_l^{\prime }=\theta {\omega }_l$ (thereinto, $\theta =(1-\epsilon {\omega }_j)/(1-{\omega }_j)$, $l\ne j$, $l=1,2,\dots ,n$), which should also meet the following condition:

$$\epsilon {\omega }_j+{\displaystyle \sum _{l=1,l\ne j}^n\theta {\omega }_l^{\prime }}=1$$

(38)

For 16 evaluation indexes, we conduct 64 sensitive analysis experiments. According to Table 1, the results of the sensitivity analysis are divided into operation service group (shown in Figure 5a and customer service group (shown in Figure 5b)).

In experiments 1–32, the evaluation results are obtained through the weight variation of index C1–C8 in the OS group as shown in Figure 5a. We can see that with the weight variation of index C1–C8, the eigenvalue of the B charging station remains relatively stable and ranks first. Although the eigenvalue of the A charging station has little fluctuation, it remains second. The eigenvalue of the C charging station also has some fluctuation in experiments 12 and 16 but holds in third place. Thus, despite the index weights of C1–C8 having extra changes, the ranking result of three charging stations is still B > A > C.

In experiments 33–64, we can see from Figure 5b that the eigenvalues of A and B are close to each other in experiment 40, which illustrates that the ranking result is sensitive to index C10, but this does not influence the ranking result. In addition, the final ranking result is still B > A > C.

By performing sensitive analysis, we can see that charging price and parking cost are two important factors affecting the service of charging stations; therefore, charging station operators should pay more attention to improve the two aspects. The implementation of the sensitive analysis is to find out the factors that have a greater impact on charging station operators so as to improve their operation efficiency and provide users with a better experience.

In China, although electric vehicle charging stations have been deployed very fast, the service level of EVCS still needs to be improved further. This paper provides the following implications for the government, operators, and users so that the service level of charging stations can be enhanced. The following implications proposed in this paper and the valuable experience of EV infrastructure development promoted by China’s government are a good reference for the development of charging stations in some aboard sites.

(1)

The local governments should follow the guidance of national policies and subsidies for the EVCS properly to improve operators’ revenue to spur the market investment in charging stations.

(2)

The operators should make full use of present technology to enhance the numerical and intelligent level of charging stations’ relevant facilities. This can make the charging service more convenient and effective.

(3)

The charging stations’ relevant applications can cooperate with many financial banks to diversify the payment methods and enhance users’ satisfaction.

(4)

Users consider charging price and parking cost per hour first when choosing charging stations. The charging stations need to investigate customer preference and affordability for the service price and conduct pertinent marketing devices.

5. Conclusions

Due to the rapid development and vigorous promotion, the charging stations as one of the infrastructures have drawn more and more attention. Meanwhile, the service level becomes an important factor that determines customers’ intention to buy and use electric vehicles. This paper employs an improved matter-element extension model to assess the service level of three typical charging stations in Beijing, as well as proves the robustness of the proposed methodology. The main conclusions are as follows:

(1)

Referring to the previous index system constructed by scholars, this paper categorizes the charging station service indexes into subject and object evaluation metrics and then constructs the evaluation index system of the EVCS service level.

(2)

This paper uses an improved matter-element extension model to assess the service of charging stations. The index data can be expressed by crisp value, interval number, and linguistic variable. The comprehensive weights are calculated through integrated subjective weights and objective weights.

(3)

According to the empirical analysis, the ranking of three charging stations is B > A > C, and the result of index weights indicates that charging price (C10), parking cost per hour (C12), and trading convenience (C13) are the top factors influencing service level.

(4)

The sensitive analysis proves that charging price is the sensitive index of influencing EVCS service evaluation. The government and operators should regulate proper charging prices to improve the service level or EVCS.

The improved matter-element extension model proposed in the paper has already been widely used in various research fields. This is the first time to apply the model to charging stations’ service evaluation, but there are some limitations. For example, the proposed index system involves a large number of indexes, and some of them are indirectly related. Therefore, future research can be conducted to deal with their relevance and screen key indexes.