Geometric and Topological Bases of a New Classification of Wood Vascular Tissues Part 1: Shape and Arrangement Classifications of Vessels
Abstract
:1. Introduction
2. Methods and Materials
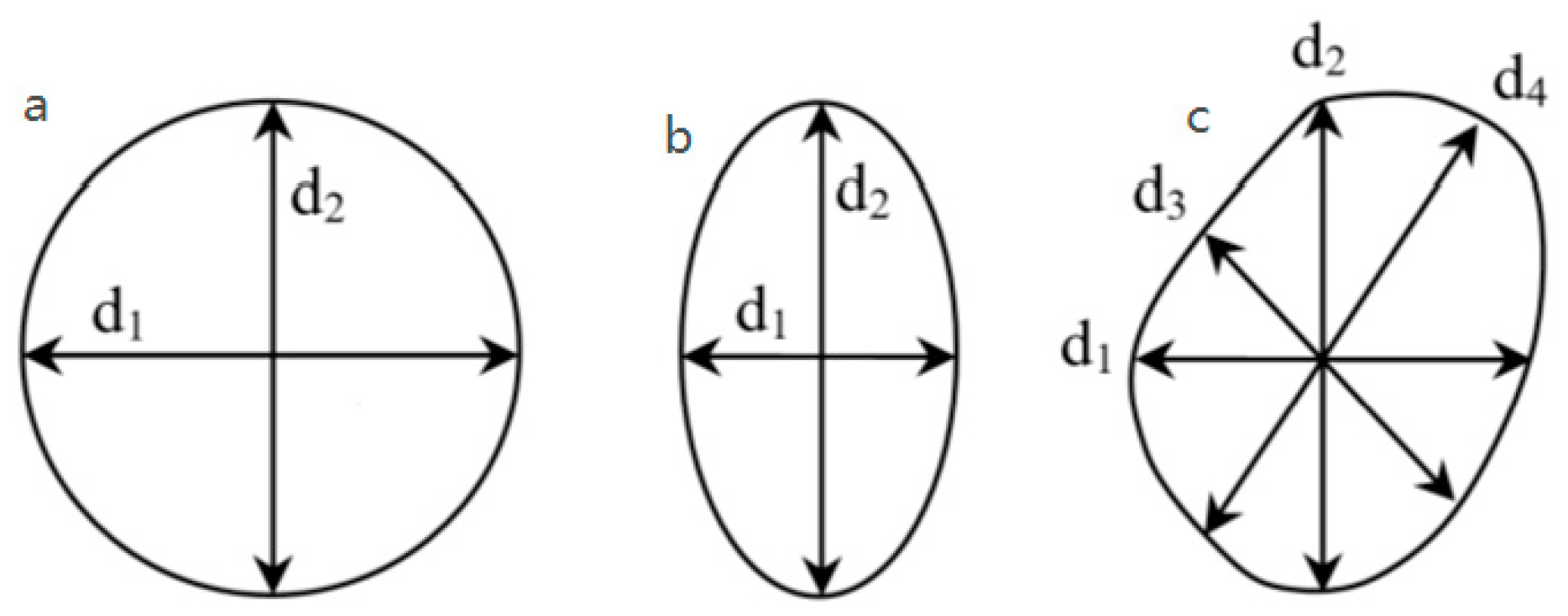
2.1. Classification of Vessels According to Their Geometric Shape: Geometry Classes of Vessels
- di—measured diameters of the vessel, as i varies from 1 to 4;
- d1—the diameter in the tangential direction, in µm;
- d2—the diameter in the radial direction, in µm;
- d3, d4—diameters located below 45° degrees relative to the tangential and radial directions, in µm.
2.2. The Classification of Vessels According to Their Mutual Position (Arrangement)
2.2.1. Density Arrangement Classes of Vessels
2.2.2. Orientation Arrangement Classes of Vessels
- -
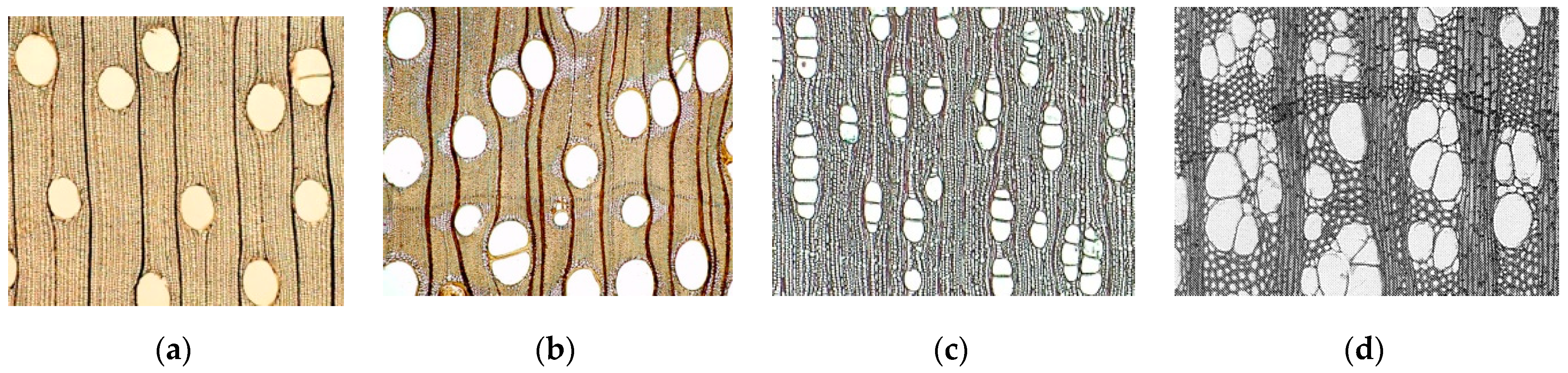
- Radial Orientation Class. Includes all vessels that are in contact with or close to their tangential walls (Figure 5a).
- -
- Tangential Orientation Class. It is defined by all cells that are in contact with or close to their radial walls (Figure 5b).
- -
- Diagonal Orientation Class. In the third group, there is mixed contact with both radial and tangential walls. If the vessels are arranged in a chain, the groups are defined as diagonal (Figure 5c).
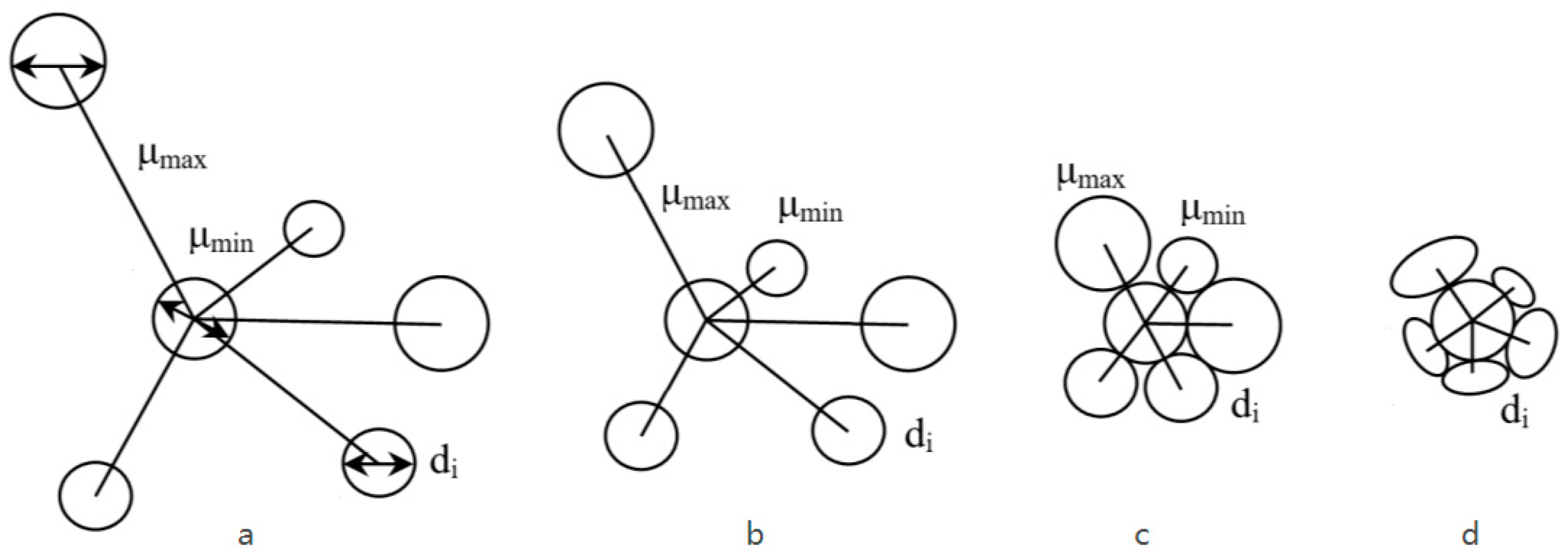
2.3. Quantitative Indicators Used in the Analysis of the Relative Position of the Vessels
- —the average diameter of the two measured vessels, in µm;
- µi—the distance between the centers of the two measured vessels, in µm;
- δ—density of vessels in the sample, number/mm2.
- S—the total area of the vessels in the tiny, microscopic samples, in µm2 (The most commonly used magnification is 25 to 32×).
2.4. Methodology of Experimental Research
- µmax—the maximum distance between the centers of the vessels, in µm;
- µmin—the minimum distance between the centers of the vessels, in µm;
- µmean—the intermediate distance between the centers of the vessels, in µm;
- n—the number of distances ranging from 2 to 3.
3. Results and Discussion
3.1. By Quantitative Indicators
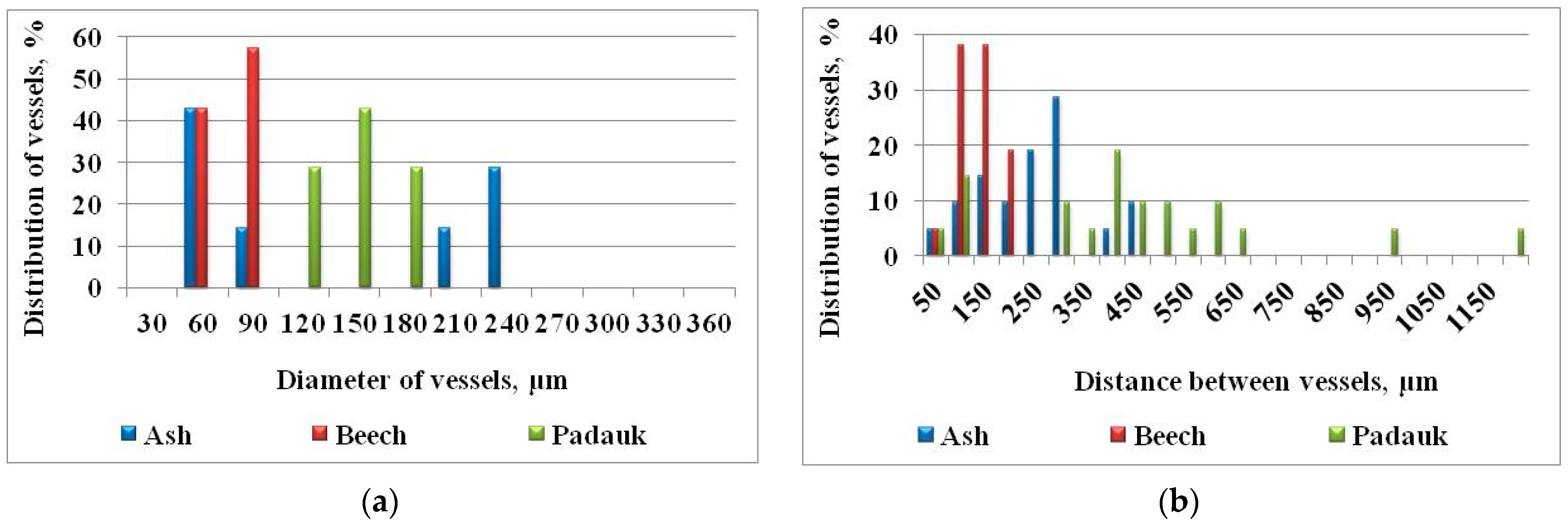
3.1.1. Diameter of Vessels
3.1.2. Distance between Vessels
3.1.3. Coefficient of Distribution A
3.1.4. Coefficient of Site B
3.1.5. Coefficient of Concentration C
3.1.6. Coefficient of Diffusion D
3.2. According to the Main Wood Structures
3.2.1. Ring-Porous Tree Species
3.2.2. Diffuse-Porous Tree Species
3.2.3. Tropical Tree Species
3.2.4. Wood with a Transitional Structure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Enchev, E.A. Wood Science, Textbook; Publishing House of Zemizdat: Sofia, Bulgaria, 1984; pp. 32–46. [Google Scholar]
- Wagenführ, R. Anatomie des Holzes; VEB Fachbuchverlag: Leipzig, Germany, 1984; pp. 78–173. [Google Scholar]
- Wagenführ, R. Holzatlas; Springer: Berlin, Germany, 1996; pp. 22–27. [Google Scholar]
- Bluskova, G.S. Wood Science, Textbook; University of Forestry Publishing House: Sofia, Bulgaria, 2009; pp. 99–121. [Google Scholar]
- Bardarov, N.S. A Guide to the Identification of Tree Species by the Anatomical Features of Wood; Publishing House at LTU: Sofia, Bulgaria, 2014; pp. 19–65. [Google Scholar]
- van der Graaff, N.A.; Baas, P. Wood anatomical variation in relation to latitude and altitude. Blumea 1974, 22, 101–121. [Google Scholar]
- Chen, F.F.; Evans, R. Automated measurement of vessel properties in birch and poplar wood. Holzforschung 2010, 64, 369–374. [Google Scholar] [CrossRef]
- Wheeler, E.A.; Baas, P.; Rodgers, S. Variations in Dicot Wood Anatomy: A Global Analysis Based on the Inside wood Database. IAWA J. 2007, 28, 229–258. [Google Scholar] [CrossRef]
- Burggraaf, P.D. Some observations on the course of the vessels in the wood of Fraxinus excelsior L. Acta Bot. Neerl. 1972, 21, 32–47. [Google Scholar] [CrossRef]
- Aloni, R.; Zimmermann, M.H. The control of vessel size and density along the plant axis. A new hypothesis. Differentiation 1983, 24, 203–208. [Google Scholar] [CrossRef]
- Greguss, P. Holzanatomie der Europäischen Laubiiölzer und Sträucher; Budapest Akademiai Kiado: Budapest, Hungary, 1959. [Google Scholar]
- Zimmermann, M.H.; Jeje, A.A. Vessel-length distribution in stems of some American woody plants. Can. J. Bot. 1981, 59, 1882–1892. [Google Scholar] [CrossRef]
- Baas, P. Terminology of imperforate tracheary elements -in defense of ubriform fibres with minutely bordered pits. IAWA Bull. 1986, 7, 82–86. [Google Scholar] [CrossRef]
- Carlquist, S. Non-random Vessel Distribution in Woods: Patterns, Modes, Diversity, Correlations. Aliso 2009, 27, 39–58. [Google Scholar] [CrossRef] [Green Version]
- Rosell, J.A.; Olson, M.E.; Aguirre-Hernandez, R.; Carlquist, S. Logistic regression in comparative wood anatomy: Tracheid types, wood anatomical terminology, and new inferences from the Carlquist and Hoekman southern Californian data set. Bot. J. Linn. Soc. 2007, 154, 331–351. [Google Scholar] [CrossRef] [Green Version]
- Ewers, F.W.; Ewers, J.M.; Jacobsen, A.L.; López-Portillo, J. Vessel redundancy: Modeling safety in numbers. IAWA J. 2007, 28, 373–388. [Google Scholar] [CrossRef] [Green Version]
- Hwang, S.W.; Sugiyama, J. Computer vision-based wood identification and its expansion and contribution potentials in wood science: A review. Plant Methods 2021, 17, 1–21. [Google Scholar] [CrossRef] [PubMed]
- da Silva, N.R.; De Ridder, M.; Baetens, J.M.; Van den Bulcke, J.; Rousseau, M.; Bruno, O.M.; Beeckman, H.; Van Acker, J.; De Baets, B. Automated classification of wood transverse cross section micro-imagery from 77 commercial central-african timber species. Ann. For. Sci. 2017, 74, 30. [Google Scholar] [CrossRef]
- Barmpoutis, P.; Dimitropoulos, K.; Barboutis, I.; Grammalidis, N.; Lefakis, P. Wood species recognition through multidimensional texture analysis. Comput. Electron. Agric. 2018, 144, 241–248. [Google Scholar] [CrossRef]
- Ibrahim, I.; Khairuddin, A.S.M.; Arof, H.; Yusof, R.; Hanafi, E. Statistical feature extraction method for wood species recognition system. Eur. J. Wood Wood Prod. 2018, 76, 345–356. [Google Scholar] [CrossRef]
- Sugiarto, B.; Prakasa, E.; Wardoyo, R.; Damayanti, R.; Krisdianto; Dewi, L.M.; Pardede, H.; Rianto, Y. Wood identification based on histogram of oriented gradient (hog) feature and support vector machine (svm) classifier. In Proceedings of the 2017 2nd International conferences on Information Technology, Information Systems and Electrical Engineering (ICITISEE), Yogyakarta, Indonesia, 1–2 November 2017; pp. 337–341. [Google Scholar]
- de Andrade, B.G.; Basso, V.M.; de Figueiredo Latorraca, J.V. Machine vision for field-level wood identification. IAWA J. 2020, 41, 681–698. [Google Scholar] [CrossRef]
- Liu, S. Realtime classification of rubber wood boards using an ssr-based cnn. IEEE Trans. Instrum. Meas. 2020, 69, 8725–8734. [Google Scholar] [CrossRef]
- Sun, Y.; Lin, Q.; He, X.; Zhao, Y.; Dai, F.; Qiu, J.; Cao, Y. Wood species recognition with small data: A deep learning approach. Int. J. Comput. Intell. Syst. 2021, 14, 1451–1460. [Google Scholar] [CrossRef]
- Christoff, N.; Bardarov, N.; Manolova, A.; Tonchev, K. Feature Extraction and Automatic Detection of Wooden Vessels from Raster Images. In Proceedings of the 2020 XXIX International Scientific Conference Electronics (ET), Sozopol, Bulgaria, 16–18 September 2020; pp. 1–4. [Google Scholar]
- Richter, H.G.; Dallwitz, M.J. 2000 Onwards. Commercial Timbers: Descriptions, Illustrations, Identification, and Information Retrieval. In English, French, German, Portuguese, and Spanish. Available online: https://www.delta-intkey.com/wood/en/index.htm (accessed on 4 July 2021).



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bardarov, N.; Todorov, V.; Christoff, N. Geometric and Topological Bases of a New Classification of Wood Vascular Tissues Part 1: Shape and Arrangement Classifications of Vessels. Sustainability 2021, 13, 7545. https://doi.org/10.3390/su13147545
Bardarov N, Todorov V, Christoff N. Geometric and Topological Bases of a New Classification of Wood Vascular Tissues Part 1: Shape and Arrangement Classifications of Vessels. Sustainability. 2021; 13(14):7545. https://doi.org/10.3390/su13147545
Chicago/Turabian StyleBardarov, Nikolai, Vladislav Todorov, and Nicole Christoff. 2021. "Geometric and Topological Bases of a New Classification of Wood Vascular Tissues Part 1: Shape and Arrangement Classifications of Vessels" Sustainability 13, no. 14: 7545. https://doi.org/10.3390/su13147545
APA StyleBardarov, N., Todorov, V., & Christoff, N. (2021). Geometric and Topological Bases of a New Classification of Wood Vascular Tissues Part 1: Shape and Arrangement Classifications of Vessels. Sustainability, 13(14), 7545. https://doi.org/10.3390/su13147545






