A Critical Review on Mathematical Descriptions to Study Flux Processes and Environmental-Related Interactions of Mangroves
Abstract
:1. Introduction
2. Methodology
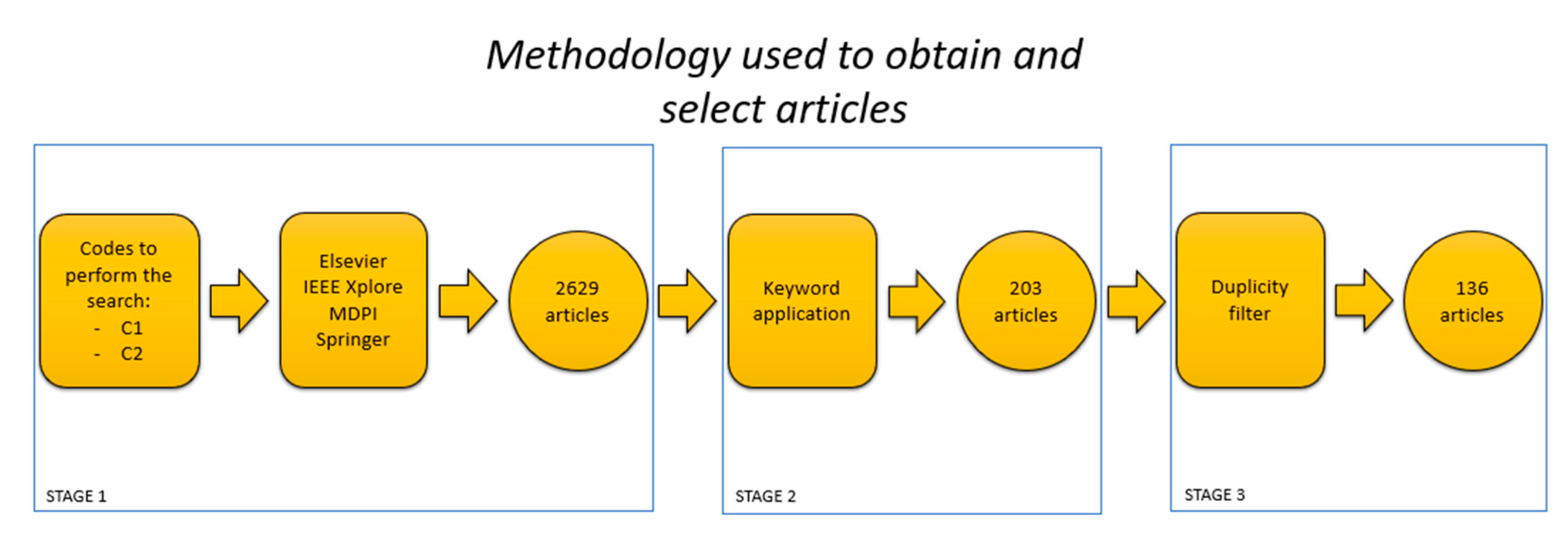
2.1. Literature Search Strategy
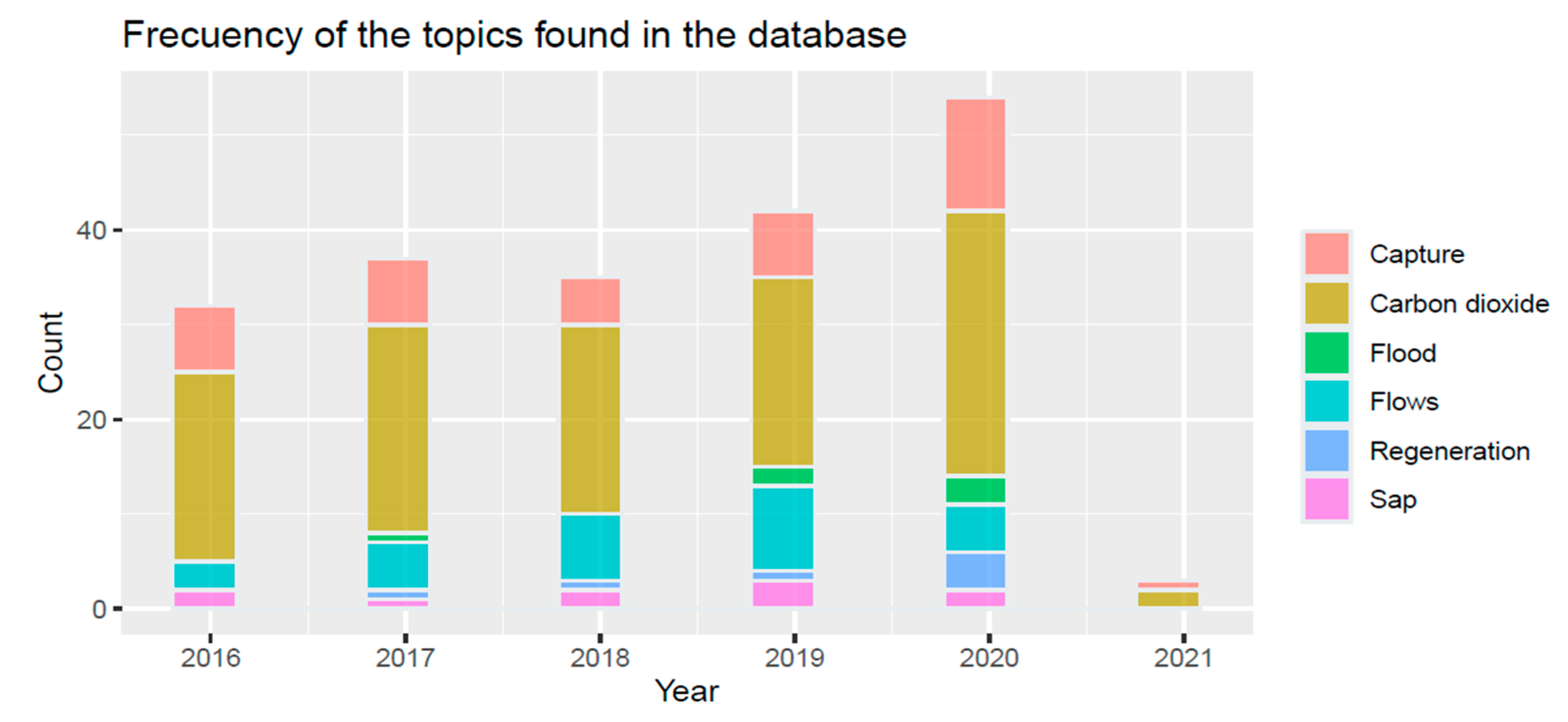
2.2. Bibliometric Analysis
3. Results: Relevance of Mangroves Modeling to Reap Their Benefits
3.1. Depollution
3.2. Biomass Content
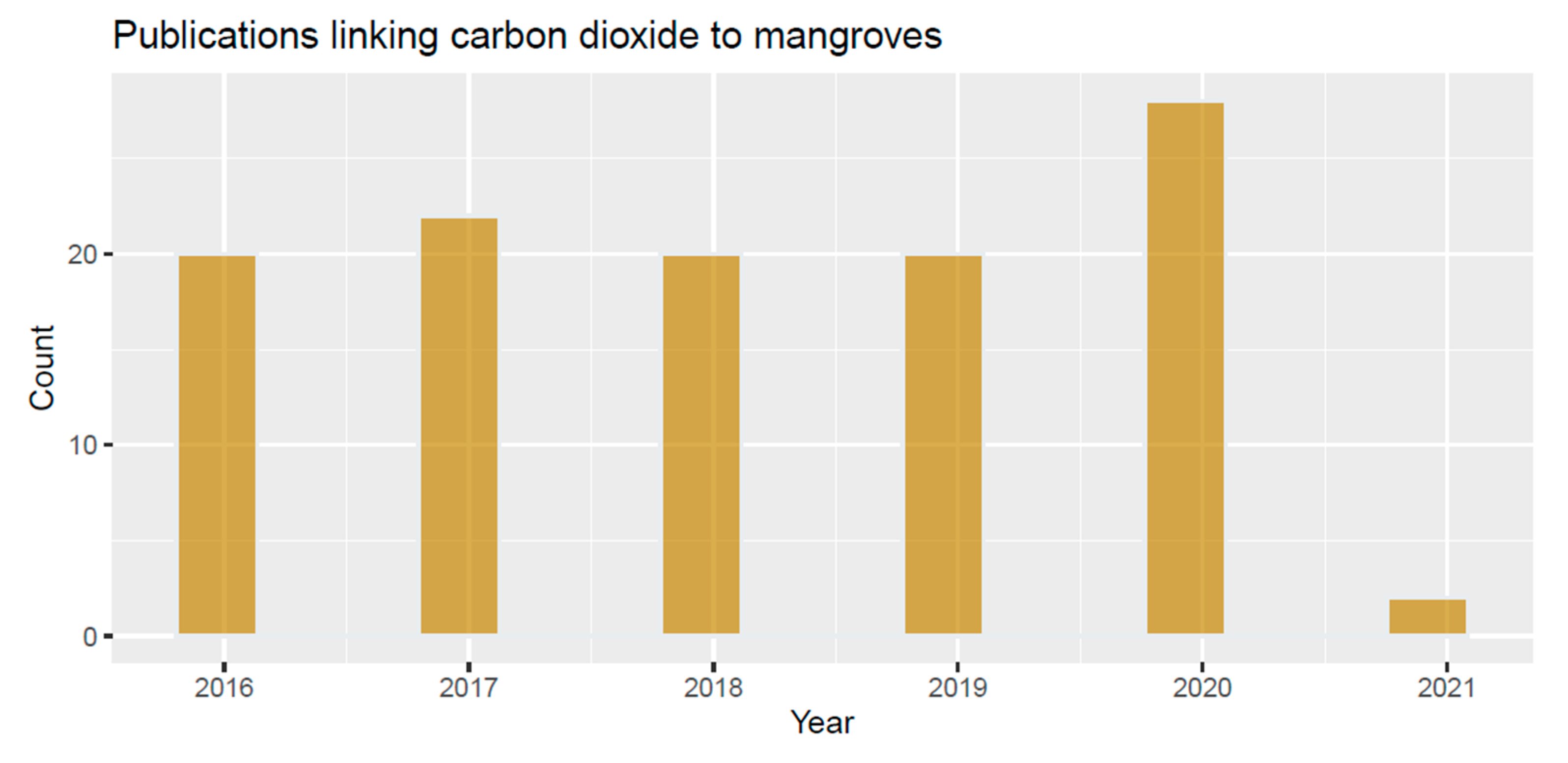
3.3. Carbon Sequestration
3.4. Rate of Growth
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Parameter | Definition | Units | Source |
|---|---|---|---|
| AGB | aboveground biomass | kg | - |
| AG | annual mangrove growth | - | [6] |
| A, B | constant | - | [58] |
| Ab | forest area | ha | - |
| Ad | accretion rate obtained by the radiometric system | cm · y −1 | - |
| Aba, Am, At | base, middle, and top areas | m2 | - |
| b | trophic magnification slope | - | [50] |
| BD | average bulk density | g-soil · cm −3 | - |
| BAF | bioaccumulation factor | - | [50] |
| BGB | below ground biomass | kg | - |
| b2 | growth constants of the species | - | [6] |
| b3 | growth constants of the species | - | [6] |
| Bi | initial biomass in the area | ton | - |
| Bdb | dry branch biomass | kg | - |
| bwj | average weight of the branches | kg | - |
| CD | crown diameter | m | - |
| Cconc | average concentration of carbon in the soil | g-C · g-soil −1 | - |
| Cf | fixed carbon | ton | - |
| Cseq | carbon sequestration | g-C · cm −2 · y −1 | - |
| DBH | diameter at breast height | cm | - |
| D0 | diameter just above the soil surface | cm | - |
| DMax | maximum diameter of the species | cm | - |
| E | bioclimatic variables | - | [52] |
| EF | enrichment factor | - | [50] |
| G | annual growth rate | - | [17] |
| Gy | growth constants of the species | - | [6] |
| h | stem height | m | - |
| H | stem height | cm | - |
| Hf | hafnium | - | [50] |
| HMax | maximum height of the species | cm | - |
| K | carbon in biomass (45%) | - | - |
| Ldb | dry leaf biomass | kg | - |
| Lwj | average dry weight of extracted leaves | kg | - |
| n | effect of nutrients | - | [6] |
| nj | number of branches in each tree | - | - |
| Nj | number of trees | - | - |
| rel | effects of light intensity | - | [6] |
| S | effect of salinity | - | [6] |
| t | time | y | - |
| TF | translocation factor | - | [50] |
| te | temperature effects | - | [6] |
| V | volume of stem biomass | m3 | - |
| δ13C | stable carbon isotope | - | [50] |
| ρe | tree species density | g · cm−3 | - |
References
- Altieri, M. Cambio climático y agricultura campesina: Impactos y respuestas adaptativas. LEISA Rev. Agroecol. 2009, 14, 5–8. [Google Scholar]
- Castro, M. Derretimiento de Los Polos: Evolución, Causas, Consecuencias, Soluciones-Lifeder. Available online: https://www.lifeder.com/derretimiento-de-los-polos/ (accessed on 17 July 2020).
- Food and Agriculture Organization of the United Nations. Carbono Organico del Suelo: El Potencial Oculto; Food & Agriculture Org: Rome, Italy, 2017; ISBN 978-92-5-309681-7. [Google Scholar]
- FAO. The World’s Mangroves 1980–2005; FAO: Rome, Italy, 2007; ISBN 978-92-5-105856-5. [Google Scholar]
- Dat Pham, T.; Xia, J.; Thang Ha, N.; Tien Bui, D.; Nhu Le, N.; Tekeuchi, W. A Review of Remote Sensing Approaches for Monitoring Blue Carbon Ecosystems: Mangroves, Sea Grasses and Salt Marshes during 2010–2018. Sensors 2019, 19, 1933. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodríguez-Rodríguez, J.A.; Mancera-Pineda, J.E.; Rodríguez-P., J.M. Validación y Aplicación de Un Modelo de Restauración de Manglar Basado En Individuos Para Tres Especies En La Ciénaga Grande de Santa Marta. Caldasia 2016, 38, 285–299. [Google Scholar] [CrossRef]
- Das, S.; Crépin, A.-S. Mangroves Can Provide Protection against Wind Damage during Storms. Estuar. Coast. Shelf Sci. 2013, 134, 98–107. [Google Scholar] [CrossRef]
- Mosquera, L.P.; Riaño-Herrera, N.M.; Arcila-Pulgarín, J.; Ponce-Dávila, C.A.; Fotosíntesis, Respiración y Fotorrespiración. 7. Available online: https://www.cenicafe.org/es/publications/arc050%2803%29215-221.pdf (accessed on 14 May 2020).
- Solarte, M.E.; Moreno, L.; Melgarejo, L.M., VI; Fotosíntesis y Pigmentos Vegetales. 16. Available online: https://www.researchgate.net/publication/295010397_Fotosintesis_y_pigmentos_vegetales (accessed on 14 May 2020).
- Fetcher, N.; Oberbauer, S.F.; Rojas, G.; Strain, B.R. Efectos Del Régimen de Luz Sobre La Fotosíntesis y El Crecimiento En Plántulas de Árboles de Un Bosque Lluvioso Tropical de Costa Rica. Rev. Biol. Trop. 1987, 35, 97–110. [Google Scholar]
- Colombo, R.; Marín, O. Relaciones hídricas, Fotosíntesis, y anatomía foliar de dos especies del género Calotropis. Interciencia 2007, 32, 7. [Google Scholar]
- Mazda, Y.; Wolanski, E. Hydrodynamics and Modeling of Water Flow in Mangrove Areas, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2009; ISBN 978-0-444-53103-2. [Google Scholar]
- Ishida, A.; Yamamura, Y.; Hori, Y. Roles of Leaf Water Potential and Soil-to-Leaf Hydraulic Conductance in Water Use by Understorey Woody Plants. Ecol. Res. 1992, 7, 213–223. [Google Scholar] [CrossRef]
- Carrasco, O. Transporte de Agua En Plantas. El Balance Hídrico En Tallos de Árboles Nativos Del Norte de Argentina: Uso e Importancia de Los Reservorios Internos de Agua. Ph.D. Thesis, Universidad de Buenos Aires, Buenos Aires, Argentina, 2018. [Google Scholar]
- Edwards, W.R.N.; Jarvis, P.G.; Landsberg, J.J.; Talbot, H. A Dynamic Model for Studying Flow of Water in Single Trees. Tree Physiol. 1986, 1, 309–324. [Google Scholar] [CrossRef]
- Sobrado, M.A. Relation of Water Transport to Leaf Gas Exchange Properties in Three Mangrove Species. Trees 2000, 14, 0258–0262. [Google Scholar] [CrossRef]
- Torres, Y.L. Los Sumideros De Carbono: Un Anàlisis De La Potencialidad Económica En Un Bosque De Manglar Del Pacìfico Colombiano. Ing. Recur. Nat. Ambiente 2007, 6, 82–92. [Google Scholar]
- Ali, S.A.; Khatun, R.; Ahmad, A.; Ahmad, S.N. Application of GIS-Based Analytic Hierarchy Process and Frequency Ratio Model to Flood Vulnerable Mapping and Risk Area Estimation at Sundarban Region, India. Model. Earth Syst. Environ. 2019, 5, 1083–1102. [Google Scholar] [CrossRef]
- Zhang, K.; Gann, D.; Ross, M.; Biswas, H.; Li, Y.; Rhome, J. Comparison of TanDEM-X DEM with LiDAR Data for Accuracy Assessment in a Coastal Urban Area. Remote Sens. 2019, 11, 876. [Google Scholar] [CrossRef] [Green Version]
- Deb Burman, P.K.; Sarma, D.; Williams, M.; Karipot, A.; Chakraborty, S. Estimating Gross Primary Productivity of a Tropical Forest Ecosystem over North-East India Using LAI and Meteorological Variables. J Earth Syst Sci 2017, 126, 99. [Google Scholar] [CrossRef] [Green Version]
- Fatoyinbo, T.; Feliciano, E.A.; Lagomasino, D.; Lee, S.K.; Trettin, C. Estimating Mangrove Aboveground Biomass from Airborne LiDAR Data: A Case Study from the Zambezi River Delta. Environ. Res. Lett. 2018, 13, 025012. [Google Scholar] [CrossRef] [Green Version]
- Wong, C.J.; James, D.; Besar, N.A.; Kamlun, K.U.; Tangah, J.; Tsuyuki, S.; Phua, M.-H. Estimating Mangrove Above-Ground Biomass Loss Due to Deforestation in Malaysian Northern Borneo between 2000 and 2015 Using SRTM and Landsat Images. Forests 2020, 11, 1018. [Google Scholar] [CrossRef]
- Gress, S.K.; Huxham, M.; Kairo, J.G.; Mugi, L.M.; Briers, R.A. Evaluating, Predicting and Mapping Belowground Carbon Stores in Kenyan Mangroves. Glob. Chang. Biol. 2017, 23, 224–234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adegboyega, S.A.; Oloukoi, J.; Olajuyigbe, A.E.; Ajibade, O.E. Evaluation of Unsustainable Land Use/Land Cover Change on Ecosystem Services in Coastal Area of Lagos State, Nigeria. Appl. Geomat. 2019, 11, 97–110. [Google Scholar] [CrossRef]
- Nurda, N.; Noguchi, R.; Ahamed, T. Forest Productivity and Carbon Stock Analysis from Vegetation Phenological Indices Using Satellite Remote Sensing in Indonesia. Asia-Pac. J. Reg. Sci. 2020, 4, 657–690. [Google Scholar] [CrossRef]
- Etemadi, H.; Smoak, J.M.; Karami, J. Land Use Change Assessment in Coastal Mangrove Forests of Iran Utilizing Satellite Imagery and CA–Markov Algorithms to Monitor and Predict Future Change. Environ. Earth Sci. 2018, 77, 208. [Google Scholar] [CrossRef]
- Wicaksono, P. Mangrove Above-Ground Carbon Stock Mapping of Multi-Resolution Passive Remote-Sensing Systems. Int. J. Remote Sens. 2017, 38, 1551–1578. [Google Scholar] [CrossRef]
- Wicaksono, P.; Danoedoro, P.; Hartono, H.; Nehren, U. Mangrove Biomass Carbon Stock Mapping of the Karimunjawa Islands Using Multispectral Remote Sensing. Int. J. Remote Sens. 2016, 37, 26–52. [Google Scholar] [CrossRef]
- Slamet, N.S.; Dargusch, P.; Aziz, A.A.; Wadley, D. Mangrove Vulnerability and Potential Carbon Stock Loss from Land Reclamation in Jakarta Bay, Indonesia. Ocean Coast. Manag. 2020, 195, 105283. [Google Scholar] [CrossRef]
- Soper, F.M.; MacKenzie, R.A.; Sharma, S.; Cole, T.G.; Litton, C.M.; Sparks, J.P. Non-Native Mangroves Support Carbon Storage, Sediment Carbon Burial, and Accretion of Coastal Ecosystems. Glob. Chang. Biol. 2019, 25, 4315–4326. [Google Scholar] [CrossRef]
- Wang, M.; Cao, W.; Guan, Q.; Wu, G.; Jiang, C.; Yan, Y.; Su, X. Potential of Texture Metrics Derived from High-Resolution PLEIADES Satellite Data for Quantifying Aboveground Carbon of Kandelia Candel Mangrove Forests in Southeast China. Wetl. Ecol. Manag. 2018, 26, 789–803. [Google Scholar] [CrossRef]
- Cao, B.; Domke, G.M.; Russell, M.B.; Walters, B.F. Spatial Modeling of Litter and Soil Carbon Stocks on Forest Land in the Conterminous United States. Sci. Total Environ. 2019, 654, 94–106. [Google Scholar] [CrossRef] [PubMed]
- Elmahdy, S.I.; Ali, T.A.; Mohamed, M.M.; Howari, F.M.; Abouleish, M.; Simonet, D. Spatiotemporal Mapping and Monitoring of Mangrove Forests Changes From 1990 to 2019 in the Northern Emirates, UAE Using Random Forest, Kernel Logistic Regression and Naive Bayes Tree Models. Front. Environ. Sci. 2020, 8, 1–23. [Google Scholar] [CrossRef]
- Sidik, F.; Fernanda Adame, M.; Lovelock, C.E. Carbon Sequestration and Fluxes of Restored Mangroves in Abandoned Aquaculture Ponds. J. Indian Ocean Reg. 2019, 15, 177–192. [Google Scholar] [CrossRef]
- Mohanta, M.R.; Mohanta, A.; Mohapatra, U.; Mohanty, R.C.; Sahu, S.C. Carbon Stock Assessment and Its Relation with Tree Biodiversity in Tropical Moist Deciduous Forest of Similipal Biosphere Reserve, Odisha, India. Trop. Ecol. 2020, 61, 497–508. [Google Scholar] [CrossRef]
- Simpson, L.T.; Osborne, T.Z.; Duckett, L.J.; Feller, I.C. Carbon Storages along a Climate Induced Coastal Wetland Gradient. Wetlands 2017, 37, 1023–1035. [Google Scholar] [CrossRef]
- Ravelo, F.N.; Pérez, M.U.; Quiroz, D.; Vásquez, B.; Belmonte, D. CO\textlessinf\textgreater2\textless/Inf\textgreater Flow in Soils Dominated by Mangroves Avicennia Germinans and Conocarpus Erectus [Flujo de CO\textlessinf\textgreater2\textless/Inf\textgreater En Suelos Dominados Por Manglares Avicennia Germinans y Conocarpus Erectus]. Rev. Geogr. Venez. 2019, 60, 284–299. [Google Scholar]
- Wang, G.; Guan, D.; Xiao, L.; Peart, M.R. Ecosystem Carbon Storage Affected by Intertidal Locations and Climatic Factors in Three Estuarine Mangrove Forests of South China. Reg. Environ. Chang. 2019, 19, 1701–1712. [Google Scholar] [CrossRef]
- Rovai, A.S.; Coelho, C., Jr.; de Almeida, R.; Cunha-Lignon, M.; Menghini, R.P.; Twilley, R.R.; Cintrón-Molero, G.; Schaeffer-Novelli, Y. Ecosystem-Level Carbon Stocks and Sequestration Rates in Mangroves in the Cananéia-Iguape Lagoon Estuarine System, Southeastern Brazil. For. Ecol. Manag. 2021, 479, 118553. [Google Scholar] [CrossRef]
- Shaltout, K.H.; Ahmed, M.T.; Alrumman, S.A.; Ahmed, D.A.; Eid, E.M. Evaluation of the Carbon Sequestration Capacity of Arid Mangroves along Nutrient Availability and Salinity Gradients along the Red Sea Coastline of Saudi Arabia. Oceanologia 2020, 62, 56–69. [Google Scholar] [CrossRef]
- Sheehan, L.; Sherwood, E.T.; Moyer, R.P.; Radabaugh, K.R.; Simpson, S. Blue Carbon: An Additional Driver for Restoring and Preserving Ecological Services of Coastal Wetlands in Tampa Bay (Florida, USA). Wetlands 2019, 39, 1317–1328. [Google Scholar] [CrossRef]
- Herrera Silveira, J.A.; Rico, A.C.; Pech, E.; Pech, M.; Ramírez, J.R.; Hernández, C.T. Carbon Dynamics (Stocks and Fluxes) in Mangroves of Mexico [Dinámica Del Carbono (Almacenes y Flujos) En Manglares de México]. Terra Latinoam. 2016, 34, 61–72. [Google Scholar]
- Thorhaug, A.; Gallagher, J.B.; Kiswara, W.; Prathep, A.; Huang, X.; Yap, T.-K.; Dorward, S.; Berlyn, G. Coastal and Estuarine Blue Carbon Stocks in the Greater Southeast Asia Region: Seagrasses and Mangroves per Nation and Sum of Total. Mar. Pollut. Bull. 2020, 160, 111168. [Google Scholar] [CrossRef]
- Bhomia, R.K.; Kauffman, J.B.; McFadden, T.N. Ecosystem Carbon Stocks of Mangrove Forests along the Pacific and Caribbean Coasts of Honduras. Wetl. Ecol. Manag. 2016, 24, 187–201. [Google Scholar] [CrossRef]
- Wang, Q.; Zeng, J.; Leng, S.; Fan, B.; Tang, J.; Jiang, C.; Huang, Y.; Zhang, Q.; Qu, Y.; Wang, W.; et al. The Effects of Air Temperature and Precipitation on the Net Primary Productivity in China during the Early 21st Century. Front. Earth Sci. 2018, 12, 818–833. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, S.; Guo, X.; Peng, C.; Gu, X.; Deng, C.; Chen, L. Anatomical Explanations for Acute Depressions in Radial Pattern of Axial Sap Flow in Two Diffuse-Porous Mangrove Species: Implications for Water Use. Tree Physiol. 2018, 38, 277–287. [Google Scholar] [CrossRef]
- Gnanamoorthy, P.; Selvam, V.; Ramasubramanian, R.; Nagarajan, R.; Chakraborty, S.; Deb Burman, P.K.; Karipot, A. Diurnal and Seasonal Patterns of Soil CO\textlessinf\textgreater2\textless/Inf\textgreater Efflux from the Pichavaram Mangroves, India. Environ. Monit. Assess. 2019, 191, 258. [Google Scholar] [CrossRef] [PubMed]
- Thorhaug, A.L.; Poulos, H.M.; López-Portillo, J.; Barr, J.; Lara-Domínguez, A.L.; Ku, T.C.; Berlyn, G.P. Gulf of Mexico Estuarine Blue Carbon Stock, Extent and Flux: Mangroves, Marshes, and Seagrasses: A North American Hotspot. Sci. Total Environ. 2019, 653, 1253–1261. [Google Scholar] [CrossRef] [PubMed]
- Couvreur, V.; Ledder, G.; Manzoni, S.; Way, D.A.; Muller, E.B.; Russo, S.E. Water Transport through Tall Trees: A Vertically Explicit, Analytical Model of Xylem Hydraulic Conductance in Stems. Plant Cell Environ. 2018, 41, 1821–1839. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ray, R.; Dutta, B.; Mandal, S.K.; González, A.G.; Pokrovsky, O.S.; Jana, T.K. Bioaccumulation of Vanadium (V), Niobium (Nb) and Tantalum (Ta) in Diverse Mangroves of the Indian Sundarbans. Plant Soil 2020, 448, 553–564. [Google Scholar] [CrossRef]
- Pittarello, M.; Busato, J.G.; Carletti, P.; Sodré, F.F.; Dobbss, L.B. Dissolved Humic Substances Supplied as Potential Enhancers of Cu, Cd, and Pb Adsorption by Two Different Mangrove Sediments. J. Soils Sedim. 2019, 19, 1554–1565. [Google Scholar] [CrossRef] [Green Version]
- Mohd Zaki, N.A.; Abd Latif, Z.; Suratman, M.N.; Zainal, M.Z. Aboveground Biomass and Carbon Stocks Modelling Using Non-Linear Regression Model. In IOP Conference Series: Earth and Environmental Science; IOP: London, UK, 2016; Volume 37. [Google Scholar]
- da Motta Portillo, J.T.; Londe, V.; Moreira, F.W.A. Aboveground Biomass and Carbon Stock Are Related with Soil Humidity in a Mangrove at the Piraquê-Açu River, Southeastern Brazil. J. Coast. Conserv. 2017, 21, 139–144. [Google Scholar] [CrossRef]
- Vinh, T.V.; Marchand, C.; Linh, T.V.K.; Vinh, D.D.; Allenbach, M. Allometric Models to Estimate Above-Ground Biomass and Carbon Stocks in Rhizophora Apiculata Tropical Managed Mangrove Forests (Southern Viet Nam). For. Ecol. Manag. 2019, 434, 131–141. [Google Scholar] [CrossRef]
- Simpson, L.T.; Stein, C.M.; Osborne, T.Z.; Feller, I.C. Mangroves Dramatically Increase Carbon Storage after 3 Years of Encroachment. Hydrobiologia 2019, 834, 13–26. [Google Scholar] [CrossRef]
- Chatting, M.; LeVay, L.; Walton, M.; Skov, M.W.; Kennedy, H.; Wilson, S.; Al-Maslamani, I. Mangrove Carbon Stocks and Biomass Partitioning in an Extreme Environment. Estuar. Coastal Shelf Sci. 2020, 244, 106940. [Google Scholar] [CrossRef]
- Kelleway, J.J.; Saintilan, N.; Macreadie, P.I.; Skilbeck, C.G.; Zawadzki, A.; Ralph, P.J. Seventy Years of Continuous Encroachment Substantially Increases “blue Carbon” Capacity as Mangroves Replace Intertidal Salt Marshes. Glob. Chang. Biol. 2016, 22, 1097–1109. [Google Scholar] [CrossRef]
- Clough, B.F.; Dixon, P.; Dalhaus, O. Allometric Relationships for Estimating Biomass in Multi-Stemmed Mangrove Trees. Aust. J. Bot. 1997, 45, 1023. [Google Scholar] [CrossRef]
- Prasanna, J.; Anand, M.; Vijayasekaran, D.; Kumaraguru, A.K. Allometric Model for Estimating above Ground Biomass and Carbon Storage in Karankadu Mangrove Swamp, Palk Bay, Southeast Coast of India. Indian J. Geo-Mar. Sci. 2017, 46, 1682–1692. [Google Scholar]
- Makinde, E.O.; Womiloju, A.A.; Ogundeko, M.O. The Geospatial Modelling of Carbon Sequestration in Oluwa Forest, Ondo State, Nigeria. Eur. J. Remote Sens. 2017, 50, 397–413. [Google Scholar] [CrossRef]
- Kusmana, C.; Hidayat, T.; Tiryana, T.; Rusdiana, O. Istomo Allometric Models for Above- and below-Ground Biomass of Sonneratia Spp. Glob. Ecol. Conserv. 2018, 15, 15. [Google Scholar] [CrossRef]
- Marchio, D.A.; Savarese, M.; Bovard, B.; Mitsch, W.J. Carbon Sequestration and Sedimentation in Mangrove Swamps Influenced by Hydrogeomorphic Conditions and Urbanization in Southwest Florida. Forests 2016, 7, 116. [Google Scholar] [CrossRef] [Green Version]
- Morgado, E.; Günther, B. On the Hidden Physical Dimensions of the Allometric Equation. Arch. Biol. Med. Exp. 1990, 23, 29–39. [Google Scholar]
| Topics | Reference |
|---|---|
| Carbon stored by remote sensing/satellite images | [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33] |
| Monitoring of stored carbon | [5,34,35,36,37,38,39,40] |
| Carbon quantification through literature | [41,42,43,44,45] |
| Mangrove flows | [46,47,48,49] |
| Filtration of heavy metals and pollutants | [50,51] |
| Author | Equation | Species | T (°C) | Mean Annual Rainfall (mm y−1) | |
|---|---|---|---|---|---|
| Mohd zaki et al. [52] | (5) | L.t.t.s. | 22.9–27.7 | 2178 | |
| Da Motta et al. [53] | (6) | L.r.—R.m. A.s. | - | 1320 | |
| Van Vinh et al. [54] | (7) | R.a. | 27 | 1800 | |
| Simpson et al. [55] | (8) | L.r.–A.g. R.m. | 21–29 | - | |
| Chatting et al. [56] | (9) | A.m. | - | 54 | |
| Kelleway et al. [57] | (10) | A.m. | - | 1084 | |
| Clough et al. [58] | (11) | R.s.–A.m. | 35 | 1750 | |
| Prasanna et al. [59] | (12) | A.m. | 28–34.2 | - | |
| (13) | |||||
| (14) | |||||
| Makinde et al. [60] | (15) | T.g.–G.a. I.e. | - | 1850 |
| Reference | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | [52] | [53] | [54] | [55] | [56] | [57] | [58] | [59] | [60] |
| DBH | |||||||||
| D0 | |||||||||
| E | |||||||||
| ρe | |||||||||
| H | |||||||||
| CD | |||||||||
| V | |||||||||
| h | |||||||||
| Author | Equation | Species | T (°C) | Mean Annual Rainfall (mm y−1) | Objective | |
|---|---|---|---|---|---|---|
| Lozano [17] | (16) | R.s.–A.m. | 26 | - | Carbon sequestration | |
| Marchio et al. [62] | (17) | A.g.–L.r. R.m. | 23.6 | 1346 | ||
| Chatting et al. [56] | (18) | A.m. | - | 54 | below ground biomass | |
| Makinde et al. [60] | (19) | T.g.–G.a. I.e. | - | 1850 | ||
| Rodriguez et al. [6] | (20) | R.m.–A.g. L.r. | 26.6 | 2300 | Annual mangrove growth |
| Equation | Parameters | Fundamental Dimensions | Result Using Rayleigh’s Method |
|---|---|---|---|
| (5) | |||
| (6) | |||
| (12) | |||
| (13) | |||
| (14) | |||
| (16) | |||
| (17) | |||
| (19) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brooks, J.; Chen Austin, M.; Mora, D.; Tejedor-Flores, N. A Critical Review on Mathematical Descriptions to Study Flux Processes and Environmental-Related Interactions of Mangroves. Sustainability 2021, 13, 6970. https://doi.org/10.3390/su13126970
Brooks J, Chen Austin M, Mora D, Tejedor-Flores N. A Critical Review on Mathematical Descriptions to Study Flux Processes and Environmental-Related Interactions of Mangroves. Sustainability. 2021; 13(12):6970. https://doi.org/10.3390/su13126970
Chicago/Turabian StyleBrooks, Jefferson, Miguel Chen Austin, Dafni Mora, and Nathalia Tejedor-Flores. 2021. "A Critical Review on Mathematical Descriptions to Study Flux Processes and Environmental-Related Interactions of Mangroves" Sustainability 13, no. 12: 6970. https://doi.org/10.3390/su13126970
APA StyleBrooks, J., Chen Austin, M., Mora, D., & Tejedor-Flores, N. (2021). A Critical Review on Mathematical Descriptions to Study Flux Processes and Environmental-Related Interactions of Mangroves. Sustainability, 13(12), 6970. https://doi.org/10.3390/su13126970









