Water-Quality Data Imputation with a High Percentage of Missing Values: A Machine Learning Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodology Description
- Pre-processing data: The dataset was pre-processed before any analysis to deal with the different units, orders of magnitude, not unified variable names and different sampling frequencies.
- Data profiling: The dataset was analyzed with the aim of studying the distribution of the variables, their missing data and data quality (the dataset is described in Section 2.2, and the results of this step are reported in Section 3.1).
- Variable correlations: Correlations among variables were considered to help the multivariate imputation techniques (Section 2.5).
- Imputation: The selected imputation models were assessed, and their loss functions were computed (the imputation techniques and the imputation performance evaluation are described in Section 2.3 and Section 2.4, respectively).
- Best model selection: For each variable at each monitoring site, the model with the highest performance was selected as “the best model” (Section 3.2).
2.2. Dataset Description
2.3. Imputation Techniques
2.4. Imputation Performance Evaluation
2.5. Helper Variables for the Imputation Process
3. Results and Discussion
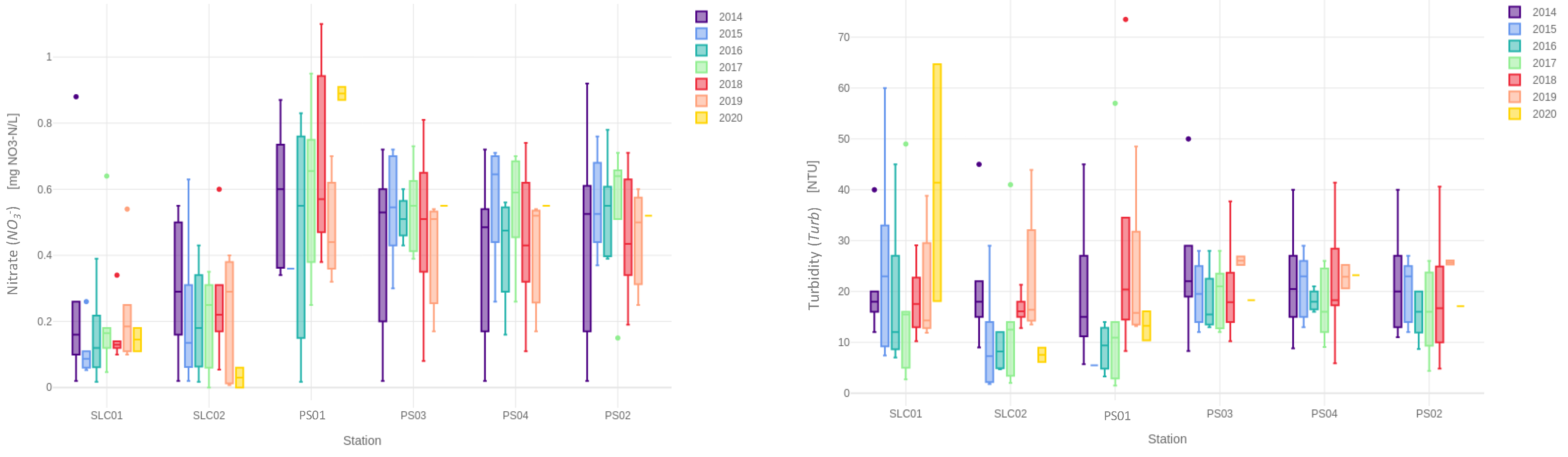
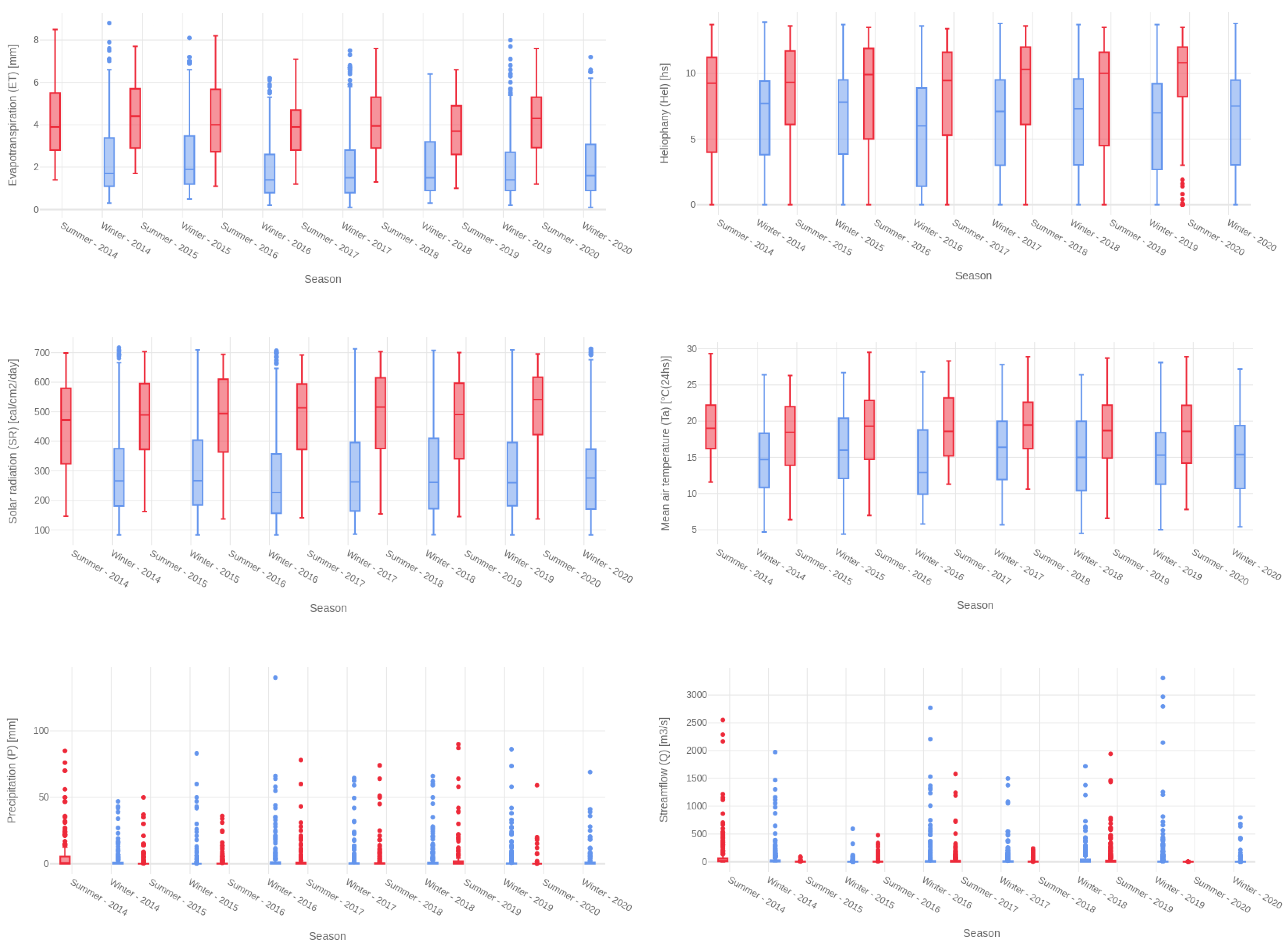
3.1. Dataset Profiling
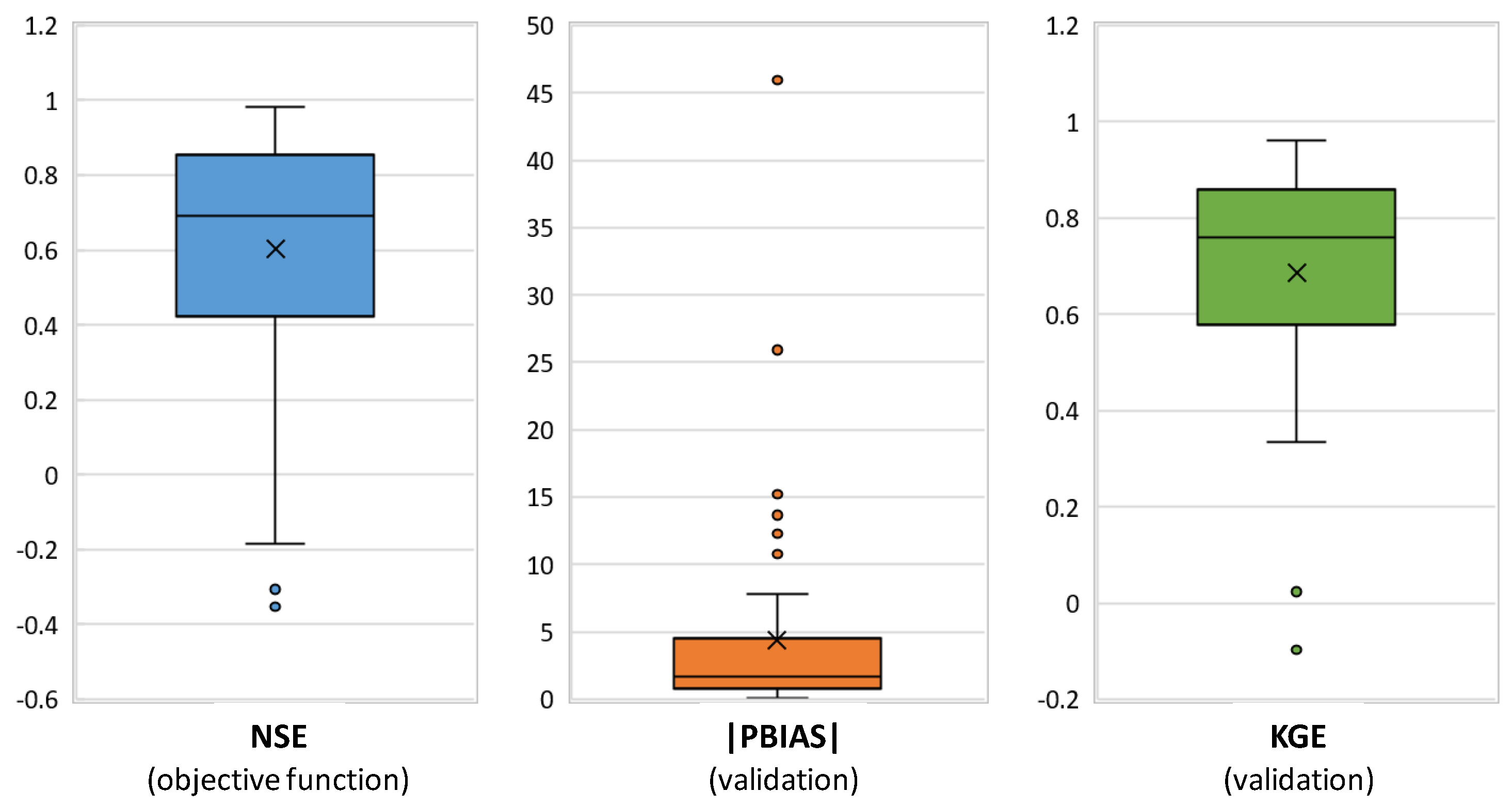
3.2. Imputation Results
3.3. Further Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Whitehead, P.; Dolk, M.; Peters, R.; Leckie, H. Water Quality Modelling, Monitoring, and Management. In Water Science, Policy, and Management; Dadson, S.J., Garrick, D.E., Penning-Rowsell, E.C., Hall, J.W., Hope, R., Hughes, J., Eds.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2019. [Google Scholar]
- Gorgoglione, A.; Castro, A.; Chreties, C.; Etcheverry, L. Overcoming Data Scarcity in Earth Science. Data 2020, 5, 5. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.V.; Aly, A.; Pathak, C.S.; Ahlquist, J.; Fuelberg, H.; Hood, J. Infilling missing precipitation records using variants of spatial interpolation and data-driven methods: Use of optimal weighting parameters and nearest neighbour-based corrections. Int. J. Climatol. 2018, 38, 776–793. [Google Scholar] [CrossRef]
- Mital, U.; Dwivedi, D.; Brown, J.B.; Faybishenko, B.; Painter, S.L.; Steefel, C.I. Sequential imputation of missing spatio-temporal precipitation data using random forests. Front. Water 2020, 2, 20. [Google Scholar] [CrossRef]
- Aguilera, H.; Guardiola-Albert, C.; Serrano-Hidalgo, C. Estimating extremely large amounts of missing precipitation data. J. Hydroinformatics 2020, 22, 578–592. [Google Scholar] [CrossRef]
- Buhi, E. Out of sight, not out of mind: Strategies for handling missing data. Am. J. Health Behav. 2008, 32, 83–92. [Google Scholar] [CrossRef]
- Ratolojanahary, R.; Ngouna, R.H.; Medjaher, K.; Junca-Bourié, J.; Dauriac, F.; Sebilo, M. Model selection to improve multiple imputation for handling high rate missingness in a water quality dataset. Expert Syst. Appl. 2019, 131, 299–307. [Google Scholar] [CrossRef]
- Lo Presti, R.; Barca, E.; Passarella, G. A methodology for treating missing data applied to daily rainfall data in the Candelaro River Basin (Italy). Environ. Monit. Assess. 2010, 160, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.W.; Liu, C.W. Estimation of the spatial rainfall distribution using inverse distance weighting (IDW) in the middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
- Barrios, A.; Trincado, G.; Garreaud, R. Alternative approaches for estimating missing climate data: Application to monthly precipitation records in South-Central Chile. For. Ecosyst. 2018, 5, 28. [Google Scholar] [CrossRef]
- Gong, G.; Mattevada, S.; O’Bryant, S.E. Comparison of the accuracy of kriging and IDW interpolations in estimating groundwater arsenic concentrations in Texas. Environ. Res. 2014, 130, 59–69. [Google Scholar] [CrossRef] [PubMed]
- Aissia, M.-A.B.; Chebana, F.; Ouarda, T. Multivariate missing data in hydrology–Review and applications. Adv. Water Resour. 2017, 110, 299–309. [Google Scholar] [CrossRef]
- Chivers, B.D.; Wallbank, J.; Cole, S.C.; Sebek, O.; Stanley, S.; Fry, M.; Leontidis, G. Imputation of missing sub-hourly precipitation data in a large sensor network: A machine learning approach. J. Hydrol. 2020, 588, 125126. [Google Scholar] [CrossRef]
- Sattari, M.-T.; Rezazadeh-Joudi, A.; Kusiak, A. Assessment of different methods for estimation of missing data in precipitation studies. Hydrol. Res. 2017, 48, 1032–1044. [Google Scholar] [CrossRef]
- Oriani, F.; Borghi, A.; Straubhaar, J.; Mariethoz, G.; Renard, P. Missing data simulation inside flow rate time series using multiple-point statistics. Environ. Model. Softw. 2016, 86, 264–276. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H. Recontrsuction of river water quality missing data using artificial neural networks. Water Qual. Res. J. Can. 2015, 50, 4. [Google Scholar] [CrossRef]
- Srebotnjak, T.; Carr, G.; de Sherbinin, A.; Rickwood, C. A global Water Quality Index and hot-deck imputation of missing data. Ecol. Indic. 2012, 17, 108–119. [Google Scholar] [CrossRef]
- Hastings, F.; Fuentes, I.; Perez-Bidegain, M.; Navas, R.; Gorgoglione, A. Land-Cover Mapping of Agricultural Areas Using Machine Learning in Google Earth Engine. In Computational Science and Its Applications—ICCSA 2020. ICCSA 2020. Lecture Notes in Computer Science; Gervasi, O., Murgante, B., Misra, S., Garau, C., Blečić, I., Taniar, D., Apduhan, B.O., Rocha, A.M.A.C., Tarantino, E., Torre, C.M., et al., Eds.; Springer: Cham, Switzerland, 2020; Volume 12252. [Google Scholar]
- Gorgoglione, A.; Gregorio, J.; Ríos, A.; Alonso, J.; Chreties, C.; Fossati, M. Influence of land use/land cover on surface-water quality of Santa Lucía river, Uruguay. Sustainability 2020, 12, 4692. [Google Scholar] [CrossRef]
- OAN—Observatorio Ambiental Nacional. Available online: https://www.dinama.gub.uy/oan/geoportal/ (accessed on 11 January 2021).
- Goyenola, G.; Meerhoff, M.; Teixeira-de Mello, F.; González-Bergonzoni, I.; Graeber, D.; Fosalba, C.; Vidal, N.; Mazzeo, N.; Ovesen, N.B.; Jeppesen, E.; et al. Phosphorus dynamics in lowland streams as a response to climatic, hydrological and agricultural land use gradients. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 3349–3390. [Google Scholar]
- Aubriot, L.; Delbene, L.; Haakonson, S.; Somma, A.; Hirsch, F.; Bonilla, S. Evolución de la eutrofización en el Río Santa Lucía: Influencia de la intensificación productiva y perspectivas. Innotec 2017, 14, 7–17. [Google Scholar] [CrossRef]
- Gorgoglione, A.; Alonso, J.; Chreties, C.; Fossati, M. Assessing temporal and spatial patterns of surface-water quality with a multivariate approach: A case study in Uruguay. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Changchun, China, 21–23 August 2020; Volume 612, p. 012002. [Google Scholar]
- Wolpert, D.; Macready, W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bartier, P.M.; Keller, C.P. Multivariate interpolation to incorporate thematic surface data using inverse distance weighting (IDW). Comput. Geosci. 1996, 22, 195–799. [Google Scholar] [CrossRef]
- Tang, F.; Ishwaran, H. Random Forest Missing Data Algorithms. Stat. Anal Data Min. 2017, 10, 363–377. [Google Scholar] [CrossRef]
- Farebrother, R.W. Further results on the mean square error of ridge regression. J. R. Stat. Soc. 1976, 38, 248–250. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Drucker, H. Improving Regressors using Boosting Techniques. In Proceedings of the Fourteenth International Conference on Machine Learning (ICML’97), Nashville, TN, USA, 8–12 July 1997; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1997; pp. 107–115. [Google Scholar]
- Art, O. A robust hybrid of lasso and ridge regression. Contemp. Math. 2007, 443, 59–72. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Dang, X.; Peng, H.; Wang, X.; Zhang, H. Theil-Sen Estimators in a Multiple Linear Regression Model. Mater. Sci. 2009. Available online: https://www.semanticscholar.org/paper/THE-THEIL-SEN-ESTIMATORS-IN-A-MULTIPLE-LINEAR-MODEL-Wang-Dang/63167c5dbb9bae6f0a269237a9b6a28fa7e1ac20 (accessed on 2 June 2021).
- Mucherino, A.; Papajorgji, P.J.; Pardalos, P.M. k-Nearest Neighbor Classification. In Data Mining in Agriculture; Springer Optimization and Its Applications, 34; Springer: New York, NY, USA, 2009. [Google Scholar]
- Narbondo, S.; Gorgoglione, A.; Crisci, M.; Chreties, C. Enhancing physical similarity approach to predict runoff in ungauged watersheds in sub-tropical regions. Water 2020, 12, 528. [Google Scholar] [CrossRef]
- Chen, H.; Luo, Y.; Potter, C.; Moran, P.J.; Grieneisen, M.L.; Zhang, M. Modeling pesticide diuron loading from the San Joaquin watershed into the Sacramento-San Joaquin Delta using SWAT. Water Res. 2017, 121, 374–385. [Google Scholar] [CrossRef]
- Gorgoglione, A.; Bombardelli, F.A.; Pitton, B.J.L.; Oki, L.R.; Haver, D.L.; Young, T.M. Role of Sediments in Insecticide Runoff from Urban Surfaces: Analysis and Modeling. Int. J. Environ. Res. Public Health 2018, 15, 1464. [Google Scholar] [CrossRef]
- Rogelis, M.C.; Werner, M.; Obregón, N.; Wright, N. Hydrological model assessment for flood early warning in a tropical high mountain basin. Hydrol. Earth Syst. Sci. Discuss. 2016, 1–36. [Google Scholar] [CrossRef]
- Andersson, J.C.M.; Arheimer, B.; Traoré, F.; Gustafsson, D.; Ali, A. Process refinements improve a hydrological model concept applied to the Niger River basin. Hydrol. Process. 2017, 31, 4540–4554. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Woods, R.A.; Freer, J.E. A Quantitative Hydrological Climate Classification Evaluated with Independent Streamflow Data. Water Resour. Res. 2018, 54, 5088–5109. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash-Sutcliffe and Kling-Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Soil Water Div. Asabe 2007, 50, 885–900. [Google Scholar]
- Hayashi, M. Temperature-Electrical Conductivity Relation of Water for Environmental Monitoring and Geophysical Data Inversion. Environ. Monit. Assess. 2004, 96, 119–128. [Google Scholar] [CrossRef] [PubMed]
- Beretta-Blanco, A.; Carrasco-Letelier, L. Relevant factors in the eutrophication of the Uruguay River and the Río Negro. Sci. Total Environ. 2021, 761, 143299. [Google Scholar] [CrossRef]
- Bakhtiar Jemily, N.H.; Ahmad Sa’ad, F.N.; Mat Amin, A.R.; Othman, M.F.; Mohd Yusoff, M.Z. Relationship between Electrical Conductivity and Total Dissolved Solids as Water Quality Parameter in Teluk Lipat by Using Regression Analysis. In Progress in Engineering Technology; Abu Bakar, M., Mohamad Sidik, M., Öchsner, A., Eds.; Advanced Structured Materials; Springer: Cham, Switzerland, 2019; Volume 119, pp. 169–173. [Google Scholar]
- Paaijmans, K.P.; Takken, W.; Githeko, A.K.; Jacobs, A.F. The effect of water turbidity on the near-surface water temperature of larval habitats of the malaria mosquito Anopheles gambiae. Int. J. Biometeorol. 2008, 52, 747–753. [Google Scholar] [CrossRef] [PubMed]
- Lintern, A.; Wbb, J.A.; Ryu, D.; Liu, S.; Bende-Michl, U.; Waters, D.; Leahy, P.; Wilson, P.; Western, A.W. Key factors influencing differences in stream water quality across space. WIREs Water 2018, 5, e1260. [Google Scholar] [CrossRef]
- Pandas_Profiling Library. Available online: https://github.com/pandas-profiling/ (accessed on 29 December 2020).
- Reisinger, A.J.; Groffman, P.M.; Rosi-Marshall, E.J. Nitrogen-cycling process rates across urban ecosystems. FEMS Microbiol. Ecol. 2016, 92, 198. [Google Scholar] [CrossRef] [PubMed]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-Validation. In Encyclopedia of Database Systems; Liu, L., Özsu, M.T., Eds.; Springer: Boston, MA, USA, 2009. [Google Scholar]
- Río, A. Implementación de un Modelo Hidrodinámico Tridimensional en el Embalse de Paso Severino. Aportes Para la Modelación de Calidad de Agua. Master’s Thesis, Graduate Program of Applied Fluid Mechanics, Universidad de la República, Montevideo, Uruguay, 2019. Available online: https://www.colibri.udelar.edu.uy/jspui/handle/20.500.12008/21553 (accessed on 29 April 2021).
- Jácome, G.; Valarezo, C.; Yoo, C. Assessment of water quality monitoring for the optimal sensor placement in lake Yahuarcocha using pattern recognition techniques and geographical information systems. Environ. Monit. Assess. 2018, 190, 259. [Google Scholar] [CrossRef] [PubMed]
- Kanga, I.S.; Naimi, M.; Chikhaoui, M. Groundwater quality assessment using water quality index and geographic information system based in Sebou River Basin in the North-West region of Morocco. Int. J. Energ. Water Res. 2020, 4, 347–355. [Google Scholar] [CrossRef]
- Barreto, P.; Dogliotti, S.; Perdomo, C. Surface water quality of intensive farming areas within the Santa Lucia River basin of Uruguay. Air Soil Water Res. 2017, 10, 1178622117715446. [Google Scholar] [CrossRef]

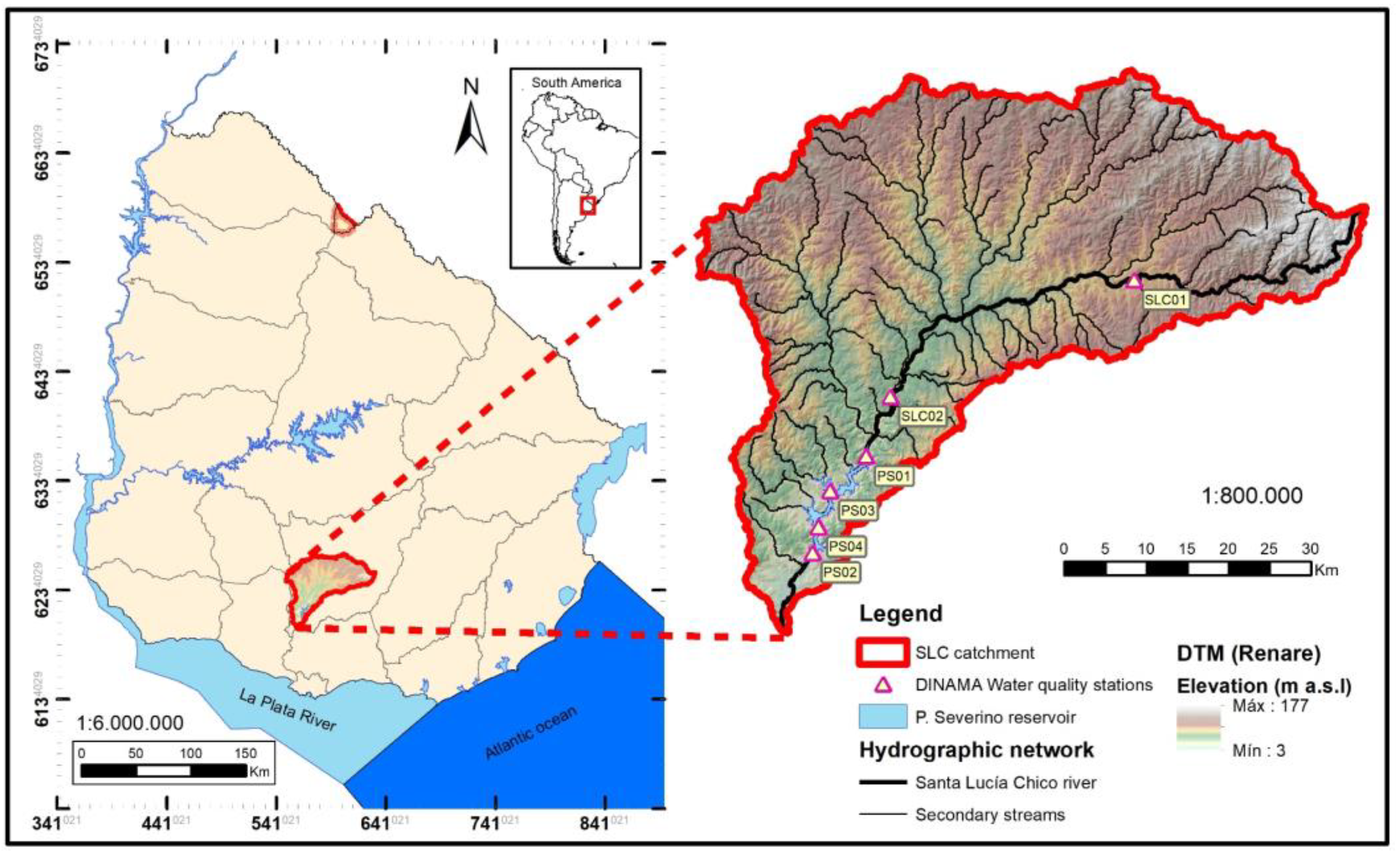
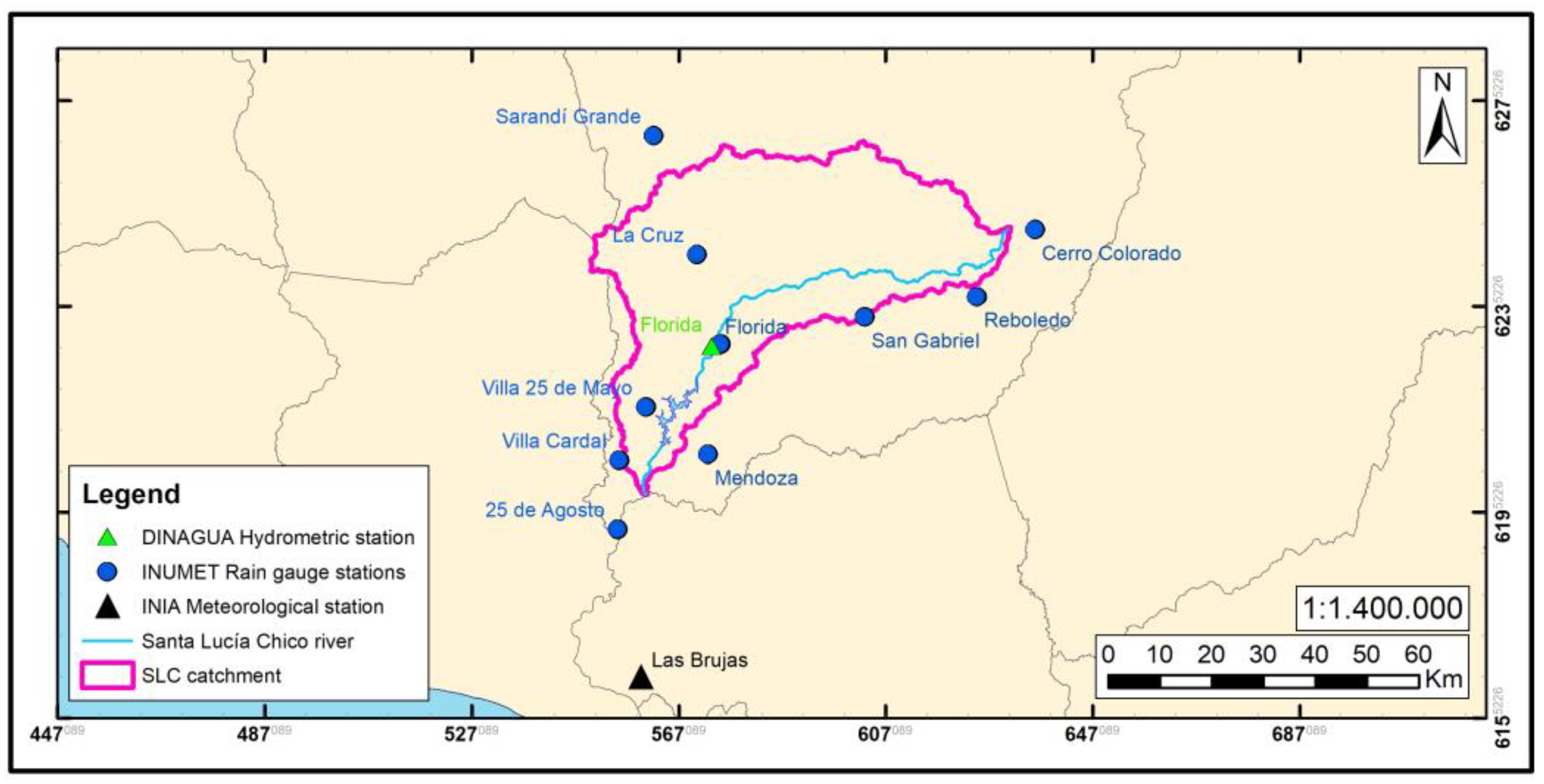
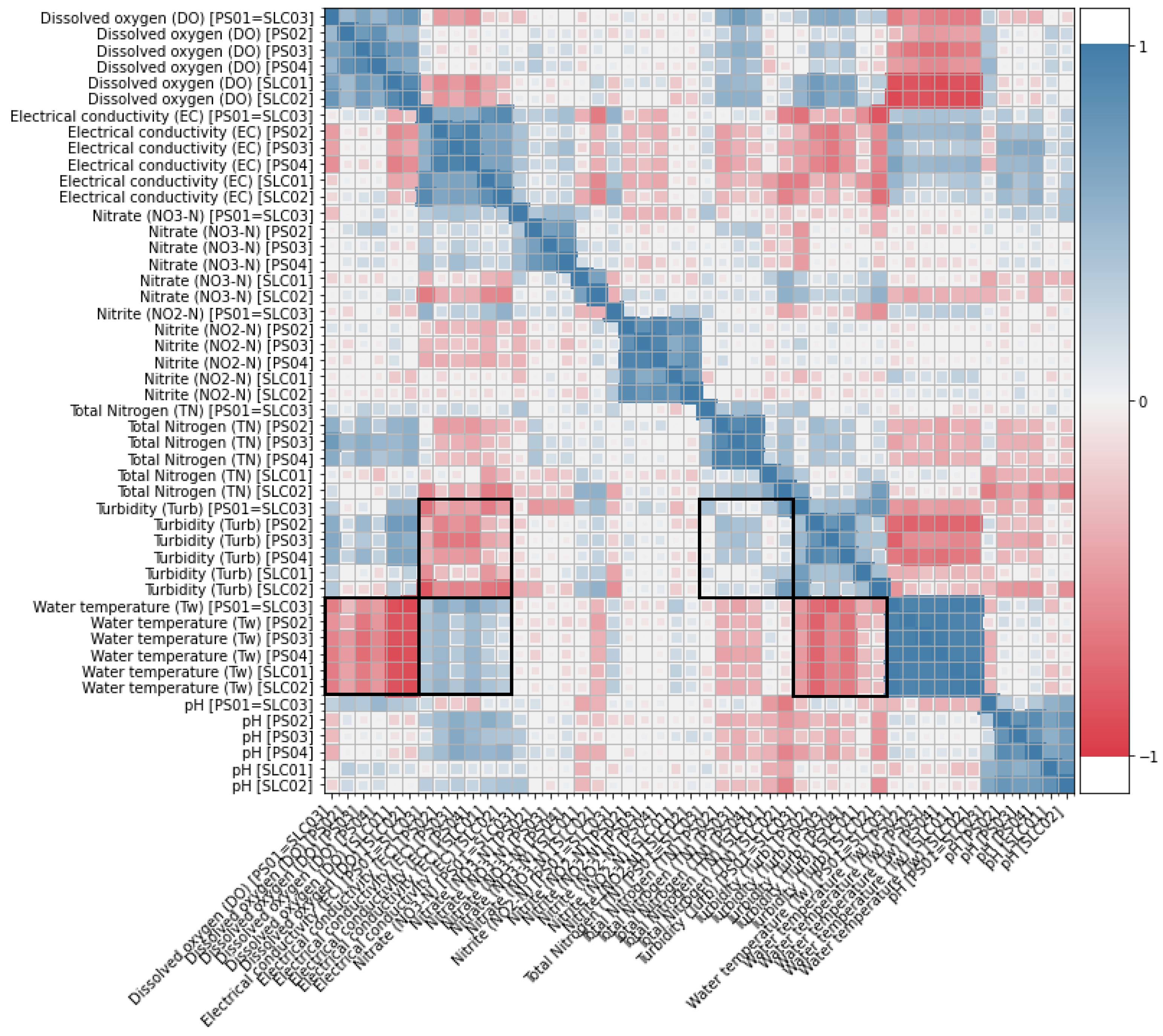
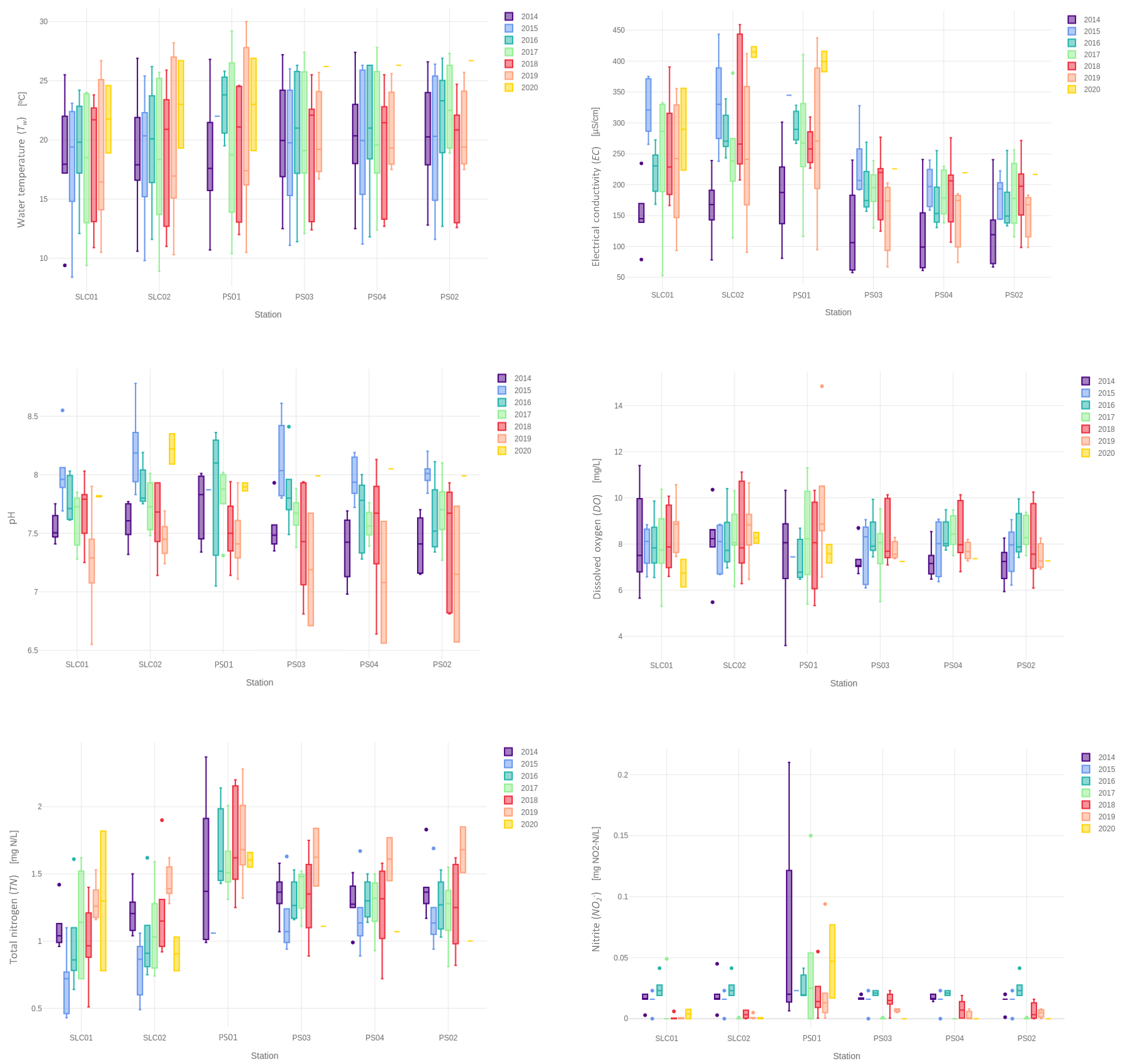
| Variable | % Missing Data | ||||||
|---|---|---|---|---|---|---|---|
| SLC01 | SLC02 | PS01 | PS03 | PS04 | PS02 | ||
| Physical | Tw | 51.5 | 51.5 | 64.7 | 57.6 | 57.6 | 59.1 |
| EC | 51.5 | 51.5 | 64.7 | 57.6 | 57.6 | 57.6 | |
| pH | 52.9 | 52.9 | 66.2 | 59.1 | 59.1 | 59.1 | |
| DO | 51.5 | 51.5 | 64.7 | 57.6 | 57.6 | 57.6 | |
| Turb | 52.9 | 52.9 | 66.2 | 60.6 | 60.6 | 59.1 | |
| Chemical | TN | 52.9 | 52.9 | 66.2 | 60.6 | 60.6 | 59.1 |
| NO2− | 51.5 | 51.5 | 64.7 | 59.1 | 59.1 | 57.6 | |
| NO3− | 51.5 | 51.5 | 64.7 | 59.1 | 59.1 | 57.6 | |
| Performance Rating | Physical Water Quality Variables | Chemical Water Quality Variables |
|---|---|---|
| NSE | ||
| Very good | NSE > 0.80 | NSE > 0.65 |
| Good | 0.70 < NSE ≤ 0.80 | 0.50 < NSE ≤ 0.65 |
| Satisfactory | 0.45 < NSE ≤ 0.70 | 0.35 < NSE ≤ 0.50 |
| Unsatisfactory | NSE ≤ 0.45 | NSE ≤ 0.35 |
| PBIAS | ||
| Very good | |PBIAS| < 10 | |PBIAS| < 15 |
| Good | 10 ≤ |PBIAS| < 15 | 15 ≤ |PBIAS| < 20 |
| Satisfactory | 15 ≤ |PBIAS| < 20 | 20 ≤ |PBIAS| < 30 |
| Unsatisfactory | |PBIAS| ≥ 20 | |PBIAS| ≥ 30 |
| KGE | ||
| Satisfactory/Good | KGE ≥ −0.41 | KGE ≥ −0.41 |
| Unsatisfactory | KGE < −0.41 | KGE < −0.41 |
| Variable to Impute | Helper Variable |
|---|---|
| Water temperature (Tw) | Air temperature (Ta) |
| Solar radiation (SR) | |
| Heliophany (Hel) | |
| Turbidity (Turb) | |
| Electrical Conductivity (EC) | Water temperature (Tw) |
| Turbidity (Turb) | |
| Dissolved oxygen (DO) | Water temperature (Tw) |
| Nitrite (NO2−) | Streamflow (Q) |
| Nitrate (NO3−) | Streamflow (Q) |
| Turbidity (Turb) | Streamflow (Q) |
| Precipitation (P) | |
| Air temperature (Ta) | |
| Evapotranspiration (ET) | |
| Total Nitrogen (TN) | Nitrite (NO2−) |
| Nitrate (NO3−) | |
| Turbidity (Turb) | |
| Streamflow (Q) |
| Variable | Station | Model | NSE | NSE Rating | PBIAS | PBIAS Rating | KGE | KGE Rating |
|---|---|---|---|---|---|---|---|---|
| Tw | SLC01 | Random Forest Regressor | 0.95 | Very good | 0.09 | Very good | 0.91 | Good |
| SLC02 | IDW | 0.97 | Very good | −2.54 | Very good | 0.95 | Good | |
| PS01 | IDW | 0.95 | Very good | −3.77 | Very good | 0.94 | Good | |
| PS03 | IDW | 0.98 | Very good | −0.21 | Very good | 0.96 | Good | |
| PS04 | IDW | 0.98 | Very good | 1.49 | Very good | 0.96 | Good | |
| PS02 | IDW | 0.97 | Very good | 0.89 | Very good | 0.93 | Good | |
| EC | SLC01 | SVR | 0.67 | Satisfactory | −0.12 | Very good | 0.76 | Good |
| SLC02 | SVR | 0.71 | Good | 0.43 | Very good | 0.67 | Good | |
| PS01 | Ridge | 0.67 | Satisfactory | −1.70 | Very good | 0.77 | Good | |
| PS03 | Ridge | 0.85 | Very good | 1.35 | Very good | 0.86 | Good | |
| PS04 | IDW | 0.94 | Very good | 4.71 | Very good | 0.87 | Good | |
| PS02 | IDW | 0.89 | Very good | −3.89 | Very good | 0.88 | Good | |
| pH | SLC01 | Bayesian Ridge | 0.39 | Unsatisfactory | −0.63 | Very good | 0.54 | Good |
| SLC02 | Random Forest Regressor | 0.75 | Good | 0.95 | Very good | 0.80 | Good | |
| PS01 | Random Forest Regressor | 0.25 | Unsatisfactory | 0.44 | Very good | 0.40 | Good | |
| PS03 | Bayesian Ridge | 0.66 | Satisfactory | −0.31 | Very good | 0.78 | Good | |
| PS04 | IDW | 0.68 | Satisfactory | −1.10 | Very good | 0.79 | Good | |
| PS02 | Huber Regressor | 0.65 | Satisfactory | −3.29 | Very good | 0.77 | Good | |
| DO | SLC01 | Bayesian Ridge | 0.81 | Very good | −2.79 | Very good | 0.83 | Good |
| SLC02 | Random Forest Regressor | 0.73 | Good | −1.80 | Very good | 0.73 | Good | |
| PS01 | AdaBoost | 0.27 | Unsatisfactory | −1.65 | Very good | 0.48 | Good | |
| PS03 | Ridge | 0.80 | Good | −0.15 | Very good | 0.86 | Good | |
| PS04 | Huber Regressor | 0.89 | Very good | −0.28 | Very good | 0.89 | Good | |
| PS02 | IDW | 0.69 | Satisfactory | −0.24 | Very good | 0.79 | Good | |
| TN | SLC01 | IDW | 0.19 | Unsatisfactory | 2.72 | Very good | 0.49 | Good |
| SLC02 | Ridge | 0.65 | Good | 1.90 | Very good | 0.72 | Good | |
| PS01 | Random Forest Regressor | −0.35 | Unsatisfactory | −0.91 | Very good | −0.10 | Good | |
| PS03 | IDW | 0.63 | Good | −7.79 | Very good | 0.75 | Good | |
| PS04 | Random Forest Regressor | 0.77 | Very good | −1.38 | Very good | 0.71 | Good | |
| PS02 | IDW | 0.70 | Very good | −15.22 | Good | 0.71 | Good | |
| NO2− | SLC01 | Huber Regressor | 0.59 | Good | −0.83 | Very good | 0.62 | Good |
| SLC02 | Random Forest Regressor | 0.36 | Satisfactory | −10.79 | Very good | 0.54 | Good | |
| PS01 | KNN | −0.31 | Unsatisfactory | 25.94 | Satisfactory | 0.02 | Good | |
| PS03 | TheilSen Regressor | 0.74 | Very good | 1.09 | Very good | 0.72 | Good | |
| PS04 | KNN | 0.92 | Very good | 3.35 | Very good | 0.86 | Good | |
| PS02 | Huber Regressor | 0.75 | Very good | −4.53 | Very good | 0.78 | Good | |
| NO3− | SLC01 | TheilSen Regressor | 0.21 | Unsatisfactory | 13.68 | Very good | 0.33 | Good |
| SLC02 | Huber Regressor | 0.42 | Satisfactory | −4.95 | Very good | 0.58 | Good | |
| PS01 | Random Forest Regressor | 0.10 | Unsatisfactory | 5.14 | Very good | 0.36 | Good | |
| PS03 | IDW | 0.69 | Very good | −0.80 | Very good | 0.80 | Good | |
| PS04 | Huber Regressor | 0.80 | Very good | −1.08 | Very good | 0.84 | Good | |
| PS02 | SVR | 0.61 | Good | −1.57 | Very good | 0.75 | Good | |
| Turb | SLC01 | SVR | −0.10 | Unsatisfactory | −1.93 | Very good | 0.03 | Good |
| SLC02 | SVR | 0.56 | Satisfactory | −5.74 | Very good | 0.67 | Good | |
| PS01 | IDW | −0.18 | Unsatisfactory | −45.97 | Unsatisfactory | 0.35 | Good | |
| PS03 | IDW | 0.66 | Satisfactory | −12.30 | Good | 0.71 | Good | |
| PS04 | IDW | 0.85 | Very good | 3.94 | Very good | 0.88 | Good | |
| PS02 | IDW | 0.88 | Very good | −3.27 | Very good | 0.87 | Good |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez, R.; Pastorini, M.; Etcheverry, L.; Chreties, C.; Fossati, M.; Castro, A.; Gorgoglione, A. Water-Quality Data Imputation with a High Percentage of Missing Values: A Machine Learning Approach. Sustainability 2021, 13, 6318. https://doi.org/10.3390/su13116318
Rodríguez R, Pastorini M, Etcheverry L, Chreties C, Fossati M, Castro A, Gorgoglione A. Water-Quality Data Imputation with a High Percentage of Missing Values: A Machine Learning Approach. Sustainability. 2021; 13(11):6318. https://doi.org/10.3390/su13116318
Chicago/Turabian StyleRodríguez, Rafael, Marcos Pastorini, Lorena Etcheverry, Christian Chreties, Mónica Fossati, Alberto Castro, and Angela Gorgoglione. 2021. "Water-Quality Data Imputation with a High Percentage of Missing Values: A Machine Learning Approach" Sustainability 13, no. 11: 6318. https://doi.org/10.3390/su13116318
APA StyleRodríguez, R., Pastorini, M., Etcheverry, L., Chreties, C., Fossati, M., Castro, A., & Gorgoglione, A. (2021). Water-Quality Data Imputation with a High Percentage of Missing Values: A Machine Learning Approach. Sustainability, 13(11), 6318. https://doi.org/10.3390/su13116318







