Prediction of Depth of Seawater Using Fuzzy C-Means Clustering Algorithm of Crowdsourced SONAR Data
Abstract
1. Introduction
- The fuzzy-logic-based FCM algorithm was implemented in the field to predict depth data.
- The proposed method obtained more accurate depth data by clustering the data, which is experimentally proven.
- To obtain accurate results, the proposed model divided the data into the parts (blocks) with sizes approximately 100 to 100 m by location of the data measurements according to domain knowledge.
- The accuracy of the proposed model was measured by calculating the mean absolute error of the mean value of each block of the real data and the FCM value of each block.
2. Related Works
3. Materials and Methods
3.1. Observation Technology of Depth of Seawater
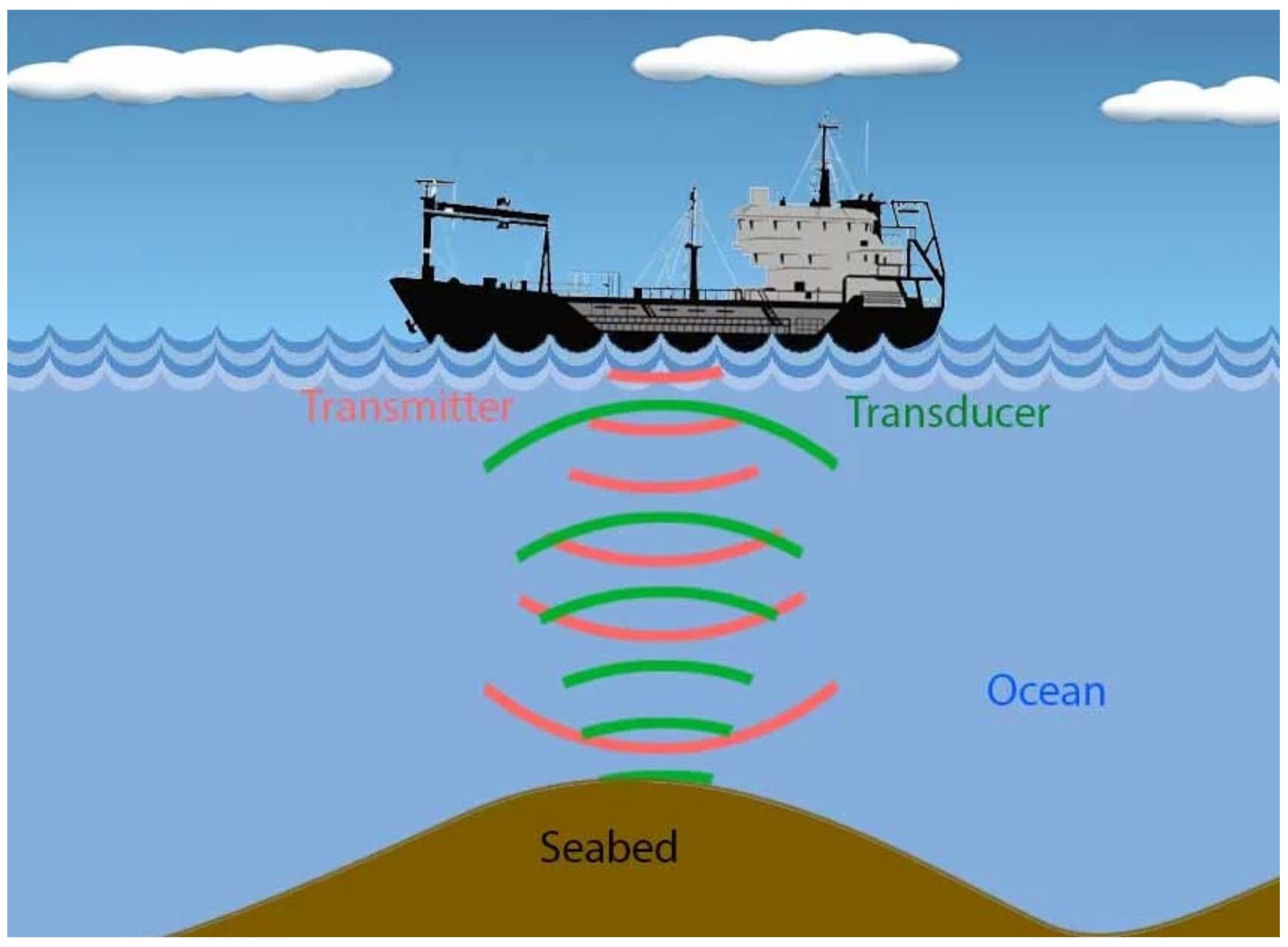
3.1.1. SONAR
3.1.2. Crowdsourced Bathymetry
- Vessels should be equipped with a global navigation satellite system (GNSS) for the calculation of the location and single-beam echo sounders (SBAS) for measurement of depth.
- The equipment (software and hardware) of the vessels must meet the recommendations of the IMO on performance standards so that vessels have the ability to gather bathymetric data (along with location and time) of standardized reliability.
- The collected data from GNSS and SBES on ships will be transferred to the National Marine Electronics Association (NMEA) and must be saved on board. Saved data will be transferred from vessels to the trusted node.For the purpose of achieving the required level of standardization, the IHO Data Center for Digital Bathymetry accepts bathymetric information in specific (default) formats. These formats are the CSV, XYZT, or GeoJson format. The XYZT format contains longitude, latitude, depth, and time. On depth measurement, the vertical distance between the line of the water surface and the thrust position of the SONAR transducer can play a significant role. Therefore, the IHO automatically recommends setup sensors according to the issue. The data collected in this way have a significant value in a whole range of activities related to improving seabed mapping.
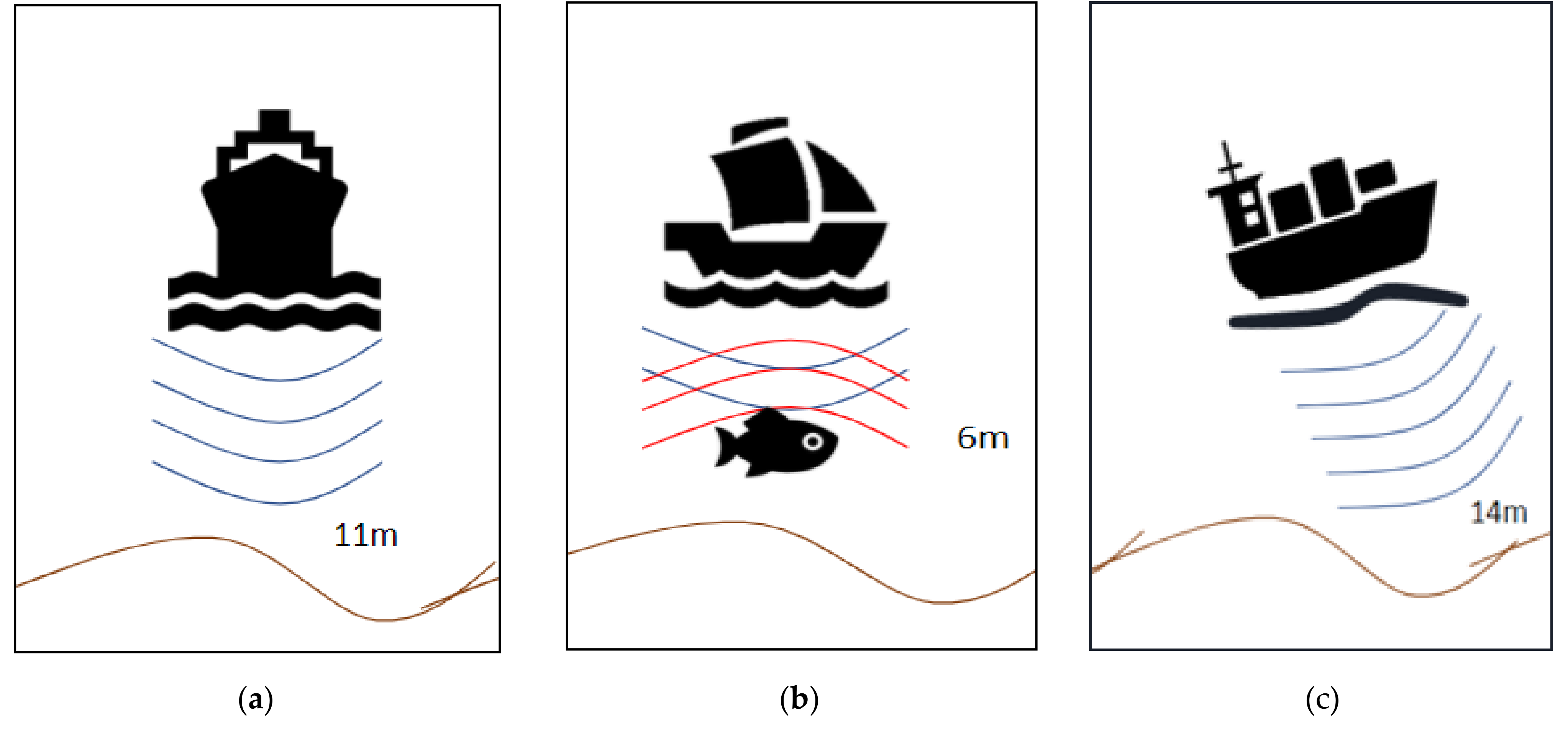
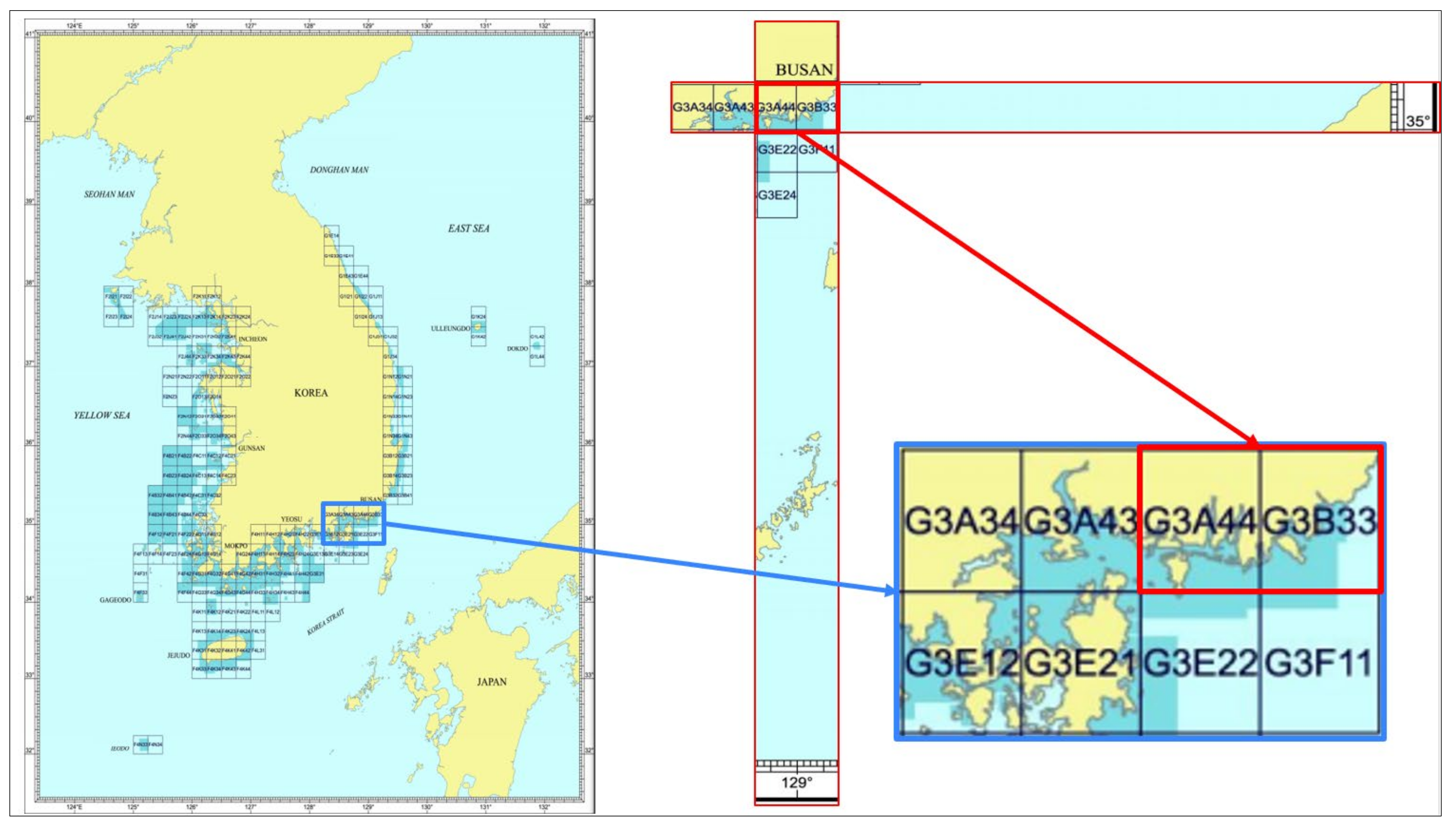
3.2. Problem Analysis
3.3. Possible Solutions
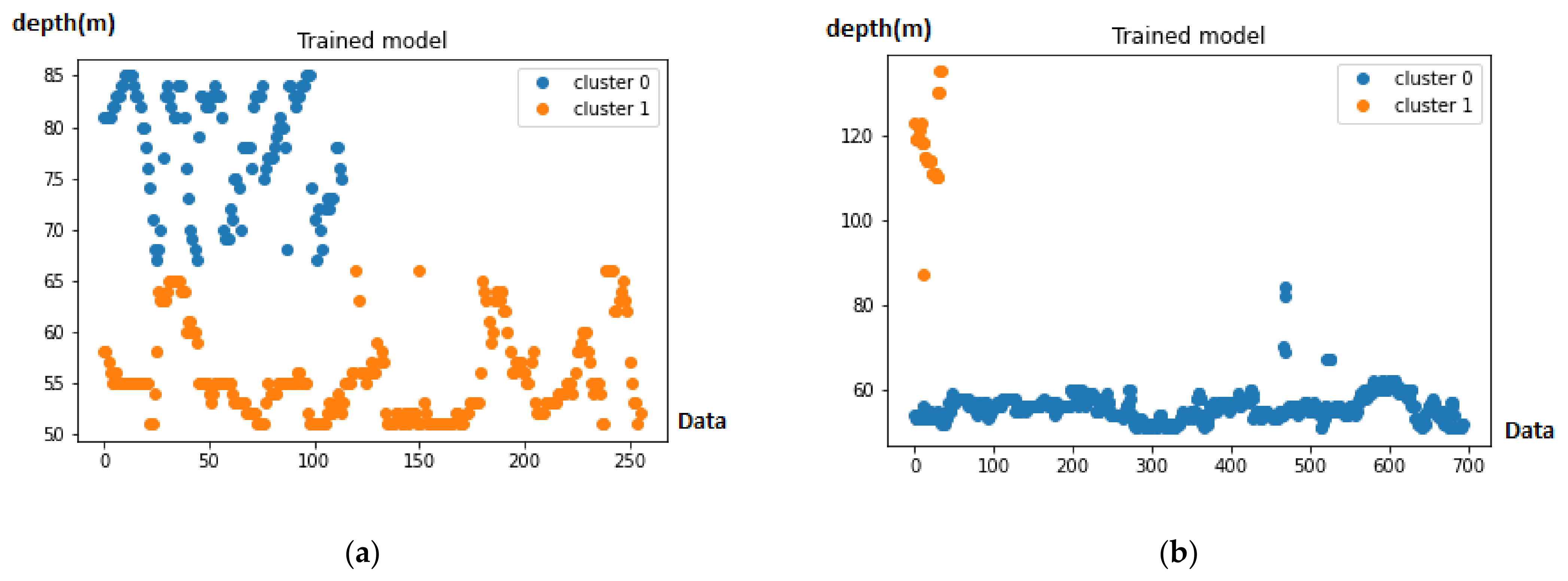
3.4. Proposed Method
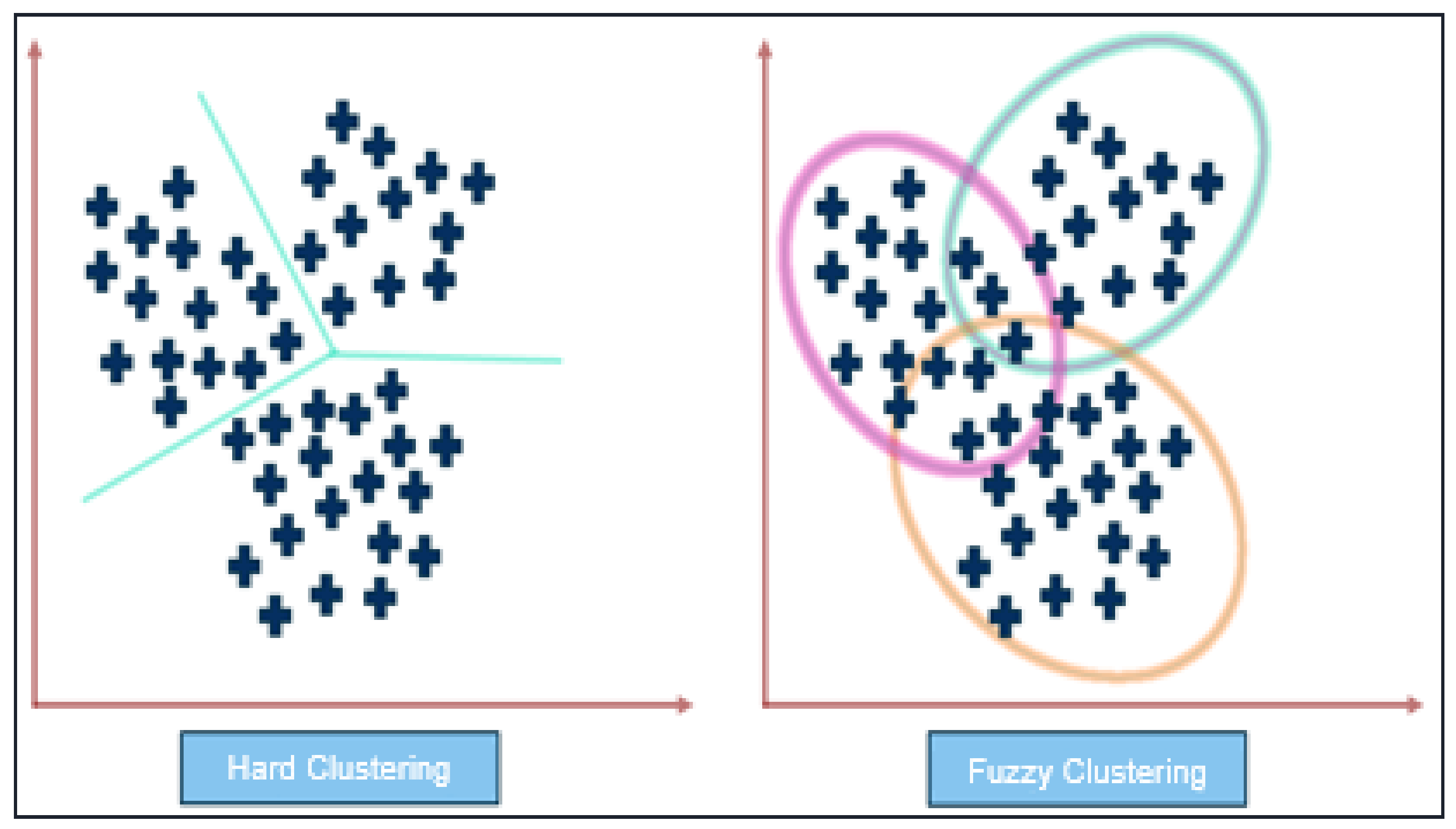
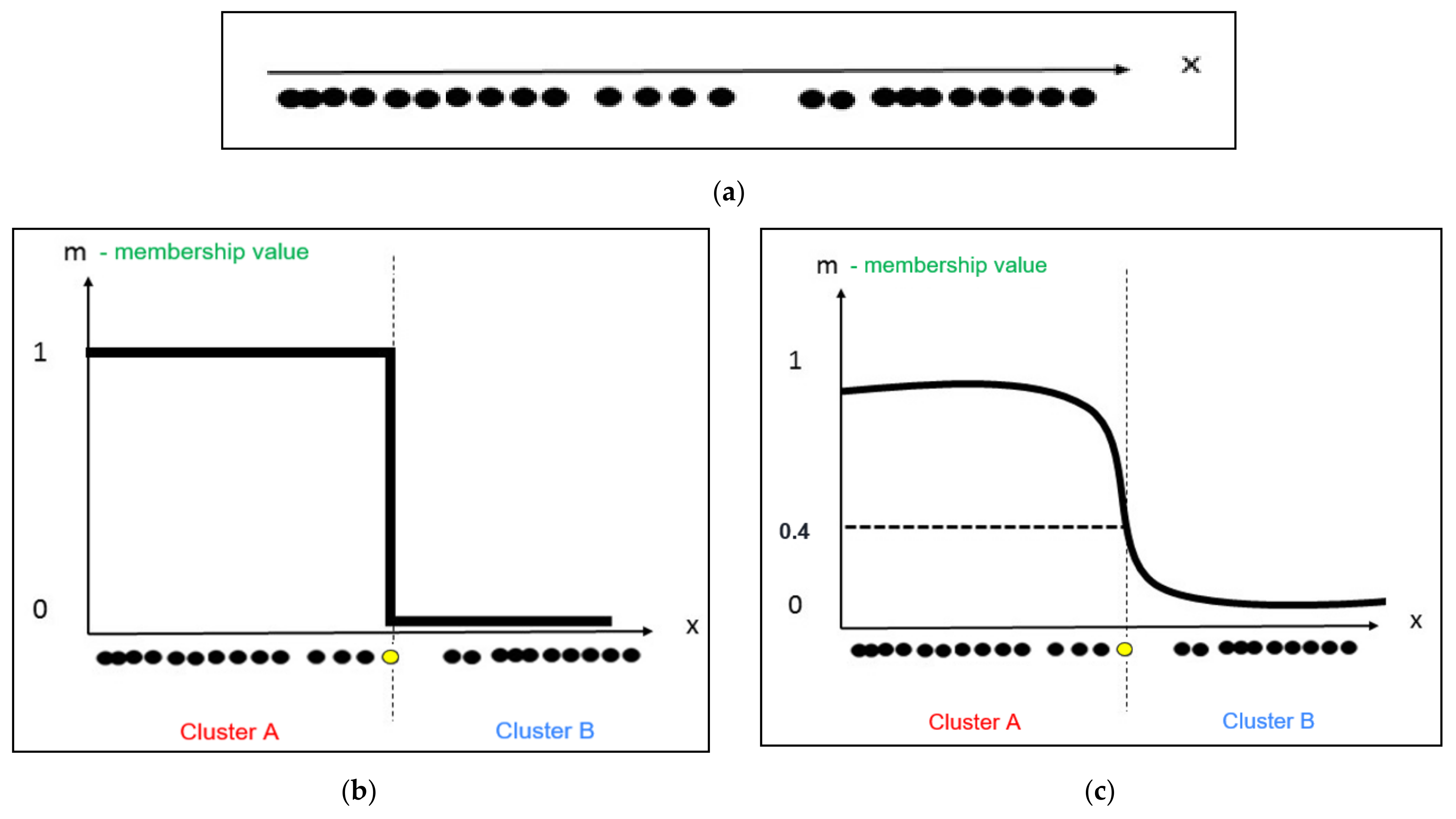
3.4.1. Fuzzy C-Means Clustering
- Clustering algorithm based on partition-k-means, k-medoids, PAM, CLARA, CLARANS
- Clustering algorithm based on hierarchy—BIRCH, CURE, ROCK, chameleon
- Clustering algorithm based on fuzzy theory—FCM, FCS, MM
- Clustering algorithm based on distribution—DBCLASD, GMM
- Clustering algorithm based on density—DBSCAN, OPTICS, Mean-shift
- Clustering algorithm based on graph theory—CLICK, MST
- Clustering algorithm based on grid—STING, CLIQUE
- Clustering algorithm based on fractal theory—FC
- Clustering algorithm based on model—COBWEB, GMM, SOM, ART
- Clustering algorithm based on kernel—kernel k-means, kernel SOM, kernel FCM, SVC, MMC, MKC
- Clustering algorithm based on ensemble—methods for generating the set of clusters: 4 types of consensus function: CSPA, HGPA, MCLA, VM, HCE, LAC, WPCK, sCSPA, sMCLA, sHBGPA
- Clustering algorithm based on swarm intelligence—ACO_based (LF), PSO_based, SFLA_based, ABC_based
- Clustering algorithm based on quantum theory—QC, DQC
- Clustering algorithm based on spectral graph theory—SM, NJW
- Clustering algorithm based on affinity propagation—AP
- Clustering algorithm based on density and distance—DD
- Clustering algorithm for spatial data—DBSCAN, STING, Wavecluster, CLARANS
- Clustering algorithm for data stream—STREAM, CluStream, HPStream, DenStream
- Clustering algorithm for large-scale data-k-means—BIRCH, CLARA, CURE, DBSCAN, DENCLUE, Wavecluster, FC
- Step 1.
- Set values for c (number of clusters), m (fuzziness exponent), ε
- Step 2.
- Initialize fuzzy partition matrix
- Step 3.
- At k-step: calculate the c cluster centers(centroids) with . Where calculates with Equation (3)
- Step 4.
- Calculate and update membership matrix . Equation (2)
- Step 5.
- If < ε then stop, otherwise set k = k+1 and return to Step 3
3.4.2. Experiment Parameters and Environment
- OS: Windows 10 Pro
- Processor: Intel(R) Core (TM) i7-10700 CPU @2.90 GHz
- RAM: 32 GB
- System Type: 64 bit
- Platform: Jupyter Notebook (Python)
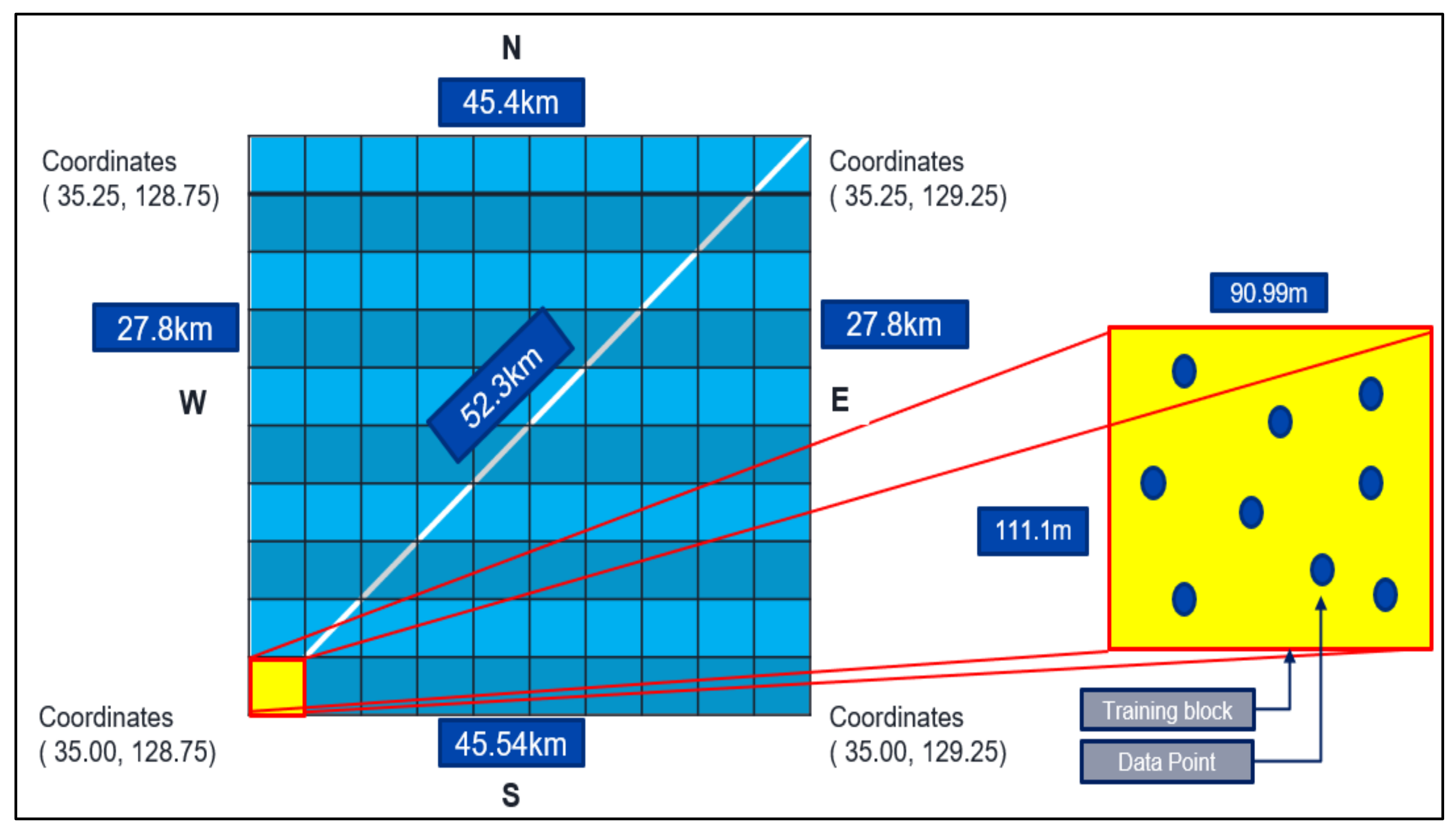
3.4.3. Data Training Method
- Define minimum and maximum coordinates (latitude, longitude).
- Divide the whole training zone into the blocks. The approximate size of the blocks should be 100 to 100 m.
- Sort blocks that have more than 200 data points. If there are fewer data points in the blocks, no use of FCM in that block.
- Implement FCM to each block.
- Compare with real data.
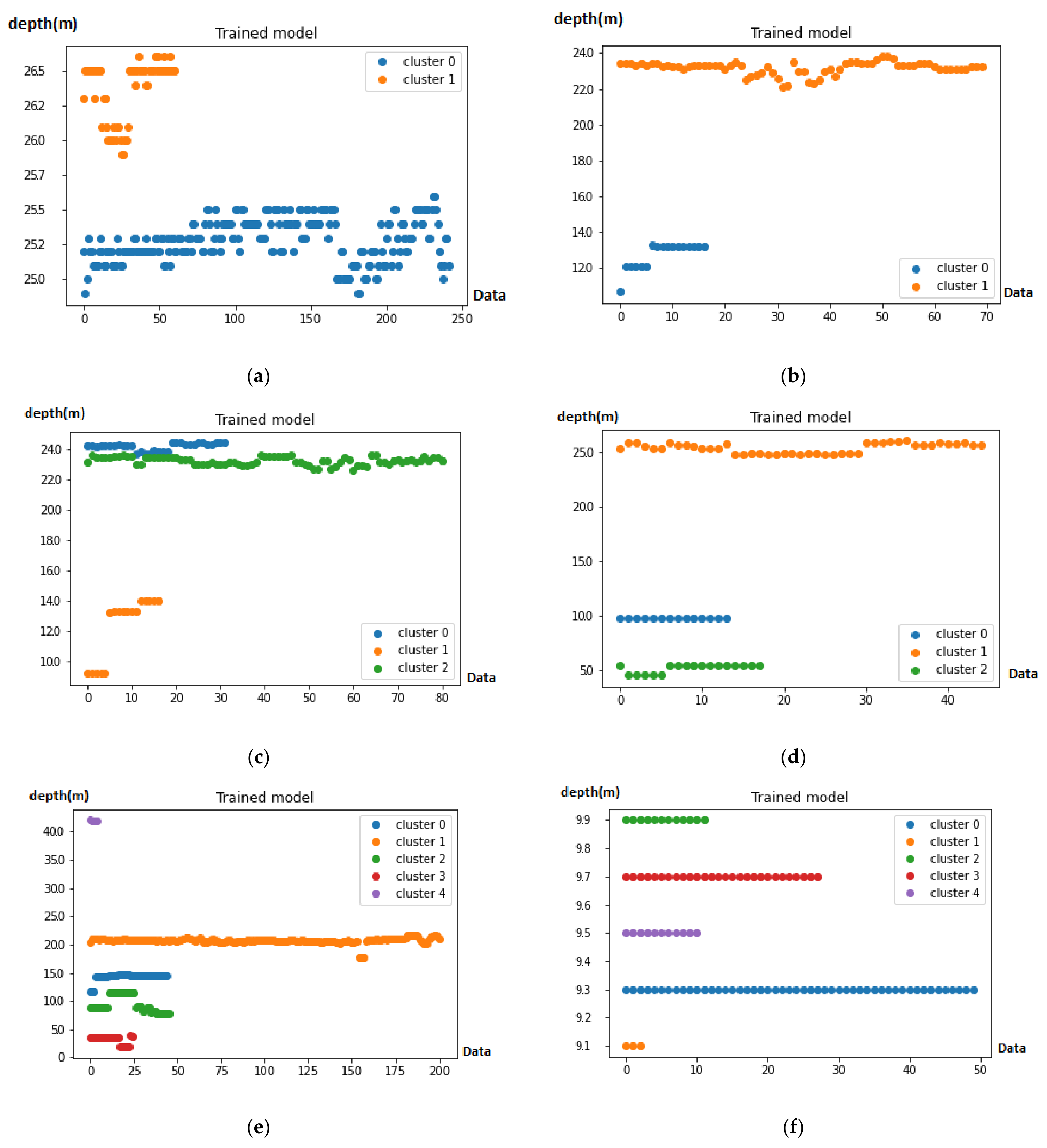
4. Results
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kamolov, A.; Park, S.H. An IoT Based Smart Berthing (Parking) System for Vessels and Ports. In ICMWT 2018: Mobile and Wireless Technology 2018; Kim, K., Kim, H., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2019; Volume 513. [Google Scholar]
- Kamolov, A.; Al-Absi, M.A.; Lee, H.J.; Park, S.H. Smart Flying Umbrella Drone on Internet of Things: AVUS. In Proceedings of the 21st International Conference on Advanced Communication Technology (ICACT), PyeongChang, Korea, 17–20 February 2019. [Google Scholar]
- Hyundai Heavy Industries Debuts ‘Smart Ship’ Solution. Available online: https://www.marinelink.com/news/industries-solution427522 (accessed on 9 February 2021).
- Japan Develops Smart Ship Platform. Available online: https://www.rivieramm.com/opinion/opinion/japan-develops-smart-ship-platform-31339 (accessed on 10 February 2021).
- We4Sea—Efficiency Solutions for Ships. Available online: https://www.we4sea.com/ (accessed on 10 February 2021).
- Hamburg Port—Interactive port map of the Port of Hamburg. Available online: https://www.hafen-hamburg.de/en/portmap (accessed on 10 February 2021).
- Amsterdam Port. Available online: https://www.portofamsterdam.com/en/shipping/arrivals-and-departures (accessed on 10 February 2021).
- Kamolov, A.; Park, S. An IoT-Based Ship Berthing Method Using a Set of Ultrasonic Sensors. Sensors 2019, 19, 5181. [Google Scholar] [CrossRef] [PubMed]
- Kamolov, A.; Park, S.H. IoT based smart reporting and mooring system for vessels. In Proceedings of the Korean Institute of Information and Communication Sciences Conference, Chungcheongnam-do, Korea, 10 October 2017; Volume 21, pp. 0395–0398. [Google Scholar]
- Geertsma, R.D.; Negenborn, R.R.; Visser, K.; Hopman, J.J. Design and control of hybrid power and propulsion systems for smart ships: A review of developments. Appl. Energy 2017, 194, 30–54. [Google Scholar] [CrossRef]
- Mapping the Ocean Floor by 2030. Available online: https://www.gislounge.com/mapping-the-ocean-floor-by-2030/ (accessed on 11 February 2021).
- Fuzzy Clustering. Available online: https://en.wikipedia.org/wiki/Fuzzy_clustering (accessed on 14 December 2020).
- Wölfl, A.-C.; Snaith, H.; Amirebrahimi, S.; Devey, C.W.; Dorschel, B.; Ferrini, V.; Huvenne, V.A.I.; Jakobsson, M.; Jencks, J.; Johnston, G.; et al. Seafloor Mapping—The Challenge of a Truly Global Ocean Bathymetry. Front. Mar. Sci. 2019, 6, 283. [Google Scholar] [CrossRef]
- Sagawa, T.; Yamashita, Y.; Okumura, T.; Yamanokuchi, T. Satellite Derived Bathymetry Using Machine Learning and Multi-Temporal Satellite Images. Remote Sens. 2019, 11, 1155. [Google Scholar] [CrossRef]
- Caballero, I.; Stumpf, R.P.; Meredith, A. Preliminary Assessment of Turbidity and Chlorophyll Impact on Bathymetry Derived from Sentinel-2A and Sentinel-3A Satellites in South Florida. Remote Sens. 2019, 11, 645. [Google Scholar] [CrossRef]
- Salameh, E.; Frappart, F.; Almar, R.; Baptista, P.; Heygster, G.; Lubac, B.; Raucoules, D.; Almeida, L.P.; Bergsma, E.W.J.; Capo, S.; et al. Monitoring Beach Topography and Nearshore Bathymetry Using Spaceborne Remote Sensing: A Review. Remote Sens. 2019, 11, 2212. [Google Scholar] [CrossRef]
- Su, H.; Liu, H.; Wu, Q. Prediction of Water Depth from Multispectral Satellite Imagery—The Regression Kriging Alternative. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2511–2515. [Google Scholar]
- Lyzenga, D.R. Passive remote-sensing techniques for mapping water depth and Bottom Features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2258. [Google Scholar] [CrossRef]
- Kao, H.-M.; Ren, H.; Lee, C.-S.; Chang, C.-P.; Yen, J.-Y.; Lin, T.-H. Determination of shallow water depth using optical satellite images. Int. J. Remote Sens. 2009, 30, 6241–6260. [Google Scholar] [CrossRef]
- Dekker, A.G.; Phinn, S.R.; Anstee, J.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.; Hedley, J.; Klonowski, W.; Lee, Z.P.; et al. Intercomparison of shallow water bathymetry, hydro-optics, and benthos mapping techniques in Australian and Caribbean coastal environments: Intercomparison of shallow water mapping methods. Limnol. Oceanogr.-Meth. 2011, 9, 396–425. [Google Scholar] [CrossRef]
- Kanno, A.; Tanaka, Y.; Kurosawa, A.; Sekine, M. Generalized Lyzenga’s predictor of shallow water depth for multispectral satellite imagery. Mar. Geod. 2013, 36, 365–376. [Google Scholar] [CrossRef]
- Manessa, M.D.M.; Kanno, A.; Sekine, M.; Haidar, M.; Yamamoto, K.; Imai, T.; Higuchi, T. Satellite-derived bathymetry using random forest algorithm and worldview-2 Imagery. Geoplanning J. Geomat. Plan. 2016, 3, 117–126. [Google Scholar] [CrossRef]
- Traganos, D.; Poursanidis, D.; Aggarwal, B.; Chrysoulakis, N.; Reinartz, P. Estimating Satellite-Derived Bathymetry (SDB) with the Google Earth Engine and Sentinel-2. Remote Sens. 2018, 10, 859. [Google Scholar] [CrossRef]
- Mavraeidopoulos, A.K.; Pallikaris, A.; Oikonomou, E. Satellite Derived Bathymetry (SDB) and Safety of Navigation. Int. Hydrogr. Rev. 2017, 17, 7–20. [Google Scholar]
- Banic, J.; Sizgoric, S. Scanning Lidar bathymeter for water depth measurement. Laser Radar Technol. Appl. 1986, 187–195. [Google Scholar] [CrossRef]
- Wilson, N.; Parrish, C.E.; Battista, T. Mapping Seafloor Relative Reflectance and Assessing Coral Reef Morphology with EAARL-B Topobathymetric Lidar Waveforms. Estuaries Coasts 2019, 1–15. [Google Scholar] [CrossRef]
- Irish, J.L.; White, T.E. Coastal engineering applications of high-resolution LiDAR bathymetry. Coast. Eng. 1998, 35, 47–71. [Google Scholar] [CrossRef]
- Wang, C.; Li, Q.; Liu, Y.; Wu, G.; Liu, P.; Ding, X. A comparison of waveform processing algorithms for single-wavelength LiDAR bathymetry. ISPRS J. Photogramm. Remote Sens. 2015, 101, 22–35. [Google Scholar] [CrossRef]
- Bincai, C.; Yong, F.; Li, G.; Haiyan, H.; Zhengzhi, J.; Bijiao, S.; Lele, L. An active-passive fusion strategy and accuracy evaluation for shallow water bathymetry based on ICESat-2 ATLAS laser point cloud and satellite remote sensing imagery. Int. J. Remote Sens. 2021, 42, 2783–2806. [Google Scholar]
- Lyzenga, D.R. Shallow-water bathymetry using combined Lidar and passive multispectral scanner data. Int. J. Remote Sens. 1985, 6, 115–125. [Google Scholar] [CrossRef]
- Saylam, K.; Brown, R.A.; Hupp, J.R. Assessment of depth and turbidity with airborne Lidar bathymetry and multiband satellite imagery in shallow water bodies of the Alaskan North Slope. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 191–200. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Liu, Z.; Yang, B.; Yang, F.; Wang, X.H.; Li, S. Satellite-derived bathymetry using the ICESat-2 lidar and Sentinel-2 imagery datasets. Remote Sens. Environ. 2020, 250, 112047. [Google Scholar] [CrossRef]
- Pike, S.; Traganos, D.; Poursanidis, D.; Williams, J.; Medcalf, K.; Reinartz, P.; Chrysoulakis, N. Leveraging Commercial High-Resolution Multispectral Satellite and Multibeam Sonar Data to Estimate Bathymetry: The Case Study of the Caribbean Sea. Remote Sens. 2019, 11, 1830. [Google Scholar] [CrossRef]
- Tian, J.; Li, C.; Liu, J.; Yu, F.; Cheng, S.; Zhao, N.; Wan Jaafar, W.Z. Groundwater Depth Prediction Using Data-Driven Models with the Assistance of Gamma Test. Sustainability 2016, 8, 1076. [Google Scholar] [CrossRef]
- Yang, F.; Qiao, Y.; Wei, W.; Wang, X.; Wan, D.; Damaševičius, R.; Woźniak, M. DDTree. A Hybrid Deep Learning Model for Real-Time Waterway Depth Prediction and Smart Navigation. Appl. Sci. 2020, 10, 2770. [Google Scholar] [CrossRef]
- Kang, C. A Differential Dynamic Positioning Algorithm Based on GPS/Beidou. Procedia Eng. 2016, 137, 590–598. [Google Scholar] [CrossRef]
- Shiri, J. Wavelet and neuro-fuzzy conjunction model for predicting water table depth fluctuations. Hydrol. Res. 2012, 43, 286–300. [Google Scholar]
- Vodas, M.; Pelekis, N.; Theodoridis, Y.; Ray, C.; Karkaletsis, V.; Petridis, S.; Miliou, A. Efficient AIS Data Processing for Environmentally Safe Shipping. Spoud. J. Econ. Bus. 2014, 63, 181–190. [Google Scholar]
- Li, S.; Chen, X.; Chen, L.; Chen, L.; Zhao, Y.; Sheng, T.; Bai, Y. Data Reception Analysis of the AIS on board the TianTuo-3 Satellite. J. Navig. 2017, 70, 761–774. [Google Scholar] [CrossRef]
- Yang, D.; Wu, L.; Wang, S.; Jia, H.; Li, K.X. How big data enriches maritime research–a critical review of automatic identification system (AIS) data applications. Transp. Rev. 2019, 39, 755–773. [Google Scholar] [CrossRef]
- How is Sound Used to Measure Water Depth? Available online: https://dosits.org/people-and-sound/navigation/how-is-sound-used-to-measure-water-depth/ (accessed on 12 February 2021).
- Sea Floor Mapping. Available online: https://oceanexplorer.noaa.gov/explorations/lewis_clark01/background/seafloormapping/seafloormapping.html (accessed on 11 February 2021).
- Depth Sounding Techniques That Preceded the Modern Day SONAR Technology. Available online: https://www.thevintagenews.com/2017/02/23/depth-sounding-techniques-that-preceded-the-modern-day-sonar-technology/ (accessed on 13 February 2021).
- How is Sound Used to Map the Seafloor? Available online: https://dosits.org/people-and-sound/examine-the-earth/map-the-sea-floor/ (accessed on 14 February 2021).
- Eakins, B.W.; Sharman, G.F. Volumes of the World’s Oceans from ETOPO2v2; NOAA National Geophysical Data Center: Boulder, CO, USA, 2010. [Google Scholar]
- Mao, K.; Capra, L.; Harman, M.; Jia, Y. A Survey of the Use of Crowdsourcing in Software Engineering. J. Syst. Softw. 2017, 126, 57–84. [Google Scholar] [CrossRef]
- Pavić, I.; Mišković, J.; Kasum, J.; Alujević, D. Analysis of Crowdsourced Bathymetry Concept and It’s Potential Implications on Safety of Navigation. TransnavInt. J. Mar. Navig. Saf. Sea Transp. 2020, 14, 681–686. [Google Scholar] [CrossRef]
- Xu, D.; Tian, Y. A comprehensive survey of clustering algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef]
- MacQUEEN, J.B. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability: Weather Modification; Lucien, M., Le, C., Jerzy, N., Eds.; University of California Press: Berkeley/Los Angeles, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
- Dunn, J.C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Bezdek, J.C. Objective function clustering. In Pattern Recognition with Fuzzy Objective Function Algorithms, 1st ed.; Springer Inc.: Secaucus, NJ, USA, 1981; pp. 43–93. ISBN 978-1-4757-0452-5. [Google Scholar]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Fuzzy C-Means Clustering. Available online: https://matteucci.faculty.polimi.it/Clustering/tutorial_html/cmeans.html (accessed on 10 December 2020).
- Kodinariya, T.M.; Makwana, P.R. Review on determining number of Cluster in K-Means Clustering. Int. J. Adv. Res. Comput. Sci. Manag. Stud. 2013, 1, 2321–7782. [Google Scholar]
- Bholowalia, P.; Kumar, A. EBK-Means: A Clustering Technique based on Elbow Method and K-Means in WSN. Int. J. Comput. Appl. 2014, 105, 17–24. [Google Scholar]
- Choi, K. Electronic Navigation Chart Standards and Viewers. Available online: https://www.slideshare.net/KyusungChoi/ss-72798127 (accessed on 20 May 2021).


| Latitude | Longitude | Depth(m) |
|---|---|---|
| 35.136863 | 129.192551 | 10 |
| 35.136863 | 129.192551 | 11 |
| 35.136863 | 129.192551 | 20 |
| 35.136863 | 129.192551 | 23 |
| 35.136863 | 129.192551 | 21 |
| 35.136863 | 129.192551 | 20 |
| Device_id | Time | Latitude | Longitude | Depth |
|---|---|---|---|---|
| SY-T02 | 2020-02-27 11:19:03 | 35.0001678466797 | 128.919357299805 | 14.5 m |
| SY-T02 | 2020-02-28 10:10:28 | 35.0003662109375 | 128.919677734375 | 14.5 m |
| SY-T04 | 2019-08-27 09:50:45 | 35.0004158020020 | 128.919662475586 | 26.4 m |
| SY-T05 | 2019-02-27 08:19:08 | 35.0001335144043 | 128.919326782227 | 26.5 m |
| SY-T02 | 2019-01-21 12:11:50 | 35.0006332397461 | 128.919570922852 | 25.5 m |
| SY-T04 | 2018-09-23 07:23:07 | 35.0006484985352 | 128.919067382812 | 9.8 m |
| SY-T03 | 2020-04-21 13:11:50 | 35.0006332397461 | 128.919570922852 | 25.7 m |
| SY-T04 | 2021-01-10 17:13:09 | 35.0006484985352 | 128.919067382812 | 10.2 m |
| By Mean Value of Each Block | By FCM Value of Each Block | |
|---|---|---|
| Mean Absolute Error | 2.09 m | 1.67 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamolov, A.A.; Park, S. Prediction of Depth of Seawater Using Fuzzy C-Means Clustering Algorithm of Crowdsourced SONAR Data. Sustainability 2021, 13, 5823. https://doi.org/10.3390/su13115823
Kamolov AA, Park S. Prediction of Depth of Seawater Using Fuzzy C-Means Clustering Algorithm of Crowdsourced SONAR Data. Sustainability. 2021; 13(11):5823. https://doi.org/10.3390/su13115823
Chicago/Turabian StyleKamolov, Ahmadhon Akbarkhonovich, and Suhyun Park. 2021. "Prediction of Depth of Seawater Using Fuzzy C-Means Clustering Algorithm of Crowdsourced SONAR Data" Sustainability 13, no. 11: 5823. https://doi.org/10.3390/su13115823
APA StyleKamolov, A. A., & Park, S. (2021). Prediction of Depth of Seawater Using Fuzzy C-Means Clustering Algorithm of Crowdsourced SONAR Data. Sustainability, 13(11), 5823. https://doi.org/10.3390/su13115823





