Assessing the Environmental Performance of Municipal Solid Waste Collection: A New Predictive LCA Model
Abstract
1. Introduction
2. Review of Existing Models
3. Materials and Methods
3.1. Selection of Pre-Existing Models for Review and Comparison
- ORWARE: This model is based on the calculation of fuel consumption and emissions for waste collection trucks, considering two different situations: while collecting waste and while traveling from the collection area to the unloading site. Data on average load, average speed, etc. are used as input parameters. Data on energy consumption (MJ/(t.km)) were obtained from average data provided by the Uppsala Public Service Work in 1994 and emissions from a simulation of an average bus tour in an urban area with many stop-and-go cycles and a rather low average speed. The author explicitly mentions that this model is only valid for the collection of waste in urban areas. Data for energy consumption (converted to the international system of units (SI)) are shown in Table 2. A complete description can be found in [71].
- MSW-DST: This model includes a set of equations to calculate the time required for the individual activities of the collection vehicles in a typical working day (driving to the collection area, driving in stop-and-go cycles, and idling at the stops). These times are then used to calculate the associated fuel consumption, based on corresponding fixed consumption factors (gallons per mile and gallons per hour)—see Table 2 for the values converted to SI. A complete description of the model and equations can be found in [72].
- Ecoinvent dataset for collection trucks (”CH: transport, municipal waste collection, lorry 21 t”): This dataset is based on five case studies for German and Swiss municipalities, from which an average consumption rate of 4 L/t was obtained. The (fixed) transportation distance was estimated from the standard transport distance to municipal solid waste incineration plants in Ecoinvent, i.e., 10 km. From these values, an average fuel consumption factor expressed as L/(t·km) was derived—also included in Table 2. For further details, the reader is referred to Doka [73].
3.2. Experimental Data Collection
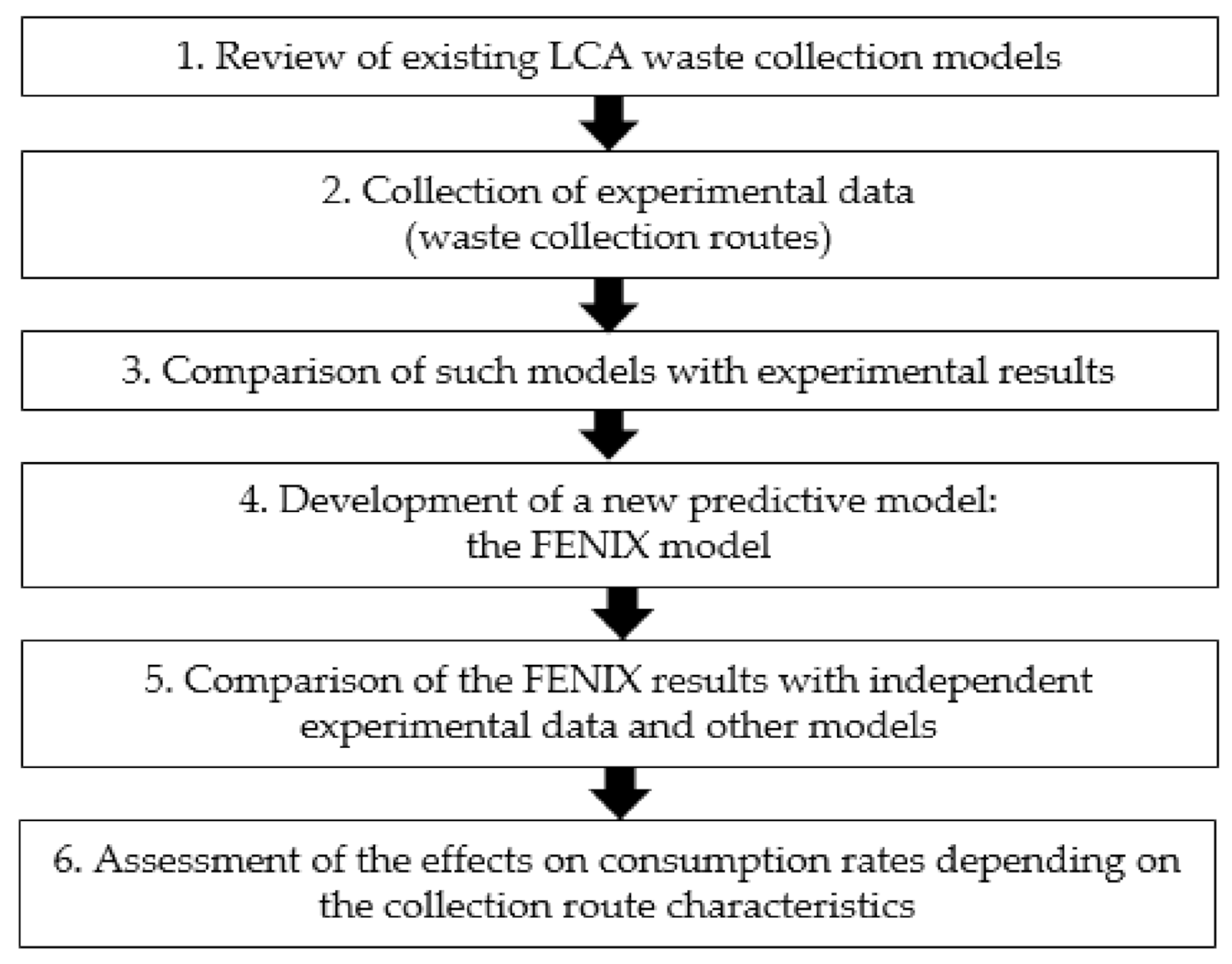
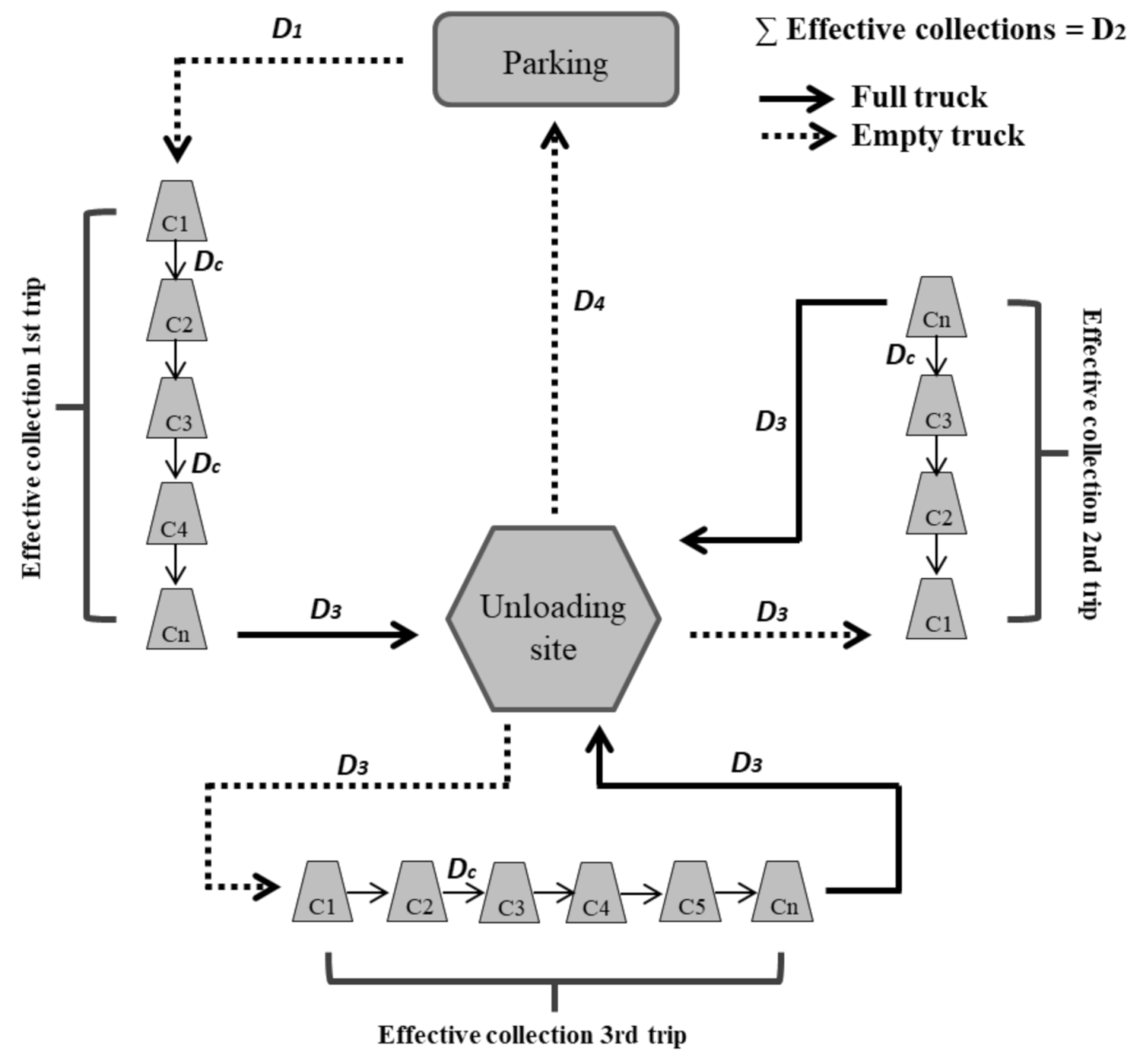
3.3. Development of a New Model: The FENIX Model
3.3.1. Starting Point: A Conventional Commercial Truck
3.3.2. Adaptation of the Conventional Truck to Waste Collection Vehicles
4. Results
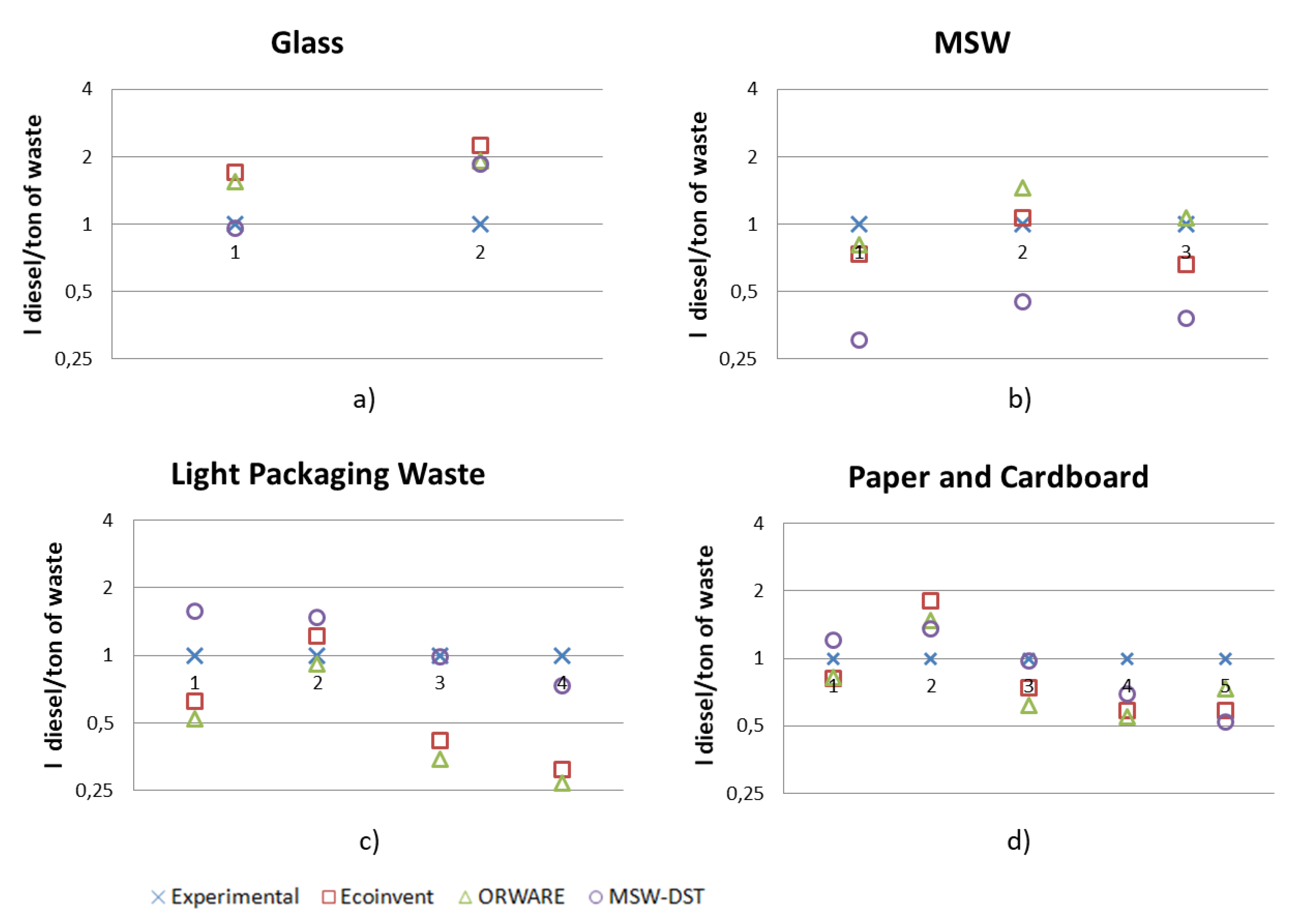
4.1. Comparison of Experimental Data to Results of Existing Models
4.2. Comparison of FENIX Model Results to Those Produced by Previous Models and to Experimental Data
4.3. Sensitivity to Model Parameters
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hauschild, M.; Barlaz, M.A. LCA in Waste Management: Introduction to Principle and Method. In Solid Waste Technology & Management; Christensen, T.H., Ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2010; Volume 1, pp. 111–136. [Google Scholar]
- Laurent, A.; Bakas, I.; Clavreul, J.; Bernstad, A.; Niero, M.; Gentil, E.; Hauschild, M.Z.; Christensen, T.H. Review of LCA studies of solid waste management systems–Part I: Lessons learned and perspectives. Waste Manag. 2014, 34, 573–588. [Google Scholar] [CrossRef] [PubMed]
- Khandelwal, H.; Dhar, H.; Thalla, A.K.; Kumar, S. Application of life cycle assessment in municipal solid waste management: A worldwide critical review. J. Clean. Prod. 2019, 209, 630–654. [Google Scholar] [CrossRef]
- Iqbal, A.; Liu, X.; Chen, G.-H. Municipal solid waste: Review of best practices in application of life cycle assessment and sustainable management techniques. Sci. Total Environ. 2020, 729, 138622. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Qin, Q.; Li, G.; Tseng, C.-H. Sustainable municipal waste management strategies through life cycle assessment method: A review. J. Environ. Manag. 2021, 287, 112238. [Google Scholar] [CrossRef] [PubMed]
- Finnveden, G.; Ekvall, T. Life-cycle assessment as a decision-support tool—the case of recycling versus incineration of paper. Resour. Conserv. Recycl. 1998, 24, 235–256. [Google Scholar] [CrossRef]
- Güereca, L.P.; Gassó, S.; Baldasano, J.M.; Jiménez-Guerrero, P. Life cycle assessment of two biowaste management systems for Barcelona, Spain. Resour. Conserv. Recycl. 2006, 49, 32–48. [Google Scholar] [CrossRef]
- Merrild, H.; Damgaard, A.; Christensen, T.H. Life cycle assessment of waste paper management: The importance of technology data and system boundaries in assessing recycling and incineration. Resour. Conserv. Recycl. 2008, 52, 1391–1398. [Google Scholar] [CrossRef]
- Villanueva, A.; Wenzel, H. Paper waste–Recycling, incineration or landfilling? A review of existing life cycle assessments. Waste Manag. 2007, 27, S29–S46. [Google Scholar] [CrossRef] [PubMed]
- Wollny, V.; Dehoust, G.; Fritsche, U.R.; Weinem, P. Comparison of Plastic Packaging Waste Management Options: Feedstock Recycling versus Energy Recovery in Germany. J. Ind. Ecol. 2001, 5, 49–63. [Google Scholar] [CrossRef]
- Lazarevic, D.; Aoustin, E.; Buclet, N.; Brandt, N. Plastic waste management in the context of a European recycling society: Comparing results and uncertainties in a life cycle perspective. Resour. Conserv. Recycl. 2010, 55, 246–259. [Google Scholar] [CrossRef]
- Rigamonti, L.; Grosso, M.; Møller, J.; Sanchez, V.M.; Magnani, S.; Christensen, T. Environmental evaluation of plastic waste management scenarios. Resour. Conserv. Recycl. 2014, 85, 42–53. [Google Scholar] [CrossRef]
- Kim, M.H.; Song, H.B.; Song, Y.; Jeong, I.T.; Kim, J.W. Evaluation of food waste disposal options in terms of global warming and energy recovery: Korea. Int. J. Energy Environ. Eng. 2013, 4, 1. [Google Scholar] [CrossRef]
- Ahamed, A.; Yin, K.; Ng, B.; Ren, F.; Chang, V.-C.; Wang, J.-Y. Life cycle assessment of the present and proposed food waste management technologies from environmental and economic impact perspectives. J. Clean. Prod. 2016, 131, 607–614. [Google Scholar] [CrossRef]
- Edwards, J.; Othman, M.; Crossin, E.; Burn, S. Life cycle assessment to compare the environmental impact of seven contemporary food waste management systems. Bioresour. Technol. 2018, 248, 156–173. [Google Scholar] [CrossRef] [PubMed]
- Margallo, M.; Aldaco, R.; Irabien, A.; Carrillo, V.; Fischer, M.; Bala, A.; Fullana, P. Life cycle assessment modelling of waste-to-energy incineration in Spain and Portugal. Waste Manag. Res. 2014, 32, 492–499. [Google Scholar] [CrossRef] [PubMed]
- Arena, U.; Ardolino, F.; Di Gregorio, F. A life cycle assessment of environmental performances of two combustion- and gasification-based waste-to-energy technologies. Waste Manag. 2015, 41, 60–74. [Google Scholar] [CrossRef] [PubMed]
- Di Maria, F.; Micale, C. Life cycle analysis of incineration compared to anaerobic digestion followed by composting for managing organic waste: The influence of system components for an Italian district. Int. J. Life Cycle Assess. 2015, 20, 377–388. [Google Scholar] [CrossRef]
- Lombardi, L.; Carnevale, E.A. Evaluation of the environmental sustainability of different waste-to-energy plant configurations. Waste Manag. 2018, 73, 232–246. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Tang, Y.; Nzihou, A.; Chi, Y.; Weiss-Hortala, E.; Ni, M. Life cycle assessment of pyrolysis, gasification and incineration waste-to-energy technologies: Theoretical analysis and case study of commercial plants. Sci. Total Environ. 2018, 626, 744–753. [Google Scholar] [CrossRef]
- Denison, R.A. Environmental Life-Cycle Comparisons of Recycling, Landfilling, and Incineration: A Review of Recent Studies. Annu. Rev. Energy Environ. 1996, 21, 191–237. [Google Scholar] [CrossRef]
- Muñoz, I.; Rieradevall, J.; Domènech, X.; Milà, L. LCA application to integrated waste management planning in Gipuzkoa (Spain). Int. J. Life Cycle Assess. 2004, 9, 272–280. [Google Scholar] [CrossRef]
- Liikanen, M.; Havukainen, J.; Hupponen, M.; Horttanainen, M. Influence of different factors in the life cycle assessment of mixed municipal solid waste management systems–A comparison of case studies in Finland and China. J. Clean. Prod. 2017, 154, 389–400. [Google Scholar] [CrossRef]
- Saraiva, A.B.; Souza, R.; Valle, R. Comparative lifecycle assessment of alternatives for waste management in Rio de Janeiro–Investigating the influence of an attributional or consequential approach. Waste Manag. 2017, 68, 701–710. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Wang, X.; Li, J.; Yan, B.; Wang, Y.; Wu, X.; Velichkova, R.; Cheng, Z.; Ma, W. Environmental, energy, and economic analysis of integrated treatment of municipal solid waste and sewage sludge: A case study in China. Sci. Total Environ. 2019, 647, 1433–1443. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, A.; Zan, F.; Liu, X.; Chen, G.-H. Integrated municipal solid waste management scheme of Hong Kong: A comprehensive analysis in terms of global warming potential and energy use. J. Clean. Prod. 2019, 225, 1079–1088. [Google Scholar] [CrossRef]
- Paes, M.X.; de Medeiros, G.A.; Mancini, S.D.; Bortoleto, A.P.; de Oliveira, J.A.P.; Kulay, L.A. Municipal solid waste management: Integrated analysis of environmental and economic indicators based on life cycle assessment. J. Clean. Prod. 2020, 254, 119848. [Google Scholar] [CrossRef]
- Fernández-Nava, Y.; del Río, J.; Rodríguez-Iglesias, J.; Castrillón, L.; Marañón, E. Life cycle assessment of different municipal solid waste management options: A case study of Asturias (Spain). J. Clean. Prod. 2014, 81, 178–189. [Google Scholar] [CrossRef]
- Beigl, P.; Salhofer, S. Comparison of ecological effects and costs of communal waste management systems. Resour. Conserv. Recycl. 2004, 41, 83–102. [Google Scholar] [CrossRef]
- Banar, M.; Cokaygil, Z.; Ozkan, A. Life cycle assessment of solid waste management options for Eskisehir, Turkey. Waste Manag. 2009, 29, 54–62. [Google Scholar] [CrossRef]
- Iriarte, A.; Gabarrell, X.; Rieradevall, J. LCA of selective waste collection systems in dense urban areas. Waste Manag. 2009, 29, 903–914. [Google Scholar] [CrossRef] [PubMed]
- Tulokhonova, A.; Ulanova, O. Assessment of municipal solid waste management scenarios in Irkutsk (Russia) using a life cycle assessment-integrated waste management model. Waste Manag. Res. 2013, 31, 475–484. [Google Scholar] [CrossRef] [PubMed]
- Kulczycka, J.; Lelek, Ł.; Lewandowska, A.; Zarebska, J. Life cycle assessment of municipal solid waste management–comparison of results using different LCA models. Polish J. Environ. Stud. 2015, 24, 125–140. [Google Scholar] [CrossRef]
- Rigamonti, L.; Grosso, M.; Sunseri, M.C. Influence of assumptions about selection and recycling efficiencies on the LCA of integrated waste management systems. Int. J. Life Cycle Assess. 2009, 14, 411–419. [Google Scholar] [CrossRef]
- Dri, M.; Canfora, P.; Antonopoulos, I.; Gaudillat, P. Best Environmental Management Practice for the Waste Management Sector; EUR 29136 EN; Publications Office of the European Union: Luxembourg, 2018; ISBN 978-92-79-80361-1. JRC111059. [Google Scholar] [CrossRef]
- Dalemo, M.; Sonesson, U.; Björklund, A.; Mingarini, K.; Frostell, B.; Jönsson, H.; Nybrant, T.; Sundqvist, J.-O.; Thyselius, L. ORWARE–A simulation model for organic waste handling systems. Part 1: Model description. Resour. Conserv. Recycl. 1997, 21, 17–37. [Google Scholar] [CrossRef]
- Eriksson, O.; Frostell, B.; Björklund, A.; Assefa, G.; Sundqvist, J.-O.; Granath, J.; Carlsson, M.; Baky, A.; Thyselius, L. ORWARE—a simulation tool for waste management. Resour. Conserv. Recycl. 2002, 36, 287–307. [Google Scholar] [CrossRef]
- Haight, M. EPIC/CSR Integrated Solid Waste Management Model Final Report; Technical Report. Waterloo, ON, Canada, 1999; p. 23. Available online: https://uwaterloo.ca/integrated-waste-management-model-for-municipalities/sites/ca.integrated-waste-management-model-for-municipalities/files/uploads/files/tech_report_mar9_2004.pdf (accessed on 20 March 2021).
- Haight, M. Integrated Solid Waste Management Model Technical Report; University of Waterloo, School of Planning: Waterloo, ON, Canada, 2004; p. 101. [Google Scholar]
- EPIC & CSR Integrated Solid Waste Management’s Tool: Measuring the Environmental Performance of Waste Management Systems; Mississauda, ON, Canada, 2000.
- Weitz, K.; Barlaz, M.; Ranjithan, R.; Brill, D.; Thorneloe, S.; Ham, R. Life Cycle Management of Municipal Solid Waste. Int. J. Life Cycle Assess. 1999, 4, 195–201. [Google Scholar] [CrossRef]
- Thorneloe, S.A.; Weitz, K.; Jambeck, J. Application of the US decision support tool for materials and waste management. Waste Manag. 2007, 27, 1006–1020. [Google Scholar] [CrossRef]
- Ecobilan Life Cycle Research Programme for Waste Management: Inventory Development for Waste Management Operations: Landfill Final Report; Environment Agency: Bristol, UK, 1997.
- McDougall, F.R.; White, P.R.; Franke, M.; Hindle, P. Integrated solid waste management: A Life Cycle Inventory. Int. J. Life Cycle Assess. 2001, 6, 320. [Google Scholar] [CrossRef]
- Tanaka, M.; Matsui, Y.; Nishimura, A. WLCA (Waste LCA) for Strategic Solid Waste Management. In Proceedings of the Proceedings of The Sixth International Conference on EcoBalance: Developing and systematizing of EcoBalance Tools based on Life-Cycle-Thinking, Tsukuba, Japan, 25–27 October 2004. [Google Scholar]
- Tanaka, M. Strategic Solid Waste Management: Challenges for Sustainable Society; Okayama University Press: Tokyo, Japan, 2008; p. 356. (In Japanese) [Google Scholar]
- Den Boer, E.; Den Boer, J.; Jager, J.; Rodrigo, J.; Meneses, M.; Castells, F.; Schanne, L. Deliverable Report on D3.1 and D3.2: Environmental Sustainability Criteria and Indicators for Waste Management (Work Package 3) The Use of Life Cycle Assessment Tool for the Development of Integrated Waste Management Strategies for Cities and Regions with Rapid Growing Economies; Technische Universitaet Darmstadt: Darmstadt, Germany, 2005. [Google Scholar]
- Den Boer, E.; Den Boer, J.; Jager, J. Waste Management Planning and optimisation. In Handbook for Municipal Waste Prognosis and Sustainability Assessment of Waste Management Systems; LCA-IWM: Darmstadt, Germany, 2005. [Google Scholar]
- Boer, J.D.; Jager, J. LCA-IWM: A decision support tool for sustainability assessment of waste management systems. Waste Manag. 2007, 27, 1032–1045. [Google Scholar] [CrossRef] [PubMed]
- Gentil, E.; Hall, D.; Thomas, B.; Shiels, S.; Collins, M. LCA Tool in Waste Management: New Features and Functionalities. In Proceedings of the Tenth International Waste Management and Landfill Symposium, Sardinia, Italy, 3–7 October 2005. [Google Scholar]
- Coleman, T. Life Cycle Assessment for Municipal Waste: Supporting Decisions. Resources Recovery Forum. Annual General Meeting. 19 July 2006. Available online: https://www.tdx.cat/bitstream/handle/10803/289634/abg1de1.pdf?sequence=1 (accessed on 20 March 2021).
- Kirkeby, J.T.; Birgisdottir, H.; Hansen, T.L.; Christensen, T.H.; Bhander, G.S.; Hauschild, M. Environmental assessment of solid waste systems and technologies: EASEWASTE. Waste Manag. Res. 2006, 24, 3–15. [Google Scholar] [CrossRef]
- Clavreul, J.; Baumeister, H.; Christensen, T.H.; Damgaard, A. An environmental assessment system for environmental technologies. Environ. Model. Softw. 2014, 60, 18–30. [Google Scholar] [CrossRef]
- Levis, J.W.; Barlaz, M.A.; DeCarolis, J.F.; Ranjithan, S.R. A generalized multistage optimization modeling framework for life cycle assessment-based integrated solid waste management. Environ. Model. Softw. 2013, 50, 51–65. [Google Scholar] [CrossRef]
- White, P.R.; Franke, M.; Hindle, P. Integrated Solid Waste Management: A Lifecycle Inventory; Blackie Academic and Professional: London, UK, 1995. [Google Scholar]
- Gentil, E.C.; Damgaard, A.; Hauschild, M.; Finnveden, G.; Eriksson, O.; Thorneloe, S.; Kaplan, P.O.; Barlaz, M.; Muller, O.; Matsui, Y.; et al. Models for waste life cycle assessment: Review of technical assumptions. Waste Manag. 2010, 30, 2636–2648. [Google Scholar] [CrossRef] [PubMed]
- Björklund, A.; Finnveden, G.; Roth, L. Application of LCA in Waste Management. In Solid Waste Technology & Management; Wiley: Hoboken, NJ, USA, 2010; Volume 1&2, pp. 137–160. [Google Scholar]
- Hansen, T.L.; Christensen, T.H.; Schmidt, S. Environmental modelling of use of treated organic waste on agricultural land: A comparison of existing models for life cycle assessment of waste systems. Waste Manag. Res. 2006, 24, 141–152. [Google Scholar] [CrossRef] [PubMed]
- Winkler, J.; Bilitewski, B. Comparative evaluation of life cycle assessment models for solid waste management. Waste Manag. 2007, 27, 1021–1031. [Google Scholar] [CrossRef]
- Rimaityte, I.; Denafas, G.; Jager, J. Report: Environmental assessment of Darmstadt (Germany) municipal waste incineration plant. Waste Manag. Res. 2007, 25, 177–182. [Google Scholar] [CrossRef] [PubMed]
- Sonesson, U. Modelling of waste collection–a general approach to calculate fuel consumption and time. Waste Manag. Res. J. Sustain. Circ. Econ. 2000, 18, 115–123. [Google Scholar]
- Ekvall, T.; Finnveden, G. The Application of Life Cycle Assessment to Integrated Solid Waste Management. Process. Saf. Environ. Prot. 2000, 78, 288–294. [Google Scholar] [CrossRef]
- Eriksson, O.; Reich, M.C.; Frostell, B.; Björklund, A.; Assefa, G.; Sundqvist, J.-O.; Granath, J.; Baky, A.; Thyselius, L. Municipal solid waste management from a systems perspective. J. Clean. Prod. 2005, 13, 241–252. [Google Scholar] [CrossRef]
- Larsen, A.W. Environmental Assessment of Waste Collection Seen in a System Perspective; Technical University of Denmark: Lyngby, Denmark, 2009. [Google Scholar]
- European Union. Supporting Environmentally Sound Decisions for Waste Management–A Technical Guide to Life Cycle Thinking (LCT) and Life Cycle Assessment (LCA) for Waste Experts and LCA Practitioners; Publications Office of the European Union: Luxembourg, 2011; ISSN 1831-9424. (online). [Google Scholar]
- Directive 2008/98/EC of the European Parliament and of the Council of 19 November 2008 on waste and repealing certain Directives. Official Journal of the European Union L312, 22 of November 2008. pp. 3–30. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2008:312:0003:0030:en:PDF (accessed on 20 March 2021).
- Klang, A.G. Sustainable Waste Management. Methods and Framework for Analysis. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2005. [Google Scholar]
- Tanskanen, J.-H.; Kaila, J. Comparison of methods used in the collection of source-separated household waste. Waste Manag. Res. 2001, 19, 486–497. [Google Scholar] [CrossRef] [PubMed]
- Salhofer, S.; Schneider, F.; Obersteiner, G. The ecological relevance of transport in waste disposal systems in Western Europe. Waste Manag. 2007, 27, S47–S57. [Google Scholar] [CrossRef] [PubMed]
- Aryan, Y.; Yadav, P.; Samadder, S.R. Life Cycle Assessment of the existing and proposed plastic waste management options in India: A case study. J. Clean. Prod. 2019, 211, 1268–1283. [Google Scholar] [CrossRef]
- Sonesson, U. Modelling of the Compost and Transport Process in the ORWARE Simulation Model; Department of Agricultural Engineering, Swedish University of Agricultural Sciences: Uppsala, Sweden, 1996; p. 35. [Google Scholar]
- Curtis, E.M.; Dumas, R.D. A Spreadsheet Process Model for Analysis of Costs and Life-Cycle Inventory Parameters Associated With Collection of Municipal Solid Waste; North Carolina State University: Raleigh, NC, USA, 2000; p. 272. [Google Scholar]
- Doka, G. Life Cycle Inventories of Waste Treatment Services. Ecoinvent Report no 13; Swiss Centre for Life Cycle Inventories: Dübendorf, Switzerland, 2009. [Google Scholar]
- Baumann, H.; Tillman, A.-M. The Hitch Hiker’s Guide to LCA: An Orientation in Life Cycle Assessment Methodology and Applications; Studentlitteratur: Lund, Sweden, 2004. [Google Scholar]
- Bjarnadóttir, H.J.; Friðriksson, G.B.; Johnsen, T.; Sletsen, H. Guidelines for the Use of LCA in the Waste Management Sector; Nordtest Report TR 517; Nordtest: Espoo, Finland, 2002. [Google Scholar]
- Larsen, A.W.; Vrgoc, M.; Christensen, T.H.; Lieberknecht, P. Diesel consumption in waste collection and transport and its environmental significance. Waste Manag. Res. 2009, 27, 652–659. [Google Scholar] [CrossRef] [PubMed]
| Software | Country | Launch Time | Reference |
|---|---|---|---|
| ORWARE (a) | Sweden | 1997 | [36,37] |
| EPIC/CSR (b) | CA | 1999 | [38,39,40] |
| MSW-DTS (c) | USA | 1999 | [41,42] |
| WIZARD (d) | UK, FR, NZ | 1999 | [43] |
| IWM-2 (e) | United Kingdom | 2001 | [44] |
| SSWMSS (f) | Japan | 2004 | [45,46] |
| LCA IWM (g) | European Union | 2005 | [47,48,49] |
| WRATE (h) | United Kingdom | 2007 | [50,51] |
| EASEWASTE (i) | Denmark | 2008–2009 | [52] |
| EASETECH (j) | Denmark | 2013 | [53] |
| SWOLF (k) | USA | 2014 | [54] |
| Units of Energy Consumption | Waste Truck, in Collecting Route | Waste Truck, from the Collection Area to the Unloading Point | Waste Truck, Idling | |
|---|---|---|---|---|
| ORWARE (a) | L/(t.km) | 0.24 | 0.13 | |
| MSW-DST (a) | L/km | 1.18 | 0.47 | |
| L/h | 0.26 | |||
| Ecoinvent | L/(t.km) | 0.42 |
| Input Data | Default Parameters and Intermediate Calculations |
|---|---|
| WT: total amount of waste collected (kg) dens: waste density (kg/m3) Freq: collection frequency (year-1) C: number of containers (-) Vc: average volume per container (m3/C) Vt: volume capacity of the truck (m3/truck) D1: distance between the parking lot and the collection route (a) (km) D3: distance from the collection area (a) to the unloading site (km) Dc: distance in between individual containers (km/C) D4: distance between the unloading site and the parking lot (km) TT: duration of the working day (h) | βj: consumption truck correction factor (-) Pl: maximum payload capacity of the truck (kgload) Aj: diesel consumption of the empty truck, depending on the type of road (kgdiesel/km) Bj: diesel consumption of the full truck, depending on the type of road (kgdiesel/km) Fcomp: diesel consumption factor while the truck is lifting containers and compacting waste (kgdiesel/h) Wbox: weight of the box truck (kg) Fillc: average container fill ratio (%) crt: compaction ratio of the truck (-) ef: collection efficiency in number of containers collected per hour (C/h) Scol: average speed while collecting (km/h) Stransp: average speed while transporting (km/h) Tcomp: time spent loading and compacting waste (h) Tunload: time spent unloading waste (h) Tluch: time for lunch break (h) Ttransp: total time spent while transporting (h) Tcol: time spent collecting (h) D2: total distance spent while collecting waste (effective collection distance) (km) N: number of trips per truck (-) |
| Output Data | |
| αj: share of km traveled in each type of road (-) Ur: utilization (fill) ratio of the truck by mass (-) DT: distance of one full trip of the waste collection truck (km) |
| Waste Fraction Collected | Route Code | Amount Collected (t/year) | Annual Distance (km/year) | Annual Diesel Consumption (L/year) | Performance Indicators | |
|---|---|---|---|---|---|---|
| L/100 km | L/t | |||||
| Glass | G1 | 189 | 5996 | 1716 | 28.6 | 9.1 |
| G2 | 124 | 2637 | 755 | 28.6 | 6.1 | |
| MSW | MSW1 | 2039 | 22,919 | 24,935 | 108.8 | 12.2 |
| MSW2 | 3015 | 47,265 | 30,216 | 63.9 | 10.0 | |
| MSW3 | 1990 | 35,078 | 23,475 | 66.9 | 11.8 | |
| Light Packaging Waste | LP1 | 76 | 3877 | 1956 | 50.4 | 25.6 |
| LP2 (a) | 139 | 2990 | 1765 | 59.1 | 12.7 | |
| LP3 | 165 | 5347 | 4390 | 82.1 | 26.6 | |
| LP4 | 92 | 2147 | 2335 | 108.8 | 25.3 | |
| Paper and Cardboard | P1 | 144 | 2773 | 1606 | 57.9 | 11.2 |
| P2 (a) | 248 | 2584 | 1525 | 59.1 | 6.2 | |
| P3 | 293 | 6747 | 5540 | 82.1 | 18.9 | |
| P4 | 201 | 2651 | 2884 | 108.8 | 14.4 | |
| P5 | 332 | 5788 | 3873 | 66.9 | 11.7 | |
| Waste Fraction Collected | Route Code | Experimental(L/t) | Relative Deviation from Experimental Data | |||
|---|---|---|---|---|---|---|
| FENIX | ORWARE | MSW-DST | Ecoinvent | |||
| Glass | G1 | 9.1 | −0.34 | 0.54 | −0.04 | 0.70 |
| G2 | 6.1 | 0.20 | 0.92 | 0.85 | 1.25 | |
| MSW | MSW1 | 12.2 | 0.44 | −0.19 | −0.69 | −0.26 |
| MSW2 | 10.0 | −0.11 | 0.46 | −0.55 | 0.07 | |
| MSW3 | 11.8 | 0.63 | 0.06 | −0.62 | −0.34 | |
| Light Packaging Waste | LP1 | 25.6 | −0.11 | −0.48 | 0.57 | −0.38 |
| LP2 | 12.7 | −0.13 | −0.09 | 0.48 | 0.22 | |
| LP3 | 26.6 | −0.25 | −0.66 | −0.01 | −0.58 | |
| LP4 | 25.3 | 0.26 | −0.73 | −0.27 | −0.69 | |
| Paper and Cardboard | P1 | 11.2 | −0.01 | −0.17 | 0.20 | −0.19 |
| P2 | 6.2 | 0.12 | 0.48 | 0.36 | 0.80 | |
| P3 | 18.9 | −0.11 | −0.38 | −0.02 | −0.26 | |
| P4 | 14.4 | 0.19 | −0.45 | −0.31 | −0.42 | |
| P5 | 11.7 | 0.65 | −0.27 | −0.48 | −0.41 | |
| Sum of the squared deviations | 1.41 | 3.27 | 3.01 | 4.35 | ||
| INPUT DATA | CALCULATED DATA | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Waste (t) | Working Day (h) | Yearly Freq. | N. Cont | Container Volume (m3) | Truck Volume (m3) | Dist Parking-Fist Cont | Dist End Coll-Unloading | Dist Unloading Point -Parking | Dist between Collection Areas | Performance (n.cont/h) | (kg diesel/(t.km)) | Annual km Traveled | km/trip | l/year | l/t | |
| Baseline | 92.2 | 8 | 55 | 449 | 0.25 | 22 | 1.7 | 10.2 | 10.7 | 0 | 41.2 | 0.86 | 3462 | 31 | 2928.48 | 31.76 |
| 1 | 92.2 | 8 | 55 | 269 | 0.25 | 22 | 1.7 | 10.2 | 10.7 | 0 | 41.2 | 0.49 | 2184 | 40 | 2171.13 | 23.55 |
| 2 | 92.2 | 8 | 55 | 494 | 0.25 | 22 | 1.7 | 10.2 | 10.7 | 0 | 41.2 | 1.00 | 3462 | 31 | 3419.55 | 37.09 |
| 3 | 92.2 | 8 | 70 | 449 | 0.25 | 22 | 1.7 | 10.2 | 10.7 | 0 | 41.2 | 1.20 | 4406 | 31 | 4123.59 | 44.72 |
| 4 | 92.2 | 8 | 110 | 449 | 0.25 | 22 | 1.7 | 10.2 | 10.7 | 0 | 41.2 | 1.88 | 6923 | 31 | 6435.03 | 69.79 |
| 5 | 92.2 | 6 | 55 | 449 | 0.25 | 22 | 1.7 | 10.2 | 10.7 | 0 | 41.2 | 1.20 | 4739 | 29 | 3853.33 | 41.79 |
| 6 | 92.2 | 4 | 55 | 449 | 0.25 | 22 | 1.7 | 10.2 | 10.7 | 0 | 41.2 | 1.44 | 6016 | 27 | 4280.64 | 46.43 |
| 7 | 92.2 | 8 | 55 | 449 | 0.25 | 22 | 3.4 | 20.4 | 21.4 | 25 | 39.3 | 0.67 | 7257 | 66 | 4915.81 | 53.32 |
| 8 | 92.2 | 8 | 55 | 449 | 0.25 | 22 | 3.4 | 20.4 | 21.4 | 50 | 37.5 | 0.64 | 8602 | 78 | 5469.50 | 59.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bala, A.; Raugei, M.; Teixeira, C.A.; Fernández, A.; Pan-Montojo, F.; Fullana-i-Palmer, P. Assessing the Environmental Performance of Municipal Solid Waste Collection: A New Predictive LCA Model. Sustainability 2021, 13, 5810. https://doi.org/10.3390/su13115810
Bala A, Raugei M, Teixeira CA, Fernández A, Pan-Montojo F, Fullana-i-Palmer P. Assessing the Environmental Performance of Municipal Solid Waste Collection: A New Predictive LCA Model. Sustainability. 2021; 13(11):5810. https://doi.org/10.3390/su13115810
Chicago/Turabian StyleBala, Alba, Marco Raugei, Carlos Afonso Teixeira, Alberto Fernández, Francisco Pan-Montojo, and Pere Fullana-i-Palmer. 2021. "Assessing the Environmental Performance of Municipal Solid Waste Collection: A New Predictive LCA Model" Sustainability 13, no. 11: 5810. https://doi.org/10.3390/su13115810
APA StyleBala, A., Raugei, M., Teixeira, C. A., Fernández, A., Pan-Montojo, F., & Fullana-i-Palmer, P. (2021). Assessing the Environmental Performance of Municipal Solid Waste Collection: A New Predictive LCA Model. Sustainability, 13(11), 5810. https://doi.org/10.3390/su13115810








