Electrification of Highway Transportation with Solar and Wind Energy

Abstract

Global warming has triggered waves of public awareness to surface very strongly worldwide, urging to eliminate all greenhouse gas emissions in a timely fashion. Among all feasible approaches to achieving this goal, using renewables to replace fossil fuels and electric vehicles (EVs) to replace conventional internal combustion engine vehicles is arguably a top-priority task. However, there is a severe lack of practical approaches to measuring a proper renewable mix for powering EVs in a large highway network while also considering renewables’ seasonal availability and the possible need to regulate the production and consumption of renewable energy with grid-scale battery arrays installed at certain locations. This urgent need motivates developing the mixed-integer programming model as presented in this paper. Furthermore, a comprehensive case study on Taiwan’s national highways covers such useful knowledge as the process to prepare key numeric data, especially local solar and wind energy and highway traffic, in-depth analysis on model solutions to reveal the overall availability of renewable energy across the highway network, and close measurements on the required investments. These findings support using renewable energy to power EVs on a national highway and reveal the importance of local business involvements. However, a relatively small country, such as Taiwan, can still display significant variations in renewable power availability. In a stand-alone setting for power usage, these variations would result in massive volumes of renewable energy not used by highway travel in some seasons. These details demonstrate the applicability and values of the proposed model in a real situation.

1. Introduction

Excessive use of coal, oil and other fossil fuels by mankind has created environmental problems of various magnitudes worldwide. Among these problems, global warming, triggered by high volumes of greenhouse gases (GHGs) continuously released into the atmosphere for many decades, receives the most attention due to its potentials to create disastrous impacts on the entire world. In response, delegates from those 195 countries participating in the 21st session of the Conference of the Parties made a landmark decision on 12 December 2015 that they unanimously agreed to adopt The Paris Agreement [1], thereby declaring a specific temperature-mitigation target for all mankind to achieve so that global warming can be kept in check:

“Holding the increase in the global average temperature to well below 2 °C above pre-industrial levels and to pursue efforts to limit the temperature increase to 1.5 °C above pre-industrial levels, recognizing that this would significantly reduce the risks and impacts of climate change”.

[1]

Reducing GHGs emitted into the atmosphere is key to mitigating global warming. In terms of global emission volume, transport emits the second-most GHGs among all major economic sectors (only next to the power sector). As an example, transport alone was responsible for creating 7.3 GtCO₂e (gigatonnes of equivalent carbon dioxide), or 23%, of the entire world’s CO₂ emissions in 2012 [2]. A significant portion of these emissions is produced by internal combustion engine vehicles (ICEVs) burning petroleum fuels. In many industrialized countries, this dependency on fossil fuel for road transportation is so heavy that as much as 96% of transportation energy is extracted from petroleum fuels [3]. In the wake of global warming, this situation has naturally stimulated strong motivations worldwide to decarbonize road transport as quickly as possible, and replacing conventional ICEVs with new vehicles designed to use so-called alternative fuels is perceived by many as an essential strategy among all possible approaches. Using such fuels as electricity, natural gas, hydrogen or biodiesel rather than conventional fossil fuels, these alternative-fuel vehicles (AFVs) [4,5,6,7,8,9,10] are more environmentally friendly than ICEVs. According to United Nations Environment Programme (UNEP), by adopting AFVs, improving fuel efficiency and adopting other effective measures, global road transport can potentially reduce emissions by as much as 2.88 GtCO₂e annually around 2030 [11]. This will certainly make a significant contribution to the worldwide campaign against global warming.

There are several types of electric vehicles (EVs) [12]. Among them, battery electric vehicles (BEVs) are those EVs powered with pure electricity, which means they do not produce any exhaust emissions to pollute the air or nourish global warming. When moving on the road, BEVs are also quieter than other vehicles because their power source is an electric motor. Fuel efficiency is another major attracting feature of BEVs. According to Lorf et al. [13], the power source is the single most important factor influencing vehicle energy consumption. In their comprehensive study, which covers 40 different vehicles, BEVs deliver a group average of 144 Wh/km. In other words, they require an approximate 144 Watt-hour of electricity to travel one kilometer of distance. In the same study, the fuel performance for plug-in hybrid electric vehicles (PHEVs), hybrid electric vehicles (HEVs) and ICEVs is 271, 389 and 550 Wh/km, respectively. Hence, on average, ICEVs require several times of energy than BEVs to travel the same distance; moreover, the higher the degree of electrification, the better the vehicle fuel economy [13] (p.15)! The attractiveness of BEVs further includes a lower manufacturing resource requirement because their powertrain is generally simpler in configuration than other types of vehicles [14]. This also implies fewer resources required to process BEVs at the end of their lifecycle. Last but not the least, when there is a sufficient number of BEVs running on the road one day, they can collectively be used as a gigantic, mobile energy reservoir, saving or releasing power whenever and wherever needed. Called vehicle-to-grid (V2G) [15,16], this is an emerging technology, which is expected to improve power grid utilization by a better balancing power supply with actual demand. Therefore, BEVs can bring various benefits to the economy, environment and society, that is, the “triple bottom line” of sustainable development [17,18]. As the major concerns surrounding their convenience of use, especially limited driving range and restricted battery charging locations, are being and will continue to be improved, BEVs are arguably a very attractive substitute for conventional ICEVs.

Although the aforementioned electrification of road transport is a promising strategy, it is still necessary to power BEVs with as much renewable energy (RE) as possible. According to European Environment Agency (2016), if BEVs are totally powered with RE, their lifecycle CO₂ emissions will be approximately 50% less than the volumes emitted by PHEVs also powered with renewables, and two-thirds less than the volumes emitted by ICEVs powered with petroleum fuels. On the other hand, when totally using coal electricity, BEVs will ironically surpass ICEVs to become the champion of CO₂-producing vehicles [12] (p.45)! Noori et al. [19] also confirm the significance of power sources to the true effectiveness of BEVs in combating global warming. The necessity to enable BEVs to run on RE is further supported by the fact that electricity/heat is the top CO₂-emitting sector, and the top-two sectors (that is, electricity/heat and transport) are already responsible for creating nearly two-thirds of global CO₂ emissions [2]. Therefore, it makes perfect sense to coordinate these two sectors, so their decarbonization can receive the effect of “one plus one greater than two” [20,21]. In recent years, the rapid decline in solar and wind energy costs, which have fallen below 3.0 US cents/kWh (kilowatt-hour) in more than one country [22], has created a cost-competitive situation for these renewables, allowing them to accelerate market expansion in the current power mix. At the same time, there are also studies confirming the feasibility of using only renewables to drive the entire economy [19,21,23]. For road transport, García-Olivares et al. [24] confirm the feasibility of a 100% renewable transportation and expect it to deliver energy savings as much as 69% (while maintaining the same service level as provided in 2014). Chandra Mouli et al. [25] and Bhatti et al. [26] investigate technical issues for using solar energy on EVs. Onat et al. [27] observe a notably lower water consumption in most American states when their EVs use solar PV (photovoltaic) as the only power source. Moreover, in addition to rooftop and open ground, solar PV can now be installed at several new locations, such as road surface [28] and water surface [29]. All these are contributions accomplished to facilitate/accelerate the decarbonization of the power and road transport sectors.

Although a good volume of EV/BEV research findings is available at the present time, there are not enough studies focusing on large-scale RE planning. Especially, there are only a handful of papers addressing issues concerning solar/wind energy planning for large transportation networks such as national highways. To be precise, there is still not enough study on hybrid RE planning for national highways with various types of BEVs (sedan, trucks, buses, etc.) constantly moving, and some require a battery recharge on the highway to complete the travel. Compared to other RE, solar and wind energy is available around the globe. However, they are different from conventional power in their availability; that is, they are generally available across a region in a decentralized fashion. In addition, their availability is intermittent throughout the day, with supply volumes varying from one day/season to the next (sometimes, the variation is quite significant). Moreover, due to the differences in regional climates, a specific solar/wind energy mix is rarely ideal for all charging locations in the transportation network. These differences create serious challenges for policymakers, as it is clearly very difficult to determine an appropriate set of locations for BEVs to recharge batteries using locally produced RE (that is, the energy is produced by solar panels or wind turbines at nearby locations). This location-sizing problem [30] has another challenge due to the possible need to install grid-scale battery arrays at some charging locations, saving enough solar or wind energy for later usage. Therefore, it is these reasons providing enough momentums for researching this paper. The objective is to develop a practical approach to deploying appropriate solar/wind/battery capacities at selected locations to enable the electrification of highway transportation with RE. As discussed in preceding paragraphs, the impact of this research will be global, therefore, very significant.

The rest of this paper proceeds as follows: Related research is reviewed in the next section. A mixed-integer programming (MIP) model formulated to serve as the main decision tool is presented in Section 3. This MIP model is then used in a comprehensive case study in Section 4, creating an appropriate solar/wind energy mix for Taiwan’s national highway network. Finally, conclusions and future research are elaborated in Section 5.

2. Literature Review

The location-sizing problem concerns locating refueling or charging stations in the transportation network with appropriate capacities to service corresponding demands. Generally, the construction of these facilities requires substantial investments to cover various expenditures, including charger payments, installation management, and power utility connections [31]. Take chargers as an example. Each charger capable of doing 150 kW super-fast charging would cost USD 76,000 to USD 100,000 [32]. Since stations must have capacities to serve multiple vehicles at any time, the required investments can easily reach a million or more. The location and capacity of these facilities have direct impacts on economic activities. If not planned well, they cause serious traffic problems and lead to a tremendous economic loss. Consequently, this problem has attracted substantial worldwide attention, with various solution approaches developed for different settings.

There are three major approaches to solving a location-sizing problem, that is, node-based, flow-based, and equilibrium-based [33]. The node-based approach solves problems with refueling or charging demands occurring at certain nodes. Generally, this approach considers the origin or destination of a traffic flow, which can be a household, workplace, or shopping mall, as a potential service location [34,35,36]. In addition to nodes, charging/refueling demand could also have a flow appearance, e.g., traffic flows moving on a national highway. In this case, the demand representation is often an origin-destination (O–D) flow, and the corresponding solution approach would attempt to satisfy the most traffic flows. According to Shen et al. [33] and Ghamami et al. [37], the flow-based approach is superior to its node-based counterpart in capturing drivers’ refueling/recharging behaviors. As for the equilibrium-based approach [38,39], it often considers driver behavior in choosing a route. Typically, drivers would choose a route with minimum social costs or maximum social welfare to refuel or recharge their vehicle.

The focus of this study is flow-based. Early flow-based work is the flow-capturing location model [40], which targets the capturing (that is, satisfying) of as much traffic flow as possible for a given set of refueling facilities. This model considers vehicle satisfaction as one or more facilities located anywhere on a vehicle’s travel route to refuel that vehicle. In other words, drivers can finish their journey as long as they can refuel the vehicle once and no matter where on the road. Obviously, such a viewpoint does not reflect the real situation. As an improvement to that, Kuby and Lim [5] proposed the flow refueling location model (FRLM) to allow vehicles to make multiple refueling stops. The execution of the FRLM consists of two steps: The first step runs a preprocessing procedure to generate all possible node combinations, with each capable of refueling all travel routes; the second step uses these combinations to solve the model. The calculation of node combinations is quite time-consuming, thus limiting the practical usage of the FRLM. Later, Lim and Kuby [7] developed several heuristic algorithms to improve its runtime.

Among all location-sizing problems, solving the scenario of intercity travel is arguably the most challenging. This kind of travel requires EVs to run long distances. Consequently, most people would do “en-route charging” to mitigate range anxieties [41]. In other words, EV drivers would recharge whenever they can on the road; sometimes, this may even require a detour). At present, there is already a significant body of research investigating various scenarios/issues in intercity travel. Many of these works are extensions from the FRLM; therefore, they are also mixed-integer linear or nonlinear programming (MILP or MINLP) formulations. For instance, Capar and Kuby [10] improved the efficiency of the FRLM by erasing its uses of node combinations. Calling their solution “node cover-path cover”, they use binary variables to determine whether a candidate node is refuelable, meaning whether it can support vehicles with enough fuels to reach the next node where they may refuel again. For any vehicle to reach its destination, there must exist a set of refuelable nodes along its travel route. This feasible spacing of refuelable nodes thus creates a model with higher computation efficiencies than the FRLM. Later, Capar et al. [42] developed a similar “arc cover-path cover” (AC-PC) approach by measuring arc coverage and tested the performance on the highway network in Florida. Jochem et al. [43] investigated the problem of locating fast-charging stations for EVs traveling in two German states where the autobahn is available. They extended AC-PC [42] by considering EVs with different ranges; they observed a positive correlation between EV ranges and coverage rates.

The location-sizing problem also has occurred in very large transportation networks, e.g., a national highway system. Motivated by the emerging dynamic wireless charging technology to allow charging while driving, Fuller [44] developed an MILP model to explore the possibility of using that technology in California. Incorporating the logic of flow-based set covering [6], that model evaluated EV-related factors, including battery capacity, travel routes, and range limits, suggesting USD 2.5 billion as the minimum costs for California to use wireless charging. The idea of optimizing lane selections is significantly different from the mainstream idea of optimizing node selections. Another study on the US is the work of He et al. [45] to explore the possibility of replacing all conventional cars with EVs. Their model is also an FRLM extension, with improvements to pre-create feasible links to reduce flow-equilibrium constraints. They also adopted the K-means clustering technique to reduce other data, but still, a supercomputer was required to generate solutions. They identified 100-mile-range-EVs with charging support from 200 stations installed nationwide to be the most cost-effective. As for Europe, Jochem et al. [46] conducted cost–benefit studies on EVs doing transnational travel in eight European countries.

In addition to general highway travel, there are also works focusing on corridors, i.e., high-volume commuting corridors dedicated to long-distance highway travel. Recognizing the potential costs associated with EV adaptions on a global scale, Nie and Ghamami [47] used a nonlinear model to balance the size of EV batteries with the charging power of highway corridors. The nonlinear parts are constraints formulated to handle charging time, which is a function of battery size and charging power. This model was evaluated against a 150-mile highway corridor with all EVs making the same trip. Later, Ghamami et al. [37] considered EVs making different trips on the same corridor, followed by Ghamami et al. [48] considering the case of different corridors (which in essence are the same as general highway travel) with MINLP. They considered charging delays as well as driver behaviors due to range anxiety, using simulated annealing to identify solutions for Michigan’s highway network.

The papers reviewed so far share a common feature: They all address a single-period problem with static charging or refueling demands. However, with the entire world accelerating to embrace EVs, charging demands are growing and will probably keep growing at an exponential rate. This has stimulated a strong need to expedite the deployment of charging facilities as well as to conduct location-sizing research in a multiperiod setting [49,50]. There are several scenarios studied thus far for this research category. Chung and Kwon [49] addressed charging station deployment for South Korea’s expressway network in a six-time-period planning horizon, adding three new stations in period two to period six to cope with growing demands. Their work is an extension of the MILP model developed by MirHassani and Ebrazi [51]. Li et al. [52] developed a multiperiod, multipath refueling location model (M²PRLM) to consider station relocation (i.e., relocating an existing station) while allowing battery recharge via multiple paths. M²PRLM is an extension of the single-period multipath model developed by Huang et al. [41]. Motivated by the stochasticity of charging activities, mainly EV arrival rates and charging times, Xie et al. [53] adapted M²PRLM to locate charging stations in a multiperiod, stochastic planning setting and used M/M/c queuing models to handle those stochastic activities. Zhang et al. [50] enhanced the AC-PC model [42] to deploy charging stations in the northeast region of the US, accounting for capacity limits and time-varying demands. More recently, Tran and Nguyen [54] investigated the impact of failing alternative-fuel stations on the highway. Their MINLP model is FRLM-based, with each station possessing a certain probability to fail; their optimization target is the stations to be added in each period.

Recently, the power source has received rising attention in location-sizing research. The main cause for this phenomenon is EVs. As their number is increasing exponentially, securing their energy supply has become a priority issue. Generally, this energy would come from the power grid or new energy sources, such as solar or wind power. Among research related to this subject, there are studies investigating the suitable moment to recharge EVs, as charging activities may start to affect power grid operations once EVs have reached a certain total volume. Furthermore, there are grid restrictions that influence the deployment of charging facilities [55,56]. These are also studies exploring the potential of using solar power to charge EVs directly at common locations, such as households [57,58], workplaces [25], parking lots [59], and gas stations [60]. For RE applications like these, costs and impacts to the power grid are key research issues.

At present, there is only a handful of studies addressing power issues for highway travel. Zhang et al. [55] extended the capacitated FRLM to study power distribution and node voltage for locating fast chargers on the highway. In another work, Zhang et al. [61] used solar energy to alleviate carbon emissions; they formulated the problem as a second-order cone-programming model and then used an iterative column generation algorithm to create solutions. Zhang et al. [55] and Zhang et al. [61] conducted numerical tests on the same 25-node highway example [62]. For real highways, Mourad et al. [63] used MIP to locate fast-charging stations for small electric cars and heavy electric trucks traveling in the Paris-Saclay region. Their power source includes both conventional and solar power. To measure solar energy generation, they used a given number of solar panels and evaluated local solar radiance, cloudiness index, and seasonal factors. Neither Zhang et al. [61] nor Mourad et al. [63] covered location-sizing decision-making for using the renewables. To our best understanding, the research setting of Xie et al. [30] is the closest to this work. They used off-grid solar power to supply energy to charging stations on the highway. Their solution is a two-stage optimization approach, with the first one making the location decision and the second one making the sizing decision on solar power and battery capacity. They also addressed the stochastic nature of traffic demand and solar power with distributionally robust optimization (DRO), which describes uncertainties with a collection of inexact distributions.

Table 1. Classification of prior studies of intercity/highway travel.

Prior Study	Modeling Approach	Objective Function	Vehicle Types	Time Period	Grid Energy	RE	Batteries
Capar and Kuby [10]	NC-PC	Max flow served	AFVs	Single	No	No	No
Capar et al. [42]	AC-PC	Max flow served	AFVs	Single	No	No	No
Nie and Ghamami [47]	NLP	Min social cost	Electric cars	Single	No	No	No
Chung and Kwon [49]	MFRLM	Max flow served	Electric cars	Multi	No	No	No
Jochem et al. [43]	FRLM	Max flow served	Electric cars	Single	No	No	No
Li et al. [52]	M2PRLM	Min total cost	Electric cars	Multi	No	No	No
Fuller [44]	FSCM	Min total cost	Electric cars	Single	No	No	No
Ghamami et al. [37]	MINLP	Min total cost	Electric cars	Single	No	No	No
Zhang et al. [50]	MCACPC	Max flow served	Electric cars	Multi	No	No	No
Xie et al. [53]	MCCSM	Min total cost	Electric cars	Multi	No	No	No
Tran and Nguyen [54]	FRLM	Max flow served	AFVs	Multi	No	No	No
He et al. [45]	FRLM	Max flow served	Electric cars	Single	No	No	No
Jochem et al. [46]	FRLM	Min number of fast charging stations	Electric cars	Single	No	No	No
Ghamami et al. [48]	MINLP	Min total cost and travel time	Multiple classes of EVs and ICEVs	Single	No	No	No
Zhang et al. [55]	CFRLM	Min total cost	Electric cars	Single	Yes	No	No
Xie et al. [30]	TSM	Min total cost	Electric cars	Multi	No	Solar	Yes
Zhang et al. [61]	SOCP	Min social cost	Electric cars	Single	Yes	Solar	No
Mourad et al. [63]	MIP	Max flow served	Electric cars and electric heavy trucks	Single	Yes	Solar	No
This work	MIP	Min total cost	Multiple categories of EVs	Multi	Yes	Solar and Wind	Yes

Vehicle related: AFV = alternative fuel vehicle; EV = electric vehicle; ICEV = internal combustion engine vehicle. Planning period related: Multi = multiperiod location decisions, or multiperiod power demands/generations. Energy related: RE = renewable energy. Modeling related: FRLM = flow refueling location model; CFRLM = capacitated FRLM; AC-PC = arc cover-path cover; MFRLM = multiperiod FRLM; MCACPC = multiperiod capacitated AC-PC; NC-PC = node cover-path cover; M²PRLM = multiperiod, multipath refueling location model; MCCSM = multiperiod chance-constrained stochastic model; MINLP = mixed-integer nonlinear programming; MIP = mixed-integer programming; NLP = nonlinear programming; TSM = two-stage optimization model; SOCP = second-order cone programming; FSCM = flow-based set covering model.

is a summary of selected location-sizing studies published after 2012 with a special focus on intercity/highway travel. The following highlights their major differences from this study:

• Several papers proposed multiperiod location models. Researchers, including Zhang et al. [50] and Xie et al. [53], also considered charging capacities. However, none addressed power source issues;
• Zhang et al. [61] and Mourad et al. [63] conducted numerical tests with a single renewable to supply the required energy; their highway setting is simulated or real, but small-scale;
• With consideration of location, sizing, and battery capacity for using solar power, the research setting of Xie et al. [30] is the closest to this study. However, they only considered a single renewable and applied the solution to a 24 h example, with simulated energy demands and supplies created for each hour. The applicability of that solution remains unclear in a real situation.

3. Optimization Model

As EVs are widely recognized as a critical element in the global campaign against climate change, the electrification of road transportation has become a priority task for countries all over the world. However, it is quite difficult to estimate the required investments, or in technical terms, to measure the required energy to support these vehicles running on the road. Due to the worsening situation in global warming, the very high utilization of renewables to produce clean energy is the preferred choice naturally. This priority task would become especially challenging when it involves a very large transportation network, such as a national highway system; the reason is changing climate conditions from one location to another. This variation thus results in different availabilities of RE for different areas in the transportation network. Often, the situation is that renewables, such as solar and wind power, are in abundant supply during certain seasons, or they are preferred only in certain locations. In addition, it may be necessary to deploy battery storage systems (e.g., grid-scale battery arrays) in certain places. How to determine a proper mix of various renewables along with an optional battery array to supply EVs with uninterrupted energy while satisfying various requirements, such as budgets or local/national regulations or development plans, presents a tremendous challenge for all governments.

The above discussions thus point to mathematical programming as an appropriate decision-making methodology. It is capable of evaluating energy supplies from various sources versus charging demands from EVs, deploying a suitable size of renewable power and battery storage at the right locations, and satisfying every constraint or performance requirement with minimum costs. The following are major assumptions adopted to develop a mathematical programming model for the location-sizing problem focused on this study.

• RE will be the primary energy to recharge EVs on the highway (e.g., 90% of all charging energy or higher); the main purpose of using conventional power is peak shaving;
• Each charging location along the highway will use local renewables, e.g., a nearby solar or wind farm with a size determined by the model, to supply the required RE. The battery storage system is an optional choice to ensure uninterrupted energy supply;
• There will be no RE injected into the power grid (to meet charging demands elsewhere).

The first assumption echoes the key strategy to charge EVs with as much RE as possible to maximize their environmental benefits [12,19,21,24]. The second assumption has the purpose of maximizing utilizing local renewables; also, it provides strong stimulation to local energy businesses. As the model will evaluate all charging demands versus all potential RE supplies that are available in the network through the entire year, it will identify the right locations and use the right local renewables to produce the right volume of RE. As for the third assumption, in addition to maximizing the efficiency in using RE, it will also help avoid major technical issues, especially voltage and frequency regulation, that the power grid must handle to accommodate huge volumes of energy injected from renewable sources. (Generally, resolving these major technical issues would require a costly upgrade to the transmission and distribution network and certain critical components in the electricity network [64].)

Since EVs on the highway will receive energy supply directly from local renewables (as opposed to the power grid), the deployment of battery energy storage systems (BESSs) thus becomes a critical decision. Particularly if solar or wind power is the primary energy source, their intermittent energy production could cause substantial fluctuations in frequency and voltage. On such occasions, BESSs can provide crucial regulation to those disturbances and help stabilize the power system [65,66]. Not to mention that they also ensure a 24/7 energy supply with renewables [67]. At present, there are commercially available BESSs in the market, and there are several reports about their success worldwide. For example, there is a Tesla microgrid commissioned in Samoa in 2016 to provide the island with uninterrupted RE; that microgrid consists of 1.4 MW of solar panels and 750 kW/6 MWh of battery storage [68]. Another example. There is a 13 MW/52 MWh energy storage facility operating on the island of Kaua’i, Hawaii, since 2017. Using proprietary energy technologies, these installations are capable of providing such critical grid services as inertia and voltage smoothing, operating as grid forming to set proper frequency and voltage references [68]. There are also research works to improve BESSs, such as developing a coordination technique to control the state-of-charge of multiple distributed BESSs for a longer lifespan [69] or investigating the size of BESSs in relation to their rapid response to power mismatch [70]. All these are indications that battery technology will become more accessible in the near future.

In addition to the above, the model will use appropriate planning periods to allow EVs to start and finish travel in the same planning period. (If some EVs do possess a long trip that requires more than one planning period to finish, those vehicles will multiply themselves to become several different vehicles in the model, each with a shorter journey so that all these multiplied vehicles can start and finish travel in just one planning period). The model also assumes a linear relationship between EV energy consumption and their travel distances [43,48]:

$$\mathrm{minimize}{\displaystyle \sum _{i\in \mathrm{N}}{\displaystyle \sum _{r\in \mathrm{R}}{\mathrm{c}}_{ri}^{\mathrm{rnew}\text{-}\mathrm{u}}{G}_{ri}^{\mathrm{rnew}}}}+{\displaystyle \sum _{i\in \mathrm{N}}{\mathrm{c}}_i^{\mathrm{batt}\text{-}\mathrm{u}}{B}_i^{\mathrm{batt}}}+{\displaystyle \sum _{i\in \mathrm{N}}{\mathrm{c}}_i^{\mathrm{chrg}}{X}_i^{\mathrm{chrg}}}$$

(1)

subject to

$$G_{ri}^{\mathrm{rnew}}\le \mathrm{M}\times X_{ri}^{\mathrm{rnew}}\forall r\in \mathrm{R},i\in \mathrm{N}$$

(2)

$$B_i^{\mathrm{batt}}\le \mathrm{M}\times {\displaystyle \sum _{r\in \mathrm{R}}{X}_{ri}^{\mathrm{rnew}}}\forall i\in \mathrm{N}$$

(3)

$$E_{rit}^{\mathrm{rnew}}=G_{ri}^{\mathrm{rnew}}{\mathrm{e}}_{rit}^{\mathrm{rnew}\text{-}\mathrm{u}}\forall r\in \mathrm{R},i\in \mathrm{N},t\in \mathrm{T}$$

(4)

$$I_{it}^{\mathrm{rnew}}\le B_i^{\mathrm{batt}}\forall i\in \mathrm{N},t\in \mathrm{T}$$

(5)

$$I_{it}^{\mathrm{rnew}}=I_{i(t-1)}^{\mathrm{rnew}}+{\displaystyle \sum _{r\in \mathrm{R}}{E}_{rit}^{\mathrm{rnew}}}-{\displaystyle \sum _{v\in {\mathrm{V}}_t}{S}_{vit}^{\mathrm{rnew}}}-W_{it}^{\mathrm{rnew}}\forall i\in \mathrm{N},t\ge 2$$

(6)

$$I_{it}^{\mathrm{rnew}}={\displaystyle \sum _{r\in \mathrm{R}}{E}_{rit}^{\mathrm{rnew}}}-{\displaystyle \sum _{v\in {\mathrm{V}}_t}{S}_{vit}^{\mathrm{rnew}}}-W_{it}^{\mathrm{rnew}}\forall i\in \mathrm{N},t=1$$

(7)

$${\displaystyle \sum _{v\in {\mathrm{V}}_t}{S}_{vit}^{\mathrm{conv}}}\le \mathrm{M}\times {\displaystyle \sum _{o\in \mathrm{O}}{X}_{oi}^{\mathrm{conv}}}\forall i\in \mathrm{N},t\in \mathrm{T}$$

(8)

$${\displaystyle \sum _{r\in \mathrm{R}}{X}_{ri}^{\mathrm{rnew}}}+{\displaystyle \sum _{o\in \mathrm{O}}{X}_{oi}^{\mathrm{conv}}}\le \mathrm{M}\times X_i^{\mathrm{chrg}}\forall i\in \mathrm{N}$$

(9)

$$S_{vit}^{\mathrm{rnew}}+S_{vit}^{\mathrm{conv}}\le {\mathrm{b}}_v-E_{vit}^{\mathrm{EV}}\forall t\in \mathrm{T},v\in {\mathrm{V}}_t,i\in \mathrm{N}$$

(10)

$$E_{vit}^{\mathrm{EV}}=E_{vkt}^{\mathrm{EV}}+S_{vkt}^{\mathrm{rnew}}+S_{vkt}^{\mathrm{conv}}-{\mathrm{e}}_{vki}{F}_v\forall t\in \mathrm{T},v\in {\mathrm{V}}_t,(k,i)\in \mathrm{L}$$

(11)

$$S_{vit}^{\mathrm{rnew}}+S_{vit}^{\mathrm{conv}}\le {\mathrm{b}}_v{F}_v\forall t\in \mathrm{T},v\in {\mathrm{V}}_t,i\in \mathrm{N}$$

(12)

$${\displaystyle \sum _{t\in \mathrm{T}}{\displaystyle \sum _{v\in {\mathrm{V}}_t}{F}_v}}\ge {\rho }^{\mathrm{EV}}\times {\displaystyle \sum _{t\in \mathrm{T}}\left|{\mathrm{V}}_t\right|}$$

(13)

$${\displaystyle \sum _{t\in \mathrm{T}}{\displaystyle \sum _{v\in {\mathrm{V}}_t}{\mathrm{d}}_v{F}_v}}\ge {\rho }^{\mathrm{dist}}\times {\displaystyle \sum _{t\in \mathrm{T}}{\displaystyle \sum _{v\in {\mathrm{V}}_t}{\mathrm{d}}_v}}$$

(14)

$${\displaystyle \sum _{t\in \mathrm{T}}{\displaystyle \sum _{v\in {\mathrm{V}}_t}{\displaystyle \sum _{i\in \mathrm{N}}{S}_{vit}^{\mathrm{rnew}}}}}\ge {\rho }^{\mathrm{rnew}}\times {\displaystyle \sum _{t\in \mathrm{T}}{\displaystyle \sum _{v\in {\mathrm{V}}_t}{\displaystyle \sum _{i\in \mathrm{N}}(S_{vit}^{\mathrm{rnew}}+S_{vit}^{\mathrm{conv}})}}}$$

(15)

$$B_i^{\mathrm{batt}}\ge 0\forall i\in \mathrm{N}$$

(16)

$$G_{ri}^{\mathrm{rnew}}\ge 0\forall r\in \mathrm{R},i\in \mathrm{N}$$

(17)

$$I_{it}^{\mathrm{rnew}},W_{it}^{\mathrm{rnew}}\ge 0\forall i\in \mathrm{N},t\in \mathrm{T}$$

(18)

$$E_{rit}^{\mathrm{rnew}}\ge 0\forall r\in \mathrm{R},i\in \mathrm{N},t\in \mathrm{T}$$

(19)

$$S_{vit}^{\mathrm{rnew}},S_{vit}^{\mathrm{conv}},E_{vit}^{\mathrm{EV}}\ge 0\forall t\in \mathrm{T},v\in {\mathrm{V}}_t,i\in \mathrm{N}$$

(20)

$$X_i^{\mathrm{chrg}}=0,1\forall i\in \mathrm{N}$$

(21)

$$X_{ri}^{\mathrm{rnew}}=0,1\forall r\in \mathrm{R},i\in \mathrm{N}$$

(22)

$$X_{oi}^{\mathrm{conv}}=0,1\forall o\in \mathrm{O},i\in \mathrm{N}$$

(23)

$$F_v=0,1\forall t\in \mathrm{T},v\in {\mathrm{V}}_t$$

(24)

The model’s objective function (1) minimizes the total capital investment costs, consisting of the costs to acquire an appropriate power generating capacity $G_{ri}^{\mathrm{rnew}}$ (e.g., 20 megawatts, or 20 MW, of solar panels) for each renewable $r$ to provide clean energy at every node $i$ in the highway network (${\mathrm{c}}_{ri}^{\mathrm{rnew}\text{-}\mathrm{u}}$ is the corresponding unit acquisition cost, N is the set of nodes and R is the set of renewables under consideration), the costs to establish an appropriate battery storage capacity $B_i^{\mathrm{batt}}$ (e.g., 50 megawatt-hours, or 50 MWh, of batteries) to save surplus energy at each node $i$ (${\mathrm{c}}_i^{\mathrm{batt}\text{-}\mathrm{u}}$ is the battery’s unit cost) and the costs to provide charging service at each node $i$ ($X_i^{\mathrm{chrg}}$ is a binary variable defined as follows: $X_i^{\mathrm{chrg}}=1$ indicates that charging service will be available at node $i$ and $X_i^{\mathrm{chrg}}=0$ indicates the otherwise situation).

In constraint (2), M is a very large user-defined positive number and $X_{ri}^{\mathrm{rnew}}$ is a binary variable dictating whether renewable $r$ will be deployed at node $i$ to provide RE. Clearly, if for some reason it is not necessary to do so at node $i$ (i.e., $X_{ri}^{\mathrm{rnew}}=0,\forall r\in \mathrm{R}$), $B_i^{\mathrm{batt}}$ will be zero due to constraint (3); that is, batteries will not be needed at that node.

Using $G_{ri}^{\mathrm{rnew}}$ and ${\mathrm{e}}_{rit}^{\mathrm{rnew}\text{-}\mathrm{u}}$ (a user-provided parameter in MWh or kWh, which represents the volume of RE that each unit of $r$ is expected to produce around node $i$ during the planning period $t\in \mathrm{T}$), constraint (4) calculates the value of $E_{rit}^{\mathrm{rnew}}$, which is a decision variable defined to carry the total volume of RE produced by $r$ around node $i$ during the planning period $t$.

In constraint (5) $I_{it}^{\mathrm{rnew}}$ is a decision variable defined to carry the volume of RE that is being saved in the batteries installed at node $i$ at the end of the planning period $t$. Therefore, $I_{it}^{\mathrm{rnew}}$ must always be smaller than or equal to $B_i^{\mathrm{batt}}$. Constraints (6) and (7) calculate the actual value of $I_{it}^{\mathrm{rnew}}$, equaling the energy produced by all the renewables deployed around node $i$ during the current planning period (${\displaystyle \sum _{r\in \mathrm{R}}{E}_{rit}^{\mathrm{rnew}}}$) plus the energy left in the batteries from the previous planning period ($I_{i(t-1)}^{\mathrm{rnew}}$), then decreased by the energy transferred to EVs at that node in the current planning period (${\displaystyle \sum _{v\in {\mathrm{V}}_t}{S}_{vit}^{\mathrm{rnew}}}$, where $v$ represents an EV, ${\mathrm{V}}_t$ is the collection of EVs expected to travel on the highway during the planning period $t$ and $S_{vit}^{\mathrm{rnew}}$ is the volume of RE charged into $v$ when it arrives at node $i$), and then possibly further decreased by the energy that, for some reason, cannot be saved in the batteries for later use ($W_{it}^{\mathrm{rnew}}$). Due to the uncertain situation in energy demand and supply, it is possible that the remaining RE (that is, what is left after EVs have recharged their batteries) is so much that the batteries at node $i$ cannot save it all. Therefore, it is necessary to have $W_{it}^{\mathrm{rnew}}$ in constraints (6) and (7).

Constraint (8) is formulated to provide the option of allowing EVs to replenish their batteries with energy generated using conventional power sources, such as coal or fossil fuel, with $X_{oi}^{\mathrm{conv}}$ defined as a binary variable to indicate whether conventional energy source $o$ will be available at node $i$ or not ($X_{oi}^{\mathrm{conv}}=1$ signals the yes condition). When some $o\in \mathrm{O}$ (the set of all conventional power sources) is provided at node $i$, EVs can recharge batteries with conventional energy when arriving, and the actual energy consumption will be saved in decision variable $S_{vit}^{\mathrm{conv}}$ for each $v$.

Constraint (9) describes the scenario in which the availability of any kind of renewable or conventional energy at node $i$ implies the availability of charging service at that node. This will set the value of the binary variable $X_i^{\mathrm{chrg}}$ to one, thus activating the fixed cost ${\mathrm{c}}_i^{\mathrm{chrg}}$ of providing charging service at node $i$ to be evaluated in the objective function (1).

Constraints (10)–(12) describe how EVs consume and replenish battery power along their movement on the highway. In constraint (10), ${\mathrm{b}}_v$ denotes the battery capacity of EV $v$ and $E_{vit}^{\mathrm{EV}}$ is a decision variable indicating the power reserve of that EV when arriving at node $i$. If there is a need for v to recharge batteries at that node, the volume of additional energy that can still be held, that is, $S_{vit}^{\mathrm{rnew}}+S_{vit}^{\mathrm{conv}}$, can obviously not exceed the remaining capacity of these batteries ${\mathrm{b}}_v-E_{vit}^{\mathrm{EV}}$. Constraint (11) calculates the power reserve of the EV when finishing its travel on $(k,i)\in \mathrm{L}$, where $(k,i)$ represents a road segment in the highway with $k$ being the starting node and $i$ being the ending node, respectively, and $\mathrm{L}$ is a set containing all such road segments. This power reserve is calculated using the energy carried by the vehicle to start the travel on $(k,i)$ and the power required to complete that travel. The starting power equals the power reserve of the vehicle when it arrives at node $k$ ($E_{vkt}^{\mathrm{EV}}$) plus the new power acquired through battery recharge at that node ($S_{vkt}^{\mathrm{rnew}}+S_{vkt}^{\mathrm{conv}}$). The required power is expressed as ${\mathrm{e}}_{vki}{F}_v$ where ${\mathrm{e}}_{vki}$ is a parameter expressing the energy need for $v$ to complete the travel on $(k,i)$ and $F_v$ is a binary variable indicating the status of whether $v$ can finish its entire journey on the highway or not ($F_v=1$ indicates yes). Finally, constraint (12) prohibits EVs from consuming any kind of energy that is provided along the highway for battery recharge, if they are unable to complete the entire journey (for these EVs, constraint (11) will be reduced to $E_{vit}^{\mathrm{EV}}=E_{vkt}^{\mathrm{EV}}$ for every $(k,i)\in \mathrm{L}$).

Constraints (13)–(15) are formulated to ensure the achievement of certain performance by the highway’s RE system. In constraint (13), $\left|{\mathrm{V}}_t\right|$ represents the size of ${\mathrm{V}}_t$ and ${\rho }^{\mathrm{EV}}$ is a user-defined parameter between zero and one. Therefore, this constraint enforces the required performance that a certain percentage of EVs will have sufficient energy to complete their entire journey on the highway (i.e., they are “covered”). In constraint (14) ${\mathrm{d}}_v$ denotes the total distance of the journey that $v$ will travel on the highway and ${\rho }^{\mathrm{dist}}$, again, is a parameter between zero and one. Since the left-hand side of the inequality calculates the total distance traveled by all covered EVs, the purpose of this constraint is to enforce coverage from a distance perspective. Constraint (15) enforces the requirement that certain energy consumption must be renewable (${\rho }^{\mathrm{rnew}}$ is a parameter representing the desired percentage).

Finally, constraints (16) through (24) specify the range of allowable values for each decision variable.

4. Case Study

This section contains a comprehensive case study using Taiwan’s highway network as the study subject. By viewing all vehicles running on the highway as pure BEVs, the MIP model (Section 3) will measure the volume of RE and batteries, which are potentially required to sustain such a 100% electrification of highway transportation. Since solar and wind are the main source of RE in Taiwan, they will be used to recharge BEVs when needed.

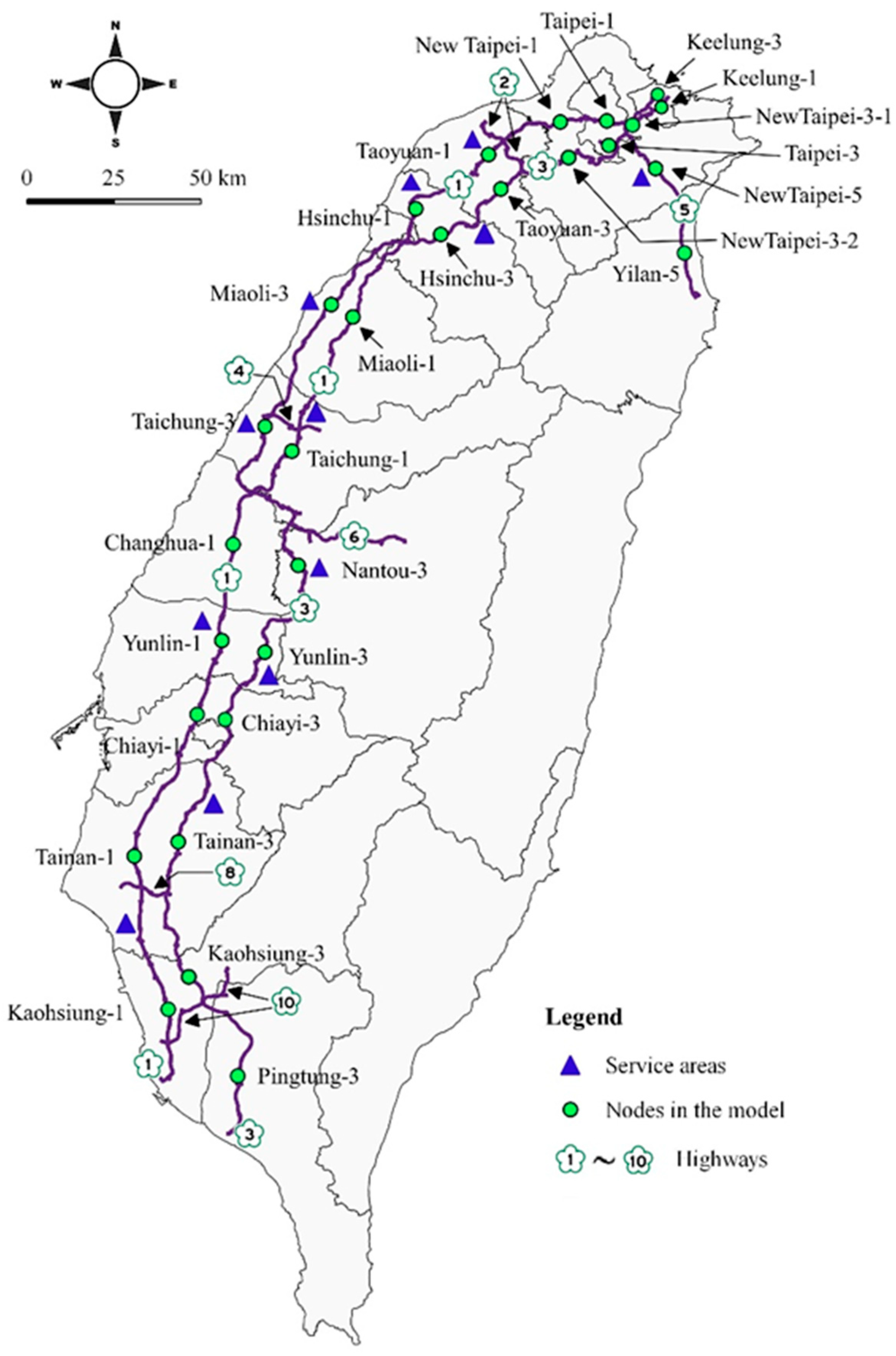
Taiwan is an island country with a total of 36,197 square kilometers of land area. The main island of Taiwan has a shape resembling a sweet potato; the distance between this potato’s north and south tips is approximately 400 km (Figure 1). Mostly covered by mountains, Taiwan has a strip of flat land situated along its west coast. Naturally, this flat area has attracted most of the 23-million Taiwanese people to congregate, thus creating a chain of heavily populated cities and counties. In 1978, Taiwan completed the construction of its first national highway, Highway #1, to connect those cities and counties. As seen in Figure 1, Highway #1 starts from Keelung (one of Taiwan’s major port cities) in the north and goes southward to connect every major city in the country, including Taipei (capital city), Taoyuan, Hsinchu, Taichung and Tainan. After traveling a total of 374 km (233 miles), Highway #1 reaches Kaohsiung (Taiwan’s biggest port city) in the south.

There is another main highway in Taiwan, Highway #3, which is built for people doing long-distance travel, especially traveling from the north to the south and vice versa in the country. This dedication effectively alleviates the heavy traffic frequently occurring on Highway #1. Starting from Keelung in the north and terminating in Pingtung in the south, Highway #3 mostly travels through suburban or rural areas and has a total length of 432 km (268 miles). There is another odd-numbered highway in Taiwan, Highway #5, which is built to connect Taipei/New Taipei and Yilan (a small city in eastern Taiwan). Finally, there are five even-numbered highways (#2, 4, 6, 8 and 10) in Taiwan. These highways have an east–west orientation to connect Highway #1 and Highway #3 or serve as a passageway between coastal areas and the mountains situated in central Taiwan. In terms of lengths, Highway #5 and those even-numbered highways are much shorter than Highway #1 and Highway #3.

4.1. Creating Highway Network and Traffic

Highways are monitored 24/7 in Taiwan. There are cameras and sensors deployed at every entrance/exit gate and along every highway to collect traffic information. Such information would go to a government database [71], where it will become available to the public. This case study uses one of the CSV files in that database to create traffic flows on the highway. With “M06A” in the filename, these CSV files contain records of essential information on every vehicle ever using the highway, including vehicle category (e.g., it is a sedan or a bus), start and finish time, start and finish gate, travel distance, and the exact route. There are many vehicles making short-distance travel on the highway; generally, these vehicles rarely need to refuel or recharge during such a trip. Therefore, this study would only consider trips that are at least 100 km long. This case study would also convert the travel time of each vehicle to categorize it as traveling in one and only one of the six-hour time slots that divide the day evenly into four parts, that is, 0:00–6:00, 6:00–12:00, 12:00–18:00, and 18:00–24:00. The consideration behind using these six-hour time slots includes the time required to make the longest highway trip in Taiwan as well as the different availability between solar and wind energy. It also means that the unit time (i.e., planning period) in the MIP model is also six hours long. Then, with computer code to identify all unique routes contained in the adjusted M06A data, a Pareto analysis analyzes their usage and indicates the top 350 routes as being used by more than 85% of the vehicles. This implies that it suffices for the MIP model to evaluate only those traffic flows occurring on the top 350 routes. The traffic data can be further simplified by integrating individual vehicles to become vehicle fleets, with each fleet consisting of the same category of vehicles (e.g., all are buses), travel time (e.g., all traveled during the 6:00–12:00 time slot on 10 April), and travel route. This allows the MIP model to evaluate a significantly smaller data set. Please refer to Appendix A for all the details on the above data processing steps.

Using M06A files with traffic data saved in January, April, July, and October of 2019, the aforementioned data processing would create four data sets for the MIP model (one for each month). Table 2 lists the volume of highway traffic contained in each set. Compared to the original M06A files kept in the government database, where over one hundred million records are regularly created every month (one for each vehicle traveling on the highway), those numbers in Table 2 indicate a significant and necessary data size reduction. The reason for choosing those four months is to cover four distinct seasons, that is, winter, spring, summer, and autumn. This would allow the model to evaluate different highway traffic and different climate conditions during different times of the year. Table 3 summarizes key parameters for all the BEV categories appearing in the four data sets. As they have an impact on where vehicles can recharge batteries on the highway, they certainly affect the decision-making of the MIP model.

This case study uses a highway network consisting of 28 nodes, with each representing a major city or county in Taiwan (Figure 1). The location of certain sensors determines the location of these nodes; Google Map is very useful in measuring their distance. Again, please refer to Appendix A for details on these node creations.

Table 2. Traffic volume evaluated by the MIP model for each season-representing month.

	January	April	July	October
Number of vehicle fleets	145,905	141,450	146,845	147,467
(Number of actual vehicles)	(3,939,970)	(4,500,876)	(4,239,003)	(3,917,507)
Total travel distance (1000 km)	621,140	717,024	672,754	617,558

Table 2. Traffic volume evaluated by the MIP model for each season-representing month.

	January	April	July	October
Number of vehicle fleets	145,905	141,450	146,845	147,467
(Number of actual vehicles)	(3,939,970)	(4,500,876)	(4,239,003)	(3,917,507)
Total travel distance (1000 km)	621,140	717,024	672,754	617,558

Table 3. Key parameters for the five major categories of BEVs on the highway.

	Sedan 1	Small Truck 2	Bus 3	Large Truck 4	18-Wheel Cargo Truck 5
Travel range (km)	300	150	250	200	200
Energy consumption rate (kWh/km)	0.21	0.55	1.3	1.13	1.8
Battery capacity (kWh)	63	83	325	226	360
Safety energy reserve for battery (kWh)	13 (20%)	17 (20%)	65 (20%)	45 (20%)	72 (20%)
Usable battery energy (kWh)	50	66	260	181	288

¹ EPA [72]; ² Rizet et al. [73] and Liebreich [74]; ³ BYD [75]; ⁴ Rizet et al. [73] and Liebreich [74]; ⁵ E-force [76].

Table 3. Key parameters for the five major categories of BEVs on the highway.

	Sedan 1	Small Truck 2	Bus 3	Large Truck 4	18-Wheel Cargo Truck 5
Travel range (km)	300	150	250	200	200
Energy consumption rate (kWh/km)	0.21	0.55	1.3	1.13	1.8
Battery capacity (kWh)	63	83	325	226	360
Safety energy reserve for battery (kWh)	13 (20%)	17 (20%)	65 (20%)	45 (20%)	72 (20%)
Usable battery energy (kWh)	50	66	260	181	288

¹ EPA [72]; ² Rizet et al. [73] and Liebreich [74]; ³ BYD [75]; ⁴ Rizet et al. [73] and Liebreich [74]; ⁵ E-force [76].

4.2. Preparing Solar and Wind Energy

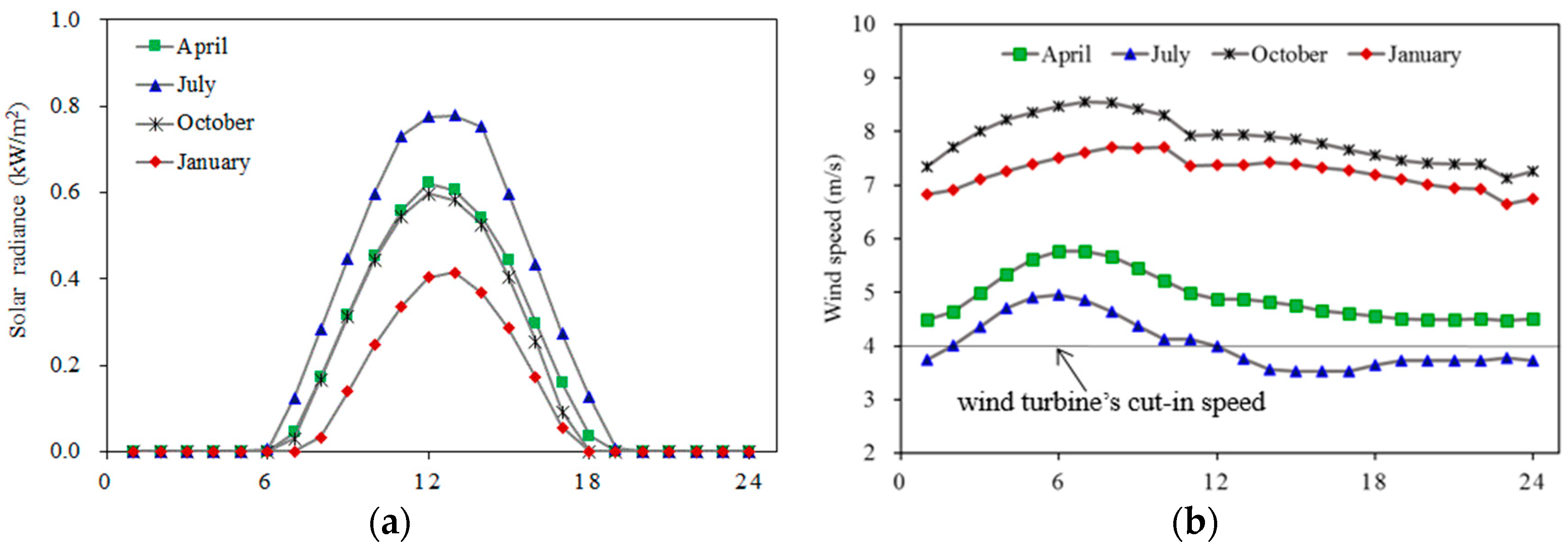
The case study used a comprehensive energy data set to determine suitable nodes to hold a solar or wind farm. For every node in the highway network, this energy data set contains the unit energy production of both renewables (i.e., the average energy produced by each MW of solar panel or wind turbine during each time slot) in January, April, July, and October. The creation of these data used the solar radiance and wind speed from 2010 to 2019 (10 years) extracted from Data Bank for Atmospheric and Hydrologic Research [77]; it also used reference information from various sources [78,79,80]. More details are available in Appendix A.

4.3. Deploying RE Optimally for Each Season-Representing Month

In addition to those aforementioned numeric data, this case study used the same assumptions as those adopted by Wang et al. [81] and Alhazmi et al. [82] such that every car in every BEV fleet would begin travel with a 50% usable energy in its battery. Furthermore, the same as Fuller [44], Li et al. [52], and Xie et al. [53], the MIP model would only consider those 12 nodes that have an existing service area (indicated by a blue triangle in Figure 1) as candidate locations to deploy a solar and/or wind farm, supplying RE to passing EVs. To evaluate capital investments, this study adopted USD 1,210,000 per MW as the unit power generation costs for solar panels, USD 1,497,000 per MW as the unit power generation costs for wind turbines [83], and USD 512,000 per MWh as the unit storage costs for battery arrays [84]. Part of these costs are expenditures to cover device installation. For overall performance, the model was adopted ${\rho }^{\mathrm{EV}}={\rho }^{\mathrm{dist}}={\rho }^{\mathrm{rnew}}=99\%$. In other words, the number of EVs that can complete their travel on the highway and these vehicles’ collective travel distance should equal (virtually) the respective total volume, and drivers should use solar or wind energy almost exclusively to recharge vehicles. Then, an Asus personal computer (equipped with an Intel i7-6700 CPU running at 3.40 GHz and 32-GB RAM) solved the MIP model with CPLEX 12.8 to identify optimal solutions for each season-representing month. These models contained approximately 140,000 binary variables and required the computer to run 40 to 90 min to reach optimality. The table in Appendix B (

Table A2. Optimal deployment of solar panels, wind turbines, and batteries for each season-representing month.

Region	Node	April (Spring)			July (Summer)
		Solar	Wind	Batteries	Solar	Wind	Batteries
Northern Taiwan	NewTaipei-5	12.1	0	10.8	7.7	0	7.5
	Taoyuan-1	14.3	286.8	0	214.1	0	367.8
	Hsinchu-1	0	134.5	4.5	0	99.2	11.0
	Hsinchu-3	0	65.5	19.8	0	52.2	12.6
	Regional total	26.4	486.8	35.1	221.8	151.4	398.9
	Capital investment	USD 31.9	USD 728.7	USD 18.0	USD 268.4	USD 226.6	USD 204.2
Central Taiwan	Miaoli-3	0	166.0	3.8	0	149.5	8.1
	Taichung-1	130.5	0	110.3	76.4	0	52.5
	Taichung-3	176.6	0	93.9	77.3	0	96.3
	Nantou-3	18.4	0	21.3	1.0	0	4.4
	Yunlin-1	298.6	0	399.4	255.9	0	363.2
	Yunlin-3	53.7	0	51.3	37.1	0	31.0
	Regional total	677.8	166.0	680.0	447.7	149.5	555.5
	Capital investment	USD 820.1	USD 248.5	USD 348.2	USD 541.7	USD 223.8	USD 284.4
Southern Taiwan	Tainan-1	291.0	0	371.3	329.0	0	493.6
	Tainan-3	102.6	0	89.2	83.7	0	71.1
	Regional total	393.6	0	460.5	412.7	0	564.7
	Capital investment	USD 476.3	USD 0	USD 235.8	USD 499.4	USD 0	USD 289.1
Total capacity		1097.8	652.8	1175.7	1082.2	300.9	1519.1
Total capital investment		USD 2907.5			USD 2537.6
Region	Node	October (Autumn)			January (Winter)
		Solar	Wind	Batteries	Solar	Wind	Batteries
Northern Taiwan	NewTaipei-5	0	3.9	4.7	0	3.9	4.1
	Taoyuan-1	0	108.9	0	0	136.8	0
	Hsinchu-1	0	63.0	0	0	80.2	0
	Hsinchu-3	0	32.5	0	0	39.8	0
	Regional total	0	208.3	4.7	0	260.7	4.1
	Capital investment	USD 0	USD 311.9	USD 2.4	USD 0	USD 390.3	USD 2.1
Central Taiwan	Miaoli-3	0	101.3	0	0	113.1	0
	Taichung-1	174.4	0	249.9	198.9	75.9	178.7
	Taichung-3	76.0	0	78.6	109.6	17.1	58.6
	Nantou-3	2.9	0	6.0	0.3	0	0.2
	Yunlin-1	42.1	0	49.9	48.2	0	46.6
	Yunlin-3	36.3	0	24.4	44.3	0	25.1
	Regional total	331.7	101.3	408.8	401.3	206.1	309.2
	Capital investment	USD 401.3	USD 151.7	USD 209.3	USD 485.5	USD 308.6	USD 158.3
Southern Taiwan	Tainan-1	360.8	0	528.1	64.8	315.6	58.6
	Tainan-3	74.3	0	62.5	45.2	33.5	14.8
	Regional total	435.1	0	590.6	110.0	349.1	73.4
	Capital investment	USD 526.5	USD 0	USD 302.4	USD 133.1	USD 522.6	USD 37.6
Total capacity		766.8	309.6	1004.1	511.3	815.9	386.7
Total capital investment		USD 1905.5			USD 2038.1

Unit for solar or wind capacity: MW; battery capacity: MWh; capital investments: USD M.

) summarizes the optimal deployment of solar and wind power and battery arrays for the four season-representing months.

The results in Table A2 exhibit a significantly different availability of RE between the north, central, and south regions in Taiwan: Wind is the preferred renewable for the north, but solar becomes the favored one for the central and the south. In northern Taiwan, the wind completely dominates the RE production in April (spring), October (autumn), and January (winter), i.e., three quarters of the year. Although the region would use a total of 221.8 MW of solar panels in July, it still relies on 151.4 MW of wind turbines to supply RE at the same time. For southern Taiwan, it is a mirror situation to the north that solar power completely dominates the RE production in April, July, and October, again, three quarters of the year. These massive deployments of solar power require very large battery arrays to ensure uninterrupted energy supply in the region, such as a total of 590.6 MWh of batteries measured for October. This is a good example of the critical role that batteries have in using solar power. In central Taiwan, solar power’s dominance occurs at five of the six nodes there. In fact, solar power has a complete dominance at three nodes that they only use to recharge EVs at all times; in addition, solar is very close to complete dominance at one other node. 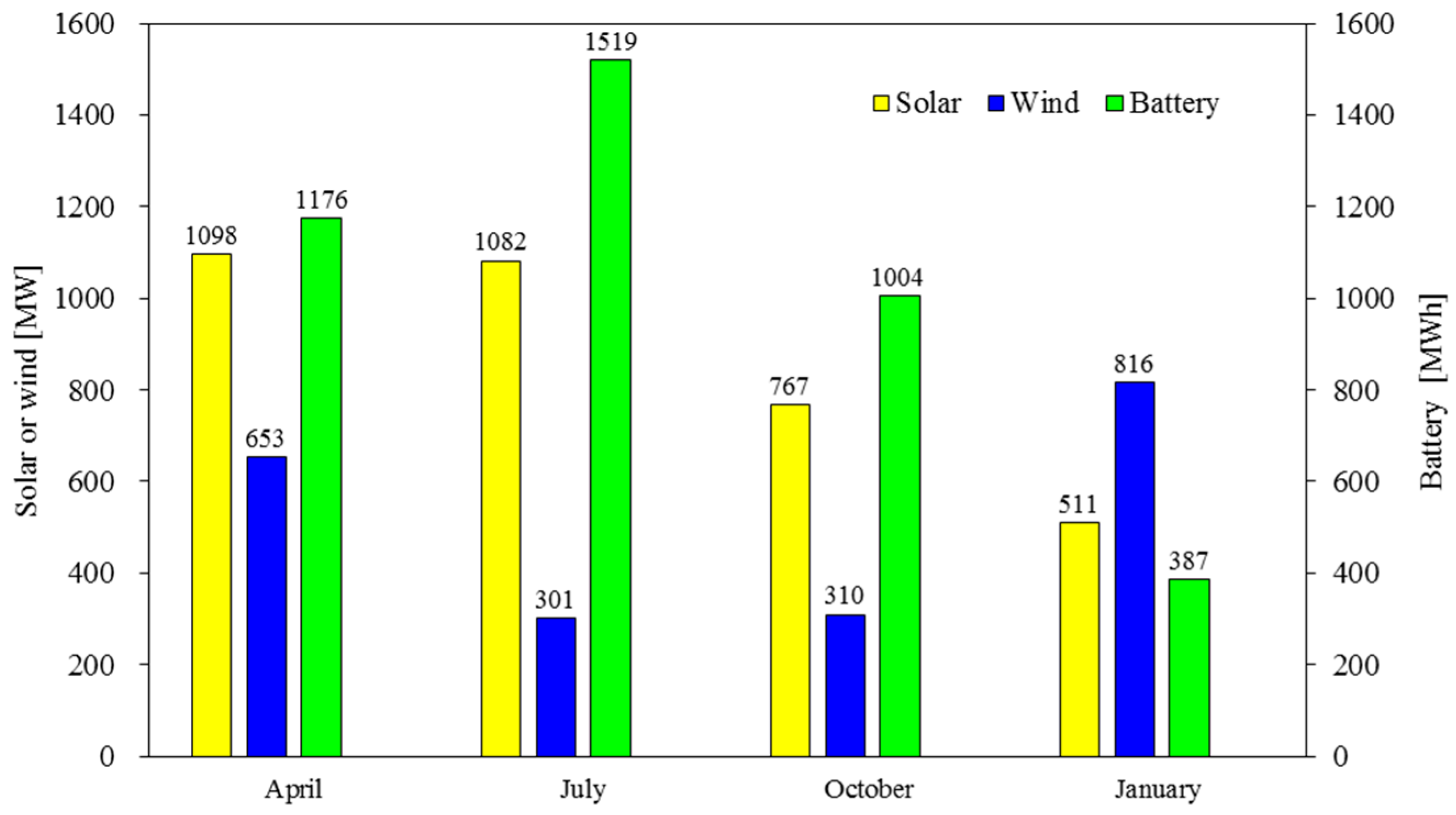Figure 2 depicts the total capacities of solar panels, wind turbines, and battery arrays deployed for each season-representing month. These distributions reflect a very different availability between solar and wind power during different seasons. In July (summer), when solar is the main source of RE, the model asked for the most volume of battery storage to reserve enough energy for the nighttime. In April (spring), when solar is still preferred over the wind, but the preference is not as much (compared to July), the battery requirements thus become much less (22.6% less than July). In January (winter), when the wind becomes the favored one, the model requested the least volume of battery storage.

The above discussions and the in-depth analysis on the four optimal deployments in Appendix B reveal the complexity of the decision-making challenge, which will surface when a large-scale RE is to be deployed to enable the electrification of highway transportation in large areas. In areas such as northern Taiwan, changing RE availability is most certainly the norm. This implies that the volume and/or source of usable RE is likely different from one season to the next and from one node (location) to another. Therefore, the situation may be that sometimes, solar energy is (much) richer than wind energy and some other times, wind energy is (much) richer than solar energy. Furthermore, there could be times when both RE is in short supply. In addition, note that solar energy is only available during daytime hours, but wind energy may be available all day long. This means when solar power appears to be the better source of RE for a particular node, but nighttime energy provision is also needed there, then a certain volume of batteries will need to be stationed at that location. Those grid-scale batteries will save enough solar energy during daytime hours and use it to satisfy nighttime charging demands, but that also means more capital investments to be required. On the other hand, battery arrays are not necessary to accompany the installation of large-scale wind turbines. The case at Taoyuan-1 is a good example: The MIP model used 214.1 MW of solar panels and 367.8 MWh of batteries to meet charging demands in July, but when using wind as the only renewable in October and January (108.9 and 136.8 MW of wind turbines, respectively), the model does not require any battery. These differences/tradeoffs between using solar and wind energy are already complicated enough. Unfortunately, the consideration further includes EVs’ charging requirements, which at a minimum are a function of travel routes, travel time, and the initial battery energy. Therefore, it is this extremely complex dynamics between BEVs and the renewables that call for developing the proposed MIP model to achieve the desired performance (${\rho }^{\mathrm{EV}}={\rho }^{\mathrm{dist}}={\rho }^{\mathrm{rnew}}=99\%$) with minimum investments!

The estimated capital investments for powering the entire national highways with virtually solar and wind energy are USD 2908 M in April, USD 2538 M in July, USD 1906 M in October, and USD 2038 M in January (Table A2). April requires the most capital investments; especially, it holds the most investments in solar power (USD 1328 M) and the second-most in wind power and batteries (USD 977 M and USD 602 M, respectively). On the other hand, October requires the least investments; specifically, its solar, wind, and battery investments are all second least among the four months (USD 928 M, USD 464 M, and USD 514 M, respectively). The investments needed for April are 52.6% higher than those for October. Overall speaking, the MIP model allocates substantially more money to acquire solar energy in April, July, and October (the ratio of solar/wind investments is 1.36, 2.91, and 2.00, respectively). Consequently, the battery investments in those months are also much higher than in January.

4.4. Determining the Final RE Deployment for the Entire Year

Since April requires the highest capital investments, the resulting deployment of solar panels, wind turbines, and battery arrays may possess sufficient capacities to achieve ${\rho }^{\mathrm{EV}}={\rho }^{\mathrm{dist}}={\rho }^{\mathrm{rnew}}=99\%$ for July, October, and January. If that is really the case, the April solution is then qualified to be the solution for the entire year as well! In other words, the April solution can serve as a significant reference case for the electrification of highway transportation in Taiwan in the future. To evaluate the performance of each MIP solution in Table A2 for the entire year, the MIP model in the previous section (called model 1 hereafter) will change as follows. All decision variables defined to handle issues of RE generation or storage in model 1 will become parameters in the new model (called model 2); next, modify every affected constraint accordingly. In other words, decision variables in model 1, including $X_{ri}^{\mathrm{rnew}}$, $G_{ri}^{\mathrm{rnew}}$, $E_{rit}^{\mathrm{rnew}}$, $B_i^{\mathrm{batt}}$, $X_i^{\mathrm{chrg}}$, and $X_{oi}^{\mathrm{conv}}$ will become given data in model 2, carrying the optimal value that model 1 has identified from the April, July, October, or January scenario. As a result, constraints (2), (3), (4), (9), (16), (17), (19), and (21)–(23) in model 1 will no longer be needed in model 2. These changes will give model 2 the same capability to produce and store RE as what model 1 has determined for April. Furthermore, model 2 will adopt the following objective function to encourage BEVs to maximize the consumption of solar/wind energy:

$$\mathrm{Maximize}{\displaystyle \sum _{t\in \mathrm{T}}{\displaystyle \sum _{i\in \mathrm{N}}{\displaystyle \sum _{v\in {\mathrm{V}}_t}{S}_{vit}^{\mathrm{rnew}}}}}$$

Table 4. Total solar panel, wind turbine, and battery capacities for each season-representing month (results from model 1), followed by the maximum volume of RE that BEVs will consume in each month (results from model 2).

	Solar	Wind	Batteries	April	July	October	January
April	1098	653	1176	154,526	152,759 (+0.4%)	147,560 (+1.0%)	151,383 (+0.1%)
July	1082	301	1519	139,851 (−9.5%)	152,077	147,560 (+1.0%)	144,813 (−4.2%)
October	767	310	1004	109,185 (−29.3%)	115,561 (−24.0%)	146,088	133,111 (−11.9%)
January	511	816	387	99,250 (−35.8%)	114,590 (−24.7%)	134,968 (−7.6%)	151,157

Unit for solar or wind capacity: MW, battery capacity: MWh, energy consumption: MWh.

summarizes the outcome of evaluation by model 2. In this table, the left part is the total solar or wind power generation capacity and the total battery array capacity that model 1 has determined for each season-representing month. As to the right part of Table 4, they are the maximum volume of RE that BEVs will consume (i.e., the optimal solution from model 2), with all that RE produced by using the optimal solution from model 1. For example, model 1 suggests deploying a total of 1098 MW of solar panels, 653 MW of onshore wind turbines, and 1176 MWh of battery arrays for April (the top row in the left part of Table 4). Then, according to model 2, using that April solution for all four months will result in a total of 154,526 MWh, 152,759 MWh, 147,560 MWh, and 151,383 MWh of RE consumed by BEVs traveling in April, July, October, and January, respectively (the top row in the right part of Table 4). As to the other three optimal deployments, they will each result in a total of 152,077 MWh, 146,088 MWh, and 151,157 MWh of RE consumed by BEVs traveling in July, October, and January. Therefore, using the April solution in those three months will allow BEVs to recharge with more RE (the numbers after the “+” sign in the top row indicate the overage volume). On the other hand, using any other solution the same way will not produce the same kind of result. For example, as indicated by those “-” signs in the bottom row, the (optimal) January deployment will result in less or much less RE used by BEVs traveling in April, July, and October. As shown in Table 4, April is the only month without a “-” sign, and using any other solution in April will all result in significantly less consumption of RE, with 9.5%, 29.3%, and 35.8% being the respective underage caused by the other three solutions. Therefore, only the April deployment is worth further investigation.

Table 5. Performance summary for using the April solution in every season-representing month.

	April	July	October	January
Total number of covered BEVs	4,466,007	4,207,516	3,892,173	3,913,905
	(99.2%)	(99.3%)	(99.4%)	(99.3%)
Total covered travel distance (1000 km)	713,316	669,789	615,232	618,728
	(99.5%)	(99.6%)	(99.6%)	(99.6%)
Total RE generation (MWh)	181,506	190,948	302,657	253,322
Total RE consumption (MWh)	154,526	152,759	147,560	151,383
	(99.0%)	(99.4%)	(100%)	(99.1%)
Total conventional energy consumption (MWh)	1561	854	0	1300
	(1.0%)	(0.6%)	(0.0%)	(0.9%)
Unused RE (MWh)	26,980	38,190	155,097	101,939

lists the key performance for using the April solution in every season-representing month. Indicated by those percentages in the first, second, and fourth rows, the April solution can deliver the required coverage in all four months, implying it does possess sufficient capacity to enable the electrification of Taiwan’s highway transportation using RE almost exclusively. However, doing so will also result in significant volumes of unused RE, that is, energy neither used to recharge BEVs nor saved in the battery. Sometimes, this unused RE is so much that it even surpasses the actual consumption, such as the case in October. There are two major causes for this phenomenon: the requirement to use local RE supply and the decision-making challenges in making investments in solar power, wind power, or battery arrays. For the first cause, the requirement to acquire RE from a nearby area (local source) can stimulate developing local businesses, but the tradeoff could be higher energy prices. On the other hand, it could be cheaper to produce RE in farther areas, but the tradeoff is to make investments in the necessary infrastructure to gather all that energy and then distribute it to different areas. As to the other cause, the current price for solar and wind energy is already very low that they are as affordable as conventional energy. However, the current battery price is still at a relatively high level (according to Lambert [84], the unit capital cost for batteries, with installation included, is USD 512,000 per MWh). The resulting situation is that sometimes, it is more cost-effective to invest money on the battery, which in turn will save more energy for later use, but some other times, it is more cost-effective to let some RE just go away. Of course, in a real situation, that RE will not really go away; rather, that energy will be useful somewhere, such as meeting the power needs of a nearby community or industrial complex. This will lower the actual capital investments as measured by model 1 in Table A2. Finally,

Table 6. Annual performance for April’s solution to power Taiwan’s highway transportation.

Measure	Annual Performance
Number of covered BEVs	49,438,803 (99.3%)
Covered travel distance (1000 km)	7,851,195 (99.6%)
RE consumption (MWh)	1,818,684 (99.4%)
Unused RE (MWh)	966,618

summarizes the annual performance for using the April solution for the entire year, with estimations obtained by tripling those volumes in Table 5.

4.5. Measuring Environmental Impacts

Table 7. Emission scenarios against using the April solution to charge BEVs in all season-representing months.

Vehicle	Scenario	April	July	October	January	Year
BEVs	Charged with non-RE on the highway	85,608	84,628	81,748	83,866	1,007,550
	Using non-RE for entire highway trip	177,367	174,253	167,717	172,021	2,074,073
ICEVs	Using fossil fuels for entire highway trip	180,300	175,388	168,319	172,074	2,088,246

Unit: ton CO₂e.

presents two emission scenarios against the scenario of using the April solution as an all-season solution. In other words, they are the environmental benefits realized under different situations. The first row lists potential CO₂ emissions generated by charging BEVs with the power grid, obtained by multiplying the total energy that BEVs would consume (from model 2) with 0.554 kg CO₂e/kWh, which is the average CO₂ emissions that the power plants in Taiwan would produce to generate one kWh of electricity [85]. In LCA (lifecycle assessment) terminology, they are the use-phase emissions for BEVs if they recharge with non-RE on the highway [86]. The numbers in the second row are CO₂ emissions generated by BEVs during their entire highway travel, assuming their initial 50% battery energy also comes from a non-renewable source. The numbers in the third row are emissions from ICEVs running on the highway. In other words, these are the CO₂ emissions on the current highway. ICEVs emit CO₂ when burning fossil fuels or releasing exhaust gases (i.e., tailpipe emissions). The measurement of these emissions uses 119, 278, 736, 625, and 817 g/km as the unit CO₂-emitting volume for sedans, small trucks, buses, large trucks, and 18-wheel cargo trucks respectively [87,88]. The right-most column contains estimated annual emissions; charging EVs with the April solution will erase all these emissions.

4.6. Measuring Charger Numbers

Although model 1 and model 2 do not measure charging capacities, that is, the maximum volume of BEVs that can recharge at the same service node during the same planning period, the two models can possess that capability with the addition of a few parameters and decision variables. There are different approaches to measuring charger numbers in the literature, with each developed under a different research setting. For example, in multiperiod strategic planning with decisions to increase chargers at each location, Xie et al. [53] used queuing theories to formulate a stochastic chance constraint to determine charger numbers, with the assurance that they will perform a desirable level of charging service with certain probabilities at all times. Mourad et al. [63] considered using the electricity distribution network and solar PV to power chargers (without BESSs to store energy). In that setting, the fixed electric capacity of the distribution network and the varying electric capacity of solar PV provide an upper bound to charger numbers.

To measure the number of chargers with model 1 and model 2, the information on the charger model is essential. Generally, each category of BEVs requires a certain charging power from the charger, such as sedans require 50 kW to charge batteries, while trucks require 250 kW [63]. Moreover, since chargers will receive electric energy from battery arrays, their power/capacity configuration (e.g., the 13 MW/52 MWh BESS installed on the island of Kaua’i) may also influence charger selection. With the right charger model (denoted by $p$ in the MIP model) being determined for each BEV category, the maximum energy that each unit $p$ can provide to charge EVs during each planning period thus becomes a known value given to the model (${\mathrm{e}}_p^{\mathrm{chrg}}$). As the MIP model already captures the energy consumption of each BEV fleet $v$ at each charging node $i$ during each planning period $t$ (that is, $S_{vit}^{\mathrm{rnew}}$), it can calculate the total consumption made by each BEV category at that node during that planning period by taking the sum of every $S_{vit}^{\mathrm{rnew}}$ with $v$ belonging to that specific BEV category. This total consumption will then determine the minimum number of charger model $p$ for performing the required charging at $i$ during $t$. Clearly, the final number required at $i$ ($H_{pi}^{\mathrm{chrg}}$, an integer decision variable) must be sufficient for every planning period. As each BEV category may require its own charger model, the total number of these chargers will ultimately contribute to the capital investments as evaluated by the objective function. Note that these measurements can be further refined with other practical considerations, such as the available land at $i$, or the maximum charging power that chargers cannot exceed (e.g., as restricted by the BESS).

5. Conclusions

In the wake of continuously rising global temperature, using EVs to replace conventional vehicles has become a priority issue for countries all over the world to combat global warming. However, the true potential of EVs in reducing GHG emissions depends on a large-scale utilization of RE to power these vehicles. Due to the lack of academic research on hybrid RE planning to power various EVs in a real national highway setting, with options to deploy grid-scale battery arrays at certain locations, this paper thus responded with the proposal of a MIP model (Section 3) to meet this urgent need. Targeting at the minimization of total capital investments while ensuring a continuous power supply, the proposed model is capable of evaluating hybrid energy sources, which could be conventional or renewable, as well as the possible need to deploy battery arrays at certain nodes to regulate the production and consumption of RE. Subsequent to the presentation of the MIP model was a comprehensive case study on Taiwan’s national highways. It covered such detail as the exact process to prepare key numeric data (local solar/wind energy and highway traffic), using model solutions to investigate changing RE supplies due to seasonality, and the determination of an all-season solution. In addition to fully demonstrating the applicability of this research in a real situation, the case study supported using RE to power EVs on a national highway and revealed the importance of having local businesses involved in developing local renewable markets. A relatively small country, such as Taiwan, can still display significant variations in renewable power availability. In a stand-alone environment for power generation and consumption, these variations would cause a massive volume of RE not used by EVs in certain seasons. This and other issues thus imply several possibilities to continue this research.

There are a number of works to extend the findings of this research. First, in a normal situation, the task of solving model 1 or model 2 for a real transportation network is time-consuming. As reported in Section 4 and Appendix A, even with much effort to process and reduce traffic data, the MIP model still contained more than 140 thousand binary variables and required the computer to spend as much time as 90 min to identify optimal solutions for some data sets. A shorter runtime is possible with developing custom solution procedures. These procedures will explore the polyhedral set as defined by the MIP model by using the special geometric structures of that polyhedral set. Consequently, a shorter runtime is achievable. Another possibility is to enhance the MIP model to account for energy losses due to such reasons as maintenance or aging equipment. For instance, wind turbines require regular inspections to examine whether their blades have cracks or other signs of damage. On such occasions, their energy production is zero because they must stop fully to ensure the safety of inspection crews. As for solar panels, they require regular surface cleaning to function at maximum efficiency. However, they will still degrade at an average rate of 1%, meaning that their energy output reduces to approximately 90% after 10 years and 80% after 20 to 25 years. These works would further increase the value of this research.

Another promising way to extend this research is to allow EVs to perform emerging practices, such as V2V (vehicle-to-vehicle). V2V is a technology to enable a direct energy exchange from one EV to another [89,90]. As it does not require any charging facility to support, EVs doing it can exchange energy freely at numerous locations. Therefore, it is a very useful solution to EVs that require battery recharge desperately. The execution of V2V requires an efficient procedure to match EVs (from numerous cars on the road) and navigate them to the right location. Timing is clearly the most important factor in this process. In a large highway network, doing V2V could be relatively harder due to longer travel distances and little flexibility in navigating the vehicles. An alternative approach would be to designate certain nodes (e.g., they do not have charging facilities) as potential locations for V2V. These nodes would offer some simple device, such as a small battery for EVs to discharge or recharge batteries. This would increase the odds for a successful match as the two vehicles no longer need to arrive at the same location at approximately the same time.