Extending the Scope of ALM to Social Investment: Investing in Population Growth to Enhance Sustainability of the Korean National Pension Service
Abstract
1. Introduction
2. Korean National Pension Service
2.1. The Korean Pension System
2.2. Analysis of Major Issues of the NPS
3. Model
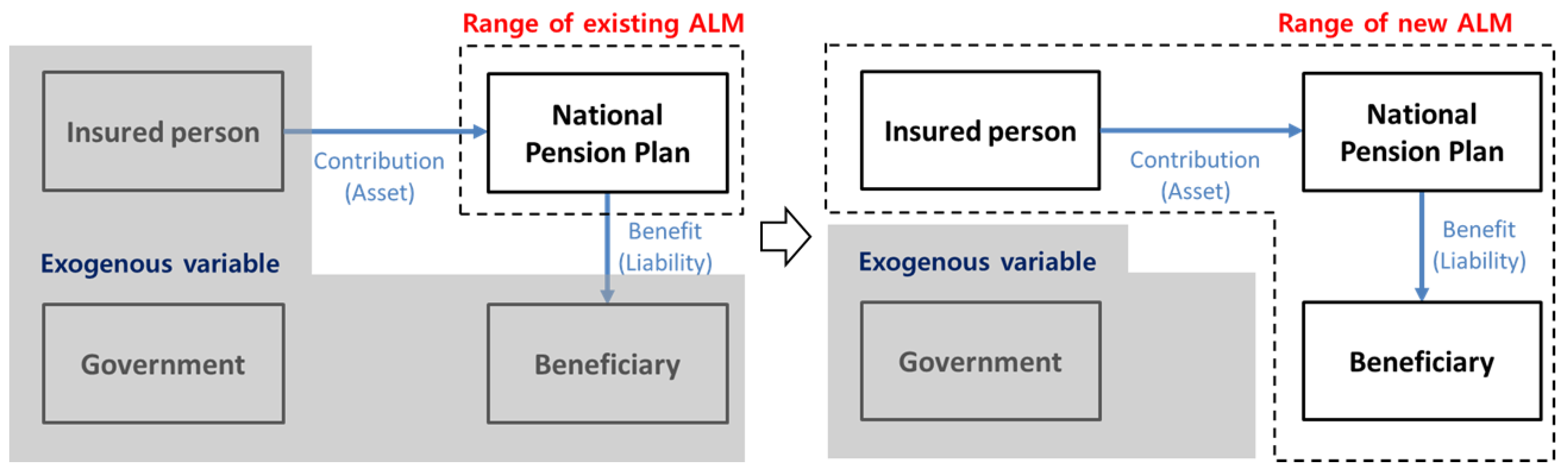
3.1. Investment in Population Growth
3.2. Demographic Structure
3.3. Model Description
3.4. MSP Formulation
- Parameters
| Length of stage t in years. | |
| Asset return during periods of stage t for asset i under scenario s. | |
| Annualized rate of the cost of borrowing. | |
| Rate of the transaction cost. | |
| Discounting factor for one year. | |
| Limit on the asset amount sold in one year. | |
| Initial wealth of NPS. | |
| Initial weight of asset i. | |
| Average pension benefit per person of age group j at stage t. | |
| Average contribution per person of age group j at stage t. | |
| Percentage of insured persons of age group j at stage t. | |
| Percentage of pension beneficiaries of age group j at stage t. | |
| Probability of scenario s, . |
- Decision Variables
| Amount allocated to asset i after rebalancing at the beginning of stage t under scenario s. | |
| Amount of asset i purchased at the beginning of stage t under scenario s ( | |
| Amount of asset i sold at the beginning of stage t under scenario s ( | |
| Amount borrowed at the beginning of stage t, under scenario s. | |
| Amount of debt paid back at the beginning of stage t, under scenario s. | |
| Age group- and sex-specific population vector at stage t under scenario s. | |
| Total Liability payment at stage t under scenario s. | |
| Total contribution of all active members at stage t under scenario s. | |
| End effect under scenario s. |
- MSP Model
| Maximize , where | (2) | |
| Subject to | ||
| (3) | ||
| (4) | ||
| (5) | ||
| (6) | ||
| (7) | ||
| (8) | ||
| (9) | ||
| (10) | ||
| (11) | ||
| (12) | ||
| (13) | ||
| (14) | ||
| (15) | ||
| , | (16) | |
| , , , | and with identical past up to time t. | (17) |
| , ,, | (18) | |
4. Scenario Tree Generations
5. Numerical Example
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- National Pension Service Actuarial Projection Committee. 2018 National Pension Service Actuarial Projection. 2018. Available online: https://fund.nps.or.kr/jsppage/fund/mpc_e/mpc_e_03.jsp (accessed on 4 January 2021).
- Ziemba, W.T.; Mulvey, J.M.; Moffatt, H. Worldwide Asset and Liability Modeling; Cambridge University Press: Cambridge, UK, 1998; Volume 10. [Google Scholar]
- Bogentoft, E.; Romeijn, H.E.; Uryasev, S. Asset/liability management for pension funds using CVaR constraints. J. Risk Financ. 2001, 3, 57–71. [Google Scholar] [CrossRef]
- Mulvey, J.M.; Simsek, K.D.; Zhang, Z. Improving investment performance for pension plans. J. Asset Manag. 2006, 7, 93–108. [Google Scholar] [CrossRef]
- Gülpınar, N.; Rustem, B.; Settergren, R. Simulation and optimization approaches to scenario tree generation. J. Econ. Dyn. Control 2004, 28, 1291–1315. [Google Scholar] [CrossRef]
- Pachamanova, D.; Gülpınar, N.; Çanakoğlu, E. Robust approaches to pension fund asset liability management under uncertainty. In Optimal Financial Decision Making Under Uncertainty; Springer: Berlin/Heidelberg, Germany, 2017; pp. 89–119. [Google Scholar]
- Høyland, K.; Wallace, S.W. Analyzing legal regulations in the Norwegian life insurance business using a multistage asset–liability management model. Eur. J. Oper. Res. 2001, 134, 293–308. [Google Scholar] [CrossRef]
- Board, J.; Sutcliffe, C. Joined-up pensions policy in the UK: An asset-liability model for simultaneously determining the Asset allocation and contribution rate. In Handbook of Asset and Liability Management; Elsevier: Amsterdam, The Netherlands, 2008; pp. 1029–1067. [Google Scholar]
- Hilli, P.; Koivu, M.; Pennanen, T.; Ranne, A. A stochastic programming model for asset liability management of a Finnish pension company. Ann. Oper. Res. 2007, 152, 115. [Google Scholar] [CrossRef]
- Haneveld, W.K.; Streutker, M.; van der Vlerk, M. Implementation of New Regulatory Rules in a Multistage ALM Model for Dutch Pension Funds; Research Report 07005; University of Groningen, Research Institute SOM (Systems, Organisations and Management): Groningen, The Netherlands, 2007. [Google Scholar]
- Haneveld, W.K.K.; Streutker, M.H.; Van Der Vlerk, M.H. An ALM model for pension funds using integrated chance constraints. Ann. Oper. Res. 2010, 177, 47–62. [Google Scholar] [CrossRef][Green Version]
- Klein Haneveld, W.K.; Streutker, M.H.; van der Vlerk, M.H. Indexation of Dutch pension rights in multistage recourse ALM models. Ima J. Manag. Math. 2010, 21, 131–148. [Google Scholar] [CrossRef]
- Dondi, G.; Herzog, F.; Schumann, L.M.; Geering, H.P. Dynamic asset and liability management for Swiss pension funds. In Handbook of Asset and Liability Management; Elsevier: Amsterdam, The Netherlands, 2008; pp. 963–1028. [Google Scholar]
- Won, C.H. Necessity of stipulate of national payment in the view of asset allocation of national pension plan. Welf. Trend (Korean) 2013, 177, 29–41. [Google Scholar]
- Colombo, L.; Haberman, S. Optimal contributions in a defined benefit pension scheme with stochastic new entrants. Insur. Math. Econ. 2005, 37, 335–354. [Google Scholar] [CrossRef]
- Angrisani, M.; Attias, A.; Bianchi, S.; Varga, Z. Sustainability of a pay-as-you-go pension system by dynamic immigration control. Appl. Math. Comput. 2012, 219, 2442–2452. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, X. Stochastic forecast of the financial sustainability of basic pension in China. Sustainability 2016, 8, 46. [Google Scholar] [CrossRef]
- Chen, X.; Yang, Z. Stochastically Assessing the Financial Sustainability of Individual Accounts in the Urban Enterprise Employees’ Pension Plan in China. Sustainability 2019, 11, 3568. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J.; Sun, S. Assessment of the Financial Sustainability of China’s New Rural Pension Plan: Does the Demographic Policy Reform Matter? Sustainability 2019, 11, 5110. [Google Scholar] [CrossRef]
- Zhao, Q.; Mi, H. Evaluation on the Sustainability of Urban Public Pension System in China. Sustainability 2019, 11, 1418. [Google Scholar] [CrossRef]
- Zhao, Y.; Bai, M.; Liu, Y.; Hao, J. Quantitative analyses of transition pension liabilities and solvency sustainability in China. Sustainability 2017, 9, 2252. [Google Scholar] [CrossRef]
- Jo, W.-H.; Kye, B.-O.; Ryu, J.-R. Ultra-Low Fertility in Korea and Social Investment by National Pension Fund Focusing on Demographic Change, Social Investment, and the National Pension Finance. Korea J. Popul. Stud. (Korean) 2018, 41, 61–90. [Google Scholar] [CrossRef]
- Milligan, K. Subsidizing the stork: New evidence on tax incentives and fertility. Rev. Econ. Stat. 2005, 87, 539–555. [Google Scholar] [CrossRef]
- Laroque, G.; Salanié, B. Fertility and financial incentives in France. Cesifo Econ. Stud. 2004, 50, 423–450. [Google Scholar] [CrossRef]
- Suk, H.W. Study on the impact of Maternity subsidies policy: Focusing on Local governments in Seoul Metropolis. Korea Local Adm. Rev. (Korean) 2011, 25, 143–180. [Google Scholar]
- Park, C.W.; Song, H.J. The Effect of Child Birth Grants on the Fertility: Evidence from South Korea. Appl. Econ. (Korean) 2014, 16, 5–34. [Google Scholar]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Mulvey, J.M.; Zenios, S.A. Capturing the correlations of fixed-income instruments. Manag. Sci. 1994, 40, 1329–1342. [Google Scholar] [CrossRef]
- Zenios, S.A. Asset/liability management under uncertainty for fixed-income securities. Ann. Oper. Res. 1995, 59, 77–97. [Google Scholar] [CrossRef]
- Carino, D.R.; Myers, D.H.; Ziemba, W.T. Concepts, technical issues, and uses of the Russell-Yasuda Kasai financial planning model. Oper. Res. 1998, 46, 450–462. [Google Scholar] [CrossRef]
- Dupačová, J.; Consigli, G.; Wallace, S.W. Scenarios for multistage stochastic programs. Ann. Oper. Res. 2000, 100, 25–53. [Google Scholar] [CrossRef]
- Gülpınar, N.; Rustem, B. Worst-case robust decisions for multi-period mean–variance portfolio optimization. Eur. J. Oper. Res. 2007, 183, 981–1000. [Google Scholar] [CrossRef]

| Pillar | Type | Income Security System |
|---|---|---|
| Third pillar | Private pension | Individual retirement savings |
| Second pillar | Company pension | |
| First pillar | Public pension | National Pension Service (NPS) |
| Pillar zero | Social welfare | Basic Old-Age Pension |
| Age Group | 20–24 | 25–29 | 30–34 | 35–39 | 40–44 | 45–49 |
|---|---|---|---|---|---|---|
| Slope | −4.3095 | 5.7131 | 7.7486 | 4.3790 | 0.6808 | −0.0180 |
| Standard error of the slope | 2.5050 | 2.6064 | 2.1829 | 1.6596 | 0.5116 | 0.0614 |
| 0.0308 | 0.0491 | 0.1193 | 0.0697 | 0.0187 | 0.0009 |
| Stage | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Number of clusters at each node | 1 | 10 | 5 | 5 | 5 | 5 | 5 |
| Period (years) | 0 | 5 | 5 | 5 | 5 | 30 | 30 |
| Number of scenarios before clustering (N) | - | 4000 | 3000 | 1000 | 1000 | 1000 | 1000 |
| Parameter | Description | Value |
|---|---|---|
| Annualized rate of the cost of borrowing. | 20% | |
| Rate of the transaction cost. | 3% | |
| Discounting factor for one year. | 0.9852 () | |
| Limit on the asset amount sold in one year. | 2% | |
| Initial wealth of NPS. | 736.7 trillion KRW | |
| Initial weight of stocks. | 52.6% |
| Contribution Rate | Weight on Each Asset (%) | Stage | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 9% (reference case) | Stock | 41.76 | 30.47 | 45.54 | 56.32 | 60.91 | 81.82 |
| Bond | 37.64 | 24.60 | 35.08 | 39.83 | 39.09 | 18.18 | |
| Population | 20.60 | 44.93 | 19.38 | 3.85 | 0 | 0 | |
| 10% | Stock | 41.76 | 32.45 | 30.94 | 56.29 | 60.86 | 87.26 |
| Bond | 37.64 | 26.39 | 22.83 | 39.94 | 39.14 | 12.74 | |
| Population | 20.60 | 41.16 | 46.22 | 3.77 | 0 | 0 | |
| 11% | Stock | 41.76 | 31.40 | 29.47 | 55.37 | 61.37 | 84.21 |
| Bond | 37.64 | 25.55 | 21.47 | 37.95 | 38.63 | 15.79 | |
| Population | 20.60 | 43.05 | 49.06 | 6.67 | 0 | 0 | |
| 12% | Stock | 41.76 | 30.28 | 29.77 | 55.50 | 62.12 | 84.96 |
| Bond | 37.64 | 24.61 | 21.07 | 37.01 | 37.88 | 15.04 | |
| Population | 20.60 | 45.11 | 49.16 | 7.48 | 0 | 0 | |
| Investment Effect in Fertility Rate | Weight on Each Asset (%) | Stage | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| High | Stock | 41.76 | 32.87 | 35.92 | 56.22 | 60.93 | 82.06 |
| Bond | 37.64 | 26.68 | 27.10 | 39.83 | 39.07 | 17.94 | |
| Population | 20.60 | 40.46 | 36.97 | 3.95 | 0 | 0 | |
| Normal (reference case) | Stock | 41.76 | 30.47 | 45.54 | 56.32 | 60.91 | 81.82 |
| Bond | 37.64 | 24.60 | 35.08 | 39.83 | 39.09 | 18.18 | |
| Population | 20.60 | 44.93 | 19.38 | 3.85 | 0 | 0 | |
| Low | Stock | 41.76 | 28.58 | 52.47 | 56.22 | 60.85 | 81.82 |
| Bond | 37.64 | 23.15 | 40.22 | 39.73 | 39.15 | 18.18 | |
| Population | 20.60 | 48.27 | 7.31 | 4.05 | 0 | 0 | |
| Risk Preference | Weight on Each Asset (%) | Stage | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Conservative ( | Stock | 41.76 | 28.19 | 54.17 | 56.78 | 60.74 | 82.08 |
| Bond | 37.64 | 22.84 | 41.64 | 40.37 | 39.26 | 17.92 | |
| Population | 20.60 | 48.98 | 4.20 | 2.85 | 0 | 0 | |
| Moderate ( (reference case) | Stock | 41.76 | 30.47 | 45.54 | 56.32 | 60.91 | 81.82 |
| Bond | 37.64 | 24.60 | 35.08 | 39.83 | 39.09 | 18.18 | |
| Population | 20.60 | 44.93 | 19.38 | 3.85 | 0 | 0 | |
| Aggressive | Stock | 41.76 | 33.92 | 34.45 | 48.62 | 59.83 | 74.36 |
| Bond | 37.64 | 27.67 | 25.51 | 35.61 | 40.17 | 25.64 | |
| Population | 20.60 | 38.41 | 40.04 | 15.77 | 0 | 0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, W.B.; Lee, D.; Kim, W.C. Extending the Scope of ALM to Social Investment: Investing in Population Growth to Enhance Sustainability of the Korean National Pension Service. Sustainability 2021, 13, 401. https://doi.org/10.3390/su13010401
Choi WB, Lee D, Kim WC. Extending the Scope of ALM to Social Investment: Investing in Population Growth to Enhance Sustainability of the Korean National Pension Service. Sustainability. 2021; 13(1):401. https://doi.org/10.3390/su13010401
Chicago/Turabian StyleChoi, Woong Bee, Dongyeol Lee, and Woo Chang Kim. 2021. "Extending the Scope of ALM to Social Investment: Investing in Population Growth to Enhance Sustainability of the Korean National Pension Service" Sustainability 13, no. 1: 401. https://doi.org/10.3390/su13010401
APA StyleChoi, W. B., Lee, D., & Kim, W. C. (2021). Extending the Scope of ALM to Social Investment: Investing in Population Growth to Enhance Sustainability of the Korean National Pension Service. Sustainability, 13(1), 401. https://doi.org/10.3390/su13010401






