Abstract
Big data from toll stations provides reliable and accurate origin-destination (OD) pair information of expressway networks. However, although the short-term traffic prediction model based on big data is being constantly improved, the volatility and nonlinearity of peak traffic flow restricts the accuracy of the prediction results. Therefore, this research attempts to solve this problem through three contributions, firstly, proposing the use the Pauta criterion from statistics as the standard for defining the anomaly criteria of expressway traffic flows. Through comparison with the common local outlier factor (LOF) method, the rationality and advantages of the Pauta criterion were expounded. Secondly, adding week attributes to data, and splitting the data based on the similarity characteristics of traffic flow time series in order to improve the accuracy and efficiency of data input. Thirdly, by introducing empirical mode decomposition (EMD) to decompose the signal before autoregressive integrated moving average (ARIMA) model training is carried out. The first two contributions are for efficiency, the third is to deal with the volatility and nonlinearity of the abnormal peak training data. Finally, the model is analyzed, based on the expressway toll data of the Jiangsu Province. The results show that the EMD-ARIMA model has more advantages than the ARIMA model when dealing with fluctuating data.
1. Introduction
1.1. Motivation
The Ministry of Transport of the People′s Republic of China issued an early warning in 2019: the short-term surge in highway traffic is the main factor leading to a substantial increase in traffic congestion and crash risks, especially causing frequent fatal crashes in the afternoon and night. Without reliable predictions on the time, the origin-destination routes and the size of a sudden increase in traffic volume on the highway network, it is hard for the government to implement effective transportation policies to ensure road safety. For the application of policy tools, such as the Advanced Traveler Information System and Advanced Traffic Management System, fast and accurate predictions of future traffic conditions are essential. Their reliability in dealing with traffic safety hazards is related to their ability to foresee the future state of the system [1]. Advances in information and communication technology (ICT), such as comprehensive highway toll station data providing accurate and detailed road network traffic measurement data for prediction research, are a prerequisite for introducing new traffic prediction models and methods [2].
While ICT collects massive amounts of data on the road network, it also needs efficient analysis methods to capture useful information within this spatiotemporal big data. Short-term traffic prediction refers to the process of directly estimating the expected traffic situation at a certain time in the future through the continuous short-term feedback of traffic information. To solve short-term traffic prediction problems, many statistical modeling efforts have been performed. Due to the randomness of traffic flow and the highly nonlinear characteristic of short-term prediction, using a traditional statistical method is inappropriate when the line network is too large. With the development of machine learning methods, a large number of researches are more inclined to use implicit traffic prediction, that is, ignoring the interaction between physical variables and only deriving dynamic relationships from the time series of observation data [3,4]. The application of the autoregressive integrated moving average (ARIMA) model in highway traffic flow prediction can be traced back to 1979 [5]. Later, it was developed into a multivariate ARIMA model [6]. Cools et al. introduced the ARIMAX model with explanatory variables and the seasonal autoregressive moving average (SARIMA) model to study the periodicity of traffic flow and predict abnormal traffic volume on holidays [7]. Due to its clear theoretical basis and prediction effectiveness [8], the ARIMA model has gradually become a standard method for comparison with newly developed prediction models. In dealing with the uncertainty and variability of time series in transportation systems, researchers used statistical volatility models to predict time-dependent variances instead of assuming constant variance. The ARCH (autoregressive conditional heteroskedasticity) model relaxes the assumption of constant variance, assuming that significant changes in time-series volatility are predictable. Bollerslev further proposed the so-called GARCH (generalized autoregressive conditional heteroskedasticity) extension to solve the problem of too many parameters describing the fluctuation process [9]. Recent studies have attempted to capture the spatial correlation between traffic variables on road networks by extending the time-series model to a multivariate form [10,11,12], Furthermore, it is proved that the obvious changes in the volatility of traffic data are predictable and may be caused by specific types of non-linear functions. Leveraging these unique attributes in different models may lead to more efficient and reliable predictions. Therefore, recent research has proposed a hybrid model that aims to be able to identify weekly trends and non-reproducible flow patterns, thereby improving prediction accuracy. Meanwhile, empirical mode decomposition (EMD) has been developed for analyzing nonlinear and non-stationary data. Since the decomposition is based on the local characteristic time scale of the data, it is applicable to nonlinear and non-stationary processes. Study from the numerical results of the classical nonlinear equation systems and data representing natural phenomena are given to demonstrate the power of this new method [13,14]. The successful application of EMD in both passenger flow forecasting and wind velocity has aroused interest regarding its potential use in traffic flow prediction [15,16].
Through the study of existing implicit traffic prediction methods, the hybrid model is used to conduct peak traffic flow predictions. Additionally, EMD preprocessing was introduced into the hybrid model to deal with the volatility and nonlinearity of the abnormal peak traffic flow.
1.2. Approaches to Traffic Predictions and Related Work
According to different types of data, there are two ways to predict traffic volume. One is a predictive model developed by tracking floating car data from GPS vehicles and mobile devices. There are three advantages of floating car data. The first is that it can inspect areas that cannot be covered by conventional fixed sensors. Secondly, the constraints of investment and the maintenance costs of fixed monitoring systems can be solved. Finally, it can obtain information on all points on the network [17], which is suitable for urban networks. This has aroused the interest of related scholars in the selection of variable points of traffic volume on the road network. Kan et al. used taxi GPS data to predict and analyze traffic congestion [18]. Zhang et al. used special vehicle data provided by Didi Chuxing (a mobile phone taxi software) [19]. Some researchers have specially configured vehicles with GPS for simulation tests [20,21]. The main disadvantage of floating car data is that it only collects the current position and speed information sent from the sample vehicles. Therefore, floating car data provides ubiquitous but only partial information. In addition, the data is completely lost on routes where the equipped vehicles are not traveling. Moreover, in cases where the sampling rules are usually specified, the actual sampling rate of each road section is unknown. Therefore, for a highway network with extreme length and low density, the second type of data, section traffic data is preferred. Freeway toll data is a particularly high-quality data source.
For the prediction of traffic volume based on cross-section data, many mature specific applications have been generated based on statistical models, including the filter theory [22], chaos theory [23], artificial neural network methods [24,25], support vector machine methods [26], and time-series models. For the short-term traffic volume abnormal value prediction, the non-linear and unstable characteristics of the flow often cause low accuracy, leading to an inappropriate reference for actual traffic induction. In particular, the parameter non-portability model is only suitable for steady-state traffic flow, and the inadequate prediction of traffic flow anomalies cannot reach the required target. In particular, when there is a large amount of calculations the modeling process is complicated and a large amount of data sets are needed to train the network. The size of the training set sample of the network has a large impact on the stability of the subsequent network. When analyzing large-capacity provincial road networks, traditional statistical methods are often unsolvable, which makes the use of machine learning a reliable choice. In addition, we recognize that a large amount of high-quality data at highway toll stations makes data-driven machine learning a valuable option.
In the past few years, various machine learning methods have been proposed in big data analysis, especially some network-based methods. Researches have focused on neural networks [27,28], Bayesian networks [17], and time series. The purpose is to take advantage of the correlations that exist between the data and process this at different time intervals and on different links of the network. This paper makes predictions from the cyclical aspect, where time series have advantages. From the perspective of the basic structure of traffic flow (cyclical trend), the popular and universal view in traffic flow theory is that traffic is mainly cyclical, and the cycle exists within the day and week. Although the frequency domain method reveals the characteristics of periodic traffic flow that changes with time and claims to effectively capture intra-day cycles [29], due to the importance of the correlation of traffic data at different times, the traffic flow prediction methods present in the literature are mainly focused on the time domain method, which regards the current value of traffic flow as its past value. Among the time domain methods, the autoregressive integrated moving average (ARIMA) model is one of the most widely used regression techniques. The research on the recent hybrid model related to time series is as follows: Song et al. applied the ARIMA-SVM model to predict the daily mean value of PM 2.5 concentration in Shenyang [30]. Sharma and Ghosh used the ARIMA-EGARCH model to make short-term predictions of wind speed variation in Maharashtra, India [31]. To predict the volatility of the securities market, EGARCH-ANN was adopted [32]. These studies show that hybrid models can improve the accuracy of traffic prediction by decomposing traffic data into different components. Although the prediction results of the hybrid prediction model reveal certain advantages compared with the traditional method, there may be overfitting problems. To address this issue, Shabri used multiple prediction techniques (ARIMA, group method of data handling (GMDH)) combined with empirical modal decomposition (EMD) to predict the number of tourists traveling to Malaysia from Singapore [33]. The results indicate that using EMD to decompose the prediction data in advance will help prevent overfitting. Wang et al. combined EMD and the ARIMA model (EMD-ARIMA) to predict the short-term traffic speed of expressways [34]. The hybrid model showed better prediction accuracy than the traditional ARIMA method. The above research results combining EMD and the ARIMA model to predict peak anomalies show that the main advantage of this model is to correct individual defects. It produces synergistic effects in short-term predictions such as traffic speed and passenger flow and can handle non-linear and non-stationary sequences. In view of the current research, this paper summarizes the mentioned forecasting models in Figure 1.
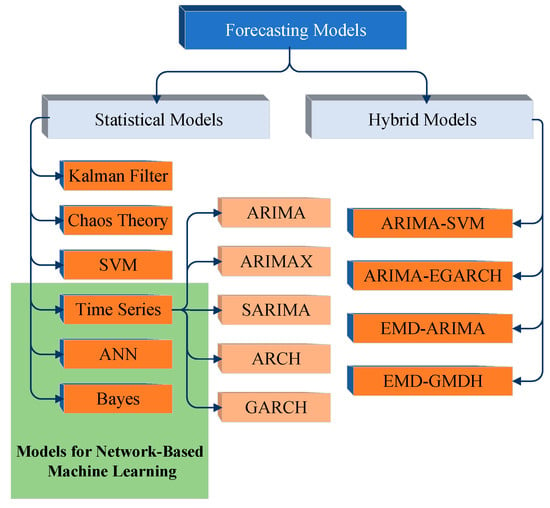
Figure 1.
Summary of mentioned forecasting models.
1.3. Paper Contribution
The feasibility of identifying traffic peak outliers lies not only in the accuracy of the predicted values, but also in the rationality of the criteria for defining the peak outliers. According to the Pauta criterion (also known as the 3σ principle), which assumes that the detection data contains only random errors, the original data is calculated and processed to obtain the mean and standard deviation. Then, an interval is determined with a certain probability. When the error exceeds this interval, it belongs to an abnormal value (the general threshold is μ + 3σ) [35]. Local outlier factor (LOF) is a classic density-based algorithm [36]. Most of the anomaly detection algorithms before LOF were either based on statistical methods, or adopted some clustering algorithms (such as DBSCAN, OPTICS) for the identification of outliers. However, statistical methods usually acquire the assumption that the data obey a specific probability distribution, and this assumption is often violated. For the clustering method, it usually gives a judgment of 0/1, which cannot quantify the degree of abnormality of each data point. The density-based LOF algorithm can solve both of these problems. This study combined the LOF and the actual data distribution, expounding the rationality of the Pauta criterion as the standard for freeway traffic volume identification.
Although many methods that improve prediction accuracy have been proposed, short-term traffic flow prediction remains a difficult challenge. Most of the research results focus on the optimization of the model, while ignoring the effective use of the similarity features of the traffic flow data. Specifically, most prediction models take all traffic flow data before the predicted time as input data. However, fluctuations in traffic flow are highly random. Prediction bias will occur if the input data of the prediction model only depends on the data of the previous moment. Yang et al. believe that the establishment of a multi-step prediction method that can fully utilize the similarity characteristics of traffic flow time series will significantly improve efficiency and accuracy [37]. Given this problem, this study presets categorical variables for dates when calibrating time series of data, then training similar time series during modeling. Cools et al. conducted a simulation analysis of Sunday′s explanatory variable (called intervention in time-series terminology) when discussing the Sunday effect, and achieved good results [7]. Analyzing the data of this study, we can find that the traffic volume of the Jiangsu expressway network fluctuated around the weekend. This paper classifies variables on Friday, Saturday, and Sunday, because it is found that there is an abnormal peak in passenger traffic on a certain number of urban origin-destination (OD) pairs in the training data; that is, Friday, Saturday, and Sunday all show unique time-series characteristics. Figure 2 is a schematic diagram of similar time series.
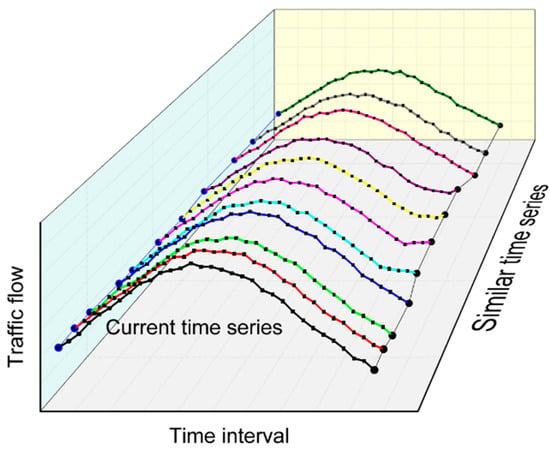
Figure 2.
Schematic diagram of similar time series.
Considering the advantages of EMD-ARIMA in abnormal peak prediction, this paper explores the potential of this hybrid model in traffic volume prediction. This study uses empirical mode decomposition (EMD) to decompose the original traffic data into independent components; that is, the original time series with nonlinear and non-stationary characteristics is decomposed into an intrinsic mode function (IMF). The main purpose of this decomposition is twofold: (1) to simplify the prediction; (2) to distinguish the intrinsic mode function with different characteristics to improve the prediction accuracy. On this basis, each IMF is modeled independently using the ARIMA model, and all results are aggregated to generate a combined prediction result. Finally, the EMD-ARIMA prediction results are compared with those of the standard ARIMA model to verify the effectiveness of the hybrid model in the prediction of short-term traffic anomalous peaks.
In summary, there are three contributions of this paper. This paper expounds on the rationality of the Pauta criterion as the standard for freeway traffic volume identification; proposes the use of the similarity features of traffic flow data based on week attributes; and introduces EMD to decompose time series with nonlinear and nonstationary characteristics.
2. Prediction Models
2.1. Empirical Mode Decomposition
EMD is a method proposed by NE, Huang et al., which has been widely used to decompose a signal into the modes with different characters. Its advantage is that any defined function will not be used as the basis, while the intrinsic mode functions (IMFs) will be adaptively generated on the base of the analyzed signal. The purpose of EMD is to decompose complex signals with nonlinear and nonstationary features into the sum of a finite number of IMFs and r(t), where the r(t) is the residual after IMFs are derived. The decomposition process of EMD is based on the local characteristic time scale and follows the order from high to low frequency. The r(t) is generally the mean trend of the signal and a monotonic trend term of the nonstationary function. Therefore, EMD can be used to analyze nonlinear and nonstationary signal series with a high signal-to-noise ratio and a good time-frequency focusing property.
The detailed procedure of the using of EMD can be summarized as follows:
- (i)
- Identify all local extreme points of in the time sequence, generate the upper and lower envelopes by the cubic spline functions, and calculate the mean envelope between the upper and lower envelopes.
- (ii)
- Calculate the difference between the original sequence and the mean value to get a new sequence, namely .
- (iii)
- Check whether satisfies the properties of an IMF. If satisfies the two conditions of an IMF, is denoted as the first IMF, i.e., , then residue is substituted into the original time series . If is not an IMF, then substitute into . Repeat (i) and (ii) until satisfies the requirements of the IMFs.
- (iv)
- Repeat (i) through (iii) until the residue becomes a constant, a monotonic function, or a function with only one maximum and one minimum from which no more IMFs can be extracted.
Finally, the signal can be presented as a summation of components and a residue is given by Equation (1):
Here, the IMFs represent components from high frequency to low frequency, while means the general tendency of the signal . This study uses the PYHHT module in PYTHON to complete the data processing work of EMD, based on which, ARIMA predictions are made on the IMF signals separated from it.
2.2. Autoregressive Integrated Moving Average Model
The autoregressive integrated moving average (ARIMA) model is one of the most recognized methods in time-series forecasting and has been implemented into various application domains after being introduced into expressway traffic prediction by Ahmed and Cook [5]. The autoregressive moving average (ARMA) model is a random time-series model which combines the autoregressive model (AR) and the moving average model (MA). Its function is to predict the optimal solution by minimizing the covariance matrix, on the basis of distinguishing the structure of the time series. The autoregressive moving average model can be expressed as ARMA (p, q), where p is the number of autoregressive terms and q is the number of moving average terms.
A general ARMA model is defined by the following Equation (2):
where is the predicted value of the next aggregate interval, is a constant value, is the value of the i-aggregate interval, and are the residual values of the predicted time interval and i-time interval, is the autocorrelation coefficient, and is the moving average coefficient.
AR, MA, and ARMA are suitable for the analysis of stationary time series, while the analysis effect of them is not ideal when the time series has an upward or downward trend. In order to solve the above problems, the stationary time series can be obtained after differencing the nonstationary series for D times, so that the model analysis can be performed on this basis. The optimal degree of differencing can be obtained by the DIFF function in PYTHON′s PANDAS module. The ARMA model after differencing for D times can be expressed as ARIMA (p, d, q), which has the following structure:
where is the sample value, is the white noise series subjecting to the independent Gaussian distribution, B is the lag operator, , is the autoregressive coefficient polynomial of the stationary invertible ARIMA (p, q) model, and d is the degree of differencing to make the formula ARIMA (p, d, q) a stationary series.
In the formula, the lag operator B represents a time pointer and gives the previous value of the series when placed in front of any variable with a time subscript.
The lag operator B can be expressed as:
The d-degree of differencing can be expressed as:
2.3. Local Outlier Factor
The LOF algorithm is a density-based algorithm for outlier detections. The scattered points with uniform density are considered as the same cluster by the LOF algorithm, while the isolated points outside the cluster with widely dispersed density are identified as dense points or outliers.
The LOF defines the k-distance as follows: . The formula satisfies:
- (i)
- There are at least k points in the set excluding , , which holds that .
- (ii)
- There are at most k − 1 points in the set excluding , , which holds that .
The k-distance neighborhood of p contains every object whose distance from p is not greater than the k-distance. The k-reachability-distance of point p with respect to point o is defined as:
It can be seen from this definition that the k-reachability-distance from point o to point p is at least the k-distance of point o, or the actual distance between point o and point p. The reachable distance from point o to the k points, which are closest to point o, is considered equal to .
The local reachability density of point p is defined as:
The formula defines the reachability distance from , the neighbors of p, to point p. If the density is high, it is more likely that all data belong to the same cluster. Otherwise, if the density is low, the possibility of the occurrence of outliers will be high. If point p and its neighbors are in the same cluster, the reachability distances are more likely equal to , which is smaller, resulting in a smaller sum of reachability distances and a higher density. Otherwise, if point p is far away from the neighbors, the reachability distance is all more likely equal to , which is larger, resulting in a lower density.
The local outlier factor of point p is defined as:
It can be seen from the formula that the local outlier factor of point p is essentially an average of the ratio of the local reachability density of point p and , its neighbors. If approaches 1, the point p and its neighbors have similar density, indicating that the data point p may belong to the same cluster as the neighborhood. If is lower than 1, the density of point p is much higher than the neighborhood and the data point p may be at the point of intensive data. In contrast, if is higher than 1, the density of point p is much lower than the neighborhood and the data point p is likely to be an outlier.
3. Data Set
The research scope is the expressway network in Jiangsu Province and neighboring provinces. The data set is about 450,000 sets of toll data from each expressway entrance and exit toll station from June to August, which is provided by the Jiangsu Transport Bureau. This paper takes the urban administrative regions of Jiangsu Province and its neighboring provinces as the aggregate object, selects the specific date of the data as the index, and add explanatory variables to Friday, Saturday, and Sunday. When Cools et al. studied the influence of the holiday effect on the abnormal peak in the expressway network [7], it was comparatively proved that using a natural day (24 h) as a scale was far better than the scale of 5–15 min in the large-scale network. In this paper, the short-term traffic volume prediction of the abnormal peak value of the Jiangsu road network takes a natural day as a set interval, counts the passenger traffic volume, constructs the time series of traffic generation and attraction between cities, and focuses on the identification of the abnormal peak value of passenger traffic between cities.
4. Case Study
4.1. Definition of Anomaly Criteria
Before identifying anomalous peak values of traffic volume on the road network, this study must first define the criteria of the anomalous peak value. To examine the rationality of the classification criteria of the anomalous peak value, the OD pairs between cities are divided into nine levels according to the amount of traffic volume: 0–10,000 pcu/D, 10,000–20,000 pcu/D, 20,000–30,000 pcu/D, 30,000–40,000 pcu/D, 40,000–50,000 pcu/D, 50,000–70,000 pcu/D, 70,000–100,000 pcu/D, 100,000–200,000 pcu/D, and >200,000 pcu/D (where pcu/D means passenger car units per day) On this basis, the traffic volume distribution of selected urban OD pairs is analyzed and verified at each level. The Pauta criterion, based on statistical rule, and the classic local outlier factor (LOF) algorithm, based on density, have been introduced in Section 2. The following is a visual analysis of the above two methods based on real data, as shown in Figure 3.
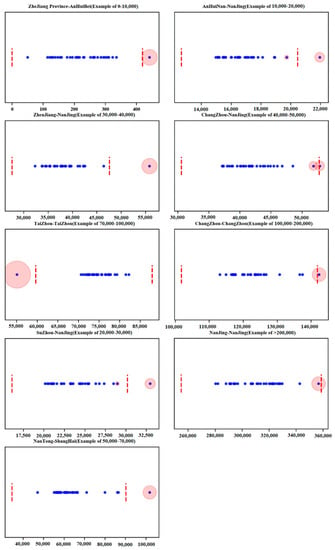
Figure 3.
Visual analysis of the standard for defining abnormal peak flow (Unit: pcu/D).
The red dotted line in Figure 3 represents the critical value calculated by the Pauta criterion, data points with red circles are the anomalies identified by the LOF algorithm, and the size of the circle represents the value of the outlier factor. A larger red circle indicates a higher possibility of anomalies in the LOF algorithm. The Pauta criterion in the levels of 0–10,000 pcu/D, 10,000–20,000 pcu/D, 20,000–30,000 pcu/D, 30,000–40,000 pcu/D, 50,000–70,000 pcu/D, 70,000–100,000 pcu/D, and 100,000–200,000 pcu/D correctly identifies the anomalies in the traffic volume. It should be noted that in the levels of 10,000–20,000 pcu/D and 20,000–30,000 pcu/D, the LOF algorithm incorrectly identifies the anomalies and accepts the false (although the value of the outlier factor is extremely small). At the same time, the critical values calculated by the Pauta criterion are more accurate in the levels of 10,000–20,000 pcu/D and 20,000–30,000 pcu/D, and its identification results are better than the LOF algorithm. In the 40,000–50,000 pcu/D and >200,000 pcu/D levels, due to the clustering effect of anomalies, the identification results of the Pauta criterion are fuzzier than those of the LOF algorithm. However, there are no obvious errors in the Pauta criterion in the levels of 10,000–20,000 pcu/D and 20,000–30,000 pcu/D, as in the LOF algorithm.
It is worth noting that the critical value calculated by the Pauta criterion is better in determining the upper bound range than the lower bound range, which is well reflected in the levels of 10,000–20,000 pcu/D, 20,000–30,000 pcu/D, 30,000–40,000 pcu/D, 40,000–50,000 pcu/D, 50,000–70,000 pcu/D, 70,000–100,000 pcu/D, and >200,000 pcu/D. It is more appropriate for this study to define the anomalous peak value of traffic volume without defining the anomalous valley value. At the same time, the LOF algorithm needs to calibrate the parameters of all urban OD pairs, and the establishment of the definition criteria in this paper does not require a specific outlier factor for each outlier. In conclusion, it is reasonable to use the Pauta criterion for defining of anomalous peak values of traffic volume on the expressway network, and the identification results are more accurate.
4.2. Comparison of Traffic Flow Prediction Methods
ARIMA has achieved mature and reliable applications in the field of prediction. In this section, an actual situation is used as the verification target to test the prediction accuracy of EMD-ARIMA for volatile traffic flow data, compared with ARIMA. It is found from the observation of actual data that the traffic flow of the highway network does not have obvious fluctuations from Monday to Thursday, and excellent fitting results have been achieved by various prediction methods. However, the fitting effect from Monday to Thursday has no obvious reference value and the goal of this study is to identify anomalous peaks in traffic flow. Although Saturday and Sunday belong to non-working days, they have different characteristics, and so they are shown in different sub-figures. This section focuses on testing the effect of traffic flow prediction on Friday, Saturday, and Sunday. Figure 4 is a schematic diagram of the results of predicting the traffic flow in the last week of June, July, and August in 2018, after machine learning the data before the last week of these three months. As the trends are similar, in order to facilitate observation, both ARIMA and EMD-ARIMA are assigned additional values to separate graphics. It also means that the Y-axis coordinates of different models are not comparable.
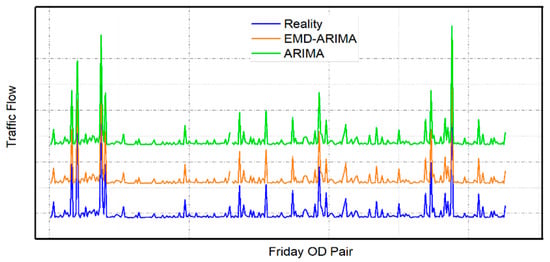
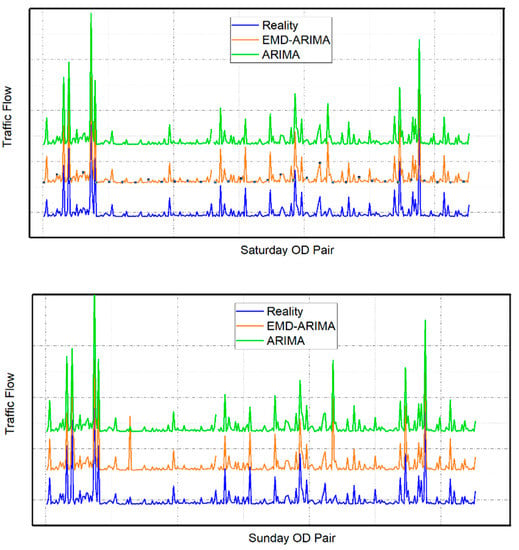
Figure 4.
Schematic diagrams of prediction results between the ARIMA model and the EMD-ARIMA model.
Intuitively, both the ARIMA model and the EMD-ARIMA model have achieved good prediction results. In order to further check the accuracy of the prediction results, test indicators of prediction accuracy are introduced: mean relative error (MRE), variance of absolute percentage error (VAPE), and root mean square error (RMSE). The specific definitions of these indicators are as follows:
where is the predicted value on day i, is the actual value on day i, is the absolute error on day i, n is the number of days, and is the mean absolute error (MAE). The results are shown in Table 1.

Table 1.
Comparison of verification parameters between the ARIMA model and the EMD-ARIMA model.
It can be ascertained from Table 1 that both the ARIMA model and EMD-ARIMA have excellent prediction effects in the prediction process of volatile traffic flow data and so both of them can be used as traffic flow prediction models.
Firstly, the EMD-ARIMA model has a slight advantage over the ARIMA model on the indicator of MRE, which indicates that the prediction effect of EMD-ARIMA show some advantages over the ARIMA model in terms of reflecting the actual situation of the predicted value error.
Secondly, the EMD-ARIMA model has a very slight advantage over the ARIMA model on the indicator of RMSE, which indicates that EMD-ARIMA presents very slight advantages over the ARIMA model in terms of measuring the deviation between the observed value and the actual value.
Thirdly, on the indicator of VAPE, the EMD-ARIMA model is better than the ARIMA model on Friday, while the ARIMA model is better than the EMD-ARIMA model on Saturday and Sunday. This result may be due to the huge difference of fluctuations in passenger traffic between the OD pairs in each city, which makes obvious fluctuations in the difference between the OD pairs and the mean error, resulting in fluctuations in the indicators of the EMD-ARIMA model and the ARIMA model.
Considering the three sets of indicators comprehensively, the prediction effects of the ARIMA model and the EMD-ARIMA model are both excellent: The EMD-ARIMA model presents a better forecasting effect of the volatility data than the ARIMA method, which shows the same result in [34,35]. It can be considered that EMD′s advantage in dealing with volatility data is that can be used in the field of transportation. It also shows a slight advantage on reflecting the error of the predicted value, while the EMD-ARIMA model has limited advantages in measuring the deviation between the observed value and the actual value. These two inferences are based on this data set and hope to be further verified in future research. It is reasonable for this paper to select the EMD-ARIMA model for the identification of abnormal peaks in traffic flow on the highway network.
4.3. Identification of Anomalous Peak Value of Traffic Volume
The anomalous peak values of traffic volume are screened from the results predicted in Section 4.2 according to the Pauta criterion verified in Section 4.1. There are 326 OD pairs between cities in total, and the results are summarized in Figure 5 according to the difference of origin and destination. The dates 25th and 26th are the weekend and the dates 27th to 31st are Monday to Friday.
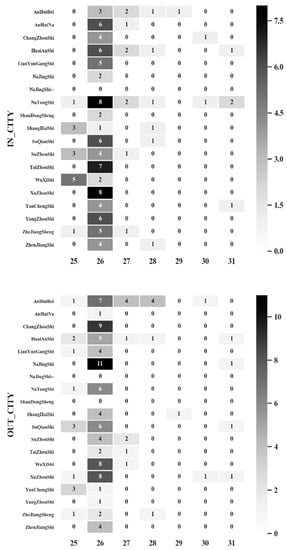
Figure 5.
Actual results of OD pairs in cities with abnormal traffic flow (ordinate unit: times).
The correct prediction results, eliminating the true errors and retaining the false errors, are analyzed statistically. It is not difficult to see in Figure 5 that most of the peaks of traffic volume occur on the weekend, especially the absolute peaks on Sunday. However, there are no absolute peaks on Friday and so the weekend effect should be analyzed, as shown in Figure 6 and Table 2. In binary classification, the model prediction results mainly have the following four cases: TP (true and positive), FN (false and negative), FP (false and positive), and TN (true and negative). The meaning of relations to our study is TP (the actual traffic volume is the anomalous peak value and it is successfully identified), FN (the actual traffic volume is the anomalous peak value, but it is not successfully identified), FP (the actual traffic volume is normal, but it is identified as anomalous peak value by mistake), and TN (the actual traffic volume is normal and it is identified as normal). The color depth represents the number of times a logical judgment occurs.
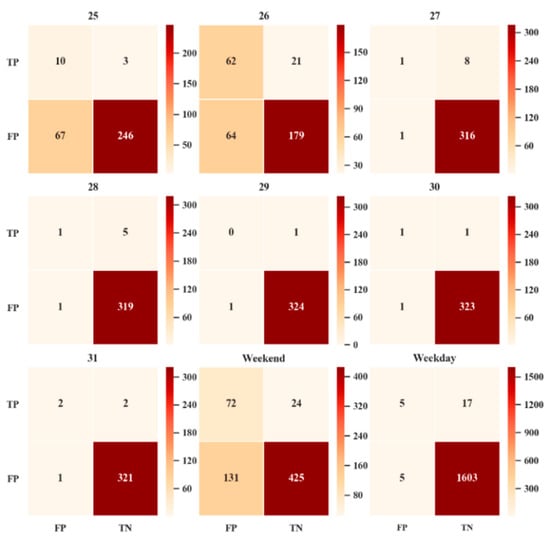
Figure 6.
Week attributes of dichotomy results (unit: times).

Table 2.
Indicators of dichotomy weekly attribute results.
To quantify the accuracy of the prediction results, accuracy, precision, recall, F-measure, and Matthews correlation coefficient (Mcc) are introduced to evaluate the effect of the outlier detection of the model. Each evaluation metric is defined as follows:
It is intuitively found in Figure 6 that TN (the actual traffic volume is normal, and it is detected as normal) occupies the absolute magnitude advantage in the classification results on weekdays, which is logical. This is also characterized in the evaluation metrics in Table 2: where accuracy is 98.65%. The weekdays receive evaluation feedback is too good, and they have no significance for metrics analysis. Therefore, the identification of peak values on the weekend is analyzed below, which is consistent with the statistical logic and subjects to the purpose of this study. The advanced traffic management system uses the prediction results for traffic management. The logical task is to identify the anomalous peak value (TP), and the least desired error is that the actual traffic volume is the anomalous peak values but the system identifies that the traffic volume is normal (FN). The corresponding metrics of accuracy and recall are 76.23% and 75% respectively, which shows that the EMD-ARIMA model of this study can identify more than 3/4 of anomalous peak values in situations where the traffic fluctuates sharply on Saturday and Sunday. Compared to pure empirical management, the accuracy of peak detection on the weekend is 14.72%. For traffic volume identified only on on Saturday, the accuracy of pure empirical management is 3.99%, while the accuracy and recall of the EMD-ARIMA model on Saturday is 78.5% and 76.9%, respectively. This shows that this study can complete the identification of anomalous peak values in fluctuating data and achieve good prediction results. At the same time, according to the precision, F-measure, and Mcc in the evaluation metrics, the identification efficiency of the model is low. However, considering that the proportion of anomalies in the total is extremely low, the efficiency loss of about 65% is within an acceptable range, and this is where the model may be improved through further research.
Figure 7 and Figure 8 analyze the impact of city attributes on the identification of anomalous peaks, where OUT-CITY is the city driving out of the expressway network and IN-CITY is the city driving in the expressway network. From the perspective of city attributes, the accuracy of each urban OD pairs fluctuates around 90% and recall is generally greater than 60%, which shows good detection performance. It is worth noting that the Pearson correlation coefficient between the accuracy of detection and the urban traffic volume is 0.165, which has no significant correlation. This shows that in the anomaly identification of fluctuation data, common sense with larger traffic volume and more accurate prediction results is not obviously reasonable.
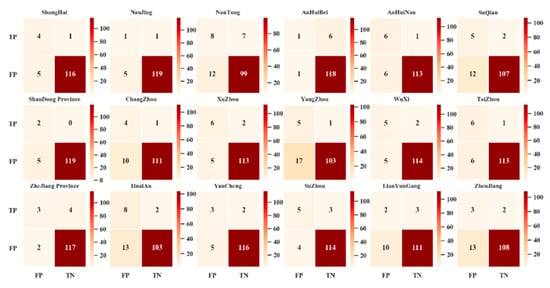
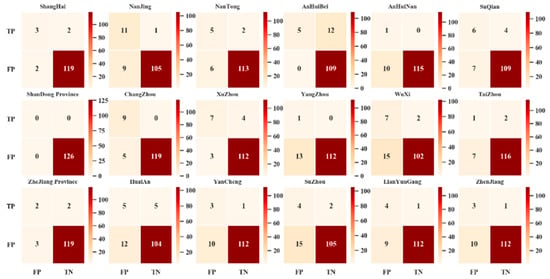
Figure 7.
Indicators of dichotomy CITY attribute results (OUT-CITY upper/IN-CITY lower) (unit: times).
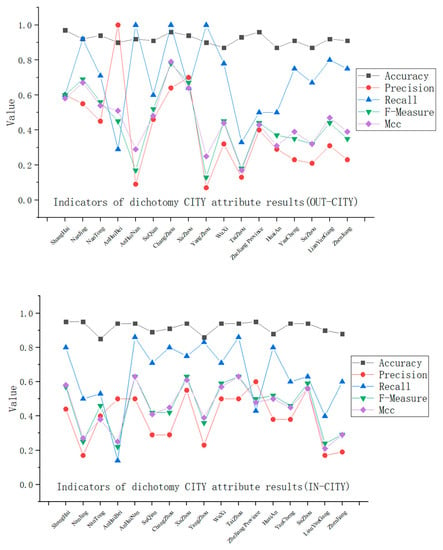
Figure 8.
Indicators of dichotomy CITY attribute results.
5. Conclusions
In order to effectively manage the safety of the expressway network, this paper advances an identification method of abnormal peak values of traffic flow. Before the prediction, in comparison with the local outlier factor (LOF) algorithm which is based on density, the Pauta criterion is proved to be better in the 10,000–20,000 pcu/D, and 20,000–30,000 pcu/D traffic flow levels. The effect of the critical value calibrated by the Pauta criterion in determining the upper bound is better than that in the lower bound, which gives it further advantages as the peak value defining standard. To sum up, this paper demonstrates the rationality of the application of the Pauta criterion in the field of expressway traffic flow.
The similarity features of traffic flow time series are used to explain the date with the same week attributes. This improves the accuracy and efficiency of the traffic flow input data. In the verification process of the test set, the weekend attribute of traffic flow fluctuation is obvious and shows that the interpretation of weekend variables conforms to machine learning logic, and the accuracy of the results also shows the feasibility of using time-series training with similar characteristics.
To ensure the reliability and validity of the machine learning model in data with obvious volatility and nonlinearity, this paper tests the effect of the EMD-ARIMA model in traffic peak prediction. In recent research, the EMD-ARIMA model has been used to predict wind speed, passenger flow, and traffic speed. This is compared to the classic ARIMA model to discuss the advantages of the hybrid model in the peak traffic flow prediction, which is embodied in the excellent results of the mean relative error (MRE) and root mean square error (RMSE). In the final verification of the results, the model can achieve good results in the weekend data with obvious volatility, even if it does not consider the weekday data with excellent performance due to the characteristics of the weekly peak distribution. The specific performance results are that both accuracy and recall are higher than 75%. In relation to urban attributes, the model performs well in all urban OD pairs: the accuracy fluctuates around 90% and recall is generally greater than 60%. Interestingly, the Pearson correlation coefficient is 0.165, and this we find that in the volatility data, the larger the traffic volume, the more stable and accurate the prediction result is, contrary to our common sense. It should be noted that the performance of the model in precision, F-measure, and MCC indicators is mediocre; that is, the recognition efficiency of the recognition model is low. Although, considering the small proportion of outliers in the total amount and the acceptable efficiency loss, it also provides the direction for further improvement of the model. In the next step of research, we hope to assess the corresponding relationship between the toll data collection point and the actual highway network, and the functions of the toll station in this level network, so that more practical research results will be obtained.
Author Contributions
Conceptualization, L.S.; Methodology, L.S. and J.L.; Project administration, L.D.; Resources, J.L. and D.G.; Writing—original draft, D.G.; Writing—review & editing, L.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [National Key R&D Program of China] grant number [2018YFB1601600].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data is provided by Transport Bureau of Jiangsu Province and managed by China Design Group Co., Ltd. If there are relevant research needs, the data can be obtained by sending an email to Shen Ling (shenling@seu.edu.cn). Please indicate the purpose of the research and the statement of data confidentiality in the email.
Acknowledgments
This research is supported by grants from National Key R&D Program of China (2018YFB1601600). The authors would like to thank Transport Bureau of Jiangsu Province and China Design Group CO., LTD. for providing the primitive data.
Conflicts of Interest
The authors declared that they have no conflict of interest to this work.
References
- Zhang, Y.; Zhang, Y.; Haghani, A. A hybrid short-term traffic flow forecastingmethod based on spectral analysis and statistical volatility model. Transp. Res. Part C Emerg. Technol. 2014, 43, 65–78. [Google Scholar] [CrossRef]
- Shi, Q.; Abdel-Aty, M. Big data applications in real-time traffic operation and safety monitoring and improvement on urban expressways. Transp. Res. Part C Emerg. Technol. 2015, 58, 380–394. [Google Scholar] [CrossRef]
- Fusco, G.; Colombaroni, C.; Isaenko, N. Short-term speed predictions exploiting big data on large urban road networks. Transp. Res. Part C Emerg. Technol. 2016, 73, 183–201. [Google Scholar] [CrossRef]
- Tettamanti, T.; Csikós, A.; Kis, K.B.; Viharos, Z.J.; Varga, I. Pattern recognition based speed forecasting methodology for urban traffic network. Transport 2018, 33, 959–970. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Cook, A.R. Analysis of Freeway Traffic Time-Series Data by Using Box-Jenkins Techniques; Transportation Research Board: Washington, DC, USA, 1979. [Google Scholar]
- Zeng, D.; Xu, J.; Gu, J.; Liu, L.; Xu, G. Short term traffic flow prediction using hybrid ARIMA and ANN models. In 2008 Workshop on Power Electronics and Intelligent Transportation System; IEEE: Piscataway Township, NJ, USA, 2008; pp. 621–625. [Google Scholar]
- Cools, M.; Moons, E.; Wets, G. Investigating the variability in daily traffic counts through use of arimax and sarimax models. Transp. Res. Rec. 2009, 2136, 57–66. [Google Scholar] [CrossRef]
- Karlaftis, M.G.; Vlahogianni, E.I. Memory properties and fractional integration in transportation time-series. Transp. Res. Part C Emerg. Technol. 2009, 17, 444–453. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, S.; Tang, J.; Wang, X. Understanding characteristics in multivariate traffic flow time series from complex network structure. Phys. A Stat. Mech. Appl. 2017, 477, 149–160. [Google Scholar] [CrossRef]
- Xue, X.; De-Xin, Y.; Xiu-Juan, T.; Shi-Guang, W. Analysis of multi-state traffic flow time series properties using visibility graph. Acta Phys. Sin. 2017, 66, 230501. [Google Scholar]
- Chen, J.; Li, D.; Zhang, G.; Zhang, X. Localized space-time autoregressive parameters estimation for traffic flow prediction in urban road networks. Appl. Sci. 2018, 8, 277. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Kopsinis, Y.; Mclaughlin, S. Development of emd-based denoising methods inspired by wavelet thresholding. IEEE Trans. Signal Process. 2009, 57, 1351–1362. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, L.; Chen, M. Short-term forecasting of high-speed rail demand: A hybrid approach combining ensemble empirical mode decomposition and gray support vector machine with real-world applications in China. Transp. Res. Part C Emerg. Technol. 2014, 2014, 44. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.N.; Srikanth, N. A novel empirical mode decomposition with support vector regression for wind speed forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1793–1798. [Google Scholar] [CrossRef]
- Fusco, G.; Colombaroni, C.; Isaenko, N. Comparative analysis of implicit models for real-time short-term traffic predictions. IET Intell. Transport. Syst. 2016, 10, 270–278. [Google Scholar] [CrossRef]
- Kan, Z.; Tang, L.; Kwan, M.P.; Ren, C.; Liu, D.; Li, Q. Traffic congestion analysis at the turn level using Taxis’ GPS trajectory data. Comput. Environ. Urban Syst. 2019, 74, 229–243. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, J.; Zhou, J.; Zhu, J.; Wan, Q. Complexities’ day-to-day dynamic evolution analysis and prediction for a didi taxi trip network based on complex network theory. Mod. Phys. Lett. B 2018, 32, 1850062. [Google Scholar] [CrossRef]
- Carrese, S.; Cipriani, E.; Mannini, L.; Nigro, M. Dynamic demand estimation and prediction for traffic urban networks adopting new data sources. Transp. Res. Part C Emerg. Technol. 2017, 81, 83–98. [Google Scholar] [CrossRef]
- Bucknell, C.; Herrera, J.C. A trade-off analysis between penetration rate and sampling frequency of mobile sensors in traffic state estimation. Transp. Res. Part C Emerg. Technol. 2014, 46, 132–150. [Google Scholar] [CrossRef]
- Guo, J.; Huang, W.; Williams, B.M. Adaptive Kalman filter approach for stochastic short-term traffic flow rate prediction and uncertainty quantification. Transp. Res. Part C Emerg. Technol. 2014, 43, 50–64. [Google Scholar] [CrossRef]
- Cheng, A.; Jiang, X.; Li, Y.; Zhang, C.; Zhu, H. Multiple sources and multiple measures based traffic flow prediction using the chaos theory and support vector regression method. Phys. A Stat. Mech. Appl. 2017, 466, 422–434. [Google Scholar] [CrossRef]
- Kumar, K.; Parida, M.; Katiyar, V.K. Short term traffic flow prediction for a non urban highway using artificial neural network. Procedia Soc. Behav. Sci. 2013, 104, 755–764. [Google Scholar] [CrossRef]
- Raza, A.; Zhong, M. Hybrid artificial neural network and locally weighted regression models for lane-based short-term urban traffic flow forecasting. Transp. Plan. Technol. 2018, 41, 901–917. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Y.; Lu, H. Seasonal autoregressive integrated moving average and support vector machine models: Prediction of short-term traffic flow on freeways. Transp. Res. Rec. 2011, 2215, 85–92. [Google Scholar] [CrossRef]
- Tang, J.; Liu, F.; Zou, Y.; Zhang, W.; Wang, Y. An improved fuzzy neural network for traffic speed prediction considering periodic characteristic. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2340–2350. [Google Scholar] [CrossRef]
- Tian, Y.; Pan, L. Predicting short-term traffic flow by long short-term memory recurrent neural network. In 2015 IEEE International Conference on Smart City/SocialCom/SustainCom (SmartCity); IEEE: Piscataway Township, NJ, USA, 2015; pp. 153–158. [Google Scholar]
- Stathopoulos, A.; Karlaftis, M.G. Spectral and cross-spectral analysis of urban traffic flows. In ITSC 2001. 2001 IEEE Intelligent Transportation Systems Proceedings (Cat. No. 01TH8585); IEEE: Piscataway Township, NJ, USA, 2001; pp. 820–825. [Google Scholar]
- Song, G.G.; Guo, X.D.; Yang, X. ARIMA-SVM combination prediction of PM2. 5 concentration in Shenyang. China Environ. Sci. 2018, 38, 4031–4039. [Google Scholar]
- Sharma, S.K.; Ghosh, S. Short-term wind speed forecasting: Application of linear and non-linear time series models. Int. J. Green Energy 2016, 13, 1490–1500. [Google Scholar] [CrossRef]
- Lahmiri, S.; Boukadoum, M. An ensemble system based on hybrid EGARCH-ANN with different distributional assumptions to predict S&P 500 intraday volatility. Fluct. Noise Lett. 2015, 14, 1550001. [Google Scholar]
- Shabri, A. A novel hybrid ensemble learning paradigm for tourism forecasting. In AIP Conference Proceedings; AIP: College Park, MD, USA, 2015; Volume 1643, pp. 192–200. [Google Scholar]
- Wang, H.; Liu, L.; Dong, S.; Qian, Z.; Wei, H. A novel work zone short-term vehicle-type specific traffic speed prediction model through the hybrid EMD-ARIMA framework. Transp. B Transp. Dyn. 2016, 4, 159–186. [Google Scholar] [CrossRef]
- Cullinane, K. Statistical and econometric methods for transportation data analysis. Technometrics 2004, 46, 492–493. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Jörg, S. LOF: Identifying Density-Based Local Outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000. [Google Scholar]
- Yang, Z.; Bing, Q.; Lin, C.; Yang, N.; Mei, D. Research on short-term traffic flow prediction method based on similarity search of time series. Math. Probl. Eng. 2014. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).