Abstract
The paper analyzes the problem of defining the potential of geothermal reservoirs and the definition of a sustainable size of a geothermal power plant in the preliminary design phase. While defining the size of a geothermal plant, the objective is to find a compromise between renewability, technical sustainability, and economic return-related issues. In the first part of the paper the simplified lumped parameter approach based on the First-Order methods and their further evolutions and limitations is proposed. Experimental data available for some geothermal reservoirs are used for critical analysis of the simplified approaches for estimating the renewability and sustainability of the production of geothermal plants. In the second part the authors analyze methods based on theoretical heat transfer analysis supported by experimental data acquired from the geothermal field (thermal properties of the rock, porosity of the reservoir, and natural heat flux) and finally consider the numerical simulation as a method to connect the two approaches discussed before. The sustainability of geothermal power production can be estimated taking into account the energy stored in the reservoir and the thermal and fluid dynamic analysis of the reservoir. From this perspective, the numerical simulation of the reservoir can be considered as an effective method for the estimation of a sustainable mass flow rate extraction. Some specific cases are analyzed and discussed.
1. Introduction
Geothermal resources, in the countries where they are available, are strategic for the possibility of direct use as well as for electricity production, in a continuous way (not affected by seasonal variation). The renewability of geothermal sources is completely recognized only if correct exploitation strategies and optimal reservoir management are pursued.
Several papers deal with the beneficial uses of geothermal energy; this has been addressed mainly in some specific cases (e.g., low depth, high temperatures, high specific enthalpy of the fluid or the availability of superheated steam) [1]. Considering the interactions between plant and reservoir, the renewability is mainly connected with the utilization rate and with the reinjection strategy. The renewability of geothermal energy is discussed in [2,3]. Moreover, the durability of a plant is directly connected to an appropriate knowledge of the reservoir assessment. In the past, the capacity of geothermal power plants was often sized at high level with the highest production rate for opportunely reducing the payback time and to compensate for the huge amount of investment.
Defining the energy potential of a geothermal reservoir is quite a complex task: the power rate can be correlated with the power density of the magmatic ascent, with the volume and the characteristic of the reservoir (fractured and porous), and with the availability of a geothermal fluid (liquid or two-phase). The problem is a complex unsteady heat transfer problem in porous media combined with the use of the energy stored in the reservoir.
Different approaches to reservoir engineering and potential assessment have been discussed and analyzed for different regional cases. Among the various contributions in literature, four are considered more relevant: the methods of surface thermal heat flux discussed in [4]; the volume method considered in [5,6]; the Planar Fracture method developed by Bodvarsson [7]; and the method of magmatic budget discussed by Noguchi, among others, with reference to Japan [8]. A good analysis of the various methods is provided by Muffler and Cataldi in [9].
The estimation of the reservoir potential (and the uncertainty associated with this value) connected to power plant sizing was frequently the object of studies and discussion [10,11,12], as clearly remarked by Steffansson in [13] and DiPippo in the classic textbook about geothermal power plants [14].
Since its beginning, the scientific and technological debate about reservoir assessment was mainly focused on the existing high potential geothermal fields, like The Geysers (USA), Larderello (Italy), Wairakei (New Zealand), Japan, and Iceland. This debate is particularly relevant today, as the medium-to-low enthalpy fields are being considered for further development of geothermal energy. As medium-to-low enthalpy fields are the most widespread around the world, this topic appears to be important for the future diffusion of geothermal energy systems. The available discussion about renewability in the above referenced literature refers mainly to the heat stored in rocks and water/steam and does not often take into account the resupply of fluid (and heat) that is really important after the common application of reinjection strategies. Resupply of heat and water to the reservoir is likely to augment significantly the geothermal resources.
In some cases, the plants showed significant reductions in power output due to the depletion of the reservoirs [10,11,12]. Wrong sizing in this case was generated by an overestimation of the reservoir potential, driven by the desire of a fast recovery of the main economic investment.
Interesting guidelines for defining a sustainable level of exploitation of geothermal resources are available in the literature, in some papers of a methodological perspective, like [9], and in more recent ones, such as [15] and [16]. The topic is still the object of research. In recent times the problem was reviewed by Axelsson [11], who introduced into the concept of sustainability the idea of considering compensative actions and implementing appropriate strategies for reservoir maintenance—like cultivation and reinjection.
The definition of a sustainable size of a geothermal power plant was the object of analysis in some papers by the authors of the present paper [12,15]. The definition of a geothermal system is very useful for the purpose of this paper: it can be seen as made up of the power plant, the geothermal reservoir, the groundwater circulation system, and all the possible connections among the various parts of the plant and the environment. In [17], the renewable behavior of geothermal systems is discussed with the objective of defining an optimized utilization strategy. A general methodology for all the varieties of geothermal fields does not exist, even if interesting analyses are available [18,19].
The objective of the paper is to provide a general analysis of the methods for the estimation of the potential assessment and to propose the best strategy for defining a sustainable size of the plant. A part of the paper concerns the analysis of the simplified lumped parameter method, as well as of the analytical methods that have been proposed in the literature. It is interesting to discuss some of the main positive elements and drawbacks, and to point out some reference data.
A discussion about the possible joint use of different First-Order methods is then provided, analyzing simple case studies for which a sustainable level of power production is identified. Finally, a specific focus is put on the numerical simulation of geothermal reservoirs, which are a useful tool for joining together the ideas contained in the other two approaches.
2. Potential Capacity of Geothermal Reservoirs and the Problems Connected with Overestimation
Geothermal energy contributes only a small part of the world energy production because it accounts for less than 1% of the world’s electricity generation output, and the total installed capacity was about 13.5 GW at the end of 2018. This level can be considered marginal, considering that the total amount of the installed power is over 6000 GW [20]. Moreover, geothermal energy has several drawbacks. A serious problem concerns the large variability of the source (enthalpy level, pressure, temperature, chemical composition). Development is burdened by high installation costs and quite long development periods. As a long-term result, in many countries geothermal energy projects have been, and are, relevant although reliant on institutional incentives.
As it can be observed from Table 1, geothermal plants are characterized by the highest total number of yearly operating hours (average value of about 7225 h) with respect to other renewable energy-based plants. Different sizes are identified in typical geothermal plants (mainly high enthalpy geofluid based) as reported in Table 2, showing a wide variability. The cases available in the literature clearly demonstrate that the installation success usually stands in the total power installed range between 150 MW and 1500 MW, which are also typical values of thermoelectric energy systems [21]. Small-sized power plants are currently increasing their markets, but these observations are related to the huge number of data coming from the traditional steam and flash-type plants. From several decades of industrial experience, it can be shown that a kind of sustainable balance is achieved by maintaining production below an appropriate limit in order to preserve this profitable exploitation level for a long time. Sustainability assessment (production/reinjection) is relevant for power plants of medium-to-low capacity (less than 5 MW). In such cases, the use of binary power plants based on the use of Organic Rankine Cycle (ORC) is a largely diffused option.

Table 1.
World power capacity and energy production by source at the end of 2014 and the trend of 2004–2014 [20].

Table 2.
The 20 biggest geothermal power plant installations in the world (data from [21]).
Anyway, the high specific costs of both exploration and erection of the ORC power plant and the high geological risks connected to the drilling could determine, in the exploration phase, an oversizing of the plant and a consequent possible overexploitation of the reservoir during the operating life. This is because the energy production must be higher in order to shorten the recovery time of the investment.
In fact, in order to obtain a quick investment payback, the highest power size achievable could be identified as design capacity, often without a proper evaluation of the technical, geological, and economic sustainability of the whole project. This would lead to a temperature or flow rate depletion, leading to a premature stop of the productivity of the plant. This problem is important particularly for plants using medium-to-low source temperatures (100 °C < Tgeo < 150 °C), typically ORC power plants. The oversizing is also a particular problem when smaller-sized power plants are considered (e.g., net power < 500 kW). In Figure 1 conceptual scheme of the interaction between plant and reservoirs is given.
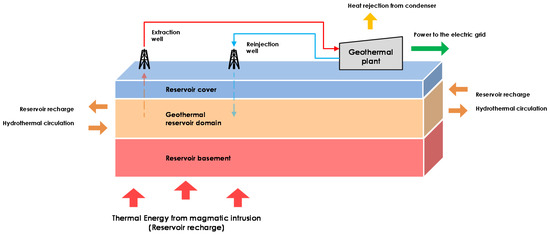
Figure 1.
Simplified scheme of the interaction of a power plant (Organic Rankine Cycle (ORC) plant, with geofluid in a closed loop between extraction and reinjection) with a geothermal reservoir.
Both with binary cycle power plants and with flash steam power plants, similar problems can occur in connection with a reduction of the thermal energy of the reservoir (e.g., resource depletion). But in this case, the reduction of the thermal input from the reservoir requires an increase of the mass flow rate extraction, and consequently, a major stress for the reservoir. In several cases, when fluid extraction is excessive, it is not possible to maintain the required long-term productivity of the plant.
The cases of the geothermal plant of Momotombo in Nicaragua, analyzed in [22], and the plants of The Geysers area represent meaningful cases [23,24,25]. At The Geysers, the plant started operation at the end of the 1960s. The increase in the size of the plants up to a level of 2200 MW, pursued until the end of the 1980s, led to an important reduction of the productivity during the 1990s (Figure 2).
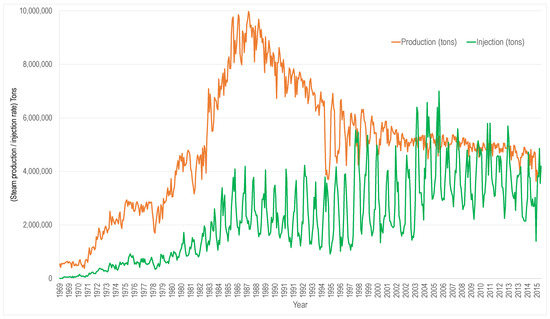
Figure 2.
The monthly production rates of the power plants at The Geysers during a period of 45 years, between January 1969 and March 2016 ([23]).
The decline of electricity production was attributed to a limited natural recharge. In the 1990s the reinjection of the geofluid started, promoting the reservoir recharge and improving the performance of the Geysers reservoir [23,24,25]. At Larderello (Italy) reinjection of geothermal fluid in the reservoir started well before, in 1974, being also the means of disposal for geothermal steam condensate. Reinjection was increased and is now an integral part of the power plant’s operation, [26]. In the Larderello area, the whole running capacity is approximately 800 MW, and no problems with the resource have been observed in the last 20 years, giving the idea of have reached a sort of equilibrium point and consequently a sustainable utilization of the source. The same cannot be said for other geothermal plants reported in Table 2.
3. The Geothermal Resources and Reservoirs: The Concepts of Renewability and Sustainability
The problem of defining the energy stored in a geothermal reservoir has been largely considered in the literature during the last 50 years, but a general methodology for every kind of geothermal field has not yet been developed. The geothermal potential will identify the maximum mass flow rate of geothermal fluid that can be extracted for a long time without reduction of the thermodynamic parameters of the reservoir (pressure, temperature, and enthalpy).
Considering the available literature, two main categories of Resource Estimation Methods can be identified: methods that do not require the use of production data, and methods that are based on the elaboration of experimental data connected to the exploitation. Table 3 provides some of the available methods. Some of those methods are analyzed in the paper, while other methods are only mentioned. In any case, none of the methods without production data appears to be completely satisfactory. All the methods require the knowledge of specific elements connected to geology and geomorphology conditions, quite a difficult a priori without the knowledge of a production history.

Table 3.
Classification of the methods for the evaluation of the energetic potential of geothermal reservoirs.
3.1. Geothermal Reservoir Potential Assessment: Power Density and Surface Heat Losses
The various geothermal fields have different histories and remarkable peculiarities regarding the development of their production capacity. In general, due to the specific peculiarities of the different geothermal resources, it is difficult to identify parameters meaningful for the exploitation.
A preliminary indication is given by the power density reported in Figure 3. This value can be calculated as the ratio between the installed power and the surface of the area of interest.
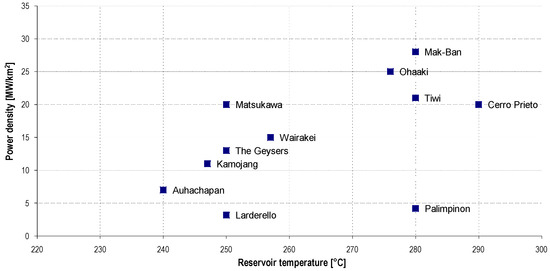
Figure 3.
Power density (out of the ground) for important geothermal areas (elaboration from [27]).
Even if the authors suggest a possible linearization of the data, the differences among geothermal fields with similar thermodynamic properties of the fluid (like temperature and pressure) can be observed (see for example the comparison of the Mak-Ban, Tiwi, and Palimpinon geothermal systems). Another important element is the extension of the area considered by the power plants, which gives an important indication about the extension of the geothermal reservoir. Observing the datum of Larderello, it appears that only 3.2 MW for each km2 of surface has been installed (the power installed is approximately 800 MW while the drilled area is about 250 km2). The plants of the geothermal area of Larderello are typical examples of sustainable use of geothermal energy. Observing the datum related to the field of Mak-Ban, a density of about 28 MW for each km2 of surface, an order of magnitude higher than the one of Larderello can be observed. But it is not possible to state that the Mak-Ban geothermal field can be defined as an example of non-sustainable use of geothermal energy. So this parameter, although interesting, seems not to be relevant.
3.2. Thermodynamic Balance of a Geothermal System: Energy and Exergy Analysis for Power Sizing
The maximum heat recoverable from the reservoir is the temperature of the fluid extracted from the reservoir, TR, with respect to the reinjection temperature (referred to as ΔT = TR – Trej); it is a finite quantity always less than the one given by the TR – T0 difference, where T0 is a reference low temperature (e.g., ambient temperature), being Trej > T0. The upper limit for the energy that can be extracted/converted is expressed by the general term Π, which can represent, alternatively, an energy, a power, or an amount of fluid dependent on the different variables that characterize the geothermal system under analysis (volume of the reservoir, porosity level, type of the fluid, etc.).
For a given power rate of the power plant, considering a well-defined difference ΔT between the temperature of the fluid that can be extracted from the geothermal reservoir and a reference temperature T0, an upper limit value of the mass flow rate extracted (m*) can be defined, identifying then the maximum potential for the required power capacity. As the value of the maximum sustainable extraction rate clearly depends on a lot of parameters and factors (both natural and technological), like permeability distribution, hydraulic linking between the production and the reinjection areas, siting of the wells, and natural recharge (meteoric water) of the reservoir, the potential (Π) is also a function of all these complex variables. The temperature difference ΔT is inversely proportional to the maximum mass flow rate that can be extracted from the reservoir without reducing its thermodynamic properties, m*. If Trej increases, as can happen while trying to mitigate particular scaling phenomena, the extraction rate (m) must be increased, and it can reach excessive values, causing an unwanted cooling-down of the whole aquifer. Each reservoir presents an optimal combination of both extractable mass flow rate and reinjection temperature, and a correct design should follow this rule. The potential (Π) must be then considered as a complex function of both natural and technological, which are very heterogeneous. From this perspective the Geothermal Potential Assessment can be seen as the result of a complex optimization problem involving the whole geothermal system (plant, reservoir, environment), and it is evident that an interdisciplinary approach becomes necessary [12]. From a more general perspective, the energy potential of a reservoir is connected to the availability of a well-defined volume of fluid at the temperature of the reservoir, TR, and it can be then determined as:
where C is the volumetric specific heat of the reservoir (considered as an aggregation of rock and fluids), while V is the total volume (including rock and fluids), TR is the reservoir temperature, and Tref is a reference temperature that can be considered as the lower bound for energy use (e.g., the environmental temperature or the reinjection temperature, Trej).
The values inside the equation can be evaluated taking into account that geothermal energy is stored partially in the rock matrix (80–90%) and the fluid contained in the porous structure (10–20%) [2,9,28,29]. Based on such a simplified approach, in a lot of cases it determines an overestimation of the potential, even if the depletion of the reservoir is neglected. In particular, in the specific case of largely spread fields, the use of a single synthetic value of porosity (with respect to the whole enormous rock domain considered) can lead to an enormous approximation. This can be explained by a simple calculation considering the typical values of the volume of the reservoir, rock density, specific heat, and a useful temperature difference. According to the authors’ evaluation, along with the analysis of data obtained by various references, reported in Table 4, amounts of stored energy of more than 1018 J can be theoretically obtained in specific cases where reservoirs have a volume of 10 km3.

Table 4.
Some reference data for typical geothermal systems [2,9,28,29].
The power size availability can also be based on exergy stored rather than on the extension of the geothermal field (Figure 3). Considering the reservoir as a mass M (equivalent) at a temperature TR > Tref, and some averaged values from the typical ones in Table 4, the useful power extractable from the reservoir (exergy) can be better defined as
It is now assumed as a simplified case study a geothermal field like the one of Larderello, according to the data by Romagnoli et al. in [30]. Referring to a reservoir dimension of 70 × 70 × 3.5 km3, the exergy available in the reservoir is in the order of 1015 MJ. For a period of exploitation of 100 years, using a typical value of the Second Law efficiency (for example, equal to 0.1), a power of 4000 ÷ 5000 MW can be installed in the area with only a temperature reduction of less than 10 °C. This is obviously not realistic, considering that the power now installed in the area is about 800 MW.
Using similar argumentation, the energy potential of different geothermal fields, as for example the Monte Amiata geothermal field, can be calculated. According to [31], this is a two-phase fluid field and the volume can be estimated as about 80 km3. Following the approach described above, a maximum power capacity of 1200 MW can be calculated. It is also evident that this value is only theoretical: the power installed is one order of magnitude lower. The reason lies in the fact that from Equation (3) an amount of energy stored in the reservoir must be defined, but only the part corresponding to the maximum permissible temperature decrease, ΔT, is extractable during the lifetime of a plant, τ (for example, 50–100 years), giving an upper limit value K expressed in terms of degrees for a reference time (e.g., a reduction of 15 °C each 10 years of operation).
In general, it is known that a simplified volumetric approach, often used in the past for a preliminary estimation of the size of the plant, leads to an overestimation of the real potential of the reservoir, while an estimation based on the time history, developed according to Equation (4), can determine a reduction of the size.
This was distinctly clear at the end of the 1970s and it is evident from [9] that the energy stored in the reservoir cannot be the only element for the potential assessment. Some additional elements must be taken into account: the boundary condition in terms of mass and energy exchange with the boundaries and the intensity of the power source available, the resupply of heat and water to the reservoirs consequent to reinjection strategy. For this reason, a plant design based on this simplified approach has sometimes encountered problems.
3.3. The Concept of Renewability and Sustainability of Geothermal Plants: Analysis of the Differences
The concept of renewability in the field of geothermal energy systems is defined as maintaining the value of the nominal power of the plant for an infinitely long time without any resource degradation and without compensative actions. However, it often occurs that renewable capacity is too small for proper investment payback and commercial development of power plants.
In recent years, as a consequence of the experiences acquired in some specific geothermal reservoirs in the world, the concept of sustainability has been proposed in papers by some authors with different approaches [2,3,12,32]. This concept can be defined as the capability of keeping almost constant the productivity of the power plant, both economically and technologically, over a period quite longer than the economic lifetime of a power plant (e.g., 50–100 years) using some compensative actions, such as cultivation and reinjection. These actions can be of fundamental importance in order to compensate for pressure drawdown and/or cooling determined by an excessive extraction of the fluid. The idea is well illustrated in the schematization of Figure 4.
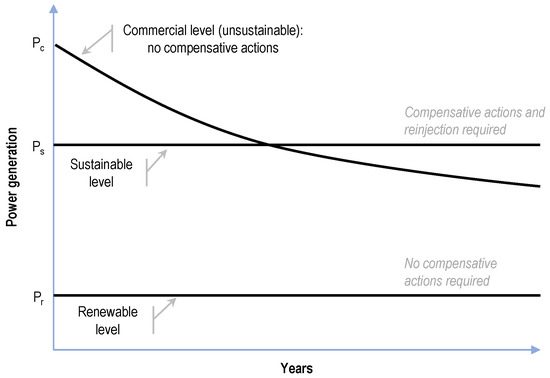
Figure 4.
Qualitative differences between renewable, sustainable, and economic production levels of geothermal reservoirs (rearranged from [11]).
4. Energy Potential and Extraction Rate: Approaches and Methods Based on a Volumetric Approach
Several approaches have been considered in the literature to analyze geothermal energy extraction. In general, the three main elements on which the energy extraction can be based are:
- -
- the amount of energy stored in the reservoir composed by rocks and fluids;
- -
- the amount of energy transferred in the reservoir from the hot part (magmatic intrusion) by natural heat flow;
- -
- the amount of energy resupplied by means of natural recharge or reinjection strategy.
Some reference values for the volumetric specific heat capacity and for the thermal conductivity, according to the experience of the authors, are reported in Table 4. The power rate obtained is based on a volumetric storage of energy determined by a geothermal heat source and the heat transfer between surface and fluid. To better explain this concept one can consider a porous reservoir as a kind of natural heat exchanger (and this approach will be discussed further in this paper), in which a rock matrix transfers the heat to a fluid flowing through it at a certain velocity.
In some of the first simplified approaches to the analysis of geothermal sources the most relevant element was the energy stored in the reservoir during the previous life of the geological system. So the first thing to do is to evaluate the heat stored in the reservoir; this can be done knowing the nature of the rocks and fluid characteristics and at an average temperature. The recoverable portion can be estimated by means of the Recovery Factor (Rg): this is the fraction of energy contained in the reservoir that could be produced feasibly by actual production wells and current conversion technology (available at the time the assessment is performed) over a reasonable project timeframe.
Considering the energy stored reduced by a recovery factor (actually a coefficient in the interval 0 ÷ 1, whose typical values can range between 0.05 and 0.5) a sustainable plant capacity for a given life of the plant can be defined [9].
To estimate the recovery factor for a geothermal field appears to be a non-trivial task, it depends on the site characterization and it is usually also strictly related to the experience. For an ideally permeable system the recovery factor may be as much as 50%. It decreases as the effective porosity decreases. For most reservoirs the recovery factor can be considered in the range between 0.15 and 0.2. It decreases to zero at an effective porosity approaching to zero (e.g., unfractured and impermeable rocks). Values from 0.25 to 0.5 are considered, too, as discussed in [33]. Table 5 provides the data for some particular cases of interest.

Table 5.
Recovery factors (Rg) and estimated values of sustainable power (P) for some reservoirs (as in [18]).
The concept of recovery factor Rg is similar to the recovery indexes considered in the oil and gas extraction industry. If all those correction factors allow us to obtain more realistic values of the energy stored and useful for conversion, though, a lot of uncertain elements need to be introduced for the estimation of the reservoir parameters, as discussed in this paper.
5. Sustainability Assessment of Geothermal Reservoirs Based on Terrestrial Heat Flux and Heat Transfer Model
Another element of the geothermal reservoir is the heat transfer to the fluid; in this case, the porous reservoir can be considered as a kind of heat exchanger with a defined surface, and the fluid gets heat from the reservoir depending on the resident time (t).
The concept here expessed were developed in some papers from the group of Stanford University in the late 70s [34,35,36]. The idea developed by the authors is to determine a kind of recovery of energy from fractured geothermal reservoirs.
The resident time of the fluid in the reservoir (t) is assumed as the time that is needed by a fluid element to get from the reinjection well to the extraction well (see Figure 1). This time can be correlated with the permeability of the reservoir, and it allows us to consider that the heat transfer phenomenon is quasi-steady. Some field tests (e.g., the tracer test) allow us to directly measure the permeability.
Coming from a traditional view according to Darcy’s law and according to this heat transfer perspective, the balance equations (heat, mass, and fluid velocity) can then be solved for a geothermal reservoir by considering it as an equivalent heat exchanger structure (allowing heat to transfer from a solid matrix to a fluid). The total thermal energy transfer can be connected to the heat transfer surface, which depends on the distribution of parameters like porosity and permeability of the reservoir (a satisfactory quality of the data from the field is then needed); this allows us to define an idealized area of the reservoir Ar.
In the case of a water-dominant geothermal system, the total power potentially extractable is correlated to both elements of available natural heat flow and conductive fraction as
The idea proposed here is to define a heat transfer area of the porous reservoir Ar and a characteristic length of the reservoir, L. In Equation (5) the power that can be extracted from the reservoir is the sum of a surface term that is surely connected to the volume and to the porosity, identifying a kind of ratio between surface and volume of the reservoir, plus a term that is connected to the length of the reservoir. This second term depends on the thermal conductivity of the reservoir (ks) and it can be evaluated by referring to the classic heat transfer problem involving two quasi-steady isothermal surfaces; it can be solved by means of the method of the shape factor S, in this case dimensionless. The values of S have been worked out for several geometries, and they are summarized in various textbooks on heat transfer or in manuals like [37].
The heat transfer problem concerning the geofluid can be seen as a superposition of two different heat transfer problems involving two different boundary conditions: imposed heat flux or imposed temperature. It is well known that the ability to transfer the thermal energy to the fluid in a heat exchanger can be correlated with the number of transfer units (NTU).
In a heat exchanger operating at steady conditions, the NTU is calculated as the ratio between the product of the overall heat transfer coefficient (U) and heat transfer area (A) and the product m·cp. Considering the geothermal reservoir as a heat exchanger, an efficiency of the system (ε) can be defined, Q can be estimated with reference to the maximum theoretically available power as:
Now that it is assumed that the geothermal system is a heat exchanger with a fixed value of the temperature of the rock, the heat transfer efficiency can be defined as:
The real problem is the definition of the number of transfer units (NTU) of the reservoir, which depends also on time:
where U (W/m2K) is the heat transfer coefficient, A (m2) is the effective contact area between fluid and reservoir, and C is the heat capacity of the reservoir (J/K). The number of transfer units (NTU), so defined, expressed in dimensionless form, represents a concept similar to the one used for thermal analysis of the heat exchangers, and it involves a combination of heat transfer surface A (dependent on the porosity and permeability of the reservoir) and the resident time (t).
An estimation of the resident time can be obtained by studying the distance between production and reinjection well, L, and the fluid flow velocity as:
where L represents the distance between the production and reinjection well, w is the velocity at which the injection front moves that is equal to the Darcy velocity wf divided by the porosity. Reinjection allows refilling the rock formation with the utilized water, then recharging in terms of fluid and thermal energy and pressure distribution.
As illustrated above, the resident time can help establish the ratio between the heat transfer surface of the reservoir and the thermal capacity of the reservoir. Thus, starting from the definition of the resident time t, the characteristic value of the NTU of the reservoir can be estimated, and the efficiency value ε is then useful to estimate the power rate Q that can be extracted from the reservoir. It is easy to demonstrate, with some simple practical calculations, that the power transmitted in a renewable way is less than one order of magnitude with respect to the energy historically stored in the reservoir, mainly in the case of single-phase fluid; the level can be higher if two-phase fluid is available, but this situation occurs in a reduced number of cases.
6. Advanced Method for Sustainable Potential Assessment: Numerical Simulation Supported by Experimental Data
The reason it is interesting to dive deeply into the sustainability of geothermal reservoir exploitation is to establish a feasible sizing of power plants that can be applied to a well-defined reservoir. The first issue to be faced is the high value of the geofluid mass flow rate, which could lead to overexploitation of the reservoir, by reducing in a significant way the useful time of the plant and the resource from the geothermal field [12], compensative actions that can be adopted in order to maximize and develop a sustainable power plant [11].
Both the methods described in the previous Section 4 and Section 5 can be considered as First-Order methods. They can be interesting and useful instruments for a preliminary evaluation of a geothermal system, but both show some serious drawbacks when defining the sustainable utilization level of a geothermal field. The joint use of the basic elements of the two methods can surely be the key point to individuating an analytical method for the power potential estimation of a reservoir.
The numerical simulation of a geothermal reservoir is a well-known field of research in the literature, as considered by the authors in [38]. Numerical models allow us to simulate the evolution of temperature and the pressure field of the aquifer and of the surrounding system under different exploitation scenarios. It has been the object of different analyses in the literature [39,40]. The transient evolution of the plant/reservoir system can be also studied [41,42,43], while taking into account that obviously there is a strong dependence of the results and model reliability on the quality of the inputs, as widely discussed by the authors (in [12,38,44,45,46]).
First of all, the input data and the geothermo-physical parameters necessary are not always available or directly measurable. Moreover, the definition of boundary conditions (e.g., hydraulic head, non-condensable gases, natural recharge) and initial conditions (e.g., thermal gradient, fluid circulation) is not a trivial task.
Numerical Simulation of a Geothermal Reservoir for Potential Assessment: Methodology
The various geothermal fields have different histories and remarkable peculiarities in the development of their production capacities. In general, due to the specific peculiarities of the different geothermal resources, it is difficult to identify parameters meaningful for the exploitation. A first indication is given by the power density provided in Figure 3.
Numerical simulation of geothermal reservoirs is surely the most promising method for defining the energy potential of a geothermal reservoir because it permits taking into account all the theoretical elements previously exposed. Considering a typical hydrothermal system, it is possible to implement the balance equations of mass, momentum, and energy in the volume domain. The balance equation must be written for each of the phases present. The basic mass and energy balance equation can be written in general form as:
The mass accumulation term and heat accumulation terms M are contained in the left part of the equation, while in the right part the term F accounts for the constitutive law (multi-phase version of Darcy’s law). The last term accounts for the heat flux.
The system is the more complex being the equilibrium of three components (rocks, water, and trapped gases) and three phases (gas, steam, or liquid). The hydrogeological elements linked to the geothermal exploitation (knowledge of the geological structures and of the groundwater system) must be connected with the engineering tasks of the design (size of the energy conversion plant). Constitutive laws are peculiar to each kind of reservoir, and the numerical simulation has two main branches:
- the natural state (unperturbed): this can be considered the natural evolution of the system without energy extraction;
- the utilization scenarios (imposing an exploitation rate).
The most relevant phases of a numerical model implementation can be identified as follows, as illustrated in Figure 5.
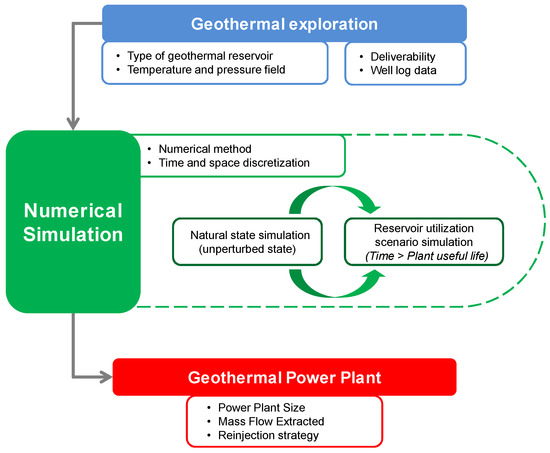
Figure 5.
Conceptual scheme of the numerical modeling of a geothermal reservoir.
- A preliminary block-model is built, together with the dataset of the main reservoir parameters at a first discretization level (e.g., geometrical features of the reservoir, hydraulic and thermal boundary conditions).
- Time and space discretization and the appropriate numerical method must be identified in order to solve the system of equations. Mass and energy balance calculation is then performed.
- Geothermal resource management: the main output from the model is the estimation of the appropriate amount of geofluid to be withdrawn/reinjected.
- The critical step for succeeding in a simulation is the calibration of the model. This should be done when geophysical log data and well tests are available, by adding geophysical measurements to the model parameters (e.g., conductivity of rocks, porosity, permeability).
The flow of information can also be upflow, mainly when feedback from the field is collected and while the calibration and refinement of the model is performed. This type of study is helpful to identify the sustainability level of a certain project, as through the simulated cases it is then possible to define the proper production scenario to match renewability and economic profitability of the investment. Sustainability is defined here according to the classic pillars: the technical, environmental, and economic definitions. If an oversizing of the plant is assumed (e.g., an excessive mass flow rate of geofluid at the design point), the lifetime of the plant would be compromised, as the resource will start to deplete soon, and also from an economic point of view the investment will not be remunerated (also treated in [38]). For this reason the classic approach to the numerical simulation of geothermal fields (e.g., during the geophysical exploration) must be extended not only to the unperturbed boundary conditions, but also to the exploitation scenario, which must be analyzed under different possible strategies in order to optimize and enlarge the useful lifetime of the resource over time (mainly), by an optimization of the reinjection strategy [36]. From a wide economic point of view, a thermo-economic analysis can be addressed, as heat recovery and exergy analyses can give a more consistent overview of the sustainability level of a geothermal project [46].
Numerical Simulation of a Geothermal Reservoir and Evaluation of the Sustainability: An Application
To understand the practical use of the methods explained, let us briefly consider a schematic model of a small reservoir in the peripheral area of the well-known Larderello field (Italy), where the presence of a moderate temperature geothermal source (90 °C–120 °C) can be assumed, estimated to be available at a relatively low depth (400–500 m below the ground level).
This kind of source was selected for the example for two different motivations: first of all, because the exploitation of such a reservoir is done using a binary cycle power plant (ORC power plant), which suffers more than the others from the temperature decrease of the reservoir; second, because in such a specific type of power plant the problem of oversizing is particularly relevant, due to the fact that in this case components with a discrete power level were used.
A three-dimensional model of the reservoir was constructed by using some standards available in the literature as [47] and discussed by one of the authors in [48]. This case was to be considered as preliminary, and so let us concentrate more on the qualitative concepts here discussed, although numerically based. The domain had an extension of 2.7 × 1.0 km2, being 0.8 km deep. The simulation was developed by means of a commercial software program (PETRASIM), in which the TOUGH2 simulator was implemented [49].
Tough2–PetraSim is an integral finite difference method for space discretization. It is First-Order fully implicit time differencing. It uses sparse direct solver or various preconditioned conjugate gradient algorithms (linear equation solution) and a quadrangular or polygonal Mesh-Finite volume grid approach. Sketches of the model domain extension and the various materials used are summarized in Figure 6 and Figure 7 and Table 6.
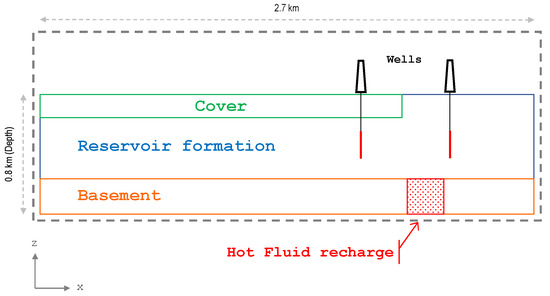
Figure 6.
Model domain and main structural features of the numerical model of the simulated geothermal reservoir (2D).
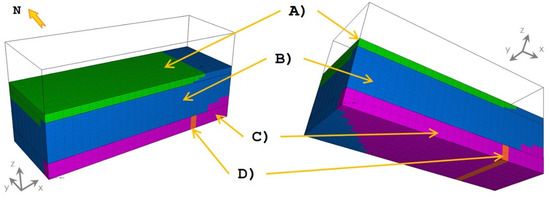
Figure 7.
Model domain 3D view and layers structure.

Table 6.
Thermophysical properties of the numerical model.
The model was constructed with the objective of defining an optimal production/reinjection strategy for the operation of a small-sized ORC plant. A simulation of the natural steady-state (unperturbed) of the field was first run, and then different exploitation scenarios were simulated. The model was made by 3672 blocks. Each block had the following dimensions: 100 m along the x-axis, 125 m along the y-axis. Each layer had then 27 blocks along the x-axis and 8 blocks along the y-axis. The blocks had different thicknesses: 25 m for the upper layer (cover), 50 m for the reservoir formation, 100 m for the basement. A hot upflow stream was assigned to simulate a fault at the base of the model.
The simulated exploitation scenarios referred to three different production/reinjections of fluid in the case of the installation of an ORC power plant, with the following assumptions:
- -
- potential size of the plant: 200 kW (case A1), 500 kW (case B1), and 1000 kW (case C1);
- -
- estimated mass flow rate values of 15 kg/s (case A1), 50 kg/s (case B1), 100 kg/s (case C1);
- -
- initial temperature of the geothermal fluid fixed at about 94 °C;
- -
- reinjection temperature fixed at 70 °C;
- -
- lifetime range considered: from 30 years to 50 years.
In a different scenario (cases B2 and C2) two production wells were at different initial temperatures (94 °C and 104 °C), while a single reinjection well was considered (the sum of the extracted flow rates was then completely reinjected). The correlation between mass flow rates and power sizes of the ORC plants came from well-known case studies and real application of the binary cycle involving Rankine cycles with both hydrocarbons and refrigerants as working fluids [44,45].
7. Results of the Numerical Analysis
The results of the three simulated cases are shown in Table 7 (for cases A1, B1, and C1) and Table 8. For case A1 (200 kW), the results gave low temperature vs. time depletion of about 2 °C in 30 years and about 4 °C in 50 years. The scenario of case A1, under these assumptions, was considered completely sustainable, also considering the low mass flow rate involved. Otherwise, when a mass flow rate extraction of 50 kg/s (for a power production of about 500 kW) was considered (case B1), the simulated temperature depletions were about 6 °C in 30 years and about 10 °C in 50 years. This was critical for the plant life and investment payback time. It can be easily concluded that the extraction of a mass flow rate of 100 kg/s of geothermal fluid (necessary for a power output of about 1 MW, case C1) is unsustainable for such a reservoir, as provided by the temperature reduction results over the lifetime of the plant for the three different exploitation strategies (Table 7). Considering such a severe scenario (case C1), the results of the simulation gave temperature reductions of about 10 °C after 25 years of exploitation. The temperature decrease could reach the level of 15 °C after 50 years of operation. So it can be concluded that in both the last two cases it would be difficult to maintain the correct working of the ORC plant during the operation, as the temperature decrease would compromise the heat exchangers pinch point and, in general, the whole exploitation strategy.

Table 7.
Simulation of the production scenarios for the tested geothermal field: temperatures at the production well at the beginning and after 25 or 50 year of exploitations (extraction/reinjection mass flow rates: 15 kg/s, 50 kg/s, and 100 kg/s, cases A1, B1, and C1).

Table 8.
Simulation of production-well temperature evolution scenarios for configuration with two extraction wells and one reinjection well (cases B2 and C2).
In Table 8 the evolution of the simulated extraction temperatures is shown (over a period of 50 years). For each production well, an extraction rate of 25 kg/s and of 50 kg/s, corresponding to scenarios B2 and C2 and to power plants of size 500 kW and 1 MW respectively, appears to be unsustainable. An extraction rate between 10 kg/s and 15 kg/s could be only considered in order to obtain a long lifetime of the plant in this case, too. In this approach, the numerical simulation of the geothermal reservoir was used to close the loop on the whole system, connecting the reservoir with the power plant flow rate utilization. In this way one simply evaluated the sustainability level by reviewing the useful lifetime of the whole geothermal system: the reservoir continuously recharging and the power plant design point conditions (underground and aboveground). As a general criterion we can say that, during the lifetime of the power plant, a temperature decrease lower than 10 °C can be accepted in the geothermal fluid contained in the reservoir.
8. Conclusions
The definition of the potential assessment of a geothermal reservoir is important in order to prevent unsustainable future use of geothermal energy systems. Today the problem is still an open field of research, even if after the late 1960s many of methodologies were proposed in the literature. In the present paper, the authors analyzed and revised the two main relevant methods.
The first group is considered as First-Order methods. These are based on the estimation of the energy stored in the reservoirs and on the definition of the amount that can be recovered. A second group of methods is based on analytic approaches. These try to define the amount of heat transfer between rocks and the fluid circulating into the reservoir.
In the final part, the numerical simulation of the reservoirs (supported by an example model) was discussed by framing this analysis as a more detailed family of methods for sustainability assessment. Considering the real exploitation of geothermal fields and the scenarios exposed in the paper, it seems clear that the estimation of the energy potential of a geothermal reservoir is a very difficult task; it is difficult to propose a general method, even if general guidelines can be defined:
- The definition of the potential assessment of a geothermal reservoir can be considered as a combination of the energy stored in the reservoir and the heat transfer rate between volumetric heat generation (magmatic ascent) and fluid;
- The classic idea of renewability is surely not good for commercial exploitation. The proper sizing of a plant should take into account the steady-state behavior of the reservoir, not only commercial needs or standard flow rates that can conflict with the proper durability of the geothermal system as a whole. The perspective of sustainability is surely more suitable for decision-making about plant capacity sizing. The sustainability of a plant must be connected to the sustainability of the resource itself, in particular when small size units are considered (<1 MW), which is properly limited by the geofluid circulation and the amount of energy stored;
- The volumetric extension of the reservoir is surely a key element of analysis; in the recent history of geothermal energy, large-sized plant (power > 100 MW) development was correlated with highly extended reservoirs. Other important elements are the measured heat flow rate (terrestrial heat flux) and the heat transfer surface of the whole geothermal system (rock–fluid heat exchange) determined by the porosity and permeability of the reservoir.
- It is evident that the potential assessment of a geothermal reservoir cannot be solved with simplified models of analysis. The First-Order methods are not useful for the definition of the size of a power plant (without integration with other methods) if the lifetime is the main goal in a complex world where small-sized power plants are increasingly under the scrutiny of the players. Small-sized units are mostly characterized by huge criticalities with respect to higher size (high flow rates, high sensitivity to geofluid temperature decrease), mainly related to a First-Order approach, and also for historical reasons.
- The experimental on-site measurements (geophysical parameters, geothermal gradient) connected with a correct 3D model simulation of the reservoir could be the most useful tools to characterize the potential of shallow geothermal reservoirs by helping to elaborate optimal production rate scenarios and the appropriate reservoir reinjection strategy.
- The geothermal potential assessment can utilize more advanced methods, however, considering the basic heat storage and heat transfer, the peculiarity of each type of plant, and the fact that the quality of the advanced method results (e.g., numerical reservoir simulation) is affected by the accuracy and scale of the input data.
Author Contributions
The two authors have contributed in equal ways to the methodology, validation, formal analysis, investigation, resources, data curation, and writing, review, and editing. All authors have read and agreed to the published version of the manuscript
Funding
This research was funded by the University of Pisa (PRA 2018–19, project n. 2018_38).
Acknowledgments
The authors would like to thank University of Pisa for the financial support.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Ar | Area of the reservoir, heat transfer area | m2 |
| C | Volumetric specific heat of the reservoir | J/K |
| cp | Specific heat capacity at constant pressure | J/kg K |
| cr | Specific rock heat capacity | J/kg K |
| E | Exergy power (from the reservoir) | W |
| F | Constitutive Law term (multi-phase version of Darcy’s law) | |
| K, ks, k | Thermal conductivity of the rocks | W/mK |
| L | Characteristic length of the reservoir (distance between prod. and reinjection wells) | m |
| m | Geofluid extraction rate | kg/s |
| m* | Upper limit of the geofluid mass flow that can be extracted | kg/s |
| M | Accumulation term | |
| NTU | Number of transfer units | |
| q | Heat flow | W/m2 |
| qR | Energy potential of a geothermal reservoir | J |
| Qgeo | Power extractable from the geothermal reservoir | W |
| Rg | Recovery factor | |
| S | Shaper factor for the conductive heat transfer problem | |
| t | Resident time | s |
| T0 | Reference (low level) temperature | *C |
| Tgeo | Geofluid temperature | *C |
| TR | Geothermal Resource Temperature | *C |
| Trej | Reinjection temperature | *C |
| U | Heat transfer coefficient | W/(m2K) |
| V | Total volume of the geothermal reservoir | m3 |
| w | Fluid velocity | m/s |
| ΔT | Temperature difference | K |
| ε | Efficiency | |
| ϕ | Porosity | |
| ϕR | Rock porosity | |
| ∏ | Geothermal potential; geothermal system function | |
| ρ | Density | kg/m3 |
| τ | Lifetime of a power plant | years |
References
- Zheng, B.; Xu, J.; Ni, T.; Li, M. Geothermal energy utilization trends from a technological paradigm perspective. Renewable Energ 2015, 77, 430–441. [Google Scholar] [CrossRef]
- Bayer, P.; Rybach, L.; Blum, P.; Branchler, R. Review on life cycle environmental effects of geothermal power generation. Sust. Energ. Rev. 2013, 26, 446–463. [Google Scholar] [CrossRef]
- Sanyal, S.K. Sustainability and Renewability of Geothermal Power Capacity. In Proceedings of the World Geothermal Congress, Antalya, Turkey, 24–29 April 2005; pp. 1–13. [Google Scholar]
- Withing, R.L.; Ramey, H.R., Jr. Application of material and energy balances to geothermal steam production. J. Pet. Technol. 1969, 21, 8939–8950. [Google Scholar]
- Baba, K. Assessment of geothermal resources in Japan. In Proceedings of the United States–Japan Geological Surveys Panel Discussion on the Assessment of Geothermal Resources, Tokyo, Japan, 17 October 1975; Suyama, J., Sund, K., Takashima, I., Yuhara, K., Eds.; Geological Survey of Japan. pp. 63–119. [Google Scholar]
- White, D.E.; Williams, D.L. Assessment of Geothermal Resources in the United States, 1975; U.S. Geological Survey: Denver, CO, USA, 1975; U.S. Geological Survey Circular 736; p. 105.
- Bodvarsson, G. Geothermal resource energetics. Geothermics 1974, 3, 83–92. [Google Scholar] [CrossRef]
- Noguchi, T. An attempted evaluation of geothermal energy in Japan. Geothermics 1970, 2, 474–477. [Google Scholar] [CrossRef]
- Cataldi, R.; Muffler, P. Methods for regional assessment of geothermal resources. Geothermics 1978, 7, 53–89. [Google Scholar]
- Varney, J.; Zarrouk, S.J.; Bean, N.; Bendall, B. Performance measures in geothermal power developments. Renew. Energy 2017, 101, 835–844. [Google Scholar] [CrossRef]
- Axelsson, G. Sustainable geothermal utilization case histories; definitions; research issues and modelling. Geothermics 2010, 39, 283–291. [Google Scholar] [CrossRef]
- Franco, A.; Vaccaro, M. An integrated “Reservoir-Plant” strategy for a sustainable and efficient use of geothermal resources. Energy 2012, 37, 299–310. [Google Scholar] [CrossRef]
- Stefansson, V. Investment cost for geothermal power plants. Geothermics 2002, 31, 263–272. [Google Scholar] [CrossRef]
- DiPippo, R. Geothermal Power Plants: Principles, Applications, Case Studies and Environmental Impact, 2nd ed.; Butterworth-Heinemann: New York, NY, USA, 2008. [Google Scholar]
- Hähnlein, S.; Bayer, P.; Ferguson, G.; Blum, P. Sustainability and policy for the thermal use of shallow geothermal energy. Energy Policy 2013, 59, 914–925. [Google Scholar] [CrossRef]
- Franco, A.; Donatini, F. Methods for the estimation of the energy stored in geothermal reservoirs. J. Phys. Conf. Ser. 2017, 796, 012025. [Google Scholar] [CrossRef]
- Fox, D.B.; Sutter, D.; Beckers, K.F.; Lukawski, M.Z.; Koch, D.L.; Anderson, B.J. Sustainable heat farming: Modeling extraction and recovery indiscretely fractured geothermal reservoirs. Geothermics 2013, 46, 42–54. [Google Scholar] [CrossRef]
- Williams, C.F. Development of revised techniques for assessing geothermal resources. In Proceedings of the Twenty-Ninth Workshop on Geothermal Reservoir Engineering, Palo Alto, CA, USA, 26–28 January 2004. [Google Scholar]
- Mendrinos, D.; Karytsas, C.; Georgilakisa, P.S. Assessment of geothermal resources for power generation. J. Optoelectron. Adv. Mater. 2008, 10, 1262–1267. [Google Scholar]
- World Energy Council, 2016. World Energy Perspective – Variable Renewables Integration in Electricity Systems: How To Get It Right. Available online: https://www.worldenergy.org/publications/entry/variable-renewable-energy-sources-integration-in-electricity-systems-2016-how-to-get-it-right (accessed on 7 May 2020).
- Bertani, R. Geothermal Power Generation in the World 2010−2014 Update Report. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 19–25 April 2015. [Google Scholar]
- Porras, E.A.; Bjornsson, G. The Momotombo reservoir performance upon 27 years of exploitation. In Proceedings of the World Geothermal Congress -2010, Bali, Indonesia, 25–29 April 2010. [Google Scholar]
- California Geothermal Energy Statistics and Data, 2016. Available online: http://www.energy.ca.gov/ (accessed on 30 March 2020).
- Khan, M.A. The Geysers Geothermal Field, an Injection Success Story. In Proceedings of the World Geothermal Congress 2010, Bali, Indonesia, 25–29 April 2010. [Google Scholar]
- Goyal, K.P.; Conant, T.T. Performance history of The Geysers steam field, California, USA. Geothermics 2010, 39, 292–313. [Google Scholar] [CrossRef]
- Cappetti, G.; Parisi, L.; Ridolfi, A.; Stefani, G. Fifteen years of reinjection in the Larderello-Valle Secolo area: Analysis of the production data. In Proceedings of the World Geothermal Congress 1995, Florence, Italy, 18–31 May 1995; pp. 1997–2000. [Google Scholar]
- Van Campen, B. 2014 Resource Assessment, Techniques & Reporting, Internal Report, The Geothermal Institute University of Auckland Santiago de Chile, 26–29 May 2014. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Events/2014/Jun/2/4_vanCampen.pdf?la=en&hash=3A91CB17646AD310A01C22595DA13A0475477B24 (accessed on 7 May 2020).
- Geothermal Systems: Principles and Case Histories; Rybach, L., Muffler, P., Eds.; John Wiley and Sons: Chichester, UK, 1981. [Google Scholar]
- Cataldi, R.; Lanzarotto, A.; Muffler, P.; Squarci, P.; Stefani, G. Assessment of geothermal potential of central and southern Tuscany. Geothermics 1978, 7, 91–131. [Google Scholar] [CrossRef]
- Romagnoli, P.; Arias, A.; Barelli, A.; Cei, C.; Casini, M. An updated numerical model of the Larderello–Travale geothermal system, Italy. Geothermics 2010, 39, 292–313. [Google Scholar] [CrossRef]
- Barelli, A.; Ceccarelli, A.; Dini, I.; Fiordelisi, A.; Giorgi, N.; Lovari, F. A review of the Mt. Amiata geothermal system, Italy. In Proceedings of the World Geothermal Congress -2010, Bali, Indonesia, 25–29 April 2010. [Google Scholar]
- Shortall, R.; Davidsdottir, B.; Axelsson, G. Development of a sustainability assessment framework for geothermal energy projects. Energy Sustain. Dev. 2015, 27, 28–45. [Google Scholar] [CrossRef]
- Ogena, M.S.; Freeston, D.H. Sensitivity analysis of the greater Tongonan field resource assessment. In Proceedings of the 10th New Zealand Geothermal Workshop 1988, Auckland, New Zeeland, 2–4 November 1988; pp. 67–72. [Google Scholar]
- Iregui, R.; Hunsbedt, A.; Kruger, P.; London, A.L. Analysis of Heat Transfer and Energy Recovery in Fractured Geothermal Reservoirs; Report Stanford University: Palo Alto, CA, USA, 1978; SGP-TR31; Available online: https://geothermal.stanford.edu/sites/g/files/sbiybj1291/f/publications/sgp-tr-031.pdf (accessed on 7 May 2020).
- Hunsbedt, A.; Kruger, P.; London, A.L. Recovery of energy from fractured geothermal reservoirs. In Proceedings of the 46th Annual California Regional Meeting of Society of Petroleum Engineers of AIME, Long Beach, CA, USA, 25–27 June 1976. [Google Scholar]
- Hunsbedt, A.; Iregui, R.; Kruger, P.; London, A.L. Energy Recovery from Fracture-Stimulated Geothermal Reservoirs. J. Pet. Technol. 1977, 29, 940–946. [Google Scholar] [CrossRef]
- Rohsenow, W.M.; Hartnett, J.P. Handbook of Heat Transfer, 2nd ed.; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Franco, A.; Vaccaro, M. Numerical simulation of geothermal reservoirs for sustainable design of energy plants: A review. Sust. Energy Rev. 2014, 30, 987–7002. [Google Scholar] [CrossRef]
- O’Sullivan, M.J.; Pruess, K.; Lippmann, M.J. State of the art of geothermal reservoir simulation. Geothermics 2001, 30, 395–429. [Google Scholar] [CrossRef]
- Ungemach, P.; Papachristou, M.; Antics, M. Renewability versus Sustainability. A reservoir Management Approach. In Proceedings of the European Geothermal Congress, Unteraching, Germany, 30 May–1 June 2007. [Google Scholar]
- Saeid, S.; Al-Khoury, R.; Barends, F. An efficient computational model for deep low-enthalpy geothermal systems. Comput. Geosci. 2013, 51, 400–409. [Google Scholar] [CrossRef]
- Mottaghy, D.; Pechnig, R.; Vogt, C. The thermal project Den Haag: 3D numerical models for temperature prediction and reservoir simulation. Geothermics 2011, 40, 199–210. [Google Scholar]
- Chen, Y.; Ma, G.; Wang, H. The simulation of thermo-hydro-chemical coupled heat extraction process in fractured geothermal reservoir. Appl. Therm. Eng. 2018, 143, 859–870. [Google Scholar] [CrossRef]
- Franco, A.; Villani, M. Optimal design of binary cycle power plants for water-dominated, medium-temperature geothermal fields. Geothermics 2009, 38, 379–391. [Google Scholar] [CrossRef]
- Franco, A. Power production from a moderate temperature geothermal resource with regenerative Organic Rankine Cycles. Energy Sustain. Dev. 2011, 15, 411–419. [Google Scholar] [CrossRef]
- Franco, A.; Vaccaro, M. A combined energetic and economic approach for the sustainable design of geothermal plants. Energy Convers. Manag. 2014, 87, 735–745. [Google Scholar] [CrossRef]
- Pollet, M.; Gosselin, L.; Dallaire, J.; Mathieu-Potvin, F. Optimization of geothermal power plant design for evolving operating conditions. Appl. Therm. Eng. 2018, 134, 118–129. [Google Scholar] [CrossRef]
- Vaccaro, M.; Conti, P. Numerical simulation of geothermal resources: A critical overlook. In Proceedings of the European Geothermal Conference, Pisa, Italy, 3–7 June 2013. Paper HS1-26. [Google Scholar]
- Pruess, K.; Oldenburg, C.; Moridis, G. TOUGH2 User’s Guide, Version 2.1. Earth Sciences Division; Lawrence Berkeley National Laboratory University of California: Berkeley, CA, USA, 2012; Volume 3, pp. 154–196. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).