Exploring the Socioeconomic Co-benefits of Global Environment Facility Projects in Uganda Using a Quasi-Experimental Geospatial Interpolation (QGI) Approach
Abstract
1. Introduction
1.1. Literature Review
2. Data and Methods
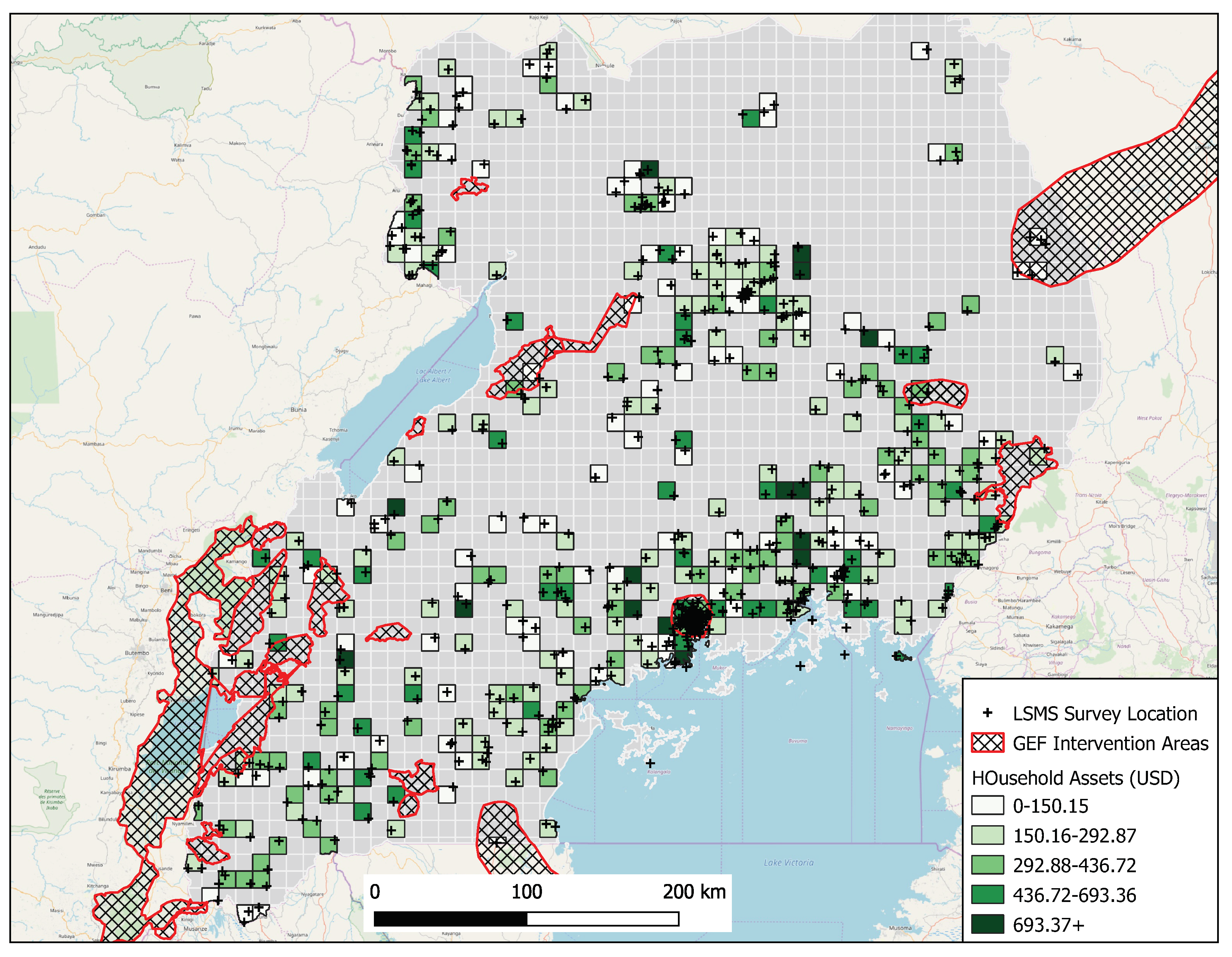
2.1. Data
2.2. Methods
2.2.1. Key Methodological Concepts
2.2.2. Quasi-Experiemental Geospatial Interpolation (QGI)
- Two hyperparameters are chosen:
- (a)
- The maximum distance () for which a treatment effect will be constructed.
- (b)
- The number of distance bands , with the geographic distance for each band denoted by .
- For each distance , we build a regression model following:
- (a)
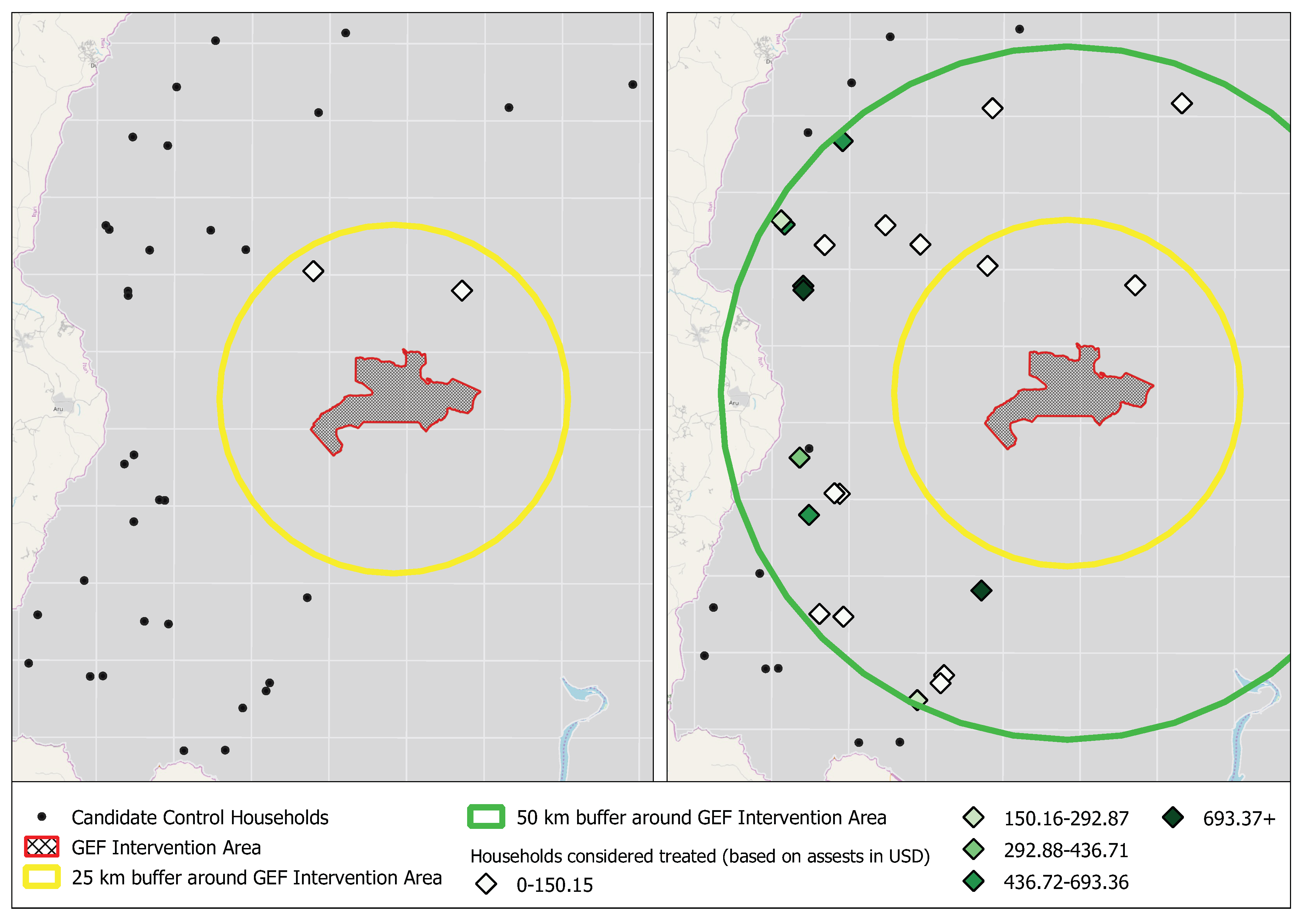
- All units of observation that are geographically closer to an intervention than the specified are considered as "treated".
- (b)
- These units are matched with eligible control units that have a minimum distance away from an intervention site of .
- (c)
- The quality of the matches () is calculated and recorded.
- (d)
- A regression model, similar to that in Equation (1), is estimated; both and the standard deviation are recorded.
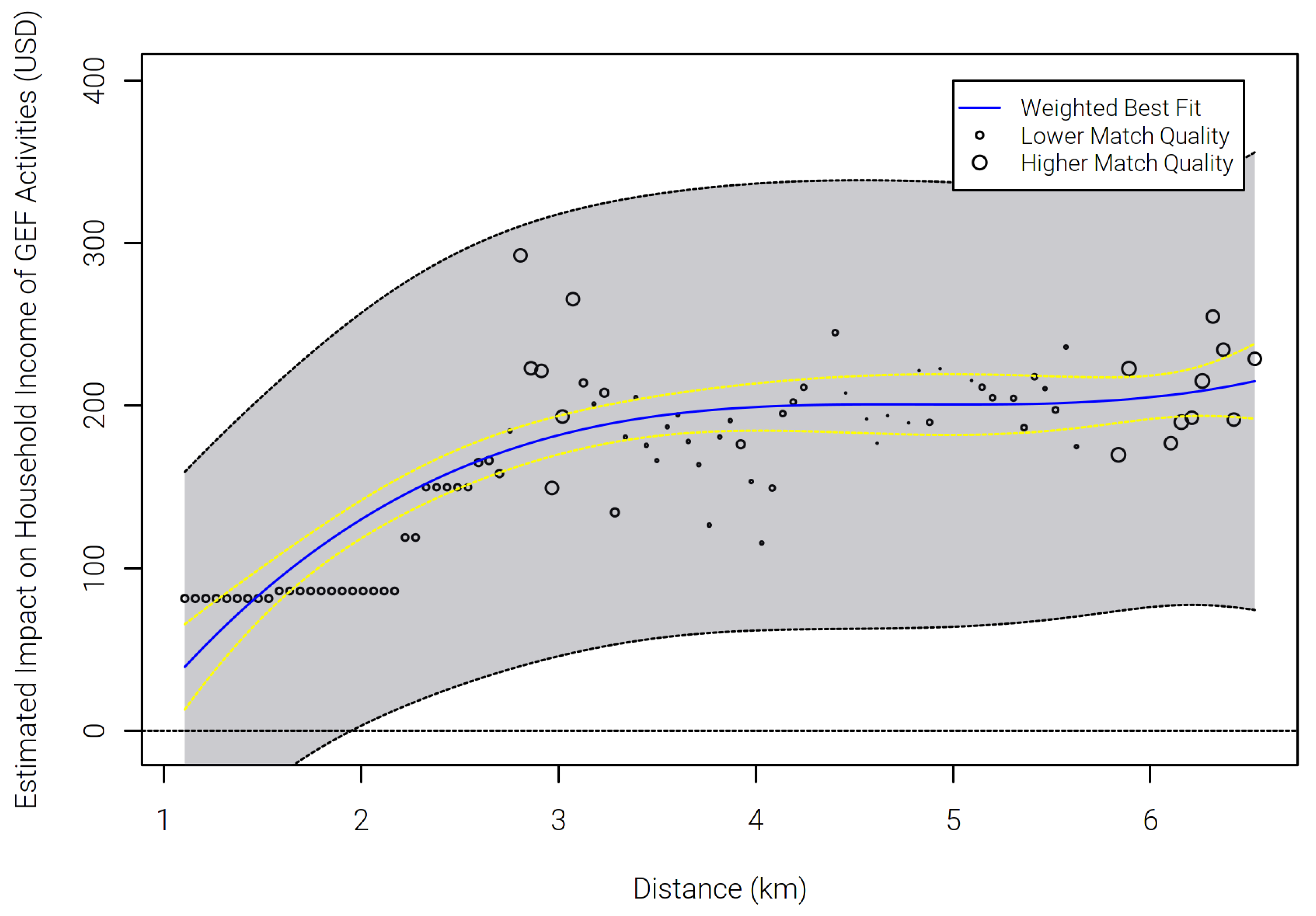
- After is recorded for all distance bands i, the relationship between distance and is estimated using a model of the users choice—i.e., spherical or polynomial, with a weighting approach in which distance bands with better match qualities () are given more weight. This is repeated for the standard deviation of the estimates ().
2.2.3. Step 1—Hyperparameter Selection
2.2.4. Step 2—Iterative Modeling
2.2.5. Step 3—Estimating the Spatial Relationship between Distances and Estimates
3. Results
3.1. Step 1—Hyperparameter Selection for the Uganda Case Study
3.2. Step 2—Iterative Modeling for the Uganda Case Study
3.3. Step 3—Distance Decay of the Observed Treatment Effects
4. Discussion and Conclusions
Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GEF | Global Environment Facility |
| QGI | Quasi-experimental Geospatial Interpolation |
| LSMS | Living Standards Measurement Survey |
References
- Alpízar, F.; Ferraro, P.J. The Environmental Effects of Poverty Programs and the Poverty Effects of Environmental Programs: The Missing RCTs. World Dev. 2020, 127, 104783. [Google Scholar] [CrossRef]
- Lech, M.; Uitto, J.I.; Harten, S.; Batra, G.; Anand, A. Improving International Development Evaluation through Geospatial Data and Analysis. Int. J. Geospat. Environ. Res. 2018, 5, 13. [Google Scholar]
- Runfola, D.; Yishay, A.B.; Tanner, J.; Buchanan, G.; Nagol, J.; Leu, M.; Goodman, S.; Trichler, R.; Marty, R. A top-down approach to estimating spatially heterogeneous impacts of development aid on vegetative carbon sequestration. Sustainability 2017, 9, 409. [Google Scholar] [CrossRef]
- Buchanan, G.M.; Parks, B.C.; Donald, P.F.; O’donnell, B.F.; Runfola, D.; Swaddle, J.P.; Tracewski, L.; Butchart, S.H.M. The Local Impacts of World Bank Development Projects Near Sites of Conservation Significance. J. Environ. Dev. 2018, 27, 299–322. [Google Scholar] [CrossRef]
- Frumhoff, P. Monitoring the Environmental Impacts of USAID-Funded Activities to Conserve Biological Diversity; U. S. Agency for International Development: Washington, DC, USA, 1995. [Google Scholar]
- Christie, P. Observed and perceived environmental impacts of marine protected areas in two Southeast Asia sites. Ocean Coast. Manag. 2005, 48, 252–270. [Google Scholar] [CrossRef]
- Carpenter, R.A.; Maragos, J.E. How to Assess Environmental Impacts on Tropical Islands and Coastal Areas; Environment and Policy Institute: Honolulu, HI, USA, 1989. [Google Scholar]
- Qdais, H.A. Environmental impacts of the mega desalination project: The Red–Dead Sea conveyor. Desalination 2008, 220, 16–23. [Google Scholar] [CrossRef]
- Boocock, C.N. Environmental impacts of foreign direct investment in the mining sector in Sub-Saharan Africa. In Foreign Direct Investment and the Environment; OECD: Paris, France, 2002; p. 19. [Google Scholar]
- Ortolano, L.; Shepherd, A. Environmental impact assessment: Challenges and opportunities. Impact Assess. 1995, 13, 3–30. [Google Scholar] [CrossRef]
- Ryberg, B.T.; Dicks, M.R.; Hebert, T. Economic impacts of the conservation reserve program on rural economies. Rev. Reg. Stud. 1991, 21, 91–105. [Google Scholar]
- Bangsund, D.A.; Hodur, N.M.; Leistritz, F.L. Agricultural and recreational impacts of the conservation reserve program in rural North Dakota, USA. J. Environ. Manag. 2004, 71, 293–303. [Google Scholar] [CrossRef]
- Olatubi, W.O.; Hughes, D.W. Natural resource and environmental policy trade-offs: A CGE analysis of the regional impact of the Wetland Reserve Program. Land Use Policy 2002, 19, 231–241. [Google Scholar] [CrossRef]
- Siegel, P.B.; Johnson, T.G. Measuring the economic impacts of reducing environmentally damaging production activities. Rev. Reg. Stud. 1993, 23, 237–254. [Google Scholar]
- Henderson, D.; Tweeten, L.; Woods, M. A multicommunity approach to community impacts: The case of the conservation reserve program. Community Dev. 1992, 23, 88–102. [Google Scholar] [CrossRef]
- Hamilton, L.L.; Levins, R.A. Local Economic Impacts of Conservation Reserve Program Enrollments: A Sub-County Analysis. In Proceedings of the Sixth Joint Conference on Food, Agriculture and the Environment, Minneapolis, MN, USA, 31 August–2 September 1998. [Google Scholar]
- Cho, S.H.; Soh, M.; English, B.C.; Yu, T.E.; Boyer, C.N. Targeting payments for forest carbon sequestration given ecological and economic objectives. For. Policy Econ. 2019, 100, 214–226. [Google Scholar] [CrossRef]
- Campiche, J.; Dicks, M.; Shideler, D.; Dickson, A. Potential economic impacts of the managed haying and grazing provision of the Conservation Reserve Program. J. Agric. Resour. Econ. 2011, 36, 573–589. [Google Scholar]
- Swartzentruber, R. The Economic Consequences of Private Lands Conservation Using Conservation Easements in Colorado. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 2019. [Google Scholar]
- Hindery, D. Social and environmental impacts of World Bank/IMF-funded economic restructuring in Bolivia: An analysis of Enron and Shell’s hydrocarbons projects. Singap. J. Trop. Geogr. 2004, 25, 281–303. [Google Scholar] [CrossRef]
- Oldekop, J.A.; Sims, K.R.; Karna, B.K.; Whittingham, M.J.; Agrawal, A. Reductions in deforestation and poverty from decentralized forest management in Nepal. Nat. Sustain. 2019, 2, 421–428. [Google Scholar] [CrossRef]
- Naidoo, R.; Gerkey, D.; Hole, D.; Pfaff, A.; Ellis, A.M.; Golden, C.D.; Herrera, D.; Johnson, K.; Mulligan, M.; Ricketts, T.H.; et al. Evaluating the impacts of protected areas on human well-being across the developing world. Sci. Adv. 2019, 5, eaav3006. [Google Scholar] [CrossRef]
- Ferraro, P.J.; Hanauer, M.M. Quantifying causal mechanisms to determine how protected areas affect poverty through changes in ecosystem services and infrastructure. Proc. Natl. Acad. Sci. USA 2014, 111, 4332–4337. [Google Scholar] [CrossRef]
- Alix-Garcia, J.; McIntosh, C.; Sims, K.R.; Welch, J.R. The ecological footprint of poverty alleviation: Evidence from mexico’s oportunidades program. Rev. Econ. Stat. 2013, 95, 417–435. [Google Scholar] [CrossRef]
- McKinnon, M.C.; Cheng, S.H.; Dupre, S.; Edmond, J.; Garside, R.; Glew, L.; Holland, M.B.; Levine, E.; Masuda, Y.J.; Miller, D.C.; et al. What are the effects of nature conservation on human well-being? A systematic map of empirical evidence from developing countries. Environ. Evid. 2016, 5, 8. [Google Scholar] [CrossRef]
- Özerol, G.; Bressers, H.; Coenen, F. Irrigated agriculture and environmental sustainability: An alignment perspective. Environ. Sci. Policy 2012, 23, 57–67. [Google Scholar] [CrossRef]
- BenYishay, A.; Heuser, S.; Runfola, D.; Trichler, R. Indigenous land rights and deforestation: Evidence from the Brazilian Amazon. J. Environ. Econ. Manag. 2017, 86, 29–47. [Google Scholar] [CrossRef]
- Marty, R.; Goodman, S.; LeFew, M.; Dolan, C.; BenYishay, A.; Runfola, D. Assessing the causal impact of Chinese aid on vegetative land cover in Burundi and Rwanda under conditions of spatial imprecision. Dev. Eng. 2019, 4. [Google Scholar] [CrossRef]
- Jain, M. The Benefits and Pitfalls of Using Satellite Data for Causal Inference. Rev. Environ. Econ. Policy 2020, 14, 157–169. [Google Scholar] [CrossRef]
- Buchanan, G.M.; Parks, B.C.; Donald, P.F.; O’donnell, B.F.; Runfola, D.; Swaddle, J.P.; Tracewski, L.; Butchart, S.H.M. The Impacts of World Bank Development Projects on Sites of High Biodiversity Importance; Technical Report; AidData at William & Mary: Williamsburg, VA, USA, 2016. [Google Scholar]
- Corrado, L.; Fingleton, B. Where is the economics in spatial econometrics? J. Reg. Sci. 2012, 52, 210–239. [Google Scholar] [CrossRef]
- Bunte, J.; Desai, H.; Gbala, K.; Parks, B.; Runfola, D.M. Natural resource sector FDI, government policy, and economic growth: Quasi-experimental evidence from Liberia. World Dev. 2018, 107, 151–162. [Google Scholar] [CrossRef]
- Goodman, S.; BenYishay, A.; Lv, Z.; Runfola, D. GeoQuery: Integrating HPC systems and public web-based geospatial data tools. Comput. Geosci. 2019, 122, 103–112. [Google Scholar] [CrossRef]
- Hsu, F.; Baugh, K.E.; Ghosh, T.; Zhizhin, M.; Elvidge, C.D. DMSP-OLS radiance calibrated nighttime lights time series with intercalibration. Remote Sens. 2015, 7, 1855–1876. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.; Zhizhin, M.; Hsu, F.C.; Ghosh, T. VIIRS night-time lights, 2017. Int. Remote Sens. 2017, 38, 5860–5879. [Google Scholar] [CrossRef]
- Center for International Earth Science Information Network-CIESIN-Columbia University, Information Technology Outreach Services-ITOS-University of Georgia. Global Roads Open Access Data Set, Version 1 (gROADSv1); NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2013. [Google Scholar] [CrossRef]
- Runfola, D.; Anderson, A.; Baier, H.; Crittenden, M.; Dowker, E.; Fuhrig, S.; Goodman, S.; Grimsley, G.; Layko, R.; Melville, G.; et al. geoBoundaries: A Global Database of Political Administrative Boundaries. PLoS ONE 2020. [Google Scholar] [CrossRef]
- Bingham, H.C.; Bignoli, J.D.; Lewis, E.; MacSharry, B.; Burgess, N.; Visconti, P.; Deguignet, M.; Misrachi, M.; Walpole, M.; Stewart, J.; et al. Sixty years of tracking conservation progress using the World Database on Protected Areas. Nat. Ecol. Evol. 2019, 3, 737–743. [Google Scholar] [CrossRef] [PubMed]
- Balk, D.L.; Deichmann, U.; Yetman, G.; Pozzi, F.; Hay, S.I.; Nelson, A. Determining global population distribution: Methods, applications and data. Adv. Parasitol. 2006, 62, 119–156. [Google Scholar] [PubMed]
- Rodriguez, E.; Morris, C.S.; Belz, J.E. A global assessment of the SRTM performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- Matsuura, K.; Willmott, C.J. Terrestrial Air Temperature & Precipitation: 1900–2014 Gridded Monthly Time Series. 2015. Available online: http://climate.geog.udel.edu/~climate/html_pages/download.htm (accessed on 10 March 2020).
- Lesiv, M.; Fritz, S.; McCallum, I.; Tsendbazar, N.; Herold, M.; Pekel, J.F.; Buchhorn, M.; Smets, B.; Van De Kerchove, R. Evaluation of ESA CCI Prototype Land cover Map at 20m. 2017. Available online: http://pure.iiasa.ac.at/id/eprint/14979/ (accessed on 10 March 2020).
- Wan, Z. MODIS Land Surface Temperature Products Users’ Guide; Institute for Computational Earth System Science, University of California: Santa Barbara, CA, USA, 2006. [Google Scholar]
- Nagol, J.R.; Vermote, E.F.; Prince, S.D. Effects of atmospheric variation on AVHRR NDVI data. Remote Sens. Environ. 2009, 113, 392–397. [Google Scholar] [CrossRef]
- Ho, D.E.; Imai, K.; King, G.; Stuart, E.A. MatchIt: Nonparametric preprocessing for parametric causal inference. J. Stat. Softw. 2011. Available online: http://gking.harvard.edu/matchit (accessed on 19 March 2020). [CrossRef]
- Imbens, G.W.; Rubin, D.B. Rubin causal model. In Microeconometrics; Palgrave Macmillan: London, UK, 2010; pp. 229–241. [Google Scholar]
- Zhao, J.; Runfola, D.M.; Kemper, P. Quantifying Heterogeneous Causal Treatment Effects in World Bank Development Finance Projects. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Technical Report; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Marty, R.; Dolan, C.; Leu, M.; Runfola, D. Taking the Aid Debate to the Sub-National Level: Impact and Allocation of Foreign Health Aid in Malawi. BMJ Global Health 2017, 2, e000129. [Google Scholar] [CrossRef]
- Carugi, C. Experiences with systematic triangulation at the Global Environment Facility. Eval. Prog. Plann. 2016, 55, 55–66. [Google Scholar] [CrossRef]
| Feature | Source | Resolution |
|---|---|---|
| Nighttime Lights | Defense Meteorological Satellite Program (DMSP-OLS) [34] | 1 km |
| Visible Infrared Imaging Radiometer Suite (VIIRS) [35] | 500 m | |
| Road Networks | Global Roads Open Access Data Set (gRoads) [36] | 1 km |
| Global Administrative Zones | geoBoundaries Administrative Zones [37] | Variable |
| Protected Areas | World Database of Protected Areas (WDPA) [38] | Variable |
| Population | Gridded Population of the World (GPW) [39] | 1 km |
| Topography | Shuttle Radar Topography Mission (SRTM) [40] | 500 m |
| Air Temperature | University of Delaware [41] | 50 km |
| Precipitation | University of Delaware [41] | 50 km |
| Land Cover | European Space Agency [42] | 300 m |
| Land Surface Temperature | MODIS [43] | 1 km |
| NDVI | NASA Long Term Data Record (LTDR) [44] | 5 km |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Runfola, D.; Batra, G.; Anand, A.; Way, A.; Goodman, S. Exploring the Socioeconomic Co-benefits of Global Environment Facility Projects in Uganda Using a Quasi-Experimental Geospatial Interpolation (QGI) Approach. Sustainability 2020, 12, 3225. https://doi.org/10.3390/su12083225
Runfola D, Batra G, Anand A, Way A, Goodman S. Exploring the Socioeconomic Co-benefits of Global Environment Facility Projects in Uganda Using a Quasi-Experimental Geospatial Interpolation (QGI) Approach. Sustainability. 2020; 12(8):3225. https://doi.org/10.3390/su12083225
Chicago/Turabian StyleRunfola, Daniel, Geeta Batra, Anupam Anand, Audrey Way, and Seth Goodman. 2020. "Exploring the Socioeconomic Co-benefits of Global Environment Facility Projects in Uganda Using a Quasi-Experimental Geospatial Interpolation (QGI) Approach" Sustainability 12, no. 8: 3225. https://doi.org/10.3390/su12083225
APA StyleRunfola, D., Batra, G., Anand, A., Way, A., & Goodman, S. (2020). Exploring the Socioeconomic Co-benefits of Global Environment Facility Projects in Uganda Using a Quasi-Experimental Geospatial Interpolation (QGI) Approach. Sustainability, 12(8), 3225. https://doi.org/10.3390/su12083225





