Evaluation of Criteria for the Implementation of High-Performance Computing (HPC) in Danube Region Countries Using Fuzzy PIPRECIA Method

Abstract

The use of computers with outstanding performance has become a real necessity in order to achieve greater efficiency and sustainability for the accomplishment of various tasks. Therefore, with the development of information technology and increasing dynamism in the business environment, it is expected that these computers will be more intensively deployed. In this paper, research was conducted in Danube region countries: Austria, Bosnia and Herzegovina, Bulgaria, Croatia, Czech Republic, Germany, Hungary, Moldova, Montenegro, Romania, Serbia, Slovakia, Slovenia, and Ukraine. The aim of the research was to determine what criteria are most significant for the introduction of high-performance computing and the real situation in each of the countries. In addition, the aim was to establish the infrastructure needed to implement such a system. In order to determine the partial significance of each criterion and thus the possibility of implementing high-performance computing, a multi-criteria model in a fuzzy environment was applied. The weights of criteria and their rankings were performed using the Fuzzy PIvot Pairwise RElative Criteria Importance Assessment—fuzzy PIPRECIA method. The results indicate different values depend on decision-makers (DMs) in the countries. Spearman’s and Pearson’s correlation coefficients were calculated to verify the results obtained.

1. Introduction

The use of supercomputers is increasing today, both in science and in economy. Advances in algorithms and software technologies at all levels are essential for further progress in problem-solving with the use of supercomputers. A supercomputer represents computer architecture of high-capacity, i.e., high performance, capable of processing large amounts of data in a very short time. Such computers are usually considered high-performance computers whose construction is not based primarily on von Neumann architecture. Typically, it enables the distribution and parallelization of computer processes. Although today’s desktop computers are more powerful than supercomputers developed just a decade ago, it can be said that common characteristics of supercomputers, regardless of the period in which they occurred, are as follows: maximum available processing speed, maximum possible memory size, the largest physical dimensions, and the highest price, compared to other computers.

Supercomputers are used to solve a variety of problems, including intensive calculations [1], e.g., in inventory management [2], military intelligence [3], climate forecasting [4], earthquake modeling [5], transport [6], production [7], human health and safety [8], medical applications [9], i.e., practically in every field of science or business. The role of supercomputers in all these fields is becoming increasingly important, and supercomputers are increasingly influencing future progress. Clustering of European supercomputers was initiated in 2002, by the project Distributed European Infrastructure for Supercomputing (DEISA), when 11 of the largest supercomputing centers from seven European countries were connected to a 10 Gbit/s network [10]. The next frontier in achieving performance for supercomputers is 1018 instructions per second and is expected to be reached around 2021–2022 [11].

The idea that computing power can be provided to customers as a useful service is not new, as it has been dating since 1966 [12]. Despite that, new technologies, as well as customer demands for high-quality services, come daily, and all of that obviously leads to day-to-day, new competition. In recent decades, the economy and industry have faced a large inflow of new and intensively data-oriented services, including data collection, storage, analysis, and use [13]. Search engines [14], social networks, and business intelligence [15] are just a few examples of such trends [16].

The amount of digital data in our world has grown enormously, with an exponential trend. The size of the digital universe is estimated to grow from 4.4 zettabytes in 2013 to 44 zettabytes by 2020 [17,18]. The vast amount of data being produced, commonly referred to as Big Data [19], provides great potential in the form of undiscovered structures and relationships [15]. In order for this potential to be exploited, new knowledge acquired, and business value gained, the produced data must be accessed, then processed, analyzed, and visualized in the most efficient way. To this end, the application of specialized architectures based on the use of supercomputers, often referred to as high-performance computing (HPC) architectures, becomes a necessity in practice [20,21,22]. This will certainly also mean the rapid transition from small, closed computers and storage architectures to large, open, and service-oriented infrastructures [23]. Since introducing early supercomputers in the 1980s, the high-performance industry has been striving for continuous performance growth. This can be noticed from the trends expressed by the list of top 500 supercomputers [24], which shows an exponential increase in computing power over the last twenty years. Traditionally, the computing power provided by HPC is mainly used in enterprises, as well as research institutes and academic organizations, which benefit from the rich offerings given by HPC. For example, from the arrangement of complex sequences in DNA to complex simulations in meteorological phenomena, HPC has been proven to be the primary basis for providing procedures for solving complex problems that require very high computational performance [25,26,27,28].

Science and industry face extensive challenges to cope with very large complex data sets. These big data needed to be processed. A collaborative exchange between scientists and data analysis experts is essential to provide insights and solutions for a specific challenge [29].

HPC providers appreciate cooperation in HPC-related aspects among national and foreign research centers, as well as mainly with national enterprises. They believe that cooperation with an industry is important for the future development of their organization and that they can help enterprises to meet their needs through HPC. On the other hand, enterprises believe that cooperation with science or industry could foster the HPC usage and their organization development [30]. HPC intermediaries, which provide consultancy or advisory services in the field of HPC, are important for connecting users of HPC services and HPC centers, as many companies and public research centers lack technical knowledge about HPC. In Europe there is a strong presence of independent software vendors whose are successfully working with research institutions. They struggle to expand their businesses successfully due to their difficulties in raising financing. Commercial banks are generally engaged in the financing of private and commercially oriented HPC centers [31].

HPC is, according to the European Commission [32], a strategic resource for Europe’s future. Creating awareness among the students about the importance of HPC topics is very important to educate a workforce to continue work in this area. Students can be introduced to HPC topics through courses, projects, and summer internship programs. Quality of education can be, according to the experiences from India [33], enhanced with better outcome in undergraduate computer science and engineering programs with the introduction of HPC courses into their curriculum.

Taking into account the increased requirements for performing complex data analyses in research and the application of HPC technologies to support those analyses, there is an objective need for an adequate evaluation and selection of an appropriate HPC architecture, which presents a challenge to the engineering community in the field of computing and informatics.

Supercomputer software, algorithms, and hardware are closely coupled. As architectures change, new software solutions are needed. If a selection of architectures is made without considering software and algorithms, the results of such a decision may be unsatisfactory.

Educated and qualified people are an important part of a supercomputing system. Professionals, i.e., multidisciplinary expert teams for supercomputers, need a set of specialized knowledge of the applications they work with, as well as of various supercomputing technologies. This further implies that both forms of support are necessary for a supercomputing system to operate effectively. In addition to the long implementation and required customizations, one of the problems that occurs when deciding to select some HPC architecture is the possibility of various types of risks occurring. As the biggest, a financial risk arises, and together with it a business risk. It implies that in addition to the resources that need to be allocated for the analysis when selecting some HPC architecture, it is also necessary to provide the resources for the architecture itself, as well as the standards that the architecture requires in order to work. In addition, a team of experts should be provided, which is also necessary to support the implementation of the HPC architecture, in order to achieve positive business results, particularly in the case of specialized problems or projects and the creation of space for future projects. Different risks can lead to the failure of the HPC architecture to be implemented, most often when it cannot meet specific requirements or needs.

In order to avoid the risk of failure of implementation and application of some HPC architecture, it is necessary to clearly define all the undertakings in the entire life cycle of the HPC architecture, starting with the analysis of the architecture selection and throughout its lifetime, in order to achieve positive business results.

A typical process for selecting some architecture could be implemented in several steps. In the first step, an assessment of the current state is important, when it is decided whether architecture changes are needed and if so, why and under what conditions. Then, the next steps would be to analyze plans and budgets, taking into consideration requirements and needs, i.e., assessing the needs for a new solution. Following these information and constraints, we explore current technologies and their capabilities. The next step is deciding which solution is appropriate for the desired changes. The whole process results in decisions that represent the basis for negotiating and creating contracts for the procurement and implementation of the desired architecture.

In such a process, it is necessary to have as much information as possible before making a decision, since when establishing some architecture in an organization, wrong decisions can be made by not paying attention to each criterion and its domain in the required way, so such an approach will not produce the desired results. Failure to achieve the desired results can lead to failure in the implementation and application of the desired HPC architecture. Therefore, it is necessary to provide a multidimensional database model and analysis procedures over such a model, in order to provide opportunities for decision simulations according to specific criteria.

Despite cost reductions and ease of access to high-performance computing platforms, they are still unavailable to most institutions and companies. Supercomputing systems consume a significant amount of energy, leading to high operating costs, reduced reliability, and waste of natural resources. This fact clearly indicates the sensitivity of a decision-making process regarding the selection and implementation of such an architecture.

2. Methods

2.1. Operations on Fuzzy Numbers

A fuzzy number [34] $\overline{A}$ on R can be a triangular fuzzy number (TFN) if its membership function ${\mu }_{\overline{A}}(x)$: R→[0,1] is equal to following Equation (1) [35,36]:

$${\mu }_{\overline{A}}(x)=\{\begin{array}{l}\frac{x-l}{m-l}l\le x\le m\\ \frac{u-x}{u-m}m\le x\le u\\ 0otherwise\end{array},$$

(1)

From Equation (1), l and u mean the lower and upper bounds of the fuzzy number $\overline{A}$, and m is the modal value for $\overline{A}$. The TFN can be denoted by $\overline{A}=(l,m,u)$.

The operational laws of TFN ${\overline{A}}_1=(l_1,m_1,u_1)$ and ${\overline{A}}_2=(l_2,m_2,u_2)$ are displayed as the following equations [37,38].

Addition:

$$\overline{A_1}+\overline{A_2}=(l_1,m_1,u_1)+(l_2,m_2,u_2)=(l_1+l_2,m_1+m_2,u_1+u_2)$$

(2)

Multiplication:

$$\overline{A_1}\times \overline{A_2}=(l_1,m_1,u_1)\times (l_2,m_2,u_2)=(l_1\times l_2,m_1\times m_2,u_1\times u_2)$$

(3)

Subtraction:

$$\overline{A_1}-\overline{A_2}=(l_1,m_1,u_1)-(l_2,m_2,u_2)=(l_1-u_2,m_1-m_2,u_1-l_2)$$

(4)

Division:

$$\frac{\overline{A_1}}{\overline{A_2}}=\frac{(l_1,m_1,u_1)}{(l_2,m_2,u_2)}=\left(\frac{l_1}{u_2},\frac{m_1}{m_2},\frac{u_1}{l_2}\right)$$

(5)

Reciprocal:

$${\overline{A_1}}^{-1}={(l_1,m_1,u_1)}^{-1}=\left(\frac{1}{u_1},\frac{1}{m_1},\frac{1}{l_1}\right)$$

(6)

2.2. Fuzzy PIvot Pairwise RElative Criteria Importance Assessment–Fuzzy (PIPRECIA) Method

The fuzzy PIPRECIA method [39] consists of 11 steps that are shown below, and so far, it has been used in a few studies. Stanković et al. [38] used fuzzy PIPRECIA in integration with the newly developed Fuzzy Measurement Alternatives and Ranking according to the COmpromise Solution (fuzzy MARCOS) for road traffic risk analysis. The significance of the six criteria for evaluating road sections was evaluated using Fuzzy PIPRECIA. The results showed that the most important criterion in their study was the number of access points on each section, i.e., the second criterion. The original study [39] in which fuzzy PIPRECIA was developed dealt with the assessment of conditions for the implementation of information technology in the warehouse. This method was integrated into Strengths, Weaknesses, Opportunities, and Threats (SWOT) analysis to obtain values of each SWOT dimension. Marković et al. [40] showed that fuzzy PIPRECIA as a subjective Multi-Criteria Decision-Making (MCDM) method can be very successfully applied in integration with other objective methods, such as Criteria Importance Through Intercriteria Correlation (CRITIC). They used an integrated model for the ranking banks in order to achieve business excellence and sustainability. Fuzzy PIPRECIA in the study in [41] was used for determining criteria weights for the evaluation of green suppliers. This method was successfully applied in integration with Rough Simple Additive Weighting (Rough SAW) method.

Step 1. Form the required benchmarking set of criteria and form a decision-making team. Sort the criteria according to marks from the first to the last, and this means that they need to be sorted unclassified. Therefore, in this step, their significance does not play any role.

Step 2. In order to determine the relative importance of criteria, each decision-maker individually evaluates pre-sorted criteria by starting from the second criterion, Equation (7):

$$\overline{s_j^r}=\{\begin{array}{l}>\overline{1}if{C}_j>C_{j-1}\\ =\overline{1}if{C}_j=C_{j-1}\\ <\overline{1}if{C}_j<C_{j-1}\end{array},$$

(7)

where $\overline{s_j^r}$ denotes the assessment of criteria by a decision-maker r.

In order to obtain a matrix $\overline{s_j^{}}$, it is necessary to perform the averaging of matrix $\overline{s_j^r}$ using a geometric mean. Decision-makers evaluate criteria by applying the defined scales in

Table 1. Scale 1–2 for the assessment of criteria [22].

			l	m	u	DFV
Almost equal value	Scale 1–2	1	1.000	1.000	1.050	1.008
Slightly more significant		2	1.100	1.150	1.200	1.150
Moderately more significant		3	1.200	1.300	1.350	1.292
More significant		4	1.300	1.450	1.500	1.433
Much more significant		5	1.400	1.600	1.650	1.575
Dominantly more significant		6	1.500	1.750	1.800	1.717
Absolutely more significant		7	1.600	1.900	1.950	1.858

and

Table 2. Scale 0–1 for the assessment of criteria [22].

	l	m	u	DFV
Scale 0–1	0.667	1.000	1.000	0.944	weakly less significant
	0.500	0.667	1.000	0.694	moderately less significant
	0.400	0.500	0.667	0.511	less significant
	0.333	0.400	0.500	0.406	really less significant
	0.286	0.333	0.400	0.337	much less significant
	0.250	0.286	0.333	0.288	dominantly less significant
		0.250	0.286	0.251	absolutely less significant

.

When the criterion is of greater importance in relation to the previous one, assessment is made using the above scale in Table 1. In order to make it easier for decision-makers to evaluate the criteria, the table shows the defuzzified value (DFV) for each comparison.

When the criterion is of less importance compared to the previous one, assessment is made using the above-mentioned scale in Table 2.

Step 3. Determine the coefficient $\overline{k_j^{}}$:

$$\overline{k_j^{}}=\{\begin{array}{l}=\overline{1}ifj=1\\ 2-\overline{s_j^{}}ifj>1\end{array}.$$

(8)

Step 4. Determine the fuzzy weight $\overline{q_j^{}}$:

$$\overline{q_j^{}}=\{\begin{array}{l}=\overline{1}ifj=1\\ \frac{\overline{q_{j-1}^{}}}{\overline{k_j}}ifj>1\end{array}.$$

(9)

Step 5. Determine the relative weight of the criterion $\overline{w_j^{}}$:

$$\overline{w_j}=\frac{\overline{q_j}}{{\displaystyle \sum _{j=1}^n\overline{q_j}}}.$$

(10)

In the following steps, the inverse methodology of fuzzy PIPRECIA method (fuzzy PIPRECIA-I) needs to be applied.

Step 6. Perform the assessment of above-defined applying scale, but this time starting from a penultimate criterion:

$$\overline{s_j^r}{}^{\prime }=\{\begin{array}{l}>\overline{1}if{C}_j>C_{j+1}\\ =\overline{1}if{C}_j=C_{j+1}\\ <\overline{1}if{C}_j<C_{j+1}\end{array},$$

(11)

where $\overline{s_j^r}{}^{\prime }$ denotes the assessment of criteria by a decision-maker r.

It is again necessary to perform the averaging of matrix $\overline{s_j^r}$ by applying a geometric mean.

Step 7. Determine the coefficient $\overline{k_j^{}}{}^{\prime }$:

$$\overline{k_j^{}}{}^{\prime }=\{\begin{array}{l}=\overline{1}ifj=n\\ 2-\overline{s_j^{}}{}^{\prime }ifj>n\end{array},$$

(12)

where n denotes a total number of criteria. Specifically, in this case, it means that the value of the last criterion is equal to the fuzzy number one.

Step 8. Determine the fuzzy weight $\overline{q_j^{}}{}^{\prime }$:

$$\overline{q_j^{}}{}^{\prime }=\{\begin{array}{l}=\overline{1}ifj=n\\ \frac{\overline{q_{j+1}^{}{}^{\prime }}}{\overline{k_j}{}^{\prime }}ifj>n\end{array}.$$

(13)

Step 9. Determine the relative weight of the criterion $\overline{w_j^{}}{}^{\prime }$:

$$\overline{w_j}{}^{\prime }=\frac{\overline{q_j}{}^{\prime }}{{\displaystyle \sum _{j=1}^n\overline{q_j}{}^{\prime }}}.$$

(14)

Step 10. In order to determine the final weights of criteria, it is first necessary to perform the defuzzification of the fuzzy values $\overline{w_j^{}}$ and $\overline{w_j^{}}{}^{\prime }$:

$$\overline{w_j^{}}{}^{″}=\frac{1}{2}(w_j+w_j{}^{\prime }).$$

(15)

Step 11. Check the results obtained by applying Spearman and Pearson correlation coefficients.

3. Input Parameters for the Evaluation of Criteria for the Implementation of HPC in Danube Region Countries

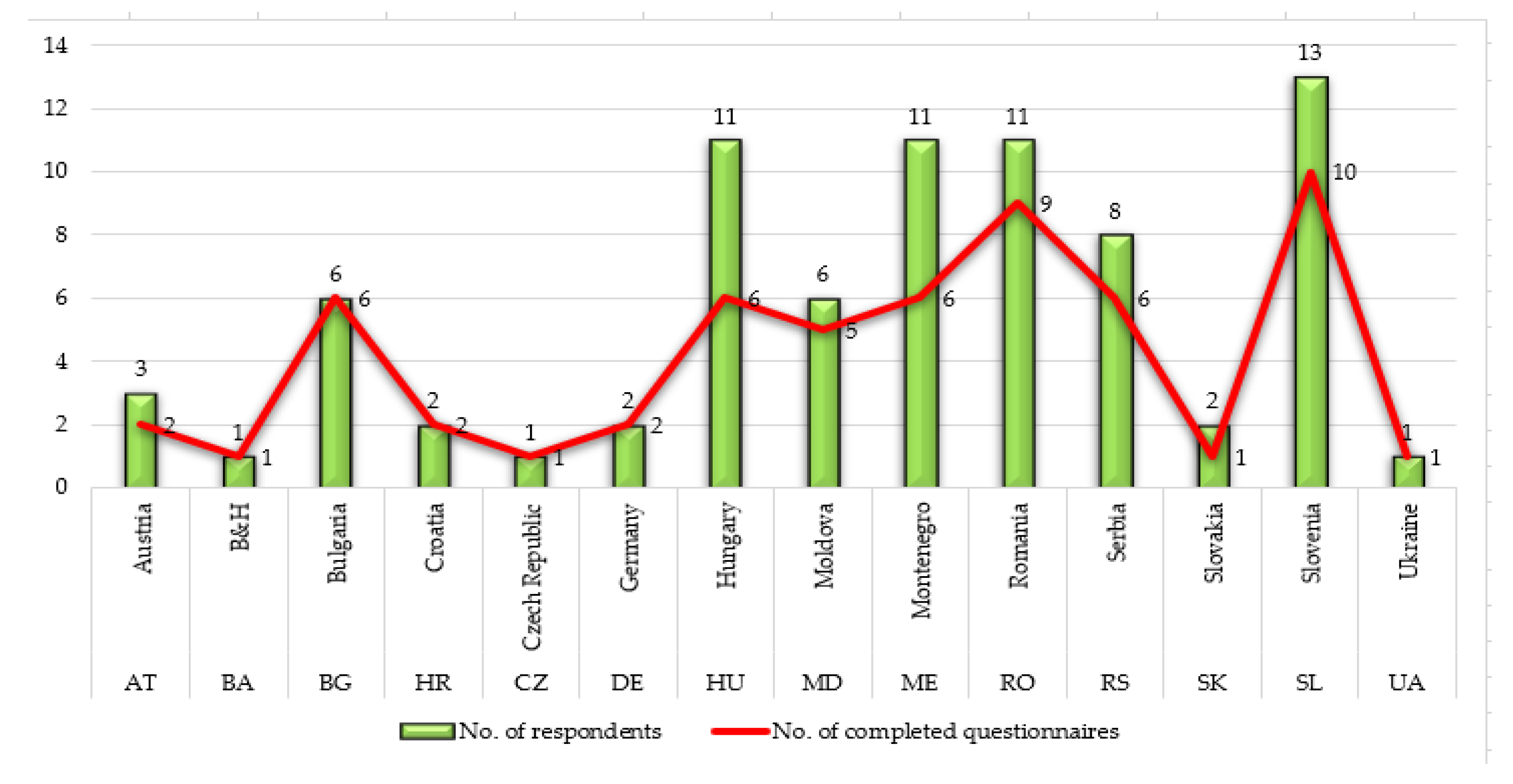
Determining the significance of the criteria relevant to the implementation of high-performance computing (HPC) was carried out in 14 countries. Countries that participated in this research were: Austria (AT), Bosnia and Herzegovina (BA), Bulgaria (BG), Croatia (HR), Czech Republic (CZ), Germany (DE), Hungary (HU), Moldova (MD), Montenegro (ME), Romania (RO), Serbia (RS), Slovakia (SK), Slovenia (SL), and Ukraine (UA). All countries were countries of Central and South-East Europe, forming the so-called Danube region. Challenges of the Danube region are, according to Coscodaru et al. [42], its backwardness and substantial disparities between its well-off westernmost parts and the rest of the region. Most HPC infrastructure and knowledge are located in the West of the Danube region. Those countries are either EU member states, pre-accession countries, or EU neighboring countries. Regional nuances were considered in this paper. Countries, as well as the number of respondents and the number of correctly completed questionnaires, are shown in Figure 1.

The total number of questionnaires sent to the experts for evaluation was 78. Since it is a very complex area still insufficiently researched, the total number of correctly completed questionnaires was 58, which represents 74.36% of the total number of questionnaires sent. The largest number of decision-makers to whom the questionnaire was forwarded was from Slovenia (13), then from Hungary, Montenegro, Romania, 11 each. For other countries, the number of questionnaires forwarded was fewer, which can be seen in Figure 1. The data for the study were gained by the online survey by the InnoHPC [43] database conducted in 2017 and by Lapuh postdoctoral research in 2018. Experts using HPC employed in the research institutions and HPC providers were part of the survey. Research institutions were chosen by the convenience, which was based on the literature review, the authors’ expert analysis on the potential usage of HPC in research organizations, and the online search. The experts were found on the basis of organizations’ website research or their published or presented scientific works in the field of HPC. The snowball sampling was used in parallel: participants were asked to suggest partners from other institutions dealing with HPC.

Data in this section represent input parameters in the model. Figure 1 shows the total number of respondents (decision-makers) per each of 14 Danube region countries. The number of respondents was various and depended on the number of experts in each country (marked with green bar). Some of the decision-makers did not properly fulfil surveys or just gave equal assessments for all criteria. Such surveys were not useful for computation in our methodology, so we have excluded them. The number of correctly completed questionnaires is presented in Figure 1 and marked with a red line. For example, in Austria, three respondents were included in the research, but one of them did not fulfil the questionnaire in the proper way, so two questionnaires were entered in the further model.

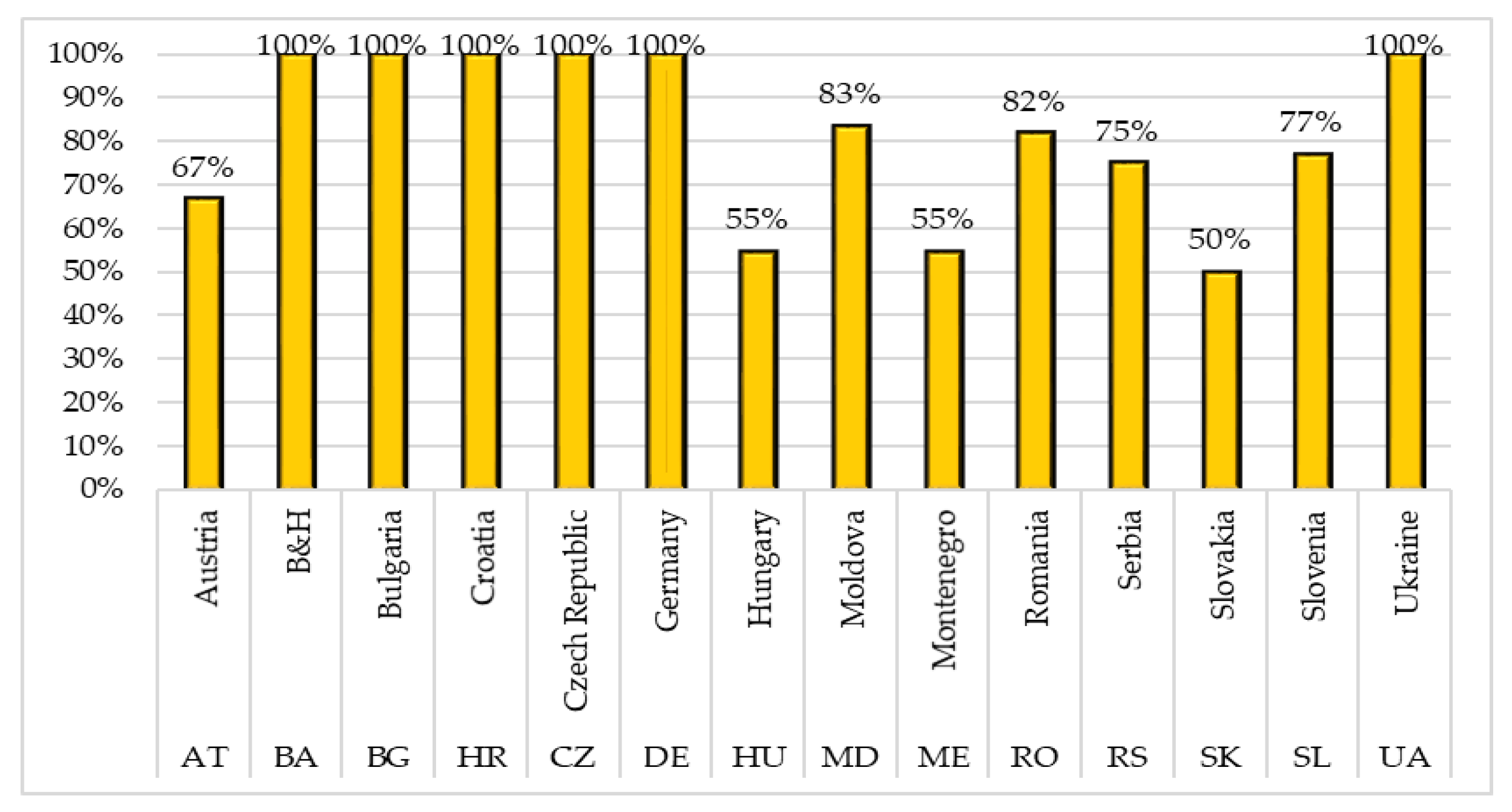
Figure 2 shows that the performance of correctly completed questionnaires was 100% in the following countries: Bosnia and Herzegovina, Bulgaria, Croatia, Czech Republic, Germany, and Ukraine. Moldova, Romania, Slovenia, and Serbia had slightly lower percentages, 83%, 82%, 77%, and 75%, respectively. Countries with 50% or more correctly completed questionnaires were Slovakia (50%), Hungary and Montenegro (55%), and Austria (67%).

The criteria, shown in

Table 3. Criteria for evaluating the implementation of high-performance computing (HPC).

Designation	Criteria
C1	Availability of free HPC infrastructure (e.g., having a sort of public funding)
C2	Availability of commercial HPC infrastructure (where you have to pay for using it)
C3	Availability of skilled human resources
C4	Degree to which universities equip students with the necessary knowledge to work in HPC
C5	Availability of competitive public funding (e.g., direct public funding, grants, awards, baseline funding)
C6	Availability of private funding for R&D related to HPC
C7	Degree of awareness about HPC benefits
C8	Degree of science-industry cooperation related to HPC
C9	Degree of industry-public authorities’ cooperation related to HPC
C10	Degree of science-public authorities’ cooperation related to HPC
C11	HPC prioritization in legislative documents and strategies

, were evaluated using fuzzy PIPRECIA and fuzzy PIPRECIA-I.

The point of interest of this study was how the experts employed in the research institutions or by the HPC providers dealing with HPC perceive the general degree of HPC development in the country they are working in. The HPC experts were asked to evaluate the HPC situation in the individual countries, regarding the HPC infrastructure, HPC competences, if curriculums contain gaining HPC skills, about the existence of project calls on gaining funding for HPC usage, about their perspective on the general awareness on advantages of using HPC in the country, if and how organizations in the selected individual countries cooperate related to HPC, and if individual countries encourage HPC usage in the legislative documents or strategies.

4. Results

A detailed calculation procedure performed on two respondents from Austria is shown in

Table 4. Respondents’ attitudes using a linguistic scale for fuzzy PIPRECIA and inverse fuzzy PIPRECIA.

	Fuzzy PIPRECIA						Inverse Fuzzy PIPRECIA
	DM1			DM2			DM1			DM2
Criterion	l	m	u	l	m	u	l	m	u	l	m	u
C1							1.100	1.150	1.200	1.000	1.000	1.000
C2	0.500	0.667	1.000	1.000	1.000	1.000	0.400	0.500	0.667	0.500	0.667	1.000
C3	1.200	1.300	1.350	1.100	1.150	1.200	1.100	1.150	1.200	0.667	1.000	1.000
C4	0.500	0.667	1.000	1.000	1.000	1.050	0.400	0.500	0.667	1.100	1.150	1.200
C5	1.200	1.300	1.350	0.500	0.667	1.000	1.300	1.450	1.500	1.200	1.300	1.350
C6	0.333	0.400	0.500	0.400	0.500	0.667	0.400	0.500	0.667	1.000	1.000	1.000
C7	1.200	1.300	1.350	1.000	1.000	1.000	1.100	1.150	1.200	0.400	0.500	0.667
C8	0.500	0.667	1.000	1.200	1.300	1.350	1.100	1.150	1.200	1.000	1.000	1.000
C9	0.500	0.667	1.000	1.000	1.000	1.000	0.400	0.500	0.667	0.500	0.667	1.000
C10	1.200	1.300	1.350	1.100	1.150	1.200	1.300	1.450	1.500	1.100	1.150	1.200
C11	0.333	0.400	0.500	0.500	0.667	1.000

,

Table 5. Details of the calculation carried out using fuzzy PIPRECIA.

		sj			kj			qj			wj		DF	Rank
	l	m	u	l	m	u	l	m	u	l	m	u
C1				1.000	1.000	1.000	1.000	1.000	1.000	0.058	0.114	0.159	0.112	5
C2	0.750	0.833	1.000	1.000	1.167	1.250	0.800	0.857	1.000	0.047	0.098	0.159	0.100	7
C3	1.150	1.225	1.275	0.725	0.775	0.850	0.941	1.106	1.379	0.055	0.127	0.219	0.130	1
C4	0.750	0.833	1.025	0.975	1.167	1.250	0.753	0.948	1.415	0.044	0.108	0.225	0.117	4
C5	0.850	0.983	1.175	0.825	1.017	1.150	0.655	0.932	1.715	0.038	0.107	0.273	0.123	3
C6	0.367	0.450	0.583	1.417	1.550	1.633	0.401	0.602	1.210	0.023	0.069	0.193	0.082	11
C7	1.100	1.150	1.175	0.825	0.850	0.900	0.445	0.708	1.467	0.026	0.081	0.233	0.097	8
C8	0.850	0.983	1.175	0.825	1.017	1.150	0.387	0.696	1.778	0.023	0.080	0.283	0.104	6
C9	0.750	0.833	1.000	1.000	1.167	1.250	0.310	0.597	1.778	0.018	0.068	0.283	0.096	9
C10	1.150	1.225	1.275	0.725	0.775	0.850	0.365	0.770	2.453	0.021	0.088	0.390	0.127	2
C11	0.417	0.533	0.750	1.250	1.467	1.583	0.230	0.525	1.962	0.013	0.060	0.312	0.094	10
Σ							6.287	8.741	17.158

,

Table 6. Details of the calculation carried out using fuzzy PIPRECIA-I.

		sj’			kj’			qj’			wj’		DF	Rank
	l	m	u	l	m	u	l	m	u	l	m	u
C1	1.050	1.075	1.100	0.900	0.925	0.950	0.339	0.834	2.031	0.019	0.075	0.270	0.098	6
C2	0.450	0.583	0.833	1.167	1.417	1.550	0.322	0.771	1.828	0.018	0.070	0.243	0.090	10
C3	0.883	1.075	1.100	0.900	0.925	1.117	0.499	1.093	2.133	0.028	0.098	0.284	0.118	3
C4	0.750	0.825	0.933	1.067	1.175	1.250	0.557	1.011	1.920	0.031	0.091	0.255	0.108	4
C5	1.250	1.375	1.425	0.575	0.625	0.750	0.697	1.188	2.048	0.039	0.107	0.272	0.123	2
C6	0.700	0.750	0.833	1.167	1.250	1.300	0.522	0.742	1.177	0.029	0.067	0.157	0.076	11
C7	0.750	0.825	0.933	1.067	1.175	1.250	0.679	0.928	1.374	0.038	0.084	0.183	0.093	8
C8	1.050	1.075	1.100	0.900	0.925	0.950	0.849	1.090	1.465	0.048	0.098	0.195	0.106	5
C9	0.450	0.583	0.833	1.167	1.417	1.550	0.806	1.008	1.319	0.045	0.091	0.175	0.097	7
C10	1.200	1.300	1.350	0.650	0.700	0.800	1.250	1.429	1.538	0.070	0.129	0.205	0.132	1
C11				1.000	1.000	1.000	1.000	1.000	1.000	0.056	0.090	0.133	0.092	9
Σ							7.520	11.093	17.833

,

Table 7. The final weights of criteria obtained from Austrian respondents.

	wp	wp-i	Final wj	Rank
C1	0.112	0.098	0.105	5
C2	0.100	0.090	0.095	9
C3	0.130	0.118	0.124	2
C4	0.117	0.108	0.113	4
C5	0.123	0.123	0.123	3
C6	0.082	0.076	0.079	11
C7	0.097	0.093	0.095	8
C8	0.104	0.106	0.105	6
C9	0.096	0.097	0.097	7
C10	0.127	0.132	0.129	1
C11	0.094	0.092	0.093	10

and

Table 8. Criteria weights according to countries.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11
AT	0.105	0.095	0.124	0.113	0.123	0.079	0.095	0.105	0.097	0.129	0.093
BA	0.180	0.084	0.142	0.117	0.097	0.082	0.099	0.099	0.099	0.121	0.085
BG	0.125	0.102	0.125	0.113	0.126	0.092	0.107	0.101	0.099	0.108	0.110
HR	0.116	0.114	0.103	0.101	0.110	0.091	0.100	0.099	0.098	0.115	0.114
CZ	0.127	0.128	0.148	0.101	0.102	0.083	0.098	0.100	0.101	0.122	0.085
DE	0.092	0.092	0.092	0.092	0.092	0.092	0.092	0.083	0.095	0.086	0.104
HU	0.144	0.106	0.116	0.105	0.105	0.094	0.109	0.104	0.094	0.113	0.113
MD	0.097	0.092	0.122	0.121	0.111	0.100	0.114	0.107	0.104	0.109	0.100
ME	0.111	0.112	0.107	0.113	0.107	0.104	0.101	0.107	0.105	0.111	0.108
RO	0.108	0.117	0.115	0.116	0.108	0.095	0.108	0.112	0.097	0.103	0.102
RS	0.119	0.114	0.124	0.133	0.104	0.092	0.097	0.097	0.094	0.109	0.095
SK	0.091	0.130	0.106	0.107	0.109	0.090	0.107	0.109	0.111	0.114	0.117
SL	0.119	0.125	0.108	0.098	0.103	0.095	0.106	0.108	0.105	0.123	0.121
UA	0.110	0.128	0.104	0.124	0.085	0.086	0.088	0.127	0.088	0.129	0.090

. Attitudes of respondents using linguistic scales (step 2) shown in Table 1 and Table 2 are presented in Table 4. It is important to note that when evaluating for fuzzy PIPRECIA, it was performed by Equation (7) and the initial criterion was the second one; therefore, cell C₁ in Table 4 is empty. The evaluation for the inverse fuzzy PIPRECIA method was performed by Equation (11), starting from the penultimate criterion C₁₀.

Aggregating the values of decision-makers using the average mean yielded the values of s_j shown in Table 5. Subsequently, using Equation (8) in the third step, the values of k_j were obtained as follows:

$$\overline{k_1}=(1.000,1.000,1.000),$$

$$\overline{k_2}=(2-1.000,2-0.833,2-0.750)=(1.000,1.167,1.250).$$

In order to obtain the values of q_j, it was necessary to apply the fourth step, i.e., Equation (9).

$$\overline{q_1}=(1.000,1.000,1.000)$$

$$\overline{q_2}=\left(\frac{1.000}{1.250},\frac{1.000}{1.167},\frac{1.000}{1.000}\right)=\left(0.800,0.857,1.000\right)$$

$$\overline{q_3}=\left(\frac{0.800}{0.850},\frac{0.857}{0.775},\frac{1.000}{0.725}\right)=\left(0.941,1.106,1.379\right)$$

In order to obtain the value of w_j, the fifth step, i.e., Equation (10), is applied. The sum previously calculated for the values of q_j was $\left(6.287,8.741,17.158\right)$, obtained in the following way:

$$\begin{array}{l}{\displaystyle \sum _{j=1}^n\overline{q_j}}=\left(6.287,8.741,17.158\right)\\ =\left(1.000+0.800+0.941+0.753+0.655+0.401+0.455+0.387+0.310+0.365+0.230\right)=6.287\\ =\left(1.000+0.857+1.106+0.948+0.932+0.602+0.708+0.696+0.597+0.770+0.525\right)=8.741\\ =\left(1.000+1.000+1.379+1.415+1.715+1.210+1.467+1.778+1.778+2.453+1.962\right)=17.158\end{array}$$

$$\overline{w_1}=\left(\frac{1.000}{17.158},\frac{1.000}{8.741},\frac{1.000}{6.287}\right)=\left(0.058,0.114,0.159\right).$$

The following equation, $d{f}_{crisp}=\frac{l+4m+u}{6}$, was then applied to perform the defuzzification of the values, as shown in the penultimate column of Table 5.

$$w_1{}_{crisp}=\frac{0.058+4\times 0.114+0.159}{6}=0.112$$

Finally, the ranks for the obtained criterion values are shown (Table 5), which were further used to determine Spearman’s correlation coefficient and determine the final ranks of the criteria.

Using the methodology of inverse fuzzy PIPRECIA, the values shown in Table 6 were obtained. It is important to note that in the same way as previously described, these values were obtained by applying Equations (11)–(14). Assessment by decision-makers from the sixth step was previously shown in Table 4.

Step 7. Determining the coefficient $\overline{k_j^{}}{}^{\prime }$:

$$\overline{k_{11}}{}^{\prime }=(1.000,1.000,1.000)$$

$$\overline{k_{10}}{}^{\prime }=(2-1.350,2-1.300,2-1.200)=(0.650,0.700,0.800).$$

Step 8. Determining the fuzzy weight $\overline{q_j^{}}{}^{\prime }$:

$$\overline{q_{11}}{}^{\prime }=(1.000,1.000,1.000)$$

$$\overline{q_{10}}{}^{\prime }=\left(\frac{1.000}{0.800},\frac{1.000}{0.700},\frac{1.000}{0.650}\right)=\left(1.250,1.429,1.538\right)$$

$$\overline{q_9}{}^{\prime }=\left(\frac{1.250}{1.550},\frac{1.429}{1.417},\frac{1.538}{1.167}\right)=\left(0.806,1.008,1.319\right).$$

In order to obtain the value of w_j, the ninth step, i.e., Equation (14), was applied. The sum previously calculated for the values of q_j was obtained in the following way:

$$\begin{array}{l}{\displaystyle \sum _{j=1}^n\overline{q_j}}{}^{\prime }=\left(7.520,11.093,17.833\right)\\ =\left(1.000+1.250+0.806+0.849+0.679+0.522+0.697+0.557+0.499+0.322+0.339\right)=7.520\\ =\left(1.000+1.429+1.008+1.090+0.928+0.742+1.188+1.011+1.093+0.771+0.834\right)=11.093\\ =\left(1.000+1.538+1.319+1.465+1.374+1.177+2.048+1.920+2.133+1.828+2.031\right)=17.833\end{array}$$

$$\overline{w_{11}}{}^{\prime }=\left(\frac{1.000}{17.833},\frac{1.000}{11.093},\frac{1.000}{7.520}\right)=\left(0.056,0.090,0.133\right).$$

The following equation, $d{f}_{crisp}=\frac{l+4m+u}{6}$, was then applied to perform the defuzzification of the values.

$$w_{11}{{}^{\prime }}_{crisp}=\frac{0.056+4\times 0.090+0.133}{6}=0.092$$

Step 10. In order to determine the final weights of criteria, it was necessary to apply Equation (15). For example:

$$\overline{w_1^{}}{}^{″}=\frac{1}{2}(0.112+0.098)=0.105.$$

The columns labeled DF in Table 5 and Table 6 contain the defuzzified weights of the criteria. On the basis of these values, the final weight of the criteria was calculated using Equation (15), as shown in Table 7 and Figure 3.

Spearman’s correlation coefficient was 0.900, while Pearson’s correlation coefficient was 0.957, which is a very high correlation of both the ranks and values of the criteria obtained by fuzzy and inverse fuzzy PIPRECIA.

As can be seen in Figure 3, the tenth criterion was the most significant—the degree of science-public authorities’ cooperation related to HPC, which also had a minor variation in weights considering both approaches. A slightly lower value was obtained for C₃—availability of skilled human resources—which was in the second position, with a variation of 0.012. The third most significant criterion was C₅—availability of competitive public funding (e.g., direct public funding, grants, awards, baseline funding)—with a value of 0.123, which indicates that it had almost the same significance as C₃. Its variation or deviation was equal to zero, since it had an identical value by applying both approaches. In the fourth position is C₄—degree to which universities equip students with the necessary knowledge to work in HPC—whose value was 0.113 and a deviation of 0.09. The fifth most significant criterion was C₁—availability of free HPC infrastructure (e.g., having some sort of public funding)—and it had a value of 0.105. Other criteria were less significant, with values below 0.100.

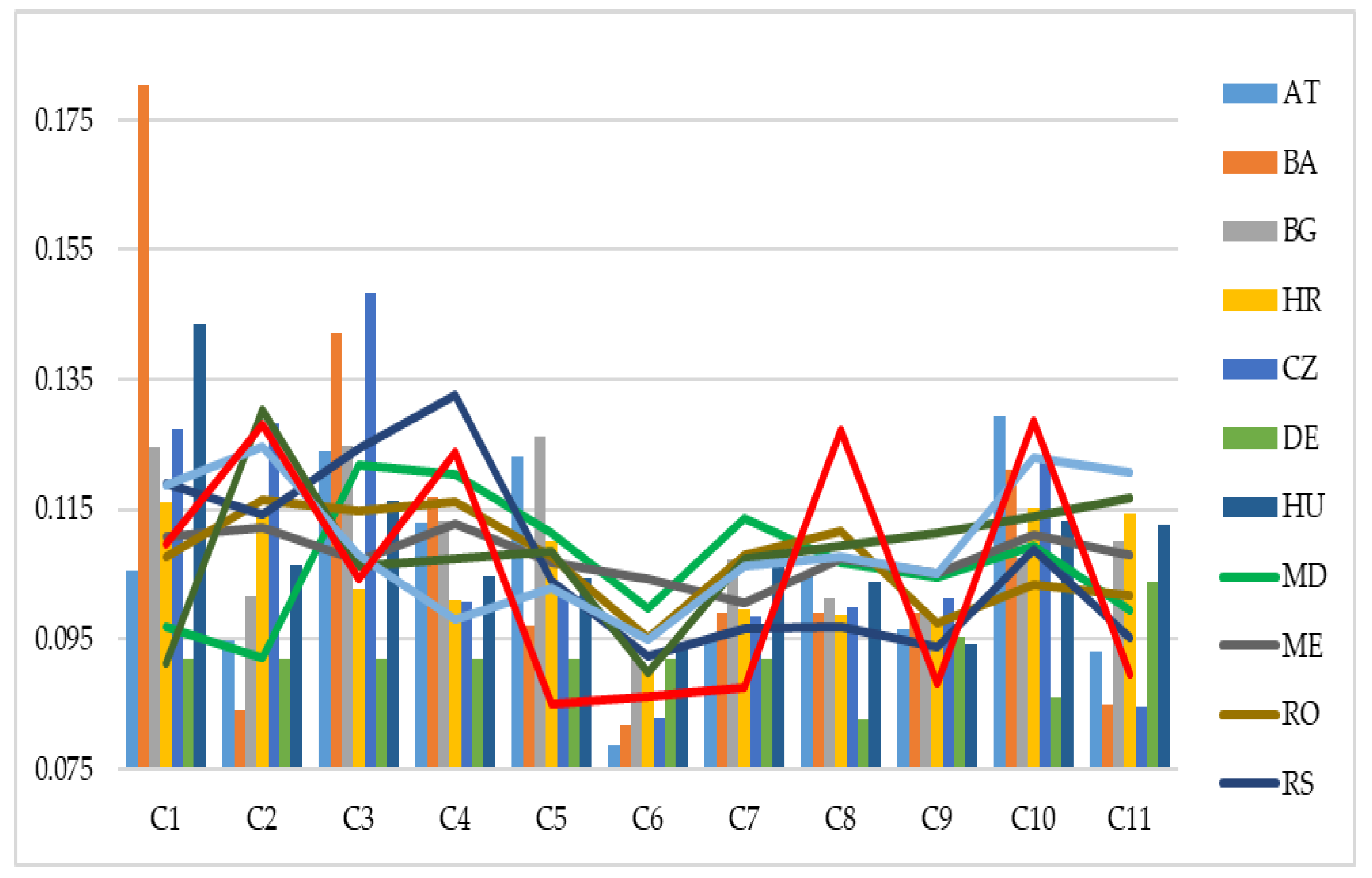
The determination of criteria weights from the remaining 13 countries was carried out in a similar way. The obtained criteria weights according to countries are shown in Table 8 and Figure 4.

The significance and ranks of criteria according to countries are shown in

Table 9. Ranks of criteria according to countries.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11
AT	5	9	2	4	3	11	8	6	7	1	10
BA	1	10	2	4	8	11	5	5	5	3	9
BG	3	8	2	4	1	11	7	9	10	6	5
HR	1	3	6	7	5	11	8	9	10	2	4
CZ	3	2	1	7	5	11	9	8	6	4	10
DE	3	3	3	3	3	3	3	11	2	10	1
HU	1	6	2	7	8	11	5	9	10	3	4
MD	10	11	1	2	4	8	3	6	7	5	9
ME	4	2	7	1	8	10	11	6	9	3	5
RO	7	1	3	2	6	11	5	4	10	8	9
RS	3	4	2	1	6	11	8	7	10	5	9
SK	10	1	9	8	6	11	7	5	4	3	2
SL	4	1	5	10	9	11	7	6	8	2	3
UA	5	2	6	4	11	10	9	3	8	1	7

and Figure 5.

As can be seen from Table 8 and Table 9, and Figure 4 and Figure 5, there was a big difference in the importance of the criteria according to the attitudes of respondents from different countries.

Based on the above, it can be seen that there were noticeable differences regarding the importance of the criteria in different countries. According to the Austrian respondents, four criteria, namely, C₃, C₄, C₅, and C₁₀, were the most influential, where criterion C₁₀—degree of science-public authorities’ cooperation related to HPC—had the highest weight, that is, 0.13. It is also significant that the weights of these criteria were approximately the same, that is, the difference between weights of criteria C₁₀ and C₄ was very small, at 0.01. According to the opinions of respondents from Bosnia and Herzegovina, criteria C₁, C₃, C₄, and C₄ were identified as the most influential, where criterion C₁—availability of free HPC infrastructure (e.g., having sort of public funding)—has the highest weight, that is, 0.18. It should be noted that a higher difference between the weight of the most influential criterion and the weight of the least influent criterion was observed in this case, at 0.01. In the case of Bulgaria, five criteria were identified as the most significant, namely C₁—availability of free HPC infrastructure (e.g., having some sort of public funding), C₃—availability of skilled human resources, C₄—degree to which universities equip students with the necessary knowledge to work in HPC, C₅—availability of competitive public funding (e.g., direct public funding, grants, awards, baseline funding), and C₁₁—HPC prioritization in legislative documents and strategies.

Based on the research conducted in Croatia, the five most influential criteria could be identified, namely C₁, C₂, C₅, C₁₀, and C₁₁. The criteria C₁—availability of free HPC infrastructure (e.g., having some sort of public funding), and C₁₀—degree of science-public authorities’ cooperation related to HPC, had approximately the same weights, while the weights of the criteria C₂, C₅, and C₁₁ were slightly smaller. In the case of the Czech Republic, the criteria C₃—availability of skilled human resources, C₂—availability of commercial HPC infrastructure (where you have to pay for using it), C₁—availability of free HPC infrastructure (e.g., having sort of public funding), and C₁₀—degree of science-public authorities’ cooperation related to HPC, were recognized as the most significant ones. In the case of Germany, the difference between the weight of the most and least influential criterion was very low at only 0.02, which is why all the criteria had approximately the same significance.

According to the respondents from Hungary, almost 50% of the total importance belonged to criteria C₁, C₃, C₁₀, and C₁₁, while according to the respondents from Moldova six criteria, namely C₃, C₄, C₅, C₇, C₈, and C₁₀, were singled out as the most influential. In the case of Montenegro respondents, the difference between the weights of the best and worst placed criteria was only 0.01, which is why almost all the criteria had approximately the same significance, and the most significant were the criteria C₄, C₂, C₁, C₉, and C₁₁, to which more than 60% of the weight belonged. According to Romanian respondents, the most important criteria were C₂—availability of commercial HPC infrastructure (where you have to pay for using it), C₄—degree to which universities equip students with the necessary knowledge to work in HPC, and C₃—availability of skilled human resources.

In the case of Serbia, the most important criteria were C₄, C₃, C₁, and C₂, while in the case of Slovakia, the most important criteria were C₂, C₁₁, and C₁₀. According to the opinion of the respondents from Slovenia, the most important criteria were C₂, C₁, C₁₁, and C₁, while according to the opinion of the respondents from Ukraine, the most important were criteria C₁₀, C₂, C₈, and C₄.

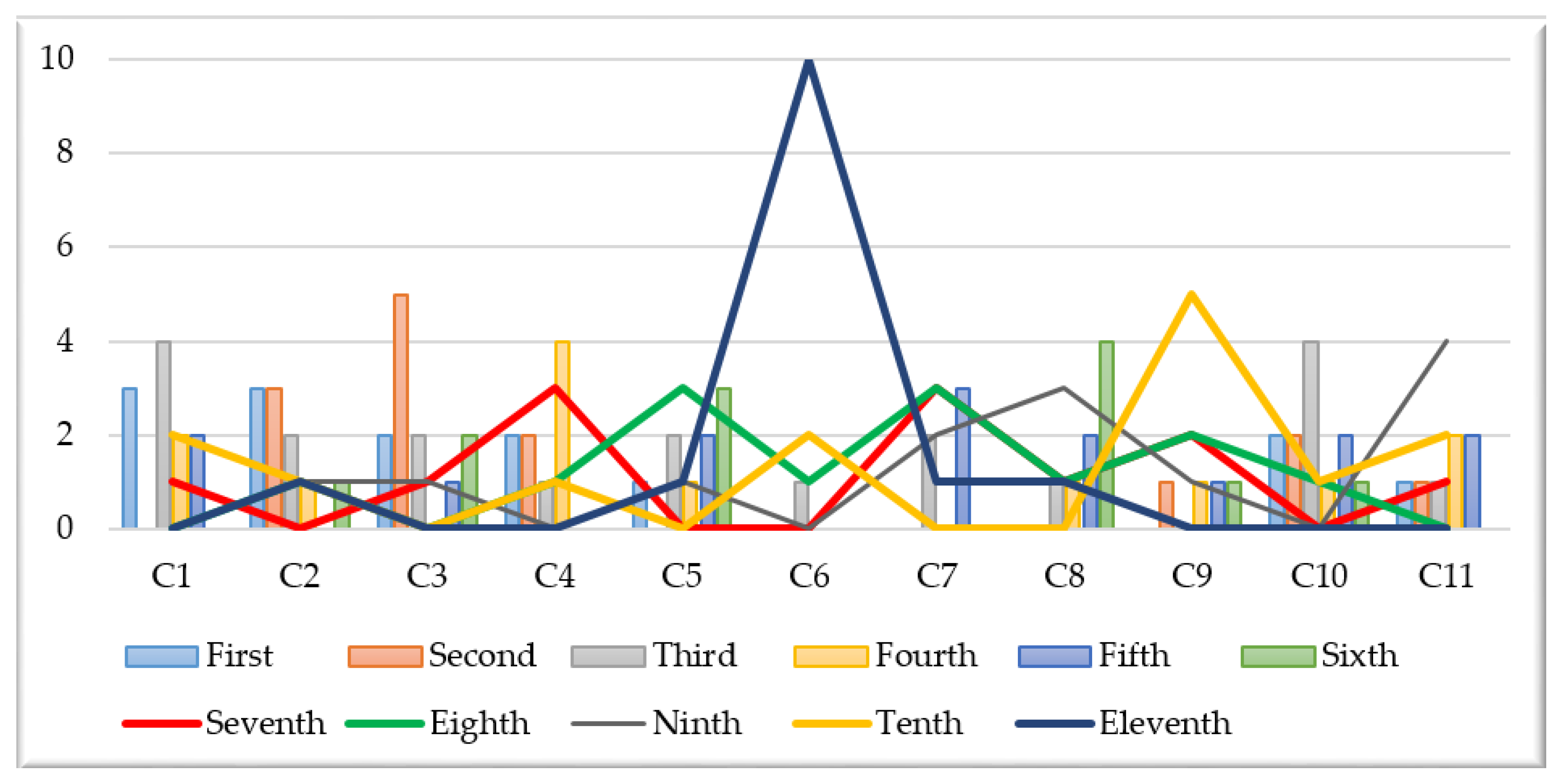
The number of occurrences of criteria from the first to eleventh position in the rankings is shown in Figure 6.

From the above table, it can be seen that criteria C₁—availability of free HPC infrastructure (e.g., having some sort of public funding), C₂—availability of commercial HPC infrastructure (where you have to pay for using it), C₃—availability of skilled human resources, C₄—degree to which universities equip students with the necessary knowledge to work in HPC, and C₁₀—degree of science-public authorities’ cooperation related to HPC were often highly ranked. Their importance was also confirmed by the high mean values of their weights.

Criteria C₁—availability of free HPC infrastructure (e.g., having some sort of public funding) and C₂—availability of commercial HPC infrastructure (where you have to pay for using it) had the highest number of appearances in the first position, three times each, while criteria C₃—availability of skilled human resources, C₄—degree to which universities equip students with the necessary knowledge to work in HPC, and C₁₀—degree of science-public authorities’ cooperation related to HPC, each had two appearances in the first position. Criterion C₂—availability of commercial HPC infrastructure (where you have to pay for using it) is also interesting because it was once identified as the least important criterion. Criterion C₆—availability of private funding for R&D related to HPC, can be mentioned as the least influential criterion because it was identified as the least important criterion based on the attitudes of respondents from nine countries.

5. Conclusions

A supercomputer represents computer architecture of high performance, capable of processing large amounts of data in a very short time. Supercomputers can be used for solving a variety of very complex problems, including intensive calculations. HPC has a very important role in computer science and until now has been used for solving a variety of computationally intensive tasks in different areas, such as quantum mechanics, molecular modeling, and physical simulations. In addition, HPC has become indispensable in the field of cryptanalysis. Therefore, the role of supercomputers is becoming increasingly important. Considering the importance of the use of supercomputers, which is evident from this research, it can be concluded that it can have a significant impact on increasing sustainability from the cost aspect. This is achieved through the higher speed of solving complex problems and greater efficiency in executing all processes, as well as decision-making based on previously implemented algorithms. The speed and success of the application of information technology will become the basic factor of the strength and usability [44].

In this paper, research was carried out regarding the evaluation of criteria for the implementation of HPC in Danube region countries by using the fuzzy PIPRECIA method. Therefore, the determination of the significance of the criteria relevant to the implementation of high-performance computing was carried out in Danube region countries. The significance of the 11 criteria was determined using the fuzzy PIPRECIA method, based on the views of 58 successfully interviewed experts from 14 Danube region countries.

Main findings and results of the study indicate that the criterion named “degree of science-public authorities’ cooperation related to HPC” was recognized as the most important, and its weight was 0.129. The second and the third influential criteria were the “availability of skilled human resources” and the “availability of competitive public funding”, whose weights were 0.124 and 0.123, respectively. Finally, the less influential was criterion “availability of private funding for R&D related to HPC”, whose weight was 0.079.