Revisiting Energy Demand Relationship: Theory and Empirical Application

Abstract

In this paper, we revisit the theoretical framework for energy demand. We then use this theoretical framework to empirically model the Saudi Arabian industrial electricity demand. We show, in the case of Saudi Arabian data, that imposing parsimonious energy demand specification on data without testing relevant assumptions can lead to biased estimations and noticeably poor approximations, while imposing general energy demand specification without accounting for the data properties can lead to redundant estimations and lower approximation than what could be obtained otherwise. Combining the theory with the data can provide unbiased and irredundant estimations with high levels of approximations. Hence, this paper recommends, based on the empirical findings, that a better strategy would be the combination of theoretical coherence with data coherence in the General to Specific Modeling (GtSM) framework for the empirical analyses of energy demand.

1. Introduction

Undoubtedly, energy is one of the key factors of not only economic activity but also social life. Moreover, it is impossible to imagine modern life without the existence of energy. As a result, countless numbers of studies have investigated different aspects of energy, including economic, environmental, and demographics. The supply- and demand-side of energy have been investigated extensively in the literature to enhance our understanding. It would not be incorrect if we state that the demand-side of energy has been examined more extensively when compared to the supply-side. One of the crucial aspects of this is to understand how various economic, technical, and demographic factors shape our demand for energy, and this has been the core task of modeling and forecasting exercises for a variety of domains such as academia, government agencies, and the private sector. Therefore, we believe that any research that helps us to understand or enhance our existing knowledge about the theoretical and empirical aspects of energy demand has a value and is worth considering.

Numerous empirical studies have investigated energy demand as a function of income and energy price (see, e.g., energy demand model surveys in [1,2,3,4]). However, if one revisits the theory of energy demand, as we do in Section 2, she/he will notice that this functional specification is a nested parsimonious form of a general specification. In other words, it is derived from the specification, in which the energy demand is a function of not only income/output and energy price, but also prices of other production factors, based on making some assumptions on the prices of other factors. Unlike in theoretical studies, in the empirical analysis of energy demand, these assumptions may or may not be held for a given country depending upon the dataset used and the time period considered (see, e.g., [2,5]) The natural question that arises here is which functional specification of energy demand should be used in empirical analysis? The General to Specific Modeling (GtSM) methodology provides insights in answering this empirically important question. The GtSM methodology articulates that the general model/specification of a given process should be considered first, and it should include all of the theoretically and empirically relevant variables to achieve a higher probability for approximating the Data Generating Process (DGP), which is never known, but researchers try to approximate at the maximum level. Then, a final parsimonious specification of the process can be achieved by checking various theoretical and empirical assumptions and excluding insignificant variables while testing properties (such as the Gaussian conditions of the residuals, or the misspecification and stability of the estimated relationship) of the final specification in each step of the exclusion ([6] inter alia). In other words, the GtSM framework advocates for the consideration of the combination of theoretical coherence with the data/statistical coherence in obtaining a final parsimonious specification from a general unrestricted specification. A number of seminal studies also suggest nesting a theory-driven approach within a data-driven approach in empirical modeling in macroeconomics ([7,8,9,10,11] inter alia).

The objective of this paper is to show the usefulness of the combination of theoretical coherence with data coherence in the GtSM framework for the empirical modeling of energy demand.

It is worth mentioning that we do not claim at all that we derive a new energy demand theory or develop a framework that combines theory-driven and data-driven approaches here. Rather, our objective here is to show the usefulness of the combination of energy demand theory with data/statistical coherence in the GtSM framework for the empirical estimation of energy demand relationships, using Saudi Arabian data as a case study.

We believe that revisiting energy demand theory would also be useful as it reminds (young) empirical researchers (a) how different industrial energy demand specifications can be theoretically derived. This would also help researchers to augment/modify energy demand specifications with other economic, social, or demographic factors if needed; (b) the specifications can be used in the empirical analysis, as they best fit the research objective given the data availability, but it should be remembered that they are based on different assumptions.

To be practically useful for empirical researchers, we revisit the theory of energy demand by re-deriving the specifications that link it to different variables in Section 2. Then, we apply these specifications to Saudi Arabian data through empirical estimations, and show the results from both the combination of the theory with the data and those from imposing the theory without accounting for the information coming from the data in Section 3. The results show that imposing general energy demand specification by ignoring the statistical properties of the data leads to redundant estimations and a lower level of approximations than what can be obtained otherwise, while imposing parsimonious specification of energy demand on the data without testing relevant assumptions leads to biased estimations and considerably poor approximations. Combining the theory with the data in the GtSM framework produces unbiased and irredundant estimations with high levels of approximations.

Thus, it may not be always possible and/or plausible to impose theory without considering the properties of a given data set. This can stem from the incompatibleness of the existing theories with the available data measures/proxies that can be caused mainly by vagueness and incompleteness of the theories, as well as the unavailability and inaccuracy of data, among other reasons (see e.g., [2,5,7,8] and references therein). Therefore, the key recommendation of this paper, which may be useful for empirical researchers, is that it is always better to apply the combination of theory-driven and data-driven approaches in the GtSM framework for the empirical modeling of energy demand.

The contribution of this paper is that it empirically shows the usefulness of the combination of theoretical coherence with data/statistical coherence in the GtSM framework for the empirical analysis of energy demand, given that such an approach is not widely used in the energy demand literature. Additionally, this study contributes to the energy demand literature of Saudi Arabia, which is the world’s primary oil exporter and has tremendous impact on energy markets and thus on global economic activities. To the best of our knowledge, this is the second paper, after [12], that applies the recommended approach to Saudi Arabian industrial energy data and investigates the drivers of industrial electricity demand. However, the objective of [12] was not to show usefulness of the combination of theoretical coherence with statistical coherence in the GtSM framework with empirical examples of modeling energy demand. The study provides information on how and to what extent the drivers of the non-oil industrial electricity demand shape it over time. Saudi Arabia embarks with the energy price and fiscal reforms in line with Saudi Vision 2030, a masterplan for the future development of the country since 2016 [13,14]. Hence, the estimated elasticities can be useful for analysis and forecasting as they can inform policymaking about at what magnitude the ongoing reforms can change the electricity demand in the non-oil industry through changes in prices and income. This information set would also be useful for the global energy and economic outlook because of Saudi Arabia’s imperative role in international energy markets.

2. Revisiting the Theory of the Energy Demand Equations

Cost Minimization Approach

This section describes the theoretical framework for the derivation of the functional specifications of energy demand for firms that produce goods and/or services. The aim of this section (and Appendix A) is to revisit the task of how energy demand specifications for firms can be theoretically derived. The same exercise can be done using the profit maximization approach, as in [15].

The Cobb–Douglas production function [16], which relates the output to the production factors is given as:

$$Q=A{K}^{\alpha }{L}^{\beta }{E}^{\gamma }{M}^{\delta }$$

(1)

where Q, K, L, E, and M are output, capital, labor, energy consumption, and materials, respectively; $\alpha ,\beta ,\gamma$ and $\delta$ are positive constants.

It can be assumed that, (a) a cost function exists as a dual function of the production function; (b) factor pricing is based on average cost and fixed markup; (c) there is also a preference function in the economy, and thus the demand for goods and services is a function of price and income; (d) all the functions follow the Cobb–Douglas type of specification; and (e) first-order conditions are derived assuming cost minimization. Based on these assumptions, the following energy demand equation can be derived, as described in Appendix A:

$$\ln E={\alpha }_0^{\prime }+{\alpha }^{\prime }\ln p_k+{\beta }^{\prime }\ln p_l+{\delta }^{\prime }\ln p_m+{\gamma }^{\prime }\ln p_e+{\eta }^{\prime }\ln Q$$

(2)

where:

$$\begin{gathered} {\alpha }_0^{\prime }=\frac{\left[-lnA+\alpha \ln \left(\frac{\gamma }{\alpha }\right)+\beta \ln \left(\frac{\gamma }{\beta }\right)+\delta \ln \left(\frac{\gamma }{\delta }\right)\right]}{\left[\alpha +\beta +\gamma +\delta \right]},{\alpha }^{\prime }=\frac{\alpha }{\left[\alpha +\beta +\gamma +\delta \right]},{\beta }^{\prime }=\frac{\beta }{\left[\alpha +\beta +\gamma +\delta \right]}, \\ {\delta }^{\prime }=\frac{\delta }{\left[\alpha +\beta +\gamma +\delta \right]},{\gamma }^{\prime }=\frac{\left(-\alpha -\beta -\delta \right)}{\left[\alpha +\beta +\gamma +\delta \right]},{\eta }^{\prime }=\frac{1}{\left[\alpha +\beta +\gamma +\delta \right]} \end{gathered}$$

(3)

Since $\alpha ,\beta ,\gamma and \delta$ are positive numbers, one can see from the above notations that ${\alpha }^{\prime }, {\beta }^{\prime }, {\delta }^{\prime } \mathrm{and} {\eta }^{\prime } \mathrm{are}\mathrm{positive}\mathrm{numbers},\mathrm{while} {\gamma }^{\prime } \mathrm{is}\mathrm{a}\mathrm{negative}\mathrm{number}.$ As a result, we derived a formula for the energy demand of the firms, which expresses it as a function of capital, labor, material and energy prices, and total output.

As discussed in [17] the demand functions of the economy for each product can be written as:

$$Q_i=f^i\left(P_1,P_2,P_3,\dots ,P_n,Y\right), i=1, \dots , n$$

(4)

where P_i’s are prices and Y is the total income. This function (in logs) can be written explicitly as:

$$\ln Q={\theta }_0+{\theta }_1\ln p_k+{\theta }_2\ln p_l+{\theta }_3\ln p_m+{\theta }_4\ln p_e+{\theta }_5\ln Y$$

(5)

where ${\theta }_{i}s$ are negative numbers, for i = 1 to 4, while ${\theta }_5>0$. Assuming market equilibrium, as in [17], one can solve (2) and (5) together. In other words, if we substitute $\ln Q$ in (2) with its expression in (5) and rearrange according to the coefficients, we find:

$$\ln E=({\alpha }_0^{\prime }+{\eta }^{\prime }{\theta }_0)+\left({\alpha }^{\prime }+{\eta }^{\prime }{\theta }_1)\ln p_k+\left({\beta }^{\prime }+{\eta }^{\prime }{\theta }_2\right)\ln p_l+({\delta }^{\prime }+{\eta }^{\prime }{\theta }_3\right)\ln p_m+({\gamma }^{\prime }+{\eta }^{\prime }{\theta }_4)\ln p_e+{\eta }^{\prime }{\theta }_5\ln Y$$

(6)

Equation (6) can be written in the following simpler form:

$$\ln E={\alpha }_0^{″}+{\alpha }^{″}\ln p_k+{\beta }^{″}\ln p_l+{\delta }^{″}\ln p_m+{\gamma }^{″}\ln p_e+{\eta }^{″}\ln Y$$

(7)

where, ${\alpha }_0^{″}={\alpha }_0^{\prime }+{\eta }^{\prime }{\theta }_0,{\alpha }^{″}={\alpha }^{\prime }+{\eta }^{\prime }{\theta }_1,{\beta }^{″}={\beta }^{\prime }+{\eta }^{\prime }{\theta }_2,{\delta }^{\prime }={\delta }^{\prime }+{\eta }^{\prime }{\theta }_3,{\gamma }^{″}={\gamma }^{\prime }+{\eta }^{\prime }{\theta }_4\mathrm{and}{\eta }^{″}={\eta }^{\prime }{\theta }_5$

Equation (7) is the derived energy demand equation and it shows that the demand for energy is a function of the prices of production factors and the total income. Based on the signs of ${\gamma }^{\prime }, {\eta }^{\prime }, {\theta }_4 and {\theta }_5$, it can be seen that ${\gamma }^{″}\langle 0, while {\eta }^{″}\rangle 0$. The comprehensive discussion of the signs of coefficients can be found in [15] and [17].

Apparently, the difference between Equations (2) and (7) is that the former links energy demand to output while the latter considers it as a function of income alongside the price measures.

Equation (7) can be reduced to Equation (8), in which the prices of other inputs are omitted based on some assumptions outlined below and energy demand is linked just to its own price and income.

$$\ln E={\alpha }_1+{\alpha }_2\ln p_e+{\alpha }_3\ln Y$$

(8)

Similarly, by making some assumptions Equation (2) can be reduced to Equation (8), where $Y$ is substituted by $Q$.

Seminal studies such as [15] and [17] assume that the price of capital goods is linearly dependent on GDP deflator and the price of labor is proportional to GDP deflator, and they end up with Equation (8). Other studies assume long-run homogeneity among the price of energy and other factors included in the energy demand equation and modify it, where the explanatory variables are just energy price and income/output. Notably, Equation (8) is the widely used specification in the empirical analyses of energy demand.

An error term should be added to the right-side of the equations discussed above to make them econometric specifications.

Lastly, depending on the research objective, Equations (2) and (7) can be further modified theoretically to include other socioeconomic variable(s) of interest in them. For example, [15] modified Equation (2) by replacing industrial production with industrial capital stock, while [12] modified Equation (7) by including a demographic variable.

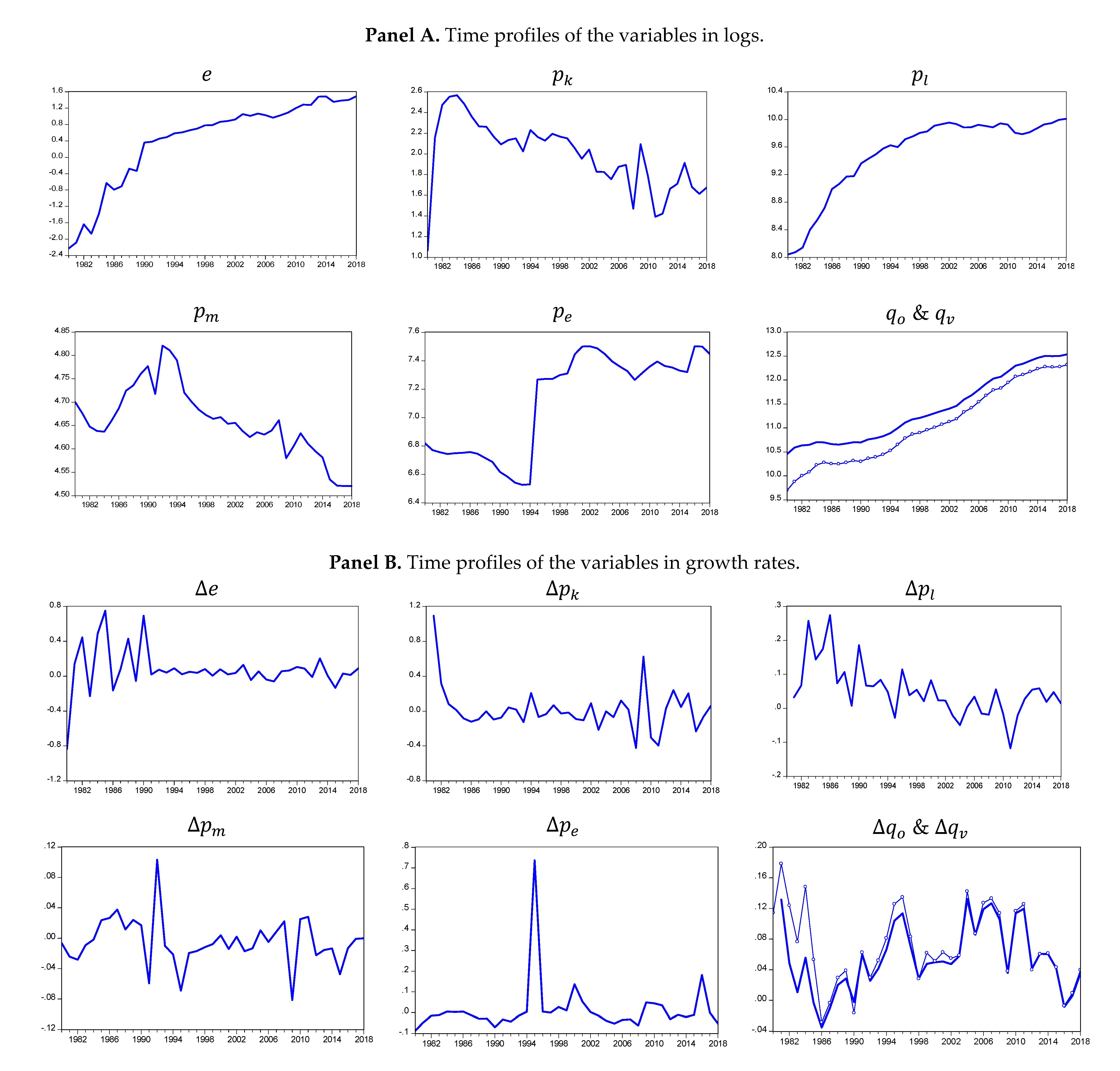
3. The Energy Demand Equations in Empirical Analysis

In this section, as an empirical application, we econometrically estimate Equations (2), (7), and (8) using time series data over the 1980–2018 period. The period is dictated by the availability of the time series data. The aim of this section is to show the result of imposing the theory by ignoring data properties and the results emerging from the combination of the theory with the data. Equally, one may apply the equations to the cross-sectional or panel data, but given the availability of the required data across the countries or across the industrial branches, especially when it comes to prices of capital and intermediate consumption data, we opt for the time series estimation here. As a country, we select Saudi Arabia because of the convenience of obtaining the required time series data. Additionally, it is the biggest oil exporter and has remarkable impact on energy markets and economic activities globally. Of course, different countries can be selected as case studies. We consider electricity consumption in the Saudi Arabian non-oil industry as a measure of energy, and, again, different energy products in different industry branches can be considered.

Table 1. Variables and their descriptions.

Variable	Notation	Description/definition	Source
Electricity consumption	$E$	The demand for electricity in non-oil industrial sector, mtoe.*	IEA [18]
Output in non-oil manufacturing in real terms	$Q_O$	This is the sum of value added and intermediate consumption both in manufacturing (excluding petroleum manufacturing) in million SAR at 2010 prices.	GSTAT [19] and OEGEM [20]
Value added in non-oil manufacturing in real terms	$Q_V$	The value added in manufacturing excluding petroleum manufacturing, in million SAR at 2010 prices.	GSTAT [19]
Price of electricity consumed in industry in real terms	$P_E$	$P_E=\frac{P_N}{P_{MAN}}*100$ $P_N$ is the nominal price of the electricity consumed in industry in SAR/toe. $P_{MAN}$ is the deflator of the non-oil manufacturing value added, which is calculated as below:    $P_{MAN}=\frac{Q_N}{Qv}*100$ $Q_N$ is the nominal value added in non-oil manufacturing, in million SAR.	Own calcula tion using GSTAT [19] data
Cost of capital in real terms	$P_K$	This is the United States Seven-Year Treasury note yield, at constant maturity, adjusted for the US inflation rate, %.	OEGEM [20]
Average annual wage in real terms	$P_L$	$P_L=\frac{W_N}{CPI}*100$ $W_N$ is the average annual wage in nominal term, which is calculated as below:    $W_N=\frac{ER}{ET}$ $ER$ is the total earnings in thousand SAR. $ET$ is total employment in thousand persons. $CPI$ is Consumer Price Index, 2010 = 100.	Own calcula tion using GSTAT [19] data
Price of intermediate consumption in real terms	$P_M$	$P_M=\frac{P_{MAN}}{P_{NOIL}}*100$ $P_{NOIL}$ is the deflator of the non-oil value added, which is calculated as below:    $P_{NOIL}=\frac{Q{N}_{NOIL}}{Q{R}_{NOIL}}*100$ $Q{N}_{NOIL}$ is the nominal value added in non-oil manufacturing, in million SAR. $Q{R}_{NOIL}$ is the real value added in non-oil manufacturing, in million SAR at 2010 prices.	Own calcula tion using GSTAT [19] data

Note: IEA = International Energy Agency; GSTAT = General Authority for Statistics of Saudi Arabia; OEGEM = Oxford Economics Global Economic Model database. We conclude that the variable is electricity consumption in the non-oil industrial sector based on our understanding of the IEA definitions for industry and energy industry own use.

presents the variables we used in the empirical analysis and their descriptions.

We use the United States Seven-Year Treasury note yield as a proxy for the Saudi long-run interest rate because such long-run interest rate data for Saudi Arabia is not available, to the best of our knowledge. There are interest rates on Saudi riyal deposits for one-, three-, six- and 12-month maturities that are available from the Saudi Arabian Monetary Authority annual statistics [21]. However, these interest rates are (a) short-run interest rates, and (b) available only from 1997. It is worth noting that earlier studies on the Saudi economy also faced the same issue of obtaining accurate interest rate data with a long sample size, and hence ended up either using the interest rates of foreign countries, especially the US, or dropping interest rates from their analyses (see [12,22,23,24,25,26,27,28]). The key justification point for those studies, as well as for us here, in using the US interest rate as a proxy for the Saudi interest rate, is that Saudi Arabian monetary policy strictly follows the monetary policy of the US because the exchange rate of the Saudi riyal has been pegged to the US dollar at the constant rate of 3.75 SAR/$ since 1986. Hence, Saudi interest rates closely track the US Federal Funds rate (see [29,30,31] inter alia). There is no available time series data on the price of the intermediate consumption that we are aware of; hence, we use also a proxy for it. The proxy is constructed as the ratio of the non-oil manufacturing price deflator to the non-oil sector price deflator, as Table 1 describes.

Figure 1 illustrates the natural logarithm and growth rate trajectories of the variables documented in Table 1. Without providing detailed information about the stochastic properties of the variables, note that they all are unit root processes at their natural logarithm levels and are stationary at their growth rate forms. In other words, they follow an integrated order of one, i.e., I (1) process. Details of the unit root test results are available from the authors upon request.

Since the variables are I (1) processes, we test whether the variables are cointegrated and estimated the level relationship among them. For this exercise, we use the Fully Modified Ordinary Least Squares (FMOLS) estimator developed by [32,33], as this method avoids over-parametrization and addresses the endogeneity issue. In line with our aim in this section, we consider the following options in our econometric analysis: (i) general energy demand specifications, i.e., Equations (2) and (7), are imposed on the data without considering the statistical properties of the variables; (ii) general energy demand specifications applied to the data and the statistical properties of the variables are accounted for, i.e., the combination of theory and data in the GtSM framework; (iii) parsimonious energy demand specification, i.e., Equation (8), is imposed on the data without considering the statistical properties of the omitted variables.

Table 2. FMOLS estimation and test results for Equations (2) and (8).

	Panel A. Estimation of Equation (2)		Panel B. Estimation of Equation (2) without ${\mathit{p}}_{\mathit{k}}$		Panel C. Estimation of Equation (8), where total output is used
Estimated long-run elasticities
Regressor	Coef.	P-value	Coef.	P-value	Coef.	P-value
$p_k$	0.097	0.643	−	−	−	−
$p_l$	1.453	0.000	1.505	0.000	−	−
$p_m$	1.980	0.086	1.493	0.087	−	−
$p_e$	−0.224	0.200	−0.285	0.075	0.630	0.392
$q_o$	0.608	0.001	0.532	0.000	0.892	0.021
$SER$	0.171098		0.168028		0.604501
$R_{ADJ}^2$	0.969779		0.970854		0.622769
Post-estimation test results
Q	0.368	0.544	0.316	0.574	0.809	0.000
$JB$	0.369	0.832	0.849	0.654	6.330	0.042
$F$ for $p_k$	−	−	0.200	0.658	0.567	0.456
$F$ for $p_l$	−	−	−	−	507.355	0.000
$F$ for $p_m$	−	−	−	−	51.613	0.000
Cointegration test results
$E{G}_{\tau }^a$	−5.492	0.027	−5.545	0.011	−2.623	0.440
$E{G}_z^a$	−34.067	0.024	−34.239	0.009	−5.674	0.852

Notes:$e$ is the dependent variable in the estimations. $SER$ is standard error of regression.$R_{ADJ}^2$ is adjusted R-Squared. Q is the Q-statistic of the first order auto-correlation coefficient with the null hypothesis that the residuals are not correlated.$JB$ is the Jarque–Bera statistic of normality test with the null hypothesis that the residuals are normally distributed.$F$ is the F-statistics of the omitted variable test with the null hypothesis that a tested variable can be omitted.$E{G}_{\tau }^a$ and $E{G}_z^a$ are the degree of freedom adjusted Engle–Granger tau- and z-statistics. Coef. and P-value mean the coefficient and its probability value. For simplicity, intercepts are not reported. Estimation period: 1980–2018.

and

Table 3. FMOLS estimation and test results for Equations (7) and (8).

	Panel D. Estimation of Equation (7)		Panel E. Estimation of Equation (7) without ${\mathit{p}}_{\mathit{k}}$		Panel F. Estimation of Equation (8), where income is used
Estimated long-run elasticities
Regressor	Coef.	P-value	Coef.	P-value	Coef.	P-value
$p_k$	0.030	0.885	−	−	−	−
$p_l$	1.368	0.000	1.439	0.000	−	−
$p_m$	1.838	0.111	1.621	0.056	−	−
$p_e$	−0.218	0.217	−0.249	0.105	0.364	0.727
$q_v$	0.540	0.002	0.499	0.000	1.019	0.029
$SER$	0.170074		0.169650		0.608458
$R_{ADJ}^2$	0.970140		0.970289		0.672940
Post-estimation test results
Q	0.594	0.441	0.669	0.413	31.490	0.000
$JB$	0.164	0.921	0.922	0.631	0.687	0.709
$F$ for $p_k$	−	−	0.029	0.865	0.808	0.375
$F$ for $p_l$	−	−	−	−	399.451	0.000
$F$ for $p_m$	−	−	−	−	67.250	0.000
Cointegration test results
$E{G}_{\tau }^a$	−5.351	0.035	−5.378	0.015	−1.853	0.795
$E{G}_z^a$	−33.126	0.031	−33.258	0.013	−5.137	0.881

Notes:$e$ is the dependent variable in the estimations. $SER$ is standard error of regression.$R_{ADJ}^2$ is adjusted R-Squared. Q is the Q-statistic of the first order auto-correlation coefficient with the null hypothesis that the residuals are not correlated. $JB$ is the Jarque–Bera statistic of normality test with the null hypothesis that the residuals are normally distributed.$F$ is the F-statistics of the omitted variable test with the null hypothesis that a tested variable can be omitted.$E{G}_{\tau }^a$ and $E{G}_z^a$ are the degree of freedom adjusted Engle–Granger tau- and z-statistics. Coef. and P-value mean the coefficient and its probability value. For simplicity, intercepts are not reported. Estimation period: 1980–2018.

document the estimation and testing results.

Three useful observations can be extracted from Table 2 and Table 3.

• Panels A and D report the results of estimations for Equations (2) and (7), respectively. All the explanatory variables have theoretically expected signs. Apparently, the cost of capital is highly statistically insignificant in both estimations. These are the results from option (i): that is, we impose the theory of energy demand on the data and ignore information coming from data, i.e., the insignificance of the capital cost. Our results are theory-driven only, and, hence, we position ourselves at the upper part of Pagan’s curve [7,11].
• Panels B and E report the results of estimations for Equations (2) and (7) without the cost of capital, respectively. In other words, we follow option (ii), such that we first apply general energy demand specifications to the data and also account for the statistical insignificance of the cost of capital and exclude it from the analysis in the GtSM framework. All the remaining variables have theoretically expected signs and are statistically significant at different levels. In other words, the estimation results are from nesting the theory of energy demand with the data in the GtSM framework, i.e., they are both theory driven and data driven, and, thus, we position ourselves at the middle part of Pagan’s curve [7,11].
• Panels C and F report the results of estimations of Equation (8), where the explanatory variables are only energy price and output/income. In other words, the estimation results are from option (iii). On data, we impose the parsimonious energy demand specification, which omits the theoretically predicted variables of prices of capital, labor, and intermediate consumption based on some assumptions made by default, as discussed in Section 2, without testing the statistical significance of the variables omitted to see whether they can contribute to the explanation of the energy demand pattern. Obviously, we miss some important information, which could come from the prices of labor and intermediate consumption, as the omitted variable tests indicate in Table 2 and Table 3. Apparently, the electricity price has an incorrect sign and is statistically insignificant, most likely due to omitting the important variables (see, e.g., the discussions in [34,35,36,37]). Obviously, if we could follow GtSM and consider both the theoretical coherence and the statistical coherence, we would not end up with such a poor specification of energy demand.

Thus, the question that occurs here is, “which of the above options should we give preference in our energy demand modeling for policy analysis and or forecasting?”. In our explanation below, we tried to justify a preferred specification, theoretically and statistically.

Undoubtedly, one should not prefer to model energy demand as we do in Panels C and F following option (iii) because such a framework for energy demand analysis yields theoretically poor (i.e., the omission of the important variables, and the incorrect sign for the energy price) and statistically poor results (the insignificance of the energy price, higher $SER,$ and lower $R_{ADJ}^2$ compared to other options, auto-correlation in the residuals, and omitted variable issue). Additionally, this specification, as a nested parsimonious form of the general specification, is based on assumptions of linear dependency, proportionality, or homogeneity between the prices of energy and other factors, which might not be representative for the country in question, Saudi Arabia in our case, given the data used and the period covered.

Perhaps theory-driven researchers, such as Computable General Equilibrium (CGE) or Dynamic Stochastic General Equilibrium (DSGE) modelers, would prefer to model energy demand as we do in Panels A and D following option (i). The researchers who are in favor of nesting theory-driven and data-driven approaches and following the GtSM framework would prefer modeling energy demand as we do in Panels B and E.

With our respect to both types of researcher, we believe that modeling energy demand following option (ii), as it is done in Panels B and E, is the relevant option to consider because of the following statistical and theoretical reasons.

Statistically, in our case, this is because of the fact that the estimated specifications without the cost of capital outperform those with the cost of capital, as the former have lower standard errors and higher levels of approximations compared to the latter. Additionally, the results of the omitted variable test indicate no information loss from excluding the cost of capital variable from the estimations.

Theoretically, the following points should be recalled briefly:

• Sometimes a variable articulated by the theory cannot be exactly measured in practice due to data inaccuracy and unavailability issues, and proxies can provide poor estimates and thus do not help us to approximate the Data Generation Process (DGP) of the variable under interest. This is exactly what we face in our analysis here. The theory in Section 2 articulates the cost of capital as an explanatory variable of energy demand. However, we cannot find the exact cost of capital data for non-oil manufacturing. It can be argued that this is not the case solely for Saudi Arabia, and, even for many developing and developed countries, the cost of capita data is not available for the different branches of industry. Following earlier studies, we proxy it, but it appears that the selected proxy does not contribute to the DGP of industrial energy demand, and it was statistically insignificant.
• Often, theories are vague about variables when it comes to considering the variables in the empirical analysis, and the selected variables may not contribute to the DGP. For example, money demand theories consider income as a scale variable in explaining the behavior of money balance. However, it is not quite clear which income measure should be considered in the empirical analysis. Therefore, GDP, retail turnover, consumption, government expenditure, and industrial production index have all been considered in the empirical analyses of money demand [38].
• All theories are based on certain assumptions, and these assumptions may not be held for the country of interest or for the time period considered (see, [2]).
• Theories do not tell us anything about structural breaks and location shifts, which can play a considerable role in explaining a given process.

Details of the points listed above, alongside others, are comprehensively discussed in [7] and in the references therein.

To conclude, imposing theory without accounting for the properties of the data may lead to biased results and, thus, to misleading policy suggestions. Thus, the recommendation of this paper, based on the empirical results above, is that it would be a better strategy to consider the combination of theoretical coherence and statistical/data coherence in the empirical analyses of energy demand.

From the Saudi Arabian standpoint, there would be value in briefly discussing the estimation results that we obtained by following the recommended approach of combining the theory with the data, although it is not our primary objective in this research. Apparently, the estimated elasticities of the electricity demand with respect to the prices of labor, intermediate consumption, and electricity reported in Panels B and E are quite similar to each other in terms of their signs, sizes, and significance levels obtained. This suggests that, regardless of whether we consider total output or value added of non-oil manufacturing, the impacts of the prices on the electricity demand follow almost the same pattern. Speaking through the estimated elasticities, holding other factors constant and in the long-run, a 1% increase (decrease) in the prices of labor and intermediate consumption leads to a 1.5–1.4% and 1.5–1.6% increase (decrease) in the electricity demand in non-oil industry, respectively, while a 1% raise in the electricity price reduces its demand by -0.3 or–0.2%. Besides, if non-oil manufacturing value added or output grows by 1%, then demand for electricity grows by 0.5%. The results are theoretically coherent as they are in line with our discussion in Section 2. They also represent the characteristics of the Saudi Arabian economy as follows. Saudi Arabia, the world’s primary oil exporter, has huge energy subsidies and, therefore, the price of energy including electricity has administratively been set very low in nominal terms and even decreases when it is adjusted for inflation (see, e.g., [12,39,40]) Even after the last increase in 2016, which followed energy price and fiscal reform programs, it was just about 0.05 USD per kWh. We think that this explains why the estimated labor price and the intermediate consumption price elasticities of electricity demand are elastic: more electricity will be used as it is very cheap if the prices of these factors are high. As an example, in the case of a resource-poor country (Greece), [41] finds long-run elasticities of energy demand with respect to the price of capital and the price of labor as low as 0.14 and 0.02, respectively. The cheap electricity price also explains why the magnitude of the own price and income/output elasticities of electricity demand are small. Since it was historically set up to be very cheap, any increases do not make significant changes in the decision of non-oil industry regarding electricity consumption. For example, the price was increased by 20% in 2016 relative to 2015, but this huge increase in percentage terms raised the price from 0.04 USD/kWh to just about 0.05 USD/kWh.

4. Concluding Remarks

Numerous studies have analyzed industrial energy demand as a function of income and energy price. By revisiting energy demand theory, one can see that this is a nested parsimonious functional specification of the general energy demand specifications, in which other explanatory variables are dropped by making some assumptions. Unlike theoretical investigations, in the empirical analysis of energy demand, these assumptions may and may not be valid for a county of interest, depending upon the dataset used and the time period considered. Then, the question becomes, “which functional specification of the energy demand should one use in her/his empirical research?”. In the case study of the empirical modeling of Saudi Arabian industrial electricity demand, we find that (a) imposing parsimonious energy demand specification on the data without checking the relevant assumptions of the data can result in biased estimations and remarkably poor approximations; (b) imposing general energy demand specifications without considering the properties of the data can end up with redundant estimations and lower approximation; (c) combining the theory with the data in GtSM framework can produce unbiased and irredundant estimations with high levels of approximations. Thus, we attempted empirically to show the usefulness of the combination of theoretical coherence with data coherence in the framework of the GtSM, to answer the question.

Additionally, the estimated elasticities can be beneficial for policy analysis and forecasting as they provide information about to what extent the ongoing energy price and fiscal reforms can change the demand for electricity in the non-oil industry through changes in prices and income in Saudi Arabia. This information set may also be useful for the global energy and economic outlook, given Saudi Arabia’s key position in international energy markets.