Electric Bus Selection with Multicriteria Decision Analysis for Green Transportation
Abstract
1. Introduction
2. Literature
2.1. Alternative Bus Technologies and Electric Buses
2.2. Decision Analysis for the Selection Process
- (1)
- To identify appropriate specific evaluation criteria for electric buses under clean technology,
- (2)
- To propose an MCDM (AHP–TOPSIS) model to select electric buses for sustainable and environmentally friendly transportation,
- (3)
- To guide planners regarding the electric vehicle selection process via the example application.
3. Methodology: An Integrated AHP–TOPSIS Method
3.1. A Brief Overview of AHP
3.2. TOPSIS
3.3. AHP-TOPSIS
4. Case Study
4.1. Criteria Definitions for Electric Bus Selection
4.2. Ranking of Alternatives with TOPSIS
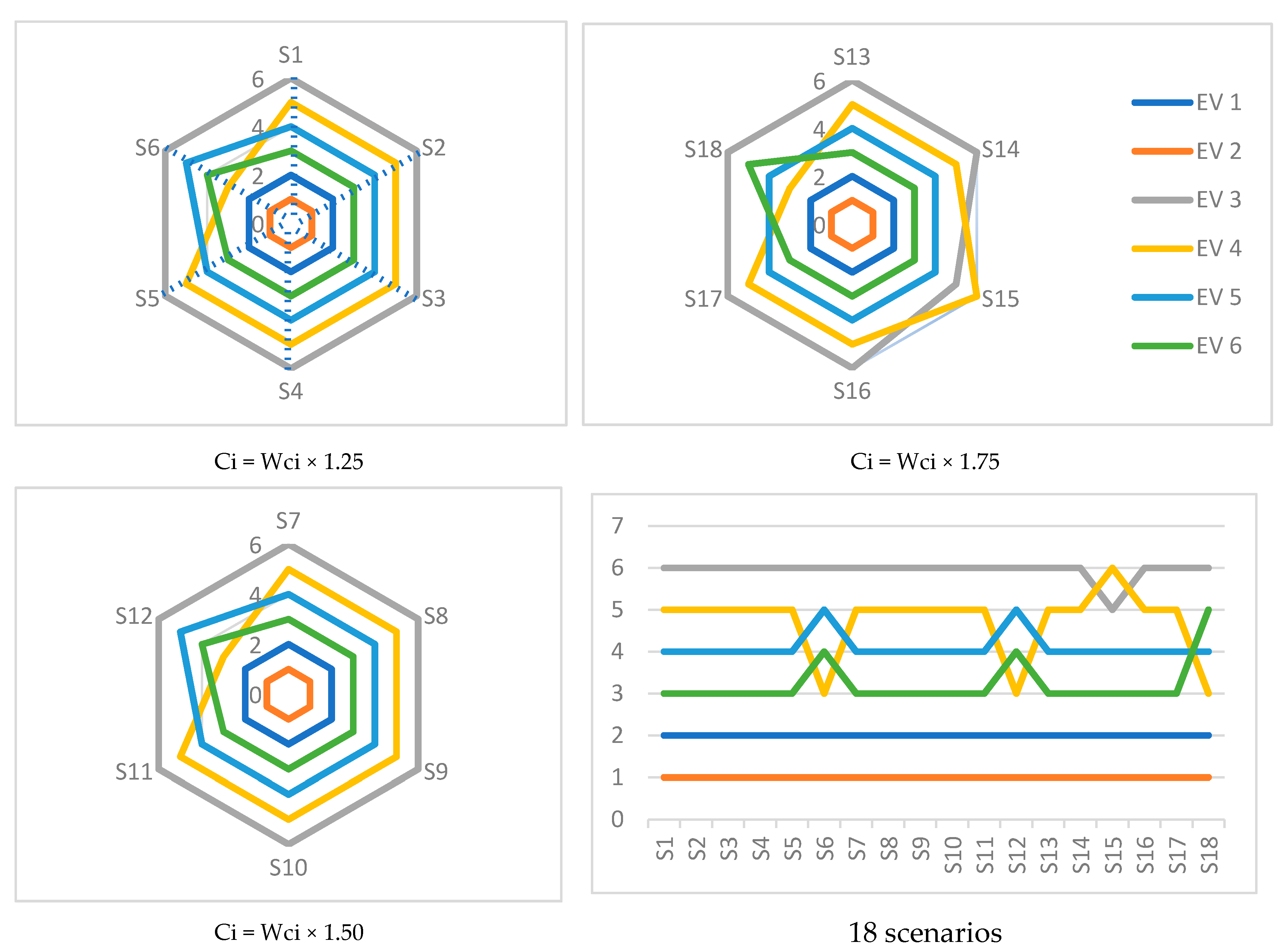
4.3. Sensitivity Analysis of the Solution
5. Results
Nomenclature-Acronyms and Symbols
| AHP | analytic hierarchy process |
| TOPSIS | technique for order performance by similarity to ideal solution |
| EV | electric vehicle |
| USA | United States of America |
| MCDM | multi-criteria decision-making |
| IEA | international energy agency |
| GHG | greenhouse gas |
| ANP | analytic network process |
| VIKOR | vise kriterijumska optimizacija I kompromisno resenje |
| ELECTRE | elimination et choix traduisant la realite |
| MOORA | multi-objective optimization on the basis of ratio analysis |
| PROMETHEE | preference ranking organization method for enrichment of evaluations |
| FMCDM | fuzzy multi-criteria decision -making |
| HSR | high-speed railway |
| CI | consistency index |
| CR | consistency ratio |
| RI | random index |
| the eigenvalue |
Author Contributions
Funding
Conflicts of Interest
References
- Dell’olio, L.; Ibeas, A.; Cecín, P. Modelling user perception of bus transit quality. Transp. Policy 2010, 17, 388–397. [Google Scholar]
- Hilmola, O.P. Benchmarking efficiency of public passenger transport in larger cities. Benchmark. Int. J. 2011, 18, 23–41. [Google Scholar] [CrossRef]
- Yaliniz, P.; Bilgic, S.; Vitosoglu, Y.; Turan, C. Evaluation of urban public transportation efficiency in Kutahya, Turkey. Proc. Soc. Behav. Sci. 2011, 20, 885–895. [Google Scholar] [CrossRef]
- Guerra, J.B.S.O.A.; Dutra, L.; Schwinden, N.B.C.; Andrade, S.F. Future scenarios and trends in energy generation in Brazil: Supply and demand and mitigation forecasts. J. Clean. Prod. 2014, 103, 197–210. [Google Scholar]
- Banister, D. Unsustainable Transport: City Transport in the New Century, 1st ed.; Routledge: Abingdon, UK, 2005. [Google Scholar]
- Shen, J.; Sakata, Y.; Hashimoto, Y. The influence of environmental deterioration and network improvement on transport modal choice. Environ. Sci. Policy 2009, 12, 338–346. [Google Scholar] [CrossRef]
- Deakin, M.; Curwell, S.; Lombardi, P. Sustainable urban development: The framework and directory of assessment methods. J. Environ. Assess. Policy Manag. 2002, 4, 171–197. [Google Scholar] [CrossRef]
- UITP. Autonomous Vehicles: Potential Game Changer for Urban Mobility; International Association of Public Transport, Policy; UITP: Brussels, Belgium, 2017. [Google Scholar]
- Mahmoud, M.; Garnett, R.; Ferguson, M.; Kanaroglou, P. Electric buses: A review of alternative powertrains. Renew. Sustain. Energy Rev. 2016, 62, 673–684. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Teoh, L.E.; Khoo, H.L.; Goh, S.Y.; Chong, L.M. Scenario-based electric bus operation: A case study of Putrajaya, Malaysia. Int. J. Transp. Sci. Technol. 2018, 7, 10–25. [Google Scholar] [CrossRef]
- Wang, T.; Yi, S.; Yang, Y. Performance evaluation method for business process of machinery manufacturer based on DEA/AHP hybrid model. Chin. J. Mech. Eng. Engl. Ed. 2007, 20, 91. [Google Scholar] [CrossRef]
- IEA. Global EV Outlook 2017; OECD/IEA: Paris, France, 2017. [Google Scholar]
- Perez, J.C.; Carrillo, M.H.; Montoya-Torres, J.R. Multi-criteria approaches for urban passenger transport systems: A literature review. Ann. Oper. Res. 2015, 226, 69–87. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook 2016; International Energy Agency: Paris, France, 2016; p. 28. [Google Scholar]
- Tie, S.F.; Tan, C.W. A review of energy sources and energy management system in electric vehicles. Renew. Sustain. Energy Rev. 2013, 20, 82–102. [Google Scholar] [CrossRef]
- International Energy Agency. CO2 Emissions from Fuel Combustion: Highlights; International Energy Agency: Paris, France, 2017. [Google Scholar]
- Jacobson, M.Z. Review of solutions to global warming, air pollution, and energy security. Energy Environ. Sci. 2009, 2, 148–173. [Google Scholar] [CrossRef]
- Enang, W.; Bannister, C. Modelling and control of hybrid electric vehicles (A comprehensive review). Renew. Sustain. Energy Rev. 2017, 74, 1210–1239. [Google Scholar] [CrossRef]
- Brahma, A.; Guezennec, Y.; Rizzoni, G. Dynamic optimization of mechanical/electrical power flow in parallel hybrid electric vehicles. In Proceedings of the 5th International Symposium in Advanced Vehicle Control, Ann Arbor, MI, USA, 22–24 August 2000. [Google Scholar]
- Schouten, N.J.; Salman, M.A.; Kheir, N.A. Energy management strategies for parallel hybrid vehicles using fuzzy logic. Control Eng. Pract. 2003, 11, 171–177. [Google Scholar] [CrossRef]
- Delprat, S.; Lauber, J.; Guerra, T.M. Control of a parallel hybrid powertrain: Optimal control. IEEE Trans. Veh. Technol. 2004, 53, 872–881. [Google Scholar] [CrossRef]
- Li, Z.; Khajepour, A.; Song, J. A comprehensive review of the key technologies for pure electric vehicles. Energy 2019, 182, 824–839. [Google Scholar] [CrossRef]
- Lajunen, A.; Lipman, T. Lifecycle cost assessment and carbon dioxide emissions of diesel, natural gas, hybrid electric, fuel cell hybrid and electric transit buses. Energy 2016, 106, 329–342. [Google Scholar] [CrossRef]
- Correa, G.; Muñoz, P.; Falaguerra, T.; Rodriguez, C.R. Performance comparison of conventional, hybrid, hydrogen and electric urban buses using well to wheel analysis. Energy 2017, 141, 537–549. [Google Scholar] [CrossRef]
- Liu, T.; Ceder, A.A. Battery-electric transit vehicle scheduling with optimal number of stationary chargers. Transp. Res. Part C Emerg. Technol. 2020, 114, 118–139. [Google Scholar] [CrossRef]
- Kühne, R. Electric buses–an energy efficient urban transportation means. Energy 2010, 35, 4510–4513. [Google Scholar]
- Ou, X.; Zhang, X.; Chang, S. Alternative fuel buses currently in use in China: Life-cycle fossil energy use, GHG emissions and policy recommendations. Energy Policy 2010, 38, 406–418. [Google Scholar] [CrossRef]
- McKenzie, E.C.; Durango-Cohen, P.L. Environmental life-cycle assessment of transit buses with alternative fuel technology. Transp. Res. Part D Transp. Environ. 2012, 17, 39–47. [Google Scholar] [CrossRef]
- Cooney, G.; Hawkins, T.R.; Marriott, J. Life cycle assessment of diesel and electric public transportation buses. J. Ind. Ecol. 2013, 17, 689–699. [Google Scholar] [CrossRef]
- Kliucininkas, L.; Matulevicius, J.; Martuzevicius, D. The life cycle assessment of alternative fuel chains for urban buses and trolleybuses. J. Environ. Manag. 2012, 99, 98–103. [Google Scholar] [CrossRef]
- Nurhadi, L.; Borén, S.; Ny, H. A sensitivity analysis of total cost of ownership for electric public bus transport systems in Swedish medium sized cities. Transp. Res. Procedia 2014, 3, 818–827. [Google Scholar] [CrossRef]
- Lajunen, A. Energy consumption and cost-benefit analysis of hybrid and electric city buses. Transp. Res. Part C Emerg. Technol. 2014, 38, 1–15. [Google Scholar] [CrossRef]
- Ribau, J.P.; Silva, C.M.; Sousa, J.M. Efficiency, cost and life cycle CO2 optimization of fuel cell hybrid and plug-in hybrid urban buses. Appl. Energy 2014, 129, 320–335. [Google Scholar] [CrossRef]
- Li, J.Q. Battery-electric transit bus developments and operations: A review. Int. J. Sustain. Transp. 2016, 10, 157–169. [Google Scholar] [CrossRef]
- Miles, J.; Potter, S. Developing a viable electric bus service: The Milton Keynes demonstration project. Res. Transp. Econ. 2014, 48, 357–363. [Google Scholar] [CrossRef]
- De Filippo, G.; Marano, V.; Sioshansi, R. Simulation of an electric transportation system at The Ohio State University. Appl. Energy 2014, 113, 1686–1691. [Google Scholar] [CrossRef]
- Chao, Z.; Xiaohong, C. Optimizing battery electric bus transit vehicle scheduling with battery exchanging: Model and case study. Procedia Soc. Behav. Sci. 2013, 96, 2725–2736. [Google Scholar] [CrossRef]
- Živanović, Z.; Nikolic, Z. The application of electric drive technologies in city buses. In New Generation of Electric Vehicles; InTech: London, UK, 2012. [Google Scholar]
- Lin, Y.; Zhang, K.; Shen, Z.J.M.; Ye, B.; Miao, L. Multistage large-scale charging station planning for electric buses considering transportation network and power grid. Transp. Res. Part C Emerg. Technol. 2019, 107, 423–443. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, D.; Meng, Q.; Ong, G.P.; Lee, D.H. A four-step method for electric-vehicle charging facility deployment in a dense city: An empirical study in Singapore. Transp. Res. Part A Policy Pract. 2019, 119, 224–237. [Google Scholar] [CrossRef]
- An, K. Battery electric bus infrastructure planning under demand uncertainty. Transp. Res. Part C Emerg. Technol. 2020, 111, 572–587. [Google Scholar] [CrossRef]
- Rogge, M.; van der Hurk, E.; Larsen, A.; Sauer, D.U. Electric bus fleet size and mix problem with optimization of charging infrastructure. Appl. Energy 2018, 211, 282–295. [Google Scholar] [CrossRef]
- Schneider, F.; Thonemann, U.W.; Klabjan, D. Optimization of battery charging and purchasing at electric vehicle battery swap stations. Transp. Sci. 2017, 52, 1211–1234. [Google Scholar] [CrossRef]
- Brendel, A.B.; Lichtenberg, S.; Brauer, B.; Nastjuk, I.; Kolbe, L.M. Improving electric vehicle utilization in carsharing: A framework and simulation of an ecarsharing vehicle utilization management system. Transp. Res. Part D Transp. Environ. 2018, 64, 230–245. [Google Scholar] [CrossRef]
- Xu, M.; Meng, Q.; Liu, Z. Electric vehicle fleet size and trip pricing for one-way carsharing services considering vehicle relocation and personnel assignment. Transp. Res. Part B Methodol. 2018, 111, 60–82. [Google Scholar] [CrossRef]
- Gao, Z.; Lin, Z.; LaClair, T.J.; Liu, C.; Li, J.M.; Birky, A.K.; Ward, J. Battery capacity and recharging needs for electric buses in city transit service. Energy 2017, 122, 588–600. [Google Scholar] [CrossRef]
- Krause, J.; Ladwig, S.; Schwalm, M. Statistical assessment of EV usage potential from user’s perspective considering rapid-charging technology. Transp. Res. Part D Transp. Environ. 2018, 64, 150–157. [Google Scholar] [CrossRef]
- Wang, Y.; Bi, J.; Guan, W.; Zhao, X. Optimising route choices for the travelling and charging of battery electric vehicles by considering multiple objectives. Transp. Res. Part D Transp. Environ. 2018, 64, 246–261. [Google Scholar] [CrossRef]
- Erdoğan, S.; Miller-Hooks, E. A green vehicle routing problem. Transp. Res. Part E Logist. Transp. Rev. 2012, 109, 100–114. [Google Scholar]
- Said, D.; Cherkaoui, S.; Khoukhi, L. Queuing model for EVs charging at public supply stations. In Proceedings of the 9th International Wireless Communications and Mobile Computing Conference (IWCMC), Cagliari, Italy, 1–5 July 2013; pp. 65–70. [Google Scholar]
- Yang, S.N.; Cheng, W.S.; Hsu, Y.C.; Gan, C.H.; Lin, Y.B. Charge scheduling of electric vehicles in highways. Math. Comput. Model. 2013, 57, 2873–2882. [Google Scholar] [CrossRef]
- Zhou, B.; Wu, Y.; Zhou, B.; Wang, R.; Ke, W.; Zhang, S.; Hao, J. Real-world performance of battery electric buses and their life-cycle benefits with respect to energy consumption and carbon dioxide emissions. Energy 2016, 96, 603–613. [Google Scholar] [CrossRef]
- Sun, X.-H.; Yamamoto, T.; Morikawa, T. Fast-charging station choice behavior among battery electric vehicle users. Transp. Res. Part D Transp. Environ. 2016, 46, 26–39. [Google Scholar] [CrossRef]
- Panchal, S.; Rashid, M.; Long, F.; Mathew, M.; Fraser, R.; Fowler, M. Degradation Testing and Modeling of 200 Ah LiFePO4 Battery; SAE Technical Paper; SAE International: Detroit, MI, USA, 2018. [Google Scholar]
- Panchal, S.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Design and simulation of a lithium-ion battery at large C-rates and varying boundary conditions through heat flux distributions. Measurement 2018, 116, 382–390. [Google Scholar] [CrossRef]
- Hamurcu, M.; Eren, T. Applications of the MOORA and TOPSIS Method for Decision of Electric Vehicle in Public Transportation Technology. Transport 2020, in press. [Google Scholar]
- Süt, N.İ.; Hamurcu, M.; Eren, T. An Application of Green Transportation in Campus: A Decision Making Process for Selection of Ring Vehicles. Gazi J. Eng. Sci. 2019, 5, 9–21. [Google Scholar]
- Büyüközkan, G.; Feyzioğlu, O.; Göçer, F. Selection of sustainable urban transportation alternatives using an integrated intuitionistic fuzzy Choquet integral approach. Transp. Res. Part D Transp. Environ. 2018, 58, 186–207. [Google Scholar]
- Dinç, S.; Hamurcu, M.; Eren, T. Multicriteria Selection of Alternative Tramway Vehicles for Urban Transportation. Gazi J. Eng. Sci. 2018, 4, 124–135. [Google Scholar]
- Mukherjee, S. Selection of alternative fuels for sustainable urban transportation under Multi-criteria intuitionistic fuzzy environment. Fuzzy Inf. Eng. 2017, 9, 117–135. [Google Scholar] [CrossRef]
- Oztaysi, B.; Cevik Onar, S.; Kahraman, C.; Yavuz, M. Multi-criteria alternative-fuel technology selection using interval-valued intuitionistic fuzzy sets. Transp. Res. Part D Transp. Environ. 2017, 53, 128–148. [Google Scholar] [CrossRef]
- Hamurcu, M.; Eren, T. Selection of Monorail Technology by Using Multicriteria Decision Making. Sigma J. Eng. Nat. Sci. 2017, 8, 303–314. [Google Scholar]
- Onat, N.C.; Gumus, S.; Kucukvar, M.; Tatari, O. Application of the TOPSIS and intuitionistic fuzzy set approaches for ranking the life cycle sustainability performance of alternative vehicle technologies. Sustain. Prod. Consum. 2016, 6, 12–25. [Google Scholar] [CrossRef]
- Onat, N.C.; Kucukvar, M.; Tatari, O.; Zheng, Q.P. Combined application of multi-criteria optimization and life-cycle sustainability assessment for optimal distribution of alternative passenger cars in U.S. J. Clean. Prod. 2016, 112, 291–307. [Google Scholar] [CrossRef]
- Lanjewar, P.B.; Rao, R.V.; Kale, A.V. Assessment of alternative fuels for transportation using a hybrid graph theory and analytic hierarchy process method. Fuel 2015, 154, 9–16. [Google Scholar] [CrossRef]
- Yavuz, M.; Oztaysi, B.; Onar, S.C.; Kahraman, C. Multi-criteria evaluation of alternative-fuel vehicles via a hierarchical hesitant fuzzy linguistic model. Expert Syst. Appl. 2015, 42, 2835–2848. [Google Scholar] [CrossRef]
- Petschnig, M.; Heidenreich, S.; Spieth, P. Innovative alternatives take action–Investigating determinants of alternative fuel vehicle adoption. Transp. Res. Part A Policy Pract. 2014, 61, 68–83. [Google Scholar] [CrossRef]
- Aydın, S.; Kahraman, C. Vehicle selection for public transportation using an integrated multi criteria decision making approach: A case of Ankara. J. Intell. Fuzzy Syst. 2014, 26, 2467–2481. [Google Scholar]
- Vahdani, B.; Zandieh, M.; Tavakkoli-Moghaddam, R. Two novel FMCDM methods for alternative-fuel buses selection. Appl. Math. Model. 2011, 35, 1396–1412. [Google Scholar] [CrossRef]
- Patil, A.; Herder, P. Investment decision making for alternative fuel public transport buses: The case of Brisbane transport. J. Public Transp. 2010, 13, 115–133. [Google Scholar] [CrossRef]
- Hsiao, H.; Chan, Y.-C.; Chiang, C.-H.; Tzeng, G.-H. Fuzzy AHP and TOPSIS for selecting low pollutant emission bus systems. In Proceedings of the 28th IAEE International Conference, Taipei, Taiwan, 3–6 June 2005; pp. 1–19. [Google Scholar]
- Tzeng, G.H.; Lin, C.W.; Opricovic, S. Multi-criteria analysis of alternative-fuel buses for public transportation. Energy Policy 2005, 33, 1373–1383. [Google Scholar] [CrossRef]
- Yedla, S.; Shrestha, R.M. Multi-criteria approach for the selection of alternative options for environmentally sustainable transport system in Delhi. Transp. Res. Part A Policy Pract. 2003, 37, 717–729. [Google Scholar] [CrossRef]
- Tavana, M.; Hatami-Marbini, A. A group AHP-TOPSIS framework for human spaceflight mission planning at NASA. Expert Syst. Appl. 2011, 38, 13588–13603. [Google Scholar] [CrossRef]
- Sánchez-Lozano, J.M.; Rodríguez, O.N. Application of Fuzzy Reference Ideal Method (FRIM) to the military advanced training aircraft selection. Appl. Soft Comput. J. 2020, 88, 106061. [Google Scholar]
- Zheng, G.; Zhu, N.; Tian, Z.; Chen, Y.; Sun, B. Application of a trapezoidal fuzzy AHP method for work safety evaluation and early warning rating of hot and humid environments. Saf. Sci. 2012, 50, 228–239. [Google Scholar] [CrossRef]
- Roy, J.; Chatterjee, K.; Bandyopadhyay, A.; Kar, S. Evaluation and selection of medical tourism sites: A rough analytic hierarchy process based multi-attributive border approximation area comparison approach. Expert Syst. 2018, 35, e12232. [Google Scholar] [CrossRef]
- Baidya, R.; Dey, P.K.; Ghosh, S.K.; Petridis, K. Strategic maintenance technique selection using combined quality function deployment, the analytic hierarchy process and the benefit of doubt approach. Int. J. Adv. Manuf. Technol. 2018, 94, 31–44. [Google Scholar] [CrossRef]
- Nazari, S.; Fallah, M.; Kazemipoor, H.; Salehipour, A. A fuzzy inference-fuzzy analytic hierarchy process-based clinical decision support system for diagnosis of heart diseases. Expert Syst. Appl. 2018, 95, 261–271. [Google Scholar] [CrossRef]
- Tseng, P.H.; Cullinane, K. Key criteria influencing the choice of Arctic shipping: A fuzzy analytic hierarchy process model. Marit. Policy Manag. 2018, 45, 422–438. [Google Scholar] [CrossRef]
- Teixeira, Z.; Marques, C.; Mota, J.S.; Garcia, A.C. Identification of potential aquaculture sites in solar saltscapes via the Analytic Hierarchy Process. Ecol. Indic. 2018, 93, 231–242. [Google Scholar] [CrossRef]
- Wu, C.; Liu, G.; Huang, C.; Liu, Q.; Guan, X. Ecological Vulnerability Assessment Based on Fuzzy Analytical Method and Analytic Hierarchy Process in Yellow River Delta. Int. J. Environ. Res. Public Health 2018, 15, 855. [Google Scholar] [CrossRef]
- Jing, M.; Jie, Y.; Shou-yi, L.; Lu, W. Application of fuzzy analytic hierarchy process in the risk assessment of dangerous small-sized reservoirs. Int. J. Mach. Learn. Cybern. 2018, 9, 113–123. [Google Scholar] [CrossRef]
- Chang, Y.; Yang, Y.; Dong, S. Comprehensive sustainability evaluation of high-speed railway (HSR) construction projects based on unascertained measure and analytic hierarchy process. Sustainability 2018, 10, 408. [Google Scholar] [CrossRef]
- Ali, Y.; Butt, M.; sabir, M.; Mumtaz, U.; Salman, A. Selection of suitable site in Pakistan for wind power plant installation using analytic hierarchy process (AHP). J. Control Decis. 2018, 5, 117–128. [Google Scholar] [CrossRef]
- Hamurcu, M.; Alakaş, H.M.; Eren, T. Selection of rail system projects with analytic hierarchy process and goal programming. Sigma J. Eng. Nat. Sci. 2017, 8, 291–302. [Google Scholar]
- Wang, J.J.; Yang, D.L. Using a hybrid multi-criteria decision aid method for information systems outsourcing. Comput. Oper. Res. 2007, 34, 3691–3700. [Google Scholar] [CrossRef]
- Dhull, S.; Narwal, M.S. Prioritizing the Drivers of Green Supply Chain Management in Indian Manufacturing Industries Using Fuzzy TOPSIS Method: Government, Industry, Environment, and Public Perspectives. Process Integr. Optim. Sustain. 2018, 2, 47–60. [Google Scholar] [CrossRef]
- Trivedi, A.; Jha, S.K.; Choudhary, S.; Shandley, R. Fuzzy TOPSIS Multi-criteria Decision Making for Selection of Electric Molding Machine. In Innovations in Computer Science and Engineering; Springer: Singapore, 2019; pp. 325–332. [Google Scholar]
- Gupta, H. Assessing organizations performance on the basis of GHRM practices using BWM and Fuzzy TOPSIS. J. Environ. Manag. 2018, 226, 201–216. [Google Scholar] [CrossRef]
- Daneshvar Rouyendegh, B.; Yildizbasi, A.; Arikan, Ü.Z. Using Intuitionistic Fuzzy TOPSIS (IFT) in Site Selection of Wind Power Plants in TURKEY. Adv. Fuzzy Syst. 2018, 2018, 6703798. [Google Scholar]
- Tang, H.; Shi, Y.; Dong, P. Public blockchain evaluation using entropy and TOPSIS. Expert Syst. Appl. 2019, 117, 204–210. [Google Scholar] [CrossRef]
- Ture, H.; Dogan, S.; Kocak, D. Assessing Euro 2020 Strategy Using Multi-criteria Decision-Making Methods: VIKOR and TOPSIS. Soc. Indic. Res. 2018, 142, 645–665. [Google Scholar] [CrossRef]
- Yadav, S.K.; Kapoor, R. Financial performance ranking of automotive companies in India using TOPSIS method. Int. J. Bus. Excell. 2018, 16, 149–161. [Google Scholar] [CrossRef]
- Çoban, V.; Onar, S.Ç.; Oztaysi, B.; Kahraman, C. Solar energy project selection by using hesitant Pythagorean fuzzy TOPSIS. In Data Science and Knowledge Engineering for Sensing Decision Support; World Scientific: Singapore, 2018; pp. 1107–1114. [Google Scholar]
- Chen, S.J.; Hwang, C.L. Fuzzy Multiple Attribute Decision Making: Methods and Applications; Springer: Berlin, Germany, 1992. [Google Scholar]
- Hwang, C.L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Noureddine, M.; Ristic, M. Route planning for hazardous materials transportation: Multicriteria decision making approach. Decis. Mak. Appl. Manag. Eng. 2019, 2, 66–85. [Google Scholar] [CrossRef]
- Shih, H.S.; Shyir, H.J.; Lee, E.S. An Extension of TOPSIS for Group Decision Making. Math. Comput. Model. 2007, 45, 801–813. [Google Scholar] [CrossRef]
- Kaliszewski, I.; Podkopaev, D. Simple additive weighting—A metamodel for multiple criteria decision analysis methods. Expert Syst. Appl. 2016, 54, 155–161. [Google Scholar] [CrossRef]
- Jain, V.; Sangaiah, A.K.; Sakhuja, S.; Thoduka, N.; Aggarwal, R. Supplier selection using fuzzy AHP and TOPSIS: A case study in the Indian automotive industry. Neural Comput. Appl. 2018, 29, 555–564. [Google Scholar] [CrossRef]
- Venkatesh, V.G.; Zhang, A.; Deakins, E.; Luthra, S.; Mangla, S. A fuzzy AHP-TOPSIS approach to supply partner selection in continuous aid humanitarian supply chains. Ann. Oper. Res. 2018, 283, 1517–1550. [Google Scholar] [CrossRef]
- Bianchini, A. 3PL provider selection by AHP and TOPSIS methodology. Benchmark. Int. J. 2018, 25, 235–252. [Google Scholar] [CrossRef]
- Kaya, A.Y.; Asyali, E.; Ozdagoglu, A. Career decision making in the maritime industry: Research of merchant marine officers using Fuzzy AHP and Fuzzy TOPSIS methods. Sci. J. Marit. Univ. Szczec. 2018, 27, 95–103. [Google Scholar]
- Torkabadi, A.; Mayorga, R. Evaluation of pull production control strategies under uncertainty: An integrated fuzzy AHP-TOPSIS approach. J. Ind. Eng. Manag. 2018, 11, 161–184. [Google Scholar] [CrossRef]
- Jabbarzadeh, A. Application of the AHP and TOPSIS in project management. J. Proj. Manag. 2018, 3, 125–130. [Google Scholar] [CrossRef]
- Karasan, A.; Erdoğan, M.; İlbahar, E. Prioritization of production strategies of a manufacturing plant by using an integrated intuitionistic fuzzy AHP & TOPSIS approach. J. Enterp. Inf. Manag. 2018, 31, 510–528. [Google Scholar]
- Sirisawat, P.; Kiatcharoenpol, T. Fuzzy AHP-TOPSIS approaches to prioritizing solutions for reverse logistics barriers. Comput. Ind. Eng. 2018, 117, 303–318. [Google Scholar] [CrossRef]
- Alakaş, H.M.; Bucak, M.; Kızıltaş, Ş. Selection of Ambulance Supplier Company with AHP-TOPSIS and AHP-VIKOR Methods. Harran Univ. J. Eng. 2019, 4, 93–101. [Google Scholar]
- Özcan, E.C.; Danışan, T.; Eren, T. A mathematical model proposal for maintenance strategies optimization of the most critical electrical equipment groups of hydroelectric power plants. Pamukkale Univ. J. Eng. Sci. 2019, 25, 498–506. [Google Scholar]
- Özcan, E.C.; Ünlüsoy, S.; Eren, T. A combined goal programming-AHP approach supported with TOPSIS for maintenance strategy selection in hydroelectric power plants. Renew. Sustain. Energy Rev. 2017, 78, 1410–1423. [Google Scholar]
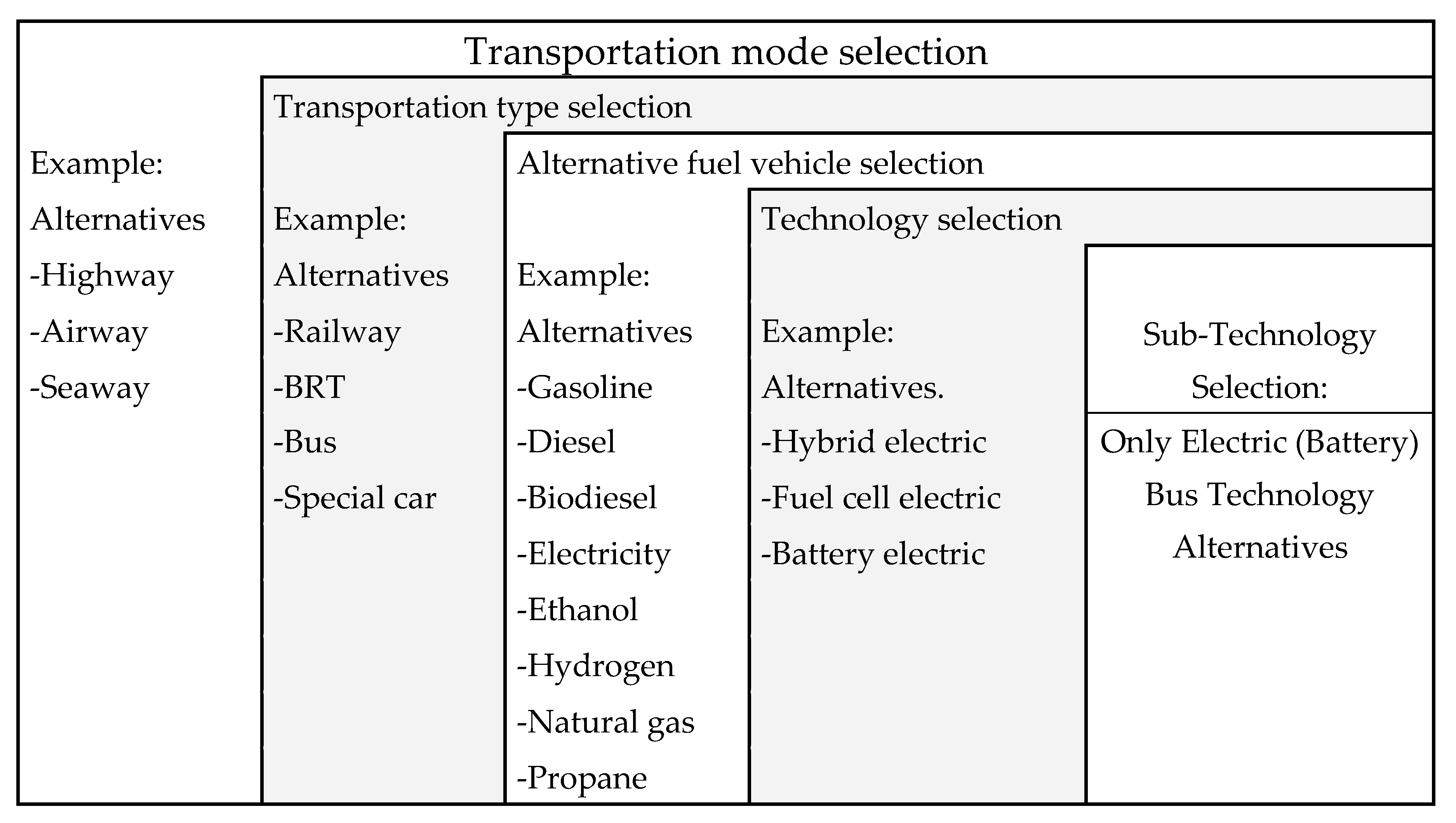
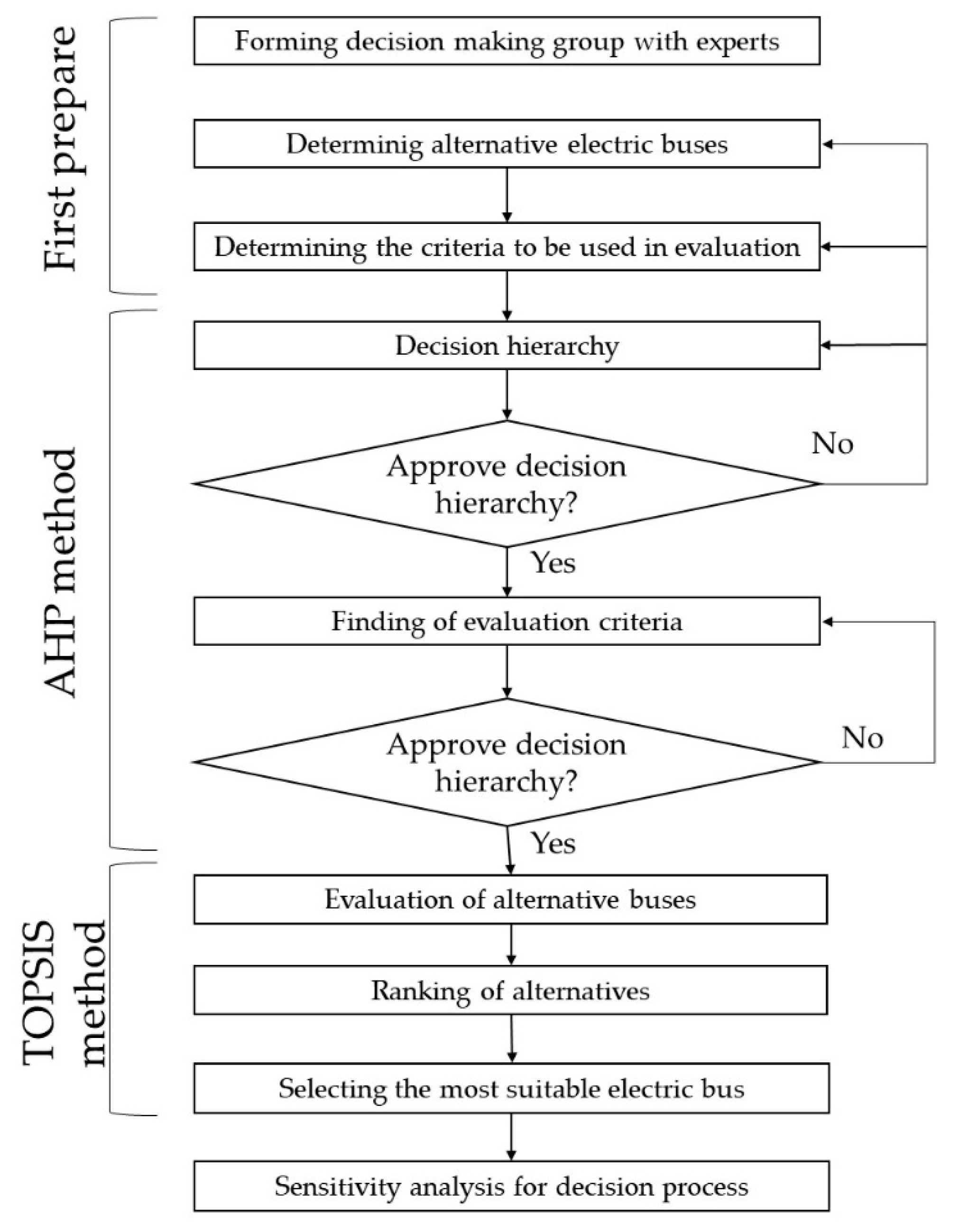
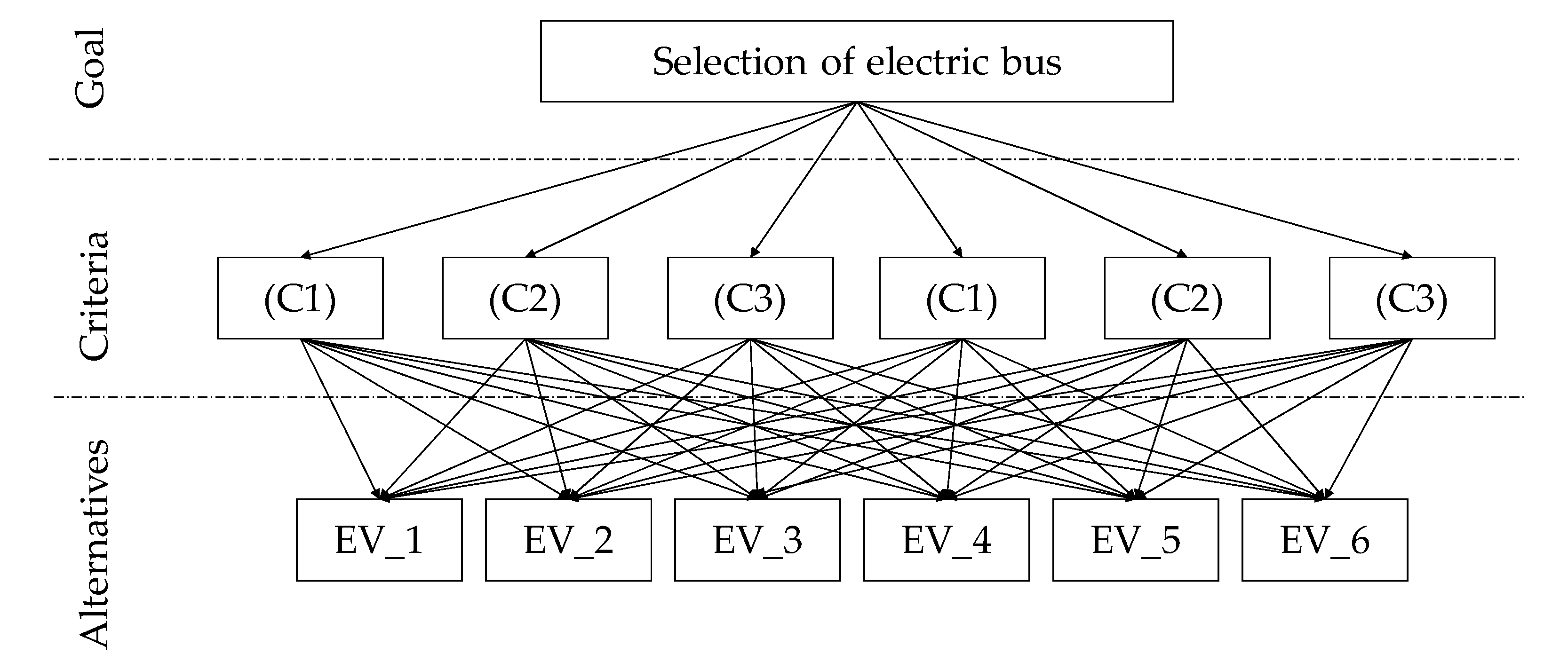
| Author (Year) | Ref. | Objective | Method |
|---|---|---|---|
| Hamurcu and Eren (2020) | [57] | To improve public transportation technology | TOPSIS-MOORA |
| Süt et al. (2019) | [58] | Selection of ring vehicles | AHP-TOPSIS |
| Büyüközkan et al. (2018) | [59] | Selection of sustainable urban transportation alternatives | Fuzzy Choquet integral |
| Dinç et al. (2018) | [60] | Tramway selection | Fuzzy AHP/AHP |
| Mukherjee (2017) | [61] | Selection of alternative fuels for sustainable urban transportation | FMCDM |
| Oztaysi et al. (2017) | [62] | Alternative-fuel technology selection | Interval-valued intuitionistic fuzzy sets |
| Hamurcu and Eren (2017) | [63] | Monorail technology selection | AHP-TOPSIS |
| Onat et al. (2016) | [64] | Ranking the life cycle sustainability performance of alternative vehicle technologies | TOPSIS- fuzzy set |
| Onat et al. (2016) | [65] | Sustainability assessment for optimal distribution of alternative passenger cars | MCDM |
| Lanjewar et al. (2015) | [66] | Fuel selection | Grap theory - AHP |
| Yavuz et al. (2015) | [67] | Evaluation of fuel-vehicle | Hesitant fuzzy logic |
| Petschnig et al. (2014) | [68] | Investigating determinants of alternative fuel vehicle adoption | Structural equation modeling |
| Aydın and Kahraman (2014) | [69] | Bus selection | Fuzzy AHP-VIKOR |
| Vahdani et al. (2011) | [70] | Alternative-fuel buses selection | FMCDM |
| Patil and Heder (2010) | [71] | Investment decision making for alternative fuel public transport buses | MCDM |
| Hsiao et al. (2005) | [72] | Selecting Low Pollutant Emission Bus Systems | FAHP-TOPSIS |
| Tzeng et al. (2005) | [73] | Alternative-fuel buses for public transportation | MCDM |
| Yedla et al. (2003) | [74] | Vehicle selection | AHP |
| Criteria | (C1) | (C2) | (C3) | (C4) | (C5) | (C6) |
|---|---|---|---|---|---|---|
| (C1) | 1.0000 | 0.3333 | 0.3333 | 1.0000 | 0.3333 | 0.3333 |
| (C2) | 3.0000 | 1.0000 | 1.0000 | 1.0000 | 0.3333 | 0.3333 |
| (C3) | 3.0000 | 1.0000 | 1.0000 | 3.0000 | 0.3333 | 0.3333 |
| (C4) | 1.0000 | 1.0000 | 0.3333 | 1.0000 | 0.3333 | 1.0000 |
| (C5) | 3.0000 | 3.0000 | 3.0000 | 3.0000 | 1.0000 | 3.0000 |
| (C6) | 3.0000 | 3.0000 | 3.0000 | 1.0000 | 0.3333 | 1.0000 |
| Criteria | AHP Weights (w) | CR | |
|---|---|---|---|
| (C1) | 0.0710 | 0.0905 | |
| (C2) | 0.1196 | ||
| (C3) | 0.1529 | CI = 0.11224 | |
| (C4) | 0.1014 | ||
| (C5) | 0.3428 | RI = 1.24 | |
| (C6) | 0.2123 |
| Characteristics | Alternatives | ||||||
|---|---|---|---|---|---|---|---|
| Unit | EV_1 | EV_2 | EV_3 | EV_4 | EV_5 | EV_6 | |
| Speed | km/h | 72 | 68.4 | 90 | 80 | 75 | 75 |
| Passenger capacity | --- | 50 | 58 | 50 | 57 | 90 | 136 |
| Range | km | 200 | 200 | 280 | 50 | 280 | 300 |
| Max. Power | kW | 360 | 360 | 103 | 200 | 250 | 250 |
| Battery Capacity | kWh | 350 | 394 | 170 | 200 | 230 | 346 |
| Charging Time | h | 2 | 1.25 | 7 | 2 | 5 | 7 |
| Alternatives | Criteria | |||||
|---|---|---|---|---|---|---|
| K1 | K2 | K3 | K4 | K5 | K6 | |
| EV_1 | 72 | 50 | 200 | 360 | 360 | 2 |
| EV_2 | 68.4 | 58 | 200 | 360 | 394 | 1.25 |
| EV_3 | 90 | 50 | 280 | 103 | 170 | 7 |
| EV_4 | 80 | 57 | 50 | 200 | 200 | 2 |
| EV_5 | 75 | 90 | 280 | 250 | 230 | 5 |
| EV_6 | 75 | 136 | 300 | 250 | 346 | 7 |
| Alternatives | Criteria | |||||
|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | |
| The weight of AHP | 0.0710 | 0.1196 | 0.1529 | 0.1014 | 0.3428 | 0.2123 |
| EV_1 | 0.027 | 0.031 | 0.053 | 0.055 | 0.170 | 0.037 |
| EV_2 | 0.026 | 0.035 | 0.053 | 0.055 | 0.186 | 0.023 |
| EV_3 | 0.034 | 0.031 | 0.075 | 0.016 | 0.080 | 0.129 |
| EV_4 | 0.030 | 0.035 | 0.013 | 0.031 | 0.095 | 0.037 |
| EV_5 | 0.028 | 0.055 | 0.075 | 0.038 | 0.109 | 0.092 |
| EV_6 | 0.028 | 0.083 | 0.080 | 0.038 | 0.163 | 0.129 |
| Alternatives | Rank | |||
|---|---|---|---|---|
| EV_1 | 0.0630 | 0.1404 | 0.6902 | 2 |
| EV_2 | 0.0552 | 0.1601 | 0.7434 | 1 |
| EV_3 | 0.1637 | 0.0618 | 0.2741 | 6 |
| EV_4 | 0.1264 | 0.0946 | 0.4281 | 5 |
| EV_5 | 0.1092 | 0.0839 | 0.4344 | 4 |
| EV_6 | 0.1099 | 0.1210 | 0.5241 | 3 |
| Alternatives | Weighted CCj | Weighted Ranking | Unweighted CCj | Unweighted Ranking |
|---|---|---|---|---|
| EV_1 | 0.6902 | 2 | 0.5855 | 2 |
| EV_2 | 0.7434 | 1 | 0.6257 | 1 |
| EV_3 | 0.2741 | 6 | 0.3339 | 6 |
| EV_4 | 0.4281 | 5 | 0.3994 | 5 |
| EV_5 | 0.4344 | 4 | 0.5198 | 4 |
| EV_6 | 0.5241 | 3 | 0.5669 | 3 |
| Scenario | Weight Criteria | Rate of Change | New Weight Criteria |
|---|---|---|---|
| S1 | C1 = 0.0710 | 1.25 × C1 | 0.0888 |
| S2 | C2 = 0.1196 | 1.25 × C2 | 0.1495 |
| S3 | C3 = 0.1529 | 1.25 × C3 | 0.1911 |
| S4 | C4 = 0.1014 | 1.25 × C4 | 0.1268 |
| S5 | C5 = 0.3428 | 1.25 × C5 | 0.4285 |
| S6 | C6 = 0.2123 | 1.25 × C6 | 0.2654 |
| S7 | C1 = 0.0710 | 1.50 × C1 | 0.1065 |
| S8 | C2 = 0.1196 | 1.50 × C2 | 0.1794 |
| S9 | C3 = 0.1529 | 1.50 × C3 | 0.2294 |
| S10 | C4 = 0.1014 | 1.50 × C4 | 0.1521 |
| S11 | C5 = 0.3428 | 1.50 × C5 | 0.5142 |
| S12 | C6 = 0.2123 | 1.50 × C6 | 0.3185 |
| S13 | C1 = 0.0710 | 1.75 × C1 | 0.1243 |
| S14 | C2 = 0.1196 | 1.75 × C2 | 0.2093 |
| S15 | C3 = 0.1529 | 1.75 × C3 | 0.2676 |
| S16 | C4 = 0.1014 | 1.75 × C4 | 0.1775 |
| S17 | C5 = 0.3428 | 1.75 × C5 | 0.5999 |
| S18 | C6 = 0.2123 | 1.75 × C6 | 0.3715 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamurcu, M.; Eren, T. Electric Bus Selection with Multicriteria Decision Analysis for Green Transportation. Sustainability 2020, 12, 2777. https://doi.org/10.3390/su12072777
Hamurcu M, Eren T. Electric Bus Selection with Multicriteria Decision Analysis for Green Transportation. Sustainability. 2020; 12(7):2777. https://doi.org/10.3390/su12072777
Chicago/Turabian StyleHamurcu, Mustafa, and Tamer Eren. 2020. "Electric Bus Selection with Multicriteria Decision Analysis for Green Transportation" Sustainability 12, no. 7: 2777. https://doi.org/10.3390/su12072777
APA StyleHamurcu, M., & Eren, T. (2020). Electric Bus Selection with Multicriteria Decision Analysis for Green Transportation. Sustainability, 12(7), 2777. https://doi.org/10.3390/su12072777





