Concreteness Fading Strategy: A Promising and Sustainable Instructional Model in Mathematics Classrooms
Abstract
1. Introduction
2. Theoretical Backgrounds
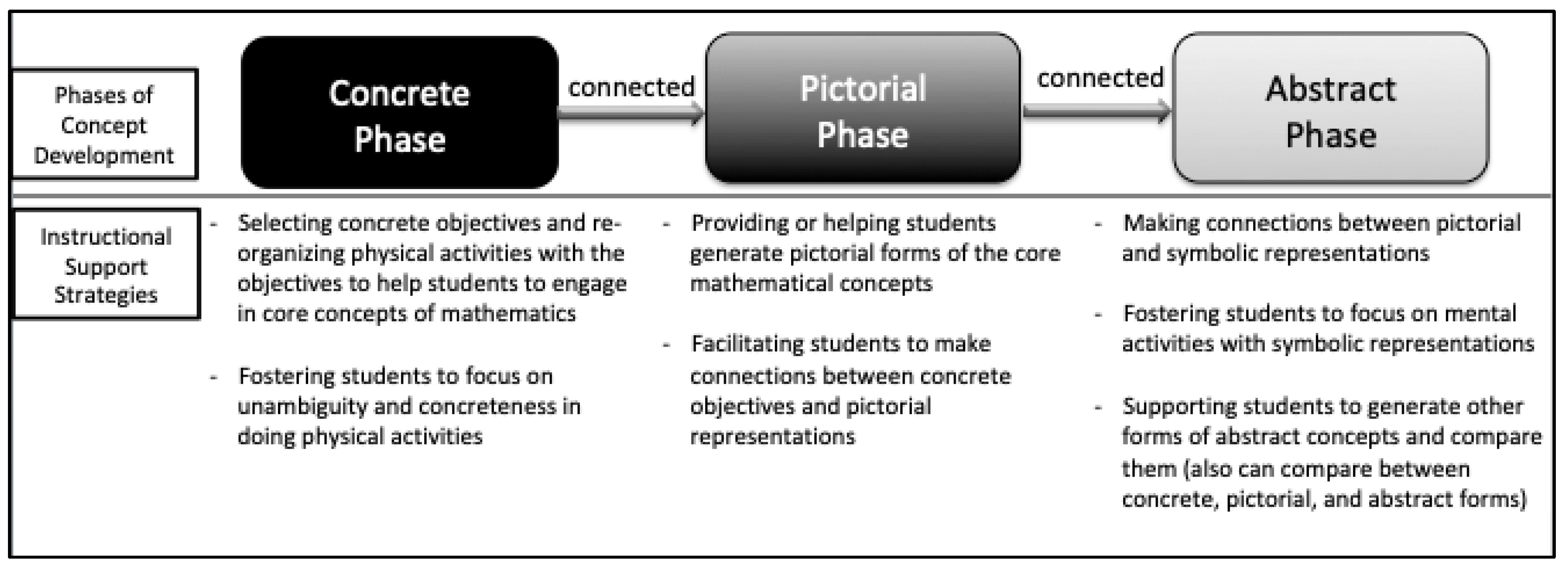
2.1. Concreteness Fading
2.2. Theoretical Framework
- (1)
- Teachers support students in interpreting their activities with manipulatives in mathematically meaningful ways (e.g., generating/providing graphical representations for concrete objectives); and
- (2)
- Teachers delete superficial features of physical activities whenever they occur in the concrete phase.
- (1)
- Introduce symbolic forms of mathematical concepts;
- (2)
- Support students in interpreting their activities with visual representations in mathematically meaningful ways; and
- (3)
- Delete superficial and unrelated features from activities with visual representations by highlighting the core structures of concepts.
3. Methods: The Empirical Case to Support Concreteness Fading Strategies
3.1. Participants and Data Sources for the Case
3.2. Context of the Case
3.3. Data Analysis
4. Results
4.1. Textbook: Abstract Instruction
4.2. Activity Sheet: Concreteness Fading Strategies
4.3. Concreteness Fading Instructional Strategies
4.3.1. Instructional Strategies in the Opening Phase
4.3.2. Instructional Strategies in Concreteness Fading Phases
- T: Can you remember how to represent 1 + 2 + 3 + 4 using blocks?S1: Yes.T: How did you do that?S1: We first made one stair model (see Figure 7) and added another model upside down. Then, we calculated the area of all blocks using the rectangle area model. Then divided by 2.T: That’s right. Can you do it in similar way for?S2: We tried, but it is not that simple.T: Then, we can dofirst. What does look like? What about ?S2: A cube? // S1: A rectangle? Square?T: Yes, a cube. You will reorganize these blocks, but the hint is that you will do this in the plane rather than thinking of a 3-D structure.
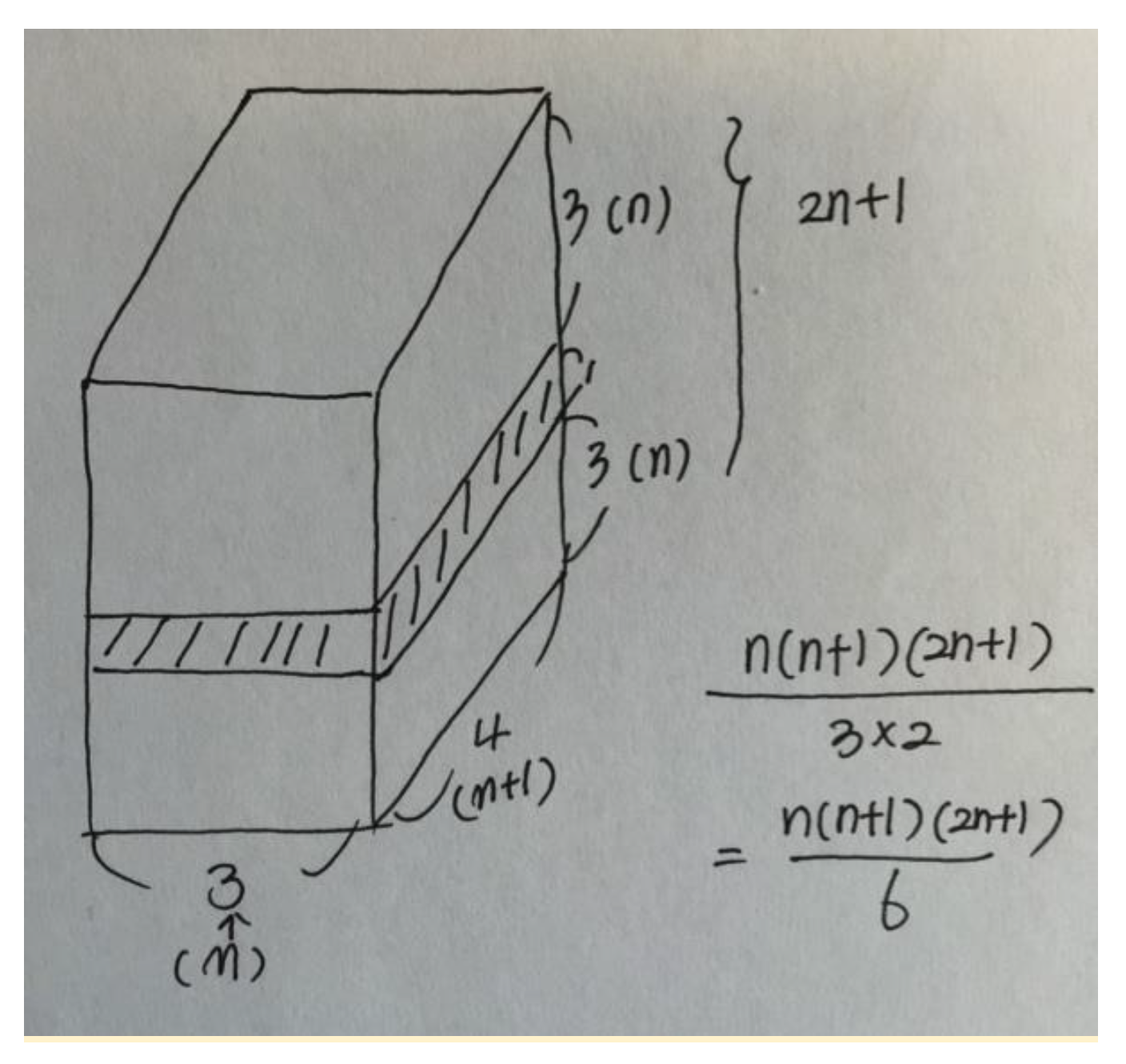
- T: So, are you disassembling the blocks of ? Then, what shape are they going to be in the plane?Students: Square!T: Yes, it looks like a square (see second diagram in Figure 8). Then, what is the length of one side of the square?S1: Oh, n? //S2: n + 1? (students had already started thinking of the generalization from the 4th model of the sum)T: That’s right. A square with n-length. Then, what about the re-assembled square? What will be the length of one side of this square (see the very right diagram in Figure 8)?S2: Oh, it’s the sum of n.T: Yes, it is going to be 1 + 2 + 3 +…+ n. Then, what will be the area of the square?Students: Wow, it’s square of (1 + 2 + 3 + n).
5. Conclusions and Discussion
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Activity Sheet that Ms. K Created and Provided to Students

Appendix B. The Visual Hint Sheet that Ms. K Provided to Students Who Struggled

References
- National Council of Teachers of Mathematics. Principles and Standards of School Mathematics; NCTM: Reston, VA, USA, 2000. [Google Scholar]
- National Governors Association Center for Best Practices and Council of Chief State School Officers. Common Core State Standards for Mathematics; National Governors Association Center for Best Practices and Council of Chief State School Officers: Washington, DC, USA, 2010. [Google Scholar]
- Freudenthal, H. Didactical Phenomenology of Mathematical Structures; Reidel: Dordrecht, The Netherlands, 1983. [Google Scholar]
- Bruner, J.S. Toward a Theory of Instruction; Harvard University Press: Cambridge, MA, USA, 1966. [Google Scholar]
- Van den Heuvel-Panhuizen, M.; Drijvers, P. Realistic mathematics education. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Kim, N.; Na, G.; Park, K.; Lee, K.; Jung, Y. Mathematics Curriculum and Lesson Research for Preservice and Inservice Teachers; Kyeongmoonsa: Seoul, Korea, 2017. [Google Scholar]
- Hwang, H.; Na, G.; Choi, S.; Park, K.; Lim, J.; Seo, D. New Theories in Mathematics Education; Moonemsa: Seoul, Korea, 2012. [Google Scholar]
- Butler, F.M.; Miller, S.P.; Crehan, K.; Babbitt, B.; Pierce, T. Fraction instruction for students with mathematics dis- abilities: Comparing two teaching sequences. Learn. Disabil. Res. Pract. 2003, 18, 99–111. [Google Scholar] [CrossRef]
- Flores, M.M.; Hinton, V.M.; Strozier, S.D.; Terry, S.L. Using the concrete-representational-abstract sequence and the strategic instruction model to teach computation to students with autism spectrum disorders and developmental disabilities. Educ. Train. Autism Dev. Disabil. 2014, 49, 547–554. [Google Scholar]
- Chang, S.H.; Lee, N.H.; Koay, P.L. Teaching and learning with concrete-pictorial-abstract sequence: A proposed model. Math. Educ. 2017, 17, 1–28. [Google Scholar]
- Fyfe, E.R.; McNeil, N.M.; Son, J.Y.; Goldstone, R.L. Concreteness Fading in Mathematics and Science Instruction: A Systematic Review. Educ. Psychol. Rev. 2014, 26, 9–25. [Google Scholar] [CrossRef]
- Goldstone, R.L.; Son, J.Y. The transfer of scientific principles using concrete and idealized simulations. J. Learn. Sci. 2005, 14, 69–110. [Google Scholar] [CrossRef]
- McNeil, N.M.; Fyfe, E.R. “Concreteness fading” promotes transfer of mathematical knowledge. Learn. Instr. 2012, 22, 440–448. [Google Scholar] [CrossRef]
- Ottmar, E.; Landy, D. Concreteness Fading of Algebraic Instruction: Effects on Learning. J. Learn. Sci. 2017, 26, 51–78. [Google Scholar] [CrossRef]
- Ainsworth, S.; Bibby, P.A.; Wood, D. Examining the effects of different multiple representational systems in learning primary mathematics. J. Learn. Sci. 2002, 11, 25–61. [Google Scholar] [CrossRef]
- Hiebert, J.; Grouws, D.A. The Effects of Classroom Mathematics Teaching on Students’ Learning. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F., Ed.; Information Age: Charlotte, NC, USA, 2007; pp. 371–404. [Google Scholar]
- Hiebert, J.; Gallimore, R.; Garnier, H.; Givvin, K.B.; Hollingsworth, H.; Jacobs, J.; Stigler, J. Teaching mathematics in seven countries: Results from the TIMSS 1999 video study. Educ. Stat. Q. 2003, 5, 7–15. [Google Scholar]
- Freudenthal, H. Revisiting Mathematics Education; Kluwer Academic: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Treffers, A. Wiskobas Doelgericht [Wiskobas Goal- Directed]; IOWO: Utrecht, The Netherlands, 1978. [Google Scholar]
- Fyfe, E.R.; McNeil, N.M.; Borjas, S. Benefits of “concreteness fading” for children’s mathematics understanding. Learn. Instr. 2015, 35, 104–120. [Google Scholar] [CrossRef]
- Flores, M.M. Using the concrete-representational-abstract sequence to teach subtraction with regrouping to students at risk for failure. Remedial Spec. Educ. 2010, 31, 195–207. [Google Scholar] [CrossRef]
- Medin, D.L.; Goldstone, R.L.; Gentner, D. Respects for similarity. Psychol. Rev. 1993, 100, 254–278. [Google Scholar] [CrossRef]
- Son, J.Y.; Smith, L.B.; Goldstone, R.G.; Leslie, M. The importance of being interpreted: Grounded words and children’s relational reasoning. Front. Dev. Psychol. 2012, 3, 45. [Google Scholar] [CrossRef] [PubMed]
- Chi, M.T.H.; Feltovich, P.J.; Glaser, R. Categorization and representation of physics problems by experts and novices. Cognit. Sci. 1981, 5, 121–152. [Google Scholar] [CrossRef]
- Woo, J.; Park, K.; Lee, J.; Park, K.; Kim, N.; Lim, J.; Kwon, S.; Nam, J.; Kim, J.; Kang, H.; et al. High School Mathematics I; Doosan Dong-A: Seoul, Korea, 2014. [Google Scholar]
- Nathan, M.J. Rethinking formalisms in formal education. Educ. Psychol. 2012, 47, 125–148. [Google Scholar] [CrossRef]
- Kilpatrick, J.; Swafford, J.; Findell, B. (Eds.) Adding It up: Helping Children Learn. Mathematics; National Academy Press: Washington, DC, USA, 2001. [Google Scholar]
- Donovan, A.M.; Fyfe, E. Connecting Concrete Objects and Abstract Symbols Promotes Children’s Mathematics Learning. 2019. Available online: https://psyarxiv.com/ye2j6 (accessed on 26 February 2020).
- Fyfe, E.R.; Nathan, M.J. Making “concreteness fading” more concrete as a theory of instruction for promoting transfer. Educ. Rev. 2019, 71, 403–422. [Google Scholar] [CrossRef]
- Kieran, C. Learning and teaching of algebra at the middle school through college levels: Building meaning for symbols and their manipulation. In Second Handbook of Research on Mathematics Teaching and Learning; Lister, F.K., Ed.; NCTM: Reston, VA, USA, 2007; pp. 707–762. [Google Scholar]
- Brown, M.C.; Mcneil, N.M.; Glenberg, A.M. Using concreteness in education: Real problems, potential solutions. Child. Dev. Perspect. 2009, 3, 160–164. [Google Scholar] [CrossRef]
- Marley, S.C.; Carbonneau, K.J. Future directions for theory and research with instructional manipulatives: Commentary on the special issue papers. Educ. Psychol. Rev. 2014, 26, 91–100. [Google Scholar] [CrossRef]
- Korean Ministry of Education. Mathematics Curriculum; No. 2015-74 [Supplement 8]; Notification of the Ministry of Education: Seoul, Korea, 2015.








| Concreteness Fading Phases | Concrete Phase | Connecting Phase | Pictorial Phase | Connecting Phase | Abstract Phase |
|---|---|---|---|---|---|
| Step-by-step approach. Representation of 1 + 2 + 3 using magnetic blocks first.  | Support in representing 1 + 2 + 3 + 4 both using a pair of blocks of 1 + 2 + 3 + 4 and implicitly expanding it into an abstract representation. | Asking students how to represent 1 + 2 + 3 +…+ n using a diagram. One student represents the exemplary diagram: 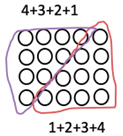 | Supporting students in expanding this diagram to generalize it to 1 + 2 + 3 + … + n by asking facilitating question, “How can we represent the finite sums of natural numbers using this diagram? Can you generalize how many dots are in the diagram?” | Students use two ways to represent the algebraic forms of : (a) (b) Ms. K summarizes that these two algebraic forms are the same as . | |
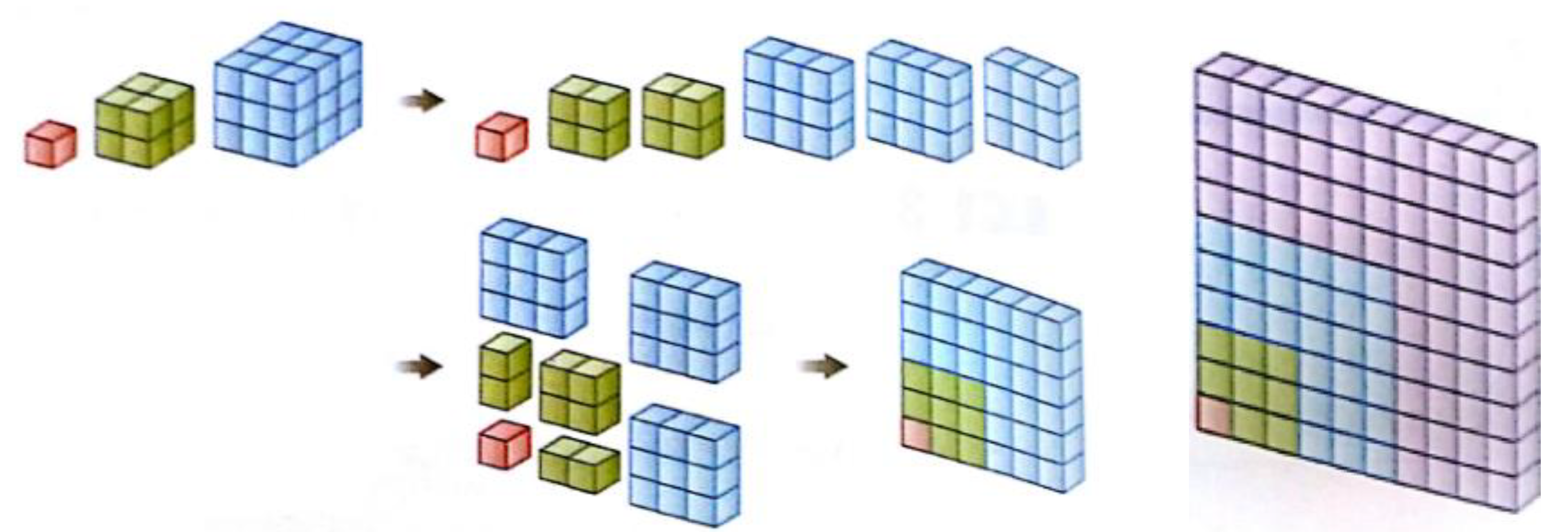
| Step-by-step approach. Representation of using magnetic blocks first.  | Representing both using blocks and implicitly expanding it into an abstract representation. →  | Asking students how to represent using re-organizing blocks. Providing a visual hint sheet for struggling students. (Figure A2) | Supporting students in interpreting their activities with magnetic blocks or the visual hint sheet. Highlighting how the re-organized blocks can be represented in algebraic forms. | Students use an algebraic form, for representation by making connections between blocks, visual diagrams and the formula. They first figure out that the re-organized blocks represent (1 + 2 + … + n)x(1 + 2 + … + n), i.e., . Ms. K summarizes the connection by rephrasing the students’ presentation (Figure 10). | |
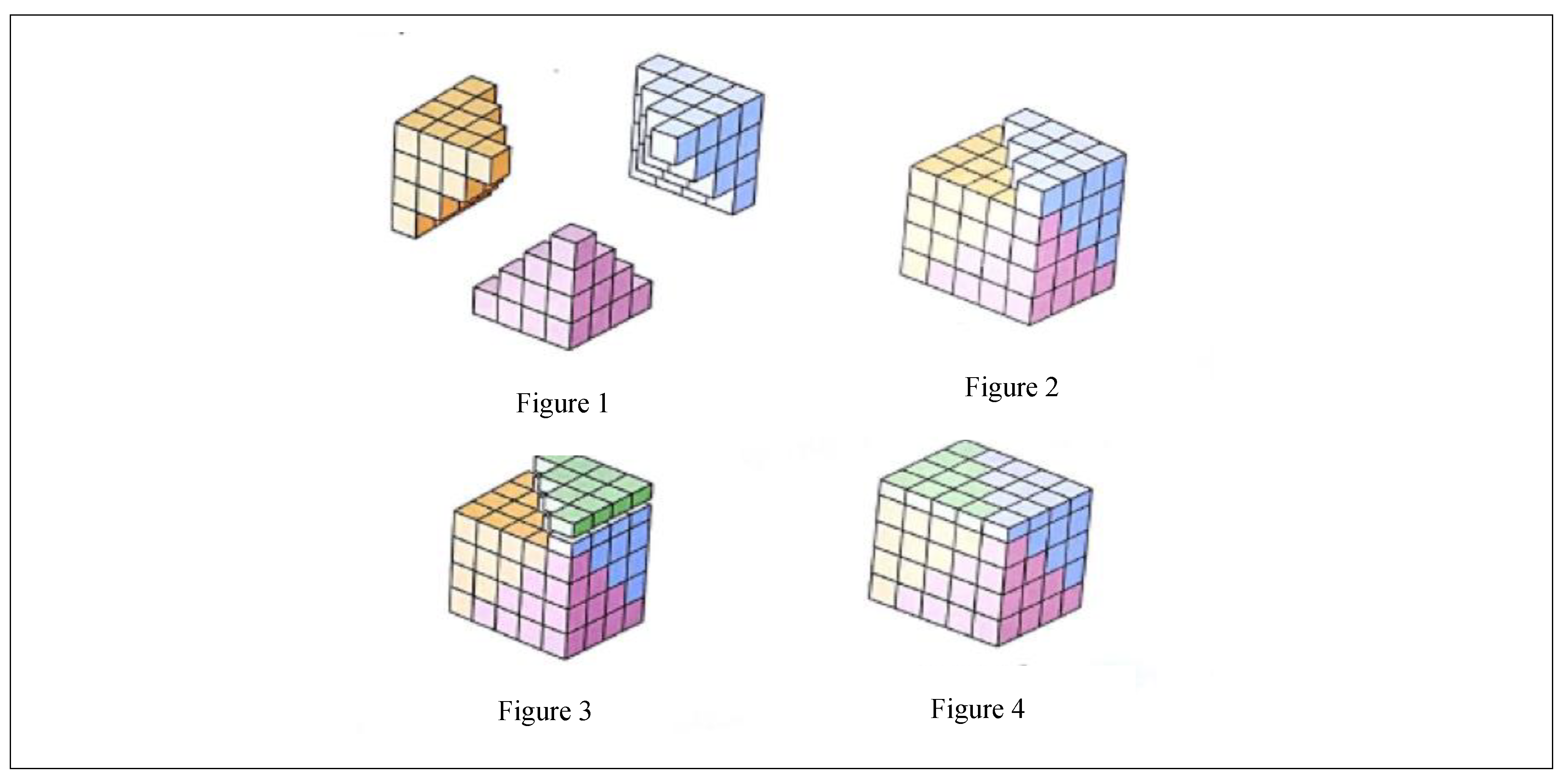
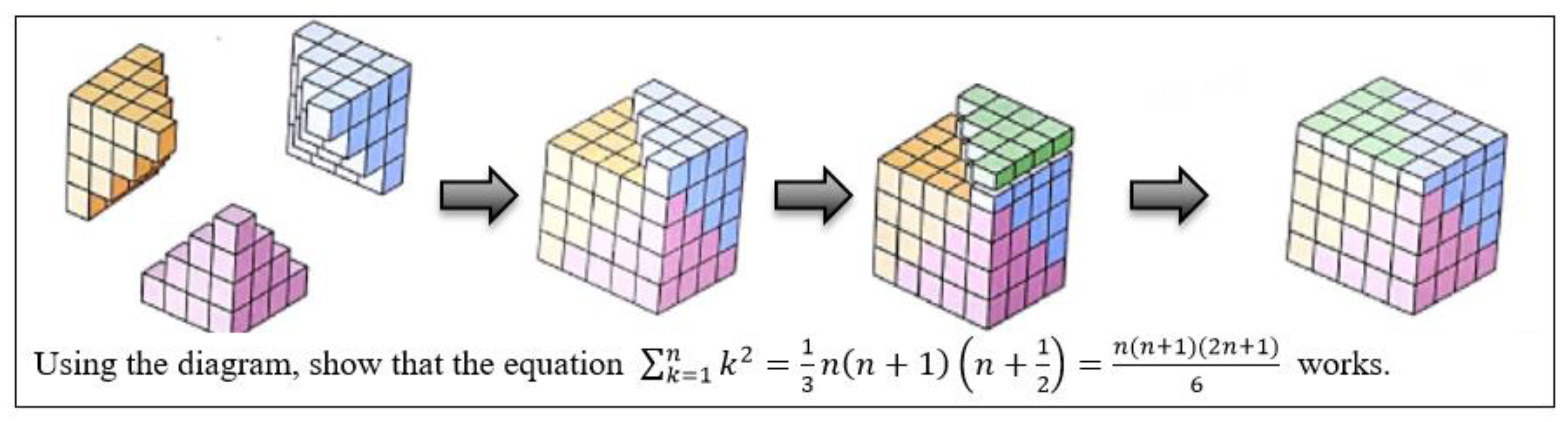
| Step-by-step approach. Representation of using magnetic blocks first.  | Representing both using three pairs of blocks of and implicitly expanding it into an abstract representation. →  | Asking students how to represent using complied three sets of blocks. Providing a visual hint sheet for struggling students. (Figure A1) | Supporting students in interpreting their activities with magnetic blocks or the visual hint sheet. Selecting a different model from the small group works to present to the whole group: A student presents her group’s model that is different from the hint sheet using a diagram (Figure 12) | Students use two ways of representing algebraic forms of : (a) (b) Several students demonstrate their understanding of connections among blocks, visuals and abstract forms of | |
| Instructional support strategies | Ms. K focuses on sense-making of each concept by supporting students in operating the magnetic blocks (i.e., concrete objectives and physical activities) with step-by-step questions. | Ms. K supports her students in representing simpler concepts with magnetic blocks, and also in interpreting their activities with manipulatives in mathematically meaningful ways. | Ms. K focuses on concept development and meaningful support by providing visual representations, especially when students are struggling with making connections between concrete activities and abstract representations. | Ms. K guides students in deleting superficial features from manipulatives or visual presentations. She highlights core structures of mathematical concepts. | Ms. K fosters students in using abstract representations of the concept by supporting generalizations and core abstract concepts. She also supports students in generating different algebraic forms of a concept from their concrete and visual representations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.-j. Concreteness Fading Strategy: A Promising and Sustainable Instructional Model in Mathematics Classrooms. Sustainability 2020, 12, 2211. https://doi.org/10.3390/su12062211
Kim H-j. Concreteness Fading Strategy: A Promising and Sustainable Instructional Model in Mathematics Classrooms. Sustainability. 2020; 12(6):2211. https://doi.org/10.3390/su12062211
Chicago/Turabian StyleKim, Hee-jeong. 2020. "Concreteness Fading Strategy: A Promising and Sustainable Instructional Model in Mathematics Classrooms" Sustainability 12, no. 6: 2211. https://doi.org/10.3390/su12062211
APA StyleKim, H.-j. (2020). Concreteness Fading Strategy: A Promising and Sustainable Instructional Model in Mathematics Classrooms. Sustainability, 12(6), 2211. https://doi.org/10.3390/su12062211





