1. Introduction
The future projections for climate change augur severe scenarios for extreme climate events, especially flooding. The predictions indicate increases of frequency in high flows by 10%–30%, while also increasing in magnitude as well [
1,
2]. The Climate Research Foundation (FIC) as part of the RESCCUE project has studied the changes in terms of rainfall intensity for two European cities, Barcelona and Bristol, with an expected increase of up to 40% [
3]. An increase in the rainfall intensity will provoke consequently higher flood depths in the surface of the cities because of the exceedance of the drainage and sewer system capacity. Consequently, current flood prone areas will be covered by higher depths and new flood prone areas will arise [
4], which will increase the likelihood of affecting critical city infrastructures.
As critical infrastructures, the electric power systems are considered the backbone of the city due to the increase of power-dependent utilities and devices. The water supply through water pumps, telecommunication centers, transport (e.g., tramway, underground, electric buses, traffic lights, etc.), and a large list of city services depend on the electrical infrastructure [
5], therefore a general system failure may end in the collapse of a city until emergency equipment is installed [
6]. Due to this, the resilience of cities is of extreme relevance.
Like any other kind of infrastructure, the electrical was designed considering certain return periods of events that could affect the system at any point, and they were protected and isolated accordingly. However, the problem arises when the intensity of the considered return period increases due to climate change, generating unexpected extreme occurrences that increase the likelihood of damaging the infrastructures that are not prepared for it [
2].
Taking into account the aforementioned points and mixing all ideas together, a plausible problem is presented; the increased probability of electric blackout provoked by flooding due to more frequent extreme rainfall events caused by climate change, and thus generating the effect of cascading failures in other urban services.
Although the problem presented above has not been extensively studied, there exist some other investigations studying similar problems but following different perspectives or focusing either on the impact assessment or on economical assessment. The most complete study found during the literature review was a GIS-based method assessing electrical grid and gas network through fragility curves focused on seismic events [
7]. When focusing on flooding events a methodology to assess the flooding impact probability of the electrical assets was proposed in [
8] where through spatial network models identified and compared the risk of critical infrastructures on flooded lands. Also, [
9] proposed a method to investigate quantitatively the robustness of the grid against flooding events based on the Hazus methodology [
10] providing a detailed risk analysis. The last relevant method found during the literature review was [
11], presenting an integrated modelling framework combining geospatial information on infrastructure and flood hazard and geospatial modelling of businesses and economic activities. Additionally, in [
12,
13] was proposed a methodology to assess the economic losses caused by flooding events to electrical assets that in fact, has been used partially on this study.
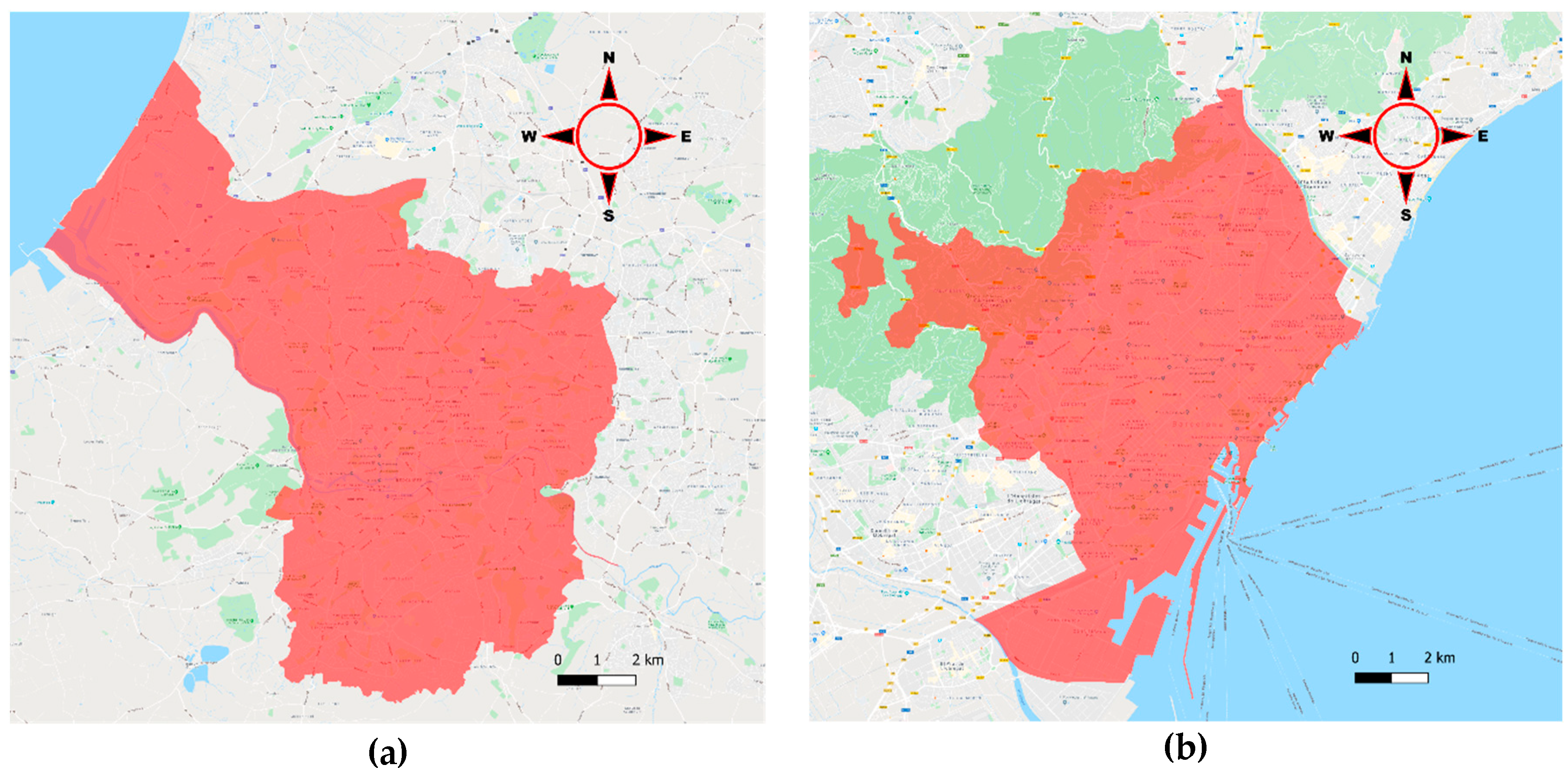
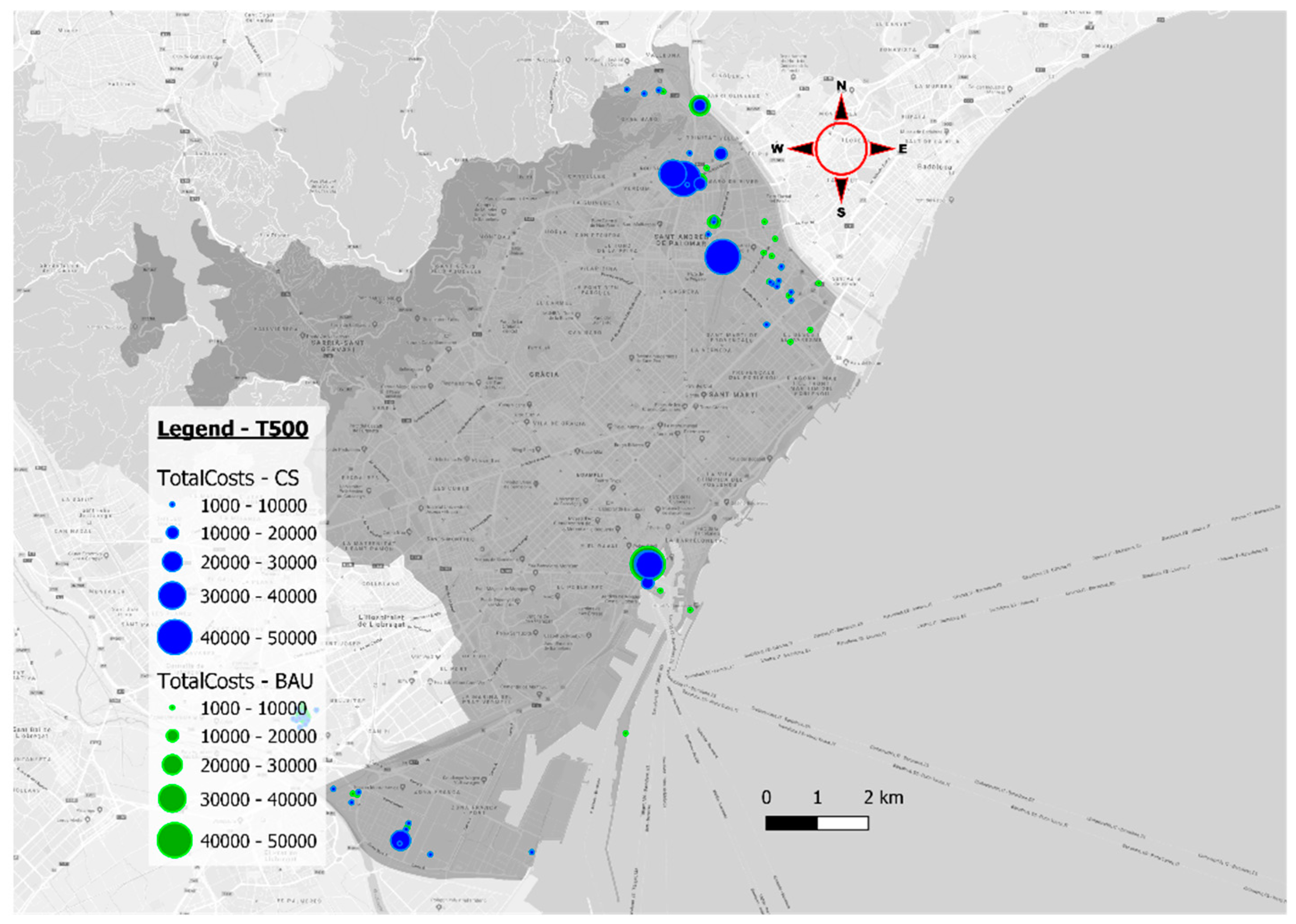
In this context, this study aims to identify first the hazards and to assess later the potential impacts caused in the electrical sector in Barcelona and Bristol cities that inevitably affect the population of the cities. This impact assessment is carried out to evaluate the probability of power system failures after a flooding event occurs, which allows identification of the most critical locations in order to implement, if necessary, adaptation measures effectively. The impact assessment will also allow an estimate of the potential cost of the energy lost during blackout periods, and damages caused to the electrical assets. Therefore, an analysis of the consequences caused by flooding to population and the electrical Distribution Systems Operators (DSO) considering failures within the electrical sector is presented here, together with the description of a novel method to assess risk and estimate losses in the distribution centers (DCs) of the power network (example given in
Figure 1). The application of these tools has been carried out for the city of Barcelona and Bristol.
The paper starts with an overview of the study areas and the data used to later explain the probabilistic GIS-based method developed and how the data was used to conduct the DC risk analysis and its corresponding risk monetization. The results are presented in different sub-sections discussing later all the details to finally conclude with the main findings and evidence drawn.
2. Study Areas and Data Used
The considered case studies have been two different cities, Bristol (UK) (
Figure 2a) and Barcelona (Spain) (
Figure 2b). Both cities are very different in almost every possible feature to consider, in the city design as house grouping, drainage systems, terrestrial topography, electrical grid, etc. and even more different in the weather conditions. Although they have a similar areal extent (Bristol 111 km
2 and Barcelona 102 km
2) the population density in Barcelona is three times bigger than in Bristol, having around 1,621,000 inhabitants while Bristol has only 460,000. However, the studied area for this energy analysis in Barcelona has been reduced up to 33% due to key data availability, therefore considering only the inhabitants living in the main city area (i.e., 326,000 inhabitants).
2.1. The Bristol Context
Bristol is recognized as one of the most susceptible cities within the top 10 Flood risk areas in the UK [
14]. This is mainly caused by the influence of the tidal river “Avon”, directly connected to the sea by mean of the “Severn Estuary”, where tides have a great effect on the river water depth. This tidal effect is transmitted to a lesser extent to the other rivers that flow into the river Avon. Bristol has undergone severe floods caused by the combination of storm surges and spring tides, but also others provoked by heavy rainfall.
Some great historical floods have occurred in Bristol throughout time. The first example is an historical flood that took place in 1607 when the death of around 2000 people was estimated. A second more recent example took place in 1896 when a tidal flood event caused a 1m water depth in the city center, and in 1968 when a combination of a great rainfall with a river flood event killed 7 people and flooded around 800 properties in the Bristol area. Also, an extreme rainfall event in 2012 caused the flooding of 25 properties due to surface water flooding [
14]. All these examples give an idea of the flooding experienced in Bristol and present a real problem that this city has suffered over time.
2.1.1. Bristol Flooding Data
From the flooding problems occurred in the past, some city plans have been born and the flooding records act as a great tool to be used in studies to try to assess the risk to the city in any sector, which in this case will be the electrical sector.
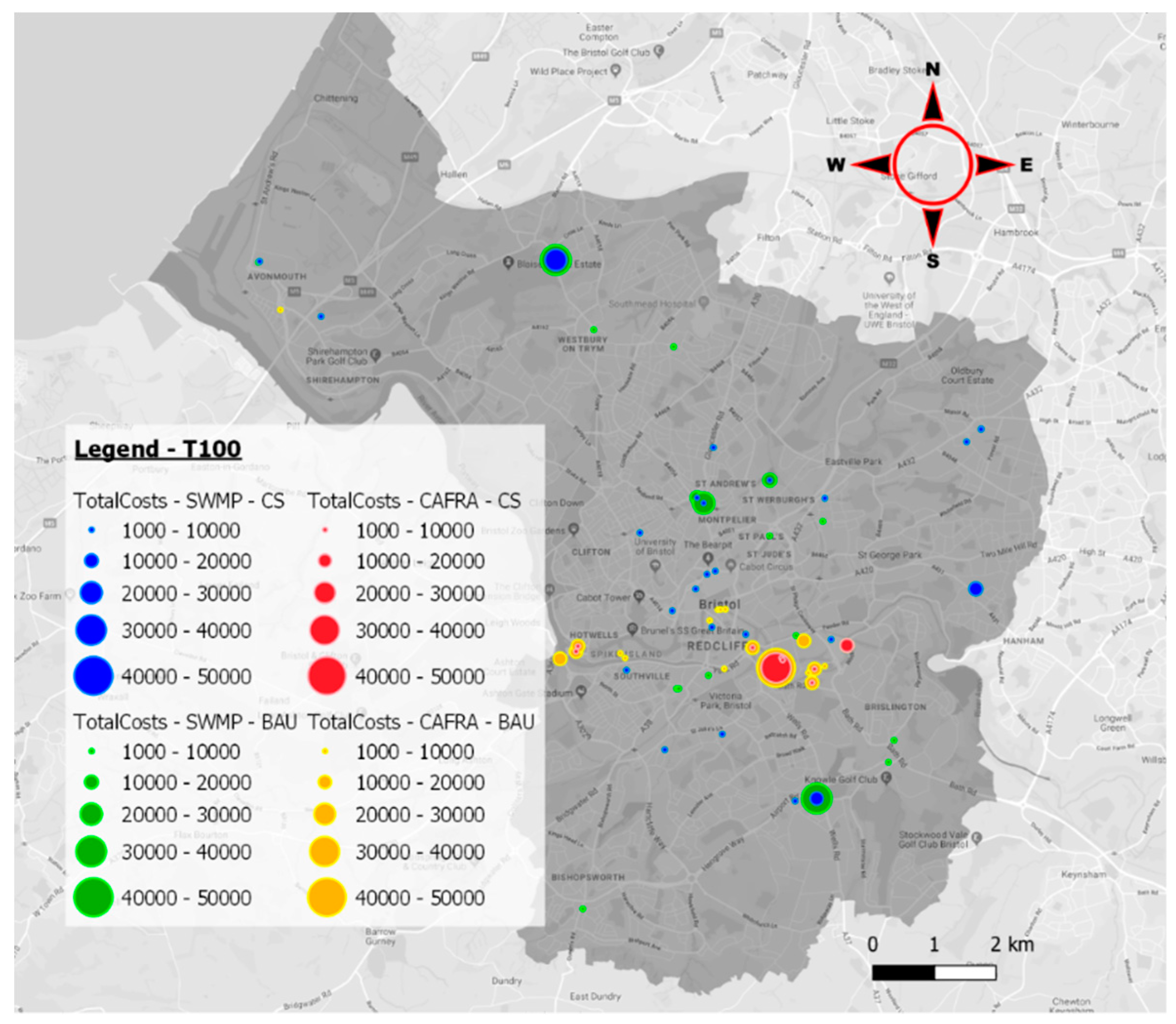
The study carried out in this paper has used two of the most recent city studies conducted by Bristol City Council; the Central Area Flood Risk Assessment (CAFRA) focused on the river and tidal flooding and the Surface Water Management Plan (SWMP), focused on the flooding caused by rainfall extreme events. In
Table 1, the return periods given for each study and scenario are introduced.
2.1.2. Bristol Electrical Data
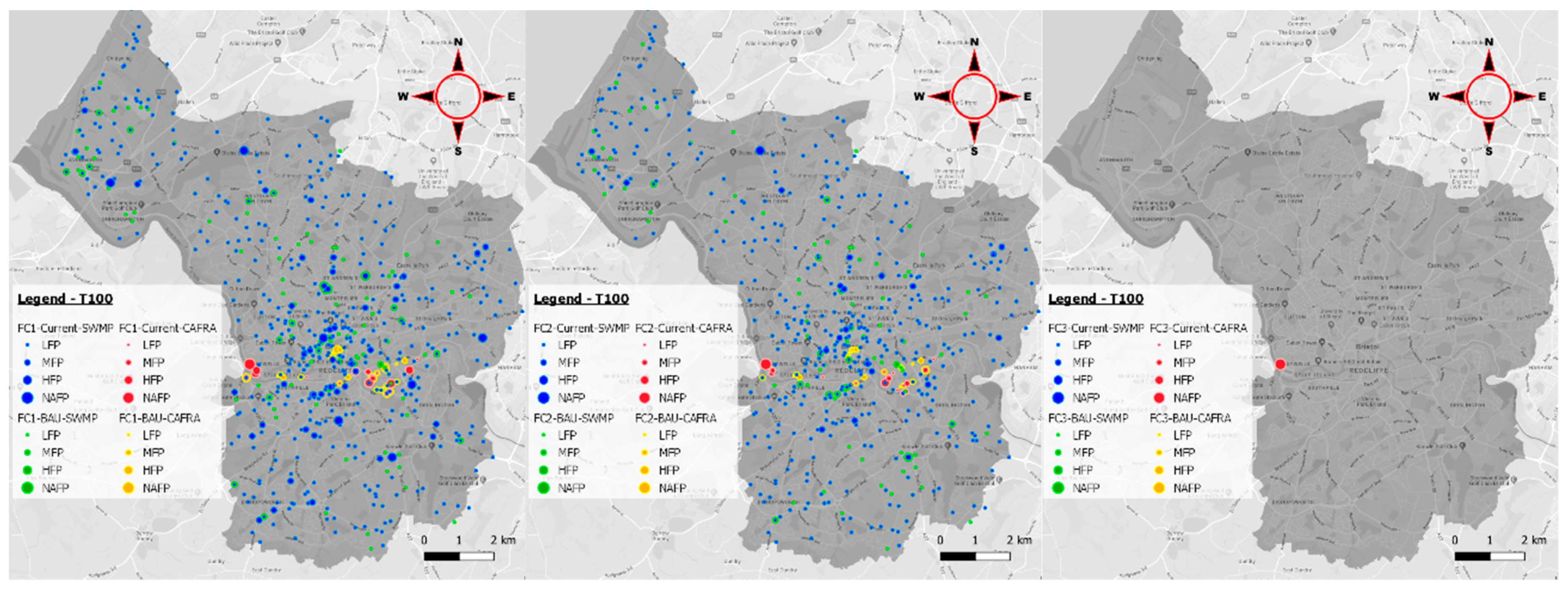
Regarding the electrical grid, Western Power Distribution is the Distribution System Operator (DSO) responsible in Bristol city who has provided part of the suitable data necessary for this study, which comprises the locations of all 11 kV DCs involved in the assessment, substantiating the risk that these assets can be exposed to.
2.2. The Barcelona Context
In Barcelona, although two main rivers (Llobregat and Besòs) cross the city and flow into the sea, the tidal influence of the Mediterranean Sea is not relevant, in that the main flooding events have been caused by heavy rainfall resulting in overtopping banks and river overflow. Every year, one or more serious rainfall events take place in Barcelona during summer and autumn, normally due to the cold drop phenomenon.
For what the Catalonia water agency (ACA) has recorded for Barcelona, in February of 1920 there was great flooding that caused the loss of around 600 properties [
15]. After that, the worst flooding of Barcelona occurred on the 25th September 1962 when 200 l/m
2 were registered in less than 3h. This caused the overflow of Besòs and Llobregat rivers making entire wards disappear through inundation, destroying whole factories and causing more than 12,000 victims and 617 people dead in several places of Barcelona province [
16]. This disaster boosted the channeling of both Llobregat and Besòs Rivers, preventing further flooding caused by river overflow. Thereafter, another example of severe flooding took place in October of 1987 when Barcelona city services such as the underground, roads, train, tram, airport, gas, communications and the electric services were blocked until the progressive restoration in the following days [
15].
Taking into account this historical record, the tidal assessment seems irrelevant, as there were no occurrences for tidal flooding. On the other hand, the extreme rainfall is the phenomenon responsible for causing the most important flooding events that critically affected the city, hence the importance of the surface cover flood risk assessment of the different city services in Barcelona.
2.2.1. Barcelona Flooding Data
The entire drainage system of Barcelona has been modelled, providing GIS layers with detailed information about flooding areas of Barcelona for different return periods and scenarios. Layers with different return periods (T1, T10, T50, T100 and T500) were generated for a current climate scenario [
17] and for a climate change scenario by considering BAU conditions [
18]. The current scenario is based on historical rainfall data. However, the BAU scenario was created by simulating extreme rainfall events considering RCP 4.5 and 8.5 by the year 2100.
2.2.2. Barcelona Electrical Data
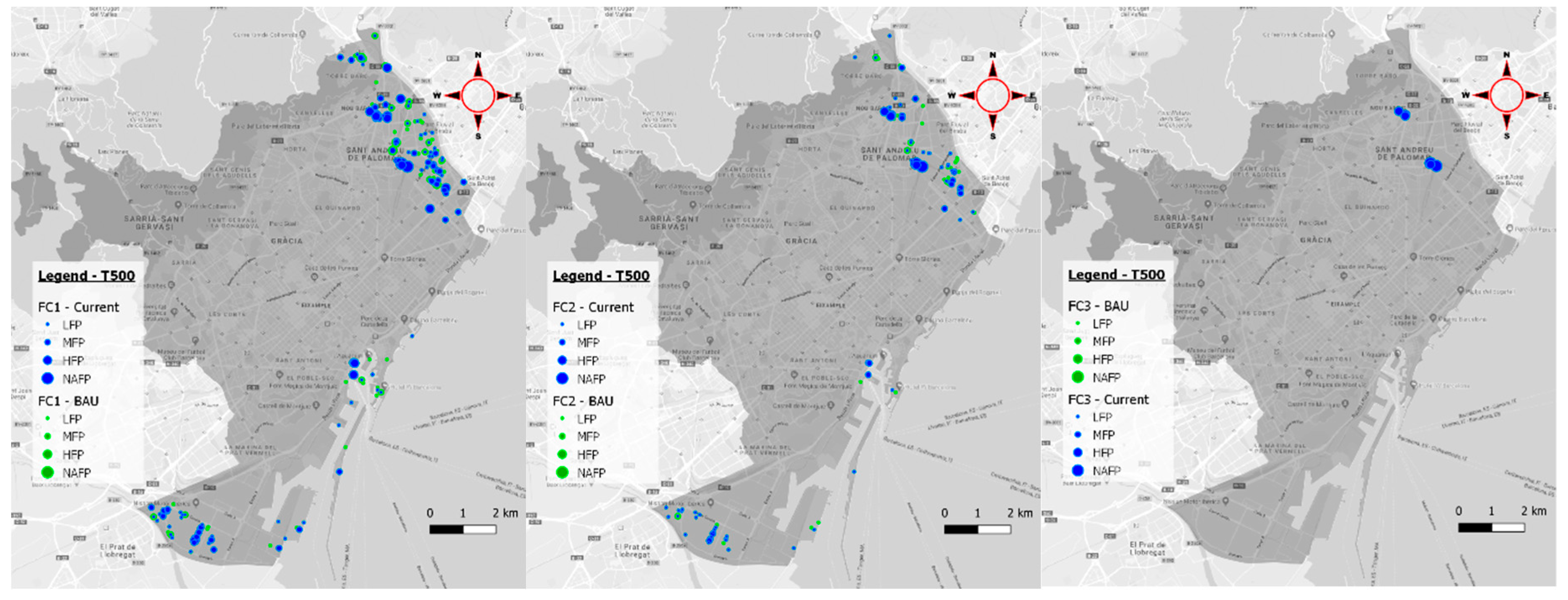
In the Barcelona case, the electrical grid is managed by Endesa DSO, who provided the location of the DCs of three important areas: Besòs riverside, Llobregat riverside, and seashore. Due to the non-availability of DCs location within the entire city, it is not possible to estimate the losses in the entire city, which makes the focus of the study on the three areas mentioned. These areas were selected by the DSO as the most relevant for their infrastructure. In addition, to keep the study based on the real data obtained, no estimations on the other zones have been made.
3. Methodology
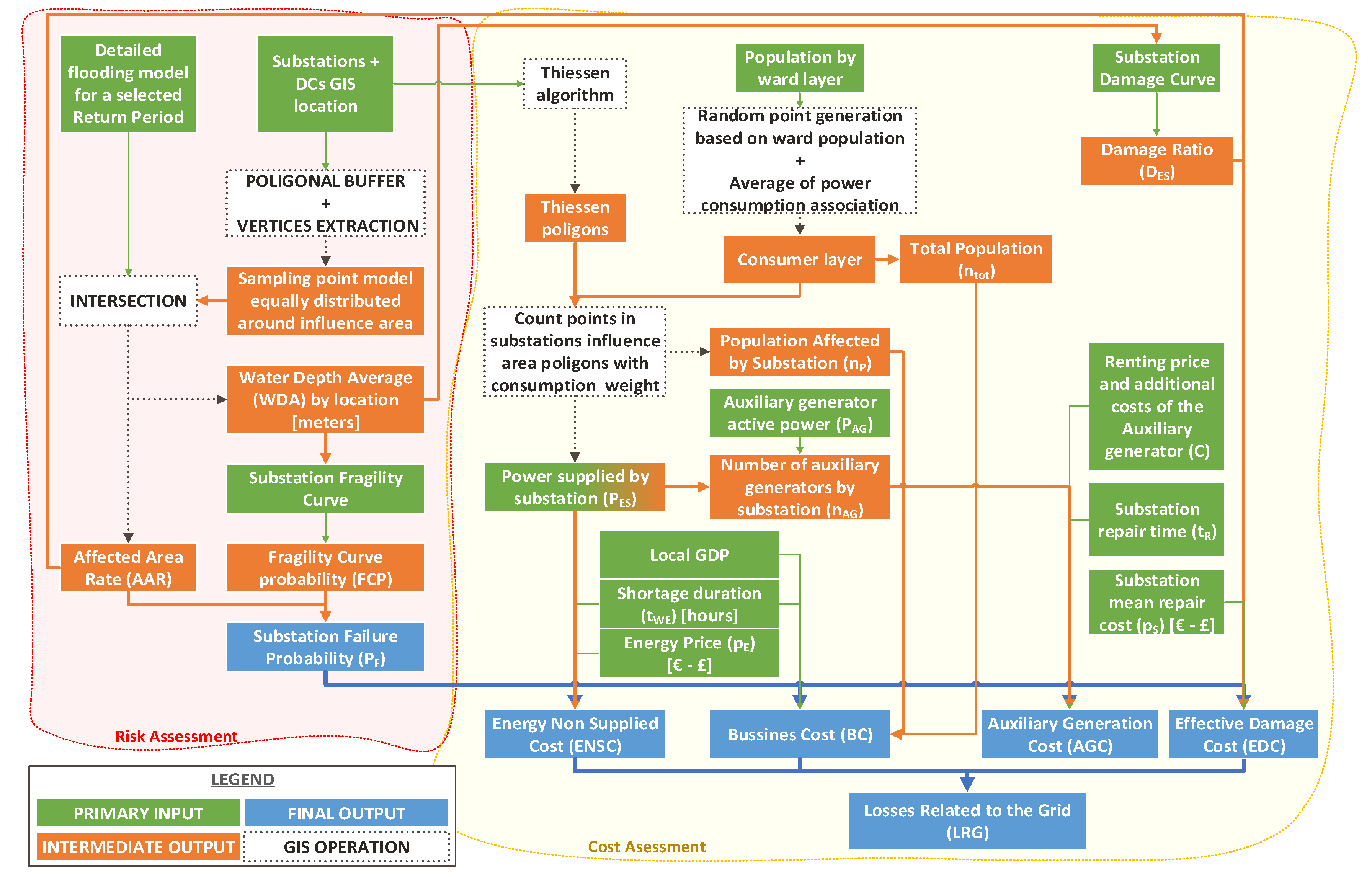
To calculate the failure probability of the DC to assess and calculate the potential cost of flooding, a new methodology has been designed. Such methodology provides an estimation of the assets impacted as well as the economic evaluation of such faulty conditions. The methodology is structured in different steps as inputs, probability evaluation, number of assets counting and finally the impact outputs. A graphical explanation of the method explained in detail in the following sections is given in
Figure 3.
3.1. Risk Assessment
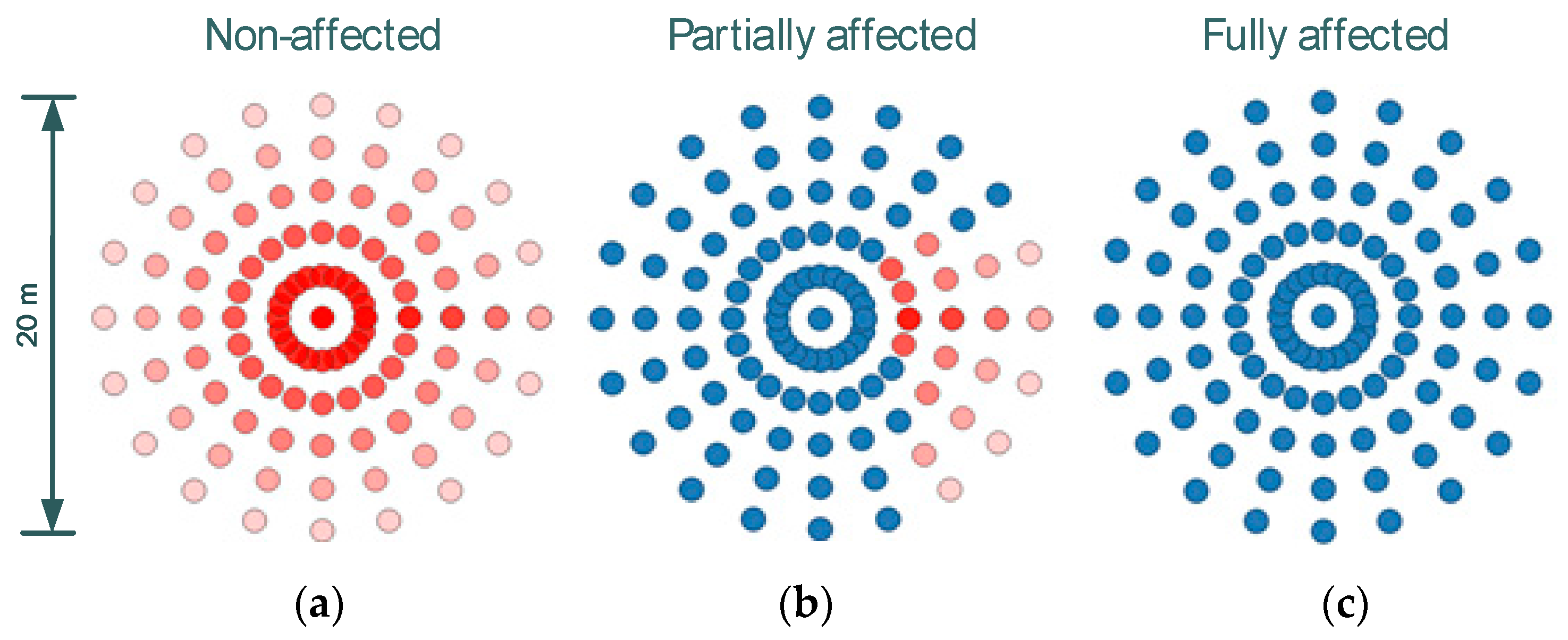
For the electrical asset risk assessment, a novel procedure has been established. The first step was to create a sampling shape layer by using an average diameter of 20 meters for the electrical DCs wanted for evaluation, with the diameter based on recommendation in the Energy Networks Association article [
19]. The diameter was used to define the influence area for each location and after that a uniformly distributed cloud of 106 sampling points was created all across the extent (
Figure 4). It is worth noting that such areas allow the tool to cope with location uncertainty in GIS data.
The second step consisted of the intersection of the sampling layer with the detailed flooding map that contained the water depth of each flooded area. After crossing both shapes, the following parameters were extracted:
The third step was to process the information obtained for every sampling point to calculate a representative figure for each location. In this way, the rate of the affected area and an average for the water depth for each location was calculated.
To calculate the Affected Area Rate (AAR), the number of sampling points affected were counted (
) and later divided by the total number of sampling points (
) (Equation (1)).
Afterwards, the Water Depth Average (WDA) was calculated for the sampling points flood depth, obtaining a general representative number of each location (Equation (2)):
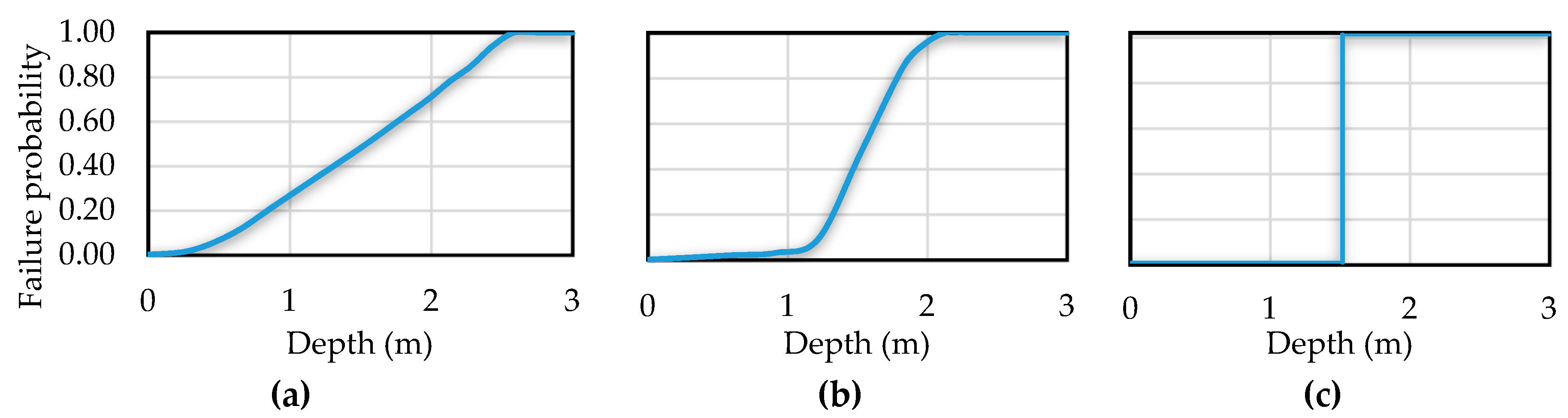
Once the water depth for each location was calculated, the fourth step was to introduce this parameter in the X-axis of each fragility curve represented in
Figure 5. The failure probability was obtained and represented from 0 to 1 in the Y-axis.
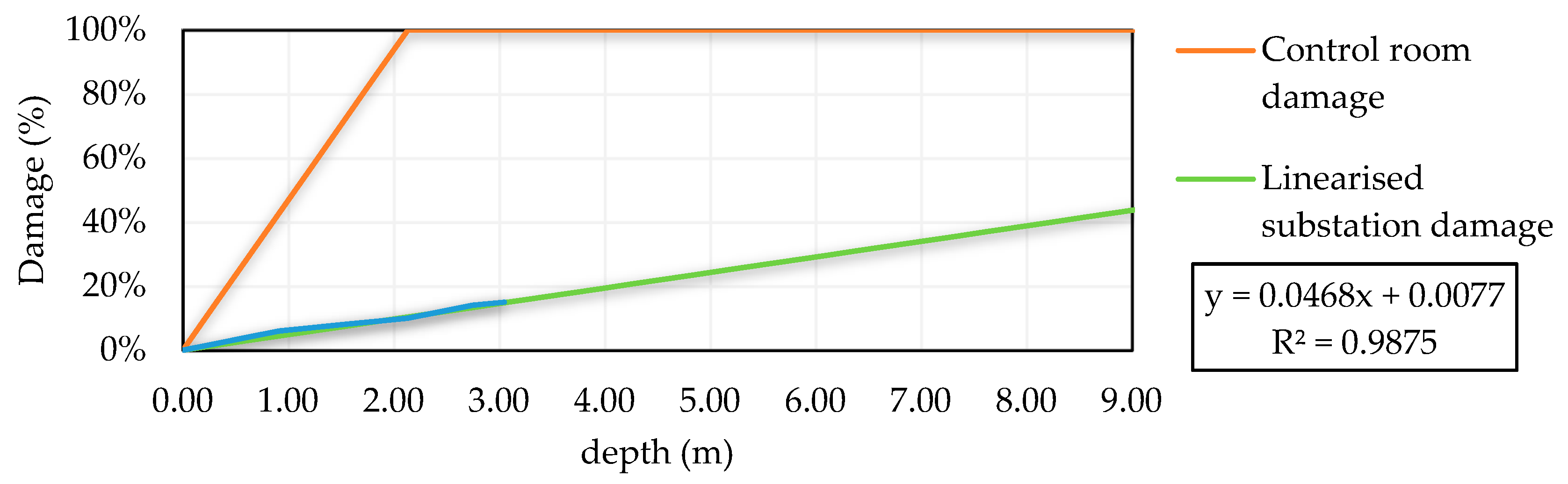
The original fragility curve (
Figure 5b) used in this study was adapted from that of the Federal Emergency Management Agency of the United States [
10], previously formed through data gathered from important disasters occurred in the US electrical grid. It must be remarked that the US grid can have different standards and protective measures compared to Europe and a different substation and DC topology. However, in further studies with more data available, the curves can be rebuilt to fit with the real conditions and features. Taking into account this dissimilarity with the grid established in Bristol or Barcelona, a sensitivity analysis was performed to assess the possible error caused by this. In this manner, it is possible to offer a better resolution by contemplating a wider spectrum (
Figure 5a,c).
After obtaining the result from the fragility curves, the fifth step was to multiply the Fragility Curve Probability (FCP) by the AAR, obtaining a final probability of failure for each analysis performed for each return period given (Equation (3)).
The last step was to classify each location studied according to the
calculated by following the categories established in
Table 2.
3.2. Economical Losses Caused by Electrical Asset Failure
Flooding can cause extensive potential economic losses due to the impact caused to the electrical assets described in the previous sections. The losses considered in this study are those caused by non-supplied electricity, damages provoked to the electrical assets, the expenditures associated with the renting of emergency electrical supply appliances, and the businesses earning losses provoked by the shortage. The methodology followed for the calculation of all mentioned losses is explained below.
3.2.1. Effective Damage Cost (EDC)
To monetize the potential damages caused to the electrical assets, a damage curve adapted from (FEMA-HAZUS) has been applied (
Figure 6). The curve initially was given for a 3m depth, but it has been interpolated from the original one up to a water depth of 9m according to the maximum water depths obtained in the flooding maps. In
Figure 6, the original curve is shown in blue, and the one that was used for the analysis in green.
After introducing the WDA (obtained by Equation (2)) in the damage curve, a percentage of damage (
) in each DC analyzed was obtained. After that, the effective damage cost (EDC) was calculated according to Equation (4) by multiplying the damage ratio (
), by the failure probability (
) and by the price of the corresponding DC (
) that has been estimated based on the substation voltage given in
Table 3. The price of a DC assumed for the cost calculation corresponds to an 11 kV substation.
3.2.2. Cost Associated with Businesses Losses (BC)
First, a GIS consumer layer based on the ward’s population of each city was created, by using databases of 2018 obtained from the open data portal of both cities studied [
20,
21].
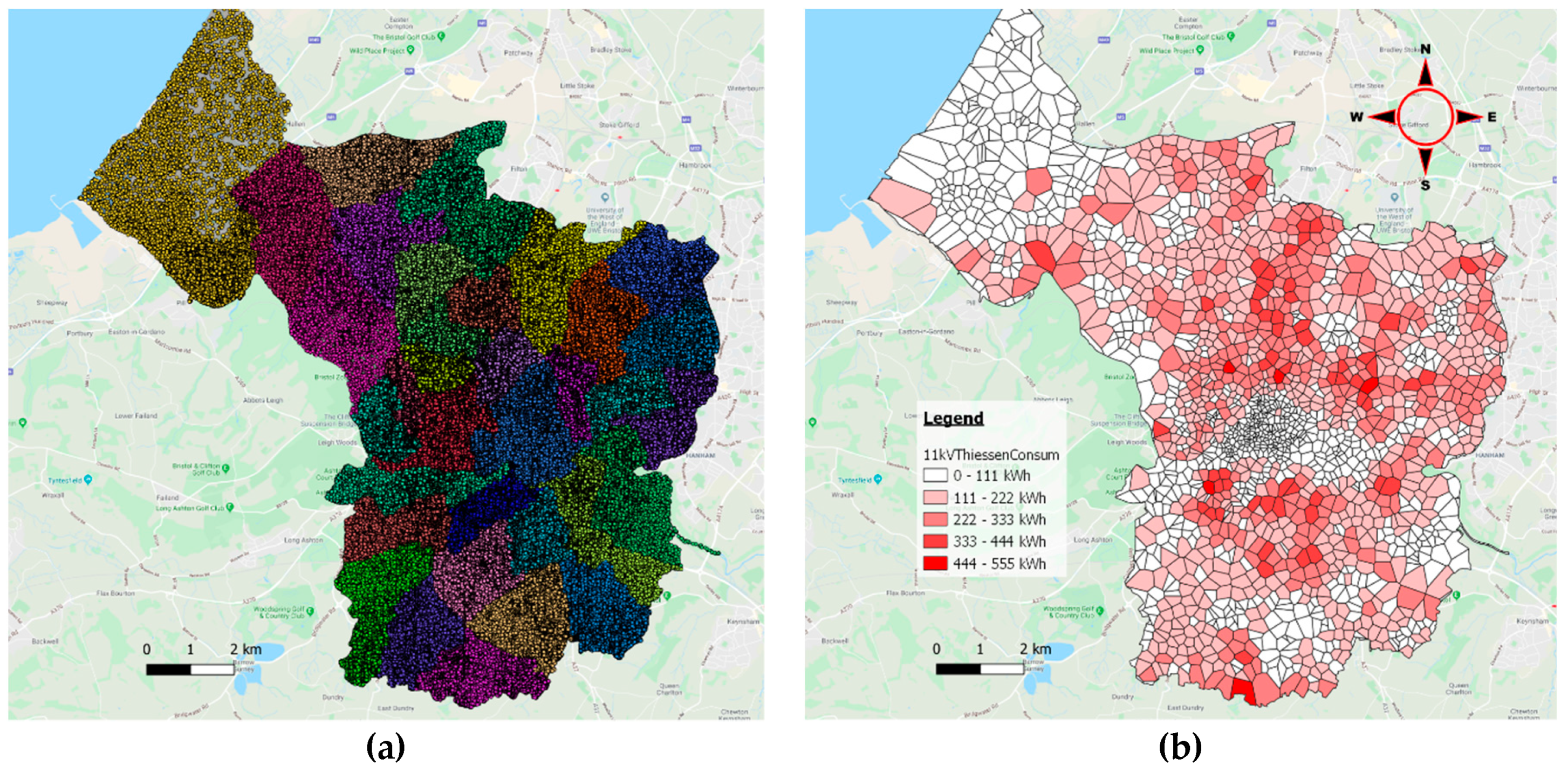
A cloud of random points based on the ward population was then generated, therefore representing the potential consumers distributed along all the study extent. After that, a Thiessen polygons layer was generated for each electrical asset, representing the supply coverage area of each DC (
Figure 7). The next step was the association of the number of consumers of each random point to the overlapping Thiessen polygon, getting a total of associated consumers for each DC. It is important to indicate that such polygons provide an averaged estimation of the population that for global risk assessment can be accepted as a reasonable result, allowing its application to larger areas.
Equations (5) and (6) are taken from a European Commission Joint Research Center (JRC) technical report [
13] analyzing climate change and critical infrastructure. These equations evaluate the losses accounted by city businesses provoked by electrical shortages. Equation (5) uses the Gross Domestic Product (GDP) of the city and multiplies it by the probability of failure of the DC (
), by a ratio of the part of population affected (number of people affected by the shortage (
) divided by the total population (
)), by the fraction of the year that the shortage takes place (shortage duration in days (
) divided by 365). In this way, the previous DC failure analysis allows the calculation of this formula that will estimate the cost of the shortage to the businesses.
Equation (6) will give the total cost of the losses associated with local businesses by adding the values previously calculated in Equation (5).
3.2.3. Energy Non-Supplied Cost (ENSC)
In this section, the electrical supply losses caused by the shortage duration have been estimated by following some different steps for the two cities studied due to the data availability.
The first step was to estimate the power supplied at each DC. In Barcelona, this step was not necessary because the real parameter was known, making the analysis performed in the selected areas quite accurate.
However, in Bristol, the average electrical demand of each DC studied was estimated based on the GIS layer generated in “3.2.2. Cost Associated with Businesses Losses (BC)” where the consumers were associated with the different DCs. The power estimation consisted of the multiplication of the total number of consumers by an average consumption of 531 kWh gathered from the world data portal [
22]. In this case, the power losses could be underestimated, due to the business locations, the industries and other possible sources of consumption were neglected.
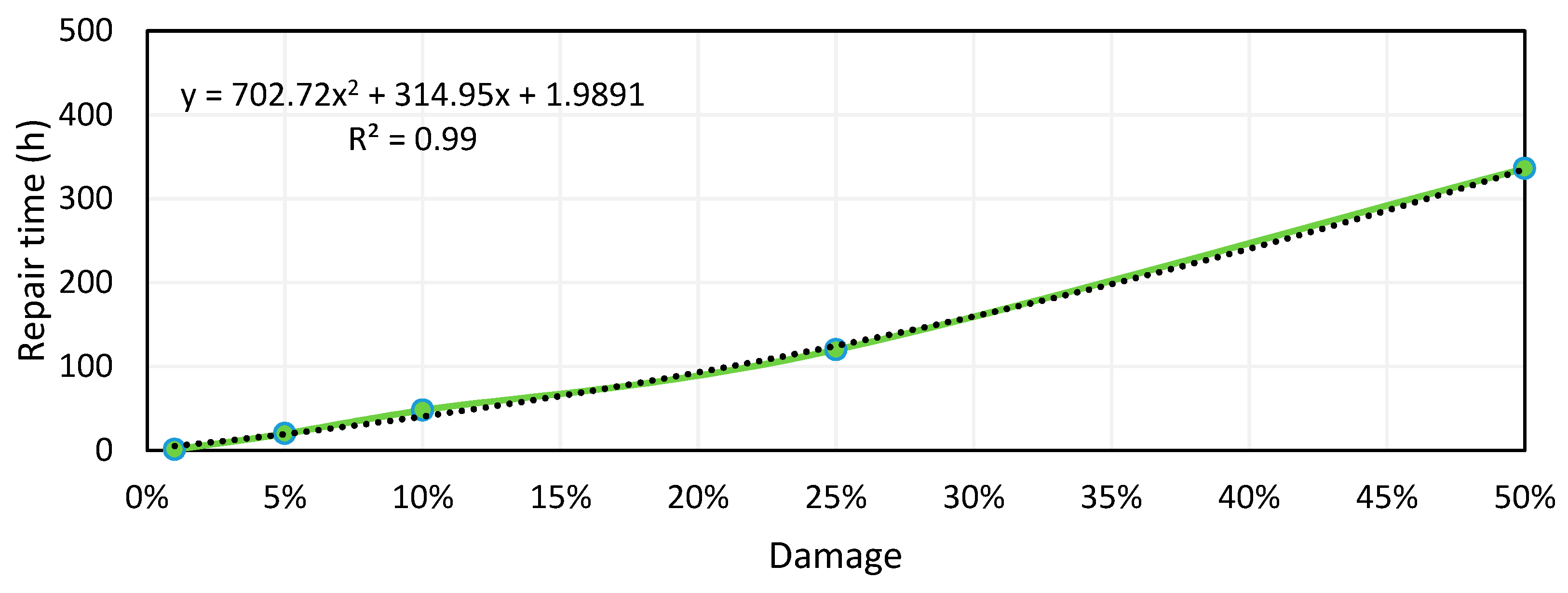
Another important parameter required for the calculation of ENSC is the repair time (
), which was calculated by associating the different damage categories to the repair time obtained from “power grid recovery after natural hazard impact” [
6], creating in such a way a damage-time curve based on these categories (
Figure 8). Because in this study the damage will never overpass the 50% mark (see
Figure 8), the categories that could exceeded that mark were discarded for a better equation curve-fitting, and the rest of categories were represented in a scatter chart, looking for a trend line that really fits the curve. In this case, it was found that a polynomial curve fitted almost to the perfection with the damage-time curve (R
2 = 0.9987). Hence, it was possible to adapt from a categorical scale to continuous by using the trend line equation.
For those future cases in which 100% damage can be reached, it is suggested to consider a total replacement.
Thus, the equation obtained from
Figure 8 was applied to the damage percentage calculated in the previous step for all locations analyzed to obtain the corresponding repair time of each one.
Thus, was applied to the trend line equation, obtaining the corresponding repair time of each location damaged.
Once the DCs power and the repair time were calculated, the energy losses were derived according to Equation (7).
where
is the failure probability,
is the DC power,
is the energy price and
is the period without energy.
In such a way, the energy blackout will be extended up to the Auxiliary Generation systems that are put into operation. From this point onwards, the cost will be directly attached to the Auxiliary Generation Cost.
3.2.4. Auxiliary Generation Cost (AGC)
In this section, the cost attached to the energy generation to avoid the prolongation of the shortage was estimated. The use of diesel emergency power generator support was assumed for when the repair time exceeded 9h of duration. This period was chosen as a hypothesis assuming the rainfall duration given for the flooding maps calculation (i.e., 3 hours) and 6h of response time to rent, transport and install the equipment. In this way, the calculation of the cost of penalties to the DSO company can be neglected in the analysis, although this, depending on the severity of the event experienced could be an underestimation.
It has been considered the transport of the equipment (
to the affected DC as 20€, and three different tranches of renting price depending on the number of days required. The first renting tranche (
) has been set as 100€/day when the period is less than 1 week. The second tranche (
) takes part when the problem is extended from one week to three weeks with a renting price of 50€/day and the third tranche (
) when the repair tasks need more than three weeks, the price is reduced up to 40€/day. The prices used for this calculation have been taken from a company of machinery renting in Barcelona [
23]. In addition, the fuel consumption cost (
) was added to the calculation as well as the number of auxiliary generators (
) (Equation (8)).
The number of auxiliary generators was calculated by dividing the DC power consumption (
) by the maximum active power given by the generator (
) and rounding up the result to the whole number (Equation (9)).
3.2.5. Estimation of the Total Losses
The total losses were calculated by adding all the cost values calculated in the previous sub-sections (Equation (10)).
5. Discussion
The risk of assets has been quantified in other studies and in several ways, but not in the same way it was conducted here. For example, a GIS-based method was proposed by JRC [
7] to assess the electrical grid and the gas network in case of seismic events using seismic fragility curves proposed by FEMA-HAZUS [
10], which is similar to what was done on the failure assessment of this study. However, it was not taken into account how to assess the economic losses, later releasing other studies, with methodologies to evaluate the economic losses caused by storms and floods to the electrical infrastructure in [
12,
13], but never fusing them in a complete methodology and using it in case of flooding. The case of [
9] builds on FEMA-HAZUS methodology [
10] and follows a much more detailed analysis by using interdependencies but with the single problem of the huge requirement of data and the added difficulty of creating the network topology, and in most of the cases that information is confidential. Considering other methodologies as the proposed in [
8] only the probability of flooding is assessed and not the probability of failure neither the economic losses. The most similar methodology can be found at [
11] where a GIS-based approach is taken for the assessment of the electrical sector in flooding events determining the system exposure and vulnerability of the grid to flooding, with the particularity of not using fragility curves. A good point here is that this study takes into account other ways to assess the economic losses considering the economic sectors involved in each area of study.
Regarding the points highlighted above and the new procedures developed, this is a novel process that allows an analytical interpretation not only of the risk that electrical assets are exposed to but also about the potential costs that these assets could produce in many different ways to the population and to the DSO company.
This process enables the user to find the distribution center most exposed to flooding within a set region, allowing them to then take preventive measures if necessary on behalf of the responsible organization or authority.
This study evaluated several scenarios by using different parameters. This allowed a check on the effectiveness of the process and to establish comparisons between the different scenarios proposed.
5.1. Comparison between Fragility Curves
The results produced in the different analyses, carried out by applying the different fragility curves modelled, offer a comprehensive view of the effect of changing the curve shape, as demonstrated in the results produced. The analysis made with FC1 (softened fragility curve) may overestimate the results because high failure rates at low water depths are considered. On the contrary, when using FC3 (hardened fragility curve) the results can be underestimated due to the curve considering zero failure probability up to water depths of 1.4m. Taking into account the results presented, FC3 is neither representative nor realistic because it omits a high number of DCs with a failure probability in the other FCs. As the arrangement of the electrical elements can vary heavily between DCs, a zero probability would be a great underestimation. In fact, taking the experiences of electrical companies’ employees, a DC can fail from very low water depths and the threshold to identify the flood risk was set to 10 cm in the risk analysis.
In general, taking FC2 as a reference point, FC1 results in a 19% cost average increase caused by the sum of all the possible small losses produced by low failure probabilities, while FC3 results in a 9% cost average reduction, as it neglects all of the small losses and keeps the gross.
In the end, the variation in the fragility curves can be taken as a pessimistic, neutral or optimistic view if choosing from FC1 to FC3, although in general, FC3 is not representative.
5.2. Comparison Between Current and BAU Scenario
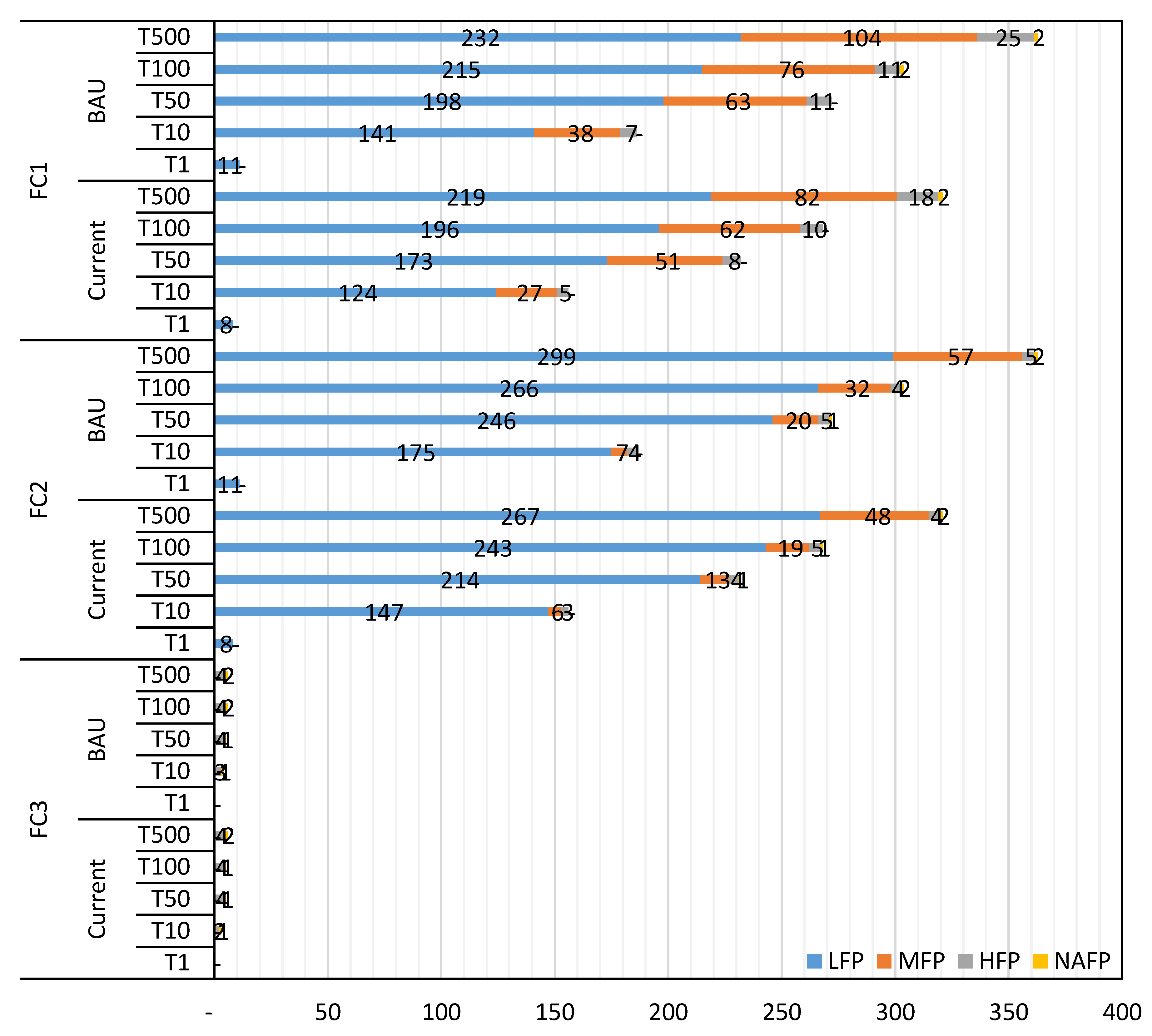
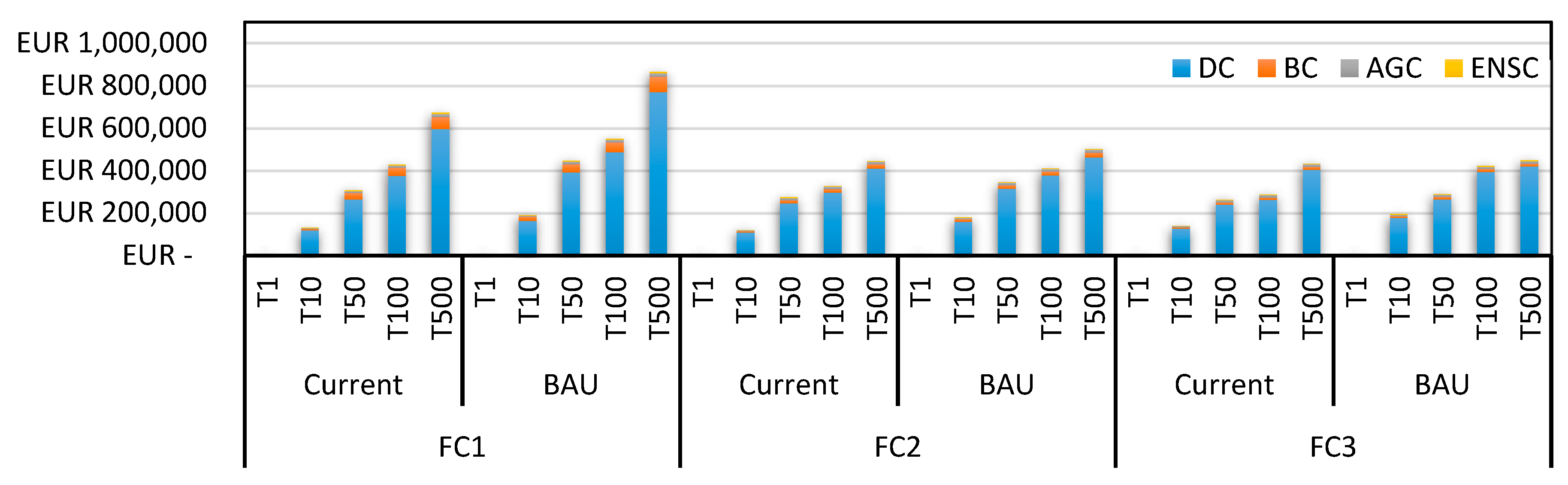
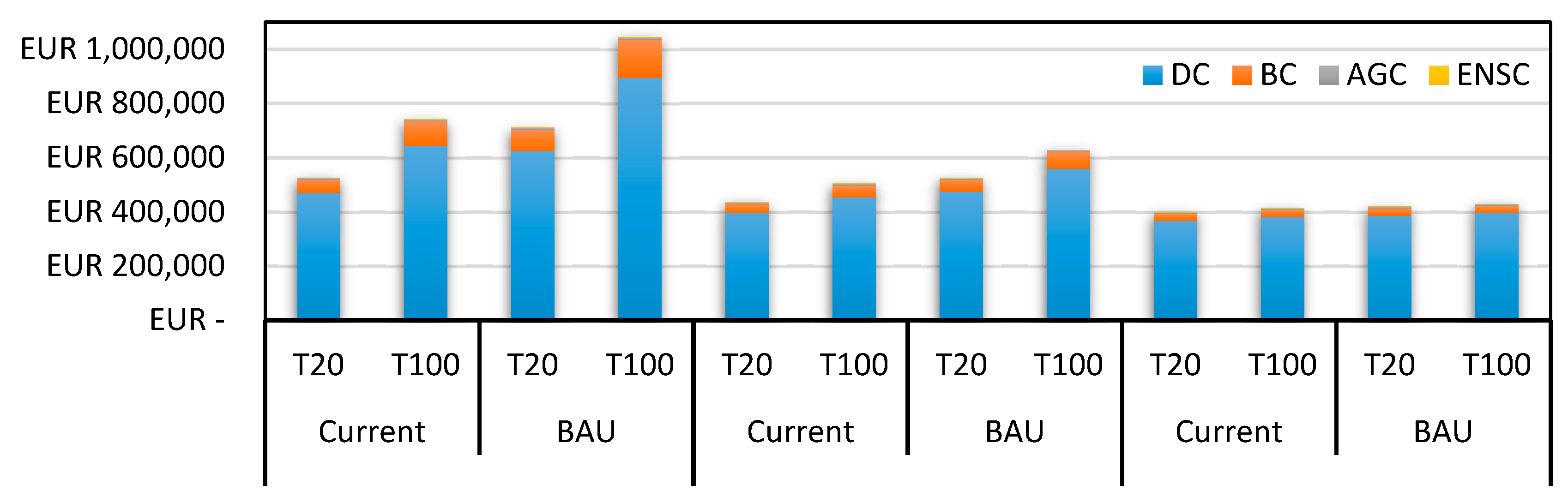
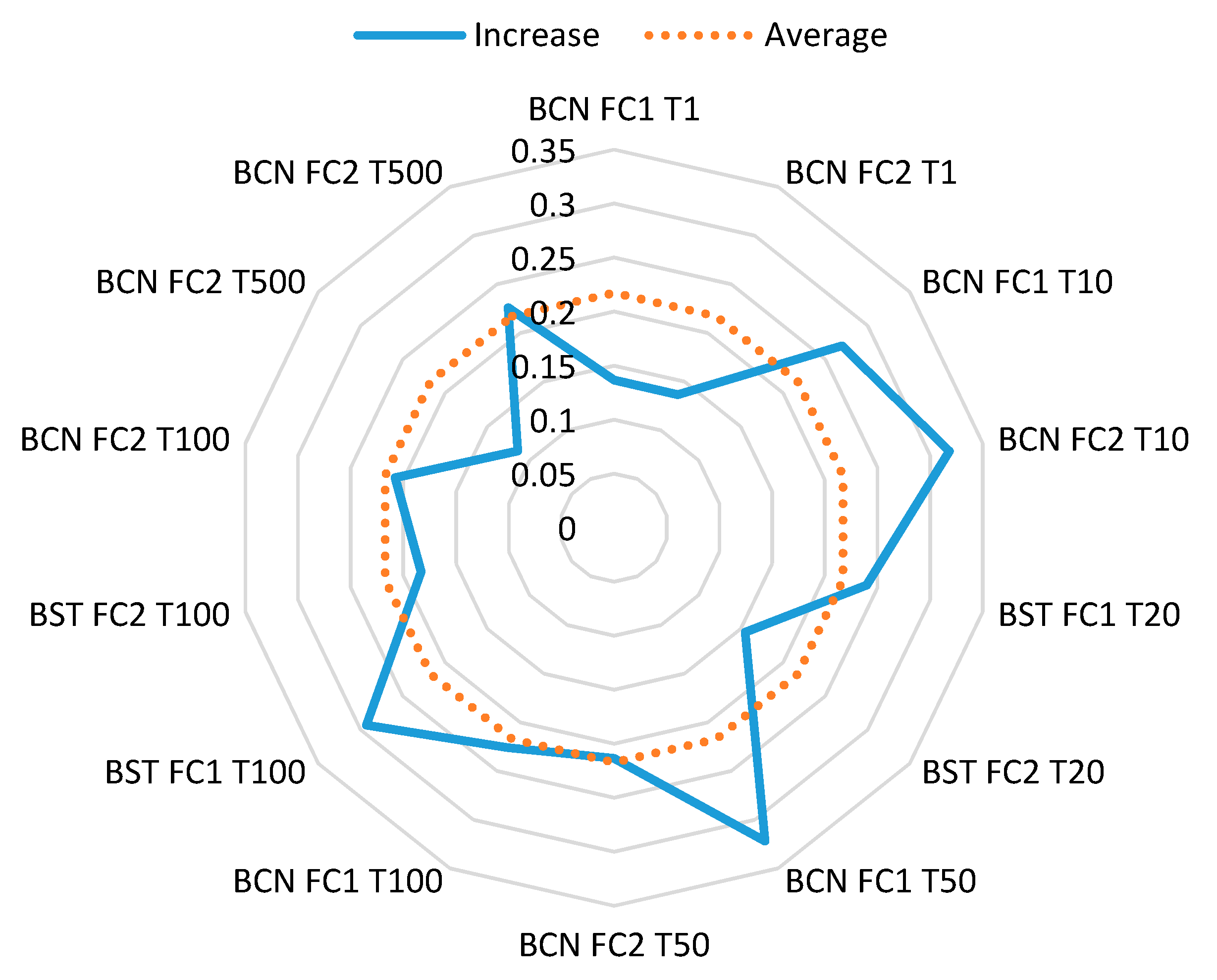
The first comparison made was between a current scenario, where different return periods based on historical data were modelled in flooding shape layers, and a BAU scenario considering climate change with an RCP 8.5, estimating the flooding that could occur in the year 2100. As is normal, in the results obtained, the BAU scenario introduced higher risk and consequently higher costs.
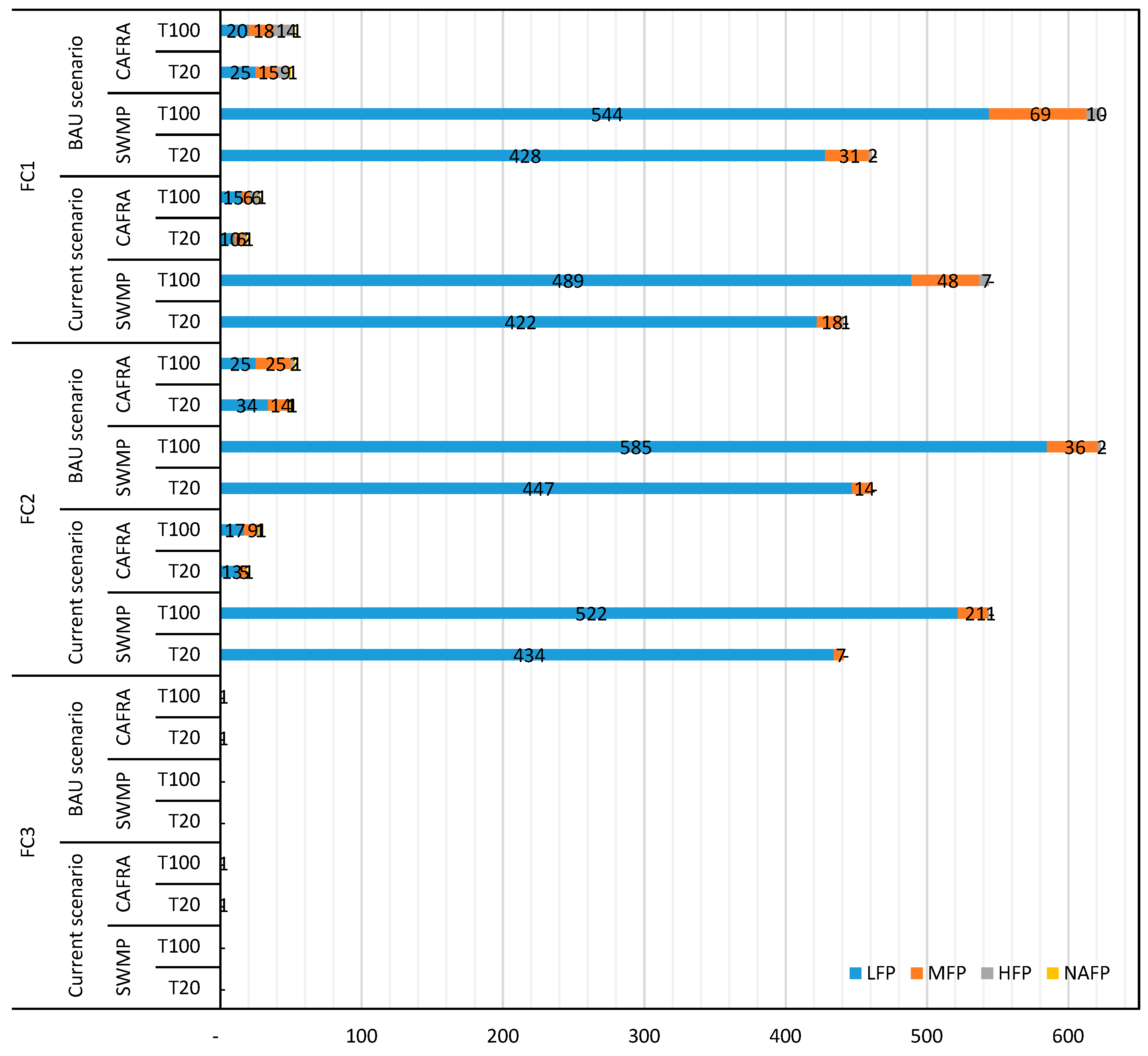
Depending on the fragility curve applied, the differences between both scenarios change, but counting the maximum change experienced in both cities, the maximum increase in the number of DCs affected goes in the LFP category with a 2.38% increment in Barcelona and 3.37% increment in Bristol. Also, big increases are presented for MFP with 1.64% rise in Barcelona and 1.12% in Bristol. These increments seem to be very low but when translated into cost, the average increase is a 22% respective difference to the current scenario, but depending on the case analyzed, the percentage can vary (
Figure 17).
5.3. Comparison between Cities
It is difficult to make a complete comparison between both cities due to different return periods being analyzed (in Bristol these were lower than in Barcelona), and because of the context of each city. With regards to context, it has to be taken into account that the extent of both cities studied is more or less within the same scale (Bristol with 111 km2 and Barcelona with 102 km2) but the effective territory studied is much less in Barcelona (only 32% which means 33km2) and also 326,000 inhabitants against 460,000 in Bristol. In this aspect, the number of inhabitants of both cities is also similar.
In addition, the hydraulic models that simulate the flooding are different. In Barcelona, the whole drainage system was included within the model, while in the underground Bristol sewer network only larger diameter pipes, although in Bristol this considered both pluvial and fluvial flood events, while in Barcelona, only the pluvial flooding was considered.
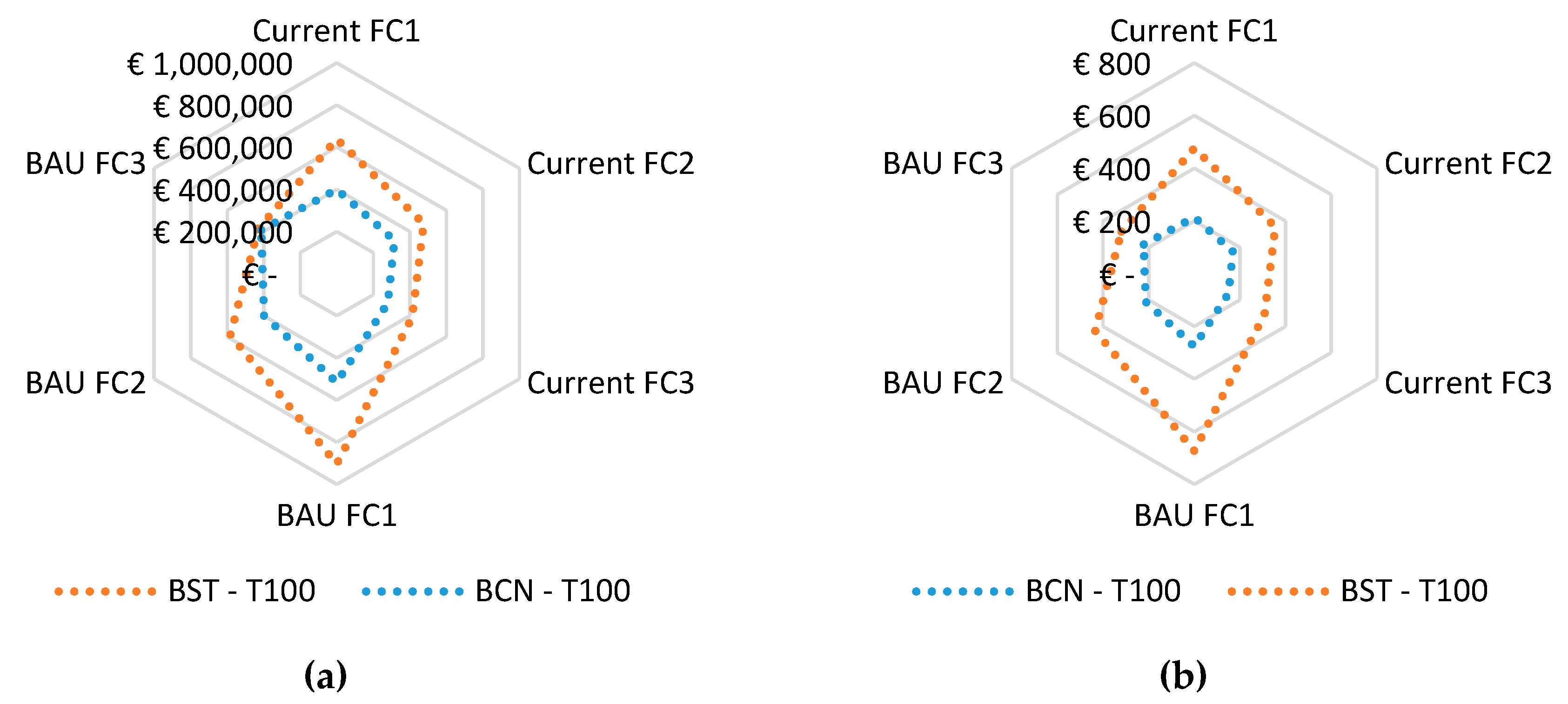
Bearing in mind the above statements and taking the unique return period (T100) run for both cities an analysis comparing the cities was performed, resulting in quite similar losses for each fragility curve applied but always resulting in Bristol being the city most affected by flooding. In
Figure 18a the total costs are represented for both cities, for the two scenarios analyzed and the different fragility curves developed, showing a clear difference between cities in almost all cases analyzed. As this difference could be linked to the number of DCs analyzed in each city, the total cost has been unified taking into account the total number of DCs analyzed in each city (
Figure 18b). In this case, the difference between cities is even more noticeable, which is something reasonable taking into account the great problem that Bristol has with flooding [
14].
6. Conclusions
This paper has gone through a methodology that aims to estimate and classify the DCs at risk of flooding in different classes set by failure probabilities, as well as the energy losses and their expenditures provoked by shortages caused by potential flooding. This methodology takes a probabilistic GIS-based approach to quantify the risk of electrical shortage in different areas caused by DCs flooded. In this research it has been demonstrated that it has become possible to implement this method to any city where the locations of the DCs and a flooding model are available.
The method used to go through different steps for each city, depending on the data availability for each one, offers several ways to estimate risk and electrical losses with, inevitably, different accuracy.
As a result, it can be drawn the potential losses incurred to put them into balance against the cost of taking protective measures if the assets analyzed are not already under protection.