1. Introduction
Smart homes are among the most significant research topics for urbanization energy optimization, which helps not only in economic reductions in energy source consumption but also in reduction of greenhouse gas emissions into the atmosphere, conferring climate change impact reductions to a certain extent. These homes are referred to under a set of terminologies including automated homes, integrated home systems and intelligent buildings, depending on the design style and convenience. Any comfort appliance for the home, including heating, ventilation, air conditioning (HVAC) and lighting, are significant units for the heating and cooling of a home. Each one of these appliances consume a certain type of energy source; consumption of fossil fuels, especially, emits greenhouse gases into the atmosphere, which adds to enhancement of undesirable impacts such as global warming and climate change. The most significant elements in any smart home are the heating and natural lighting, but recently electrical components have also been integrated into the system. As a result of technological developments, a smart home can now monitor the activities of the occupant of home, independently operate devices in set predefined patterns or independently, as the user requires [
1].
In the long run, elderly people (>60 years old) will perhaps compose more than one-quarter of the world’s population. As they will face more problematic life within a home, automatization of all comfort appliances must be integrated into a single command so that not only the elderly but also others may have more comfortable habitats.
The rapidly growing world energy use already has raised concerns about the exhaustion of energy resources and heavy environmental impacts. As a result of these concerns, a trend of green and smart cities has been increasing. In recent years, building energy performance improvement studies have increased due to greenhouse gas emissions from the homes, and hence energy efficiency, energy intensity and energy consumption reduction activities have entered into the building sector so as to reduce the emission rates to the possible minimum level. It was stated by Kibert [
2] that in the nonresidential sector, the net-zero energy strategy requires hyper-efficient buildings with consumption of energy below 50 kWh/m
2/year. In order to achieve this goal, which is not yet obtainable today, apart from the new technologically innovative developments, it is necessary to improve the mathematical models, which is the prime purpose of this paper. For instance building energy performance is not yet fully understood mathematically, and the simulation models should provide better improved results. On the mathematical model side, there are two branches, namely the physically-based analytical solutions or data-based mathematical models through the probability, statistics and stochastic simulations. The view taken in this paper is the first one, where the space in a home is modeled by physical principles. Although analytical models have restrictive assumptions, at least they provide conceptual, rational and logical principles with lack of some precision. Lu [
3] proposed a new method for modeling energy performance in buildings.
Usama [
4] stated that there are six data-based methodologies that are widely implemented in practical applications. These are data classification methods including the decision tree method, support vector machine (SVM) and artificial neural network (ANN) approaches, cluster analysis, association rule mining (ARM), statistical regression approach, summarization and anomaly detection methods. Yu et al. [
5] presented an overview of these and recent studies undertaking two tasks in the building field.
As for the stochastic models, they are useful in modeling the building occupancy and occupant behavior as crucial factors influencing the discrepancy between practical and simulated building energy consumption. Analytically, the predictions of these behaviors are difficult to model, and therefore, probabilistic, statistical and stochastic processes are used for their simulation, leading to a set of predictive patterns ([
6,
7,
8,
9]). The application of each model requires expert views; also, they are rather complicated, need huge amounts of data and, if possible, require a continuous record for better updating their procedures and verifications. Lü et al. [
10] suggested past, present and future mathematical models for buildings.
However, the data-driven methodologies are not concerned with logical and rational principles but try to relate a set of measurement records in a harmonious manner to reach the desired goal. On the other hand, data-driven models can cope with complexities. They need a substantial amount of data for the parameter identification in the data-driven models with a lack of basic physical laws (mass balance and heat flux principles).
Li et al. [
11] mentioned model-based predictive control as a promising solution for building energy efficiency improvement including building-grid resilience. Energy forecasting models are essential tools and software for the model predictive control performance. In general energy predictive models can be categorized as physical ones in the form of “white noise” and as a data-driven form as “black box”, which does not provide any information about the physical mechanism of a smart home system. Every model has its pros and cons and, especially, a set of restrictive assumptions, idealizations and simplifications that can be regarded as first approximations, which can be improved with later studies along the same direction. Furthermore, each model requires expert engineering views and computational power. Li et al. [
11] presented a novel methodology for an energy forecasting model using system identification approaches based on system characteristics, where the whole-building experiments are systematically designed and conducted to verify and validate a real commercial building. Their results showed that the methodology is able to achieve 90% forecasting accuracy within a 1-min calculation time for chiller energy and total cooling energy forecasting in a 1-day forecasting period under the experimental conditions. On the other hand, a Monte Carlo study also shows that the model is more sensitive to outdoor air temperature and direct solar radiation, but less sensitive to ventilation rate.
Molina-Solana et al. [
12] presented review about how data have been applied to address the most difficult problems faced by practitioners in the field of building sector energy management with a discussion on the challenges and opportunities concerned with the advent of better-connected devices and new computational technologies.
Chun-sheng et al. [
13] suggested the analysis for rural and urban areas with the current situation and environmental effects of household energy consumption. Their analysis was also concerned with reducing greenhouse emission for the purpose of protecting the environment from pollution. They used a SPIRPAT model to analyze the impact of population and income factors on the ecological footprint of energy use, with results showing that there are differences between the rural and urban areas in terms of the per capita energy consumption. It was shown that the rural households’ emissions are much larger than those of urban alternatives. Needless to say, both population size and income factors have promoting effects on total energy and the ecological footprints of, e.g., electricity and coal, in urban areas and on electricity and biomass in rural areas.
Mikucioniene et al. [
14] indicated that the smart home qualitative calculations are based on energy efficiency measures and evaluation. For better sustainability, energy efficiency should be selected in such a way that measurement evaluations reflect continuous attitude. They presented five main criteria (energy efficiency, environmental impact, economical rationality, comfort and duration under a life cycle point of view), which were defined and analyzed, then formed a decision tree for distribution of energy efficiency measures to better understand additional energy efficiency measures. According to their study, the case studies with five energy efficiency measures show the optimal results.
In their study, Ahmed et al. [
15] stated the impact of building connection characteristics and designs, with performances by data mining techniques leading to the appropriateness of a room in relation to energy efficiency by use of analytical methods. Model performance criterion was estimated by cross validation consisting of holding a fraction of observations out as a test set. The results were extended to show the benefits of these techniques in optimizing a building’s four basic elements (structure, systems, services and management) and the interrelationships between them. These techniques extend and enhance current methodologies to simplify modeling interior daylight and thermal comfort, further assisting building energy management decision-making. On the other hand, Yu et al. [
16] proposed a methodology for knowledge discovery through mining associations between building operational data.
Pena et al. [
17] presented a methodology for the increasing trend of smart cities with more complex buildings. They proposed a method to detect energy inefficiencies in smart buildings, which is based on a rule-based system through data mining techniques and applying the application of energy efficiency experts. Anomalies are detected by a set of useful energy efficiency indicators. The results provide a set of useable rules as a part of an optimization decision support system for energy consumption and the detection of anomalies in smart buildings. Bacecq et al.’s [
18] review study demonstrates that an exhaustive comparison of the systems encounters difficulties due to the differences between the studies with respect to experimental measurements, weather data and the lack of similar comparison criteria, such as decrement factor, efficiency and cost. Hussain et al. [
19] investigated the thermophysical property enhancement of eutectic (oleic and capric acid)-based latent thermal energy storage materials for cold storage applications. Highly porous activated carbon (AC) nanosheets were synthesized, which act as nucleators to enhance thermophysical properties. Kasaeian et al. [
20] provided review information about thermal energy storage systems with phase change materials (PCMs) as a known energy storage technology with a high potential for increasing the energy efficiency of buildings. In their work, the experimental works in the field of phase change materials (PCM)s, especially in smart buildings, are taken into account. The relevant papers are classified based on heating, cooling and air-conditioning. Thermal energy storage (TES) is a technology that stocks thermal energy by heating or cooling a storage medium so that the stored energy can be used at a later time for heating and cooling applications and power generation. Sarbu and Sebarchievici [
21] focused on TES technologies that provide a way of valorizing solar heat and reducing the energy demand of buildings. In the same work, several energy storage method principles and calculations of storage capacities are described. There are numerical solutions for a set of differential equations, whereas in this paper, an efficient analytical method with application has been provided that is practically simple to apply provided that time–temperature record data are available.
The main purpose of this paper is to present a physically-based model by taking into consideration the mass balance and the Fourier heat flow law. In the model, the building envelope is considered as homogeneous and isotropic material of uniform thickness. The model helps to identify the storage and heat conductivity coefficients of an empty space in home as a single concrete room of 3 × 5 × 2.9 = 43.5 m3 and its generation to a whole building.
2. Methodology
Although the mathematical approach in this section is used already in heat transfer and groundwater movement modeling, its adaptation to heat propagation from a single room is presented in detail. Its connection to smart houses is for numerical calculation of heat storage and transmission features, which can be related to energy consumption and regulation in such buildings. The restrictive assumptions in the model are the uniformity, isotropy and homogeneity of the construction material. For the development of an effective analytical model, a prism model as in
Figure 1 is visualized with infinite dimensions, dx, dy and dz.
Fourier (1822) provided a relationship between the material conduction rate and the temperature difference (gradient) in the energy flux direction. He stated that the heat flux, Q (W/m
2), due to thermal conduction is proportional to the magnitude of the temperature gradient, which is expressed as follows:
Herein,
is the material thermal conductivity (W/mK) and dT/dL is the temperature gradient (K/m) in the direction of heat flow, where L is the length, which might be in x, y or z directions mathematically. Equation (1) is valid in any direction at a fixed time, t, but if the space is fixed and the heat flux changes by time then it is possible to write a similar expression as:
The Fourier law can be combined with the energy conservation principle for forming the heat conduction balance analysis problems.
Under the light of the assumptions that there are no heat sources and that the material is homogeneous, isotropic with constant material properties and without any advection heat velocity, the simplest form of the heat flow equation is given by Berkman et al. [
22]. A similar approach has been used for groundwater flow mathematical modeling by Şen [
23].
where k is the thermal diffusivity coefficient, which is equal to the multiplication of the material density,
, with thermal conductivity coefficient,
.
where
Q(
x,
t) and
T(
x,
t) are the heat and temperature amounts at distance
x and time
t. For
and
, Equation (4) becomes:
The general expression for heat within the wall on one side is:
where
v(
x,
t) is the expansion velocity of the heat. After the differentiation of this expression is substituted into Equation (5), then one can obtain:
On the other hand, since the flow is laminar, the Fourier law is applicable, which is expressed as follows:
where
c is the heat conductivity coefficient. Equations (7) and (8) together represent linear flow towards the wall. The substitution of Equation (8) into Equation (7) yields in terms of temperature drop,
s(
x,
t) as:
Solution
The boundary condition and initial conditions for the solution of Equation (9) are as follows:
and
The solution of Equation (9) using Boltzmann ([
24]) transformation of variables technique is given by:
where
The values of
for any given
value can be taken from normal probability distribution function (PDF) tables,
being the normal probability distribution function percentage. In addition, the velocity distribution in the laminar flow pattern case can be found as:
where
C (a constant) depends on the initial and boundary conditions of the heat flux. Type curve for the planer source can be obtained from Equation (13) by defining dimensionless time factor,
u, and wall function
W(
u) as follows:
and
In terms of these new definitions and after some algebraic manipulations, Equation (13) becomes:
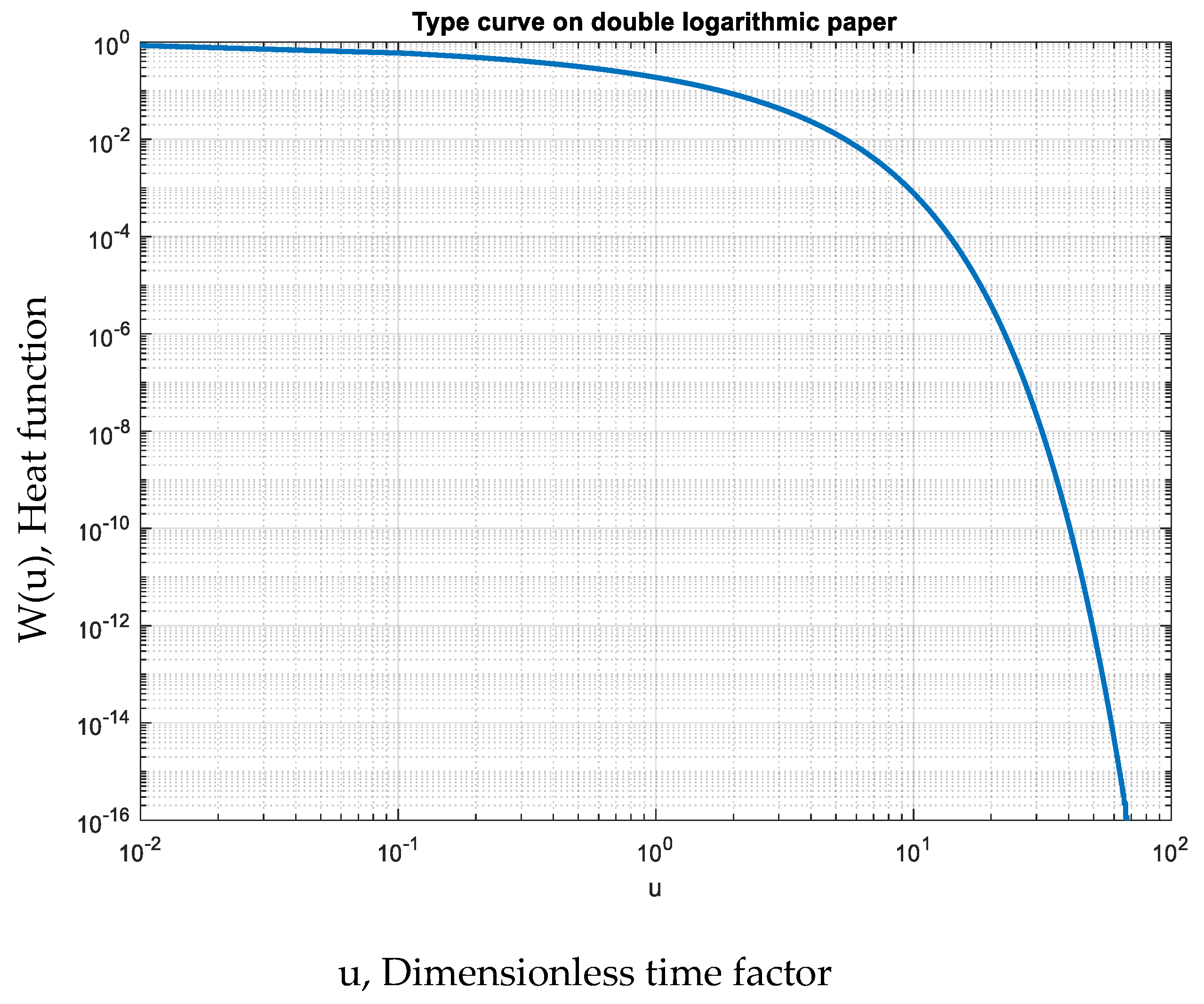
The plot of
W(
u) versus
u (a dimensionless time factor) on a double logarithmic grid gives a type curve for the wall. As
and
, Equation (16) yields that:
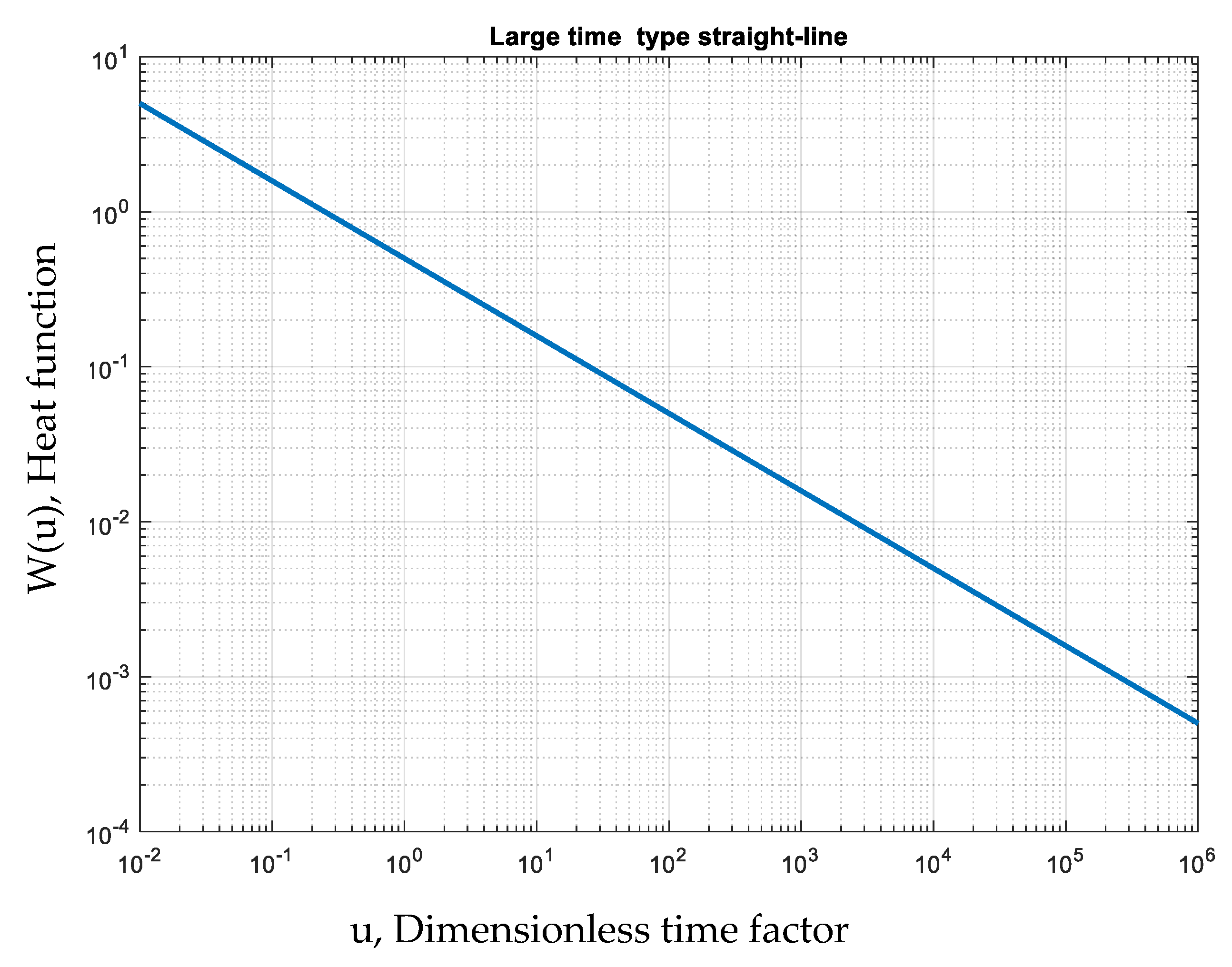
This gives a straight line on a double logarithmic grid with slope of 1/2. Equation (18) represents the late portion of the linear heat flux type curve. Consideration of Equations (15) and (16) leads to an explicit form for Equation (18), as follows:
Substitution of Equations (15) and (18) into the expression in Equation (15), after some algebraic manipulation, leads explicitly to the following form:
All of what has been explained above boils down to a standard type curve, as in
Figure 1, which shows the change of dimensionless heat function
W(
u) by dimensionless time factor (
u).
In
Figure 2 and
Figure 3, the late-time temperature fall standard curves are shown on double logarithmic and semi-logarithmic grids, which provide simple usage for the cases of incomplete record evaluation where the early time records are missing.
3. Application
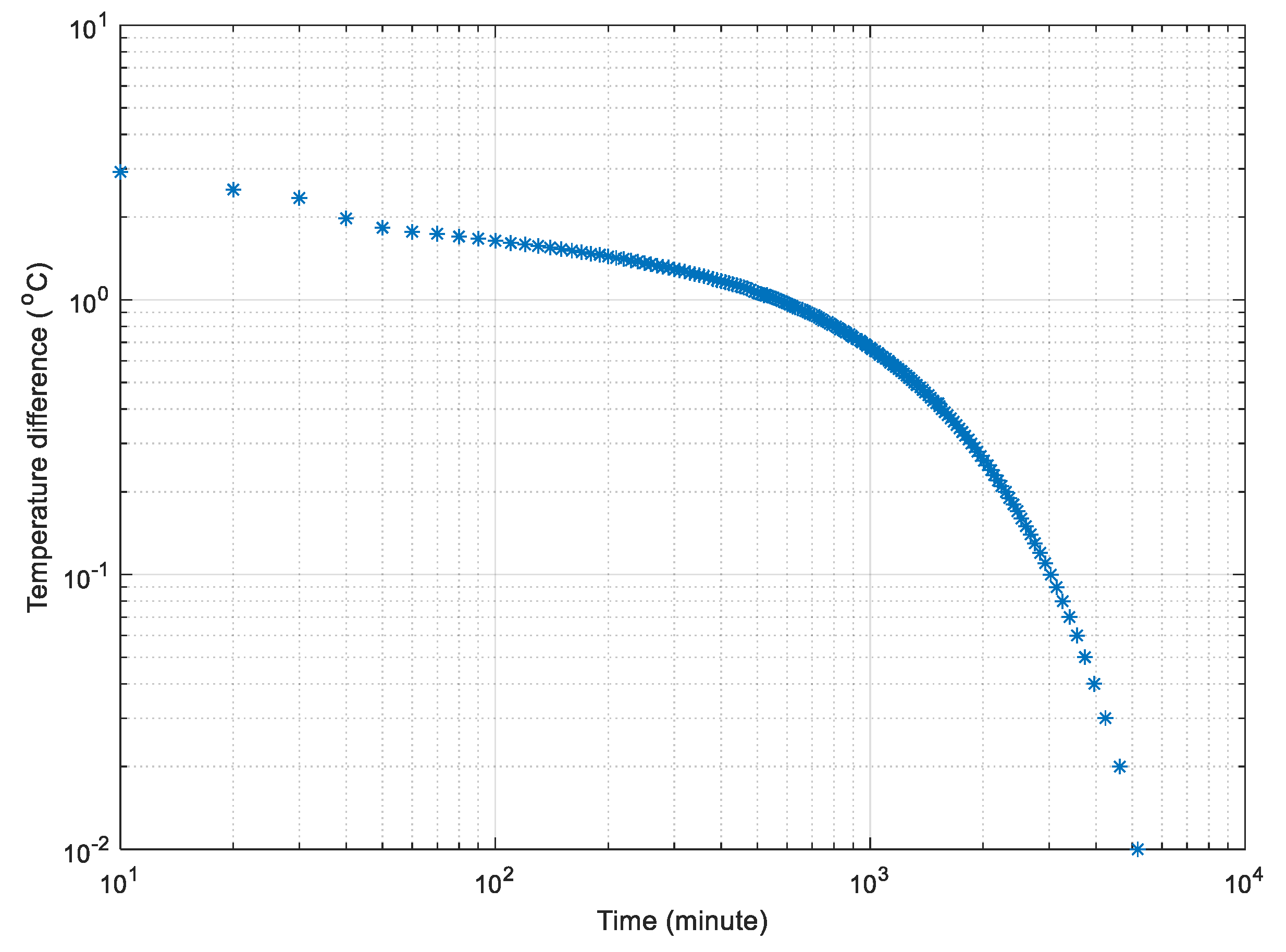
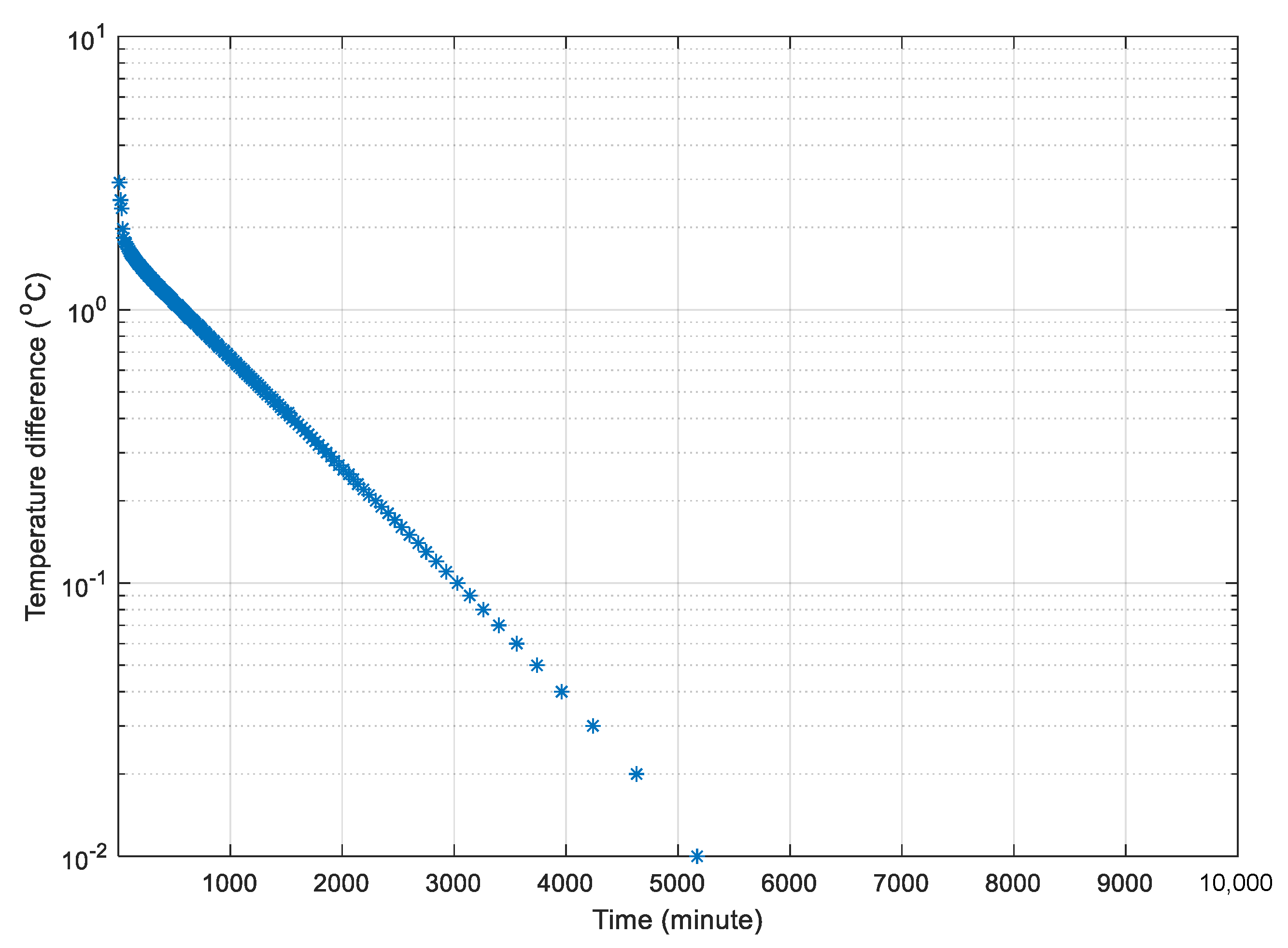
For the application, one of the rooms in a building was heated up to a high temperature and then the heating source was stopped. Starting from the stop time, the records of temperature were taken at a set of predetermined time durations. Logically, the decrease in the temperature by time appears in
Figure 4 as similar to
Figure 2, where the temperature decrease appears in a decreasing form, which reflects the actual time–temperature variation situation in the room after the turning off the heating source. It has to be remembered that the test conditions require homogeneity, isotropic uniformity and room air without any ventilation. These conditions should be available at experimental room in this case its dimensions are: floor area equal to 3 × 5 = 15 m
2; room height equal to 2.9 m; room volume as 3 × 5 × 2.9 = 43.3 m
3. The U-value for the concrete room is 2.296 W/m
2K.
The same time–temperature record decrease is given in
Figure 5 on a semi-logarithmic grid, where late-time temperature record change by time appears along a straight line, similar to the theoretical standard curve in
Figure 3.
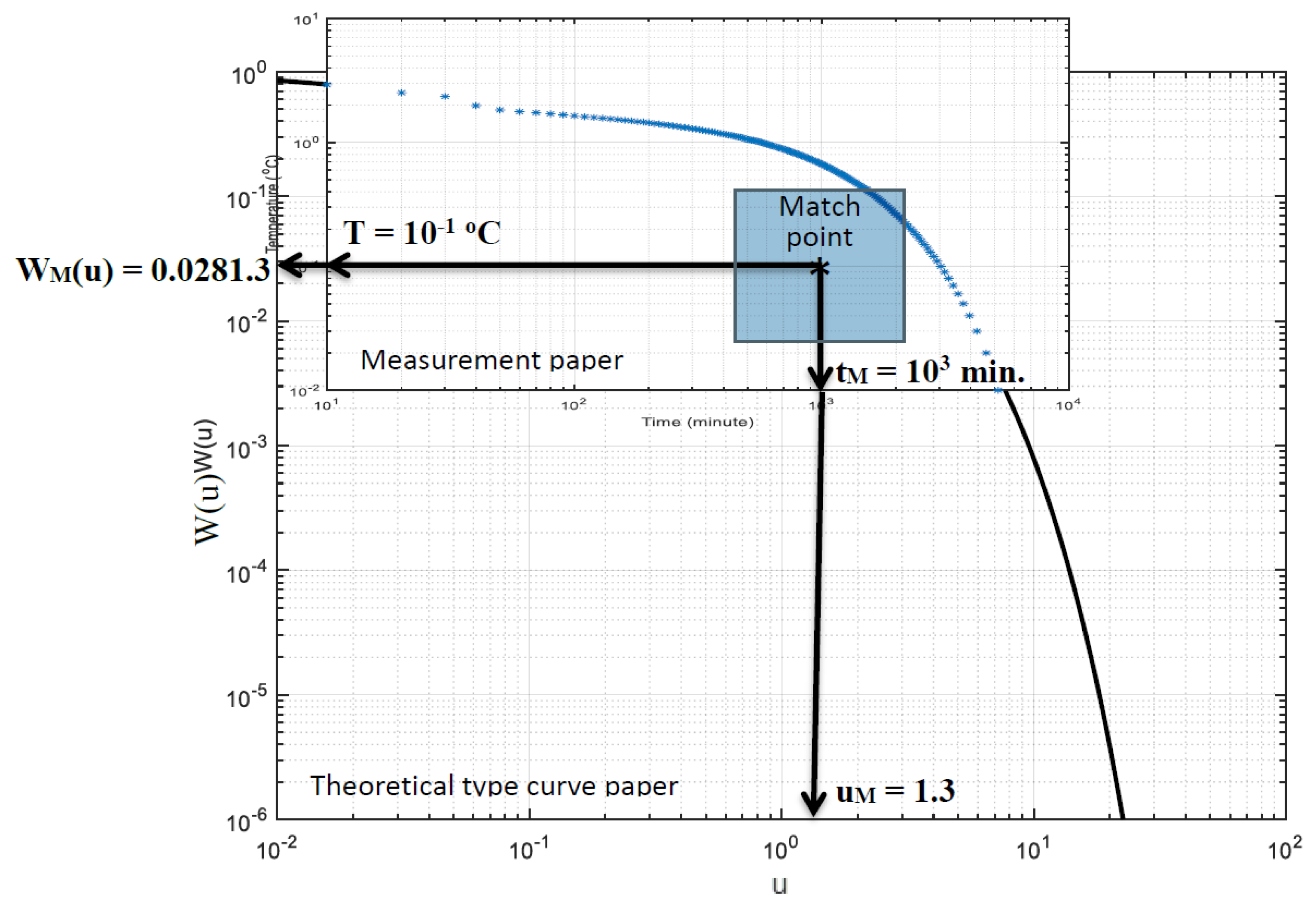
The standard curve in
Figure 1 was overlain on the same double-scale recorded time–temperature scatter diagram, and they were shifted on each other such that the corresponding axes are always parallel to each other until the best match was obtained between the theoretical standard curve and the data scatter points, which led to
Figure 6. For the numerical solution, a match point was selected on the common area of the two graphs, which is shown by M (match point) in
Figure 6. The next step is to read from this figure two theoretical standard curve values, namely W
M(u) = 0.0281 and, on the horizontal axis, u
M = 1.3. The corresponding values on the data sheet axes are T = 10
−1 °C and matching time, t
M = 10
3 min. The substitution of these values into Equations (19) and (20), respectively, yields the storativity and heat conductivity coefficients.