Technological Differences, Theoretical Consistency, and Technical Efficiency: The Case of Hungarian Crop-Producing Farms
Abstract
1. Introduction
2. Materials and Methods
2.1. Heterogeneity in Production Frontiers Models
2.2. Theoretical Consistency
2.3. Data
3. Results
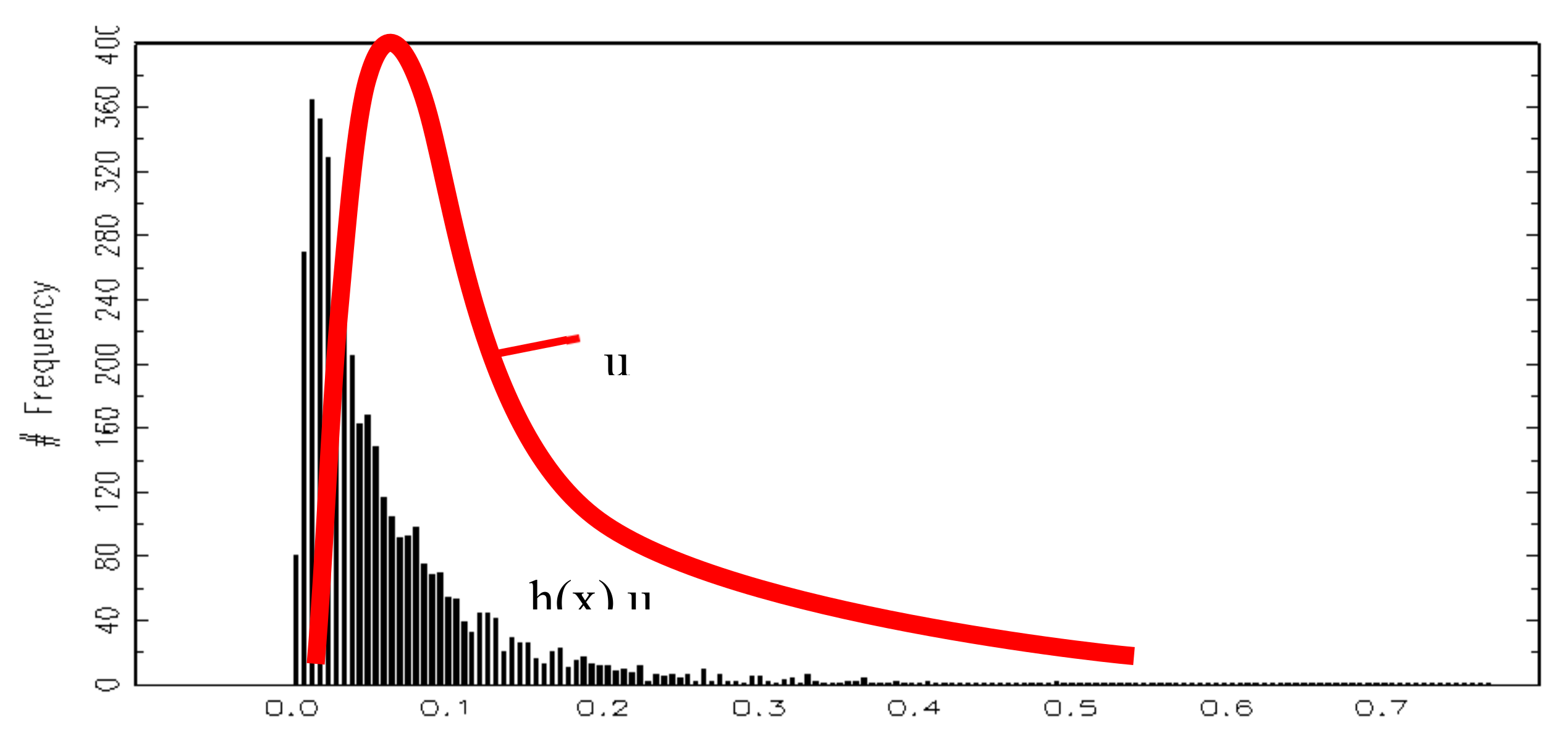
3.1. Comparison of TRE and RPM
3.2. The Effect of Constraints
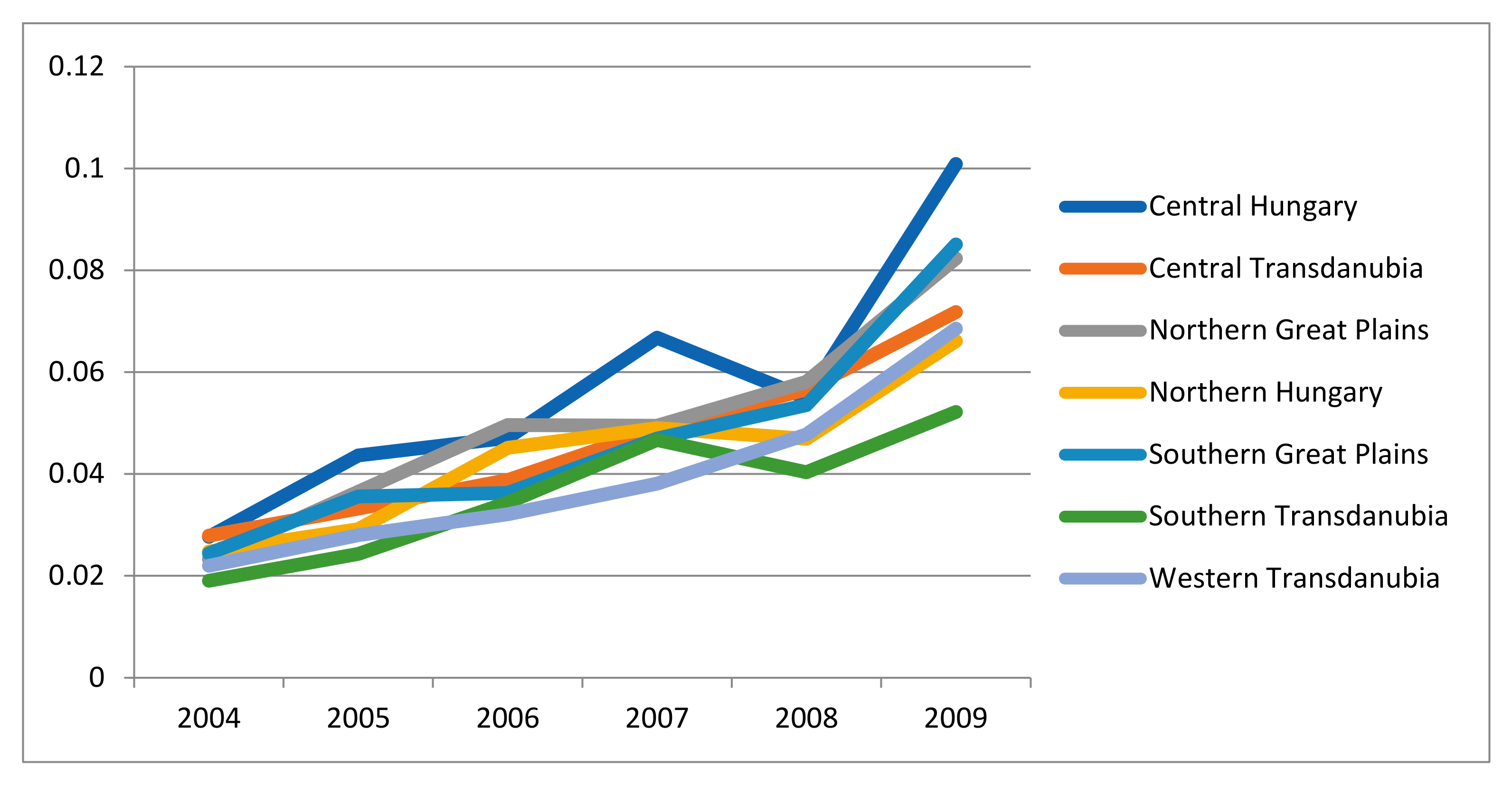
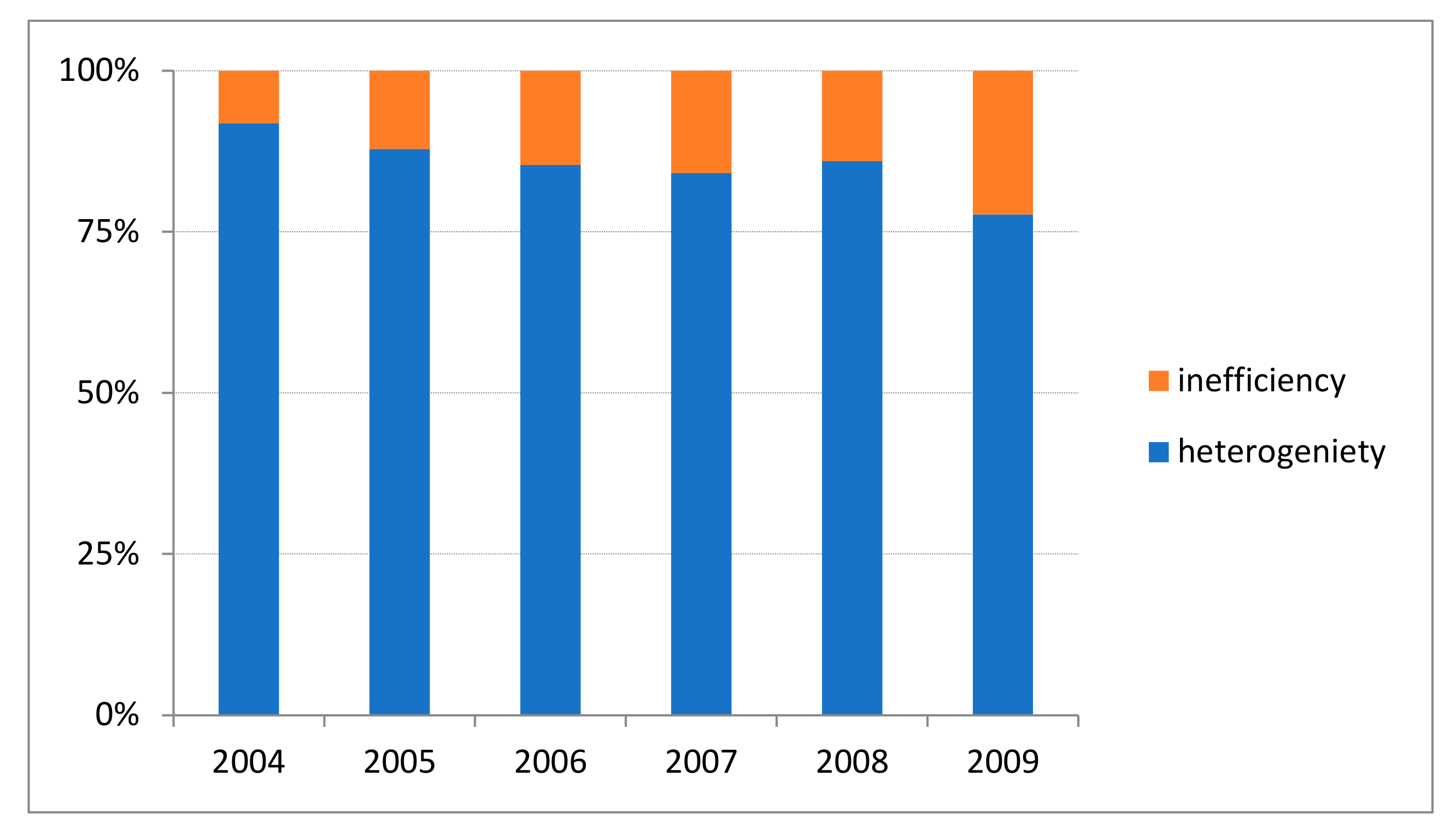
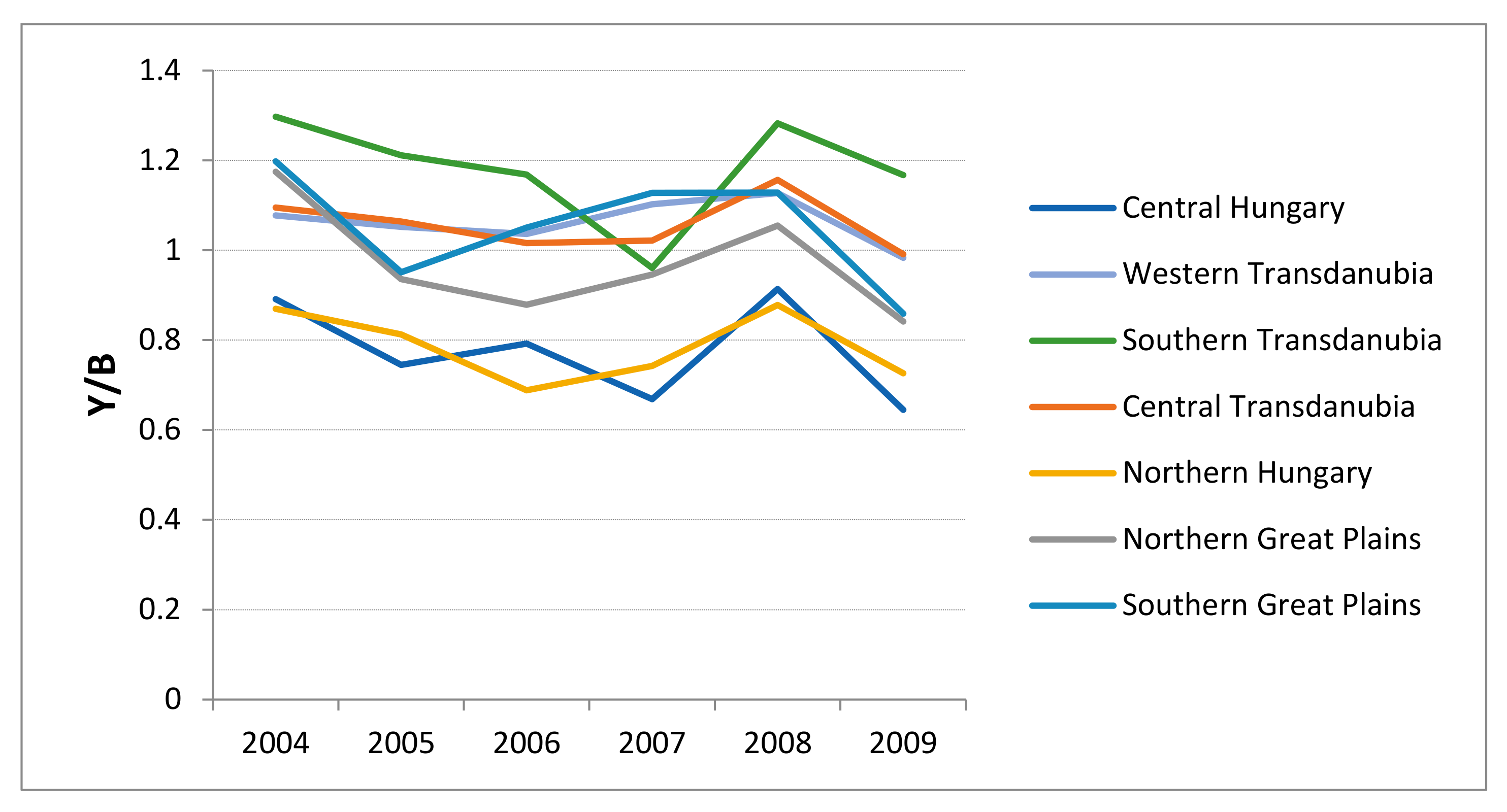
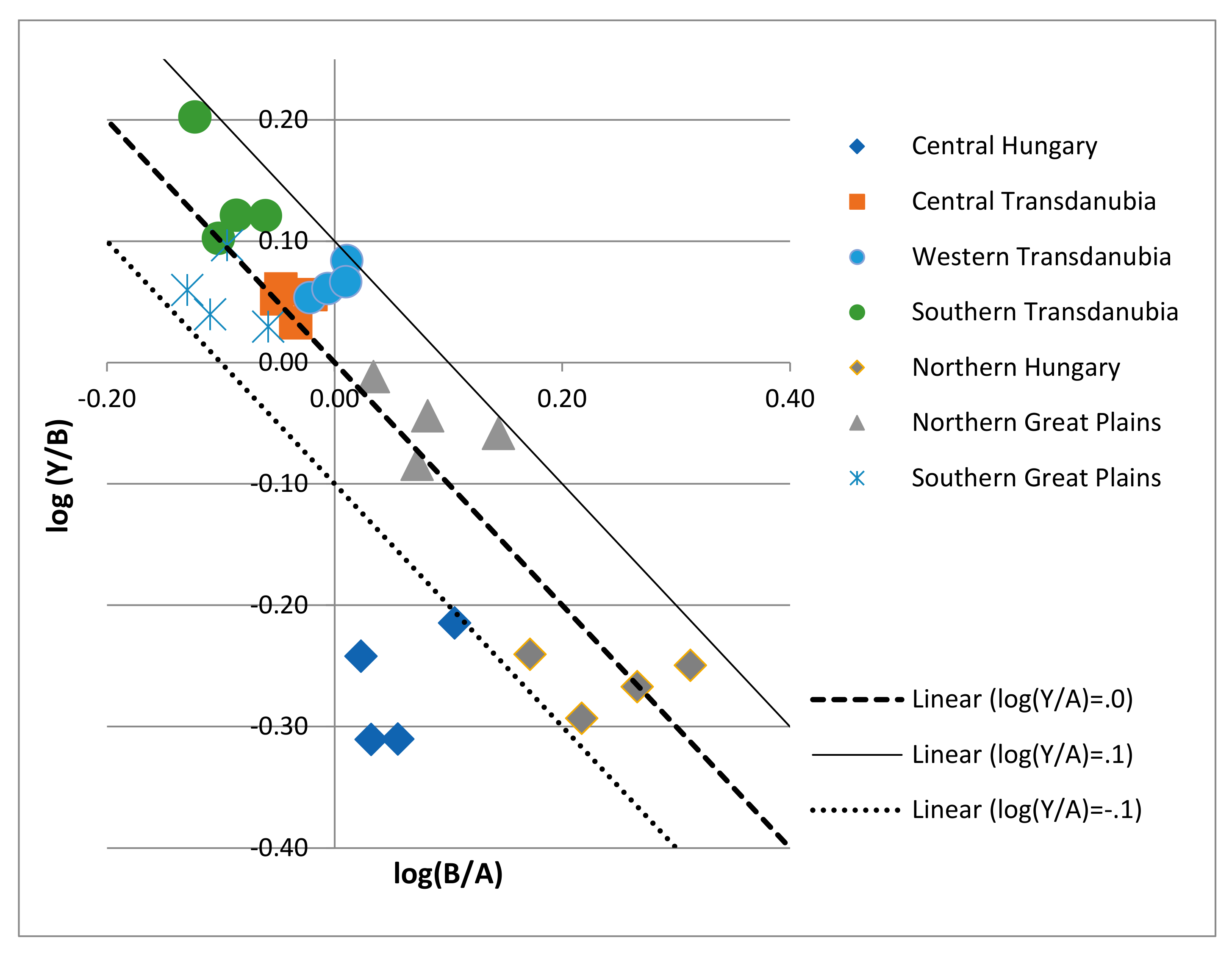
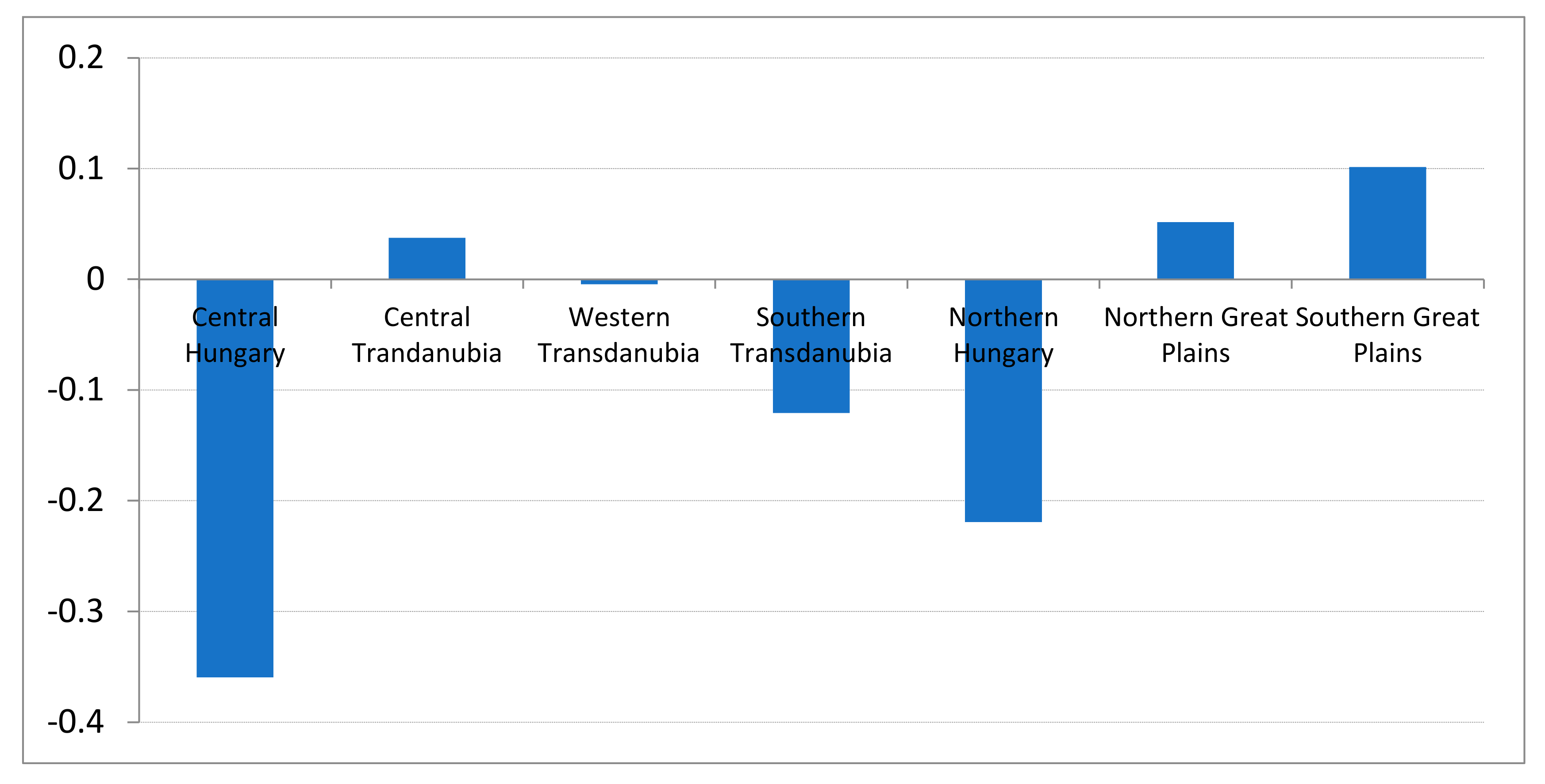
3.3. The Effect of Heterogeneity on Production and the Connection between Farms’ Economic and Natural Conditions and Unobserved Heterogeneity
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Abdulai, A.; Tietje, H. Estimating technical efficiency under unobserved heterogeneity with stochastic frontier models: Application to northern German dairy farms. Eur. Rev. Agric. Econ. 2007, 34, 393–416. [Google Scholar] [CrossRef]
- Bauer, P.W.; Berger, A.N.; Ferrier, G.D.; Humphrey, D.B. Consistency Conditions for Regulatory Analysis of Financial Institutions: A Comparison of Frontier Efficiency Method. J. Econ. Bus. 1998, 50, 85–114. [Google Scholar] [CrossRef]
- Chang, C.-H.; Wu, K.-S.; Chang, B.-G.; Lou, K.-R. Measuring Technical Efficiency and Returns to Scale in Taiwan′s Baking Industry—A case study of the 85 °C Company. Sustainability 2019, 11, 1268. [Google Scholar] [CrossRef]
- Lazikova, J.; Lazikova, Z.; Takac, I.; Rumanovska, L.; Bandlerova, A. Technical efficiency in the Agricultural Business—The case of Slovakia. Sustainability 2019, 11, 5589. [Google Scholar] [CrossRef]
- Tsionas, E.G. Stochastic frontier Models with Random Coefficients. J. Appl. Econom. 2002, 17, 127–147. [Google Scholar] [CrossRef]
- Huang, H.-C. Estimation of Technical Inefficiencies with Heterogeneous Technologies. J. Product. Anal. 2004, 21, 277–296. [Google Scholar] [CrossRef]
- Eberhardt, M.; Teal, F. No Mangoes in the Tundra: Spatial Heterogeneity in Agricultural Productivity Analysis. Oxf. Bull. Econ. Stat. 2013, 75, 914–939. [Google Scholar] [CrossRef]
- Eberhardt, M.; Teal, F. Econometrics for Grumblers: A New Look at the Literature on Cross-Country Growth Empirics. J. Econ. Surv. 2011, 25, 109–155. [Google Scholar] [CrossRef]
- Eberhardt, M.; Vollrath, D. The Effect of Agricultural Technology on the Speed of Development. World Dev. 2018, 109, 483–496. [Google Scholar] [CrossRef]
- Kuenzle, M. Cost Efficiency in Network Industries: Application of Stochastic Frontier Analysis. Ph.D. Thesis, Swiss Federal Institute of Technology Zurich, Zürich, Switzerland, 2005. [Google Scholar]
- Farsi, M.; Filippini, M.; Kuenzle, M. Unobserved heterogeneity in stochastic cost frontier models: An application to Swiss nursing homes. Appl. Econ. 2005, 37, 2127–2141. [Google Scholar] [CrossRef]
- Cillero, M.; Thorne, F.; Wallace, M.; Breen, J. Technology heterogeneity and policy change in farm-level efficiency analysis: An application to the Irish beef sector. Eur. Rev. Agric. Econ. 2019, 46, 193–214. [Google Scholar] [CrossRef]
- Alvarez, A.; del Corral, J. Identifying different technologies using a latent class model: Extensive versus intensive dairy farms. Eur. Rev. Agric. Econ. 2010, 37, 231–250. [Google Scholar] [CrossRef]
- Baráth, L.; Fertő, I. Heterogeneous technology, scale of land use and technical efficiency: The case of Hungarian crop farms. Land Use Policy 2015, 42, 141–150. [Google Scholar] [CrossRef]
- Hsiao, C. Analysis of Panel Data, 3rd ed.; Cambridge University Press: New York, NY, USA, 2014; pp. 1–539. [Google Scholar]
- Belyaeva, M.; Hockmann, H. Impact of regional diversity on production potential: An example of Russia. Stud. Agric. Econ. 2015, 117, 72–79. [Google Scholar] [CrossRef]
- Cechura, L.; Grau, A.; Hockmann, H.; Levkovych, I.; Kroupova, Z. Catching up or falling behind in European agriculture: The case of milk production. J. Agric. Econ. 2017, 68, 206–227. [Google Scholar] [CrossRef]
- Wang, X.; Hockmann, H.; Bai, J. Technical efficiency and producers’ individual technology: Accounting for within and between regional farm heterogeneity. Can. J. Agric. Econ. 2012, 60, 561–576. [Google Scholar] [CrossRef]
- Lachaud, M.; Bravo-Ureta, B.E.; Ludeña, C. Agricultural productivity in Latin America and the Caribbean in the presence of unobserved heterogeneity and climatic effects. Clim. Chang. 2017, 143, 445–460. [Google Scholar] [CrossRef]
- Njuki, E.; Bravo-Ureta, B.E.; O’Donnell, C.J. Decomposing agricultural productivity growth using a random-parameters stochastic production frontier. Empir. Econ. 2018, 57, 1–22. [Google Scholar] [CrossRef]
- Julien, J.; Bravo-Ureta, B.E.; Rada, N. Assessing farm performance by size in Malawi, Tanzania, and Uganda. Food Policy 2019, 84, 153–164. [Google Scholar] [CrossRef]
- Sauer, J. Economic theory and econometric practice: Parametric efficiency analysis. Empir. Econ. 2006, 31, 1061–1087. [Google Scholar] [CrossRef]
- Láng, I.; Csete, L.; Harnos, Z. The Agro-Ecopotential of the Hungarian Agriculture at the Turn of 2000; Mezőgazdasági Kiadó: Budapest, Hungary, 1983; pp. 1–266. [Google Scholar]
- Agrell, P.J.; Brea-Solís, H. Stationarity of Heterogeneity in Production Technology using Latent Class Modelling. Core Discuss. Pap. 2015, 47, 1–21. [Google Scholar]
- Pitt, M.; Lee, L. The measurement and sources of technical inefficiency in Indonesian weaving industry. J. Dev. Econ. 1981, 9, 43–64. [Google Scholar] [CrossRef]
- Schmidt, P.; Sickles, R. Production frontiers with panel data. J. Bus. Econ. Stat. 1984, 2, 365–374. [Google Scholar]
- Greene, W. Reconsidering heterogeneity in panel data estimators of the stochastic frontier model. J. Econom. 2005, 126, 269–303. [Google Scholar] [CrossRef]
- Alvarez, A.; Arias, C.; Greene, W. Accounting for unobservables in production models: Management and inefficiency. Working Paper. Fund. Cent. Estud. Andal. Ser. Econ. 2004, E2004/72, 1–18. [Google Scholar]
- Train, K. Halton Sequences for Mixed Logit. Economics Working Papers E00-27; Department of Economics, University of California: Berkeley, CA, USA, 2000; pp. 1–18. [Google Scholar]
- Terrell, D.; Dashti, I. Incorporating Monotonicity and Concavity Restrictions into Stochastic Cost Frontiers. In Proceedings of the Midwest Econometric Society Meeting, Columbus, OH, USA, May 1997; pp. 1–31. [Google Scholar]
- Sauer, J.; Hockmann, H. The Need for Theoretically Consistent Efficiency Frontiers. In Proceedings of the XIth EAAE Congress, Copenhagen, Denmark, 24–27 August 2005. [Google Scholar]
- Henningsen, A.; Christian, H.C.A. Henning. Imposing regional monotonicity on translog stochastic production frontiers with a simple three-step procedure. J. Product. Anal. 2009, 32, 217–229. [Google Scholar] [CrossRef]
- Coelli, T.J.; Prasada Rao, D.S.; Q′Donnell, C.J.; Battese, G.E. An Introduction to Efficiency and Productivity Analysis, 2nd ed.; Springer: Boston, MA, USA, 2005; pp. 1–349. [Google Scholar]
- Lau, J.L. Testing and imposing monotonicity, convexity and quasi-convexity constraints. In Production Economics: A Dual Approach and Application to Theory and Application, 1st ed.; Fuss, M., McFadden, D., Eds.; North Holland Publishing Company: New York, NY, USA, 1978; Volume 2, pp. 1–360. [Google Scholar]
- Keszthelyi, S.; Pesti, C. A Tesztüzemi Információs Rendszer 2008. évi Eredményei. Agrárgazdasági Inf. 2009, 3, 1–45. [Google Scholar]
- Herlemann, H.H.; Stamer, H. Produktionsgestaltung und Betriebsgröβe in der Landwirtschaft unter dem Einfluss der wirtschaftlich-technischen Entwicklung. Kiel. Stud. 1958, 44, 353–354. [Google Scholar]
- Hayami, Y.; Ruttan, V.W. Agricultural Development: An International Perspctive, 2nd ed.; Johns Hopkins University Press: Baltimore, MD, USA, 1971; pp. 1–367. [Google Scholar]
- Bakucs, L.Z.; Latruffe, L.; Fertő, I.; Fogarasi, J. The impact of EU accession on farms’ technical efficiency in Hungary. Post-Communist Econ. 2010, 22, 165–175. [Google Scholar] [CrossRef]
- Nemes-Zubor, A.; Fogarasi, J.; Molnár, A.; Kemény, G. Farmers’ responses to the changes in Hungarian agricultural insurance system. Agric. Financ. Rev. 2018, 78, 275–288. [Google Scholar] [CrossRef]
- Latruffe, L.; Fogarasi, J.; Desjeux, Y. Efficiency, productivity and technology comparison for farms in Central and Western Europe: The case of field crop and dairy farming in Hungary and France. Econ. Syst. 2012, 36, 264–278. [Google Scholar] [CrossRef]
- Jondrow, J.; Knox, C.A.; Materov, I.S.; Schmidt, P. On the Estiamtion of Technical Inefficiency in the Stochastic Frontier Production Function Model. J. Econom. 1982, 19, 233–238. [Google Scholar] [CrossRef]
| Symbol | Mean | Standard Deviation | Minimum | Maximum | |
|---|---|---|---|---|---|
| Output (EUR) | Y | 40,097.8 | 84,487.8 | 128.51 | 931,774.0 |
| Labor (AWU) | A | 3.73 | 8.30 | 0.01 | 100.09 |
| Land (ha) | L | 237.41 | 428.57 | 3.68 | 3787.0 |
| Capital (EUR) | K | 17,309.6 | 42,077.1 | 5.53 | 339,055.0 |
| Variable Inputs (EUR) | V | 28,224.6 | 60,186.5 | 323.26 | 657,902.0 |
| TRE | M_Alvarez | ||||
| Constant | 0.273 | *** | 0.241 | *** | |
| Neutr TF | T | 0.006 | ** | 0.028 | *** |
| TT | 0.009 | *** | 0.018 | *** | |
| Inputs-first order | A | 0.054 | *** | 0.074 | *** |
| L | 0.158 | *** | 0.177 | *** | |
| K | 0.132 | *** | 0.142 | *** | |
| V | 0.664 | *** | 0.571 | *** | |
| Biased technical change | A*T | −0.001 | 0.000 | ||
| L*T | −0.006 | 0.000 | |||
| K*T | 0.008 | ** | 0.007 | * | |
| V*T | −0.004 | −0.009 | |||
| Second order | AA | 0.038 | ** | 0.010 | |
| LL | 0.052 | 0.126 | ** | ||
| KK | 0.067 | *** | 0.071 | *** | |
| VV | 0.023 | 0.023 | |||
| AL | −0.107 | *** | −0.077 | *** | |
| AK | 0.017 | * | 0.010 | ||
| AV | 0.046 | ** | 0.051 | ** | |
| LK | 0.015 | −0.008 | |||
| LV | 0.002 | −0.057 | |||
| KV | −0.082 | *** | −0.051 | ** | |
| Unobserved heterogeneity | AM | 0.181 | *** | 0.179 | *** |
| AM_T | - | 0.018 | *** | ||
| AM_A | - | 0.027 | *** | ||
| AM_L | - | 0.015 | ** | ||
| AM_K | - | −0.001 | |||
| AM_V | - | −0.070 | *** | ||
| Auxiliary para-meters | SV | 0.167 | *** | 0.167 | *** |
| SU | 0.395 | *** | 2.083 | *** | |
| () | 2.368 | 2.232 | |||
| RTS | 1.008 | 0.964 | |||
| Model selection | Log L | −1011.391 | −853.328 | ||
| AIC | 2070.782 | 1764.656 | |||
| BIC | 2109.190 | 1811.065 |
| Mono-Tonicity | Quasi-Concavity | Consistent | Binding Restrictions | ||
|---|---|---|---|---|---|
| Linear | Nonlinear | ||||
| RPM without constraints | 88% | 75% | 73% | ||
| RPM with constraints | 97% | 93% | 92% | 7 | 3 |
| RPM without Constraints | RPM with Constraints | Difference (%) + | ||||
| Constant | 0.2412 | *** | 0.2513 | *** | 4.0% | *** |
| T | 0.0283 | *** | 0.0288 | *** | 1.7% | *** |
| TT | 0.0176 | *** | 0.0176 | *** | 0.0% | |
| A | 0.0735 | *** | 0.0750 | *** | 2.0% | *** |
| L | 0.1768 | *** | 0.1748 | *** | −1.1% | *** |
| K | 0.1423 | *** | 0.1397 | *** | −1.9% | *** |
| V | 0.5711 | *** | 0.5716 | *** | 0.1% | |
| A*T | 0.0001 | 0.0007 | 85.7% | *** | ||
| L*T | −0.0003 | 0.0021 | 114.3% | *** | ||
| K*T | 0.0073 | * | 0.0070 | ** | −4.3% | *** |
| V*T | −0.0092 | −0.0116 | ** | 20.7% | *** | |
| AA | 0.0102 | 0.0087 | −17.2% | *** | ||
| LL | 0.1263 | ** | 0.0882 | ** | −43.2% | *** |
| KK | 0.0713 | *** | 0.0481 | *** | −48.2% | *** |
| VV | 0.023 | −0.0147 | 256.5% | *** | ||
| AL | −0.0771 | *** | −0.0592 | *** | −30.2% | *** |
| AK | 0.0104 | 0.0082 | −26.8% | *** | ||
| AV | 0.0512 | ** | 0.0416 | ** | −23.1% | *** |
| LK | −0.0075 | −0.0063 | −19.0% | *** | ||
| LV | −0.0569 | −0.0324 | −75.6% | *** | ||
| KV | −0.0507 | ** | −0.0300 | *** | −69.0% | *** |
| AM | 0.179 | *** | 0.1746 | *** | −2.5% | *** |
| AM_T | 0.0178 | *** | 0.0173 | *** | −2.9% | *** |
| AM_A | 0.0267 | *** | 0.0240 | *** | −11.3% | *** |
| AM_L | 0.0148 | ** | 0.0155 | *** | 4.5% | *** |
| AM_K | 0.0006 | 0.0025 | 76.0% | *** | ||
| AM_V | −0.0697 | *** | −0.0714 | *** | 2.4% | *** |
| SV | 0.1671 | *** | 0.1681 | *** | 0.6% | *** |
| SU | 2.0828 | *** | 2.1287 | *** | 2.2% | *** |
| 2.232 | 2.211 | 0.9% | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baráth, L.; Fertő, I.; Hockmann, H. Technological Differences, Theoretical Consistency, and Technical Efficiency: The Case of Hungarian Crop-Producing Farms. Sustainability 2020, 12, 1147. https://doi.org/10.3390/su12031147
Baráth L, Fertő I, Hockmann H. Technological Differences, Theoretical Consistency, and Technical Efficiency: The Case of Hungarian Crop-Producing Farms. Sustainability. 2020; 12(3):1147. https://doi.org/10.3390/su12031147
Chicago/Turabian StyleBaráth, Lajos, Imre Fertő, and Heinrich Hockmann. 2020. "Technological Differences, Theoretical Consistency, and Technical Efficiency: The Case of Hungarian Crop-Producing Farms" Sustainability 12, no. 3: 1147. https://doi.org/10.3390/su12031147
APA StyleBaráth, L., Fertő, I., & Hockmann, H. (2020). Technological Differences, Theoretical Consistency, and Technical Efficiency: The Case of Hungarian Crop-Producing Farms. Sustainability, 12(3), 1147. https://doi.org/10.3390/su12031147






