Abstract
Effective agricultural policymaking requires the accurate estimation of the production technology and efficiency of farms. However, several methodological issues should be considered when modelling production and estimating technical efficiency. In this paper, we focus on two of these—technological heterogeneity and theoretical consistency—as implied in microeconomic theory. Heterogeneity in the efficiency literature is often evaluated using a variable intercept model. However, in farm production, it is likely that heterogeneity also affects the marginal productivity of production factors. Some earlier papers investigated the effect of unobserved heterogeneity on technical efficiency using latent class models, but the application of random parameter models is limited. One of our main contributions in this paper is that we apply a modified version of a random parameter model to investigate the effect of unobserved heterogeneity on production factors and efficiency. The second aim was to impose regularity conditions into the model through introducing linear and non-linear constraints and thereby investigate their significance. Third, we examined the relationship between unobserved heterogeneity and the natural and economic conditions of farms. Our findings show that heterogeneity has a greater effect on variation in output than technical efficiency; furthermore, the violation of theoretical consistency significantly influences the results. These findings also reveal that the explanatory power of regional natural and economic conditions is significant but not sufficient on the variance of estimated unobserved heterogeneity.
1. Introduction
Analyses of farm efficiency using frontier methods can deliver significant insight into the competitiveness of farms and their potential to increase productivity and improve resource use. Policymakers are particularly interested in the potential impact of their decisions on the performance of firms. Thus, findings about technical efficiency (TE) have far-reaching policy implications [1,2].
Numerous papers have been written about the technical efficiency [3,4], but in the majority of the technical efficiency literature, homogeneous technology is assumed for farms. Technology, in this context, refers to the shape of the production function. However, farms may adopt different technologies or face different natural resource and economic conditions for a variety of reasons [5]. Without taking into account this possible heterogeneity, estimates about the efficiency and productivity of farms can be under-estimated [6]
There is a growing body of macro-agricultural productivity literature which emphasizes the importance of modelling heterogeneous technologies [7,8,9]. In a recent paper, Eberhardt and his co-authors [7] describe an extensive comparison of different linear parametric models and reveal that the assumption of a homogeneous production function in the farm sector may mask or distort important insights into development [7]. The author also demonstrates that failure to account for technological heterogeneity leads to misspecified empirical models with serious implications for any total factor productivity (TFP) estimates thereby obtained [5].
In a Stochastic Frontier context, intensive investigation using farm-level data has already been conducted to examine which model is best able to separate technical efficiency from unobserved heterogeneity. Most papers have found that the true random effect (TRE) model is most appropriate for this task (e.g., references [1,10,11]). Additionally, some authors have investigated the effect of heterogeneous technology using latent class models (LCM) [12,13,14]
Although the TRE Model is able to separate TE and heterogeneity, it is insufficient for capturing the underlying variation in agricultural technology. However, as Hsiao argues, in farm production, it is likely that unobserved heterogeneity also impacts the marginal productivity of inputs [15]. In this context, random parameter models (RPMs) appear to be more capable of capturing the unobserved heterogeneity than models with only individual- and/or time-specific effects (variable-intercept models). Despite this fact, variable-coefficient models have not gained such wide acceptance in empirical work as variable-intercept models, perhaps because of their computational complexity. However, this does not mean that there is less need to take account of parameter heterogeneity [15]. The number of papers that applied RPM in agricultural context is very limited (e.g., references [16,17,18,19,20,21]).
The first aim of this paper is to apply a modified version of a random parameter model, which has favorable characteristics for investigating the effect of unobserved heterogeneity on production factors and efficiency. In addition, the robustness of policy suggestions based on inferences about efficiency measures crucially depends on having theoretically well-founded estimates. Theoretically inconsistent frontiers over- or understate real relative inefficiency and hence lead to severe misperceptions and, ultimately, inadequate as well as counterproductive policy measures [22]. Despite this fact, only a few applications exist that emphasize the need for theoretically consistent frontier estimation.
The second aim is to check for the effect of the fulfilment of theoretical consistency, namely monotonicity and quasi-concavity requirements. In order to fulfil this aim, we estimate the model with and without monotonicity and quasi-concavity constraints and check the differences between the results. Monotonicity is imposed through linear constraints: i.e., we impose the condition that the gradient of the function with respect to each input should be positive. Quasi-concavity is imposed through non-linear constraints—i.e., we impose the condition that the bordered Hessian matrix of the function should be semi-definite.
The third aim is to examine the effect of heterogeneity on the variation in output and the connection between unobserved heterogeneity and farms’ economic and natural conditions. For the empirical analysis, we use data from the Hungarian Farm Accountancy Data Network (FADN). In terms of the characteristics of Hungarian agriculture, we assume that there exist at least two significant background factors that imply that technological parameters are different across farms; thus, the estimation of a homogeneous production function might lead to inadequate policy implications. First, Hungarian agriculture has a typical dual structure, with a large number of small-scale farms on the one hand and a small number of large-scale farms on the other, while within these categories, there are further significant differences among farms (i.e., the standard deviation of output and input variables are high). Second, ecological conditions are very diverse—according to a survey of agro-economic potential, 35 ecological regions may be distinguished [23]. Because of these facts, we think that the use of an RPM is an adequate approach to modelling production structure and efficiency in such a diverse production environment.
The remainder of the paper is organized as follows. We begin by briefly examining earlier studies involving heterogeneity, and we then outline the methods used in the analysis (Section 2). In Section 3, we present the data used in our analysis. The following section (Section 4) discusses results. Here, special weight is put on the estimated efficiencies and the interpretation of unobserved heterogeneity. Finally, Section 4 summarizes our findings and draws conclusions for future modelling.
2. Materials and Methods
2.1. Heterogeneity in Production Frontiers Models
Early work on heterogeneity focused on including environmental variables into production models [24]. However, in many cases, it may not be feasible to include such kind of variables because of shortages of degrees of freedom or multicollinearity, or they may simply not be observable [15]. Therefore, later work explored various statistical techniques for determining the omitted variables (i.e., unobserved heterogeneity) [24].
Conventional panel data models such as fixed-effects or random-effects models [25,26] are able to handle heterogeneity, but these models have two major limitations—(i) treatment of the inefficiency term as time-invariant, which raises a fundamental identification problem, and (ii) they fail to distinguish between cross individual heterogeneity and inefficiency [1,27]
To account for these limitations, Greene proposed two stochastic frontier models that are time-variant and that distinguish unobserved heterogeneity from the inefficiency component [27]. These models are termed the “true” fixed effects (TFE) and “true” random effects (TRE) models [1]. However, as pointed out by Greene the TFE model might produce biased individual effects and efficiency estimates because the presence of individual effects creates an incidental parameter problem [27]. In contrast, TRE models produce unbiased inefficiency estimates, therefore we focus here on the description of TRE model only.
The TRE model may be written as follows:
where represents the output of the i-th farm, , is a vector of inputs, is a vector of unknown parameters, is a symmetric random error, which accounts for statistical noise and is a non-negative random variable associated with technical inefficiency; is a time-invariant, firm-specific random term intended to capture farm-specific heterogeneity; is a firm specific intercept; denotes average value of . The estimation procedure is similar to that used with one of the models discussed below. In order to avoid duplication, we omit a detailed description of the estimation procedure here.
Although TRE is able to separate TE and heterogeneity, it is insufficient for modelling the effect of unobserved heterogeneity on production technology. In other words, heterogeneity influences only the intercept; the slope parameters are common for every cross-sectional units. However, there are cases in which there are changing economic structures or unobserved but different socioeconomic, demographic, or climatic background factors imply that the response parameters of the included variables may be different for different cross-sectional units. For instance, in farm production it is likely that variables not included in the specification could also impact the marginal productivity of production factors [15]. In these situations, varying coefficient models appear to be more capable of capturing unobserved heterogeneity than models with only individual-specific and/or time-specific effects (variable-intercept models) [15].
One way of allowing differences in the coefficients across individual units is that each regression coefficient can be viewed as a random variable with a probability distribution (random parameter models). Different specifications of RPMs can be found in the literature. As our aim was to examine the effect of unobserved heterogeneity on production technology, we applied such a specification that is favorable for examining the effect of unobserved heterogeneity.
The key feature of the applied specification is that the random component of each random parameter is the same, and only the constant and first-order terms are randomly distributed. This specification is similar to the TRE Model, the only difference being that unobserved heterogeneity influences not only the intercept of the model, but also the slope parameters. Alternatively, this model can be seen as a modification of the Alvarez, Arias, and Greene model [28] with a different interpretation. The difference between this model and the Alvarez model is as follows: in the Alvarez model, the square of the random component also appears in the model. However, because of the inclusion of the square component in the Alvarez model, the crucial assumption of the independence of “u” and the explanatory variable does not necessarily hold. Without the inclusion of the second term, this problem can be avoided. Additionally, Alvarez and his co-authors [28] interpret the latent variable as an effect that accounts for management differences between firms. However, recent empirical papers [18,29] have argued that this term might capture the effect of various sources of unobserved heterogeneity such as differences in regional/farm characteristics, input quality, environmental conditions, or socioeconomic characteristics, etc. We follow this interpretation.
A Random Parameter Model might be written out as follows:
where
Equation (1) is clearly similar to that for the TRE model. In the TRE model, unobserved heterogeneity () influences only the intercept (), while in this specification also influences—in addition to the intercept—the explanatory variables and t.
The parameters of the model can be estimated using the maximum simulated likelihood technique, we refer the reader for further discussion of this technique to references [27,28,29] for discussion. The estimation strategy applied in this paper can be found in Appendix A.
Technical efficiency can be defined similarly as in reference [28]. Farms generally do not exploit their full production capacities (); i.e., their actual output () may be less than the optimal level of output. The optimal level of production can be achieved with the maximum level of the unobserved components ( ), while the actual level of production can can be produced with the actual level of (), where ().
Having defined the optimal and actual level of production, we can now define technical efficiency (TEit or )—which is the ratio of observed to potential output:
For estimation, a critical assumption is the absence of any correlation between and the input levels (); therefore [28] highlight that it is important to show explicitly how TE is defined in the model. In the original Alvarez model, however, it is not possible to separate properly and the other input variables because of the inclusion of the square term of the unobserved variable. In our modified version, it can be seen that the effect of x and the unobserved variable can be separated:
2.2. Theoretical Consistency
Measures of firm efficiency appear quite sensitive to the choice of the functional form. If the functional form lacks flexibility, inefficiency tends to be overestimated by attributing some portion of the misspecification error to firm inefficiency. This fact suggests the need to choose a very flexible form to approximate the unknown function. While a more flexible form has the advantage of reducing misspecification error, most flexible functional forms (such as the translog or generalized Leontief) frequently violate conditions of monotonicity and concavity. However, if the estimated frontier fails to adhere to the theory, it is problematic to attribute deviations resulting from that form to inefficiency [30].
The findings of previous studies clearly show that concavity and monotonicity violations are a serious problem in efficiency analysis [22,30,31]. Despite their importance, most empirical studies do not impose demands for monotonicity and quasi-concavity. According to Henningsen and Henning [32], the reason for this may be that existing approaches are rather complex and laborious [32].
There are different approaches to imposing regularity conditions. One is to undertake a constrained maximum likelihood (ML) estimation, i.e., the likelihood function is maximized subject to the restriction that the theoretically derived properties of the frontier function are fulfilled. As another solution, Coelli and his co-authors [33] use the Bayesian MCMC method to estimate a stochastic frontier distance function with all desirable theoretical conditions imposed at all data points [32]. Recently, a three-step procedure has been suggested for imposing monotonicity [32]. This latter method is adequate for imposing monotonicity but cannot be used to impose quasi-concavity. However, without satisfying the demands of both curvature and monotonicity, the second-order conditions for optimizing behaviour fail, and duality theory fails [31]
In this paper, we use the constrained maximum likelihood method. In order to maintain the flexibility of our function, we do not impose regularity conditions globally. However, imposing restrictions locally—at only one point (the usual practice is to impose them at the sample mean)—is not sufficient for obtaining reasonable efficiency estimates [32]. Therefore, we identify several approximation points and impose constraints at these points.
The approximation points were calculated as follows: for each variable the one-sigma deviation from the mean was calculated. All observations inside of the one-sigma deviation were excluded. For the resulting data sets, the mean of each variable was computed; these means in the newly constructed data set were then used as new approximation points. Since we had four exogenous variables, we constructed eight approximation points.
For each point, we had a four linear monotonicity restriction and a one-sign restriction for the impact of unobserved heterogeneity (Equation (2)). In addition, there were four nonlinear curvature restrictions for each of the approximation points. This procedure gives us consistent results from an economic perspective for a wide range of observations.
In order to fulfil the monotonicity criteria, linear constraints were built into the model, as follows:
where denotes the linear constraints for observed inputs and denotes the linear constraint for the unobserved heterogeneity (), and other variables as defined earlier. The model was forced to fulfil these criteria at every defined approximation point.
Similarly, in order to fulfil the criteria of quasi-concavity we built nonlinear constraints into the model and guaranteed that the bordered Hessian at the different approximation points is negative semidefinite. For this, we applied Cholesky decomposition [34]. Accordingly, every bordered Hessian Matrix H can be written in the following form,
Here, the matrix A refers to the second derivatives of the production function with respect to inputs, and a represents the vector of first derivatives of the production function. The Cholesky factorization of is L’DL [34]. The matrix D represents the Cholesky factors dii for i = 1,4, and L is a lower triangular matrix with element lij, for i, j = 1,4 and lii = 1.
Using , the above expression changes to
This results in the following curvature restrictions:
2.3. Data
For the purposes of empirical analysis, we used data from the Hungarian Farm Accountancy Data Network (FADN); more specifically, data about specialized cereal, oilseed and, protein crop (COP)-producing farms over the 2004–2009 period. Agricultural farms can join and leave the Hungarian FADN system; thus, to maintain representativeness, farms that leave the system are replaced by similarly characterized farms [35]. Our primary goal was to examine technological differences between farms. This can be better done if, in every year, the same farms remain in the sample, so we used a balanced panel. Our sample contains 3984 observations, 664 for each year. Data were provided by the Research Institute for Agricultural Economics.
We estimated the model with one output (Y—total agricultural production in constant EUR) and the following four inputs: (1) labor in Annual Work Units (A), (2) utilized agricultural area (UAA) in hectares (L), (3) capital input (as a sum of depreciation and services) in constant EUR (K), and (4) variable input (intermediate consumption) in constant EUR (V). All of the variables expressed in nominal prices were deflated to 2005 prices with the use of the appropriate deflators; namely, output (Y) was deflated by the agricultural output price index, total specific costs (V) by the price index of purchased goods and services, and the corresponding values of total fixed assets (K) by the price index of agricultural investments. Some descriptive statistics are presented in Table 1.

Table 1.
Descriptive statistics.
The high variance of individual variables is apparent; e.g., labor input had a minimum value of 0.01 AWU and a maximum of 100 AWU, while the values for (UAA) ranged from 8.5–3787 hectares. These significant differences suggest that heterogeneity plays an important role in Hungarian agriculture. The huge differences between the minimum and maximum values also imply that the marginal products of these inputs are different among farms; thus, it seems reasonable to assume that farms with such heterogeneous input endowments use different technologies, and it is important to account for these differences in production models.
3. Results
3.1. Comparison of TRE and RPM
We start with a discussion of parameter coefficients without constraints. Table 1 reports the parameter estimates for the estimated TRE and Random Parameter Models (RPMs). All variables were divided by their geometric mean; thus, the first-order coefficients can be interpreted as output elasticities evaluated using the geometric mean of the sample.
First, the effect of the unobserved latent variable assumed to capture the effect of heterogeneity is significant in both models. However, the interaction of this variable is significant not only with the constant (the assumption of TRE) but also with most of the observed inputs, which suggests that it is important to also model these interactions in order to get unbiased results. In other words, it shows that there exist significant technological differences among Hungarian farms and neglecting this heterogeneity effect might lead to inadequate policy outcomes.
Second, Table 2 clearly shows that the first-order coefficients are different among the estimated models. The biggest difference can be seen regarding the estimates of material inputs. The elasticity of material inputs is round 10% lower in the RPM. Furthermore, all models suggest that technological progress occurred, and the growth rate increased in Hungarian agriculture over the analysed period. However, the RPM suggests that technological progress was much greater. There are no differences among the models in terms of the characteristics of technological change: all models suggest that it was capital-using.

Table 2.
Parameter estimates—model comparison.
Third, and are significant in both models, and the estimates of are much higher than , suggesting that variations in inefficiency have a significantly larger impact on output variation than statistical noise and confirming that technical inefficiency is an important phenomenon in Hungarian agriculture. In the case of the RPM, is much higher compared to TRE. However, when calculating for the modified RPM the different definition of should be taken into account. Computing this expression at the sample mean gives . Thus, both models give similar results for the significance of inefficiency.
Fourth, the consequence of the different definitions of can be also seen in Figure 1. The red line represents the distribution of u for both models. The line represents only a rough characterization of the distribution of u. Since it is used for illustrative purpose only, this procedure appears reasonable. However, this distribution of u also represents the distribution of technical efficiency in the first model. The distribution of technical efficiency in the RPM is illustrated by the histogram in Figure 1. At first glance it is convincing that the efficiencies of the first model are much lower than in the other model. While in the first model a large share of farms has an efficiency lower than 25% (e-u, u > 0.3), the share of farms that operate at low efficiency is reduced to a marginal fraction in the second model. Given that farms are operating in a homogeneous institutional environment, this wide range of efficiencies is difficult to justify. Thus, we conclude that the RPM depicts inefficiency more appropriately than the TRE model.
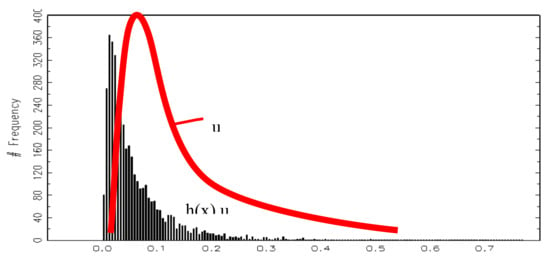
Figure 1.
Distribution of inefficiencies by model. Source: Authors’ calculation.
Fifth, returns to scale are also different between the models. TRE suggest slightly increasing return to scale, whereas applied RPM suggests slightly decreasing RTS.
To select the most appropriate specification we used model selection criteria; namely, we used Akaike Information Criteria (AIC) and Bayesian information criterion (BIC) (also known as Schwarz Criterion, SBC, or SBIC). The preferred model is the one for which the values of these statistics are lowest. Table 1 clearly shows that both the values of AIC and BIC are lower in the case of RPM; thus, RPM is the preferred model for these data. Therefore, in the following analysis, we only use this model for further investigation.
3.2. The Effect of Constraints
In the next step of our analysis, we examined the effect of constraints. Before discussing the different parameter estimates with and without constraints, we checked what percentage of observations were consistent with and without constraints and the number of binding restrictions. Results are presented in Table 3.

Table 3.
Checking theoretical consistency (% of observations, n).
Table 3 reveals that the proportion (%) of consistent estimates increased substantially. Despite the fact that we estimated the model with a great number of restrictions, only 10 of these were binding.
The imposition of constraints in the estimation changes all parameter values (Table 4). This is surprising since only a few constraints were found to be binding. Our interpretation is that the binding constraint forms an envelope of all-parameter constraints that forces the variation in the optimal parameters. The changes in the first-order parameters are very marginal compared to the changes in the second-order parameters. The change in the second-order parameter often exceeds 30%, and in one case even 250%. This confirms that it is mainly the relationship of the values in the matrix Bkk that determines whether the results are theoretically consistent. This concerns not only the pure absolute value of the estimated parameter but also, in many cases, the sign.

Table 4.
Parameter estimates—the effect of constraints.
3.3. The Effect of Heterogeneity on Production and the Connection between Farms’ Economic and Natural Conditions and Unobserved Heterogeneity
In the following, we restrict our attention to the model with constraints. First, we move to the regional distribution of estimated efficiencies (Figure 2). In general, inefficiencies are very low (much of the variation in output is explained by technology and by the impact of unobserved heterogeneity). Regional differences in the inefficiency scores are hardly seen. The only pronounced effects in inefficiency are the declines in efficiency in the years 2007 and 2009. For these years, we noted the severe weather conditions that similarly affected all regions in Hungary. Moreover, efficiency over time follows a negative trend. This can be seen in connection with the significant impact of technical change in Hungarian grain production. The frontier is determined by the farms that use the most modern technology. Farmers who hesitate to do this increasingly fall behind or show greater inefficiencies.
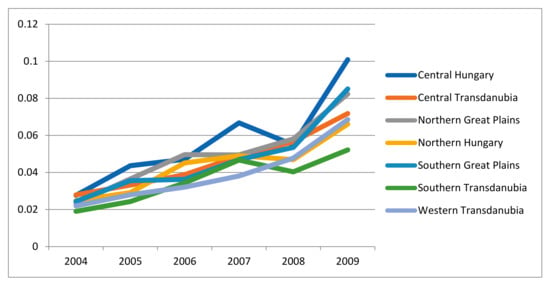
Figure 2.
Regional development of inefficiencies, 2004–2009. Source: authors’ estimation.
It has already been mentioned that heterogeneity might have a greater impact on production than inefficiency. To check this conjecture, the share of heterogeneity and inefficiency on variation of output was calculated (Figure 3). Results confirm that heterogeneity is much more important than inefficiency. The latter is only responsible for 5–20% of the total variance of these sources. This suggests that not considering heterogeneity in estimations can lead to totally misguided policy recommendations.
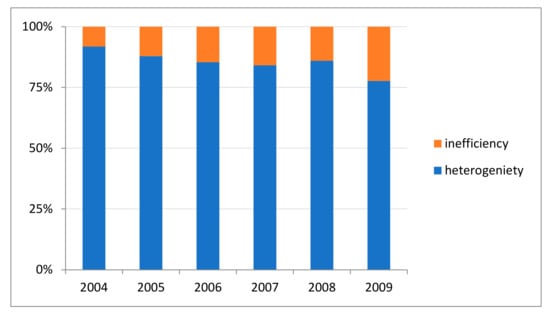
Figure 3.
Joint impact of the variance of heterogeneity and efficiency. Source: authors’ estimation.
Moreover, because of the expected overestimation of efficiency when neglecting heterogeneity, policies may not only be misdirected, but the impact on increasing efficiency measures may be overestimated as well. The increased impact of inefficiency at the end of the period of investigation can be seen (as explained in the last paragraph) as a consequence of the high speed of technical change in the sector (see Table 4) and/or the severe weather conditions at the end of the period under investigation.
In the following, how the sources of heterogeneity were investigated is described in more detail. For this, we refer to two partial productivities that can be viewed as indicators of the natural and economic factors of location.
Figure 4 shows the development of land productivity in the Hungarian regions (NUTS 2 level) over the period of investigation. In this figure, land productivity in the regions is measured relative to the average land productivity in the sample. Two regions had below-average land productivity—Northern Hungary and Central Hungary. The other regions had above-average productivity, with the highest in Southern Transdanubia. In these regions, land productivity was about 20% higher than average. One more issue had to be considered—the ranking of the regions according to land productivity remained relatively constant over the years. This suggests that our conjecture that we could assume a constant term for the impact of heterogeneity was supported by the data.
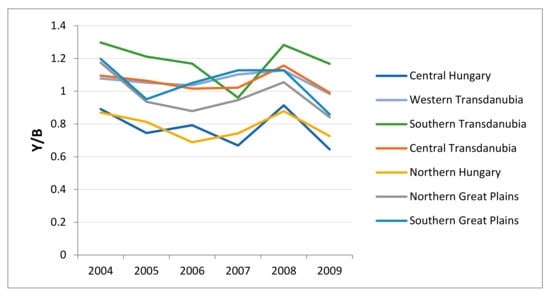
Figure 4.
Development of relative land productivity by region (2004–2009). Source: authors’ calculations.
Figure 5 provides more details of the technologies used in Hungarian grain production. It displays the relationship between the three indicators labor productivity (Y/A), land productivity (Y/B), and land-man ratio (B/A) for all regions over time according to references [36,37].
or, in log terms,
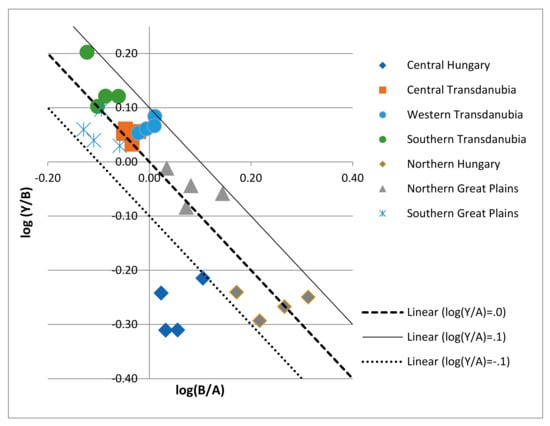
Figure 5.
Partial productivities and the man-land ratio in Hungarian grain production 2005–2008, according to region. Note: Y/A land productivity; Y/B land productivity; B/A land-man ratio; all variables are normalized using the geometric average of the total sample. Source: authors’ calculations.
Land productivity can be seen as an indicator of the natural condition of location. This indicator basically reflects soil conditions, availability of water and sunshine, etc. However, land productivity is also influenced by the level of economic development in relationship to the availability of sufficient production-enhancing inputs such as fertilizer or pesticide. However, given the homogeneous institutional conditions in Hungary it can be assumed that this impact is of minor importance for land productivity differences across regions. On the other hand, differences in labor productivity can be regarded more as a consequence of the economic conditions of location. The opportunity cost of labor determines how much labor is devoted to this sector. Moreover, in combination with factor prices the land-man ratio determines the capital-to-labor ratio in the sector, which depends at least partially on the economic infrastructure in the region [36]. However, we admit that the relationship between the economic condition of the location and labor productivity is much weaker than between natural conditions and land productivity. Differences in labor productivity can be also the consequence of various farm structures: large-scale agriculture is usually less labor intensive than small-scale agriculture and is much more mechanized. The dual agricultural structure in Hungary provides some support for this interpretation. Given the lack of data, we are unfortunately not able to dig deeper into this problem. However, independent of whether the high land-man ratio is the result of economic forces or whether farm structures are due to political (institutional) decisions, higher labor productivity can be seen as an indicator of better performance.
The numbers in Figure 5 represent three-year averages. This calculation was carried out to eliminate outliers. As in Figure 4, all numbers relate to the sample average. Thus, on the horizontal axis numbers larger than zero indicate above-average land-man ratios. A similar interpretation holds for the vertical axes for land productivity. The dashed line represents average labor productivity. Above this line are regions with higher labor productivity. The solid line represents a level of labor productivity about 25% higher than average labor productivity. The dotted line corresponds to labor productivity about 25% lower than average. The figure confirms what was deduced from the previous figure. Land productivity in Central Hungary and Northern Hungary is lower than in the other regions. However, in Central Hungary the land-man ratio is lower than in Northern Hungary. As a result, labor productivity in this region is the lowest of all Hungarian regions. Poor labor productivity is also typical of the Southern Great Plains. However, together with a low land ratio this nevertheless allows above-average land productivity. The region with relatively high land and labor productivity and a high land-man ratio is the Northern Great Plains. The high land-man ratio suggests that agriculture or grain production is much more labor intensive than in other regions, especially the Southern Great Plains. The same holds for grain production in Northern Hungary.
In Figure 6, we display how we investigated how heterogeneity affects Hungarian agriculture. Central Hungary is the region in which land and labor productivity was lowest in our sample. This finds its expression in the highest negative value for unobserved heterogeneity (w*). North Hungary is similar in this respect. However, labor productivity is higher than in Central Hungary. Accordingly, the w* value for this region is also negative but also slightly higher than in Central Hungary. The highest w* values were found for the two Great Plains regions. In the northern part, we have high labor productivity but low land productivity. The partial productivities in the southern region contrast with those of the northern part: namely, high land productivity and low labor productivity. In this region we found the highest value for w*. Another region with an above-average value for w* is Central Transdanubia. This region is characterized by above-average land productivity and average labor productivity. Western Transdanubia does not fit into this pattern. Labor and land productivity are both relatively high, but the value of w* is only average.
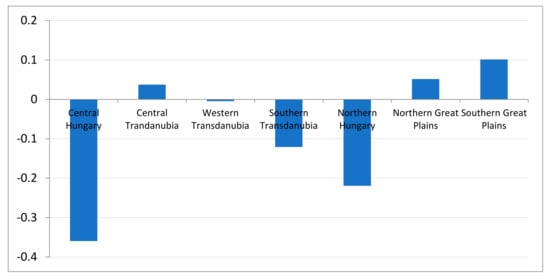
Figure 6.
Distribution of heterogeneity across Hungarian regions. Source: authors’ estimation.
This analysis provides support for the view that unobserved heterogeneity can be regarded as an indicator of the favourability of the regions in terms of their natural and economic conditions of production (Section 3). However, some part of the variation of w* is not explained by this interpretation. Therefore, further investigation is needed to better understand factors which influence unobserved heterogeneity, (e.g., as Alvarez and his co-authors assumed managerial ability might influence it [28] or farms structural characteristics might affect it too.)
To sum up, land and labor productivity may provide some explanation for the variance in heterogeneity. The explanatory power of these two indicators appears to be relatively high but is not sufficient. The actual value of w* depends on other important factors which might not be covered by natural and economic conditions. One suggestion is that w* captures the distribution of the management abilities of farmers [28]. However, what the reasons are for the different w* among farms cannot be uniquely decided from our analysis. More work is necessary to distinguish among the various sources of w*.
4. Conclusions
The goal of the research described in this paper was to model technological differences among farms and evaluate how consideration of technological heterogeneity affects parameter estimates and technical efficiency. In order to model technological differences, we used a modified version of an RPM. The first aim was to compare the results of the RPM with those of the TRE model, which can be seen as a restricted version of an RPM, where heterogeneity affects only the intercept (i.e., it is able to separate heterogeneity and technical efficiency, but is insufficient for capturing underlying variation in technology).
Our second aim was to examine how the fulfilment of theoretical consistency influences the results. Our third aim was to examine the effect of heterogeneity on the variation in output and the connection between farms’ economic and natural conditions and the modelled unobserved heterogeneity.
Results revealed that, in addition to the separation of unobserved heterogeneity and TE, consideration of technological heterogeneity is also important and has a significant effect on parameter estimates and TE. Our results showed that the interaction of unobserved heterogeneity was significant not only with the constant, but also with observed inputs and technological change, revealing that heterogeneity also influences the technology that is used and technological change. This suggests that a model which is able to estimate these different technologies and changes might lead to more adequate policy making.
Model selection criteria also show that the applied RPM is better suited to this database. Our results suggest that the RPM depicts inefficiency more appropriately than the other models. Technical inefficiency estimates are lower in this model, and the distribution of efficiency scores seems to be more plausible. From our point of view, this result is convincing, While, in the TRE model, a large share of farms has an efficiency that is lower than 25% (e−u, u > 0.3), the share of farms with low efficiency is reduced to a marginal fraction in the RPM. Given that farms are operating in a homogeneous institutional environment, the very wide span of inefficiencies is difficult to justify.
Earlier studies using traditional SFA method reported technical efficiency score in Hungarian crop producing sector around 0.73 [14,38] studies used DEA reported around 0.5–0.6 [39,40]. Baráth and Fertő [14] using an LCM showed that when technological heterogeneity is considered the technical efficiency is higher 0.83. The result of the applied RPM shows even higher technical efficiency score of 0.9.
Moreover, the applied model suggests that heterogeneity has a greater effect on the variance of output than inefficiency. The latter is only responsible for 5–20% of the total variance of output. This calls attention to the fact that in creating more targeted development policies it is necessary to better take into account the technological heterogeneity among farms. Comparison of the model with and without constraints showed that the imposition of constraints increased substantially the proportion of consistent estimates. This result suggests that it is important to check whether demands for theoretical consistency are fulfilled, as if they are violated the method, we applied is adequate for increasing the number of consistent estimates. This method can also help to increase our knowledge about farms which are far from average ones.
Empirical results show that there are hardly any regional differences in the efficiency scores of Hungarian agriculture, while the evolution of efficiency is negative over time. This situation should be seen in connection with the significant impact of technical change in Hungarian grain production. The frontier is determined by those farms which use the most modern forms of technology. Farmers who hesitate to do this increasingly fall behind (i.e., show greater inefficiency). This also shows the divergence among Hungarian farms.
In the last step of the analysis we examined the connection between modelled heterogeneity and farms’ economic and natural conditions. Results confirm that unobserved heterogeneity can be regarded as an indicator of the favourability of a region in terms of its natural and economic conditions for production. The explanatory power of these indicators is high but appears to be insufficient. Consequently, the modelled heterogeneity effect captures natural and economic conditions and other important factors as well. One proposal is that unobserved heterogeneity captures the distribution of the management abilities of farmers, as Alvarez and his co-authors suggested [28]. However, the determinants of unobserved heterogeneity among farms cannot be uniquely decided from our analysis. More work is necessary to distinguish the various sources of heterogeneity. While our analysis showed that heterogeneity has an important impact on variation in output, identification of the sources of heterogeneity might help to improve the productivity of farms.
Author Contributions
Conceptualization, L.B. and H.H.; methodology, L.B. and H.H.; writing—original draft preparation, L.B. and H.H.; writing—review and editing, I.F.; supervision, I.F.; All authors have read and agreed to the published version of the manuscript.
Funding
Lajos Baráth gratefully acknowledges support from National Research Development and Innovation Office (Hungary); project no. K120326.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The parameters of the model can be estimated by using the maximum simulated likelihood technique (27;29 for discussion).
We assume that is standard normally distributed with zero mean and variance 1, .
We can then take several draws from this di: tribution, plug in the values of into the likelihood function, and construct the simulated maximum likelihood function, as follows:
Here, R represents the number of replications in the simulation process. According to Greene (2005) [27] “in order to achieve a reasonable approximation to the true likelihood function, a reasonably large number of random draws are required. The process can be greatly accelerated by using ‘intelligent’ draws, such as Halton sequences (see Train (1999) [29] for discussion).” Following this suggestion, we used Halton sequences for the simulation.
Authors differ in their approximations of the value of R. Train (1999) [29] recommends several hundred. We decided to use 1000 replications in the final model since we experienced that with a lower number of replications the . The results were unstable. With more than 1000 replications, the results stabilize, and we experienced only very minor changes in the estimated values when we attempted a higher number of simulations.
As can be seen, the likelihood function has the same structure as in conventional stochastic frontier analysis. However, two important modifications should be mentioned: the compound variance of the error term, and the measure of the extent of inefficiency. The variance of the compound error term in conventional SFA models is given by
Since in our model is determined through the standard calculation changes to
Similarly, the original measure for the extent of efficiency changes to
Given the estimates of the model and the expectation of , technical efficiency can be estimated according to the conventional Jondrow et al. procedure [28,41]):
The above formula can be computed directly by simulation like other quantities that involve , or the expected value of can be estimated separately via [27,28]:
where the function denotes the likelihood function for farm i evaluated at the parameter estimates and the current draw of .
Having computed the expected value of , the values of inefficiencies conditioned on these estimates and other data for farm i can be computed.
References
- Abdulai, A.; Tietje, H. Estimating technical efficiency under unobserved heterogeneity with stochastic frontier models: Application to northern German dairy farms. Eur. Rev. Agric. Econ. 2007, 34, 393–416. [Google Scholar] [CrossRef]
- Bauer, P.W.; Berger, A.N.; Ferrier, G.D.; Humphrey, D.B. Consistency Conditions for Regulatory Analysis of Financial Institutions: A Comparison of Frontier Efficiency Method. J. Econ. Bus. 1998, 50, 85–114. [Google Scholar] [CrossRef]
- Chang, C.-H.; Wu, K.-S.; Chang, B.-G.; Lou, K.-R. Measuring Technical Efficiency and Returns to Scale in Taiwan′s Baking Industry—A case study of the 85 °C Company. Sustainability 2019, 11, 1268. [Google Scholar] [CrossRef]
- Lazikova, J.; Lazikova, Z.; Takac, I.; Rumanovska, L.; Bandlerova, A. Technical efficiency in the Agricultural Business—The case of Slovakia. Sustainability 2019, 11, 5589. [Google Scholar] [CrossRef]
- Tsionas, E.G. Stochastic frontier Models with Random Coefficients. J. Appl. Econom. 2002, 17, 127–147. [Google Scholar] [CrossRef]
- Huang, H.-C. Estimation of Technical Inefficiencies with Heterogeneous Technologies. J. Product. Anal. 2004, 21, 277–296. [Google Scholar] [CrossRef]
- Eberhardt, M.; Teal, F. No Mangoes in the Tundra: Spatial Heterogeneity in Agricultural Productivity Analysis. Oxf. Bull. Econ. Stat. 2013, 75, 914–939. [Google Scholar] [CrossRef]
- Eberhardt, M.; Teal, F. Econometrics for Grumblers: A New Look at the Literature on Cross-Country Growth Empirics. J. Econ. Surv. 2011, 25, 109–155. [Google Scholar] [CrossRef]
- Eberhardt, M.; Vollrath, D. The Effect of Agricultural Technology on the Speed of Development. World Dev. 2018, 109, 483–496. [Google Scholar] [CrossRef]
- Kuenzle, M. Cost Efficiency in Network Industries: Application of Stochastic Frontier Analysis. Ph.D. Thesis, Swiss Federal Institute of Technology Zurich, Zürich, Switzerland, 2005. [Google Scholar]
- Farsi, M.; Filippini, M.; Kuenzle, M. Unobserved heterogeneity in stochastic cost frontier models: An application to Swiss nursing homes. Appl. Econ. 2005, 37, 2127–2141. [Google Scholar] [CrossRef]
- Cillero, M.; Thorne, F.; Wallace, M.; Breen, J. Technology heterogeneity and policy change in farm-level efficiency analysis: An application to the Irish beef sector. Eur. Rev. Agric. Econ. 2019, 46, 193–214. [Google Scholar] [CrossRef]
- Alvarez, A.; del Corral, J. Identifying different technologies using a latent class model: Extensive versus intensive dairy farms. Eur. Rev. Agric. Econ. 2010, 37, 231–250. [Google Scholar] [CrossRef]
- Baráth, L.; Fertő, I. Heterogeneous technology, scale of land use and technical efficiency: The case of Hungarian crop farms. Land Use Policy 2015, 42, 141–150. [Google Scholar] [CrossRef]
- Hsiao, C. Analysis of Panel Data, 3rd ed.; Cambridge University Press: New York, NY, USA, 2014; pp. 1–539. [Google Scholar]
- Belyaeva, M.; Hockmann, H. Impact of regional diversity on production potential: An example of Russia. Stud. Agric. Econ. 2015, 117, 72–79. [Google Scholar] [CrossRef]
- Cechura, L.; Grau, A.; Hockmann, H.; Levkovych, I.; Kroupova, Z. Catching up or falling behind in European agriculture: The case of milk production. J. Agric. Econ. 2017, 68, 206–227. [Google Scholar] [CrossRef]
- Wang, X.; Hockmann, H.; Bai, J. Technical efficiency and producers’ individual technology: Accounting for within and between regional farm heterogeneity. Can. J. Agric. Econ. 2012, 60, 561–576. [Google Scholar] [CrossRef]
- Lachaud, M.; Bravo-Ureta, B.E.; Ludeña, C. Agricultural productivity in Latin America and the Caribbean in the presence of unobserved heterogeneity and climatic effects. Clim. Chang. 2017, 143, 445–460. [Google Scholar] [CrossRef]
- Njuki, E.; Bravo-Ureta, B.E.; O’Donnell, C.J. Decomposing agricultural productivity growth using a random-parameters stochastic production frontier. Empir. Econ. 2018, 57, 1–22. [Google Scholar] [CrossRef]
- Julien, J.; Bravo-Ureta, B.E.; Rada, N. Assessing farm performance by size in Malawi, Tanzania, and Uganda. Food Policy 2019, 84, 153–164. [Google Scholar] [CrossRef]
- Sauer, J. Economic theory and econometric practice: Parametric efficiency analysis. Empir. Econ. 2006, 31, 1061–1087. [Google Scholar] [CrossRef]
- Láng, I.; Csete, L.; Harnos, Z. The Agro-Ecopotential of the Hungarian Agriculture at the Turn of 2000; Mezőgazdasági Kiadó: Budapest, Hungary, 1983; pp. 1–266. [Google Scholar]
- Agrell, P.J.; Brea-Solís, H. Stationarity of Heterogeneity in Production Technology using Latent Class Modelling. Core Discuss. Pap. 2015, 47, 1–21. [Google Scholar]
- Pitt, M.; Lee, L. The measurement and sources of technical inefficiency in Indonesian weaving industry. J. Dev. Econ. 1981, 9, 43–64. [Google Scholar] [CrossRef]
- Schmidt, P.; Sickles, R. Production frontiers with panel data. J. Bus. Econ. Stat. 1984, 2, 365–374. [Google Scholar]
- Greene, W. Reconsidering heterogeneity in panel data estimators of the stochastic frontier model. J. Econom. 2005, 126, 269–303. [Google Scholar] [CrossRef]
- Alvarez, A.; Arias, C.; Greene, W. Accounting for unobservables in production models: Management and inefficiency. Working Paper. Fund. Cent. Estud. Andal. Ser. Econ. 2004, E2004/72, 1–18. [Google Scholar]
- Train, K. Halton Sequences for Mixed Logit. Economics Working Papers E00-27; Department of Economics, University of California: Berkeley, CA, USA, 2000; pp. 1–18. [Google Scholar]
- Terrell, D.; Dashti, I. Incorporating Monotonicity and Concavity Restrictions into Stochastic Cost Frontiers. In Proceedings of the Midwest Econometric Society Meeting, Columbus, OH, USA, May 1997; pp. 1–31. [Google Scholar]
- Sauer, J.; Hockmann, H. The Need for Theoretically Consistent Efficiency Frontiers. In Proceedings of the XIth EAAE Congress, Copenhagen, Denmark, 24–27 August 2005. [Google Scholar]
- Henningsen, A.; Christian, H.C.A. Henning. Imposing regional monotonicity on translog stochastic production frontiers with a simple three-step procedure. J. Product. Anal. 2009, 32, 217–229. [Google Scholar] [CrossRef]
- Coelli, T.J.; Prasada Rao, D.S.; Q′Donnell, C.J.; Battese, G.E. An Introduction to Efficiency and Productivity Analysis, 2nd ed.; Springer: Boston, MA, USA, 2005; pp. 1–349. [Google Scholar]
- Lau, J.L. Testing and imposing monotonicity, convexity and quasi-convexity constraints. In Production Economics: A Dual Approach and Application to Theory and Application, 1st ed.; Fuss, M., McFadden, D., Eds.; North Holland Publishing Company: New York, NY, USA, 1978; Volume 2, pp. 1–360. [Google Scholar]
- Keszthelyi, S.; Pesti, C. A Tesztüzemi Információs Rendszer 2008. évi Eredményei. Agrárgazdasági Inf. 2009, 3, 1–45. [Google Scholar]
- Herlemann, H.H.; Stamer, H. Produktionsgestaltung und Betriebsgröβe in der Landwirtschaft unter dem Einfluss der wirtschaftlich-technischen Entwicklung. Kiel. Stud. 1958, 44, 353–354. [Google Scholar]
- Hayami, Y.; Ruttan, V.W. Agricultural Development: An International Perspctive, 2nd ed.; Johns Hopkins University Press: Baltimore, MD, USA, 1971; pp. 1–367. [Google Scholar]
- Bakucs, L.Z.; Latruffe, L.; Fertő, I.; Fogarasi, J. The impact of EU accession on farms’ technical efficiency in Hungary. Post-Communist Econ. 2010, 22, 165–175. [Google Scholar] [CrossRef]
- Nemes-Zubor, A.; Fogarasi, J.; Molnár, A.; Kemény, G. Farmers’ responses to the changes in Hungarian agricultural insurance system. Agric. Financ. Rev. 2018, 78, 275–288. [Google Scholar] [CrossRef]
- Latruffe, L.; Fogarasi, J.; Desjeux, Y. Efficiency, productivity and technology comparison for farms in Central and Western Europe: The case of field crop and dairy farming in Hungary and France. Econ. Syst. 2012, 36, 264–278. [Google Scholar] [CrossRef]
- Jondrow, J.; Knox, C.A.; Materov, I.S.; Schmidt, P. On the Estiamtion of Technical Inefficiency in the Stochastic Frontier Production Function Model. J. Econom. 1982, 19, 233–238. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).