Abstract
Local scour depth at complex piers (LSCP) cause expensive costs when constructing bridges. In this study, a hybrid artificial intelligence approach of random subspace (RS) meta classifier, based on the reduced error pruning tree (REPTree) base classifier, namely RS-REPTree, was proposed to predict the LSCP. A total of 122 laboratory datasets were used and portioned into training (70%: 85 cases) and validation (30%: 37 cases) datasets for modeling and validation processes, respectively. The statistical metrics such as mean absolute error (MAE), root mean squared error (RMSE), correlation coefficient (R), and Taylor diagram were used to check the goodness-of-fit and performance of the proposed model. The capability of this model was assessed and compared with four state-of-the-art soft-computing benchmark algorithms, including artificial neural network (ANN), support vector machine (SVM), M5P, and REPTree, along with two empirical models, including the Florida Department of Transportation (FDOT) and Hydraulic Engineering Circular No. 18 (HEC-18). The findings showed that machine learning algorithms had the highest goodness-of-fit and prediction accuracy (0.885 < R < 0.945) in comparison to the other models. The results of sensitivity analysis by the proposed model indicated that pile cap location (Y) was a more sensitive factor for LSCP among other factors. The result also depicted that the RS-REPTree ensemble model (R = 0.945) could well enhance the prediction power of the REPTree base classifier (R = 0.885). Therefore, the proposed model can be useful as a promising technique to predict the LSCP.
1. Introduction
Local scour is responsible for most bridge failures around the world every year. In a streambed, the flow interferes with bridge piers and leads to the creation of multiple vortices, which remove sediment in the vicinity of the piers, and a scour hole is formed [1]. When the scour hole deepens sufficiently, it causes bridge failure. The failures significantly increase the costs of temporary maintenance and also ecological impacts on downstream ecosystems, such as spawning beds [2]. Because of the complicated process of scour around bridge piers, the local scour depth at complex pier (LSCP (is a complicated phenomenon and hence its accurate predictions are a critical issue for the design of bridge foundations. In other words, overestimation of LSCP may lead to extra construction costs and even bridge failure around their foundations [3].
An accurate prediction of LSCP is a hot topic in river engineering because overestimated and underestimated predictions lead to an increase in the dimensions of the bridges, resulting in an increase of the construction costs and bridge failure, respectively [4]. Therefore, a reliable prediction of LSCP for a safe, economic and technically sound structure is of paramount importance. In a river, when a high volume of water flows, scouring of particles around the base of the bridges occurs, and then a scour hole appears around bridge piers. If the LSCP is not predicted correctly, the bottom level of the local scour hole will exceed the original level of the pier foundation. As a result, as time passes and the volume of water flowing increases, local scour depth develops and the bridge’s base loses strength, and eventually it will be destroyed [2]. Almost 53% of all bridge failures are attributed to flood and scour [5].
Over the past decades, the mechanisms and prediction of scour hole occurence at the simple pier and a group of piles have been widely investigated. Due to economic and technical issues, the piers with complex geometry have developed to become the most common foundation type of bridge piers in alluvial streambeds [6]. The term “complex pier” (CPs) is used in contrary to the simple pier. By definition, the complex pier is a term that defines a special kind of non-uniform pier that is comprised of a column, a pile cap, and a pile group [7]. At piers with complex geometry, due to scouring during a flood, the pile cap position with respect to the initial stream bed level changes. As a result, the influence of pile cap may be changed from a protective to intensifying role at the scour process when it is entirely buried and exposed to the flow, respectively [7]. Such roles increase the complicity of scour mechanisms and prediction at CPs [8].
To estimate local scour depth at complex pier (ys), a few empirical methods have been proposed including the FHWA design methodology, Hydraulic Engineering Circular No. 18. (HEC-18) [9], the Florida Department of Transportation (FDOT) bridge mechanisms scour manual [2,10,11]. In addition, a procedure was proposed by Amini and Mohammad [7] which, based on field data, gives reasonable estimates of the scour depth at CPs [12]. For calculations of scour depth, the HEC-18 and FDOT methods apply a superposition procedure to combine the effect of each element of CPs. However, the methods presented by Lee and Hong [1], Amini et al. [6], and Arneson et al. [9] provided relations for an equivalent width (be) for that around a CP to be used in simple pier equations where be is the diameter of a circular simple pier that produces scour depth equal to the CP, for the same sediment and flow conditions. Apart from HEC-18 and FDOT methods, Mueller and Wagner [13] used field data to examine the efficacy of 20 bridge pier scour depth estimation methods and found that these methods predict the scour depth inaccurately with a large number of overestimations.
In recent years, ensemble machine learning models have become popular among environmental researchers not only for classification issues to generate susceptibility maps [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36] but also for regression problems to simulate and predict an environmental variable such as wastewater hydraulics [37], saturated hydraulic conductivity [38], shear strength of soft soil [39], soil moisture [40], and soil temperature [41]. The advantages of artificial intelligence (AI) have encouraged numerous researchers to use methods and techniques based on AI to estimate the depth of scour [42,43,44,45]. Based on artificial neural networks (ANNs), some local scour depth estimation methods have been proposed. In case of bridge scouring, Cheng and Cao [46] for predicting local scour depth at simple bridge piers, proposed an intelligent fuzzy radial basis function neural network inference model (IFRIM). Their model was a hybrid of the fuzzy logic, the artificial bee colony algorithm and radial basis function neural network. Najafzadeh et al. [47] presented a group method of data handling, using the back propagation algorithm and quadratic polynomial. They found that the AI-based model provides accurate predictions of scour at simple piers. In the case of local scour prediction at pile group, Zounemat-Kermani et al. [48] and Hosseini et al. [49] reported the accuracy of the ANNs and the neuro-fuzziness system in comparison with empirical methods.
However, contrary to the simple piers and pile groups, due to the complication of the scour mechanism, and the variation of influential parameters, the ensemble machine learning methods have been rarely developed to estimate the scour around the complex piers. The positive and different point of this study with other studies is that there is no applied an ensemble model to predict the LSCP. In other words, although some models and techniques have been used and suggested for predicting the LSCP, the proposed model, RS-REPTree, has not been yielded for this purpose worldwide. Therefore, the main aim of this study was to use a hybrid intelligence model to predict current-induced local scour at complex piers. The presented model enhances the accuracy of scouring predictions and the understanding of the local scour at the complex pier and its dominant variables.
2. Methodology
2.1. Data Acquisition
In this study, two sets of experimental data on local scour at CPs (LSCP) were used. The first dataset was measured by fourth author of this paper at the National Hydraulic Research Institute of Malaysia, NAHRIM. Five models (CPs) were used and experiments were performed over the whole range of possible pile cap elevations with different geometrical characteristics. More details of the data are presented in Amini et al. [7,50] and Amini et al. [51]. The second dataset of the experiment works were carried out at Sharif University of Technology, Tehran, Iran by Ataie-Ashtiani et al. [52]. Both datasets were measured under flow and model dimensions so that the sediment size, d50, flow depth, h, and contraction effects on LSCP became insignificant. The flow intensity, U/Uc, was selected so that in all tests the clear water condition was maintained, where U is mean velocity of the approach flow and Uc is critical mean velocity for sediment motion.
2.2. Dimensional Analysis
To determine scour depth, ys, most of the empirical methods use of dimensional analysis, a functional relationship, based on an equivalent pier width, be, at CPs, from an existing equation for single piers [7,9,10,11]. The be is defined as the diameter of a simple pile for the same flow and sediment characteristics that would produce the same scour depth as the CPs. Depending on the pile cap location (Y) with respect to the undisturbed streambed, ys or be is a function of flow and sediment properties and CPs’ geometries. Therefore, a functional relationship for presenting LSCP may be written as Equation (1) using dimensional analysis:
where bc is the column width; bpc is the pile cap width; h is flow depth, d50 is median particle size of the bed sediment, Uc is critical value of U associated with initiation of motion of bed sediments, Fr is Froude number, T is the thickness of the pile cap; Lu and Lf are extensions of the pile cap upstream of and sides of the column; ksc and kspc are the shape factors for the column and pile cap; bpg is the pile diameter; m and n are the number of piles in line and normal with the flow; Sl and Sb are the pile spacing in line and normal with the flow, and Y is pile cap elevation with respect to the undisturbed streambed. A schematic drawing for flow-induced scour around a CP and the corresponding parameters are shown in Figure 1.
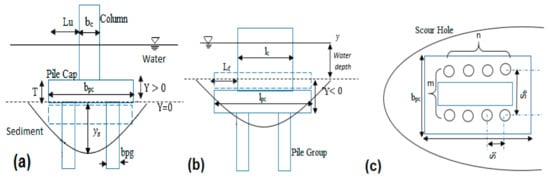
Figure 1.
The various components of the composite pier and the corresponding parameters; (a) Upstream view, (b) Side view, and (c) Plan view.
2.3. Empirical Equations
The HEC-18 [9] and FDOT methods [11] use the superposition method to predict scour depth at piers with complex geometry (i.e., column, pile cap, and pile group). The superposition method to calculate scour depth contributions from each component in HEC-18, is expressed as Equation (2):
where yscol is scour of column, yspc is the scour of pile cap, and yspg is the scour of pile group. The FDOT method calculates the equivalents single cylindrical pier that would produce the same scour depth as that complex pier component. Then, the equivalent diameter of the CPs is calculated by adding the equivalent diameters of the CP components and expressed as Equation (3):
where Dse, Decol, Depc, and Depg are equivalent diameters of the CPs, column, pile cap, and pile group, respectively. Finally, the scour depth at CPs can be calculated using the methods presented for scouring calculation at simple piers.
2.4. Machine Learning Algorithms
2.4.1. Artificial Neural Networks
The artificial neural networks (ANN), developed based on the neurons, is one of the well-known deep learning algorithms for regression, classification, and pattern recognition challenges [53,54,55,56]. A typical ANN architecture (Figure 2) has three layers: (a) input layer, in this case all the predictors of LSCP that also decide the number of neurons in the ANN architecture; (b) hidden layer, the recipient of all the neurons containing a specific weight, and (c) output layer, i.e., the predicted value of LSCP. We have discovered that the number of hidden layers and their neurons can only be decided by trial and error, and may vary case-by-case [57]. The ANN has shown promising results in predicting bridge pier scour depths [58,59,60,61,62].
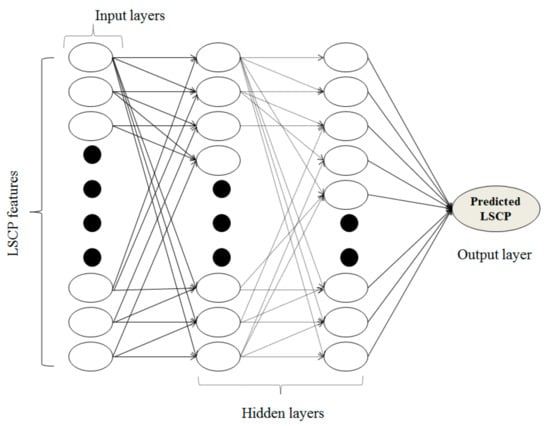
Figure 2.
A typical architecture of ANN.
2.4.2. M5P Model Tree
Although the M5P algorithm was developed in 1992 [63,64] by combining traditional decision tree and linear regression function, resulting in induced trees of regression models, Quinlan [63] reconstructed this algorithm. The M5P is one of the decision tree algorithms that has a branch node and leaf node. The first one indicates a choice between a number of alternatives and another represents a classification or decision issue [65].
Consider S as the set of examples is either associated with a leaf, or some test is chosen that splits S into subsets and this process is recursively conducted to the subsets [63,66]. In the M5P, the split process is done according to the minimizing the intra-subset variation down each branch in the output values. Then, in each node the standard deviation of the expected reduction () is calculated for the output values of the examples. Eventually, the attribute that maximizes the expected error reduction is selected. The can be formulated as follows [67]:
where S is the set of examples corresponding to S1, S2, …, Sn as the sets that result from splitting of the node according to the chosen attribute [64].
2.4.3. Support Vector Machine
Support vector machine (SVM) was recently used for efficiently predicting scour depth at simple piers [62]. SVM, a nonlinear simplified version of the generalized portrait algorithm, is one of the most known robust machine learning algorithms for both regression and classification problems. It can efficiently handle non-linear relationship between the predictors and the response in a multidimensional space [68,69,70]. Since SVM is based on the statistical learning theory and was developed using real world datasets, it is advantageous in generalizing the outcomes on the unknown data [68]. In this study, we used support vector regression (SVR), following Vapnik’s method where an alternative ε-loss function is used to minimize the error. The SVM offers four kernel functions including linear, polynomial, radial base, and sigmoid. In the SVR, a linear kernel is used, and users can set the kernel parameters. However, the regularization parameter ‘C’ and the size of error in sensitive zone ‘e’ may vary with the number of features and the context. Mathematically, SVR can be presented as below:
where and are positive Lagrange multipliers and denotes a non-linear transformation using linear kernel function of SVM, and ‘b’ stands for the ‘bias’.
2.4.4. REP Tree
The reduced error pruning tree (REPTree) is an ensemble model of decision tree (DT) and reduced error pruning (REP) algorithms, equally efficient for classification and regression problems [71]. The REPTree algorithm forms a decision regression tree by splitting and pruning the regression tree based on the highest information gain ratio (IGR) value [72]. The IGR values were calculated based on the entropy (E) function by Equation (6).
The IGR considers all the predictors of LSCP from training dataset (S) with subset Si: i = 1, 2, …, n in consecutive pruning stages. Since complex decision-trees could lead to over-fitting and the reduced-interpretability of a model, REP helps in decreasing the complexity, by removing leaves and branches of the DT structure [17,71,73,74].
2.4.5. Random Subspace Ensemble Algorithm
The random subspace (RS) is another robust ensemble method used for classification as well as regression challenges [75]. RS distinct itself from other ensemble technique and become advantageous because it trains the model on randomly selected samples of features opposed to whole feature sets, therefore, reduces correlations between estimators [76]. In this process, the first regression of original feature space is performed in L training subsets of q dimensionality. Then, base regression is applied to each of these subsets and a final decision is made on the basis of weighted majority voting [77]. In this technique, first REPTree as a base classifier is selected and, after selecting the optimal parameters, number of seeds, and iterations, the model is run and the dataset trained. In the next step, the RS meta classifier is conducted to hybrid with REPTree base classifier. The RS is created some sub-training and then for each dataset the base classifier is performed and eventually, based on majority voting, the best model is selected as the final outcome. The framework of the LSCP prediction is shown in Figure 3.
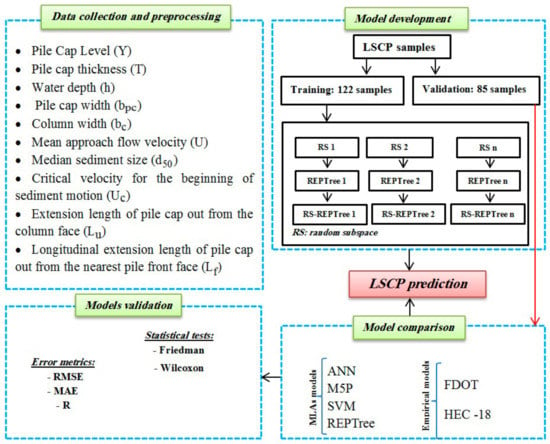
Figure 3.
A methodological framework of LSCP prediction.
2.5. Evaluation and Comparison
2.5.1. Statistical Metrics
In this study, some statistical index-based measures including correlation coefficient (R), mean absolute error (MAE), root mean square error (RMSE) and a Taylor diagram were used to evaluate and compare the performance of the models. R is a statistical measure, which represents the percentage of the variance for a dependent variable that’s explained by an independent variable. MAE measures the mean absolute value of each difference. Compared with RMSE, MAE can be given to be a more natural and unambiguous index to measure errors between estimated and actual observed values [78,79]. RMSE has been applied as a regular statistical metric to measure model performance [80]. Lower values of RMSE indicate the better result. It has been widely used different fields around the world [81]. The Taylor diagram graphically shows how the prediction models are matched with observations in terms of correlation, their root-mean-square difference, and the ratio of their variance considered in a single diagram [82]. On this diagram, the mode that is closer to the observation (validation dataset) has the highest predictive performance [83]. The abovementioned statistical indexes can be calculated by Equations (7)–(9) as below [84]:
where is the correlation coefficient, and are measured and predicted values respectively, and are the mean of measured and predicted values respectively, and N is the number of input data.
2.5.2. Non-Parametric Statistical Tests
In order to check the statistical difference between five models to enhance the prediction accuracy of LSPC, Friedman and Wilcox rank tests were used. As a null hypothesis, it was assumed that there was no statistical significance between the performances of all LSCP models at the significance level of α = 0.05. In other words, it attempted to show there was no variation between the models or a single model was no different from its mean. Regarding the P-value, if the null hypothesis is rejected (p < 0.05), it concludes that there is a significant difference between the models [85]. The Friedman test only shows the significant differences among all LSCP models but not show as pairwise comparisons. In this case, the Wilcoxon sign-rank test can be used to evaluate the pairwise differences between the LSCP models. Statistically, if the null hypothesis is rejected (p < 0.05 and z-value > (−1.96 and +1.96), there is significant differences between the performance of the models [72,85].
2.6. Sensitivity Analysis
The effect of each factor on the local scour depth is assessed by the sensitivity analysis (SA) technique [49,86]. The SA method in this study was computed by the proposed machine learning algorithm named RS-REPTree. In the SA method, each factor is removed individually from the modeling process and then the values of MAE, RMSE, and R metrics are recorded. Eventually, the sensitive factors during the modeling process are known and listed. Judgement is performed based on the effectiveness of each input factor. The higher the values of RMSE and MAE and the lower the R for each factor is, the higher sensitivity of the factor for the modeling process of local scour depth will be [49].
3. Results and Analysis
3.1. Optimal Selection of Modeling Parameters
Theoretically, an accurate model will be obtained when the parameters of the model are correctly selected and optimized. The optimal values are achieved by trial and error using the modification of the parameters. The optimal value of each machine learning parameters is shown in Table 1. In the proposed ensemble model, RS-REPTree, the most important parameters are the number of seeds and iterations during the modeling process. Figure 4 shows the best values for these two parameters of the ensemble model based on the RMSE and R metrics. According to the test/validation dataset, the result indicated that the best values for the number of seed and iteration based on the lowest RMSE metric (0.0181) were 6 and 10, respectively (Figure 4a,b). Additionally, the optimal values for the number of seeds and iterations regarding the R metric (0.945) were also 6 and 10 (Figure 4c,d). Therefore, the proposed ensemble model was constructed by the obtained parameters to enhance the prediction accuracy of LSCP.

Table 1.
Model optimal parameters in the modeling process.
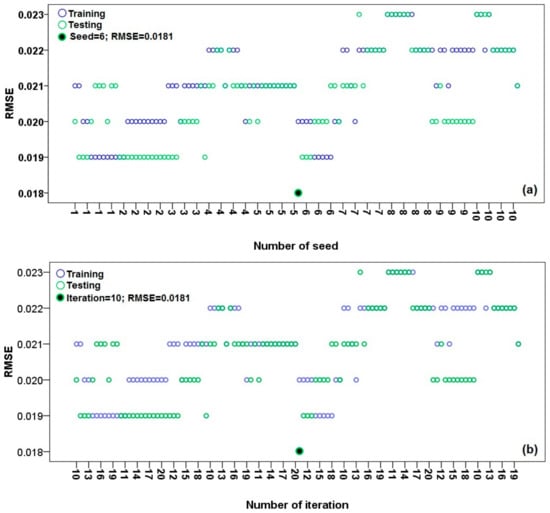
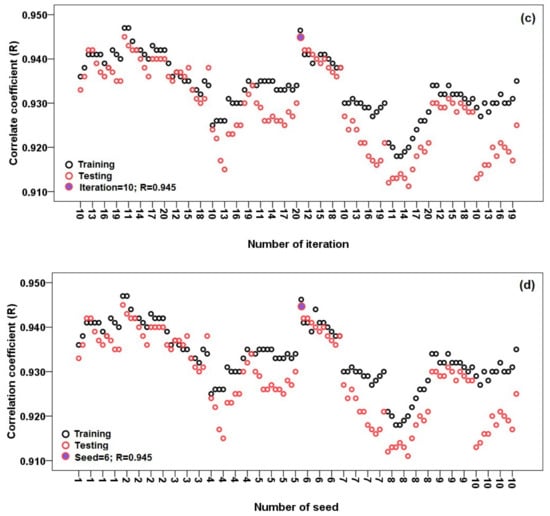
Figure 4.
Determination of the number of optimal values of iteration and seed in the modeling process based on the RMSE and R; (a) number of seed by RMSE, (b) number of iteration using RMSE, (c) number of iteration using R and (d) number of seed using R.
3.2. Model Validation and Comparison
The goodness-of-fit and performance of the models using training and testing/validation datasets are shown in Table 2 and Figure 5a–n. The experimental data of LSCP was used to compare obtained models and then their predictive accuracies were evaluated using the statistical metrics as MAE, RMSE and R. It is noteworthy that the goodness-of-fit and performance of the models are judged using training and validation datasets, respectively. However, to compare the power prediction and performance of the models testing/validation dataset were used. Basically, the number of MAE, RMSE, and R for the FDOT method were 0.058, 0.062, 0.726 and for the HECT-18 were 0.051, 0.064, and 0.620, respectively. In the ANN model, these values were 0.016, 0.021, and 0.907 while in the M5P machine learning model they were 0.017, 0.022, and 0.912, respectively. For the SVM model, the number of MAE, RMSE, and R were 0.016, 0.024, and 0.918 and for the REPTree mode were 0.018, 0.025, and 0.885, respectively. In the proposed ensemble model the values of 0.014, 0.018, and 0.945 were obtained for MAE, RMSE, and R, respectively. Overall, results indicated that, although all machine learning models had higher accuracy than the empirical models, the proposed model, RS-REPTree, well enhanced the accuracy of the based classifier of REPTree. On the other hand, this model had the highest prediction accuracy in predicting LSCP.

Table 2.
Model results and comparison using training and validation datasets.
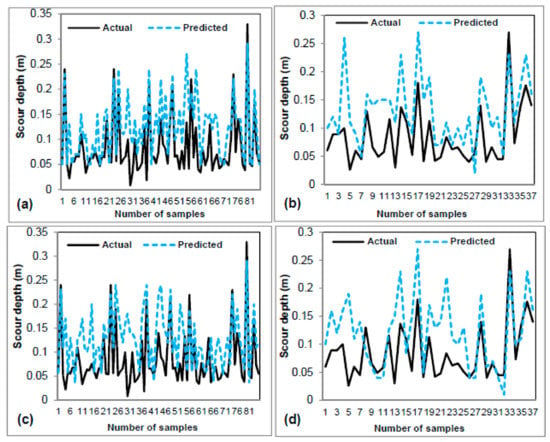
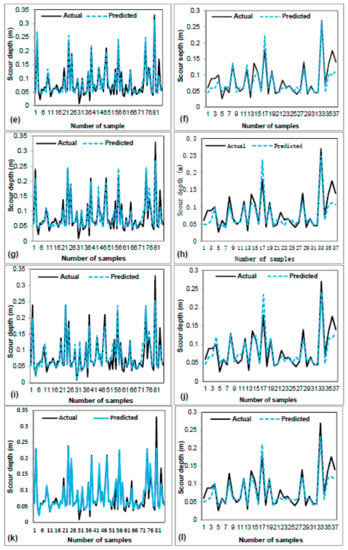
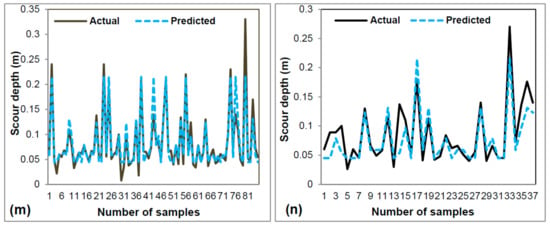
Figure 5.
Comparison between actual and predicted scour depth using training dataset; (a) FDOT model, (c) HEC-18, (e) ANNMLP, (g) M5P, (i) SVM, (k) REPTree, (m) RS-REPTree, and Testing dataset; (b) FDOT, (d) HEC-18, (f) ANNMLP, (h) M5P, (j) SVM, (l) REPTree and (n) RS-REPTree.
Figure 5a–n graphically shows the relationship between actual and predicted scour depths (m) based on the training and validation datasets. It was concluded that the empirical models had the lowest prediction because the distance between actual and predicted local scour depth was higher than the other models. The lower the MAE and RMSE and the higher R, the higher the model prediction and lower distance between actual and predicted local scour depths. Although all machine learning models had a reasonable fit of actual and predicted local scour depth, the proposed model showed the best simulating results.
Figure 6 shows the correlation between actual and predicted values of LSCP for empirical and machine learning models. Figure 6 was plotted in SPSS software to show the agreement of the actual and predicted values of local scour depth. The results illustrated that, based on the validation dataset, the values of R for the FDOT, HEC-18, ANN, M5P, SVM, REPTree, and RS-REPTree models were 0.726, 0.620, 0.907, 0.912, 0.918, 0.885, and 0.945, respectively. This implied that the lowest value of R belonged to HEC-18 as an empirical model, and the highest one was obtained for the proposed model. Overall, the result received that all machine learning models outperformed and outclassed the empirical models for predicting the local scour depth; however, the RS-REPTree ensemble model was more powerful than the other models.
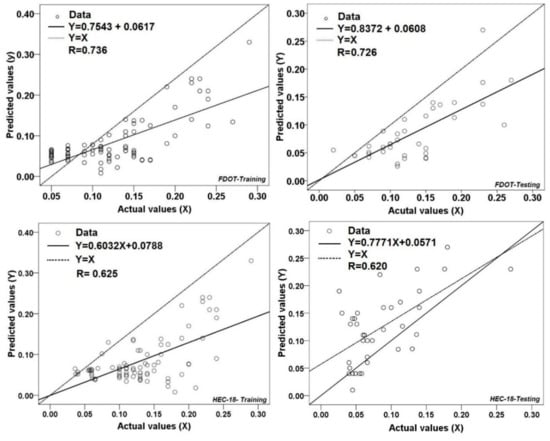
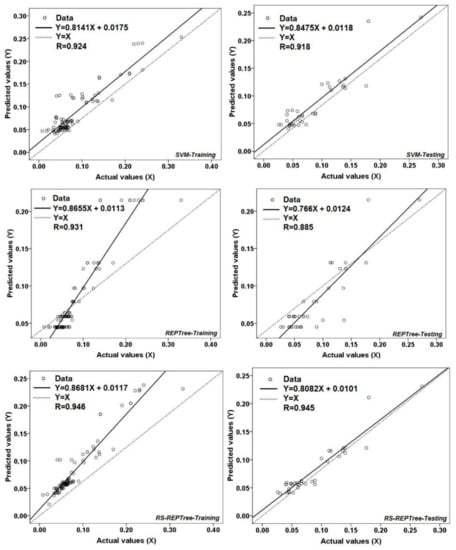
Figure 6.
Analysis of correlation between actual and predicted values of LSCP (m) for empirical models and machine learning algorithms.
A Taylor diagram was plotted to further analyze of model applicability (Figure 7). This diagram showed that although all machine learning models were close to observed LSCP, the proposed model, RS-REPTree, had the most predictive power compared to other models. The proposed model had a closer correlation (0.946), RMSE (0.018), and SD (0.044) with observed data. The results indicated that the models had good predictive power.
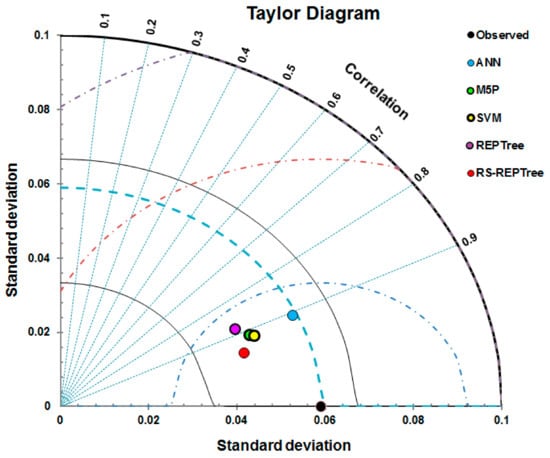
Figure 7.
Taylor diagram for displaying the correlation between the observed and predicted LSCP by different machine learning models.
Beside the above-mentioned graphs and tables, the results were assessed based on the boxplot of the models as shown in Figure 8. The box plots were plotted using the observed versus predicted LSCP for machine learning and empirical methods. The spread of measured and predicted values revealed that machine learning models present more accurate predictions in comparison to HEC-18 and FDOT models.
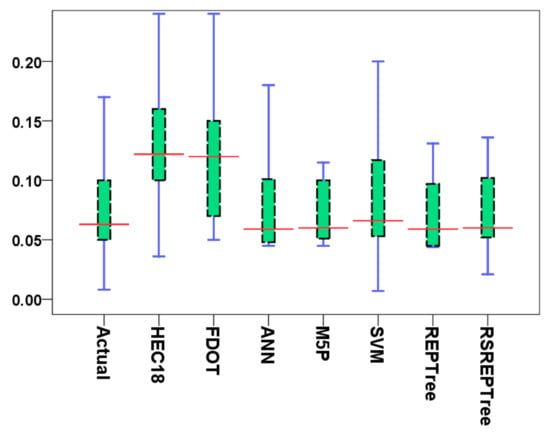
Figure 8.
Box plots of the actual and predicted values of local scour depth.
Additionally, to find significant differences among models evaluated in this research the Friedman’s test, a non-parametric test for detecting differences in treatments across multiple attempts [87], was used. Since the Friedman’s test does not show pairwise comparisons, the Wilcoxon test was used to quantify pairwise comparisons among the models. The results of the Wilcoxon test for performance of the RS-REPTree model and other LSCP models are shown in Table 3. The obtained significance value for the Friedman test was 0.000 (<0.05), which indicated that at 95% confidence level there was no evidence to accept the null hypothesis and then it was rejected that there are no differences between the mean of all models. Therefore, a significant difference between the performances of the models to predict the LSCP was indicated. In addition, the Wilcoxon sign rank test, as a pairwise comparison of the performance of the models, was used.

Table 3.
Average ranking of the seven local scour depth models using the Friedman’s test.
Table 4 shows significant differences between empirical methods predictions and actual data using Wilcoxon pairwise rank test. In compare with machine learning models, both HEC-18 and FDOT methods are with more over and under predicted data. It should be noted that avoiding under predicting data, is of most importance for bridge designers. Table 4 shows that, apart from a significant difference between the empirical models and actual experimental data, the empirical models and machine learning models are significantly different. However, no significant differences between machine learning predictions and actual data can be concluded from Table 4. Overall, according to the statistical tests, it can be safely said that the result of machine learning models to predict local scour depth is more reasonable and reliable than the empirical models.

Table 4.
Performance of the RS-REPTree model compared to other LSCP models using Wilcoxon signed-rank test (two-tailed).
3.3. Sensitivity Analysis
The role of each factor on the result of scour depth modeling was assessed by sensitivity analysis of the proposed model (Figure 9). The results are ordered according to the effectiveness of each factor that meaning the factor with removal creates higher RMSE and MAE, as well as the lower R located at the top of the list. The results stated that the pile cap level is the most important factor in the LSCP in a particular model. Moreover, other significant factors were pile cap thickness (T) and width (bpc). The rest factors have slight effect for modeling process by the proposed ensemble model (Figure 9).
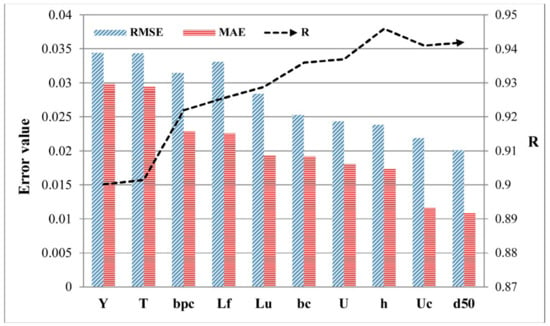
Figure 9.
Sensitivity analysis graphically based on the proposed ensemble model to predict local scour depth.
4. Discussion
The flow disturbances around obstacles such as bridge piers, inserted into an alluvial streambed, induce local scouring which is one of the most common being riverbed scour. Since the late 1950s the estimation of scour at bridges has attracted the attention of many researchers [88].
Unlike the local scour at simple pier, the scour at CPs is a complex phenomenon. However, the accurate estimation of equilibrium scour depth at CPs is vital for safe designing of the bridges. The experimental data were used to compare the most commonly used method for predicting scour depth at CPs. Based on data set analyses, an ensemble model was constructed to improve the accuracy of local scour depth prediction of REPTree as a base classifier. The statistical measurements indicated that the best values for the number of seeds and iterations were 6 and 10, respectively.
The capabilities and performance of the empirical methods and obtained models in scour prediction were evaluated using statistical tests. Overall, the statistical tests showing the relationship between observed and predicted scour depths indicated that all machine learning models are with higher power prediction than the empirical models. The inaccuracy of empirical methods at CPs scour including HEC-18 and FDOT methods was reported [6,12,52]. In contrast, the superiority of intelligent models to empirical methods for scour predicting was stated by Zounemat-Kermani et al. [48] and Hosseini et al. [49]. The same results can be concluded from the correlation between the observed and predicted values of local scour depth for empirical and machine learning models. The lowest values of R were obtained for HEC-18 and the highest belonged to the RS-REPTree as 0.620 and 0.945, respectively. Moreover, the boxplot and Friedman’s test of the models support the above statements.
In the case of detecting the dominant parameters at inducing local scour at CPs, the sensitivity analyses were conducted and the parameters were ordered according to their effectiveness. The results depicted that the pile cap location (Y) in respect to undisturbed streambed is the most important parameter which influence the scouring at CPs. These results are consistent with those reported by [51,52,89]. Furthermore, the pile cap width (bpc), thickness (T) and column width (bc) are with higher influences on LSCP, respectively. These results are in agreement with the findings of Ferraro et al. [90] and Moreno et al. [89]. It should be noted that unlike the simple piers and pile group [91], the role of the parameters at producing LSCP is various versus the pile cap level in respect to undisturbed streambed. Particularly when the pile cap is lower or inside the scour hole, the pile cap prevents scouring. This process continues until flow penetrates below the pile cap and the pile cap becomes undercut. The undercutting of pile caps intensifies the scour depth. As the level of pile cap reached the position for undercutting, apart from column and pile cap, the pile group is exposed to the flow, and contributes towards scouring. As the pile cap level increased, the pile group prevents the scouring and diminishes the LSCP [50,52]. In this case, the LSCP depends on the pile cap and pile group characteristics. It is worth noting that the bridge pier models used to obtain the data in this research were selected so that the sediment size and flow depth effects on LSCP became negligible and flow intensity was in a confined range.
The ensemble models could more decrease the noise and over-fitting problems between the training dataset, resulting in enhancing the accuracy of the model [15,17,92,93]. Basically, the findings depicted that the RS-REPTree ensemble model could well enhance the prediction accuracy of the REPTree as a classifier for the prediction of local scour depth at piers with complex geometry. This finding is in agreement with Cheng and Cao [46] who reported the capability of the IFRIM as a promising tool for civil engineers to estimate local scour at piers with simple geometry.
5. Conclusions
The complexity of the scour mechanisms at piers with non-uniform geometry caused the inaccuracy in the empirical methods presented for scouring prediction at these piers. In this research, the comprehensive datasets were used to evaluate the most commonly used empirical methods and to present a machine learning algorithms approach for predicting LSCP. The typical geometry of non-uniform piers is a complex pier (CP) composed of a column resting on a pile cap supported by a group of piles, which is investigated in this research. The most obvious findings to emerge from this study can be present as:
- The machine learning algorithms have the powerful capability to predict LSCP and the hybrid models can improve the performance of separate models in predicting LSCP.
- Computing benchmark algorithms presented in this research have the potential to alter the LSCP prediction in comparison with the most well-known empirical methods, namely HEC-18 and FDOT methods.
- The state-of-the-art RS-REPTree ensemble model, with the highest accuracy of the REPTree, is proposed as a classifier for the prediction of the LSCP.
- The pile cap location (Y) was a more sensitive factor for LSCP among other factors based on the availability of data.
Author Contributions
D.T.B., A.S., A.A., H.S., N.A.-A., S.H., S.K.S., B.T.P., and B.B.A. contributed equally to the work. A.S., A.A., H.S., and S.H. collected field data and conducted the analysis. A.S., A.A., H.S., N.A.-A., S.H., S.K.S. and B.T.P. wrote the manuscript. D.T.B., N.A.-A., S.K.S., B.T.P., B.B.A. and P.T.G. provided critical comments in planning this paper and edited the manuscript. All the authors were involved in discussing the results. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| RMSE | Root Mean Squared Error |
| LSCP | Local Scour Depth at Complex Piers |
| RS | Random Subspace |
| ANN | Artificial Neural Network |
| R | Correlation Coefficient |
| d50 | Median Sediment Size |
| Ys | Scour Depth |
| h | Water Depth |
| bc | Column Width |
| lc | Column Length |
| bpc | Pile Cap Width |
| lpc | Pile Cap Length |
| T | Pile Cap Thickness |
| Lu | Extension length of pile cap out from the column face |
| Lf | Extension width of pile cap out from the column |
| ksc | Shape factor for the column |
| kspc | Shape factor for the pile cap |
| bpg | Pile diameter |
| Fr | Froude number |
| m | Number of piles in line with the flow |
| n | Number of piles normal with the flow |
| Sl | Pile spacing in line with the flow |
| Sb | Pile spacing normal with the flow |
| Y | Pile cap elevation in respect to undisturbed streamflow |
| be | Equivalent width/diameter |
| yscol | Column’s scour |
| yspc | Pile cap’s scour |
| yspg | Scour of pile group |
| Dse | Equivalent diameters of the complex pier |
| Decol | Equivalent diameters of the column |
| Depc | Equivalent diameters of the pile cap |
| Depg | Equivalent diameters of the pile group |
| X | Training dataset |
| S | Subset of training dataset |
| Uc | Critical velocity for the beginning of sediment motion |
| U | Mean approach flow velocity |
References
- Lee, S.O.; Hong, S.H. Turbulence Characteristics before and after Scour Upstream of a Scaled-Down Bridge Pier Model. Water 2019, 11, 1900. [Google Scholar] [CrossRef]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publication: Littleton, CO, USA, 2000. [Google Scholar]
- Ghodsi, H.; Khanjani, M.; Beheshti, A. Evaluation of harmony search optimization to predict local scour depth around complex bridge piers. Civ. Eng. J. 2018, 4, 402–412. [Google Scholar] [CrossRef]
- Ghazvinei, P.T.; Mohamed, T.A.; Ghazali, A.H.; Huat, B.K. Scour hazard assessment and bridge abutment instability analysis. Electron. J. Geotech. Eng. 2012, 17, 2213–2224. [Google Scholar]
- Wardhana, K.; Hadipriono, F.C. Analysis of recent bridge failures in the United States. J. Perform. Constr. Facil. 2003, 17, 144–150. [Google Scholar] [CrossRef]
- Amini, A.; Melville, B.W.; Ali, T.M. Local scour at piled bridge piers including an examination of the superposition method. Can. J. Civ. Eng. 2014, 41, 461–471. [Google Scholar] [CrossRef]
- Amini, A.; Mohammad, T.A. Local scour prediction around piers with complex geometry. Mar. Georesour. Geotechnol. 2017, 35, 857–864. [Google Scholar] [CrossRef]
- Baghbadorani, D.A.; Ataie-Ashtiani, B.; Beheshti, A.; Hadjzaman, M.; Jamali, M. Prediction of current-induced local scour around complex piers: Review, revisit, and integration. Coast. Eng. 2018, 133, 43–58. [Google Scholar] [CrossRef]
- Arneson, L.; Zevenbergen, L.; Lagasse, P.; Clopper, P. Evaluating Scour at Bridges; U.S. Department of TransportationFederal Highway Administration: Washington, DC, USA, 2012.
- Coleman, S.E. Clearwater local scour at complex piers. J. Hydraul. Eng. 2005, 131, 330–334. [Google Scholar] [CrossRef]
- Sheppard, D.; Renna, R. Bridge Scour Manual; Florida Department of Transportation: Tallahassee, FL, USA, 2005. [Google Scholar]
- Jannaty, M.; Eghbalzadeh, A.; Hosseini, S. Using field data to evaluate the complex bridge piers scour methods. Can. J. Civ. Eng. 2015, 43, 218–225. [Google Scholar] [CrossRef]
- Mueller, D.S.; Wagner, C.R. Field Observations and Evaluations of Streambed Scour at Bridges; U.S. Department of TransportationFederal Highway Administration: Washington, DC, USA, 2005.
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Thai Pham, B.; Prakash, I.; Dou, J.; Singh, S.K.; Trinh, P.T.; Trung Tran, H.; Minh Le, T.; Tran, V.P.; Kim Khoi, D.; Shirzadi, A. A novel hybrid approach of landslide susceptibility modeling using rotation forest ensemble and different base classifiers. Geocarto Int. 2018, 14, 1–38. [Google Scholar]
- Shafizadeh-Moghadam, H.; Valavi, R.; Shahabi, H.; Chapi, K.; Shirzadi, A. Novel forecasting approaches using combination of machine learning and statistical models for flood susceptibility mapping. J. Environ. Manag. 2018, 217, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Bui, D.T. Landslide susceptibility modeling using Reduced Error Pruning Trees and different ensemble techniques: Hybrid machine learning approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Wang, Y.; Hong, H.; Chen, W.; Li, S.; Panahi, M.; Khosravi, K.; Shirzadi, A.; Shahabi, H.; Panahi, S.; Costache, R. Flood susceptibility mapping in dingnan county (China) using adaptive neuro-fuzzy inference system with biogeography based optimization and imperialistic competitive algorithm. J. Environ. Manag. 2019, 247, 712–729. [Google Scholar] [CrossRef] [PubMed]
- Ahmadlou, M.; Karimi, M.; Alizadeh, S.; Shirzadi, A.; Parvinnejhad, D.; Shahabi, H.; Panahi, M. Flood susceptibility assessment using integration of adaptive network-based fuzzy inference system (ANFIS) and biogeography-based optimization (BBO) and BAT algorithms (BA). Geocarto Int. 2019, 34, 1252–1272. [Google Scholar] [CrossRef]
- Khosravi, K.; Shahabi, H.; Pham, B.T.; Adamowski, J.; Shirzadi, A.; Pradhan, B.; Dou, J.; Ly, H.-B.; Gróf, G.; Ho, H.L. A comparative assessment of flood susceptibility modeling using Multi-Criteria Decision-Making Analysis and Machine Learning Methods. J. Hydrol. 2019, 573, 311–323. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Li, S.; Shahabi, H.; Wang, Y.; Wang, X.; Ahmad, B.B. Flood susceptibility modelling using novel hybrid approach of reduced-error pruning trees with bagging and random subspace ensembles. J. Hydrol. 2019, 575, 864–873. [Google Scholar] [CrossRef]
- Tien Bui, D.; Khosravi, K.; Shahabi, H.; Daggupati, P.; Adamowski, J.F.; M Melesse, A.; Thai Pham, B.; Pourghasemi, H.R.; Mahmoudi, M.; Bahrami, S. Flood spatial modeling in northern Iran using remote sensing and gis: A comparison between evidential belief functions and its ensemble with a multivariate logistic regression model. Remote Sens. 2019, 11, 1589. [Google Scholar] [CrossRef]
- Bui, D.T.; Panahi, M.; Shahabi, H.; Singh, V.P.; Shirzadi, A.; Chapi, K.; Khosravi, K.; Chen, W.; Panahi, S.; Li, S. Novel hybrid evolutionary algorithms for spatial prediction of floods. Sci. Rep. 2018, 8, 15364. [Google Scholar] [CrossRef]
- Tien Bui, D.; Khosravi, K.; Li, S.; Shahabi, H.; Panahi, M.; Singh, V.; Chapi, K.; Shirzadi, A.; Panahi, S.; Chen, W. New hybrids of anfis with several optimization algorithms for flood susceptibility modeling. Water 2018, 10, 1210. [Google Scholar] [CrossRef]
- Chen, W.; Pradhan, B.; Li, S.; Shahabi, H.; Rizeei, H.M.; Hou, E.; Wang, S. Novel hybrid integration approach of bagging-based fisher’s linear discriminant function for groundwater potential analysis. Nat. Resour. Res. 2019, 28, 1–20. [Google Scholar] [CrossRef]
- Miraki, S.; Zanganeh, S.H.; Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Pham, B.T. Mapping groundwater potential using a novel hybrid intelligence approach. Water Resour. Manag. 2019, 33, 281–302. [Google Scholar] [CrossRef]
- Rahmati, O.; Naghibi, S.A.; Shahabi, H.; Bui, D.T.; Pradhan, B.; Azareh, A.; Rafiei-Sardooi, E.; Samani, A.N.; Melesse, A.M. Groundwater spring potential modelling: Comprising the capability and robustness of three different modeling approaches. J. Hydrol. 2018, 565, 248–261. [Google Scholar] [CrossRef]
- Rahmati, O.; Choubin, B.; Fathabadi, A.; Coulon, F.; Soltani, E.; Shahabi, H.; Mollaefar, E.; Tiefenbacher, J.; Cipullo, S.; Ahmad, B.B. Predicting uncertainty of machine learning models for modelling nitrate pollution of groundwater using quantile regression and uneec methods. Sci. Total Environ. 2019, 688, 855–866. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Li, Y.; Xue, W.; Shahabi, H.; Li, S.; Hong, H.; Wang, X.; Bian, H.; Zhang, S.; Pradhan, B. Modeling flood susceptibility using data-driven approaches of naïve Bayes tree, alternating decision tree, and random forest methods. Sci. Total Environ. 2020, 701, 134979. [Google Scholar] [CrossRef]
- Khosravi, K.; Melesse, A.M.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hong, H. Flood susceptibility mapping at Ningdu catchment, China using bivariate and data mining techniques. In Extreme Hydrology and Climate Variability; Elsevier: Amsterdam, The Netherlands, 2019; pp. 419–434. [Google Scholar]
- He, Q.; Shahabi, H.; Shirzadi, A.; Li, S.; Chen, W.; Wang, N.; Chai, H.; Bian, H.; Ma, J.; Chen, Y. Landslide spatial modelling using novel bivariate statistical based Naïve Bayes, RBF Classifier, and RBF Network machine learning algorithms. Sci. Total Environ. 2019, 663, 1–15. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shirzadi, A.; Shahabi, H.; Chapi, K.; Omidavr, E.; Pham, B.T.; Talebpour Asl, D.; Khaledian, H.; Pradhan, B.; Panahi, M. A Novel Ensemble Artificial Intelligence Approach for Gully Erosion Mapping in a Semi-Arid Watershed (Iran). Sensors 2019, 19, 2444. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Omidvar, E.; Shirzadi, A.; Geertsema, M.; Clague, J.J.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Chapi, K. Shallow landslide prediction using a novel hybrid functional machine learning algorithm. Remote Sens. 2019, 11, 931. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shirzadi, A.; Chapi, K.; Shahabi, H.; Pradhan, B.; Pham, B.T.; Singh, V.P.; Chen, W.; Khosravi, K.; Bin Ahmad, B. A Hybrid Computational Intelligence Approach to Groundwater Spring Potential Mapping. Water 2019, 11, 2013. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hoang, N.-D.; Pham, B.; Bui, Q.-T.; Tran, C.-T.; Panahi, M.; Bin Ahamd, B. A novel integrated approach of relevance vector machine optimized by imperialist competitive algorithm for spatial modeling of shallow landslides. Remote Sens. 2018, 10, 1538. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.-X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using GIS-based machine learning techniques for Chongren County, Jiangxi Province, China. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef] [PubMed]
- Granata, F.; de Marinis, G. Machine learning methods for wastewater hydraulics. Flow Meas. Instrum. 2017, 57, 1–9. [Google Scholar] [CrossRef]
- Parasuraman, K.; Elshorbagy, A.; Si, B.C. Estimating saturated hydraulic conductivity in spatially variable fields using neural network ensembles. Soil Sci. Soc. Am. J. 2006, 70, 1851–1859. [Google Scholar] [CrossRef]
- Pham, B.T.; Hoang, T.-A.; Nguyen, D.-M.; Bui, D.T. Prediction of shear strength of soft soil using machine learning methods. Catena 2018, 166, 181–191. [Google Scholar] [CrossRef]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Soil moisture forecasting by a hybrid machine learning technique: ELM integrated with ensemble empirical mode decomposition. Geoderma 2018, 330, 136–161. [Google Scholar] [CrossRef]
- Kazemi, S.; Minaei Bidgoli, B.; Shamshirband, S.; Karimi, S.M.; Ghorbani, M.A.; Chau, K.-W.; Kazem Pour, R. Novel genetic-based negative correlation learning for estimating soil temperature. Eng. Appl. Comput. Fluid Mech. 2018, 12, 506–516. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Hong, H.; Akgun, A.; Tian, Y.; Liu, J.; Zhu, A.-X.; Li, S. Novel hybrid artificial intelligence approach of bivariate statistical-methods-based kernel logistic regression classifier for landslide susceptibility modeling. Bull. Eng. Geol. Environ. 2019, 78, 4397–4419. [Google Scholar] [CrossRef]
- Jaafari, A.; Zenner, E.K.; Panahi, M.; Shahabi, H. Hybrid artificial intelligence models based on a neuro-fuzzy system and metaheuristic optimization algorithms for spatial prediction of wildfire probability. Agric. For. Meteorol. 2019, 266, 198–207. [Google Scholar] [CrossRef]
- Alizadeh, M.; Alizadeh, E.; Asadollahpour Kotenaee, S.; Shahabi, H.; Beiranvand Pour, A.; Panahi, M.; Bin Ahmad, B.; Saro, L. Social vulnerability assessment using artificial neural network (ANN) model for earthquake hazard in Tabriz city, Iran. Sustainability 2018, 10, 3376. [Google Scholar] [CrossRef]
- Chen, W.; Shirzadi, A.; Shahabi, H.; Ahmad, B.B.; Zhang, S.; Hong, H.; Zhang, N. A novel hybrid artificial intelligence approach based on the rotation forest ensemble and naïve Bayes tree classifiers for a landslide susceptibility assessment in Langao County, China. Geomat. Nat. Hazards Risk 2017, 8, 1955–1977. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Cao, M.-T. Hybrid intelligent inference model for enhancing prediction accuracy of scour depth around bridge piers. Struct. Infrastruct. Eng. 2015, 11, 1178–1189. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Barani, G.-A.; Azamathulla, H.M. GMDH to predict scour depth around a pier in cohesive soils. Appl. Ocean. Res. 2013, 40, 35–41. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Beheshti, A.-A.; Ataie-Ashtiani, B.; Sabbagh-Yazdi, S.-R. Estimation of current-induced scour depth around pile groups using neural network and adaptive neuro-fuzzy inference system. Appl. Soft Comput. 2009, 9, 746–755. [Google Scholar] [CrossRef]
- Hosseini, R.; Fazloula, R.; Saneie, M.; Amini, A. Bagged neural network for estimating the scour depth around pile groups. Int. J. River Basin Manag. 2018, 16, 401–412. [Google Scholar] [CrossRef]
- Amini, A.; Ali, T.M.; Ghazali, A.H.; Aziz, A.A.; Akib, S.M. Impacts of land-use change on streamflows in the Damansara Watershed, Malaysia. Arab. J. Sci. Eng. 2011, 36, 713–720. [Google Scholar] [CrossRef]
- Amini, A.; Mohammad, T.A.; Aziz, A.A.; Ghazali, A.H.; Huat, B.B. A local scour prediction method for pile caps in complex piers. In Proceedings of the Institution of Civil Engineers-Water Management; ICE: Washington, DC, USA, 2019; pp. 73–80. [Google Scholar]
- Ataie-Ashtiani, B.; Baratian-Ghorghi, Z.; Beheshti, A. Experimental investigation of clear-water local scour of compound piers. J. Hydraul. Eng. 2010, 136, 343–351. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; McClelland, J.L. Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Volume 1. Foundations; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Haykin, S. Support vector machines. Neural Netw. A Compr. Found. 1999, 12, 318–350. [Google Scholar]
- Dreiseitl, S.; Ohno-Machado, L. Logistic regression and artificial neural network classification models: A methodology review. J. Biomed. Inform. 2002, 35, 352–359. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, C.; Hong, H.; Zhou, Q.; Wang, D. Mapping earthquake-triggered landslide susceptibility by use of artificial neural network (ANN) models: An example of the 2013 Minxian (China) Mw 5.9 event. Geomat. Nat. Hazards Risk 2019, 10, 1–25. [Google Scholar] [CrossRef]
- Shirzadi, A.; Shahabi, H.; Chapi, K.; Bui, D.T.; Pham, B.T.; Shahedi, K.; Ahmad, B.B. A comparative study between popular statistical and machine learning methods for simulating volume of landslides. Catena 2017, 157, 213–226. [Google Scholar] [CrossRef]
- Bateni, S.M.; Borghei, S.; Jeng, D.-S. Neural network and neuro-fuzzy assessments for scour depth around bridge piers. Eng. Appl. Artif. Intell. 2007, 20, 401–414. [Google Scholar] [CrossRef]
- Kia, M.B.; Pirasteh, S.; Pradhan, B.; Mahmud, A.R.; Sulaiman, W.N.A.; Moradi, A. An artificial neural network model for flood simulation using GIS: Johor River Basin, Malaysia. Environ. Earth Sci. 2012, 67, 251–264. [Google Scholar] [CrossRef]
- Kaya, A. Artificial neural network study of observed pattern of scour depth around bridge piers. Comput. Geotech. 2010, 37, 413–418. [Google Scholar] [CrossRef]
- Choi, S.U.; Cheong, S. Prediction of local scour around bridge piers using artificial neural networks 1. J. Am. Water Resour. Assoc. 2006, 42, 487–494. [Google Scholar] [CrossRef]
- Pal, M.; Singh, N.; Tiwari, N. Support vector regression based modeling of pier scour using field data. Eng. Appl. Artif. Intell. 2011, 24, 911–916. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Tasmania, 16–18 November 1992; pp. 343–348. [Google Scholar]
- Balouchi, B.; Nikoo, M.R.; Adamowski, J. Development of expert systems for the prediction of scour depth under live-bed conditions at river confluences: Application of different types of ANNs and the M5P model tree. Appl. Soft Comput. 2015, 34, 51–59. [Google Scholar] [CrossRef]
- Etemad-Shahidi, A.; Mahjoobi, J. Comparison between M5′ model tree and neural networks for prediction of significant wave height in Lake Superior. Ocean Eng. 2009, 36, 1175–1181. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Siek, M.B.L. Flexible and optimal M5 model trees with applications to flow predictions. In Hydroinformatics: (In 2 Volumes, with CD-ROM); World Scientific: Singapore, 2004; pp. 1719–1726. [Google Scholar]
- Bhattacharya, B.; Solomatine, D.P. Neural networks and M5 model trees in modelling water level–discharge relationship. Neurocomputing 2005, 63, 381–396. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Jordan, M., Lauritzen, S.L., Lawless, J.L., Nair, V., Eds.; Springer: NewYork, NY, USA, 1995. [Google Scholar]
- Micheletti, N.; Foresti, L.; Robert, S.; Leuenberger, M.; Pedrazzini, A.; Jaboyedoff, M.; Kanevski, M. Machine learning feature selection methods for landslide susceptibility mapping. Math. Geosci. 2014, 46, 33–57. [Google Scholar] [CrossRef]
- Vapnik, V. Pattern recognition using generalized portrait method. Autom. Remote Control 1963, 24, 774–780. [Google Scholar]
- Quinlan, J.R. Simplifying decision trees. Int. J. Man-Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Prakash, I.; Bui, D.T. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz watershed, northern Iran. Sci. Total Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef]
- Mohamed, W.N.H.W.; Salleh, M.N.M.; Omar, A.H. A comparative study of reduced error pruning method in decision tree algorithms. In Proceedings of the Control System, Computing and Engineering (ICCSCE), 2012 IEEE International Conference on, Penang, Malaysian, 23 November 2012; pp. 392–397. [Google Scholar]
- Galathiya, A.; Ganatra, A.; Bhensdadia, C. Improved decision tree induction algorithm with feature selection, cross validation, model complexity and reduced error pruning. Int. J. Comput. Sci. Inf. Technol. 2012, 3, 3427–3431. [Google Scholar]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Skurichina, M.; Duin, R.P. Bagging, boosting and the random subspace method for linear classifiers. Pattern Anal. Appl. 2002, 5, 121–135. [Google Scholar] [CrossRef]
- Shirzadi, A.; Bui, D.T.; Pham, B.T.; Solaimani, K.; Chapi, K.; Kavian, A.; Shahabi, H.; Revhaug, I. Shallow landslide susceptibility assessment using a novel hybrid intelligence approach. Environ. Earth Sci. 2017, 76, 60. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Veerasamy, R.; Rajak, H.; Jain, A.; Sivadasan, S.; Varghese, C.P.; Agrawal, R.K. Validation of QSAR models-strategies and importance. Int. J. Drug Des. Discov. 2011, 3, 511–519. [Google Scholar]
- Bonadonna, C.; Costa, A. Estimating the volume of tephra deposits: A new simple strategy. Geology 2012, 40, 415–418. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Sigaroodi, S.K.; Chen, Q.; Ebrahimi, S.; Nazari, A.; Choobin, B. Long-term precipitation forecast for drought relief using atmospheric circulation factors: A study on the Maharloo Basin in Iran. Hydrol. Earth Syst. Sci. 2014, 18, 1995–2006. [Google Scholar] [CrossRef]
- Barnston, A.G. Correspondence among the correlation, RMSE, and Heidke forecast verification measures; refinement of the Heidke score. Weather Forecast. 1992, 7, 699–709. [Google Scholar] [CrossRef]
- Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Bui, D.T.; Pham, B.T.; Khosravi, K. A novel hybrid artificial intelligence approach for flood susceptibility assessment. Environ. Model. Softw. 2017, 95, 229–245. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Rezaie Balf, M.; Rashedi, E. Prediction of maximum scour depth around piers with debris accumulation using EPR, MT, and GEP models. J. Hydroinform. 2016, 18, 867–884. [Google Scholar] [CrossRef]
- Beasley, T.M.; Zumbo, B.D. Comparison of aligned Friedman rank and parametric methods for testing interactions in split-plot designs. Comput. Stat. Data Anal. 2003, 42, 569–593. [Google Scholar] [CrossRef]
- Lee, S.O.; Hong, S.H. Reproducing Field Measurements Using Scaled-Down Hydraulic Model Studies in a Laboratory. Adv. Civ. Eng. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Moreno, M.; Maia, R.; Couto, L. Effects of relative column width and pile-cap elevation on local scour depth around complex piers. J. Hydraul. Eng. 2015, 142, 04015051. [Google Scholar] [CrossRef]
- Ferraro, D.; Tafarojnoruz, A.; Gaudio, R.; Cardoso, A.H. Effects of pile cap thickness on the maximum scour depth at a complex pier. J. Hydraul. Eng. 2013, 139, 482–491. [Google Scholar] [CrossRef]
- Amini, A.; Solaimani, N. The effects of uniform and nonuniform pile spacing variations on local scour at pile groups. Mar. Georesour. Geotechnol. 2018, 36, 861–866. [Google Scholar] [CrossRef]
- Shirzadi, A.; Soliamani, K.; Habibnejhad, M.; Kavian, A.; Chapi, K.; Shahabi, H.; Chen, W.; Khosravi, K.; Thai Pham, B.; Pradhan, B. Novel GIS based machine learning algorithms for shallow landslide susceptibility mapping. Sensors 2018, 18, 3777. [Google Scholar] [CrossRef] [PubMed]
- Shirzadi, A.; Solaimani, K.; Roshan, M.H.; Kavian, A.; Chapi, K.; Shahabi, H.; Keesstra, S.; Ahmad, B.B.; Bui, D.T. Uncertainties of prediction accuracy in shallow landslide modeling: Sample size and raster resolution. Catena 2019, 178, 172–188. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).