Analytical Mathematical Modeling of the Thermal Bridge between Reinforced Concrete Wall and Inter-Floor Slab
Abstract
1. Introduction
The Building Context and Techniques
2. Methodology
3. Results and Calculation
3.1. Inapplicability of Existing Manuals/Atlases for the Calculation of Thermal Bridges
3.2. Numerical Model
3.3. Non-Linear Regression
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Type of Floor | dp | di | Ψi THERM 7.4 | ds | dpi = dp + di | Upi | Up | Us | Ψi Equation (4) | ΔΨi |
|---|---|---|---|---|---|---|---|---|---|---|
| Reinforced concrete slab | 0.14 | 0.02 | 0.957 | 0.160 | 0.160 | 128.454 | 359.081 | 313.077 | 0.926 | −3.18% |
| 0.04 | 1.049 | 0.160 | 0.180 | 0.78217 | 359.081 | 313.077 | 1.058 | 0.85% | ||
| 0.06 | 1.054 | 0.160 | 0.200 | 0.56228 | 359.081 | 313.077 | 1.077 | 2.18% | ||
| 0.08 | 1.033 | 0.160 | 0.220 | 0.43889 | 359.081 | 313.077 | 1.054 | 2.08% | ||
| 0.10 | 1.003 | 0.160 | 0.240 | 0.35991 | 359.081 | 313.077 | 1.014 | 1.04% | ||
| 0.16 | 0.02 | 0.927 | 0.160 | 0.180 | 127.035 | 348.208 | 313.077 | 0.915 | −1.28% | |
| 0.04 | 1.025 | 0.160 | 0.200 | 0.77689 | 348.208 | 313.077 | 1.041 | 1.59% | ||
| 0.06 | 1.032 | 0.160 | 0.220 | 0.55954 | 348.208 | 313.077 | 1.059 | 2.60% | ||
| 0.08 | 1.015 | 0.160 | 0.240 | 0.43722 | 348.208 | 313.077 | 1.036 | 2.12% | ||
| 0.10 | 0.987 | 0.160 | 0.260 | 0.35879 | 348.208 | 313.077 | 0.996 | 0.88% | ||
| 0.18 | 0.02 | 0.901 | 0.160 | 0.200 | 125.647 | 337.975 | 313.077 | 0.901 | 0.01% | |
| 0.04 | 1.003 | 0.160 | 0.220 | 0.77168 | 337.975 | 313.077 | 1.021 | 1.82% | ||
| 0.06 | 1.012 | 0.160 | 0.240 | 0.55683 | 337.975 | 313.077 | 1.038 | 2.54% | ||
| 0.08 | 0.997 | 0.160 | 0.260 | 0.43556 | 337.975 | 313.077 | 1.015 | 1.77% | ||
| 0.10 | 0.972 | 0.160 | 0.280 | 0.35767 | 337.975 | 313.077 | 0.975 | 0.28% | ||
| 0.20 | 0.02 | 0.872 | 0.160 | 0.220 | 124.289 | 328.326 | 313.077 | 0.884 | 1.37% | |
| 0.04 | 0.977 | 0.160 | 0.240 | 0.76653 | 328.326 | 313.077 | 0.999 | 2.27% | ||
| 0.06 | 0.993 | 0.160 | 0.260 | 0.55415 | 328.326 | 313.077 | 1.014 | 2.11% | ||
| 0.08 | 0.981 | 0.160 | 0.280 | 0.43392 | 328.326 | 313.077 | 0.991 | 1.02% | ||
| 0.10 | 0.957 | 0.160 | 0.300 | 0.35656 | 328.326 | 313.077 | 0.952 | −0.48% | ||
| 0.14 | 0.02 | 1.041 | 0.200 | 0.160 | 128.454 | 359.081 | 296.911 | 1.002 | −3.73% | |
| 0.04 | 1.152 | 0.200 | 0.180 | 0.78217 | 359.081 | 296.911 | 1.144 | −0.71% | ||
| 0.06 | 1.165 | 0.200 | 0.200 | 0.56228 | 359.081 | 296.911 | 1.165 | 0.00% | ||
| 0.08 | 1.147 | 0.200 | 0.220 | 0.43889 | 359.081 | 296.911 | 1.140 | −0.56% | ||
| 0.10 | 1.113 | 0.200 | 0.240 | 0.35991 | 359.081 | 296.911 | 1.096 | −1.53% | ||
| 0.16 | 0.02 | 1.008 | 0.200 | 0.180 | 127.035 | 348.208 | 296.911 | 0.989 | −1.80% | |
| 0.04 | 1.128 | 0.200 | 0.200 | 0.77689 | 348.208 | 296.911 | 1.126 | −0.24% | ||
| 0.06 | 1.138 | 0.200 | 0.220 | 0.55954 | 348.208 | 296.911 | 1.145 | 0.57% | ||
| 0.08 | 1.125 | 0.200 | 0.240 | 0.43722 | 348.208 | 296.911 | 1.120 | −0.39% | ||
| 0.10 | 1.093 | 0.200 | 0.260 | 0.35879 | 348.208 | 296.911 | 1.077 | −1.51% | ||
| 0.18 | 0.02 | 0.977 | 0.200 | 0.200 | 125.647 | 337.975 | 296.911 | 0.974 | −0.34% | |
| 0.04 | 1.096 | 0.200 | 0.220 | 0.77168 | 337.975 | 296.911 | 1.104 | 0.75% | ||
| 0.06 | 1.116 | 0.200 | 0.240 | 0.55683 | 337.975 | 296.911 | 1.122 | 0.53% | ||
| 0.08 | 1.105 | 0.200 | 0.260 | 0.43556 | 337.975 | 296.911 | 1.097 | −0.66% | ||
| 0.10 | 1.076 | 0.200 | 0.280 | 0.35767 | 337.975 | 296.911 | 1.055 | −2.01% | ||
| 0.20 | 0.02 | 0.947 | 0.200 | 0.220 | 124.289 | 328.326 | 296.911 | 0.956 | 0.99% | |
| 0.04 | 1.071 | 0.200 | 0.240 | 0.76653 | 328.326 | 296.911 | 1.080 | 0.88% | ||
| 0.06 | 1.094 | 0.200 | 0.260 | 0.55415 | 328.326 | 296.911 | 1.096 | 0.22% | ||
| 0.08 | 1.086 | 0.200 | 0.280 | 0.43392 | 328.326 | 296.911 | 1.072 | −1.30% | ||
| 0.10 | 1.059 | 0.200 | 0.300 | 0.35656 | 328.326 | 296.911 | 1.030 | −2.73% | ||
| 0.14 | 0.02 | 1.121 | 0.240 | 0.160 | 128.454 | 359.081 | 282.332 | 1.091 | −2.66% | |
| 0.04 | 1.246 | 0.240 | 0.180 | 0.78217 | 359.081 | 282.332 | 1.246 | 0.00% | ||
| 0.06 | 1.265 | 0.240 | 0.200 | 0.56228 | 359.081 | 282.332 | 1.269 | 0.25% | ||
| 0.08 | 1.250 | 0.240 | 0.220 | 0.43889 | 359.081 | 282.332 | 1.242 | −0.66% | ||
| 0.10 | 1.224 | 0.240 | 0.240 | 0.35991 | 359.081 | 282.332 | 1.194 | −2.44% | ||
| 0.16 | 0.02 | 1.082 | 0.240 | 0.180 | 127.035 | 348.208 | 282.332 | 1.078 | −0.43% | |
| 0.04 | 1.215 | 0.240 | 0.200 | 0.77689 | 348.208 | 282.332 | 1.226 | 0.88% | ||
| 0.06 | 1.239 | 0.240 | 0.220 | 0.55954 | 348.208 | 282.332 | 1.247 | 0.64% | ||
| 0.08 | 1.226 | 0.240 | 0.240 | 0.43722 | 348.208 | 282.332 | 1.220 | −0.45% | ||
| 0.10 | 1.201 | 0.240 | 0.260 | 0.35879 | 348.208 | 282.332 | 1.173 | −2.37% | ||
| 0.18 | 0.02 | 1.049 | 0.240 | 0.200 | 125.647 | 337.975 | 282.332 | 1.061 | 1.10% | |
| 0.04 | 1.186 | 0.240 | 0.220 | 0.77168 | 337.975 | 282.332 | 1.203 | 1.38% | ||
| 0.06 | 1.211 | 0.240 | 0.240 | 0.55683 | 337.975 | 282.332 | 1.222 | 0.90% | ||
| 0.08 | 1.202 | 0.240 | 0.260 | 0.43556 | 337.975 | 282.332 | 1.195 | −0.59% | ||
| 0.10 | 1.182 | 0.240 | 0.280 | 0.35767 | 337.975 | 282.332 | 1.149 | −2.79% | ||
| 0.20 | 0.02 | 1.018 | 0.240 | 0.220 | 124.289 | 328.326 | 282.332 | 1.041 | 2.31% | |
| 0.04 | 1.156 | 0.240 | 0.240 | 0.76653 | 328.326 | 282.332 | 1.176 | 1.79% | ||
| 0.06 | 1.186 | 0.240 | 0.260 | 0.55415 | 328.326 | 282.332 | 1.194 | 0.68% | ||
| 0.08 | 1.181 | 0.240 | 0.280 | 0.43392 | 328.326 | 282.332 | 1.167 | −1.15% | ||
| 0.10 | 1.161 | 0.240 | 0.300 | 0.35656 | 328.326 | 282.332 | 1.122 | −3.40% | ||
| Hollow brick floor | 0.14 | 0.02 | 0.611 | 0.160 | 0.160 | 128.454 | 359.081 | 215.900 | 0.597 | −2.38% |
| 0.04 | 0.690 | 0.160 | 0.180 | 0.78217 | 359.081 | 215.900 | 0.681 | −1.27% | ||
| 0.06 | 0.686 | 0.160 | 0.200 | 0.56228 | 359.081 | 215.900 | 0.694 | 1.16% | ||
| 0.08 | 0.660 | 0.160 | 0.220 | 0.43889 | 359.081 | 215.900 | 0.679 | 2.79% | ||
| 0.10 | 0.630 | 0.160 | 0.240 | 0.35991 | 359.081 | 215.900 | 0.653 | 3.54% | ||
| 0.16 | 0.02 | 0.602 | 0.160 | 0.180 | 127.035 | 348.208 | 215.900 | 0.589 | −2.14% | |
| 0.04 | 0.671 | 0.160 | 0.200 | 0.77689 | 348.208 | 215.900 | 0.670 | −0.15% | ||
| 0.06 | 0.673 | 0.160 | 0.220 | 0.55954 | 348.208 | 215.900 | 0.682 | 1.26% | ||
| 0.08 | 0.650 | 0.160 | 0.240 | 0.43722 | 348.208 | 215.900 | 0.667 | 2.71% | ||
| 0.10 | 0.621 | 0.160 | 0.260 | 0.35879 | 348.208 | 215.900 | 0.641 | 3.22% | ||
| 0.18 | 0.02 | 0.587 | 0.160 | 0.200 | 125.647 | 337.975 | 215.900 | 0.580 | −1.22% | |
| 0.04 | 0.662 | 0.160 | 0.220 | 0.77168 | 337.975 | 215.900 | 0.658 | −0.61% | ||
| 0.06 | 0.663 | 0.160 | 0.240 | 0.55683 | 337.975 | 215.900 | 0.668 | 0.82% | ||
| 0.08 | 0.642 | 0.160 | 0.260 | 0.43556 | 337.975 | 215.900 | 0.653 | 1.79% | ||
| 0.10 | 0.615 | 0.160 | 0.280 | 0.35767 | 337.975 | 215.900 | 0.628 | 2.05% | ||
| 0.20 | 0.02 | 0.570 | 0.160 | 0.220 | 124.289 | 328.326 | 215.900 | 0.569 | −0.11% | |
| 0.04 | 0.649 | 0.160 | 0.240 | 0.76653 | 328.326 | 215.900 | 0.643 | −0.88% | ||
| 0.06 | 0.654 | 0.160 | 0.260 | 0.55415 | 328.326 | 215.900 | 0.653 | −0.25% | ||
| 0.08 | 0.634 | 0.160 | 0.280 | 0.43392 | 328.326 | 215.900 | 0.638 | 0.61% | ||
| 0.10 | 0.608 | 0.160 | 0.300 | 0.35656 | 328.326 | 215.900 | 0.613 | 0.89% | ||
| 0.14 | 0.02 | 0.638 | 0.200 | 0.160 | 128.454 | 359.081 | 194.931 | 0.631 | −1.11% | |
| 0.04 | 0.735 | 0.200 | 0.180 | 0.78217 | 359.081 | 194.931 | 0.721 | −1.98% | ||
| 0.06 | 0.738 | 0.200 | 0.200 | 0.56228 | 359.081 | 194.931 | 0.734 | −0.58% | ||
| 0.08 | 0.715 | 0.200 | 0.220 | 0.43889 | 359.081 | 194.931 | 0.718 | 0.45% | ||
| 0.10 | 0.683 | 0.200 | 0.240 | 0.35991 | 359.081 | 194.931 | 0.691 | 1.16% | ||
| 0.16 | 0.02 | 0.628 | 0.200 | 0.180 | 127.035 | 348.208 | 194.931 | 0.623 | −0.80% | |
| 0.04 | 0.719 | 0.200 | 0.200 | 0.77689 | 348.208 | 194.931 | 0.709 | −1.30% | ||
| 0.06 | 0.724 | 0.200 | 0.220 | 0.55954 | 348.208 | 194.931 | 0.721 | −0.34% | ||
| 0.08 | 0.703 | 0.200 | 0.240 | 0.43722 | 348.208 | 194.931 | 0.706 | 0.40% | ||
| 0.10 | 0.672 | 0.200 | 0.260 | 0.35879 | 348.208 | 194.931 | 0.678 | 0.90% | ||
| 0.18 | 0.02 | 0.612 | 0.200 | 0.200 | 125.647 | 337.975 | 194.931 | 0.614 | 0.28% | |
| 0.04 | 0.705 | 0.200 | 0.220 | 0.77168 | 337.975 | 194.931 | 0.696 | −1.34% | ||
| 0.06 | 0.713 | 0.200 | 0.240 | 0.55683 | 337.975 | 194.931 | 0.707 | −0.83% | ||
| 0.08 | 0.695 | 0.200 | 0.260 | 0.43556 | 337.975 | 194.931 | 0.691 | −0.50% | ||
| 0.10 | 0.666 | 0.200 | 0.280 | 0.35767 | 337.975 | 194.931 | 0.664 | −0.19% | ||
| 0.20 | 0.02 | 0.595 | 0.200 | 0.220 | 124.289 | 328.326 | 194.931 | 0.602 | 1.28% | |
| 0.04 | 0.691 | 0.200 | 0.240 | 0.76653 | 328.326 | 194.931 | 0.681 | −1.57% | ||
| 0.06 | 0.701 | 0.200 | 0.260 | 0.55415 | 328.326 | 194.931 | 0.691 | −1.45% | ||
| 0.08 | 0.686 | 0.200 | 0.280 | 0.43392 | 328.326 | 194.931 | 0.675 | −1.56% | ||
| 0.10 | 0.657 | 0.200 | 0.300 | 0.35656 | 328.326 | 194.931 | 0.649 | −1.28% | ||
| 0.14 | 0.02 | 0.665 | 0.240 | 0.160 | 128.454 | 359.081 | 178.084 | 0.680 | 2.34% | |
| 0.04 | 0.775 | 0.240 | 0.180 | 0.78217 | 359.081 | 178.084 | 0.777 | 0.28% | ||
| 0.06 | 0.784 | 0.240 | 0.200 | 0.56228 | 359.081 | 178.084 | 0.791 | 0.92% | ||
| 0.08 | 0.764 | 0.240 | 0.220 | 0.43889 | 359.081 | 178.084 | 0.774 | 1.37% | ||
| 0.10 | 0.737 | 0.240 | 0.240 | 0.35991 | 359.081 | 178.084 | 0.745 | 1.00% | ||
| 0.16 | 0.02 | 0.651 | 0.240 | 0.180 | 127.035 | 348.208 | 178.084 | 0.672 | 3.22% | |
| 0.04 | 0.754 | 0.240 | 0.200 | 0.77689 | 348.208 | 178.084 | 0.765 | 1.34% | ||
| 0.06 | 0.772 | 0.240 | 0.220 | 0.55954 | 348.208 | 178.084 | 0.778 | 0.76% | ||
| 0.08 | 0.751 | 0.240 | 0.240 | 0.43722 | 348.208 | 178.084 | 0.761 | 1.29% | ||
| 0.10 | 0.726 | 0.240 | 0.260 | 0.35879 | 348.208 | 178.084 | 0.731 | 0.78% | ||
| 0.18 | 0.02 | 0.634 | 0.240 | 0.200 | 125.647 | 337.975 | 178.084 | 0.662 | 4.31% | |
| 0.04 | 0.745 | 0.240 | 0.220 | 0.77168 | 337.975 | 178.084 | 0.750 | 0.62% | ||
| 0.06 | 0.757 | 0.240 | 0.240 | 0.55683 | 337.975 | 178.084 | 0.762 | 0.71% | ||
| 0.08 | 0.742 | 0.240 | 0.260 | 0.43556 | 337.975 | 178.084 | 0.745 | 0.52% | ||
| 0.10 | 0.718 | 0.240 | 0.280 | 0.35767 | 337.975 | 178.084 | 0.716 | −0.27% | ||
| 0.20 | 0.02 | 0.619 | 0.240 | 0.220 | 124.289 | 328.326 | 178.084 | 0.649 | 4.95% | |
| 0.04 | 0.728 | 0.240 | 0.240 | 0.76653 | 328.326 | 178.084 | 0.734 | 0.75% | ||
| 0.06 | 0.746 | 0.240 | 0.260 | 0.55415 | 328.326 | 178.084 | 0.745 | −0.25% | ||
| 0.08 | 0.732 | 0.240 | 0.280 | 0.43392 | 328.326 | 178.084 | 0.728 | −0.52% | ||
| 0.10 | 0.709 | 0.240 | 0.300 | 0.35656 | 328.326 | 178.084 | 0.699 | −1.30% | ||
| Predalles floor | 0.14 | 0.02 | 0.562 | 0.160 | 0.160 | 128.454 | 359.081 | 196.885 | 0.547 | −2.62% |
| 0.04 | 0.639 | 0.160 | 0.180 | 0.78217 | 359.081 | 196.885 | 0.625 | −2.19% | ||
| 0.06 | 0.634 | 0.160 | 0.200 | 0.56228 | 359.081 | 196.885 | 0.636 | 0.36% | ||
| 0.08 | 0.610 | 0.160 | 0.220 | 0.43889 | 359.081 | 196.885 | 0.623 | 2.11% | ||
| 0.10 | 0.581 | 0.160 | 0.240 | 0.35991 | 359.081 | 196.885 | 0.599 | 3.08% | ||
| 0.16 | 0.02 | 0.555 | 0.160 | 0.180 | 127.035 | 348.208 | 196.885 | 0.541 | −2.61% | |
| 0.04 | 0.622 | 0.160 | 0.200 | 0.77689 | 348.208 | 196.885 | 0.615 | −1.12% | ||
| 0.06 | 0.623 | 0.160 | 0.220 | 0.55954 | 348.208 | 196.885 | 0.625 | 0.40% | ||
| 0.08 | 0.600 | 0.160 | 0.240 | 0.43722 | 348.208 | 196.885 | 0.612 | 2.01% | ||
| 0.10 | 0.572 | 0.160 | 0.260 | 0.35879 | 348.208 | 196.885 | 0.588 | 2.85% | ||
| 0.18 | 0.02 | 0.541 | 0.160 | 0.200 | 125.647 | 337.975 | 196.885 | 0.532 | −1.70% | |
| 0.04 | 0.613 | 0.160 | 0.220 | 0.77168 | 337.975 | 196.885 | 0.603 | −1.62% | ||
| 0.06 | 0.614 | 0.160 | 0.240 | 0.55683 | 337.975 | 196.885 | 0.613 | −0.11% | ||
| 0.08 | 0.593 | 0.160 | 0.260 | 0.43556 | 337.975 | 196.885 | 0.600 | 1.04% | ||
| 0.10 | 0.568 | 0.160 | 0.280 | 0.35767 | 337.975 | 196.885 | 0.576 | 1.50% | ||
| 0.20 | 0.02 | 0.525 | 0.160 | 0.220 | 124.289 | 328.326 | 196.885 | 0.522 | −0.53% | |
| 0.04 | 0.602 | 0.160 | 0.240 | 0.76653 | 328.326 | 196.885 | 0.590 | −1.98% | ||
| 0.06 | 0.607 | 0.160 | 0.260 | 0.55415 | 328.326 | 196.885 | 0.599 | −1.33% | ||
| 0.08 | 0.587 | 0.160 | 0.280 | 0.43392 | 328.326 | 196.885 | 0.586 | −0.24% | ||
| 0.10 | 0.561 | 0.160 | 0.300 | 0.35656 | 328.326 | 196.885 | 0.563 | 0.29% | ||
| 0.14 | 0.02 | 0.598 | 0.200 | 0.160 | 128.454 | 359.081 | 177.827 | 0.584 | −2.32% | |
| 0.04 | 0.693 | 0.200 | 0.180 | 0.78217 | 359.081 | 177.827 | 0.667 | −3.75% | ||
| 0.06 | 0.696 | 0.200 | 0.200 | 0.56228 | 359.081 | 177.827 | 0.679 | −2.43% | ||
| 0.08 | 0.673 | 0.200 | 0.220 | 0.43889 | 359.081 | 177.827 | 0.665 | −1.22% | ||
| 0.10 | 0.642 | 0.200 | 0.240 | 0.35991 | 359.081 | 177.827 | 0.639 | −0.44% | ||
| 0.16 | 0.02 | 0.581 | 0.200 | 0.180 | 127.035 | 348.208 | 177.827 | 0.577 | −0.71% | |
| 0.04 | 0.669 | 0.200 | 0.200 | 0.77689 | 348.208 | 177.827 | 0.656 | −1.88% | ||
| 0.06 | 0.674 | 0.200 | 0.220 | 0.55954 | 348.208 | 177.827 | 0.668 | −0.95% | ||
| 0.08 | 0.653 | 0.200 | 0.240 | 0.43722 | 348.208 | 177.827 | 0.653 | 0.04% | ||
| 0.10 | 0.632 | 0.200 | 0.260 | 0.35879 | 348.208 | 177.827 | 0.628 | −0.65% | ||
| 0.18 | 0.02 | 0.566 | 0.200 | 0.200 | 125.647 | 337.975 | 177.827 | 0.568 | 0.33% | |
| 0.04 | 0.657 | 0.200 | 0.220 | 0.77168 | 337.975 | 177.827 | 0.644 | −2.00% | ||
| 0.06 | 0.664 | 0.200 | 0.240 | 0.55683 | 337.975 | 177.827 | 0.654 | −1.48% | ||
| 0.08 | 0.646 | 0.200 | 0.260 | 0.43556 | 337.975 | 177.827 | 0.640 | −0.95% | ||
| 0.10 | 0.618 | 0.200 | 0.280 | 0.35767 | 337.975 | 177.827 | 0.615 | −0.50% | ||
| 0.20 | 0.02 | 0.550 | 0.200 | 0.220 | 124.289 | 328.326 | 177.827 | 0.557 | 1.34% | |
| 0.04 | 0.644 | 0.200 | 0.240 | 0.76653 | 328.326 | 177.827 | 0.630 | −2.21% | ||
| 0.06 | 0.653 | 0.200 | 0.260 | 0.55415 | 328.326 | 177.827 | 0.639 | −2.11% | ||
| 0.08 | 0.638 | 0.200 | 0.280 | 0.43392 | 328.326 | 177.827 | 0.625 | −2.04% | ||
| 0.10 | 0.610 | 0.200 | 0.300 | 0.35656 | 328.326 | 177.827 | 0.600 | −1.56% | ||
| 0.14 | 0.02 | 0.618 | 0.240 | 0.160 | 128.454 | 359.081 | 163.004 | 0.635 | 2.76% | |
| 0.04 | 0.727 | 0.240 | 0.180 | 0.78217 | 359.081 | 163.004 | 0.726 | −0.17% | ||
| 0.06 | 0.735 | 0.240 | 0.200 | 0.56228 | 359.081 | 163.004 | 0.739 | 0.46% | ||
| 0.08 | 0.716 | 0.240 | 0.220 | 0.43889 | 359.081 | 163.004 | 0.723 | 0.98% | ||
| 0.10 | 0.690 | 0.240 | 0.240 | 0.35991 | 359.081 | 163.004 | 0.695 | 0.77% | ||
| 0.16 | 0.02 | 0.607 | 0.240 | 0.180 | 127.035 | 348.208 | 163.004 | 0.628 | 3.46% | |
| 0.04 | 0.713 | 0.240 | 0.200 | 0.77689 | 348.208 | 163.004 | 0.714 | 0.12% | ||
| 0.06 | 0.725 | 0.240 | 0.220 | 0.55954 | 348.208 | 163.004 | 0.726 | 0.21% | ||
| 0.08 | 0.706 | 0.240 | 0.240 | 0.43722 | 348.208 | 163.004 | 0.711 | 0.66% | ||
| 0.10 | 0.681 | 0.240 | 0.260 | 0.35879 | 348.208 | 163.004 | 0.683 | 0.30% | ||
| 0.18 | 0.02 | 0.592 | 0.240 | 0.200 | 125.647 | 337.975 | 163.004 | 0.618 | 4.42% | |
| 0.04 | 0.700 | 0.240 | 0.220 | 0.77168 | 337.975 | 163.004 | 0.701 | 0.03% | ||
| 0.06 | 0.711 | 0.240 | 0.240 | 0.55683 | 337.975 | 163.004 | 0.712 | 0.13% | ||
| 0.08 | 0.696 | 0.240 | 0.260 | 0.43556 | 337.975 | 163.004 | 0.696 | 0.05% | ||
| 0.10 | 0.673 | 0.240 | 0.280 | 0.35767 | 337.975 | 163.004 | 0.669 | −0.64% | ||
| 0.20 | 0.02 | 0.577 | 0.240 | 0.220 | 124.289 | 328.326 | 163.004 | 0.606 | 5.10% | |
| 0.04 | 0.684 | 0.240 | 0.240 | 0.76653 | 328.326 | 163.004 | 0.685 | 0.17% | ||
| 0.06 | 0.702 | 0.240 | 0.260 | 0.55415 | 328.326 | 163.004 | 0.695 | −0.89% | ||
| 0.08 | 0.687 | 0.240 | 0.280 | 0.43392 | 328.326 | 163.004 | 0.680 | −1.03% | ||
| 0.10 | 0.664 | 0.240 | 0.300 | 0.35656 | 328.326 | 163.004 | 0.653 | −1.66% |
References
- World Health Organization. Technical and Policy Recommendations to Reduce Health Risks Due to Dampness and Mould; Project Report; WHO: Copenhagen, Denmark, 2009. [Google Scholar]
- Hanafi, M.H.; Umar, M.U.; Razak, A.A.; Rashid, Z.Z.A.; Noriman, N.Z.; Dahham, O.S. An introduction to thermal bridge assessment and mould risk at dampness surface for heritage building. IOP Conf. Ser. Mater. Sci. Eng. 2018, 454, 1–8. [Google Scholar] [CrossRef]
- Fantucci, S.; Isaia, F.; Serra, V.; Dutto, M. Insulating coat to prevent mold growth in thermal bridges. Energy Procedia 2017, 134, 414–422. [Google Scholar] [CrossRef]
- Berggren, B.; Wall, M. State of Knowledge of Thermal Bridges—A Follow up in Sweden and a Review of Recent Research. Sustainability 2018, 8, 154. [Google Scholar] [CrossRef]
- Kalousek, L.; Brzoň, R.; Fišarová, Z. Analysis of thermal bridges in loggias of pre-cast concrete apartment buildings. MATEC Web Conf. 2019, 279, 1–6. [Google Scholar] [CrossRef]
- Jedidi, M.; Benjeddou, O. Effect of thermal bridges on the heat balance of buildings. IJSRCE 2018, 2, 41–49. [Google Scholar]
- Berggren, B.; Wall, M. Calculation of thermal bridges in (Nordic) building envelopes—Risk of performance failure due to inconsistent use of methodology. Energy Buildings 2013, 65, 331–339. [Google Scholar] [CrossRef]
- Citterio, M.; Cocco, M.; Erhorn-Kluttig, H. Thermal bridges in the EBPD context: Overview on MS approaches in regulations. In Build Up. The European Portal for Energy Efficiency in Buildings; Information Paper P64 of the EPBD Buildings Platform, European Communities; 2008; pp. 1–9. Available online: http://www.buildingsplatform.eu/ (accessed on 22 September 2020).
- Kotti, S.; Telia, D.; James, P.A.B. Quantifying thermal bridge effects and assessing retrofit solutions in a Greek residential building. Procedia Environ. Sci. 2017, 38, 306–313. [Google Scholar] [CrossRef]
- Theodosiou, T.G.; Papadopoulos, A.M. The impact of thermal bridges on the energy demand of buildings with double brick wall constructions. Energy Build. 2008, 40, 2083–2089. [Google Scholar] [CrossRef]
- Ilomets, S.; Kuusk, K.; Paap, L.; Arumägi, E.; Kalamees, T. Impact of linear thermal bridges on thermal transmittance of renovated apartment buildings. J. Civ. Eng. Manag. 2016, 1–9. [Google Scholar] [CrossRef]
- Bergero, S.; Chiari, A. The influence of thermal bridge calculation method on the building energy need-: A case study. Energy Proced. 2018, 148, 1042–1049. [Google Scholar] [CrossRef]
- Gao, Y.; Roux, J.J.; Zhao, L.H.; Jiang, Y. Dynamical building simulation: A low order model for thermal bridges losses. Energy Build. 2008, 40, 2236–2243. [Google Scholar] [CrossRef]
- Ben-Nakhi, A.E. Minimizing thermal bridging through window systems in buildings of hot regions. Appl. Therm. Eng. 2002, 22, 989–998. [Google Scholar] [CrossRef]
- Cappelletti, F.; Corrado, V.; Gasparella, A.; Gorrino, A. Detailed assessment of thermal bridges in highly insulated buildings. In Proceedings of the CLIMA 2010, 10th Rehva World Congress Sustainable Energy Use in Buildings, Antalya, Turkey, 9–12 May 2010. [Google Scholar]
- Dilmac, S.; Guner, A.; Senkal, F.; Kartal, S. Simple method for calculation of heat loss through floor/beam-wall intersections according to ISO 9164. Energy Convers Manag. 2007, 48, 826–835. [Google Scholar] [CrossRef]
- Evola, G.; Margani, G.; Marletta, L. Cost-effective design solutions for low-rise residential Net ZEBs in Mediterranean climate. Energy Build. 2014, 68, 7–18. [Google Scholar] [CrossRef]
- Karabulut, K.; Buyruk, E.; Fertelli, A. Numerical investigation of the effect of insulation on heat transfer of thermal bridges with different types. Therm. Sci. 2016, 20, 185–195. [Google Scholar] [CrossRef]
- Ghazi Wakili, K.; Simmler, H.; Frank, T. Experimental and numerical thermal analysis of a balcony board with integrated glass fibre reinforced polymer GFRP elements. Energy Build. 2007, 39, 76–81. [Google Scholar] [CrossRef]
- Baldinelli, G.; Bianchi, F.; Rotili, A.; Costarelli, D.; Seracini, M.; Vinti, G.; Asdrubali, F.; Evangelisti, L. A model for the improvement of thermal bridges quantitative assessment by infrared thermography. Appl Energy 2018, 211, 854–864. [Google Scholar] [CrossRef]
- O’Grady, A.; Lechowska, A.; Harte, A.M. Assessment of thermal bridging heat loss by means of the Infrared thermography technique: Sustainable Buildings in Cold Climates. In Cold Climate HVAC 2018; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Asdrubali, F.; Baldinelli, G.; Bianchi, F.; Costarelli, D.; Rotili, A.; Seracini, M.; Vinti, G. Detection of thermal bridges from thermographic images by means of image processing approximation algorithms. Appl. Math. Comput. 2018, 317, 160–171. [Google Scholar] [CrossRef]
- Garrido, I.; Lagüela, S.; Arias, P.; Balado, J. Thermal-based analysis for the automatic detection and characterization of thermal bridges in buildings. Energy Build. 2018, 158, 1358–1367. [Google Scholar] [CrossRef]
- Tejedor, B.; Barreira, E.; Almeida, R.M.S.F.; Casals, M. Thermographic 2D U-value map for quantifying thermal bridges in building façades. Energy Build. 2020, 224. [Google Scholar] [CrossRef]
- Ge, J.; Xue, Y.; Fan, Y. Methods for evaluating and improving thermal performance of wall-to-floor thermal bridges. Energy Build. 2020. [Google Scholar] [CrossRef]
- Capozzoli, A.; Corrado, V.; Gorrino, A.; Soma, P. Atlante Nazionale dei Ponti Termici. Conforme alle UNI EN ISO 14683 e UNI EN ISO 10211; Edizioni EDILCLIMA: Novara, Italy, 2011. [Google Scholar]
- Centro per lo Sviluppo Tecnologico, L’energia e la Competitività (CESTEC SPA). Associazione regionale dei costruttori edili lombardi (ANCE Lombardia). In Abaco dei Ponti Termici; Politecnico di Milano: Milano, Italy, 2011. [Google Scholar]
- Office Fédéral de L’ÉNergie (OFEN). Catalogue des Ponts Thermiques; Office Fédéral de L’ÉNergie (OFEN): Bern, Switzerland, 2003. [Google Scholar]
- Ben, L.A. Statistical modelling of heat transfer for thermal bridges of buildings. Energy Build. 2005, 37, 945–951. [Google Scholar] [CrossRef]
- Theodosiou, T.; Tsikaloudaki, K.; Kontoleon, K.; Giarma, C. Assessing the accuracy of predictive thermal bridge heat flow methodologies. Renew. Sust. Energy Rev. 2021, 136. [Google Scholar] [CrossRef]
- Passive House Institute (PHI). Thermal Bridge Catalogue; Passive House Institute: Darmstadt, Germany, 2019. [Google Scholar]
- Carini, A. Housing in Europa; Luigi Parma Editions: Bologna, Italy, 1978. [Google Scholar]
- Basiricò, T.; Bertorotta, S. L‘Industrializzazione nei Quartieri di Edilizia Residenziale Pubblica; ARACNE: Roma, Italy, 2013. [Google Scholar]
- Marchigiani, S. Cooperative edili e industrializzazione: Appunti critici. Edil. Pop. 1978, 142, 47–50. [Google Scholar]
- Basiricò, T.; Cottone, A. Sustainable retrofitting of the ‘70s public housing. In An application to the ZEN 2 district in Palermo. Proceedings of the 30th IAHS Changing, Needs, Adaptive Buildings, Smart Cities; Milano, Italy, 15–17 September 2013, pp. 151–161.
- Basiricò, T. Degrado, Manutenzione, Recupero. Il Caso del Quartiere ZEN 2 a Palermo; Fotograf: Palermo, Italy, 2009. [Google Scholar]
- Zedan, M.F.; Al-Sanea, S.; Al-Mujahid, A.; Al-Suhaibani, Z. Effect of thermal bridges in insulated walls on air-conditioning loads using whole building energy analysis. Sustainability 2016, 8, 560. [Google Scholar] [CrossRef]
- Dell’Acqua, A.C.; Degli Esposti, V.; Ferrante, A.; Mochi, G. Caratteri Tipologici del Costruito e Criteri di Adeguamento Tecnologico e Ambientale; Alinea Editrice: Firenze, Italy, 2011. [Google Scholar]
- Basiricò, T.; Cottone, A. Performance analysis and durability of environmental and energy sustainability interventions on existing buildings. In Proceedings of the XIII International Conference on Durability of Building Materials and Components (DBMC), Sao Paolo, Brasil, 2–5 September 2014; pp. 166–173. [Google Scholar]
- Mineo, A.M. Una Guida All’utilizzo Dell’ambiente Statistico R; Free Software Foundation: Cambridge, MA, USA, 2003. [Google Scholar]
- Venturini, S.; Poli, M. Statistica 4038 (ver.1.2) Software Didattico per L’insegnamento della Statistica; Istituto di Metodi Quantitativi, Università “L. Bocconi”: Milan, Italy, 2001. [Google Scholar]
- Borelli, D.; Cavalletti, P.; Marchitto, A.; Schenone, C. A comprehensive study devoted to determine linear thermal bridges transmittance in existing buildings. Energy Build. 2020, 224. [Google Scholar] [CrossRef]
- National Fenestration Rating Council, Inc. THERM 7, NFRC Simulation Manual; NFRC: Greenbelt, MD, USA, 2017. [Google Scholar]
- Basiricò, T.; Cottone, A. Thermal bridge in industrialized building. The case of reinforced concrete wall/floor junction. In Proceedings of the 42th IAHS World Congress the Housing for the Dignity of Mankind, Naples, Itay, 10–13 April 2018; pp. 109–120. [Google Scholar]
- Lombardy Region, Prezzario Regionale delle Opere Pubbliche. 2020. Available online: https://www.regione.lombardia.it (accessed on 19 November 2020).







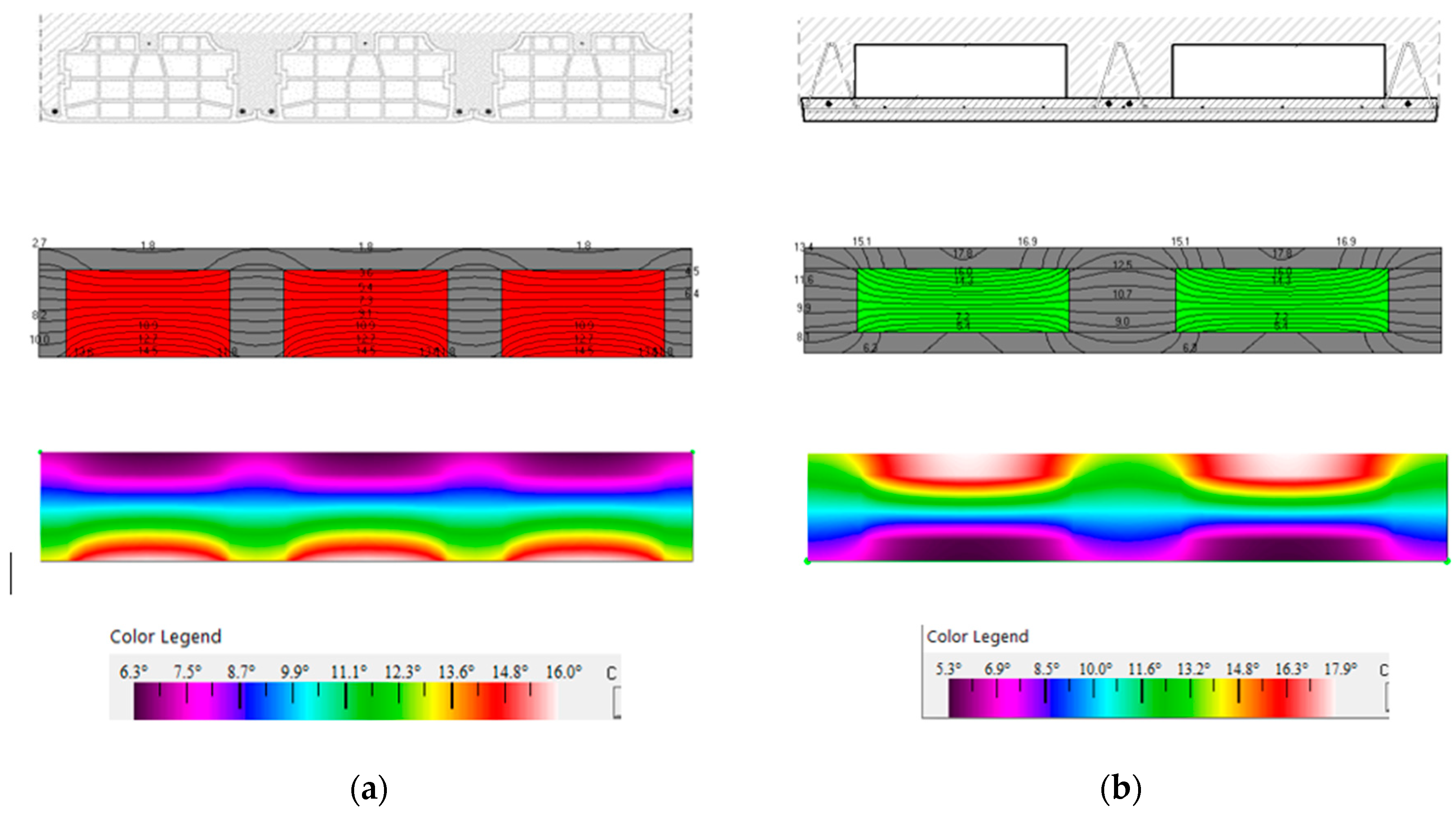


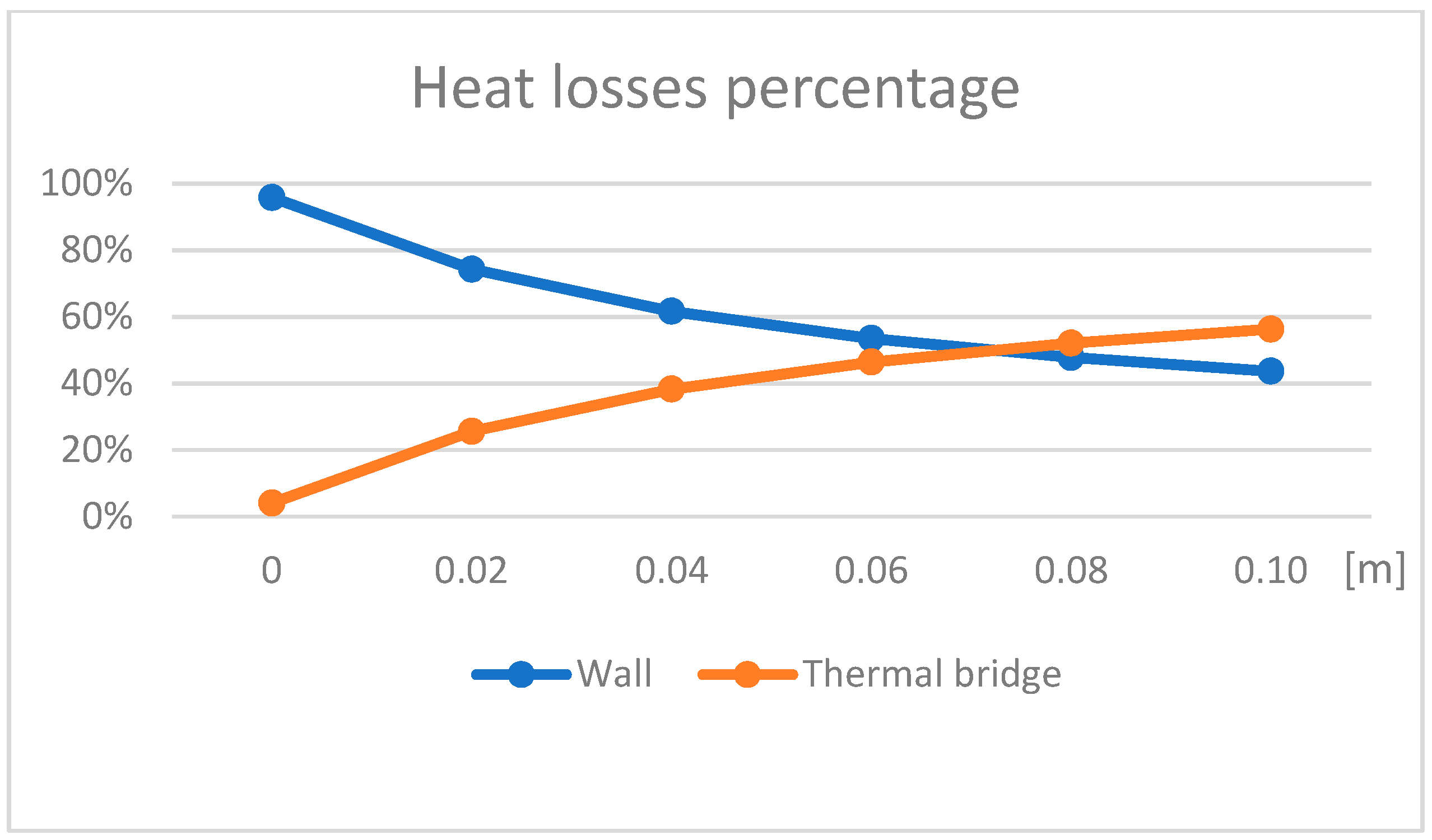
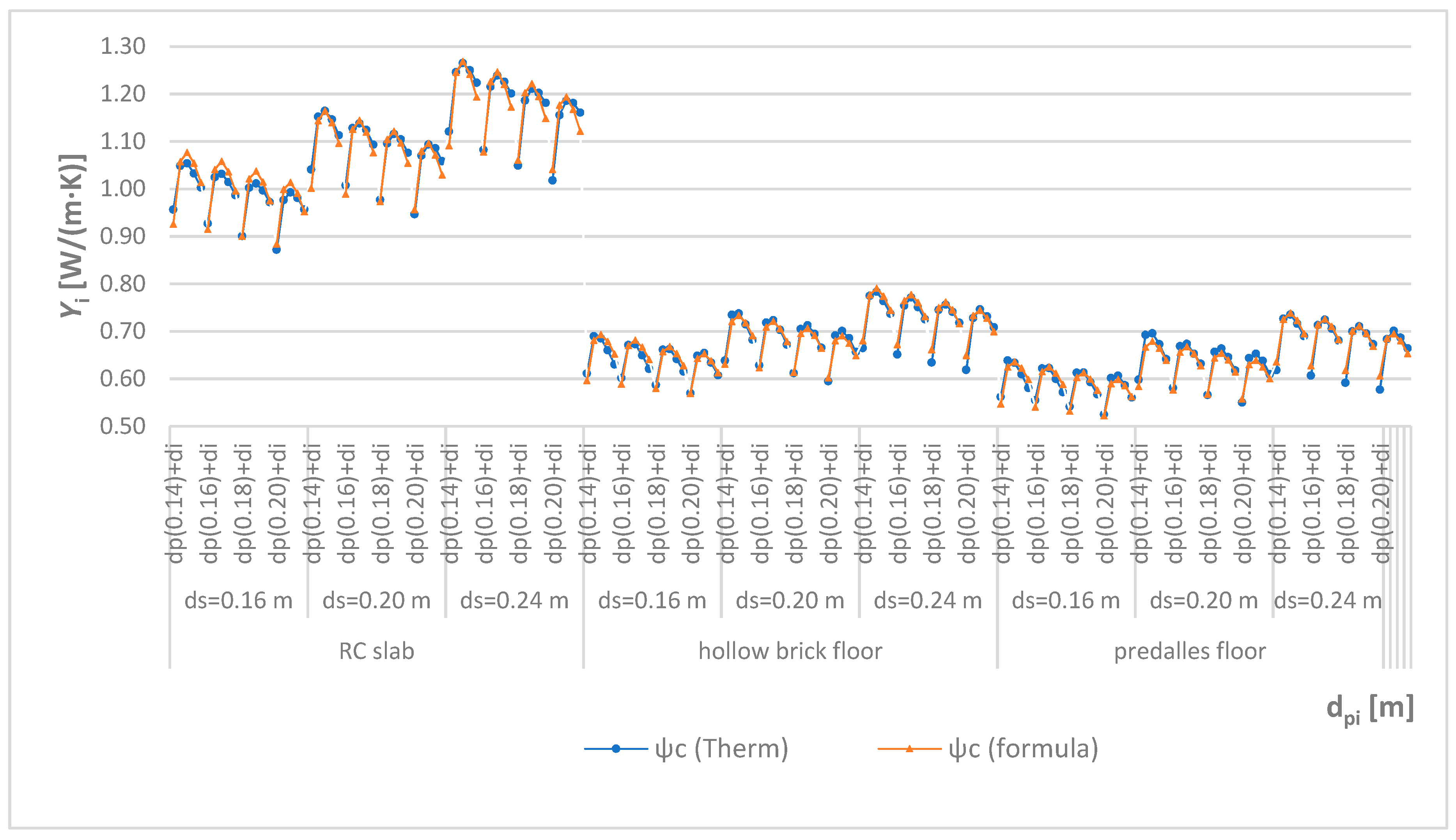
| THERM 7.4 Version | UNI EN ISO 14683:2001 | UNI EN ISO 14683:2018 | Edilclima | CESTEC | OFEN | |
|---|---|---|---|---|---|---|
| ψi (W/(m·K)) | 1.059 | 0.8 | 1.0 | 0.82 | 0.719 | 0.88 |
| Δ (%) | - | −24.4 | −5.6 | −22.6 | −32.1 | −16.9 |
| External Temperature (°C) | Internal Temperature (°C) | External Surface Thermal Resistance (Rse) (m2·K/W) | Internal Surface Thermal Resistance (Rsi) (m2·K/W) |
|---|---|---|---|
| +5 | +20 | 0.04 | 0.13 |
| Technical Element | Thickness (m) | Thermal Conductivity (W/(m·K)) |
|---|---|---|
| RC wall | 0.14–0.16–0.18–0.20 | 2.3 |
| Thermal insulation | 0–0.02–0.04–0.06–0.08–0.10 | 0.04 |
| RC floor | 0.16–0.20–0.24 | 2.3 |
| “Predalles” floor | 0.16–0.20–0.24 | 0.62–0.64–0.66 * |
| Hollow brick floor | 0.16–0.20–0.24 | 0.75–0.76–0.77 * |
| Mortar and plaster | 0.01 | 0.43 |
| Floor | 0.02 | 1.2 |
| Screed | 0.05 | 1.6 |
| Plasterboard | 0.01 | 0.21 |
| di(m) | UFiup (W/(m2·K)) | liup (m) | UFidown (W/(m2·K)) | lidown (m) | Up (W/(m2·K)) | le (m) | ψi (W/(m·K)) |
|---|---|---|---|---|---|---|---|
| 0.00 | 4.18730 | 0.99 | 4.19430 | 0.94 | 3.59081 | 2.16 | 0.332 |
| 0.02 | 1.93190 | 0.99 | 1.93490 | 0.94 | 1.28454 | 2.16 | 0.957 |
| 0.04 | 1.41870 | 0.99 | 1.41910 | 0.94 | 0.78217 | 2.16 | 1.049 |
| 0.06 | 1.17570 | 0.99 | 1.17530 | 0.94 | 0.56228 | 2.16 | 1.054 |
| 0.08 | 1.02780 | 0.99 | 1.02490 | 0.94 | 0.43889 | 2.16 | 1.033 |
| 0.10 | 0.92440 | 0.99 | 0.92060 | 0.94 | 0.35991 | 2.16 | 1.003 |
| Thickness [m] | IF3a | IF3b | IF3c | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Wall | Floor | 0.16 | 0.20 | 0.24 | 0.16 | 0.20 | 0.24 | 0.16 | 0.20 | 0.24 | |
| Insulation | |||||||||||
| 0.14 | 0.00 | 0.332 | 0.331 | 0.322 | 0.035 | 0.025 | 0.092 | 0.062 | 0.008 | −0.053 | |
| 0.02 | 0.957 | 1.041 | 1.121 | 0.562 | 0.598 | 0.618 | 0.611 | 0.638 | 0.665 | ||
| 0.04 | 1.049 | 1.152 | 1.246 | 0.639 | 0.693 | 0.727 | 0.690 | 0.735 | 0.775 | ||
| 0.06 | 1.054 | 1.165 | 1.265 | 0.634 | 0.696 | 0.735 | 0.686 | 0.738 | 0.784 | ||
| 0.08 | 1.033 | 1.146 | 1.250 | 0.610 | 0.673 | 0.716 | 0.660 | 0.715 | 0.764 | ||
| 0.10 | 1.003 | 1.113 | 1.224 | 0.581 | 0.642 | 0.690 | 0.630 | 0.683 | 0.737 | ||
| 0.16 | 0.00 | 0.310 | 0.309 | 0.303 | 0.019 | 0.033 | 0.081 | 0.056 | 0.005 | −0.050 | |
| 0.02 | 0.927 | 1.008 | 1.082 | 0.555 | 0.581 | 0.607 | 0.602 | 0.628 | 0.651 | ||
| 0.04 | 1.025 | 1.128 | 1.215 | 0.622 | 0.669 | 0.713 | 0.671 | 0.719 | 0.754 | ||
| 0.06 | 1.032 | 1.138 | 1.239 | 0.623 | 0.674 | 0.725 | 0.673 | 0.724 | 0.772 | ||
| 0.08 | 1.015 | 1.125 | 1.226 | 0.600 | 0.653 | 0.706 | 0.650 | 0.703 | 0.751 | ||
| 0.10 | 0.987 | 1.093 | 1.201 | 0.572 | 0.632 | 0.681 | 0.621 | 0.672 | 0.726 | ||
| 0.18 | 0.00 | 0.293 | 0.292 | 0.285 | 0.019 | 0.031 | 0.076 | 0.053 | 0.005 | −0.048 | |
| 0.02 | 0.901 | 0.977 | 1.049 | 0.541 | 0.566 | 0.592 | 0.587 | 0.612 | 0.634 | ||
| 0.04 | 1.003 | 1.096 | 1.186 | 0.613 | 0.657 | 0.700 | 0.662 | 0.705 | 0.745 | ||
| 0.06 | 1.012 | 1.116 | 1.211 | 0.614 | 0.664 | 0.711 | 0.663 | 0.713 | 0.757 | ||
| 0.08 | 0.997 | 1.105 | 1.202 | 0.593 | 0.646 | 0.696 | 0.642 | 0.695 | 0.742 | ||
| 0.10 | 0.972 | 1.076 | 1.182 | 0.568 | 0.618 | 0.673 | 0.615 | 0.666 | 0.718 | ||
| 0.20 | 0.00 | 0.275 | 0.274 | 0.268 | 0.019 | 0.028 | 0.073 | 0.052 | 0.006 | −0.043 | |
| 0.02 | 0.872 | 0.947 | 1.018 | 0.525 | 0.550 | 0.577 | 0.570 | 0.595 | 0.619 | ||
| 0.04 | 0.977 | 1.071 | 1.156 | 0.602 | 0.644 | 0.684 | 0.649 | 0.691 | 0.728 | ||
| 0.06 | 0.993 | 1.094 | 1.186 | 0.607 | 0.653 | 0.702 | 0.654 | 0.701 | 0.746 | ||
| 0.08 | 0.981 | 1.086 | 1.181 | 0.587 | 0.638 | 0.687 | 0.634 | 0.686 | 0.732 | ||
| 0.10 | 0.957 | 1.059 | 1.161 | 0.561 | 0.610 | 0.664 | 0.608 | 0.657 | 0.709 | ||
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 1 | m5 = 1.573001 | m4 = 0.612972 | m3 = 0.66599 | m2 = 0.028051 | m1 = 44.0864 | b = 2.118112 |
| 2 | se5 = 0.002431 | se4 = 0.026652 | se3 = 0.011054 | se2 = 0.126889 | se1 = 0.0402 | seb = 0.125843 |
| 3 | r2 = 0.995554 | sey = 0.017018 | ||||
| 4 | F = 7791.857 | df = 174 | ||||
| 5 | ssreg = 11.2829 | ssresid = 0.050392 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basiricò, T.; Cottone, A.; Enea, D. Analytical Mathematical Modeling of the Thermal Bridge between Reinforced Concrete Wall and Inter-Floor Slab. Sustainability 2020, 12, 9964. https://doi.org/10.3390/su12239964
Basiricò T, Cottone A, Enea D. Analytical Mathematical Modeling of the Thermal Bridge between Reinforced Concrete Wall and Inter-Floor Slab. Sustainability. 2020; 12(23):9964. https://doi.org/10.3390/su12239964
Chicago/Turabian StyleBasiricò, Tiziana, Antonio Cottone, and Daniele Enea. 2020. "Analytical Mathematical Modeling of the Thermal Bridge between Reinforced Concrete Wall and Inter-Floor Slab" Sustainability 12, no. 23: 9964. https://doi.org/10.3390/su12239964
APA StyleBasiricò, T., Cottone, A., & Enea, D. (2020). Analytical Mathematical Modeling of the Thermal Bridge between Reinforced Concrete Wall and Inter-Floor Slab. Sustainability, 12(23), 9964. https://doi.org/10.3390/su12239964






