1. Introduction
Information and Communication Technologies (ICT) offer an enormous breadth of important new pedagogical tools. These tools turn out to be remarkably appealing to students, increasing their motivation in the learning process [
1]. In this study, out of the wide range of technological resources applicable to schools, we focus on teaching programming. The essential core of computer education is the incorporation of programming into school contexts, rather than ICT, which is more focused on useful skills for the knowledge society. Various reports influence this conceptual differentiation [
2,
3]. Computer Science Education (CSE) is a research field with decades of research about teaching programming [
4,
5].
The inclusion of education in programming in the classroom is a reality in educational processes today [
6,
7]. Traditionally, the integration of Information and Communication Technologies has been focused on activities in support of learning curriculum subjects throughout the different educational levels, but education in programming requires going further. It involves the inclusion of programming under essential principles such as problem-solving and creativity [
8].
Current and future schoolchildren should be considered technology consumers and creators. Furthermore, in terms of lifelong learning, the European Commission considers education in programming as a fundamental skill to be integrated into schools throughout the 21st century [
9], considering its instrumental and transversal nature in the acquisition of other skills [
10,
11]. Teacher training, together with the early integration of learning these skills, is especially important in achieving this [
12,
13,
14,
15,
16,
17]. There are multiple occurrences of integration of programming into schools [
10,
18,
19,
20,
21,
22,
23], including the work of mathematical content through programming [
24,
25,
26,
27,
28,
29].
One of the foundations of this integration of education in programming in schools may be the development of the Sustainable Development Goals (SDGs); the search for practical and innovative solutions to certain situations and problems could justify such a relationship. The SDGs are part of a 15-year action plan adopted by all United Nations member states in 2015 as part of the 2030 Agenda for Sustainable Development, which seeks to increase prosperity, promote peace, and eradicate global poverty before 2030. Through 17 SDG and 169 targets, it is an attempt to make human rights a reality for all [
30]. The research presented below is particularly related to three goals: Goal 4—Quality Education, Goal 5—Gender Equality, and Goal 12—Sustainable Consumption and Production.
The first of those goals, Quality Education, seeks the achievement of inclusive, equitable, and quality education that promotes learning opportunities throughout life for all. Its targets include the development of the necessary skills (technical and professional competencies) in the population to access the labor market and stimulate entrepreneurship. To achieve this goal, the use of technology in educational processes is a key issue in all stages of the educational system [
31,
32]. There is a need to adjust educational practices to the innovations and transformations that have resulted from the integration of emerging technologies in schools. This generates progress and change and makes it essential to be able to adapt the teaching and learning processes. Innovation generates quality in education, and technology is an ideal instrument for establishing a connection between them.
The second SDG, Gender Equality, is a fundamental right to put an end to any type of discrimination between men and women. One of the targets proposed for this goal is to ensure the effective participation of women in all contexts, facilitating their leadership, decision-making, and empowerment at all levels. Despite this, there are still some problems regarding full parity [
33,
34,
35]; a clear example being the existing inequality in scientific disciplines between men and women in different domains, as indicated by various studies [
36,
37,
38,
39,
40], including mathematics [
41,
42,
43,
44,
45,
46].
Finally, the third goal, Sustainable Consumption and Production, highlights the need to increase the efficiency of resources and promote healthier and more responsible lifestyles. Among the targets for this goal, one thing that stands out is the importance of supporting countries in strengthening their scientific and technological capacities, in order to promote more sustainable consumption and production habits. It is necessary to combat the idea that technological consumption only causes harm to the environment [
47,
48]. As an example, in this study, we applied an assessment instrument electronically to a large sample of students instead of using a pencil and paper format, with consequent energy savings in courier transportation and paper consumption.
Therefore, this study establishes a connection between the three aforementioned SDGs. The application of this educational experience is aimed at providing students with strategies to solve problems and communicate ideas through the computer and the work of a programming language applied to mathematics, under the title of the project “Learn mathematics (and other things) with the new Scratch 3”. The main contribution of this article is to offer a contribution to mathematics learning, in this case, through education in programming. The study objective was to compare the results in an online version of the Battery of Mathematical Competence Evaluation (BECOMA On) between two groups of students, a control and an experimental group, at two different timepoints, pretest and post-test. Between the two timepoints, the students carried out a project with the Scratch 3 programming language; this made it possible to measure the impact of that project. In short, the study aimed to assess students’ mathematics progress via education in programming. In addition, this method of evaluation via ICT allowed a thorough evaluation of a school population, giving information about their competence and potential in mathematics.
3. Results
The reliability at both study timepoints was high, with a Cronbach Alpha of 0.81 at the pretest and 0.84 at the post-test. The descriptive statistics for the two timepoints are shown in
Table 2.
The scores increased between the two study timepoints, the mean at the pretest being 36.08 (SD = 9.27) and at post-test, 38.79 (SD = 9.59). We conducted an analysis of covariance (ANCOVA) in order to examine the impact of the mathematics programming project and determine any statistically significant differences at the post-test between the experimental group and the control group. We found statistically significant differences, with an F value = 17.76 and a significance
p < 0.001. The effect size of the intervention project for both groups and both study timepoints was 0.45, reflecting a medium or moderate effect [
50]. This showed that the intervention project had a significant impact on the mathematical competence of the students in the experimental group, in contrast to the children in the control group.
In order to look more deeply into those differences, to examine which items had the greater impact on the differences in the results between the study timepoints, we performed
t-tests for a comparison of means for each timepoint, assessing the items that make up the BECOMA On and the total score. The results at the pretest are shown in
Table 3.
Table 3 shows that there were significant differences between the two groups in various items at the pretest. The experimental group scored higher in Items 25 (
p < 0.05) and 27 (
p < 0.05), the control group scored higher in in items 7 (
p < 0.01), 8 (
p < 0.01), 9 (
p < 0.05), 10 (
p < 0.01), 11 (
p < 0.001), and 21 (
p < 0.01). In all these items with statistically significant differences, the effect size indices ranged between 0.16 and 0.32.
The post-test results are shown in
Table 4.
In the post-test, we found the opposite pattern to the pretest, with the experimental group scoring higher with statistically significant differences in more items; in this case, Items 14 (
p < 0.01), 21 (
p < 0.05), 27 (
p < 0.01), 29 (
p < 0.001), and 30 (
p < 0.01). For the control group, the statistically significant difference continued in Item 8 (
p < 0.01). In terms of the total score in the instrument, the experimental group had a higher mean score (38.65; SD = 9.66), than the control group (36.84; SD = 9.53), although the difference was not statistically significant (
p = 0.070). The effect size at the post-test of the items with statistically significant differences ranged between 0.23 and 0.44, significantly higher than the values at the pretest, demonstrating the effectiveness of the education in programming program with the students in the experimental group.
Table 5 shows the difference in the mean scores between the two groups for the two study timepoints.
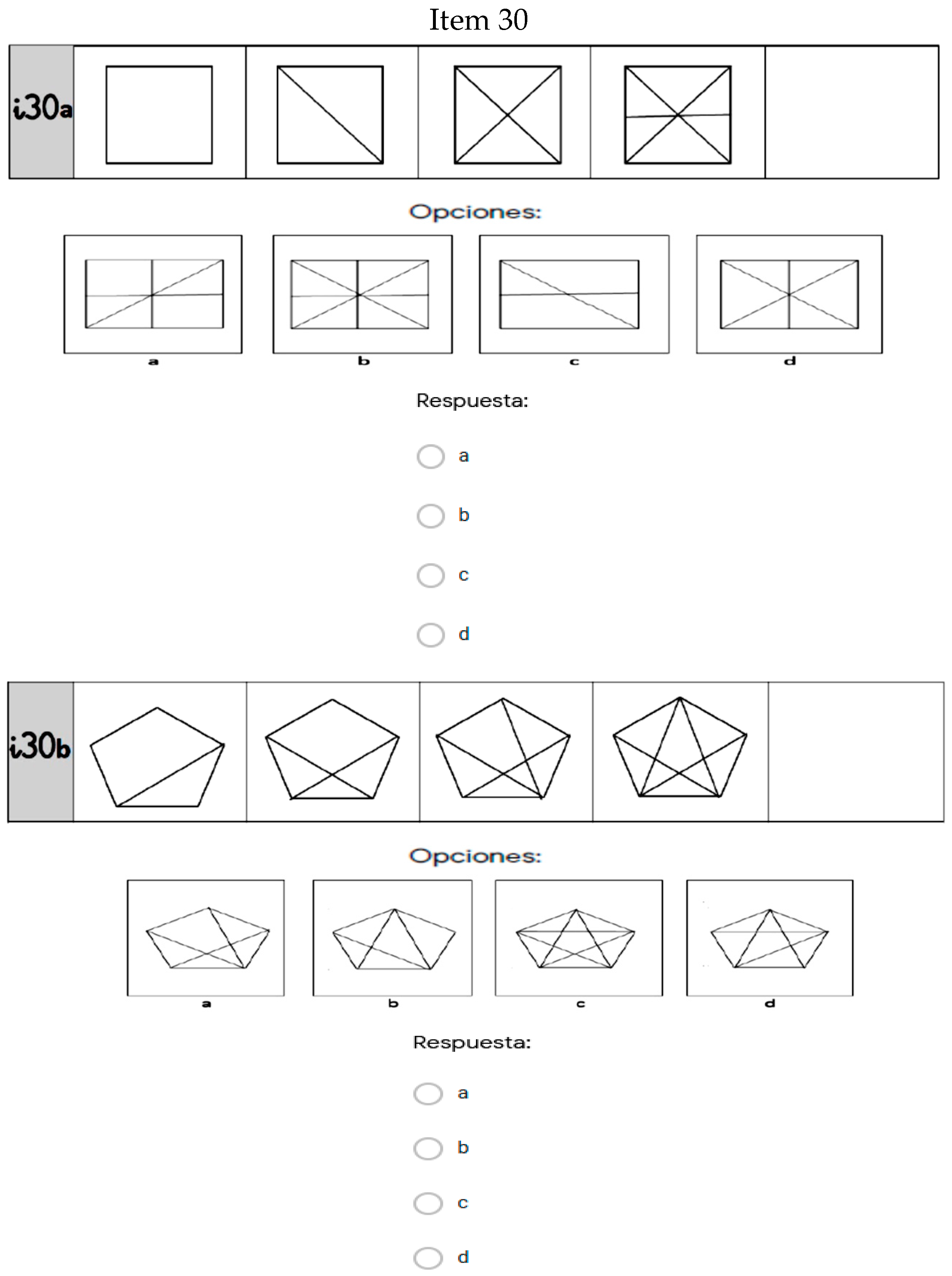
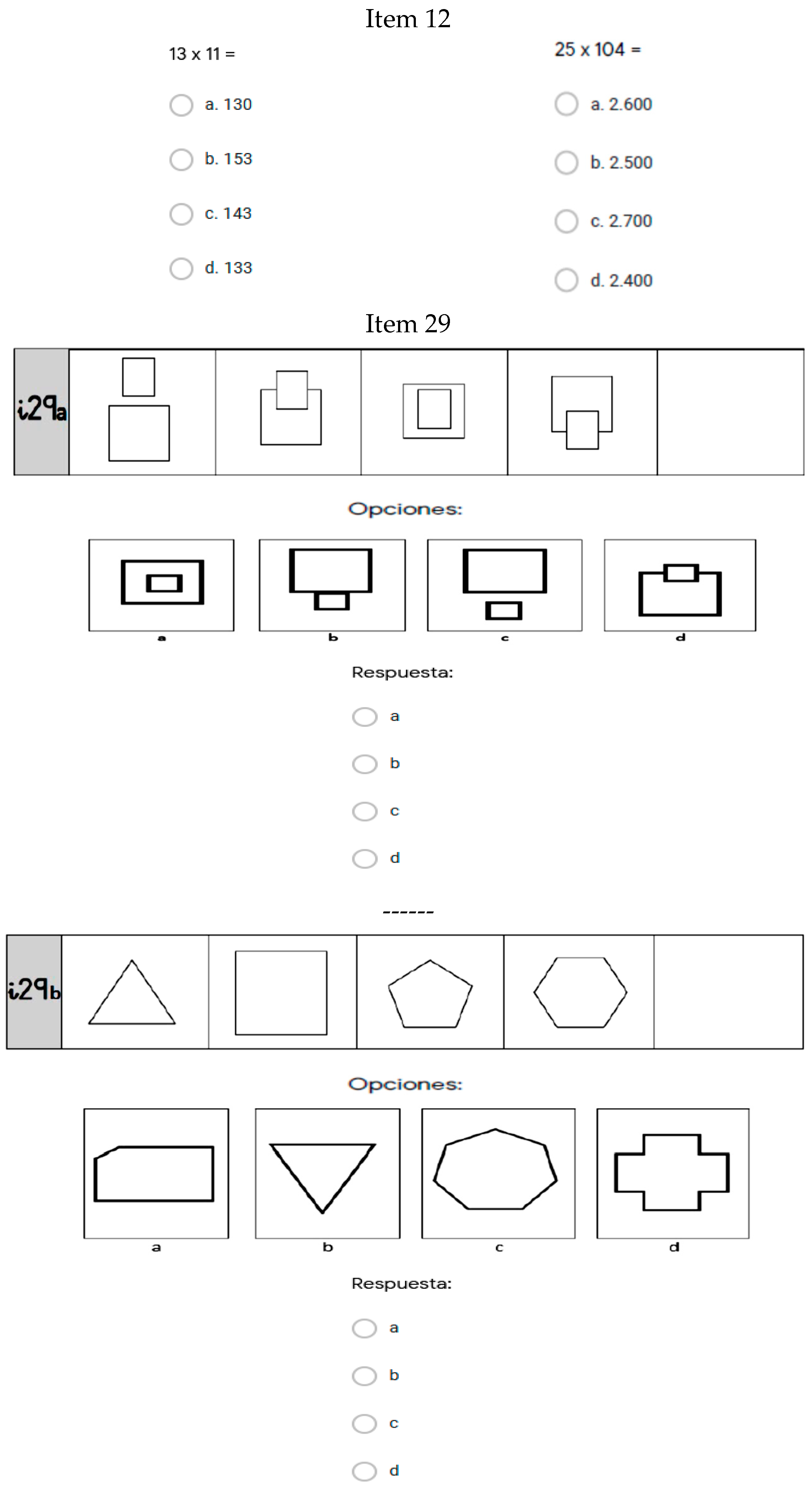
The differences between the group means at the two study timepoints were greater for the experimental group than for the control group, the total difference between the pretest and post-test for the experimental group was 3.85, and for the control group, 1.46. It is striking that there were no negative scores in the experimental group; in other words, there was no lower score in any of the instrument items at the post-test compared to the pretest, something that did occur in the control group in 8 out of the 30 items in the instrument. The items that stood out as having the greatest differences between the pre- and post-test in the experimental group were Items 10 (difference of 0.25), 11 (difference of 0.24), 12 (difference of 0.23), 29 (difference of 0.24), and 30 (difference of 0.21). In the control group, the items with the greatest differences were Items 12 (difference of 0.23) and 15 (difference of 0.19), in terms of positive differences, and 20 (difference of −0.15) and 21 (difference of −0.23), in terms of negative differences.
The differences we found in effect sizes between the two groups at the two study timepoints are shown in
Table 6.
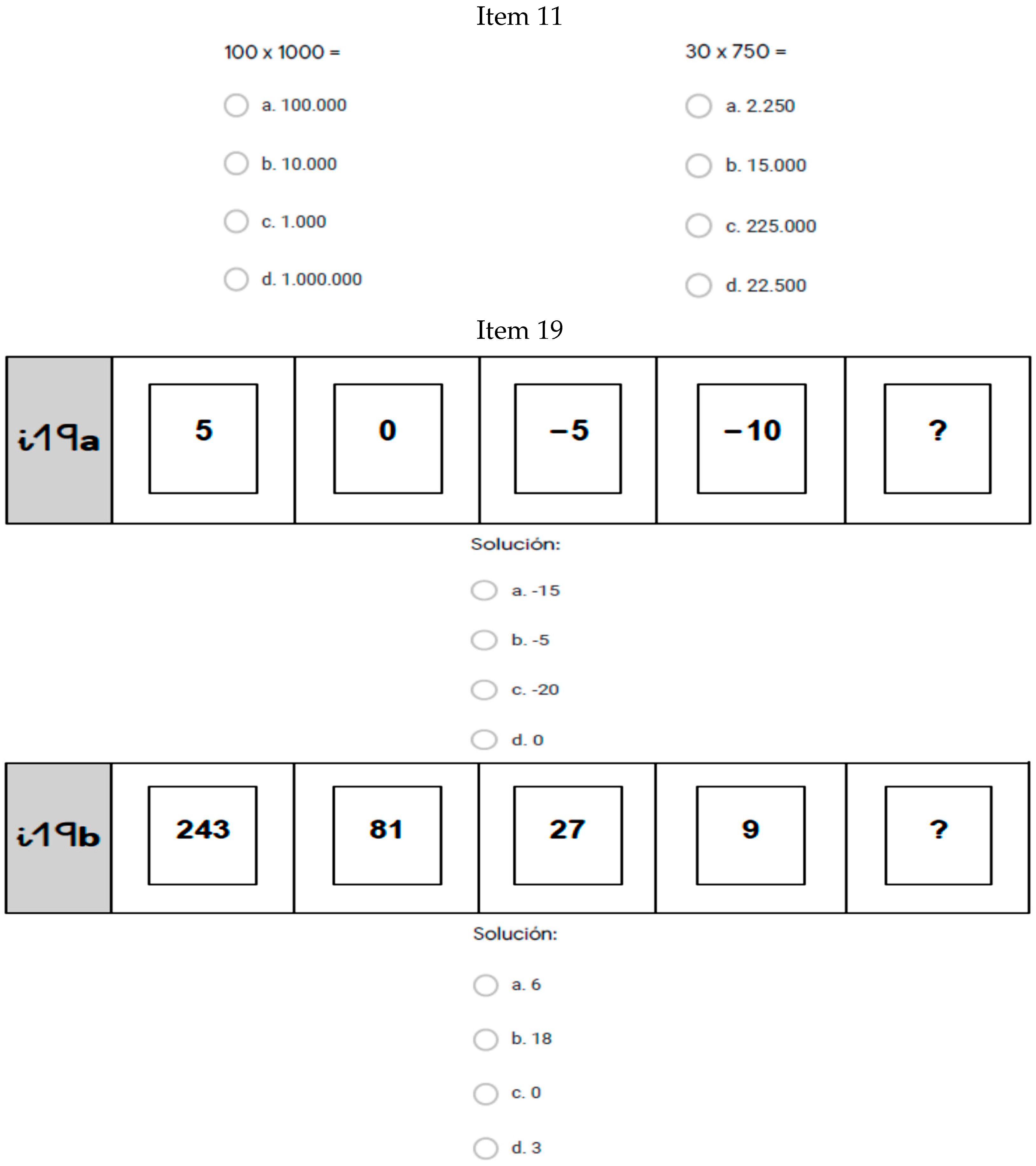
The total effect size of the study was higher in the experimental group (0.40) compared to the control group (0.15), with the difference between the effect size of the two groups being 0.25. The largest effect sizes for the differences between the pre- and post-test in the experimental group were in Items 10 (0.32), 11 (0.28), 12 (0.28), 29 (0.32), and 30 (0.27). In the control group, the largest effect sizes were in items 5 (0.26), 12 (0.30), 15 (0.25), and 21 (0.26). The items with the greatest differences in effect sizes between the two groups were Items 11 (0.25), 19 (0.19), and 30 (0.23), with the experimental group having higher values. It is worth mentioning that in 21 of the 30 items, the higher values for effect size were in the experimental group.
In summary, on comparing the means and effect sizes for the two timepoints, we found that Items 11, 19, and 30 demonstrated the largest differences between the experimental and control groups after the project (Items 11 and 19 were about arithmetic content, Item 30 was about geometry). The items are shown in
Figure 1.
It is also worth noting Items 10, 11, 12, 29, and 30, (two about arithmetic content, and three about geometry), as they were the items with the largest differences between the pre- and post-test in the experimental group. The items are shown in
Figure 2, with the exception of 11 and 30 (which appear in
Figure 1):
Finally, in accordance with the SDGs, in this case, Goal 5—Gender Equality, the results based on the sex of the participants at each timepoint are shown in
Table 7 and
Table 8.
Both boys and girls in the experimental group had higher scores. The difference in mean scores between the pre- and post-test was 4.13 for the boys and 3.58 for the girls. In the control group, the difference in mean scores between the pre-and post-test was 1.44 for the boys and 1.76 for the girls. Thus, following the program (the experimental group), both boys and girls had higher scores, something that we did not see to the same extent in the control group.
4. Discussion
Globalization is producing rapid and frequent exchanges of ideas and innovation, which changes how people assimilate society’s cultural patterns. The roadmap set out by the Sustainable Development Goals is an ideal framework for maintaining global balance at the social and environmental level, and therefore, also at the educational level. In schools, students have to learn knowledge that is continually changing; learning evolves gradually, with the need to integrate more collaborative and participatory methodologies that demand greater commitment and involvement in tasks from students [
51]. We find ourselves within a networked society that has brought about changes in the social and relational structures of the population. Coming generations will be digital natives, and artificial intelligence—machine learning—will be increasingly incorporated into the teaching and learning process. Technology offers a wide variety of opportunities for more visual and intuitive learning [
52]. Teaching design should include learning how to use these resources and methodologies, which includes education in programming being incorporated into all areas of learning in an interdisciplinary manner [
53,
54].
This study aimed to assess whether there is empirical evidence justifying the integration of education in programming into schools. To do this, we implemented a project in mathematics using Scratch and assessed its effects via a pre- and post-test with an experimental group and a control group, using a test battery to assess mathematical competence. Education in programming needs to be integrated into schools [
55,
56], and the schools’ current situations need to be assessed to facilitate their decisions about whether to include it [
57,
58]. It is essential to generalize research in order to assess whether it works and what its effects are; there are examples pursuing this goal [
59,
60], a goal that is shared by our study.
Our results show that the fifth grade primary education students who participated in the project and who worked on mathematical competence through computer programming activities developed their mathematics skills more than the students who were taught mathematics via other activities and the usual resources for this area. These differences were more apparent in specific items than in the global differences between the two groups at the pretest (p = 0.454) and at the post-test (p = 0.070). Mean scores increased between the pretest and the post-test, with a p < 0.001 and an effect size of 0.45. The difference between the pretest and the post-test was larger in the experimental group (3.85) than in the control group (1.46), as was the effect size (0.40 for the experimental group, 0.15 for the control group). The items that exhibited differences between the two groups, with the experimental group scoring higher, were in arithmetic and geometry content. In terms of sex, boys and girls in the experimental group had better results than the control group at the post-test compared with the pretest.
The inclusion of new didactic methodologies in the teaching/learning process promotes educational innovation and encourages students to take on active roles. This represents a greater cognitive load for the students but, in the case of the present study, their interest and motivation towards learning in the area of mathematics was not affected. This was analyzed by asking the students at both stages of the study to rate (on a scale from 0 to 10) their interest in and motivation towards mathematics. The results showed little difference between the study timepoints: in the pretest, we found a mean value of 7.71 (SD = 2.37) for the experimental group and 7.90 (SD = 2.63) for the control group. At the post-test, the results were 7.75 (SD = 2.37) for the experimental group and 7.97 (SD = 2.20) for the control group. The reliability of the results between timepoints was high, with values above 0.80. Therefore, the learning of mathematics and technology appear closely related, something that other studies have noted and analyzed [
61,
62].
One limitation of this study that is worth highlighting is the small size of the control group, something to be considered in subsequent studies. Replicating this study with a similar size experimental group while expanding the control group is the main line for the development of future research. We will attempt to maintain the homogeneity of the characteristics and circumstances of this current study as much as possible. There is also the possibility of establishing relationships between the results according to variables such as gender or academic performance in mathematics.
Ultimately, education systems will not be able to remain outside of the technology revolution in educational practices [
63]. This will need initial and continuous training for teachers [
64], with a goal to transmit to students, as facilitators and mediators, the importance of technology in applying, analyzing, evaluating, and creating knowledge [
65]. Putting the concepts of lifelong learning and continual learning into practice becomes important, knowledge becomes obsolete, and technology helps us move forward.