Smart-Guided Pedestrian Emergency Evacuation in Slender-Shape Infrastructure with Digital Twin Simulations
Abstract
1. Introduction
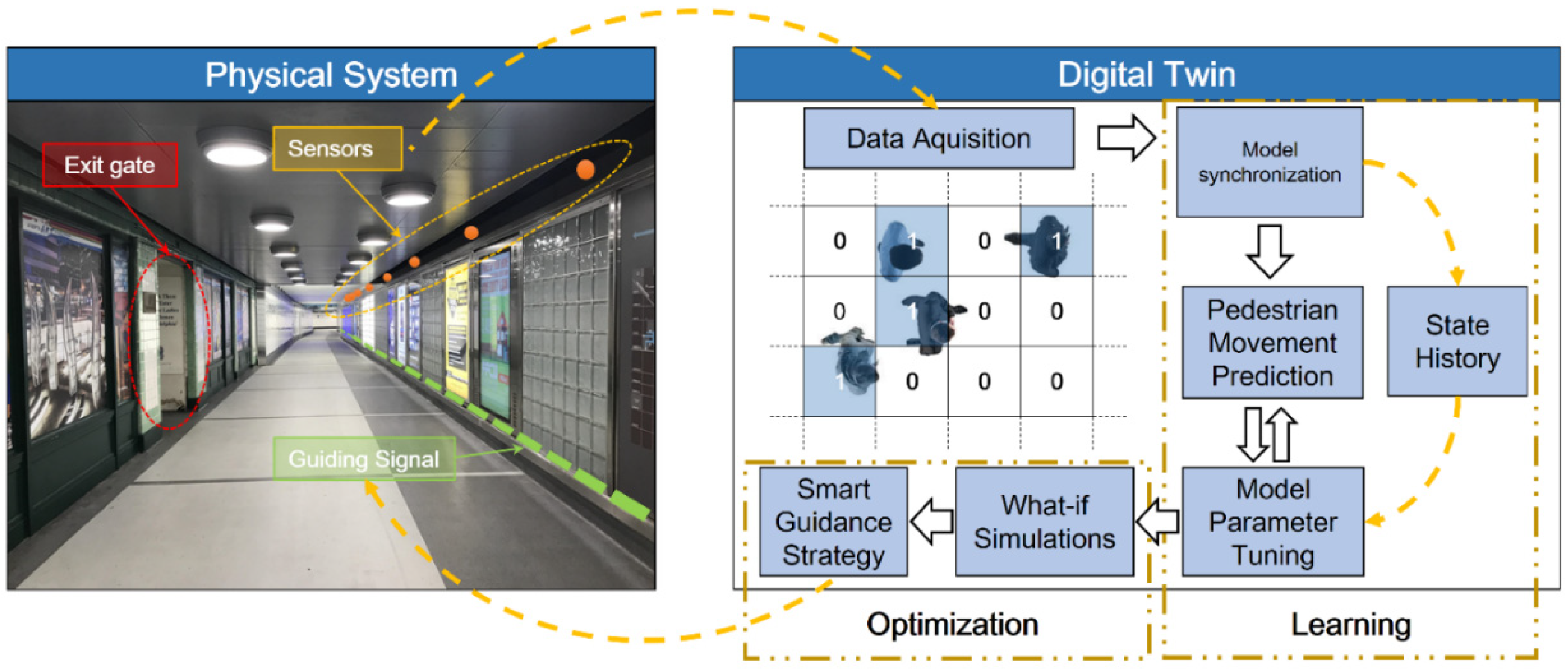
2. Smart Guidance through Digital Twin Simulations
3. Digital Twin of Evacuation Process inside Slender-Shape Infrastructure
3.1. Infrastructure Internal Space
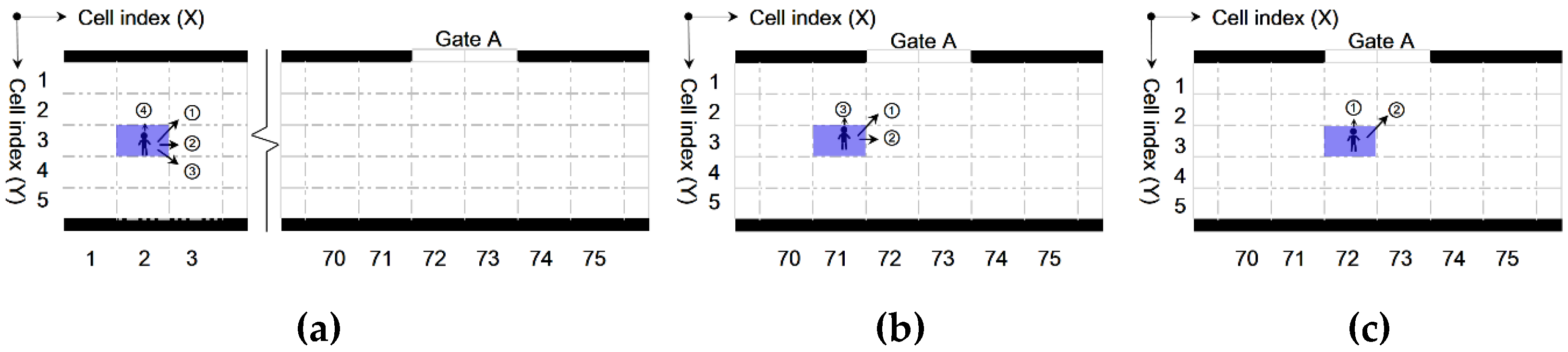
3.2. Pedestrian Movement Rules
3.3. Evacuation Guiding Strategies
- (1)
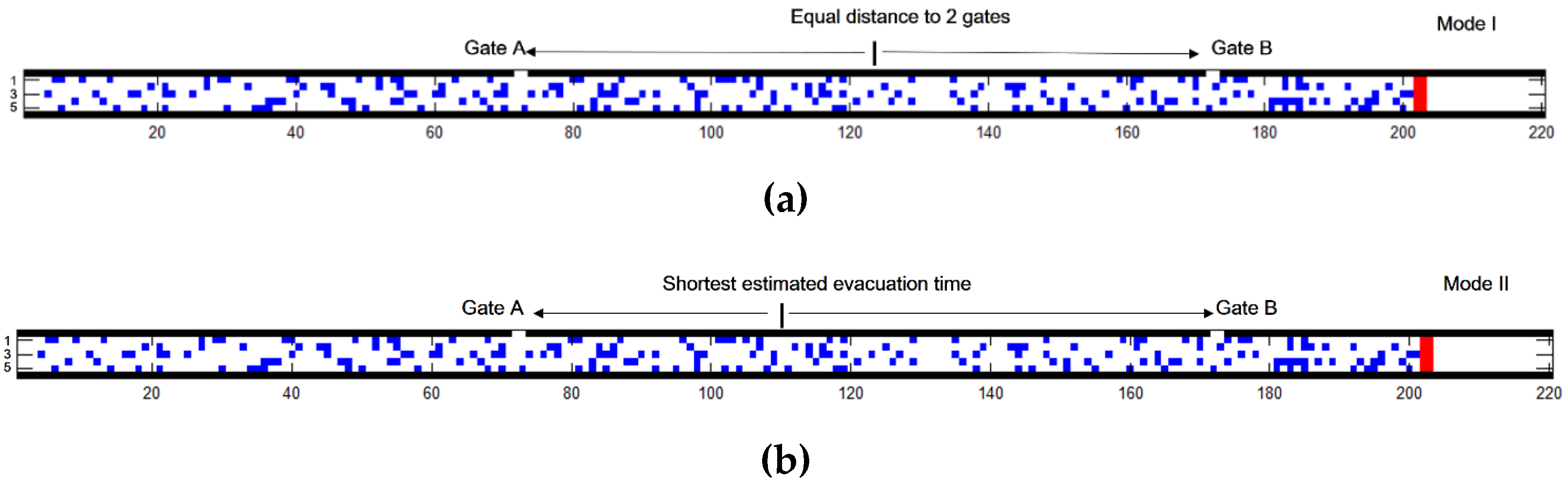
- Strategy 1: fixed guidance according to geometry of the infrastructure internal space
- (2)
- Strategy 2: smart guidance based on estimated evacuation time
4. Numerical Experiments
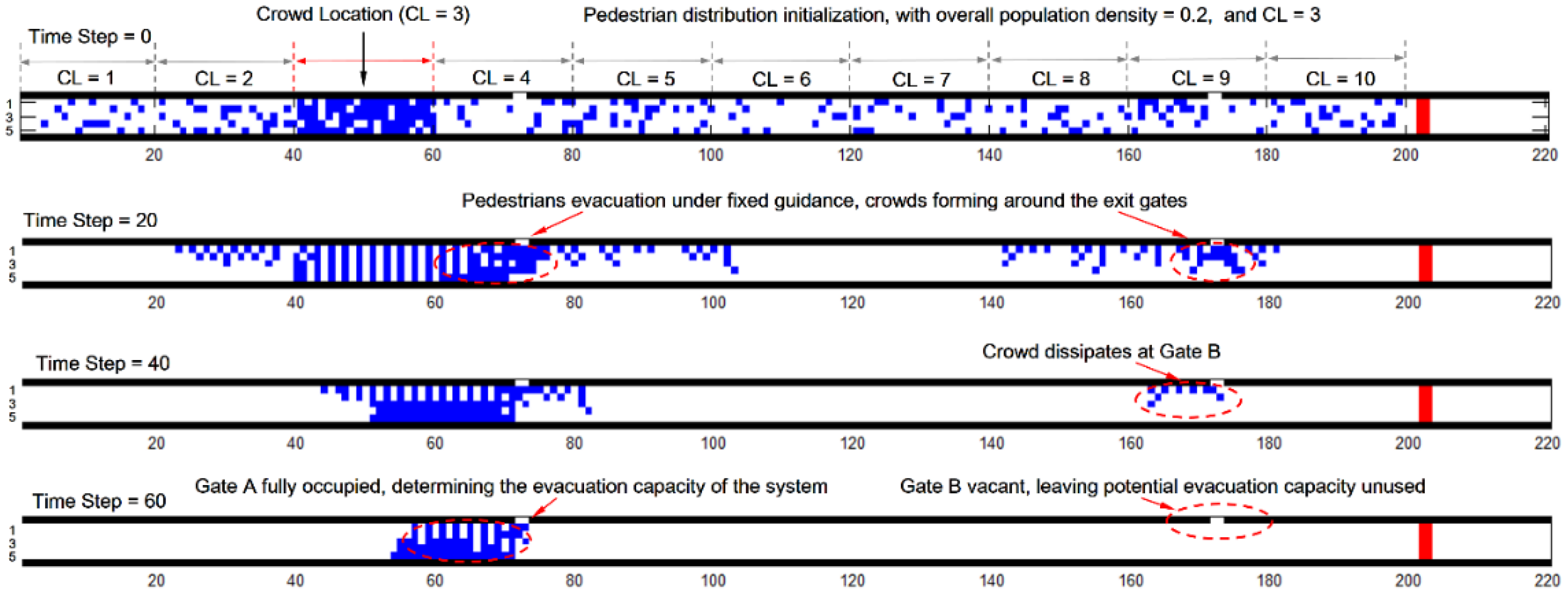
Simulation Initialization
5. Results and Discussions
6. Summary and Conclusions
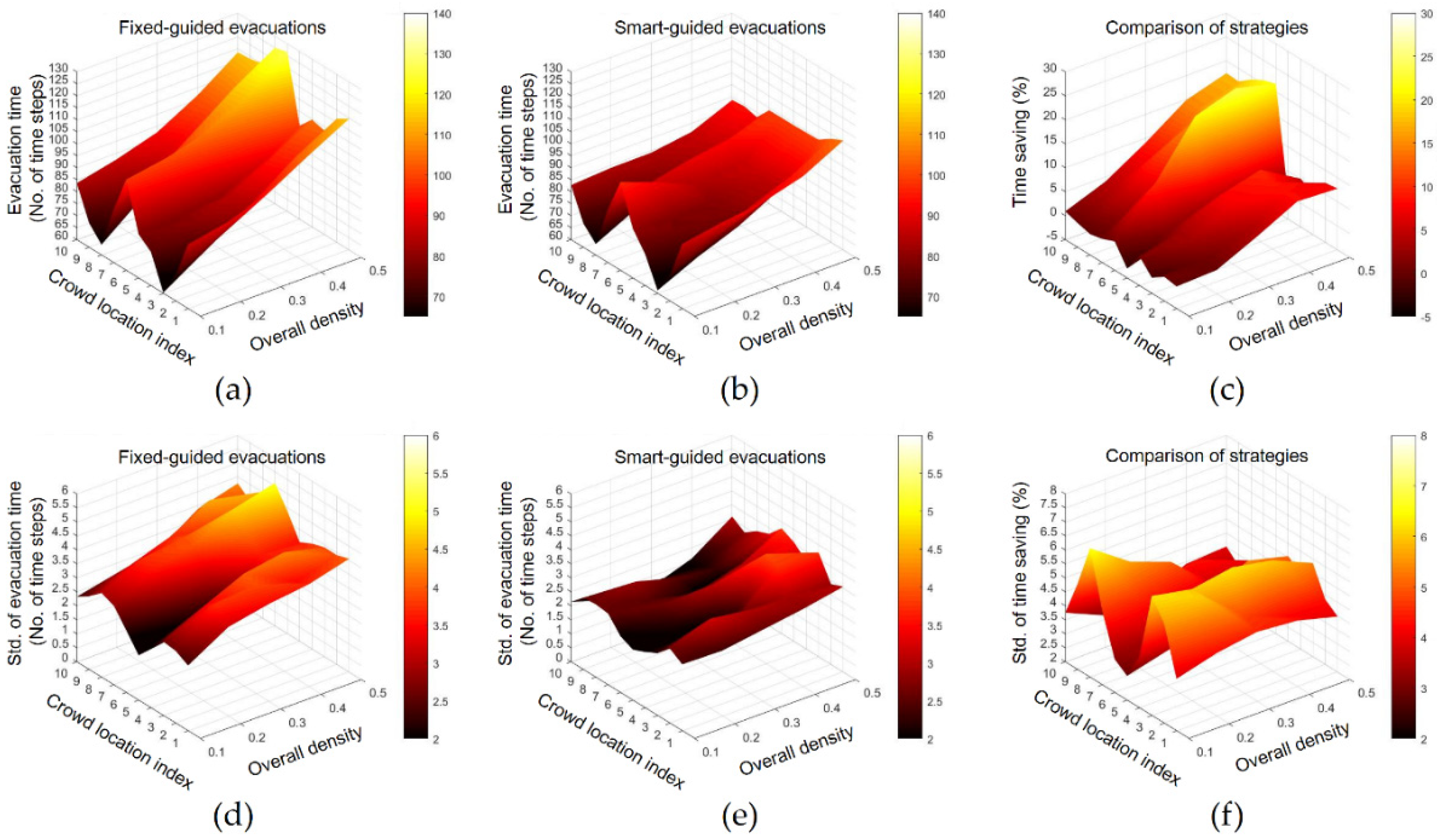
- (a)
- In general, evacuation time increases with higher overall density for both guiding strategies. However, the smart-guided simulations tends to experience slower growth in evacuation time than that of the fixed guided ones for increased density settings, and thus more resilient to pedestrian population density change.
- (b)
- Different pedestrian crowd location also influences the total evacuation time, and the performance of the smart guided system is overall more immune to the influence of the position change of these regions in comparison with the fixed guided cases.
- (c)
- The smart-guided system is found to most obviously outperform the fixed-guided system in mid to high population densities (density around 0.3 to 0.5), which results in time saving ranging from 8.7% to 23.8%. In relative lower density settings, improvements of the smart guided system over fixed guided ones are not obvious.
- (d)
- Simulation results indicate that the smart guided system demonstrates smaller discrepancy over different simulation realizations, demonstrating more consistent results, and therefore a more robust guiding system.
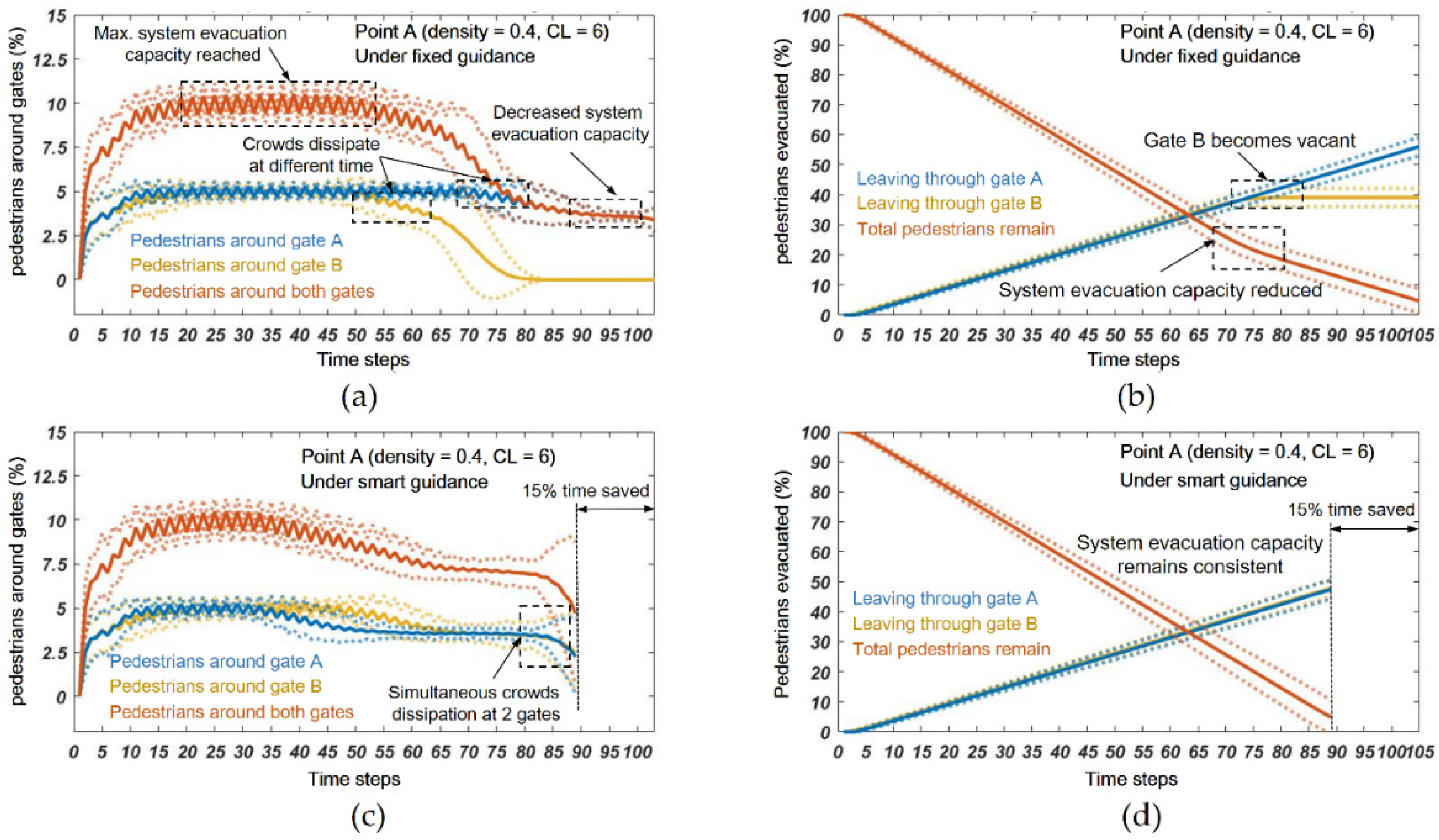
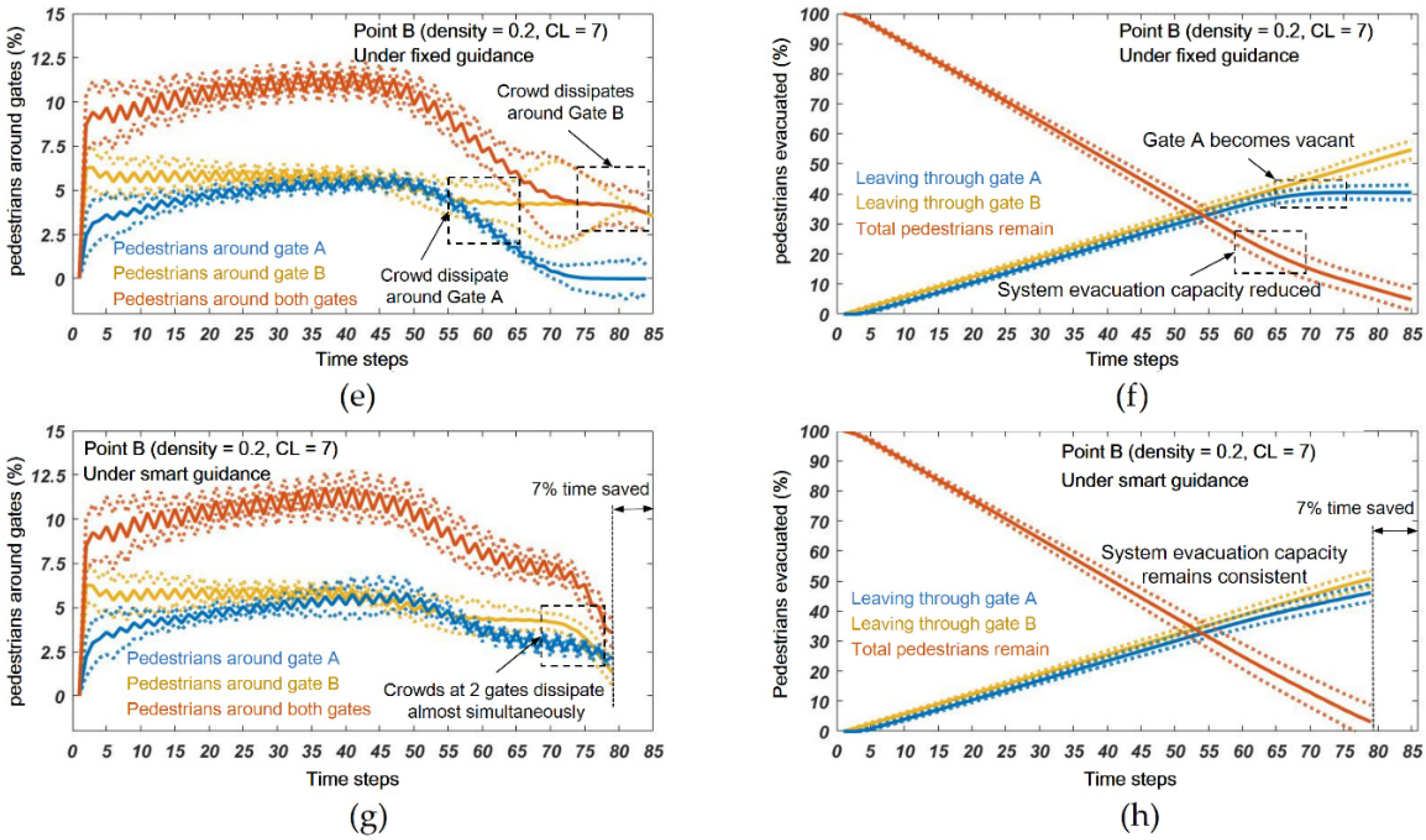
- (e)
- A closer examination of the pedestrian evacuation behavior shows that the introduction of the smart guidance helps to more scientifically divide people to evacuate through respective exit gates so that crowds tend to dissipate simultaneously, and therefore, more evacuation capacity of the exit gates can be mobilized, resulting in shorter total evacuation time and improved safety for pedestrians collectively.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fahy, R.F.; Proulx, G.; Aiman, L. Panic or not in fire: Clarifying the misconception. Fire Mater. 2012, 36, 328–338. [Google Scholar] [CrossRef]
- Helbing, D.; Johansson, A.; Al-Abideen, H.Z. Dynamics of crowd disasters: An empirical study. Phys. Rev. E 2007, 75, 046109. [Google Scholar] [CrossRef] [PubMed]
- Lin, P.; Ma, J.; Liu, T.; Ran, T.; Si, Y.; Li, T. An experimental study of the “faster-is-slower” effect using mice under panic. Phys. A Stat. Mech. Appl. 2016, 452, 157–166. [Google Scholar] [CrossRef]
- Haghani, M.; Sarvi, M. Human exit choice in crowded built environments: Investigating underlying behavioural differences between normal egress and emergency evacuations. Fire Saf. J. 2016, 85, 1–9. [Google Scholar] [CrossRef]
- Henderson, L.F. On the fluid mechanics of human crowd motion. Transp. Res. 1974, 8, 509–515. [Google Scholar] [CrossRef]
- Huang, L.; Wong, S.C.; Zhang, M.; Shu, C.W.; Lam, W.H. Revisiting Hughes’ dynamic continuum model for pedestrian flow and the development of an efficient solution algorithm. Transp. Res. Part B Methodol. 2009, 43, 127–141. [Google Scholar] [CrossRef]
- Hughes, R.L. A continuum theory for the flow of pedestrians. Transp. Res. Part B Methodol. 2002, 36, 507–535. [Google Scholar] [CrossRef]
- Hughes, R.L. The flow of human crowds. Annu. Rev. Fluid Mech. 2003, 35, 169–182. [Google Scholar] [CrossRef]
- Helbing, D.; Farkas, I.J.; Vicsek, T. Freezing by heating in a driven mesoscopic system. Phys. Rev. Lett. 2000, 84, 1240. [Google Scholar] [CrossRef]
- Varas, A.; Cornejo, M.D.; Mainemer, D.; Toledo, B.; Rogan, J.; Munoz, V.; Valdivia, J.A. Cellular automaton model for evacuation process with obstacles. Phys. A Stat. Mech. Appl. 2007, 382, 631–642. [Google Scholar] [CrossRef]
- Wolfram, S. Theory and Applications of Cellular Automata; World Scientific: Singapore, 1986. [Google Scholar]
- Wolfram, S. Cellular Automata and Complexity; Addison-Wesley: Boston, MA, USA, 1994. [Google Scholar]
- Knospe, W.; Santen, L.; Schadschneider, A.; Schreckenberg, M. Towards a realistic microscopic description of highway traffic. J. Phys. A Math. Gen. 2000, 33, L477. [Google Scholar] [CrossRef]
- Knospe, W.; Santen, L.; Schadschneider, A.; Schreckenberg, M. Single-vehicle data of highway traffic: Microscopic description of traffic phases. Phys. Rev. E 2002, 65, 056133. [Google Scholar] [CrossRef] [PubMed]
- Nagel, K.; Schreckenberg, M. A cellular automaton model for freeway traffic. J. Phys. I 1992, 2, 2221–2229. [Google Scholar] [CrossRef]
- Fukui, M.; Ishibashi, Y. Self-organized phase transitions in cellular automaton models for pedestrians. J. Phys. Soc. Jpn. 1999, 68, 2861–2863. [Google Scholar] [CrossRef]
- Fukui, M.; Ishibashi, Y. Jamming transition in cellular automaton models for pedestrians on passageway. Phys. Soc. Jpn 1999, 68, 3738–3739. [Google Scholar] [CrossRef]
- Burstedde, C.; Klauck, K.; Schadschneider, A.; Zittartz, J. Simulation of pedestrian dynamics using a two-dimensional cellular automaton. Phys. A Stat. Mech. Appl. 2001, 295, 507–525. [Google Scholar] [CrossRef]
- Kirchner, A.; Schadschneider, A. Simulation of evacuation processes using a bionics-inspired cellular automaton model for pedestrian dynamics. Phys. A Stat. Mech. Appl 2002, 312, 260–276. [Google Scholar] [CrossRef]
- Muramatsu, M.; Nagatani, T. Jamming transition in two-dimensional pedestrian traffic. Phys. A Stat. Mech. Appl. 2000, 275, 281–291. [Google Scholar] [CrossRef]
- Takimoto, K.; Nagatani, T. Spatio-temporal distribution of escape time in evacuation process. Phys. A Stat. Mech. Appl. 2003, 320, 611–621. [Google Scholar] [CrossRef]
- Yue, H.; Guan, H.; Zhang, J.; Shao, C. Study on bi-direction pedestrian flow using cellular automata simulation. Physica Phys. A Stat. Mech. Appl. 2010, 389, 527–539. [Google Scholar] [CrossRef]
- Yue, H.; Hao, H.; Chen, X.; Shao, C. Simulation of pedestrian flow on square lattice based on cellular automata model. Phys. A Stat. Mech. Appl. 2007, 384, 567–588. [Google Scholar] [CrossRef]
- Sun, Y. Simulations of bi-direction pedestrian flow using kinetic Monte Carlo methods. Phys. A Stat. Mech. Appl. 2019, 524, 519–531. [Google Scholar] [CrossRef]
- Sun, Y. Kinetic Monte Carlo simulations of bi-direction pedestrian flow with different walk speeds. Phys. A Stat. Mech. Appl. 2020, 124295. [Google Scholar] [CrossRef]
- Weng, W.; Chen, T.; Yuan, H.Y.; Fan, W.C. Cellular automaton simulation of pedestrian counter flow with different walk velocities. Phys. Rev. E 2006, 74, 036102. [Google Scholar] [CrossRef]
- Yang, L.; Li, J.; Liu, S. Simulation of pedestrian counter-flow with right-moving preference. Phys. A Stat. Mech Appl. 2008, 387, 3281–3289. [Google Scholar] [CrossRef]
- Alizadeh, R. A dynamic cellular automaton model for evacuation process with obstacles. Saf. Sci. 2011, 49, 315–323. [Google Scholar] [CrossRef]
- Zheng, Y.; Jia, B.; Li, X.G.; Zhu, N. Evacuation dynamics with fire spreading based on cellular automaton. Phys. A Stat. Mech. Appl. 2011, 390, 3147–3156. [Google Scholar] [CrossRef]
- Yang, L.; Fang, W.; Huang, R.; Deng, Z. Occupant evacuation model based on cellular automata in fire. Chin. Sci. Bull. 2002, 47, 1484. [Google Scholar] [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Moeuf, A.; Pellerin, R.; Lamouri, S.; Tamayo-Giraldo, S.; Barbaray, R. The industrial management of SMEs in the era of Industry 4.0. Int. J. Prod. Res. 2018, 56, 1118–1136. [Google Scholar] [CrossRef]
- Hermann, M.; Pentek, T.; Otto, B. Design principles for industrie 4.0 scenarios. In Proceedings of the 49th Hawaii International Conference on System Sciences (HICSS), Koloa, HI, USA, 5–8 January 2016. [Google Scholar] [CrossRef]
- Kagermann, H.; Wahlster, W.; Helbig, J. Recommendations for Implementing the Strategic Initiative Industrie 4.0: Final Report of the Industrie 4.0 Working Group; Acatech: München, Germany, 2013; pp. 19–26. [Google Scholar]
- Lasi, H.; Hussain, H.I.; Ślusarczyk, B.; Jermsittiparsert, K. Industry 4.0. Bus. Inf. Syst. Eng. 2014, 6, 239–242. [Google Scholar] [CrossRef]
- Negri, E.; Fumagalli, L.; Macchi, M. A review of the roles of digital twin in cps-based production systems. Procedia Manuf. 2017, 11, 939–948. [Google Scholar] [CrossRef]
- Schleich, B.; Anwer, N.; Mathieu, L.; Wartzack, S. Shaping the digital twin for design and production engineering. CIRP Ann. 2017, 66, 141–144. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, X. Cloud-based manufacturing equipment and big data analytics to enable on-demand manufacturing services. Robot. Comput.-Integr. Manuf. 2019, 57, 92–102. [Google Scholar] [CrossRef]
- Tao, F.; Sui, F.; Liu, A.; Qi, Q.; Zhang, M.; Song, B.; Guo, Z.; Lu, S.C.Y.; Nee, A.Y.C. Digital twin-driven product design framework. Int. J. Prod. Res. 2019, 57, 3935–3953. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, H.; Tao, F.; Juang, C.F. DT-II: Digital twin enhanced Industrial Internet reference framework towards smart manufacturing. Robot. Comput.-Integr. Manuf. 2020, 62, 101881. [Google Scholar] [CrossRef]
- Cimino, C.; Negri, E.; Fumagalli, L. Review of digital twin applications in manufacturing. Comput. Ind. 2019, 113, 103130. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, C.; Kevin, I.; Wang, K.; Huang, H.; Xu, X. Digital Twin-driven smart manufacturing: Connotation, reference model, applications and research issues. Robot. Comput.-Integr. Manuf. 2020, 61, 101837. [Google Scholar] [CrossRef]
- Ito, K. Change beyond building information modeling to a “Digital Twin” in architecture. Jpn. Archit. Rev. 2019, 2, 391. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Lian, Q. Digital twin aided sustainability-based lifecycle management for railway turnout systems. J. Clean. Prod. 2019, 228, 1537–1551. [Google Scholar] [CrossRef]
- Lu, R.; Brilakis, I. Digital twinning of existing reinforced concrete bridges from labelled point clusters. Autom. Construct. 2019, 105, 102837. [Google Scholar] [CrossRef]
- Bagheri, B.; Lee, J. Big Future for Cyber-Physical Manufacturing Systems. Des. World 2015. Available online: https://www.researchgate.net/publication/282355928_Big_future_for_cyberphysical_manufacturing_systems (accessed on 2 November 2020).


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, T.; Zhao, J.; Li, W. Smart-Guided Pedestrian Emergency Evacuation in Slender-Shape Infrastructure with Digital Twin Simulations. Sustainability 2020, 12, 9701. https://doi.org/10.3390/su12229701
Han T, Zhao J, Li W. Smart-Guided Pedestrian Emergency Evacuation in Slender-Shape Infrastructure with Digital Twin Simulations. Sustainability. 2020; 12(22):9701. https://doi.org/10.3390/su12229701
Chicago/Turabian StyleHan, Tianran, Jianming Zhao, and Wenquan Li. 2020. "Smart-Guided Pedestrian Emergency Evacuation in Slender-Shape Infrastructure with Digital Twin Simulations" Sustainability 12, no. 22: 9701. https://doi.org/10.3390/su12229701
APA StyleHan, T., Zhao, J., & Li, W. (2020). Smart-Guided Pedestrian Emergency Evacuation in Slender-Shape Infrastructure with Digital Twin Simulations. Sustainability, 12(22), 9701. https://doi.org/10.3390/su12229701




