Subtraction: More than an Algorithm?
Abstract
1. Introduction
2. Theoretical Framework
3. Materials and Methods
3.1. Sample
3.2. Instrument
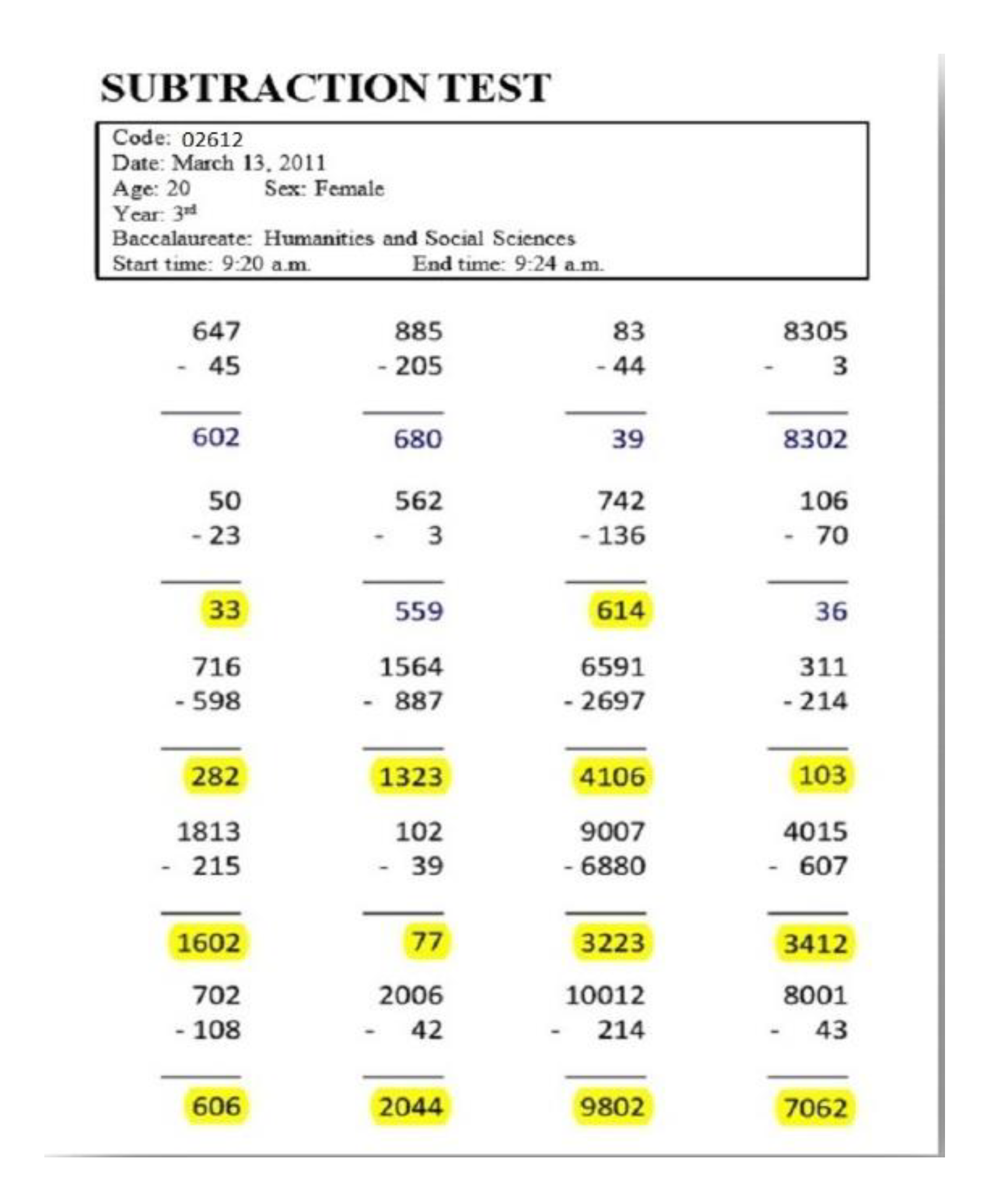
3.3. Preliminary Exploratory Test
3.4. Procedure
3.5. Data
3.6. Analysis System
4. Results
4.1. Errors Commited by University Students
4.2. Type of Error Committed by University Students in the Erroneous Subtractions
5. Discussion
6. Conclusions
- -
- Only one quarter of university students correctly answered all 20 subtractions in the questionnaire they completed. Extending the criteria for successful completion of the questionnaire to admit up to two errors resulted in only two thirds of students completing the questionnaire correctly.
- -
- There were significant differences related to the level of success in completing the questionnaire depending on the students’ sex (in favour of women), centre of studies (in favour of teaching students compared to business and statistics students) and time taken to complete the questionnaire (in favour of those who took fewer than five minutes, as against those who took longer than five minutes). There were no significant differences in terms of successful completion of the questionnaire based on age, year or previous studies.
- -
- The typology of the most frequently occurring errors committed by university students, which essentially coincides with the profile for primary students, indicates that in addition to these errors corresponding to a deficient handling of basic numerical relationships, they were also due to weaknesses in understanding zero and the place value system.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chamoso, J.M. Considering dialogue as a social instrument in the Mathematics class. Learn. Math. 2003, 23, 30–40. [Google Scholar]
- NCTM (National Council of Teachers of Mathematics). Principles and Standards for School Mathematics; NCTM: Reston, VA, USA, 2000. [Google Scholar]
- Voigt, J. Negotiation of mathematical meaning and learning mathematics. Educ. Stud. Math. 1994, 26, 275–298. [Google Scholar] [CrossRef]
- Jimenez, L.; Verschaffel, L. Development of Children´s solutions of non-standard arithmetic word problem solving. Rev. Psicodidact. 2014, 19, 93–123. [Google Scholar] [CrossRef]
- Depaepe, F.; De Corte, E.; Verschaffel, L. Teachers’ approaches towards word problem solving: Elaborating or restricting the problem context. Teach. Teach. Educ. 2010, 26, 152–160. [Google Scholar] [CrossRef]
- Kolovou, A.; Van den Heuvel-Panhuizen, M.; Bakker, A. Non-routine problem solving tasks in Primary School Mathematics textbooks-a needle in a Haystack. Mediterr. J. Res. Math. Educ. 2009, 8, 31–68. [Google Scholar]
- Reusser, K.; Stebler, R. Every word problem has a solution—The social rationality of mathematical modeling in schools. Learn. Instr. 1997, 7, 309–327. [Google Scholar] [CrossRef]
- Resnick, L.B. Education and Learning to Think; National Academic Press: Washington, DC, USA, 1987. [Google Scholar]
- Carpenter, T.P.; Franke, M.L.; Jacobs, V.R.; Fennema, E. Invention and Understanding in the Development of Multidigit Addition and Subtraction Procedures: A Longitudinal Study. In Proceedings of the Annual Meeting of the American Educational Research Association, New York, NY, USA, 8–12 April 1996. [Google Scholar]
- Fuson, K. Roles of representation and verbalization in the teaching of multi-digit addition and subtraction. Eur. J. Psychol. Educ. 1986, 1, 35–56. [Google Scholar] [CrossRef]
- Fuson, K.C.; Briars, D.J. Using a base-ten blocks learning/teaching approach for first -and second- grade place- value and multidigit addition and subtraction. J. Res. Math. Educ. 1990, 21, 180. [Google Scholar] [CrossRef]
- Hiebert, J.; Wearne, D. Instruction, understanding, and skill in multidigit addition and subtraction. Cogn. Instr. 1996, 14, 251–283. [Google Scholar] [CrossRef]
- Resnick, L.B. Syntax and semantics in learning to subtract. In Addition and Subtraction: A Developmental Perspective; Carpenter, T., Moser, J., Romberg, T., Eds.; Lawrence Erlbaum Assoc: Hillsdale, NJ, USA, 1982. [Google Scholar]
- Resnick, L.B.; Omanson, S.F. Learning to understand arithmetic. In Advances in Instructional Psychology; Glaser, R., Ed.; Lawrence Erlbaum Assoc: Hillsdale, NJ, USA, 1987. [Google Scholar]
- Sánchez-García, A.B. Algorithmic Errors. Cognitive Processes and Educational Actions. Teor. Educ. Rev. Interuniv. 2013, 25, 215–235. [Google Scholar]
- VanLehn, K. Mind Bugs: The Origins of Procedural Misconceptions; The MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Engberg, M.E.; Wolniak, G.C. College student pathways to the STEM disciplines. Teach. Coll. Rec. (1970) 2013, 115, 1–27. [Google Scholar]
- Jordan, N.C.; Kaplan, D.; Ramineni, C.; Locuniak, M.N. Early math matters: Kindergarten number competence and later mathematics outcomes. Dev. Psychol. 2009, 45, 850–867. [Google Scholar] [CrossRef] [PubMed]
- Geary, D.C. Consequences, characteristics, and causes of mathematical learning disabilities and persistent low achievement in mathematics. J. Dev. Behav. Pediatr. 2011, 32, 250–263. [Google Scholar] [CrossRef] [PubMed]
- Lefevre, J.-A.; Bisanz, J.; Daley, K.E.; Buffone, L.; Greenham, S.L. Multiple routes to solution of single-digit multiplication problems. J. Exp. Psychol. Gen. 1996, 125, 284–306. [Google Scholar] [CrossRef]
- Mitchell, J.H.; Hawkins, E.F.; Stancavage, F.B.; Dossey, J.A. Estimation Skills, Mathematics-in-Context, and Advanced Skills in Mathematics: Results from Three Studies of the National Assessment of Educational Progress 1996 Mathematics Assessment; Education Publications Center (Ed Pubs): Washington, DC, USA, 1999.
- Ohlsson, S.; Rees, E. The function of conceptual understanding in the learning of arithmetic procedures. Cogn. Instr. 1991, 8, 103–179. [Google Scholar] [CrossRef]
- Chamoso, J.; González, S.; Martín, P.; Hernández, R.W. Las Matemáticas en Las Primeras Edades Escolares; Colección Diálogos de Matemáticas, Nivola: Madrid, Spain, 2013. [Google Scholar]
- Baroody, A.J. Children’s Mathematical Thinking: A Developmental Framework for Preschool, Primary, and Special Education Teachers; Teachers College Press: New York, NY, USA, 1987. [Google Scholar]
- Hughes, M. Children and Number: Difficulties in Learning Mathematics; Blackwell Publishing: Oxford, UK, 1986. [Google Scholar]
- Starkey, P.; Cooper, R.G. Perception of numbers by human infants. Science 1980, 210, 1033–1035. [Google Scholar] [CrossRef]
- Ginsburg, H.P.; Klein, A.; Starkey, P. The development of children's mathematical thinking: Connecting research with practice. In Handbook of Child Psychology, 5th ed.; Damon, W., Sigel, I.E., Renninger, K.A., Eds.; Wiley and Sons: Hoboken, NJ, USA, 1998; Volume 4, pp. 401–476. [Google Scholar]
- Cooper, T.J.; Heirdsfield, A.; Irons, C.J. Children’s mental strategies for addition and subtraction word problems. In Children’s Number Learning; Mulligan, J.J., Mitchelmore, M., Eds.; Australian Association of Mathematics Teachers, Inc. (AAMT): Adelaide, Australia, 1996; pp. 147–162. [Google Scholar]
- Klein, A.S.; Beishuizen, M.; Treffers, A. The empty number line in Dutch second grades: Realistic versus gradual program design. J. Res. Math. Educ. 1998, 29, 443–464. [Google Scholar] [CrossRef]
- Fuson, K.C.; Wearne, D.; Hiebert, J.C.; Murray, H.G.; Human, P.G.; Olivier, A.I.; Carpenter, T.P.; Fennema, E. Children’s conceptual structures for multidigit numbers and methods of multidigit addition and subtraction. J. Res. Math. Educ. 1997, 28, 130–162. [Google Scholar] [CrossRef]
- Brownell, W.A. Psychological considerations in the learning and teaching of arithmetic. In The Teaching of Arithmetic; Reeve, D.W., Ed.; Bureau of Publications, Teachers College, Columbia University: New York, NY, USA, 1935; pp. 1–31. [Google Scholar]
- Groen, G.; Resnick, L.B. Can preschool children invent addition algorithms? J. Educ. Psychol. 1977, 69, 645–652. [Google Scholar] [CrossRef]
- Brown, J.S.; Burton, R.R. Diagnostic Models for Procedural Bugs in Basic Mathematical Skills. Cogn. Sci. 1978, 2, 155–192. [Google Scholar] [CrossRef]
- Gagne, R.M. The Conditions of Learning; Holt, Rinehart & Winston: New York, NY, USA, 1970. [Google Scholar]
- Woods, P.; Hartley, J.R. Some learning models for arithmetic tasks and their use in computer based learning. Br. J. Educ. Psychol. 1971, 41, 38–48. [Google Scholar] [CrossRef]
- Woods, S.S.; Resnick, L.B.; Groen, G.J. An Experimental Test of Five Process Models for Subtraction. J. Educ. Psychol. 1975, 67, 17–21. [Google Scholar] [CrossRef]
- Lankford, F.G. Some Computational Strategies of Seventh Grade Pupils; University of Virginia: Charlottesville, VA, USA, 1972. [Google Scholar]
- Ashlock, R.B. Error Patterns in Computation; Charles, E., Ed.; Merrill Publishing Co.: Columbus, OH, USA, 1976. [Google Scholar]
- Newell, A.; Simon, H.A. Human Problem Solving; Prentice-Hall: Englewood Cliffs, NJ, USA, 1972. [Google Scholar]
- Anderson, J.R. Language, Memory, and Thought; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1976. [Google Scholar]
- Young, R.M.; O’Shea, T. Errors in Children’s Subtraction. Cogn. Sci. 1981, 2, 153–177. [Google Scholar] [CrossRef]
- Young, R.M. Seriation by Children: An Artificial Intelligence Analysis of a Piagetian Task; Birkhauser: Basel, Switzerland, 1976. [Google Scholar]
- Young, R.M. Mixtures of strategies in structurally adaptive production systems: Examples from seriation and subtraction. ACM SIGART Bull. 1977, 63, 65–71. [Google Scholar] [CrossRef]
- Brown, J.S.; VanLehn, K. Repair Theory: A generative theory of bugs in procedural skills. Cogn. Sci. 1980, 4, 379–426. [Google Scholar] [CrossRef]
- Brown, J.S.; Vanlehn, K. Towards a generative theory of “bugs”. In Addition and Subtraction: A Cognitive Perspective; Carpenter, T.P., Moser, J.M., Romberg, T.A., Eds.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1982; pp. 117–135. [Google Scholar] [CrossRef]
- VanLehn, K. Bugs are not enough: Empirical studies of bugs, impasses and repairs in procedural skills. J. Math. Behav. 1982, 3, 3–71. [Google Scholar]
- Fuson, K.C. Research on Whole Number Addition and Subtraction. In Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics; Grouws, D.A., Ed.; Macmillan Publishing Co.: New York, NY, USA, 1992; pp. 243–275. [Google Scholar]
- Verschaffel, L.; De Corte, E. Number and arithmetic. In International Handbook of Mathematics Education; Bishop, A.J., Clements, K., Keitel, C., Kilpatrick, J., Laborde, C., Eds.; Kluwer Academic Publishers: New York, NY, USA, 1996; pp. 99–137. [Google Scholar]
- Bélanger, M. Les erreurs en arithmétique. Un siècle de présomption méricaine. Petit X 1991, 26, 49–71. [Google Scholar]
- Ashcraft, M.H. Cognitive arithmetic: A review of data and theory. Cognition 1992, 44, 75–106. [Google Scholar] [CrossRef]
- López-Fernández, R.; Sánchez-García, A.B. Los componentes generadores de errores algorítmicos. Caso particular de la sustracción. Rev. Educ. 2007, 344, 377–402. [Google Scholar]
- López-Fernández, R.; Sánchez-García, A.B. Analysis of systematic error in substraction. Enseñ. Cienc. 2009, 27, 49–58. [Google Scholar]
- Cox, L.S. Systematic errors in the four vertical algorithms in normal and handicapped populations. J. Res. Math. Educ. 1975, 6, 202–220. [Google Scholar] [CrossRef]
- Bennett, M. SUBSTITUTOR: A Teaching Program; Department of Artificial Intelligence, University of Edinburgh: Edinburgh, UK, 1976; Unpublished Project Report. [Google Scholar]
- Cebulski, L.A.; Bucher, B. Identification and remediation of children's subtraction errors: A comparison of practical approaches. J. Sch. Psychol. 1986, 24, 163–180. [Google Scholar] [CrossRef]
- Sander, E. Solving arithmetic operations: A semantic approach. In Proceedings of the 23rd Annual Conference of the Cognitive Science Society, Edinburgh, UK, 1–4 August 2001; Moore, J.D., Stenning, K., Eds.; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 2001; pp. 915–920. [Google Scholar]
- Fiori, C.; Zuccheri, L. An experimental research on error patterns in written subtraction. Educ. Stud. Math. 2005, 60, 323–331. [Google Scholar] [CrossRef]
- Barrouillet, P.; Fayol, M. From algorithmic computing to direct retrieval: Evidence from number and alphabetic arithmetic in children and adults. Mem. Cognit. 1998, 26, 355–368. [Google Scholar] [CrossRef]
- Geary, D.C.; Frensch, P.A.; Wiley, J.G. Simple and Complex Mental Subtraction: Strategy Choice and Speed-of-Processing Differences in Younger and Older Adults. Psychol. Aging 1993, 8, 242–256. [Google Scholar] [CrossRef]
- Creswell, J.W. Research Design: Qualitative, Quantitative, and Mixed Methods Approaches; Sage: London, UK, 2008. [Google Scholar]
- McMillan, J.H.; Schumacher, S. Research in Education: A Conceptual Introduction, 5th ed.; Addison Wesley Longman: New York, NY, USA, 2001. [Google Scholar]
- Kramarski, B.; Mevarech, Z.R.; Arami, M. The Effects of Metacognitive Instruction on Solving Mathematical Authentic Tasks. Educ. Stud. Math. 2002, 49, 225–250. [Google Scholar] [CrossRef]
- Polya, G. Como Plantear and Resolver Problemas; Trillas: México DF, México, 1965. [Google Scholar]
- Baroody, A.J. Kindergartners’ mental addition with single-digit combinations. J. Res. Math. Educ. 1989, 20, 159–172. [Google Scholar] [CrossRef]
- Cobb, P.; Wheatley, G. Children’s Initial Understandings of Ten. Focus Learn. Probl. Math. 1988, 10, 1–28. [Google Scholar]
- Cobb, P.; Yackel, E.; Wood, T.; Wheatley, G.; Merkel, G. Creating a problem-solving atmosphere. Arith. Teach. 1988, 36, 46–47. [Google Scholar]
- Kamii, C.; Lewis, B.A. Achievement Tests in Primary Mathematics: Perpetuating Lower-Order Thinking. Arith. Teach. 1991, 38, 4–9. [Google Scholar] [CrossRef]
- Carraher, T.N.; Carraher, D.W.; Schliemann, A.D. Mathematics in the streets and in schools. Br. J. Dev. Psychol. 1985, 3, 21–29. [Google Scholar] [CrossRef]

| Centre | First | Second | Third | Total |
|---|---|---|---|---|
| Teaching | 185 (46.1%) | 143 (35.7%) | 73 (18.2%) | 401 (100%) |
| Business | 64 (56.6%) | 0 (0.0%) | 49 (43.4%) | 113 (100%) |
| Statistics | 7 (33.3%) | 10 (47.6%) | 4 (19.0%) | 21 (100%) |
| Total | 256 (47.9%) | 153 (28.6%) | 126 (23.6%) | 535 (100%) |
| Error | Name | Description |
|---|---|---|
| E4 | 0 − N = N Except After Borrow | The student thinks that 0 − N is N except when the column has been borrowed from. |
| E5 | 1 − 1 = 0 After Borrow | If a column starts with 1 in both top and bottom and is borrowed from, the student writes 0 as the answer to that column. |
| E6 | 1 − 1 = 1 After Borrow | If a column starts with 1 at the top and bottom and is borrowed from, the student writes 1 as the answer to that column. |
| E7 | Add Borrow Decrement | Instead of decrementing, the student adds 1, carrying to the next column if necessary. |
| E8 | Add Borrow Decrement without Carry | Instead of decrementing, the student adds one. If this addition results in ten, the student does not carry but simply writes both digits in the same space. |
| E9 | Add Instead of Sub | The student adds instead of subtracts. |
| E12 | Always Borrow | The student borrows in every column regardless of whether it is necessary. |
| E19 | Borrow across Top Smaller Decrementing To | When decrementing a column in which the top is smaller than the bottom, the student adds 10 to the top digit, decrements the column being borrowed into and borrows from the next column to the left. Further, the student skips any column that has a zero over a zero or blank in the borrowing process. |
| E20 | Borrow across Zero | When borrowing across a zero, the student skips over the zero to borrow from the next column. If this requires them to borrow twice, they decrement the same number both times. |
| E22 | Borrow across Zero over Zero | Instead of borrowing across a zero that is over a zero, the student does not change the zero but decrements the next column to the left instead. |
| E28 | Borrow from All Zero | When borrowing across one or more zeros, the student changes all the zeros to nines, but does not decrement the appropriate nonzero digit. |
| E29 | Borrow from Bottom | The student borrows from the bottom instead of top row. |
| E32 | Borrow from One Is Nine | When borrowing from a 1, the student changes it to 9 instead of zero. |
| E33 | Borrow from One Is Ten | When borrowing from a 1, the student changes it to 10 instead of zero. |
| E34 | Borrow from Zero | Instead of borrowing across a zero, the student changes the zero to 9 but does not continue borrowing from the column to the left. |
| E36 | Borrow from Zero Is Ten | When borrowing across a zero, the student changes the zero to 10 but does not decrement any digit to the left. |
| E38 | Borrow into One = Ten | When a borrow is caused by a column of the form 1 − N, the student changes the 1 to 10 instead of adding 10 to it. |
| E39 | Borrow No Decrement | When borrowing, the student correctly adds 10 but does not decrement any column to the left. |
| E40 | Borrow No Decrement Except Last | The student omits decrementing unless the column to be decremented is the leftmost column in the subtraction. |
| E44 | Borrow Only Once | The student does the first borrow correctly in a problem. They subsequently only add 10 and omit the decrement. |
| E45 | Borrow Skip Equal | When decrementing, the student skips over columns where the top and bottom digits are the same. |
| E47 | Borrow Treat One as Zero | When borrowing from a 1, the student treats the 1 as if it were a 0. In other words, they change the 1 to 9 and decrement the number to the left of the 1. |
| E51 | Borrowed from Don’t Borrow | When there are two consecutive borrows, the student performs the first correctly but does not decrement with the second (although they add 10 correctly). |
| E56 | Decrement by One Plus Zeros | When there is a borrow across one or more zeros, the student decrements the number to the left of the zero(s) by an extra 1 for each zero borrowed across. |
| E61 | Decrement on First Borrow | The first column that requires a borrow is decremented before the column subtract is done. |
| E65 | Diff 0 − N = N | In columns of the form 0 − N, the student does not borrow but instead writes N as the answer. |
| E69 | Diff N − N = N | Whenever there is a column with the same number on the top and bottom, the student writes that number as the answer. |
| E75 | Don’t Decrement Zero over Blank | The student does not borrow from a zero that is over a blank. |
| E76 | Don’t Decrement Zero over Zero | The student does not borrow from a zero that is over a zero. |
| E77 | Don’t Decrement Zero Until Bottom Blank | When borrowing across a zero, the student changes the zero to 10 instead of 9, unless the zero is over a blank, in which case they borrow correctly. |
| E79 | Double Decrement One | When borrowing from a one, the student treats the one as a zero (that is, they change the one to nine and continue borrowing to the left) unless the one is over a blank, in which case they do the correct thing. |
| E80 | Forget Borrow over Blanks | The student does not decrement a number that is over a blank. |
| E81 | Ignore Leftmost One over Blank | When the leftmost column has a 1 over a blank, the student ignores that column. |
| E85 | N − 9 = N − 1 After Borrow | If a column is of the form N − 9 and has been borrowed from, when the student does that column, he subtracts one instead of nine. |
| E86 | N − N After Borrow Causes Borrow | The student borrows with columns of the form N − N (after having borrowed). |
| E88 | N − N = 1 After Borrow | If a column had the form N − N and was borrowed from, the student writes one as the answer to that column. |
| E89 | N − N = 9 Plus Decrement | When a column has the same number in the top and bottom, the student writes 9 as the answer and decrements the next column to the left, even when no borrowing is required. |
| E90 | Once Borrow Always Borrow | Once a student has borrowed, they continue borrowing in every column. |
| E94 | Smaller from Larger | The student does not borrow, but in each column subtracts the smaller digit from the larger one. |
| E95 | Smaller from Larger Except Last | The student answers all columns by taking the smaller digit from the larger one unless the column is second to the last, in which case the student borrows if necessary. |
| E100 | Smaller from Larger With Borrow | When borrowing is required, the student correctly decrements but subtracts the smaller digit from the larger one. |
| E109 | Top Instead of Borrow From Double Zero | If a column requires borrowing from multiple zeros, the student writes the top digit as the answer to that column. |
| E115 | Treat Top Zero as Ten | In a 0 − N column, the student does not borrow, but rather treats the 0 as if it were a 9. |
| E122 | Calculation | Number fact errors, such as 8 − 3 = 6. |
| E123 | Not diagnosable | |
| E301 a | Decrement By 2 in Second Borrow | When two consecutive borrows are required, the student performs the first correctly but introduces a two-unit decrement in the second. |
| E302 a | Units Column: If T < B, Add Not Subtract and Decrement | When T < B in the units column, the student adds instead of subtracting and introduces a decrement of one unit in the next column. |
| E303 a | Units Column: If T < B, Add Not Subtract and No Decrement With Borrow | When T < B in the units column, the student adds instead of subtracting and does not introduce a decrement of one unit in the next column. |
| E304 a | Units Column: If T < B, Increase Units By 1 and Decrement Borrow | When T < B in the units column, the student increases the result by one and decrements the borrow in the next column. |
| E305 a | Units Column: If T < B, Write Bottom | When T < B in the units column, the student writes the bottom digit as the result. |
| E306 a | N − 0 = N and Decrement | N − 0 = N and the student introduces a decrement of one unit in the next column. |
| E307 a | N − 0 = 0 − N and Decrement | N − 0 = 0 − N and the student introduces a decrement of one unit in the next column. If it is another number instead of a zero, the student subtracts the bottom from the top and decrements the borrow. |
| E308 a | E40 + E69 | Combination of errors 40 and 69 from VanLehn’s glossary of errors. |
| Total Errors | Teaching | Statistics | Business | Total |
|---|---|---|---|---|
| 0 | 109 (27.2%) | 2 (9.5%) | 18 (15.9%) | 129 (24.1%) |
| 1 | 85 (21.2%) | 8 (38.1%) | 27 (23.9%) | 120 (22.4%) |
| 2 | 74 (18.5%) | 2 (9.5%) | 21 (18.6%) | 97 (18.1%) |
| 3 | 58 (14.5%) | 4 (19.0%) | 12 (10.6%) | 74 (13.8%) |
| 4 | 31 (7.7%) | 2 (9.5%) | 10 (8.8%) | 43 (8.0%) |
| 5 or more | 44 (10.9%) | 3 (14.4%) | 25 (22.2%) | 72 (13.6%) |
| Total | 401 (100%) | 21 (100%) | 113 (100%) | 535 (100%) |
| Subtraction | Number of Errors | Percentage of Questionnaires |
|---|---|---|
| S13 | 128 | 23.9% 1 |
| S11 | 107 | 20.0% |
| S9 | 94 | 17.6% |
| S19 | 91 | 17.0% |
| S20 | 88 | 16.4% |
| S10 | 85 | 15.9% |
| S15 | 82 | 15.3% |
| S18 | 80 | 15.0% |
| S16 | 76 | 14.2% |
| S17 | 70 | 13.1% |
| S14 | 53 | 9.9% |
| S5 | 52 | 9.7% |
| S12 | 47 | 8.8% |
| S3 | 41 | 7.7% |
| S1 | 40 | 7.5% |
| S7 | 39 | 7.3% |
| S6 | 31 | 5.8% |
| S8 | 26 | 4.9% |
| S2 | 20 | 3.7% |
| S4 | 8 | 1.5% |
| Total erroneous subtractions: 1258 | ||
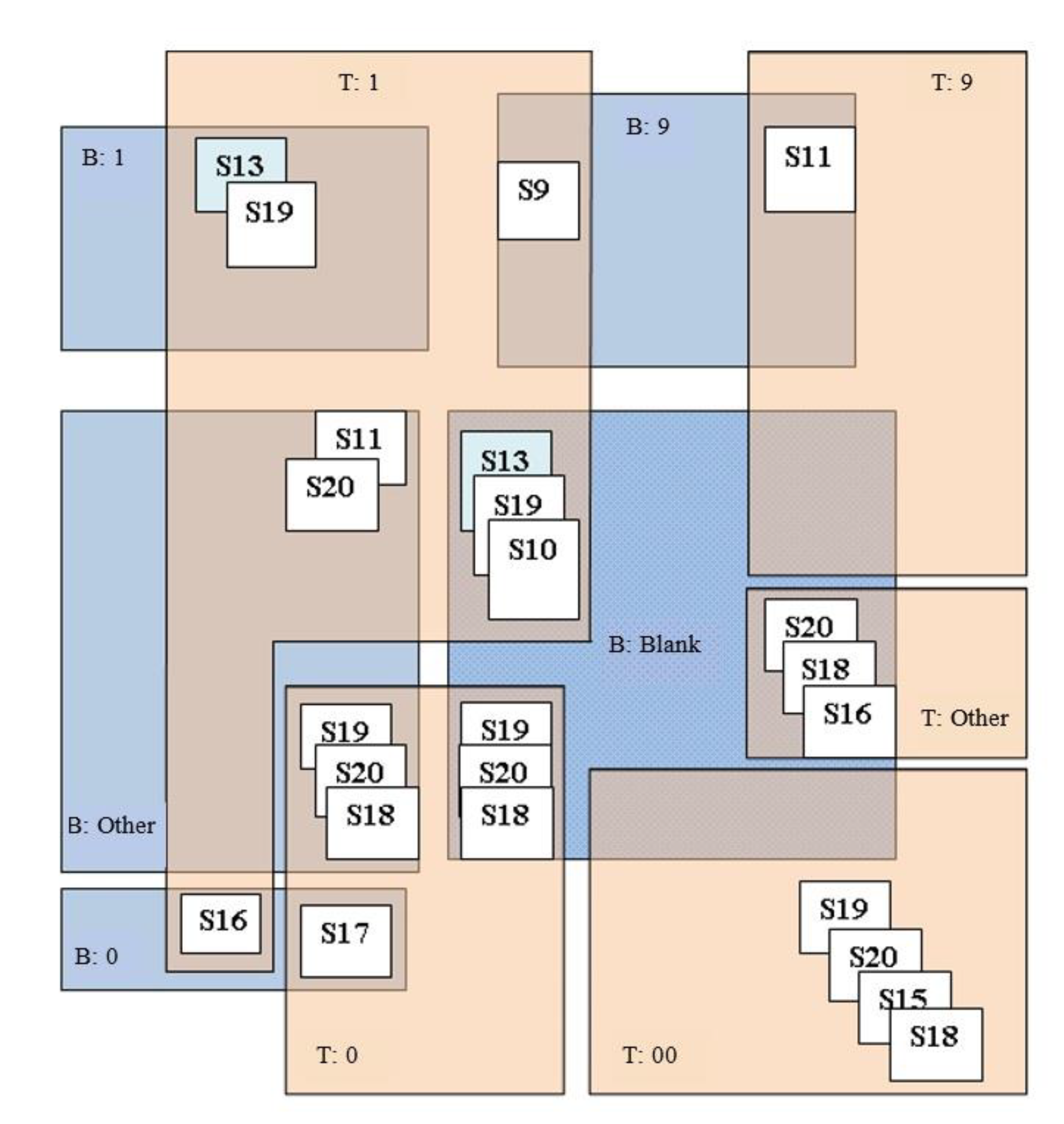
| Subtraction Number | Total Errors (%) | Most Frequent Error Types | Example of Error in Each Subtraction | Number of Errors of Each Type |
|---|---|---|---|---|
| Subtraction 13: 1813 − 215 = 1598 | 128 (23.9%) | E81 | 1813 − 215 = 598 a 1813 − 215 = 608 | 56 (25.11%) |
| E12 | 181 3 − 215 = 598 | 50 (22.42%) | ||
| E5 | 1813 − 215 = 1608 | 22 (9.83%) | ||
| E122 | 1813 − 215 = 1597 | 12 (5.38%) | ||
| E19 | 1813 − 215 = 1607 | 11 (4.93%) | ||
| E6 | 1813 − 215 = 1618 | 10 (4.48%) | ||
| E33 | 1813 − 215 = 1698 | 10 (4.48%) | ||
| Subtraction 11: 6591 − 2697 = 3894 | 107 (20.0%) | E40 | 6591 − 2697 = 3904 | 37 (15.16%) |
| E69 | 6591 − 2697 = 3994 | 33 (13.52%) | ||
| E122 | 6591 − 2697 = 3899 | 28 (11.47%) | ||
| E45 | 6591 − 2697 = 3804 | 13 (5.33%) | ||
| E89 | 6591 − 2697 = 3894 | 10 (4.1%) | ||
| E301 | 6591 − 2697 = 3794 | 10 (4.1%) | ||
| E7 | 6591 − 2697 = 4014 | 8 (3.28%) | ||
| Subtraction 9: 716 − 598 = 118 | 94 (17.6%) | E33 | 716 − 598 = 218 | 40 (30.1%) |
| E122 | 716 − 598 = 116 | 22 (16.54%) | ||
| E302 | 716 − 598 = 114 | 8 (6.01%) | ||
| E19 | 716 − 598 = 117 | 5 (3.76%) | ||
| E32 | 716 − 598 = 208 | 4 (3.01%) | ||
| E40 | 716 − 598 = 128 | 4 (3.01%) | ||
| E47 | 716 − 598 = 108 | 4 (3.01%) | ||
| Subtraction 19: 10012 − 214 = 9798 | 91 (17.0%) | E5 | 10,012 − 214 = 9808 | 14 (7.33%) |
| E80 | 10,012 − 214 = 10,798 | 14 (7.33%) | ||
| E34 | 10,012 − 214 = 19,798 | 11 (5.76%) | ||
| E75 | 10,012 − 214 = 10,798 | 11 (5.76%) | ||
| E33 | 10,012 − 214 = 9898 | 10 (5.24%) | ||
| E28 | 10,012 − 214 = 19,798 | 9 (4.71%) | ||
| E122 | 10,012 − 214 = 9998 | 9 (4.71%) | ||
| Subtraction 20: 8001 − 43 = 7958 | 88 (16.4%) | E77 | 8001 − 43 = 7968 | 13 (8.67%) |
| E34 | 8001 − 43 = 8958 | 12 (8%) | ||
| E80 | 8001 − 43 = 8058 | 12 (8%) | ||
| E122 | 8001 − 43 = 7956 | 11 (7.33%) | ||
| E28 | 8001 − 43 = 8958 | 10 (6.67%) | ||
| E75 | 8001 − 43 = 8058 | 10 (6.67%) | ||
| E38 | 8001 − 43 = 7957 | 8 (5.33%) | ||
| Subtraction 10: 1564 − 887 = 677 | 85 (15.9%) | E122 | 1564 − 887 = 657 | 31 (21.68%) |
| E44 | 1564 − 887 = 777 | 17 (18.89%) | ||
| E51 | 1564 − 887 = 1777 | 13 (9.09%) | ||
| E9 | 1564 − 887 = 2 451 | 9 (6.29%) | ||
| E29 | 1564 − 887 = 897 | 8 (5.59%) | ||
| E81 | 1564 − 887 =787 | 8 (5.59%) | ||
| E80 | 1564 − 887 = 1677 | 7 (4.89%) | ||
| Subtraction 15: 9007 − 6880 = 2127 | 82 (15.3%) | E34 | 9007 − 6880 = 3127 | 30 (19.87%) |
| E28 | 9007 − 6880 = 3117 | 28 (18.54%) | ||
| E36 | 9007 − 6880 = 3227 | 13 (8.61%) | ||
| E39 | 9007 − 6880 = 3227 | 13 (8.61%) | ||
| E56 | 9007 − 6880 = 1127 | 8 (5.3%) | ||
| E307 | 9007 − 6880 = 2113 | 7 (4.63%) | ||
| E306 | 9007 − 6880 = 2117 | 7 (4.63%) | ||
| Subtraction 18: 2006 − 42 = 1964 | 80 (15.0%) | E12 | 2006 − 42 = 1954 | 33 (24.81%) |
| E56 | 2006 − 42 = 964 | 18 (13.53%) | ||
| E75 | 2006 − 42 = 2064 | 11 (8.27%) | ||
| E80 | 2006 − 42 = 2064 | 10 (7.52%) | ||
| E115 | 2006 − 42 = 2064 | 7 (5.26%) | ||
| E122 | 2006 − 42 = 1963 | 7 (5.26%) | ||
| E28 | 2006 − 42 = 2964 | 6 (4.51%) | ||
| Subtraction 16: 4015 − 607 = 3408 | 76 (14.2%) | E12 | 4015 − 607 = 3308 | 19 (12.5%) |
| E90 | 4015 − 607 = 3308 | 16 (10.53%) | ||
| E86 | 4015 − 607 = 4308 | 13 (8.55%) | ||
| E80 | 4015 − 607 = 4408 | 12 (7.89%) | ||
| E40 | 4015 − 607 = 3418 | 11 (7.24%) | ||
| E65 | 4015 − 607 = 4608 | 9 (5.92%) | ||
| E115 | 4015 − 607 = 4408 | 9 (5.92%) | ||
| Subtraction 17: 702 − 108 = 594 | 70 (13.1%) | E34 | 702 − 108 = 694 | 26 (23.21%) |
| E122 | 702 − 108 = 596 | 10 (8.93%) | ||
| E28 | 702 − 108 = 694 | 9 (8.03%) | ||
| E76 | 702 − 108 = 604 | 7 (6.25%) | ||
| E36 | 702 − 108 = 604 | 6 (5.36%) | ||
| E19 | 702 − 108 = 603 | 5 (4.46%) | ||
| E22 | 702 − 108 = 614 | 4 (3.57%) | ||
| Total | 901 (71.6%) |
| Error | Frequency in Our Study | Order According to Frequency in Our Study | Order According to Frequency in Primary Education 1 | Systematic Errors 1 |
|---|---|---|---|---|
| E122 | 212 | 1 | 1 | |
| E12 | 140 | 2 | 6 | * |
| E39 | 96 | 3 | 2 | * |
| E34 | 94 | 4 | * | |
| E40 | 91 | 5 | * | |
| E80 | 78 | 6 | 18 | * |
| E81 | 71 | 7 | * | |
| E28 | 67 | 8 | * | |
| E33 | 67 | 9 | * | |
| E19 | 54 | 10 | 4 | |
| E94 | 50 | 11 | 21 | * |
| E115 | 50 | 12 | ||
| E9 | 48 | 13 | 10 | |
| E69 | 48 | 14 | ||
| E5 | 47 | 15 | 3 | * |
| E7 | 43 | 16 | 19 | |
| E29 | 39 | 17 | ||
| E44 | 37 | 18 | * | |
| E56 | 34 | 19 | ||
| E302 a | 34 | 20 | ||
| E65 | 32 | 21 | 20 | * |
| E75 | 32 | 22 | ||
| E308 a | 32 | 23 | ||
| E304 a | 31 | 24 | ||
| E100 | 30 | 25 | ||
| E36 | 29 | 26 | 12 | * |
| E4 | 27 | 27 | ||
| E85 | 26 | 28 | ||
| E89 | 26 | 29 | ||
| E88 | 25 | 30 | ||
| E123 b | 24 | 31 | ||
| E61 | 21 | 32 | ||
| E6 | 20 | 33 | 17 | * |
| E79 | 19 | 34 | ||
| E95 | 19 | 35 | ||
| E77 | 18 | 36 | ||
| E8 | 17 | 37 | 16 | |
| E51 | 17 | 38 | ||
| E20 | 15 | 39 | 5 | |
| E45 | 15 | 40 | ||
| E306 a | 15 | 41 | ||
| E307 a | 15 | 42 | ||
| E38 | 14 | 43 | * | |
| E47 | 14 | 44 | ||
| E301 a | 13 | 45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Sánchez, M.M.; Sánchez-García, A.B.; López-Fernández, R. Subtraction: More than an Algorithm? Sustainability 2020, 12, 9148. https://doi.org/10.3390/su12219148
Rodríguez-Sánchez MM, Sánchez-García AB, López-Fernández R. Subtraction: More than an Algorithm? Sustainability. 2020; 12(21):9148. https://doi.org/10.3390/su12219148
Chicago/Turabian StyleRodríguez-Sánchez, M. Mercedes, Ana B. Sánchez-García, and Ricardo López-Fernández. 2020. "Subtraction: More than an Algorithm?" Sustainability 12, no. 21: 9148. https://doi.org/10.3390/su12219148
APA StyleRodríguez-Sánchez, M. M., Sánchez-García, A. B., & López-Fernández, R. (2020). Subtraction: More than an Algorithm? Sustainability, 12(21), 9148. https://doi.org/10.3390/su12219148







