Photovoltaic Plant Optimization to Leverage Electric Self Consumption by Harnessing Building Thermal Mass
Abstract
1. Introduction and Motivation of the Work
2. Methodology
2.1. Building Energy Model (BEM)
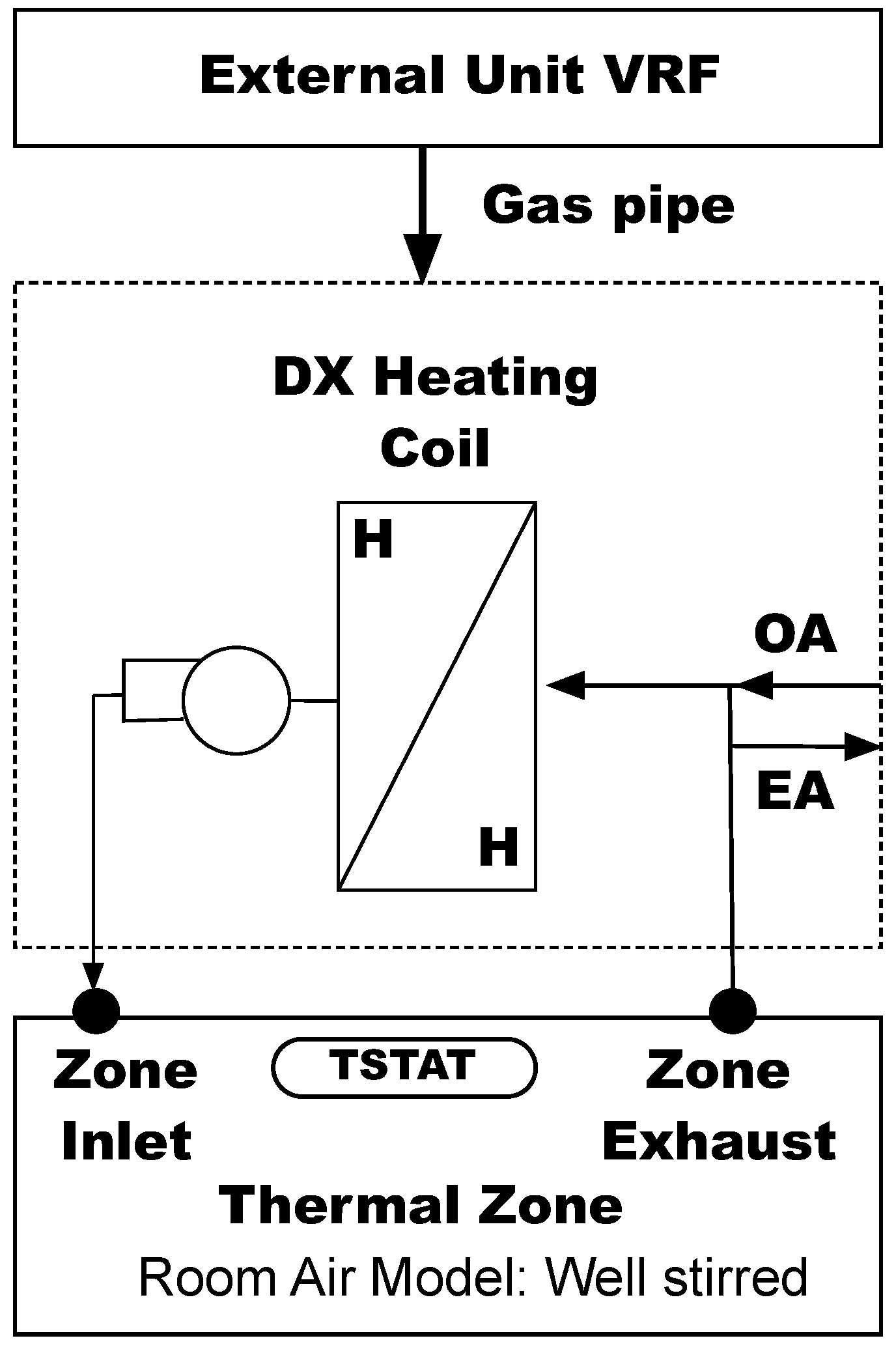
2.2. Heating System
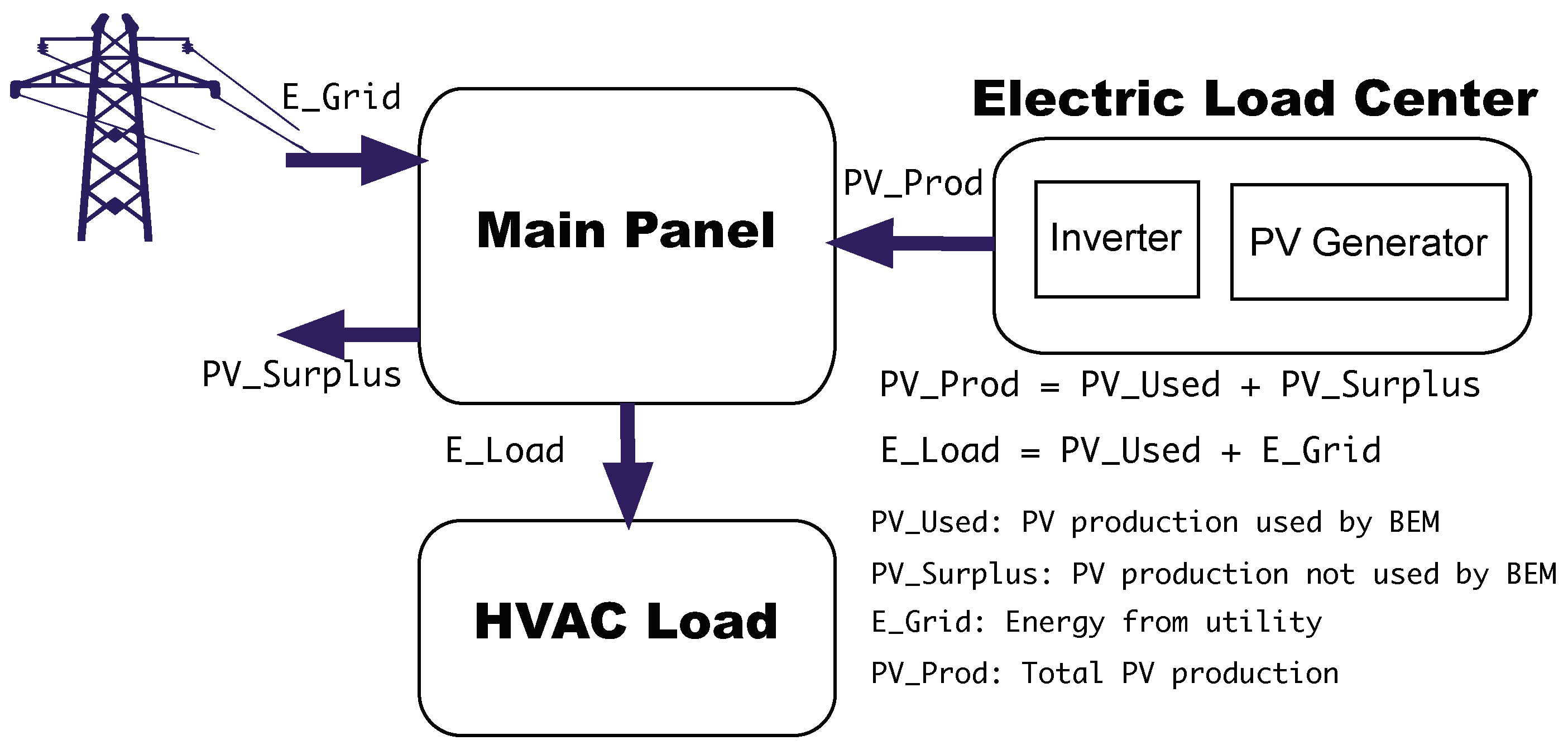
2.3. Electric Building System
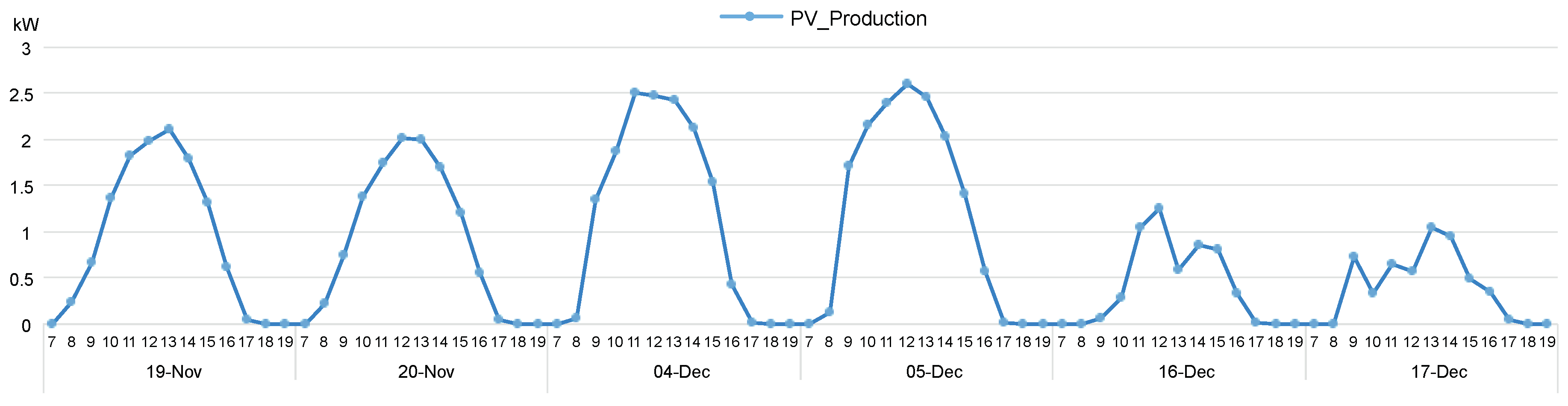
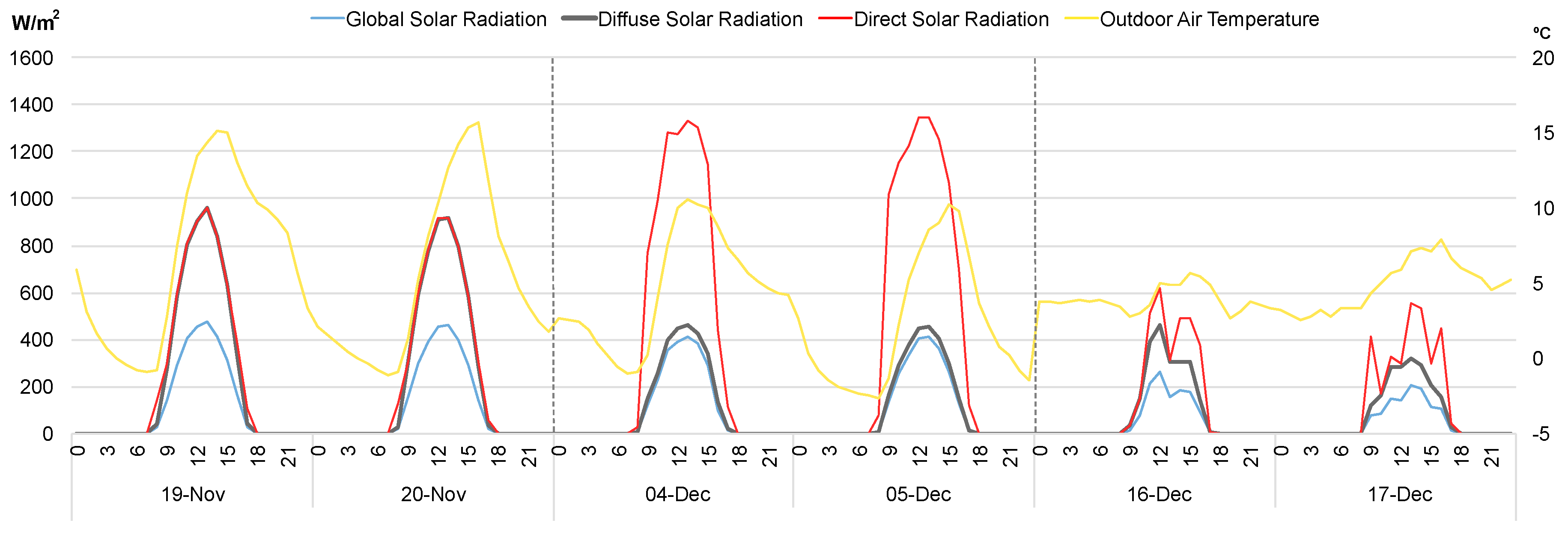
2.4. Weather Data
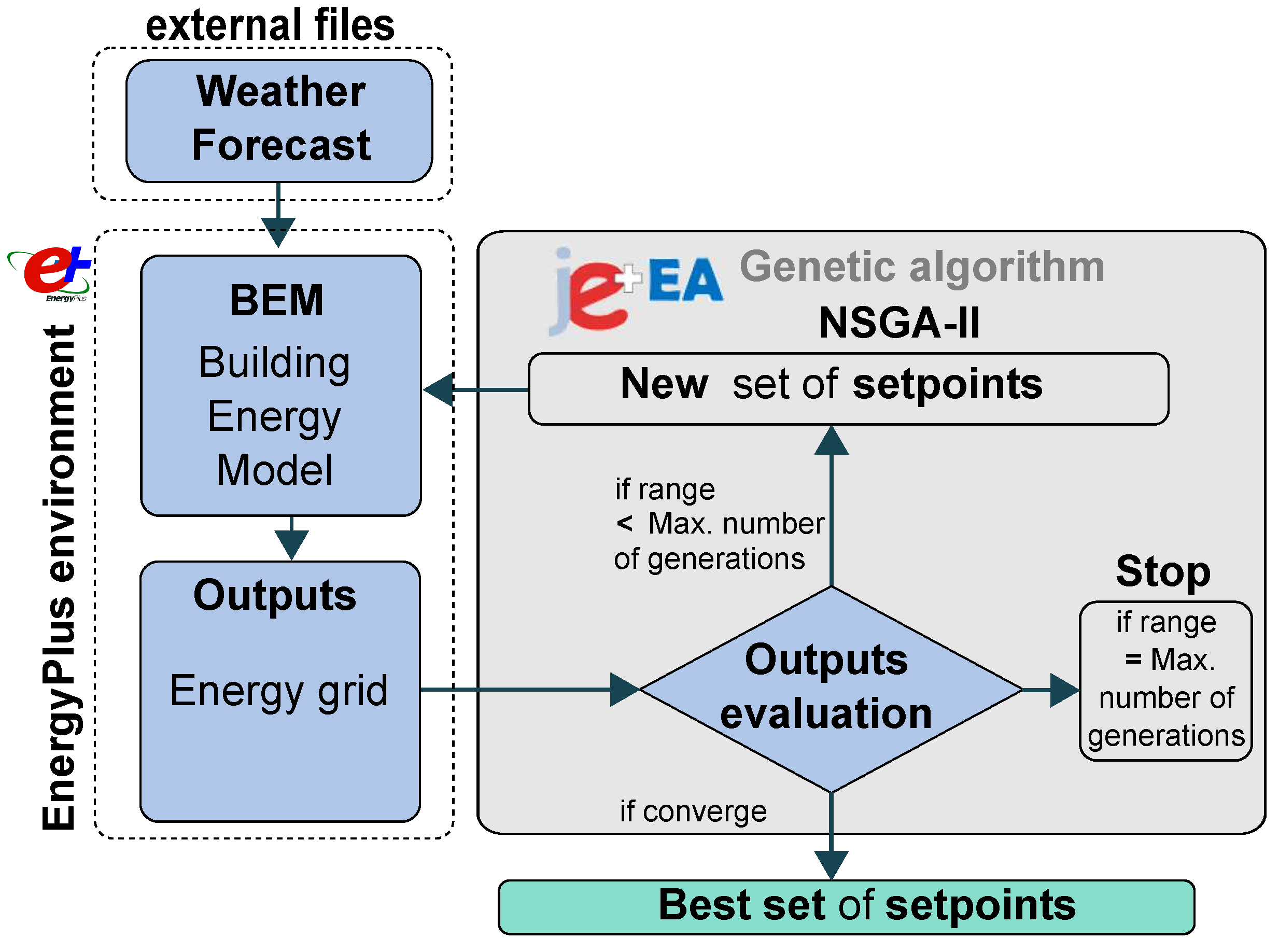
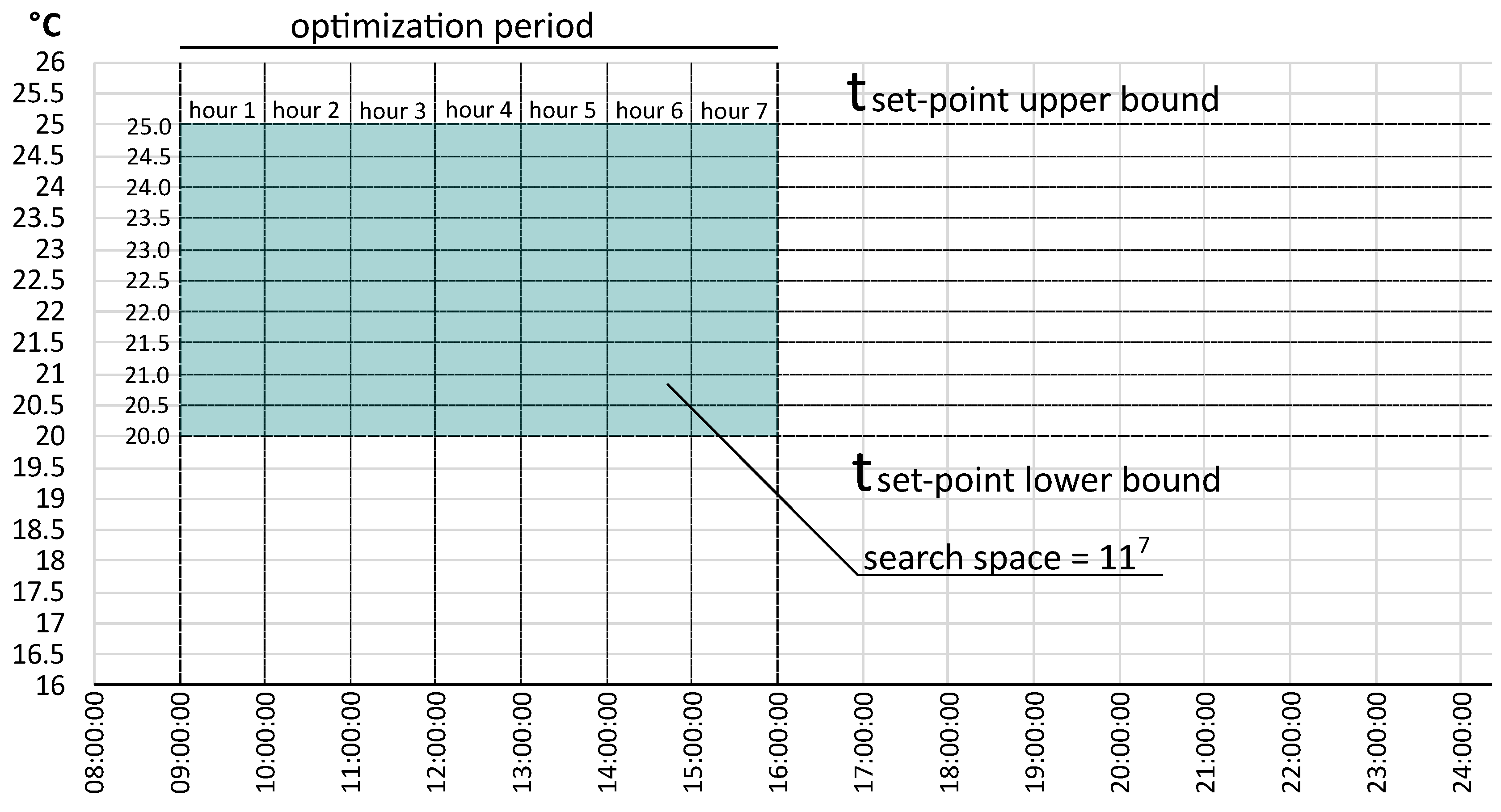
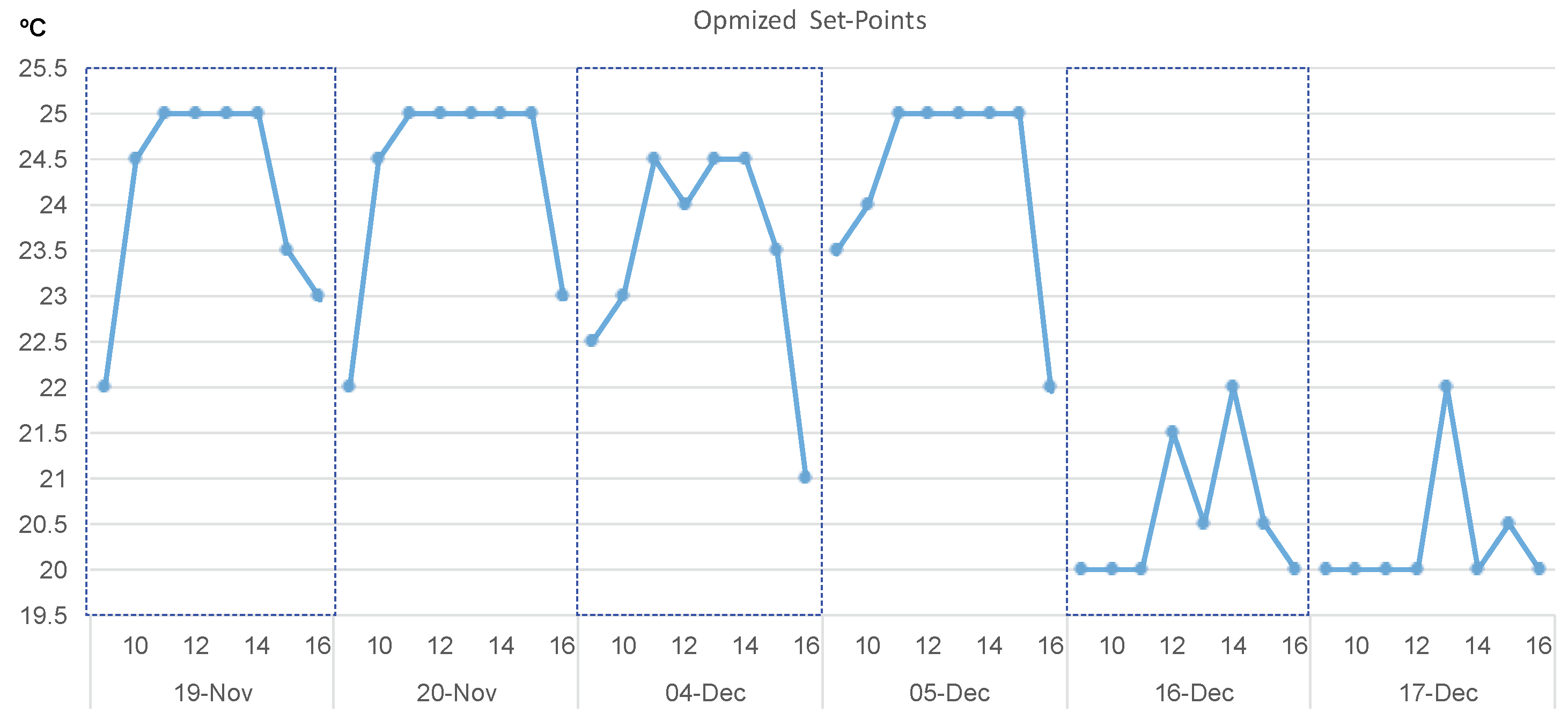
2.5. Model Predictive Control (MPC) Strategy
2.6. Evaluation Criteria
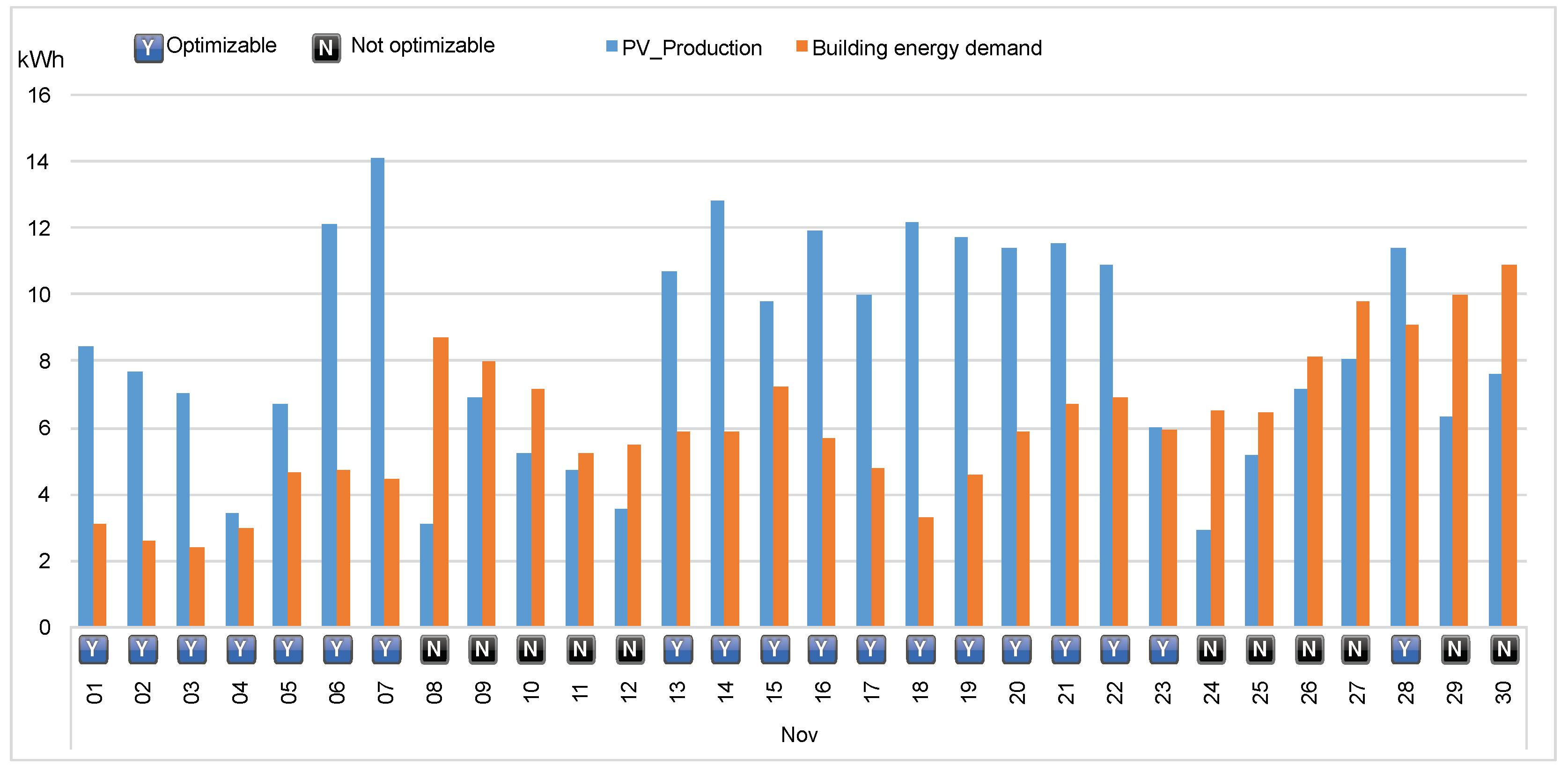
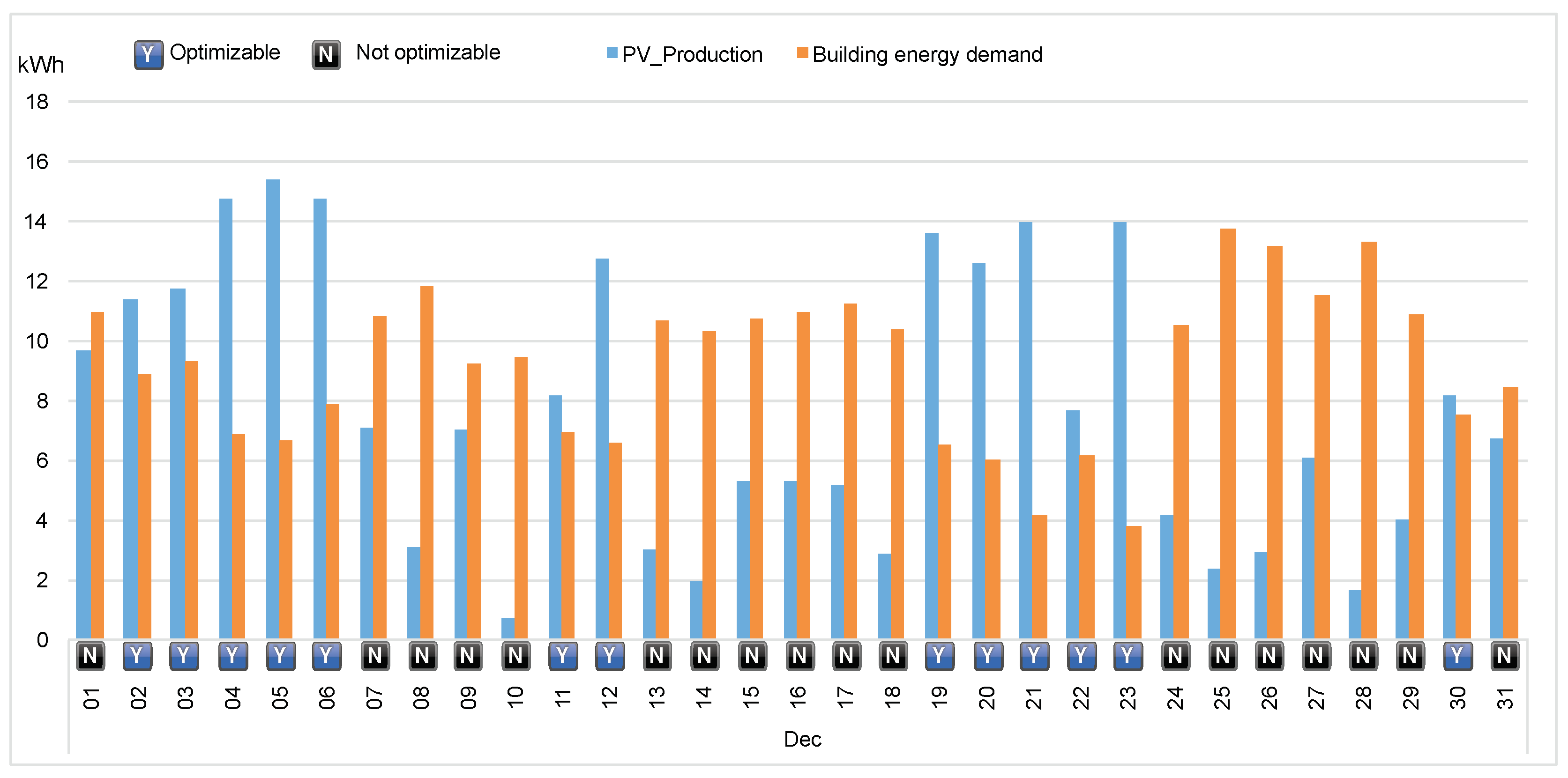
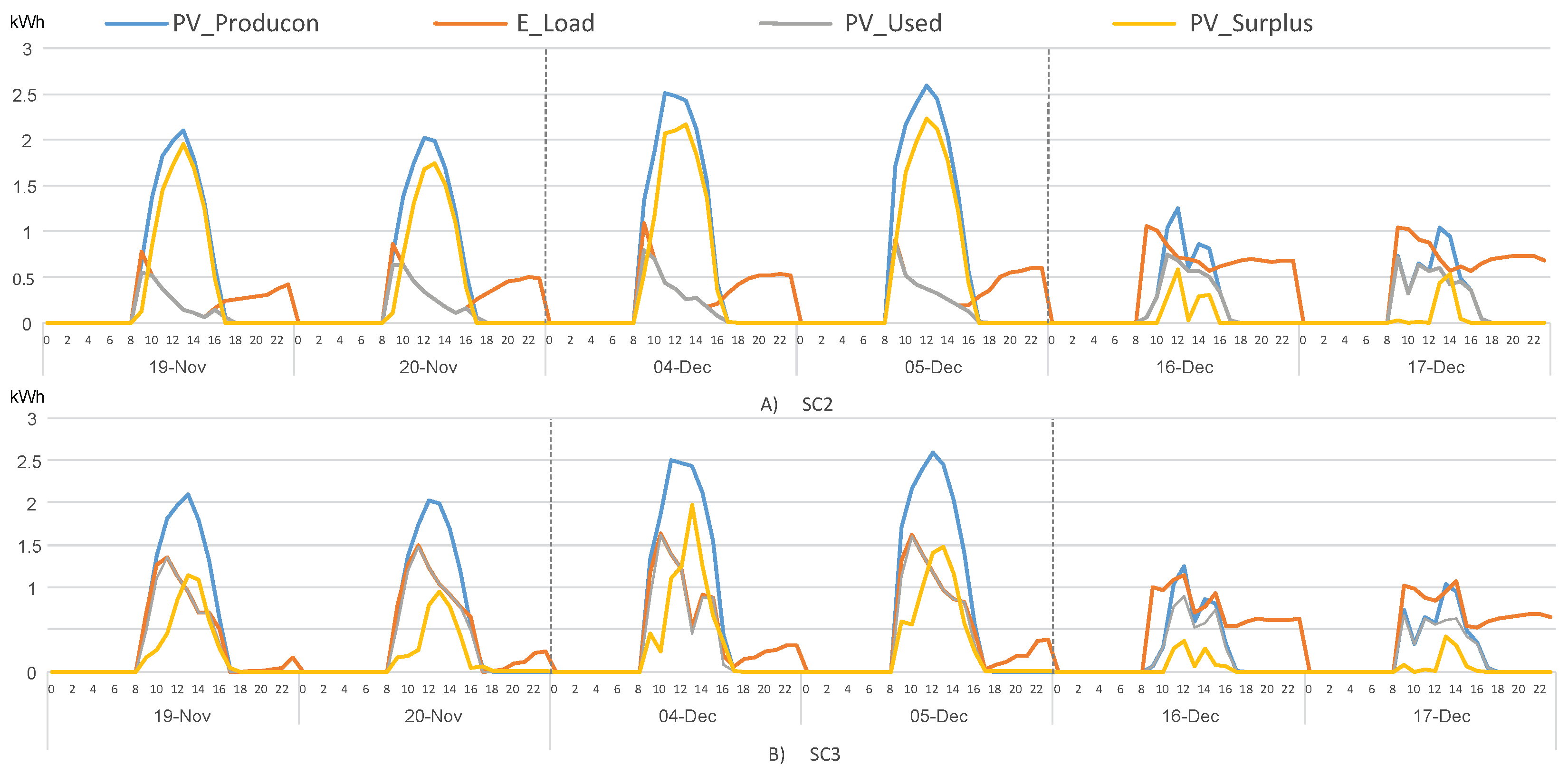
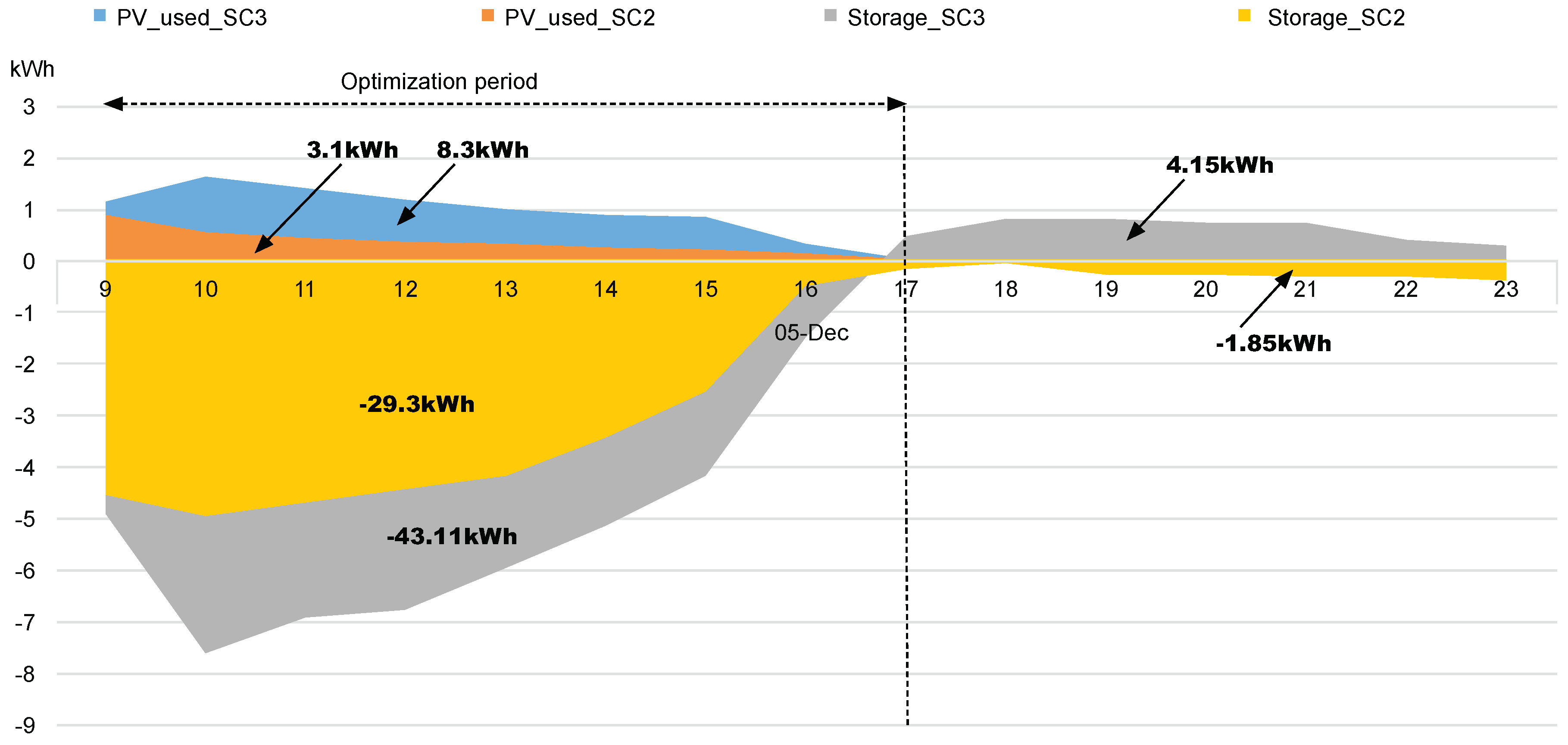
3. Analysis of Results
4. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BMS | Building Management Systems |
| BEM | Building Energy Models |
| HEMS | Home Energy Management Systems |
| HP | Heat Pump |
| HVAC | Heating Ventilation and Air Conditioning |
| MPC | Model Predictive Control |
| NSGA-II | Non dominated sorting genetic algorithm—II |
| PMV | Predicted Mean Vote |
| PV | Photolvoltaic |
| PV-T | Photovoltaic-Thermal Module (PV-T) |
| RES | Renewable Energy Sources |
| ROI | Return Of Investment |
| VRF | Variable Refrigerant Flow |
| SC1 | The model without any renewable energy |
| SC2 | The model with the renewable energy consumption but with a fixed set-point of 20 |
| SC3 | The optimized model with variable set-points |
Appendix A. Summary of Results
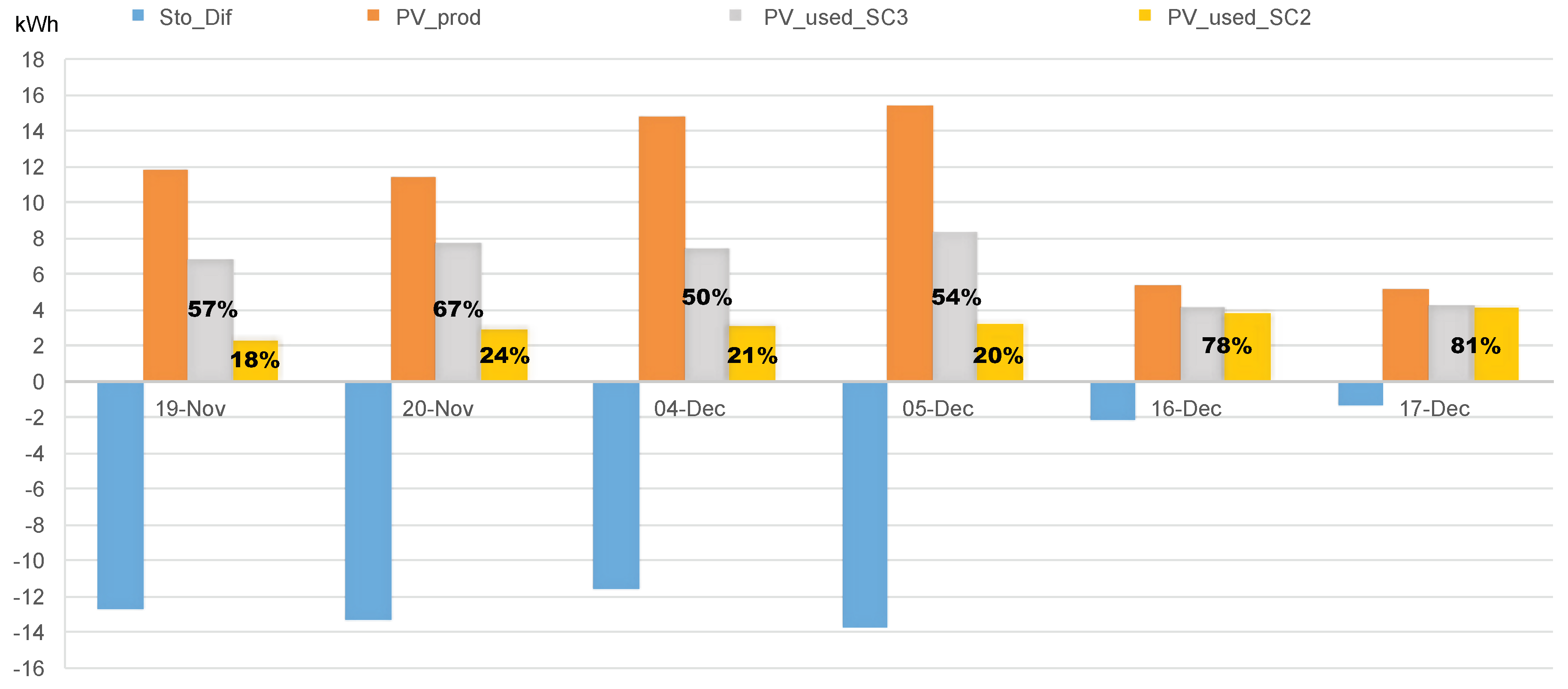
| PV Production () | PV Used () | Storage () | |||||
|---|---|---|---|---|---|---|---|
| Difference | Difference | ||||||
| 19-November | 11.72 | 2.19 (18.69%) | 6.79 (57.94%) | 4.6 (39.25%) | −17 | −29.7 | −12.8 |
| 20-November | 11.73 | 2.8 (23.87%) | 7.71 (65.73%) | 4.9 (41.77%) | −17.6 | 31 | −13.4 |
| 04-December | 14.71 | 3.09 (21.01%) | 7.4 (50.31%) | 4.3 (29.23%) | −29.7 | −41.3 | −11.63 |
| 05-December | 15.33 | 3.11 (20.29%) | 8.28 (54.01%) | 5.17 (33.72%) | −29.4 | −43.1 | −13.8 |
| 16-December | 5.26 | 3.76 (71.48%) | 4.13 (78.52%) | 0.37 (7.03%) | −17.5 | −19.6 | −2.2 |
| 17-December | 5.15 | 4.09 (79.42%) | 4.22 (81.94%) | 0.13 (2.52%) | −18.3 | −19.5 | −1.3 |
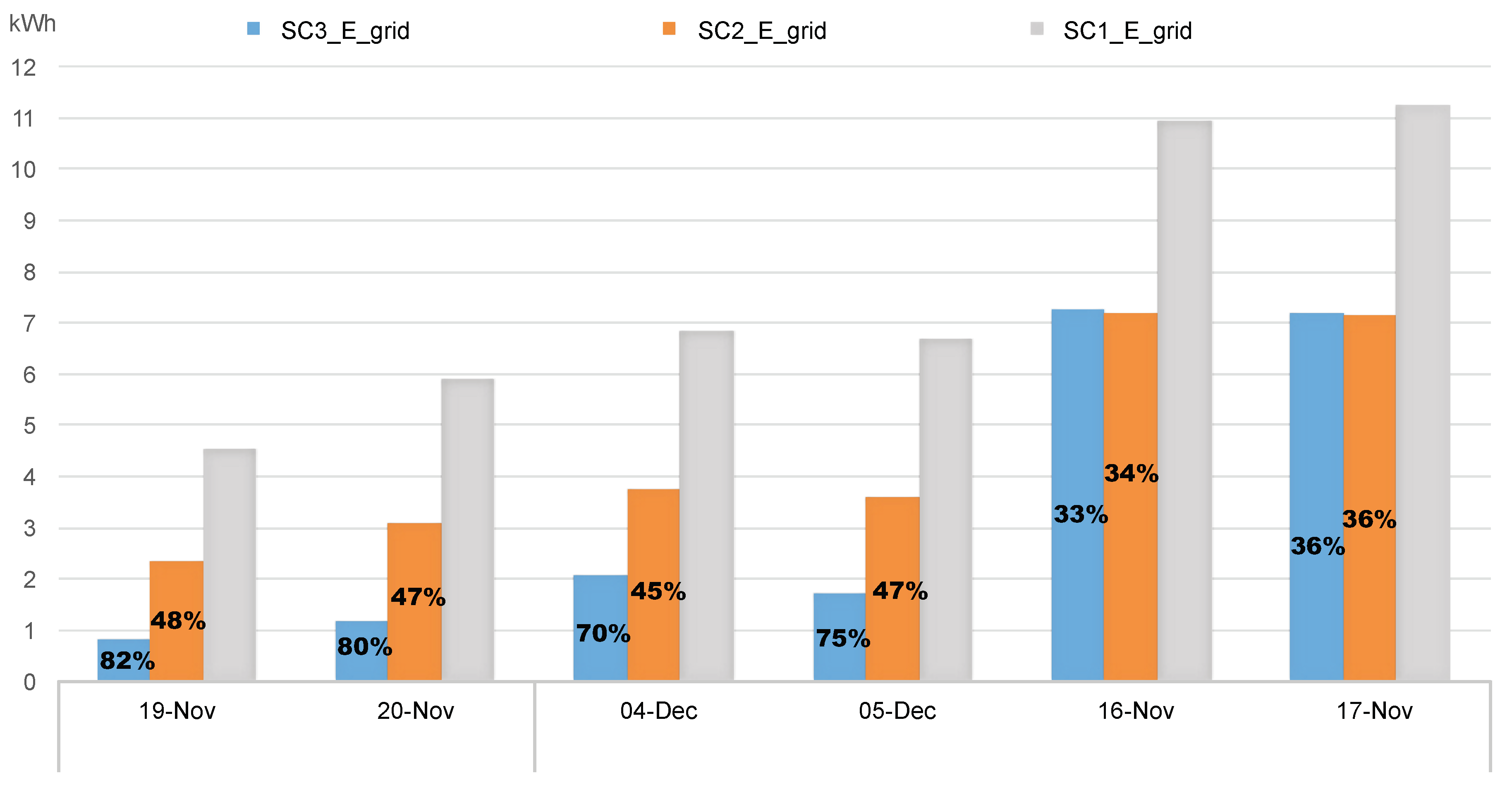
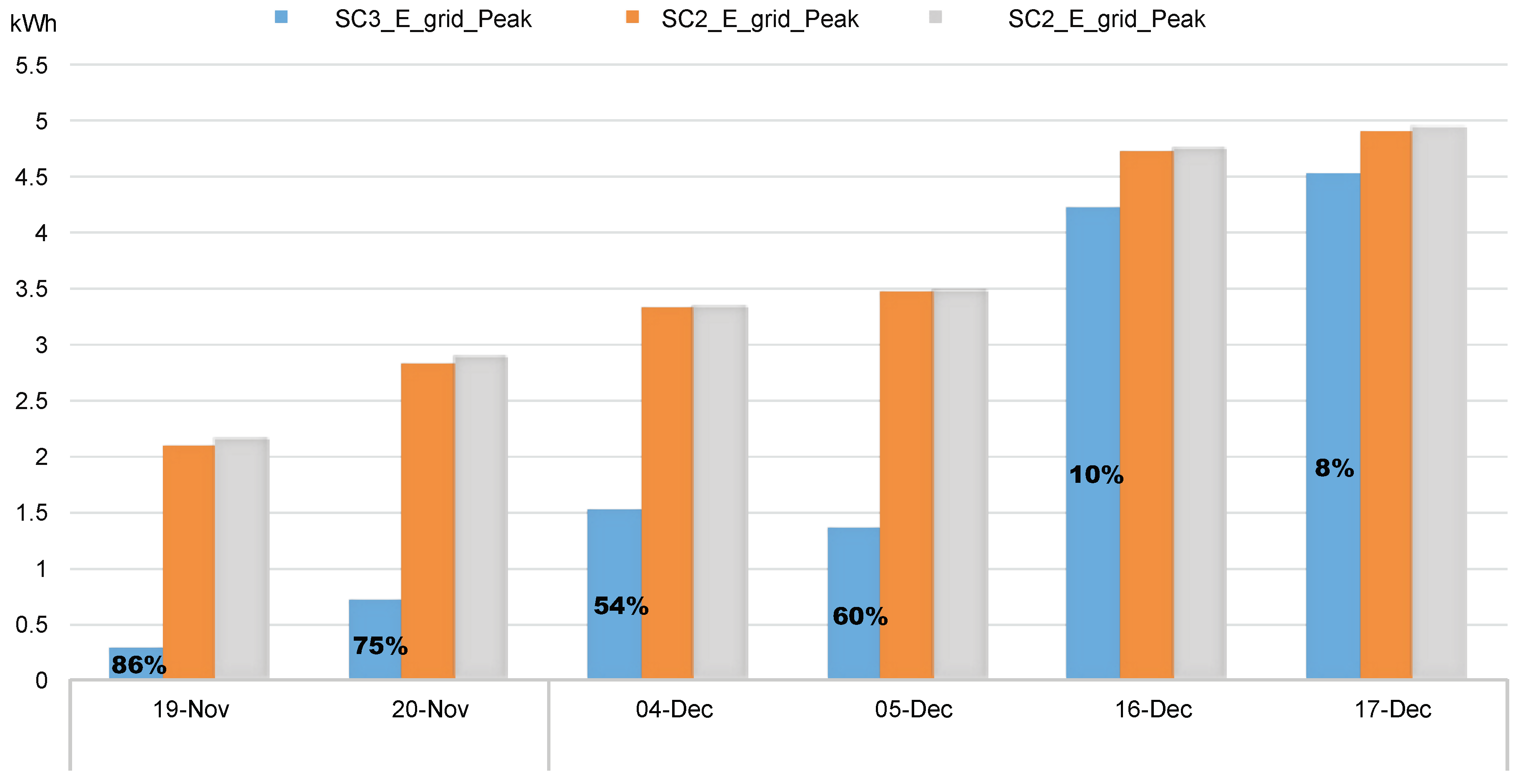
| Energy Grid (kWh)[Total–Peak] | Total Saving (kWh–[%]) | Peak-Saving (kWh–[%]) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Difference | ||||||||||
| 19-November | 4.53 | 2.13 | 2.34 | 2.08 | 0.81 | 0.29 | 2.19 (48.34%) | 3.72 (82.12%) | 1.53 (33.77%) | 1.85 (86.85%) |
| 20-November | 5.86 | 2.88 | 3.06 | 2.83 | 1.15 | 0.7 | 2.8 (47.78%) | 4.71 (80.38%) | 1.91 (32.59%) | 2.18 (75.69%) |
| 04-December | 6.82 | 3.32 | 3.73 | 3.31 | 2.04 | 1.52 | 3.09 (45.31%) | 4.78 (70.09%) | 1.69 (24.78%) | 1.8 (54.22%) |
| 05-December | 6.66 | 3.46 | 3.55 | 3.46 | 1.71 | 1.36 | 3.11 (46.70%) | 4.96 (74.47%) | 1.85 (27.78%) | 2.11 (60.98%) |
| 16-December | 10.92 | 4.74 | 7.16 | 4.72 | 7.25 | 4.22 | 3.76 (34.43%) | 3.66 (33.52%) | 0 (0.00%) | 0.52 (10.97%) |
| 17-December | 11.23 | 4.93 | 7.14 | 4.89 | 7.15 | 4.52 | 4.09 (36.42%) | 4.08 (36.33%) | 0 (0.00%) | 0.4 (8.11%) |
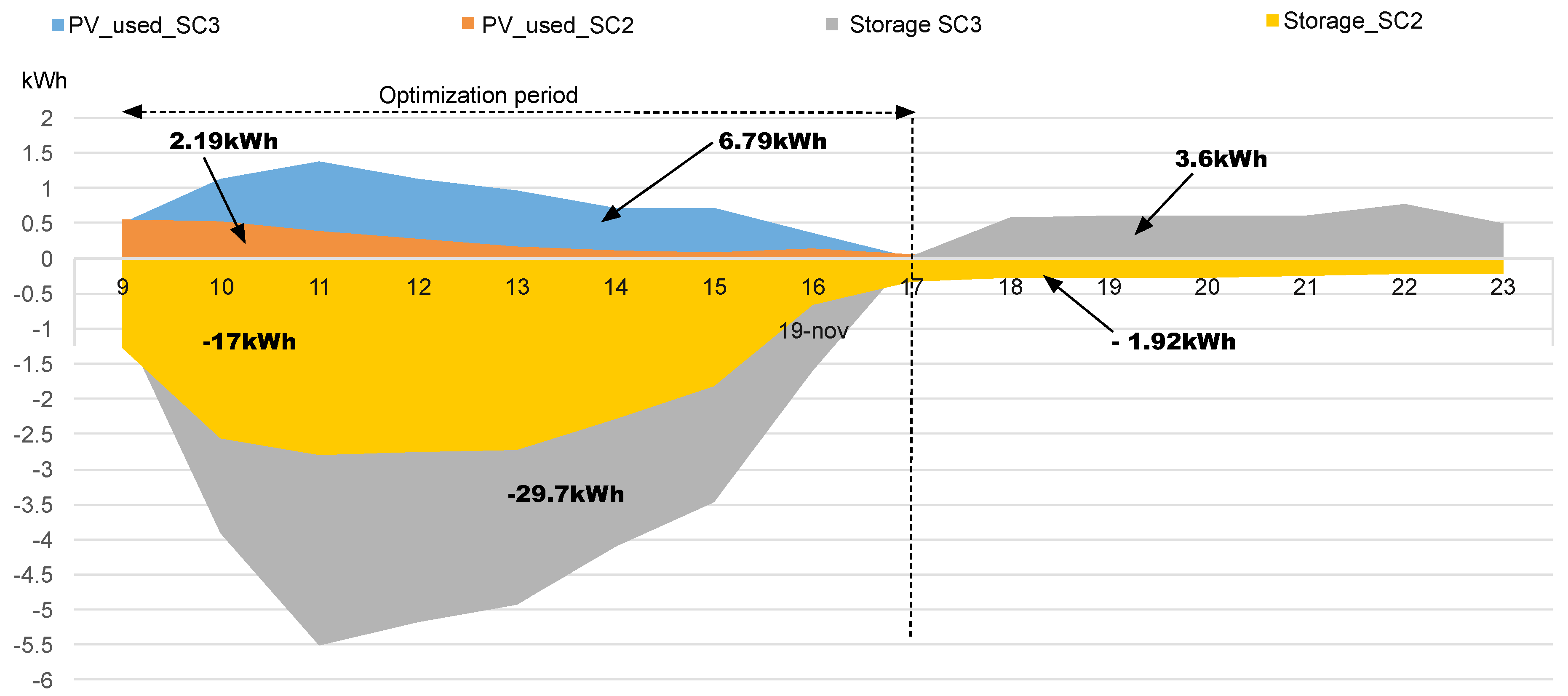

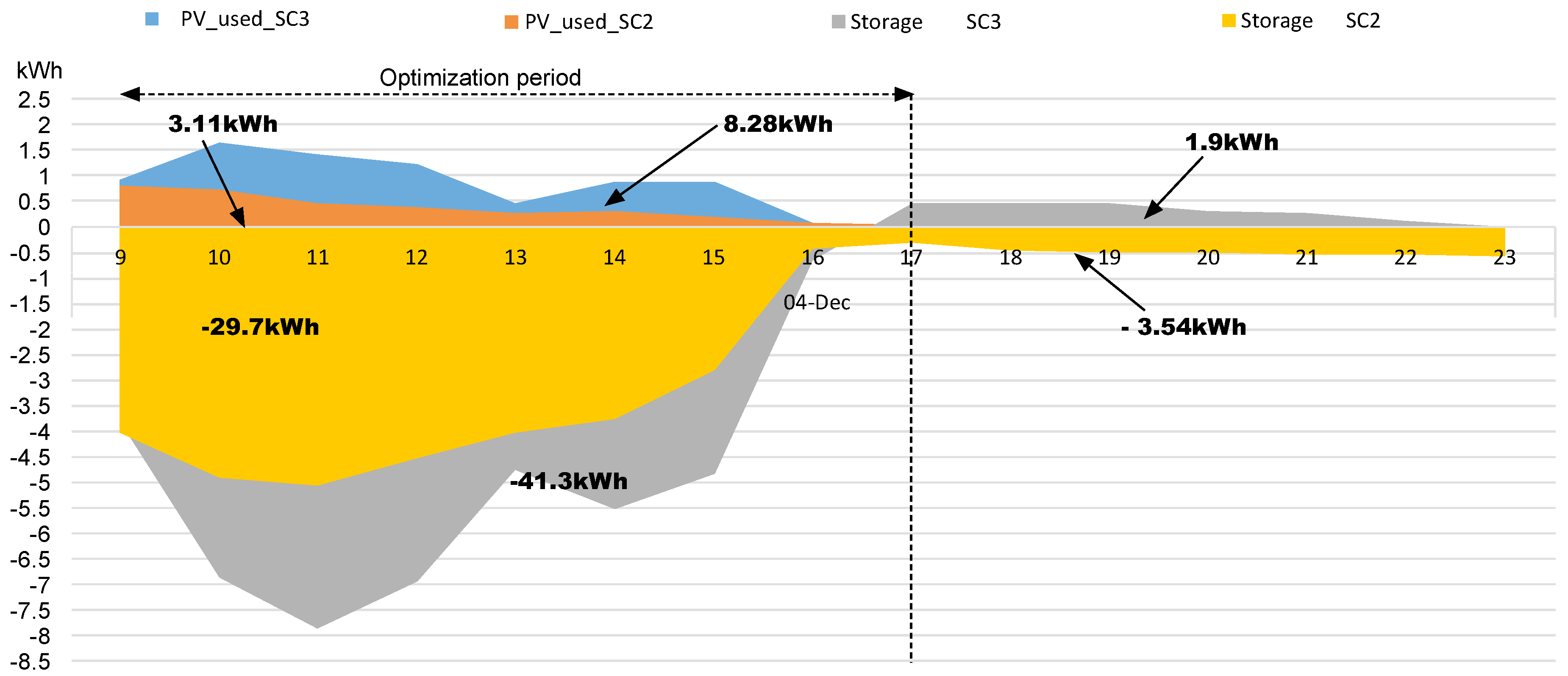
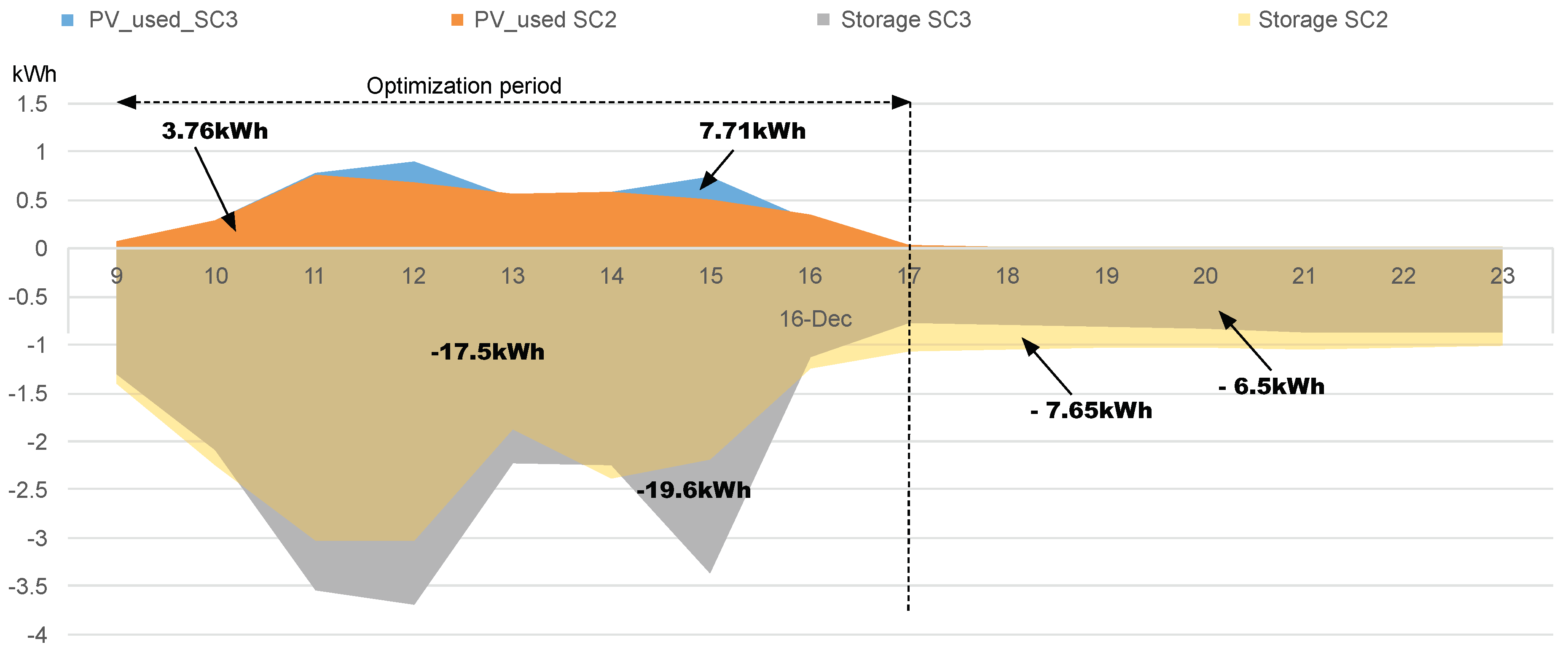
References
- Jäger-Waldau, A. Snapshot of Photovoltaics—February 2019. Energies 2019, 12, 769. [Google Scholar] [CrossRef]
- Rodríguez-Molina, J.; Martínez-Núñez, M.; Martínez, J.F.; Pérez-Aguiar, W. Business models in the smart grid: Challenges, opportunities and proposals for prosumer profitability. Energies 2014, 7, 6142–6171. [Google Scholar] [CrossRef]
- Aguilar, F.; Aledo, S.; Quiles, P. Experimental analysis of an air conditioner powered by photovoltaic energy and supported by the grid. Appl. Therm. Eng. 2017, 123, 486–497. [Google Scholar] [CrossRef]
- Nižetić, S.; Papadopoulos, A.; Tina, G.; Rosa-Clot, M. Hybrid energy scenarios for residential applications based on the heat pump split air-conditioning units for operation in the Mediterranean climate conditions. Energy Build. 2017, 140, 110–120. [Google Scholar] [CrossRef]
- Nizetic, S.; Coko, D.; Marasovic, I. Experimental study on a hybrid energy system with small-and medium-scale applications for mild climates. Energy 2014, 75, 379–389. [Google Scholar] [CrossRef]
- Hedegaard, K.; Mathiesen, B.V.; Lund, H.; Heiselberg, P. Wind power integration using individual heat pumps–Analysis of different heat storage options. Energy 2012, 47, 284–293. [Google Scholar] [CrossRef]
- Kaygusuz, K.; Kaygusuz, O. Theoretical performance of solar heat pump residential heating applications. J. Eng. Res. Appl. Sci. 2019, 8, 1099–1108. [Google Scholar]
- Noris, F.; Musall, E.; Salom, J.; Berggren, B.; Jensen, S.Ø.; Lindberg, K.; Sartori, I. Implications of weighting factors on technology preference in net zero energy buildings. Energy Build. 2014, 82, 250–262. [Google Scholar] [CrossRef]
- Salom, J.; Marszal, A.J.; Widén, J.; Candanedo, J.; Lindberg, K.B. Analysis of load match and grid interaction indicators in net zero energy buildings with simulated and monitored data. Appl. Energy 2014, 136, 119–131. [Google Scholar] [CrossRef]
- Jensen, S.Ø.; Marszal-Pomianowska, A.; Lollini, R.; Pasut, W.; Knotzer, A.; Engelmann, P.; Stafford, A.; Reynders, G. IEA EBC annex 67 energy flexible buildings. Energy Build. 2017, 155, 25–34. [Google Scholar] [CrossRef]
- Péan, T.; Ortiz, J.; Salom, J. Impact of demand-side management on thermal comfort and energy costs in a residential nZEB. Buildings 2017, 7, 37. [Google Scholar] [CrossRef]
- Henze, G.; Brandemuehl, M.; Felsmann, C.; Florita, A.; Cheng, H. Evaluation of Building Thermal Mass Savings; ASHRAE Research Project RP-1313; ASHRAE: North Atlanta, GA, USA, 2007. [Google Scholar]
- Zhai, X.; Qu, M.; Li, Y.; Wang, R. A review for research and new design options of solar absorption cooling systems. Renew. Sustain. Energy Rev. 2011, 15, 4416–4423. [Google Scholar] [CrossRef]
- Kim, D.; Ferreira, C.I. Solar refrigeration options–a state-of-the-art review. Int. J. Refrig. 2008, 31, 3–15. [Google Scholar] [CrossRef]
- Li, Z.; Sumathy, K. Technology development in the solar absorption air-conditioning systems. Renew. Sustain. Energy Rev. 2000, 4, 267–293. [Google Scholar] [CrossRef]
- Zondag, H. Flat-plate PV-Thermal collectors and systems: A review. Renew. Sustain. Energy Rev. 2008, 12, 891–959. [Google Scholar] [CrossRef]
- Fu, H.; Pei, G.; Ji, J.; Long, H.; Zhang, T.; Chow, T.T. Experimental study of a photovoltaic solar-assisted heat-pump/heat-pipe system. Appl. Therm. Eng. 2012, 40, 343–350. [Google Scholar] [CrossRef]
- Chen, H.; Riffat, S.B. Investigation of a hybrid solar heat pump system. Procedia Eng. 2011, 21, 311–318. [Google Scholar] [CrossRef]
- Lasseter, R.H.; Piagi, P. Microgrid: A conceptual solution. In Proceedings of the IEEE Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; Volume 6, pp. 4285–4291. [Google Scholar]
- Lasseter, R.H. Microgrids. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting, Conference Proceedings (Cat. No. 02CH37309), New York, NY, USA, 27–31 January 2002; Volume 1, pp. 305–308. [Google Scholar]
- Mariam, L.; Basu, M.; Conlon, M.F. A review of existing microgrid architectures. J. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Infield, D.; Li, F. Integrating micro-generation into distribution systems—A review of recent research. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–4. [Google Scholar]
- Saviuc, I.; Peremans, H.; Van Passel, S.; Milis, K. Economic Performance of Using Batteries in European Residential Microgrids under the Net-Metering Scheme. Energies 2019, 12, 165. [Google Scholar] [CrossRef]
- Koch, S.; Mathieu, J.L.; Callaway, D.S. Modeling and control of aggregated heterogeneous thermostatically controlled loads for ancillary services. In Proceedings of the PSCC, Stockholm, Sweden, 22–26 August 2011; pp. 1–7. [Google Scholar]
- McKenna, E.; Pless, J.; Darby, S.J. Solar photovoltaic self-consumption in the UK residential sector: New estimates from a smart grid demonstration project. Energy Policy 2018, 118, 482–491. [Google Scholar] [CrossRef]
- European Parliament. DIRECTIVE (EU) 2018/2001 of the European Parliament and of the Council of 11 December 2018 on the Promotion of the Use of Energy from Renewable Sources (Recast). 2018. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex:32018L2001 (accessed on 11 January 2020).
- Ministerio para la Transición Ecológica. Real Decreto 244/2019, de 5 de abril, por el que se regulan las condiciones administrativas, técnicas y económicas del autoconsumo de energía eléctrica; Boletín Oficial del Estado (BOE): Madrid, Spain, 2019; pp. 68–71.
- SABINA. SmArt BI-Directional Multi eNergy gAteway. 2016. Available online: http://sabina-project.eu (accessed on 1 November 2019).
- Péan, T.Q.; Salom, J.; Costa-Castello, R. Review of control strategies for improving the energy flexibility provided by heat pump systems in buildings. J. Process. Control. 2019, 74, 35–49. [Google Scholar] [CrossRef]
- Baeten, B.; Rogiers, F.; Helsen, L. Reduction of heat pump induced peak electricity use and required generation capacity through thermal energy storage and demand response. Appl. Energy 2017, 195, 184–195. [Google Scholar] [CrossRef]
- Pavlak, G.S.; Henze, G.P.; Cushing, V.J. Evaluating synergistic effect of optimally controlling commercial building thermal mass portfolios. Energy 2015, 84, 161–176. [Google Scholar] [CrossRef]
- Guglielmetti, R.; Macumber, D.; Long, N. OpenStudio: An Open Source Integrated Analysis Platform; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2011.
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Buhl, W.F.; Huang, Y.J.; Pedersen, C.O.; Strand, R.K.; Liesen, R.J.; Fisher, D.E.; Witte, M.J.; et al. EnergyPlus: creating a new-generation building energy simulation program. Energy Build. 2001, 33, 319–331. [Google Scholar] [CrossRef]
- Pombeiro, H.; Machado, M.J.; Silva, C. Dynamic programming and genetic algorithms to control an HVAC system: Maximizing thermal comfort and minimizing cost with PV production and storage. Sustain. Cities Soc. 2017, 34, 228–238. [Google Scholar] [CrossRef]
- Corbin, C.D.; Henze, G.P.; May-Ostendorp, P. A model predictive control optimization environment for real-time commercial building application. J. Build. Perform. Simul. 2013, 6, 159–174. [Google Scholar] [CrossRef]
- Ruiz, G.R.; Bandera, C.F.; Temes, T.G.A.; Gutierrez, A.S.O. Genetic algorithm for building envelope calibration. Appl. Energy 2016, 168, 691–705. [Google Scholar] [CrossRef]
- Ruiz, G.R.; Bandera, C.F. Analysis of uncertainty indices used for building envelope calibration. Appl. Energy 2017, 185, 82–94. [Google Scholar] [CrossRef]
- Ruiz, G.; Bandera, C. Validation of calibrated energy models: common errors. Energies 2017, 10, 1587. [Google Scholar] [CrossRef]
- Fernández Bandera, C.; Ramos Ruiz, G. Towards a new generation of building envelope calibration. Energies 2017, 10, 2102. [Google Scholar] [CrossRef]
- González, V.G.; Colmenares, L.Á.; Fidalgo, J.F.L.; Ruiz, G.R.; Bandera, C.F. Uncertainy’s Indices Assessment for Calibrated Energy Models. Energies 2019, 12, 2096. [Google Scholar] [CrossRef]
- Handbook, A.F. American Society of Heating, Refrigerating and Air-Conditioning Engineers; ASHARE Inc.: Atlanta, GA, USA, 2017. [Google Scholar]
- de la Edificación, C.T. Documento Básico he Ahorro de energía; CTE DB-HE; Ministerio de Fomento: Madrid, Spain, 2013.
- U.S. Department of Energy. Energyplus Engineering Reference: The Reference to EnergyPlus Calculations; U.S. Department of Energy: Washington, DC, USA, 2010.
- Ineichen, P.; Perez, R.; Seal, R.; Maxwell, E.; Zalenka, A. Dynamic global-to-direct irradiance conversion models. Ashrae Trans. 1992, 98, 354–369. [Google Scholar]
- Ramos Ruiz, G.; Lucas Segarra, E.; Fernández Bandera, C. Model Predictive Control Optimization via Genetic Algorithm Using a Detailed Building Energy Model. Energies 2019, 12, 34. [Google Scholar] [CrossRef]
- Zhang, Y.; Korolija, I. Performing complex parametric simulations with jEPlus. In Proceedings of the SET2010-9th International Conference on Sustainable Energy Technologies, Shanghai, China, 24–27 August 2010; pp. 24–27. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Theory and applications of HVAC control systems–A review of model predictive control (MPC). Build. Environ. 2014, 72, 343–355. [Google Scholar] [CrossRef]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers. ASHRAE Standard: Thermal Environmental Conditions for Human Occupancy; ASHRAE: Atlanta, GA, USA, 2010. [Google Scholar]
- Fanger, P.O. Thermal Comfort. Analysis and Applications in Environmental Engineering; Danish Technical Press: Copenhagen, Denmark, 1970. [Google Scholar]
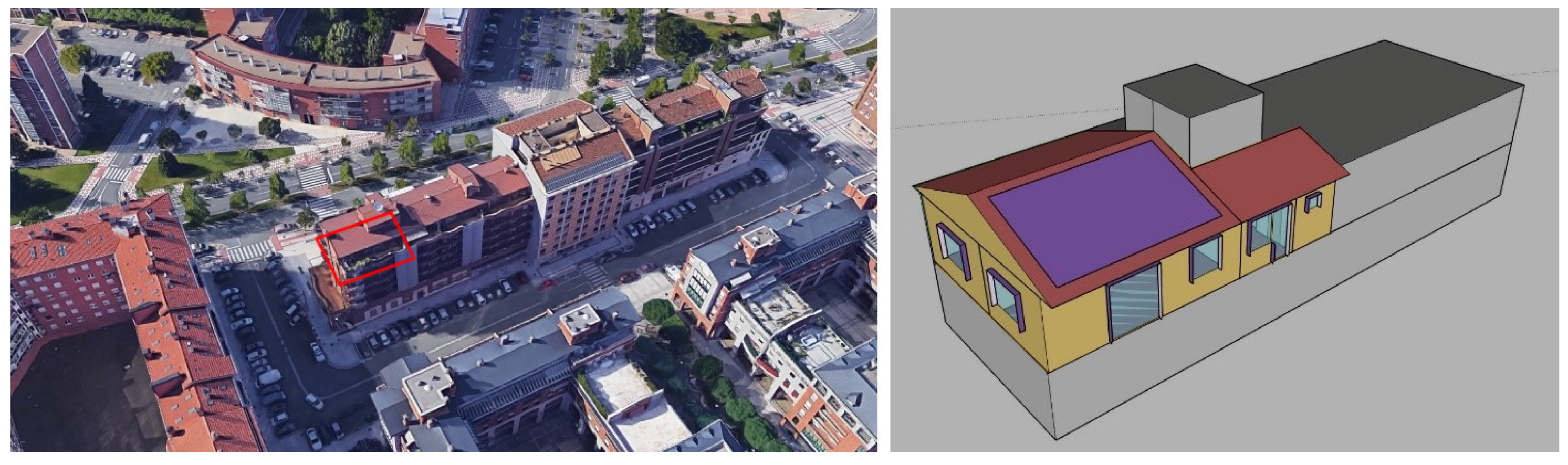
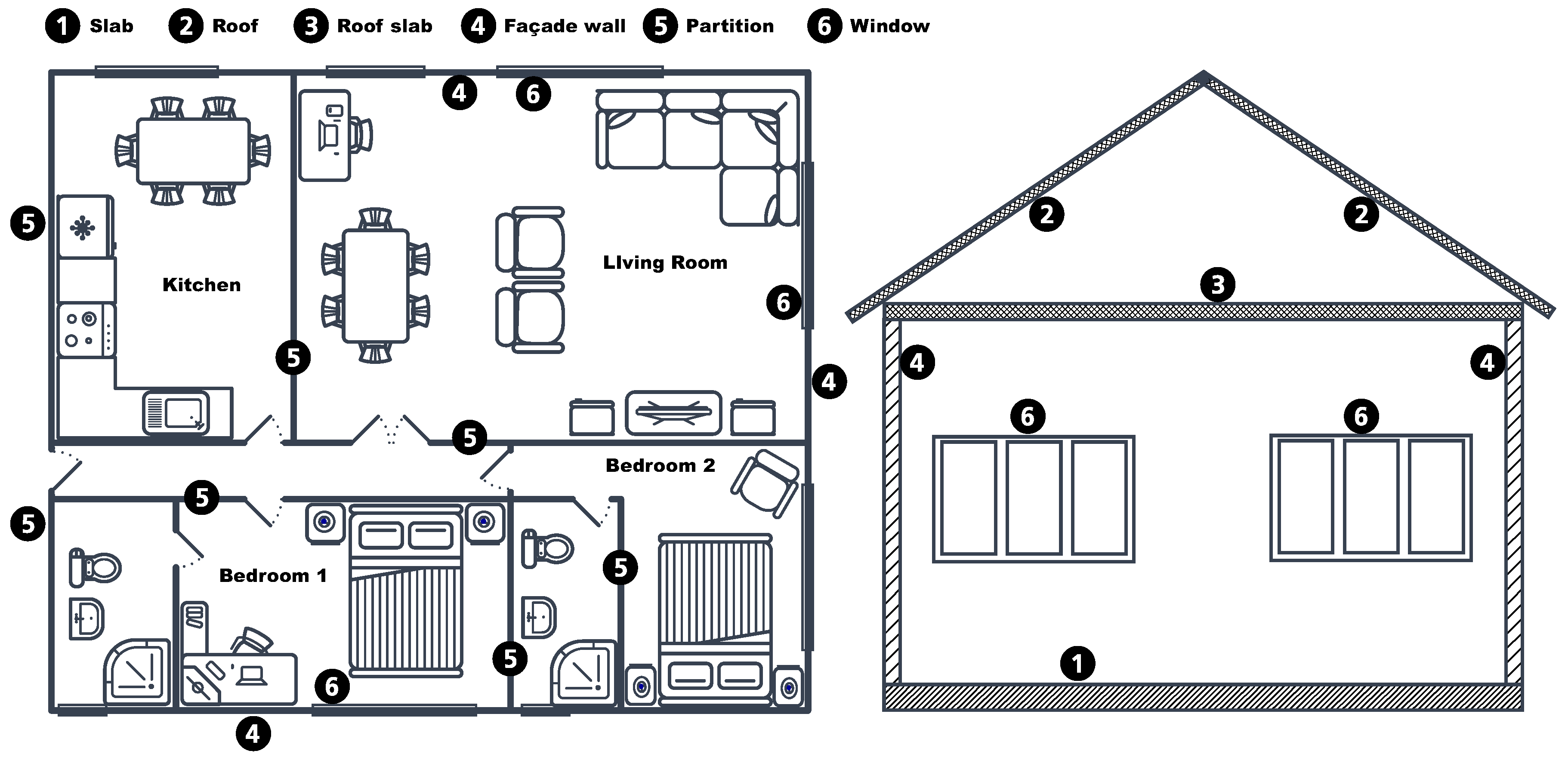

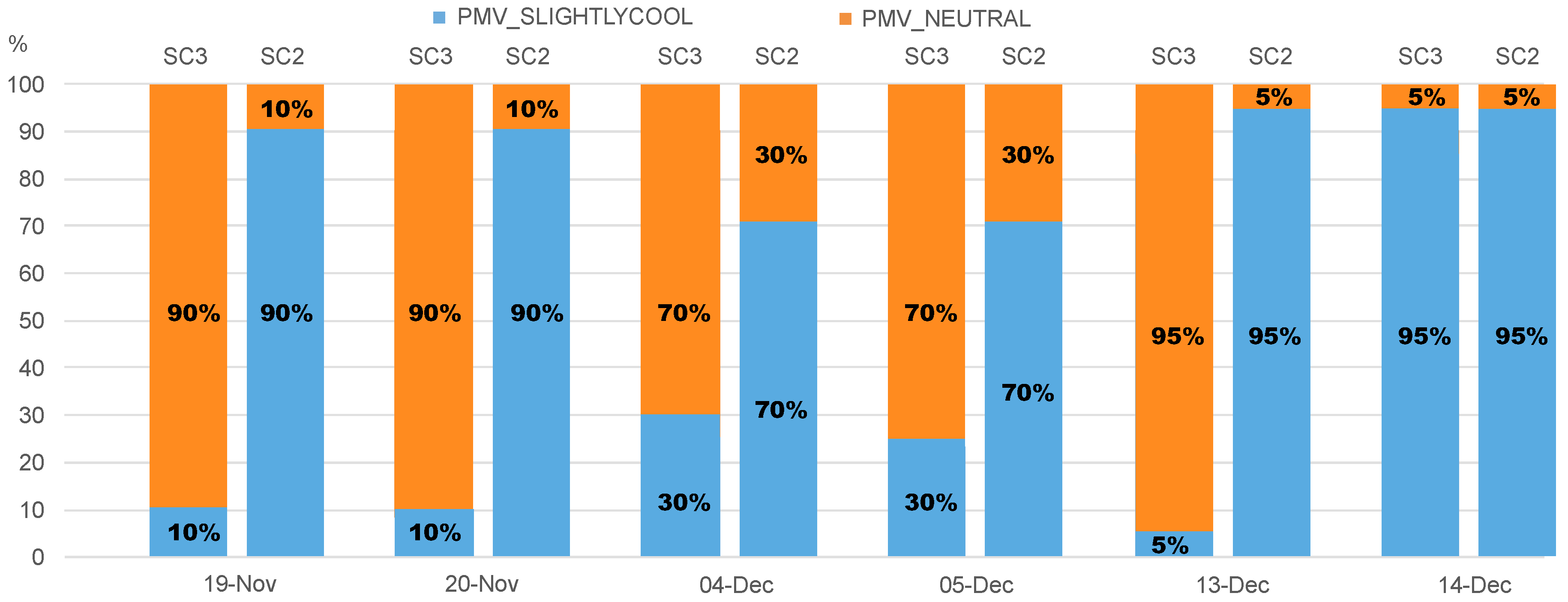
| Baseline Case Model | e m | c | ||
|---|---|---|---|---|
| Facade wall (out-in) | ||||
| Perforated brick | 0.12 | 0.53 | 900 | 1000 |
| Expanded polystyrene | 0.05 | 0.037 | 30 | 1000 |
| Hollow brick | 0.075 | 0.047 | 930 | 1000 |
| Plaster | 0.02 | 0.4 | 850 | 1000 |
| Roof (out-in) | ||||
| Ceramic tiles | 0.02 | 1 | 2000 | 800 |
| Cement mortar | 0.02 | 0.55 | 1125 | 1000 |
| Hollow brick | 0.05 | 0.28 | 670 | 1000 |
| Roof Slab (out-in) | ||||
| Expanded polystyrene | 0.05 | 0.037 | 30 | 1000 |
| Waffle slab | 0.25 | 1.67 | 1277 | 1000 |
| Plaster | 0.02 | 0.4 | 850 | 1000 |
| Slab (out-in) | ||||
| Plaster | 0.02 | 0.4 | 850 | 1000 |
| Waffle slab | 0.25 | 1.67 | 1277 | 1000 |
| Expanded polystyrene | 0.05 | 0.037 | 30 | 1000 |
| Stoneware tiles | 0.02 | 1.9 | 2350 | 1000 |
| Partition | ||||
| Plaster | 0.02 | 0.4 | 850 | 1000 |
| Hollow brick | 0.075 | 0.47 | 930 | 1000 |
| Plaster | 0.02 | 0.4 | 850 | 1000 |
| VRF Heat Pump | Unit | Min. | Nom. | Max. |
|---|---|---|---|---|
| Heating capacity | W | 600 | 4800 | 6000 |
| Heating power supply | W | 200 | 1600 | 2000 |
| SCOP | - | - | 2.9 | - |
| Type | Period | kWp | kWh |
|---|---|---|---|
| Yearly | 2017 | 4 | 6077.3 |
| Monthly | November 2017 | 2.7 | 249.7 |
| December 2017 | 3 | 236.8 | |
| Daily | 19 November | 2.1 | 11.7 |
| 20 November | 2.01 | 11.7 | |
| 4 December | 2.5 | 14.7 | |
| 5 December | 2.6 | 15.32 | |
| 16 December | 1.2 | 5.2 | |
| 17 December | 1.0 | 5.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández Bandera, C.; Pachano, J.; Salom, J.; Peppas, A.; Ramos Ruiz, G. Photovoltaic Plant Optimization to Leverage Electric Self Consumption by Harnessing Building Thermal Mass. Sustainability 2020, 12, 553. https://doi.org/10.3390/su12020553
Fernández Bandera C, Pachano J, Salom J, Peppas A, Ramos Ruiz G. Photovoltaic Plant Optimization to Leverage Electric Self Consumption by Harnessing Building Thermal Mass. Sustainability. 2020; 12(2):553. https://doi.org/10.3390/su12020553
Chicago/Turabian StyleFernández Bandera, Carlos, Jose Pachano, Jaume Salom, Antonis Peppas, and Germán Ramos Ruiz. 2020. "Photovoltaic Plant Optimization to Leverage Electric Self Consumption by Harnessing Building Thermal Mass" Sustainability 12, no. 2: 553. https://doi.org/10.3390/su12020553
APA StyleFernández Bandera, C., Pachano, J., Salom, J., Peppas, A., & Ramos Ruiz, G. (2020). Photovoltaic Plant Optimization to Leverage Electric Self Consumption by Harnessing Building Thermal Mass. Sustainability, 12(2), 553. https://doi.org/10.3390/su12020553







