Fuel Cell Characteristic Curve Approximation Using the Bézier Curve Technique
Abstract
1. Introduction
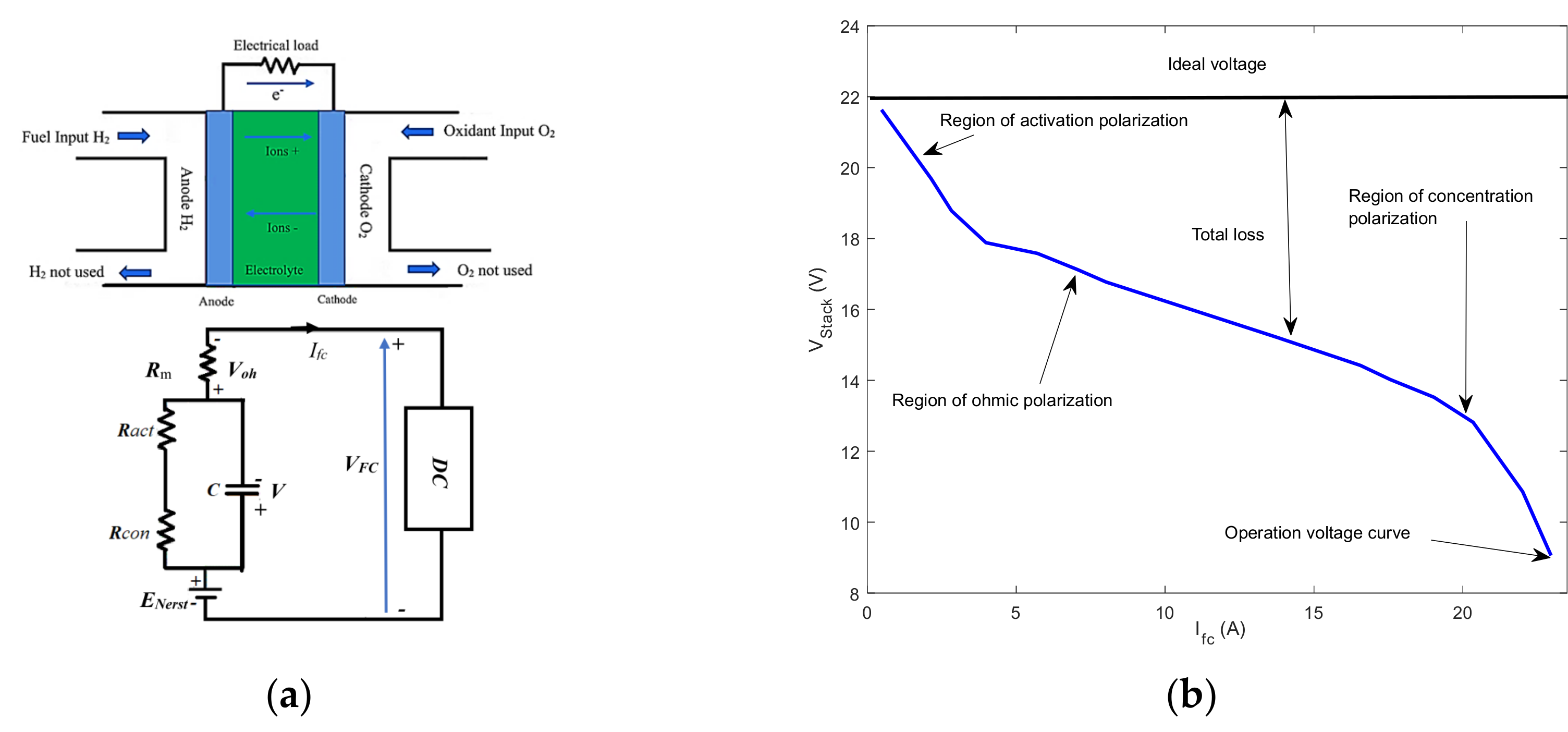
2. Fuel Cell Model
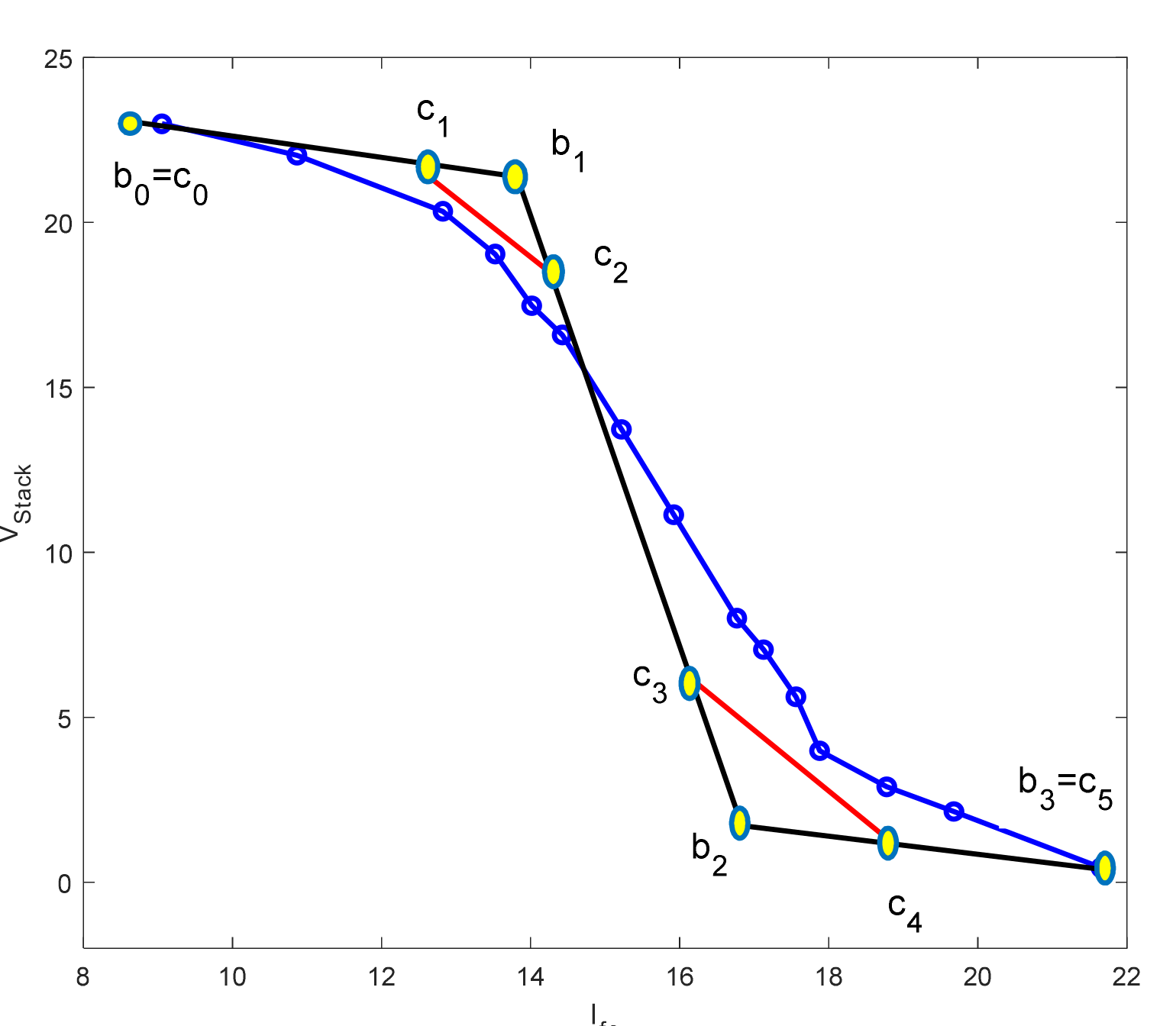
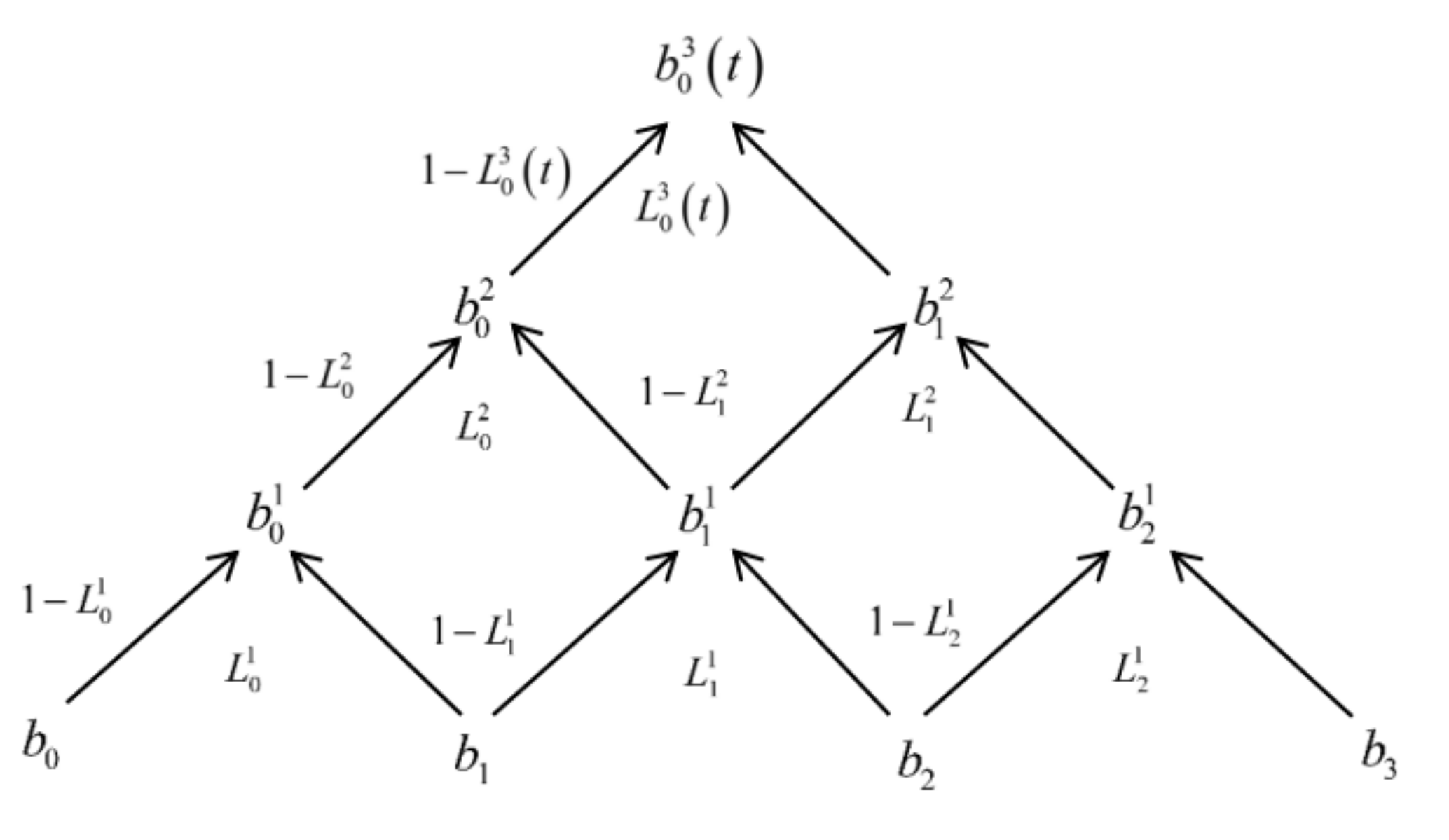
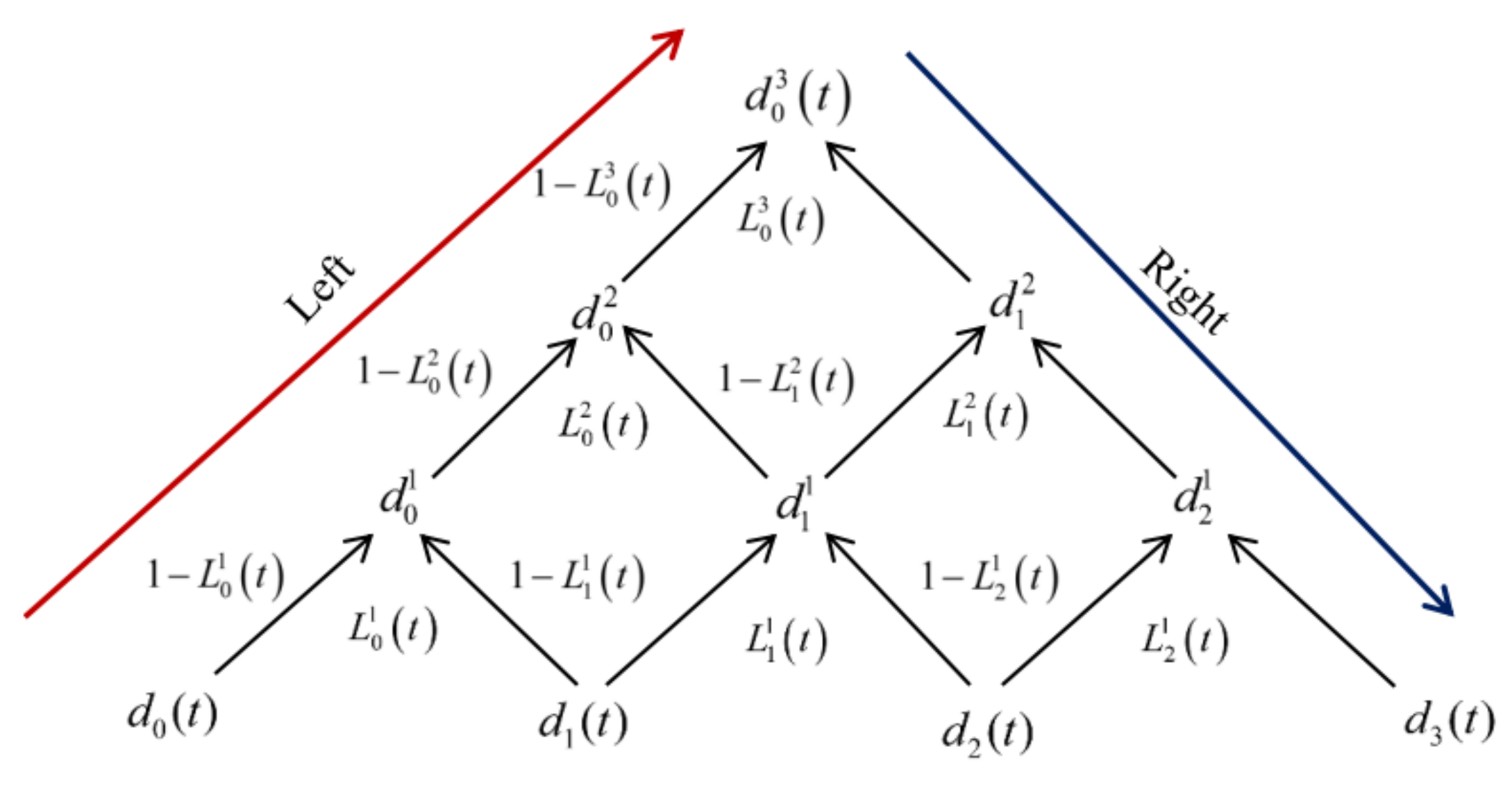
3. Bézier Curve Method
4. Proposed Method Evaluation Criteria
5. Results, Discussions, and Comparisons
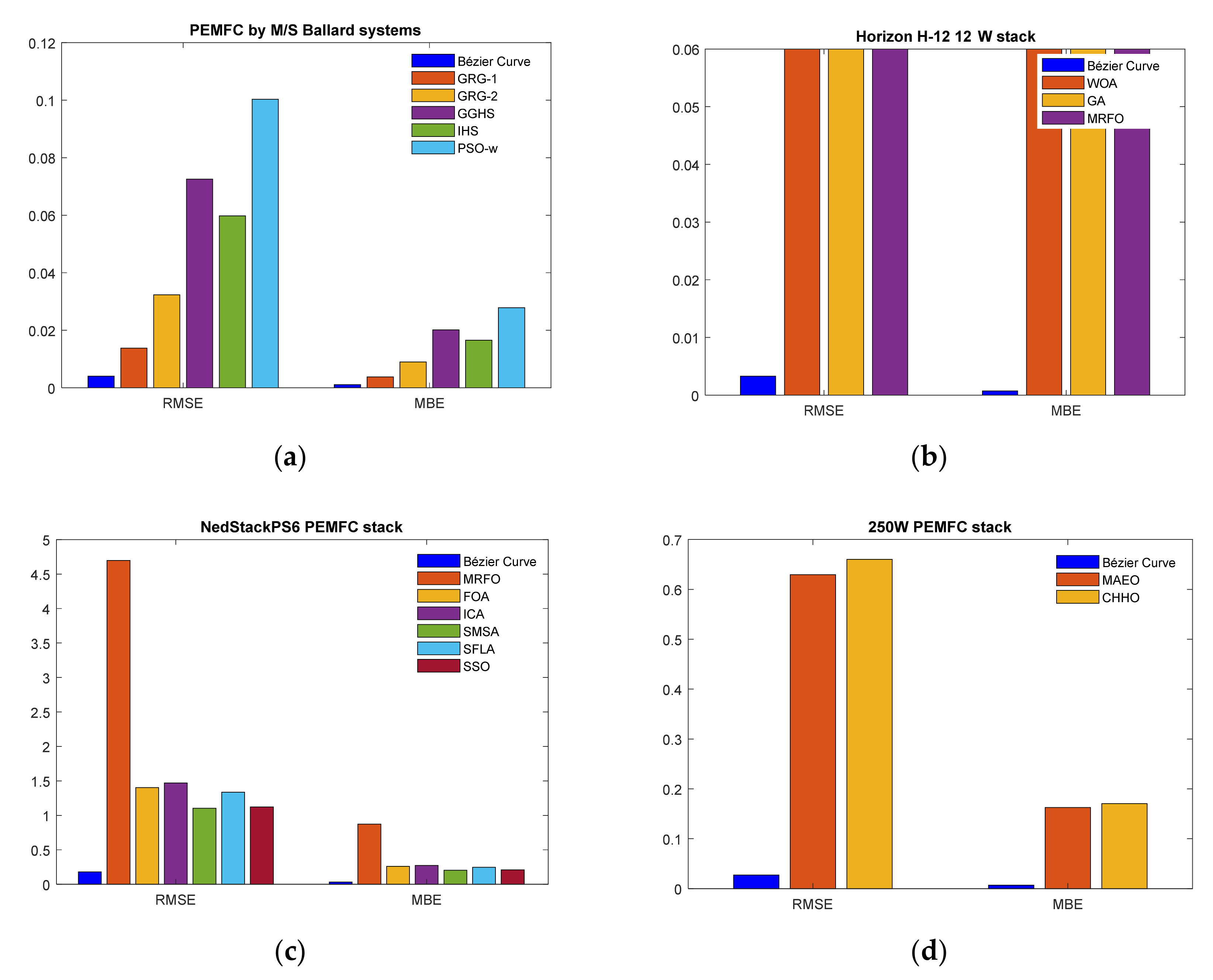
5.1. Case Study 1: Single Cell-Based PEMFC by M/S Ballard Systems
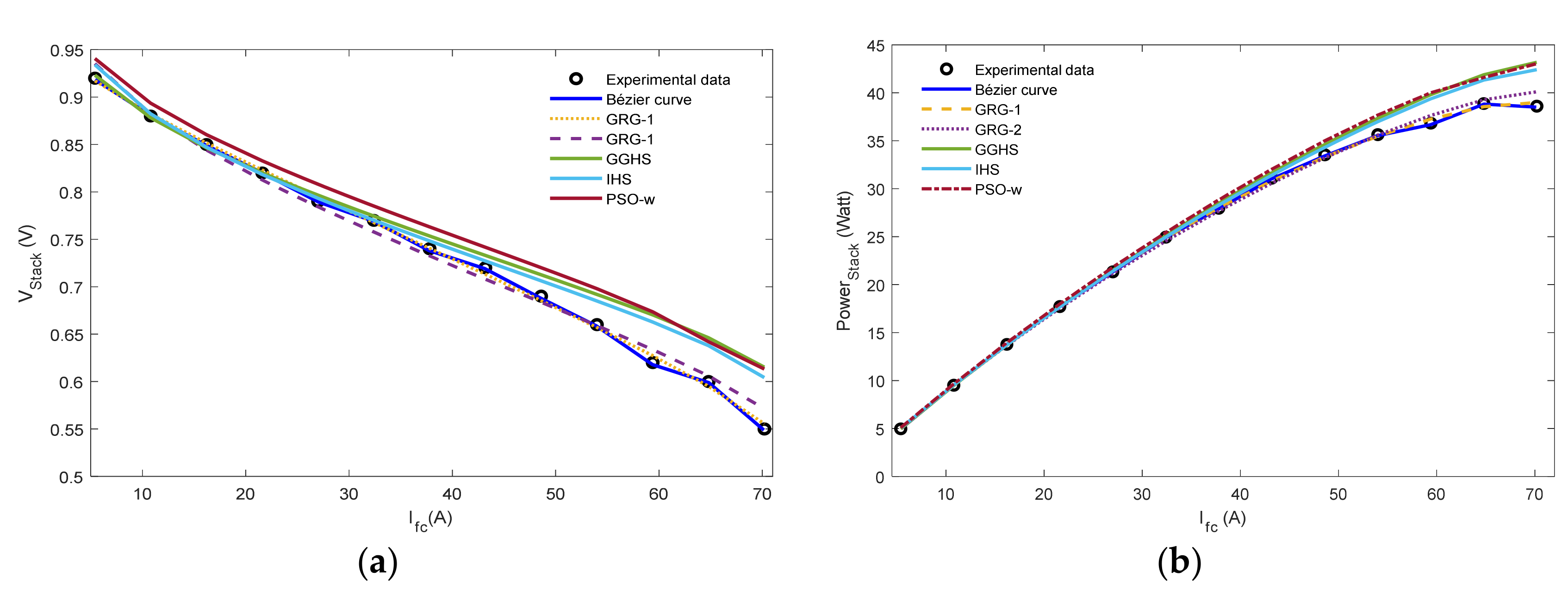
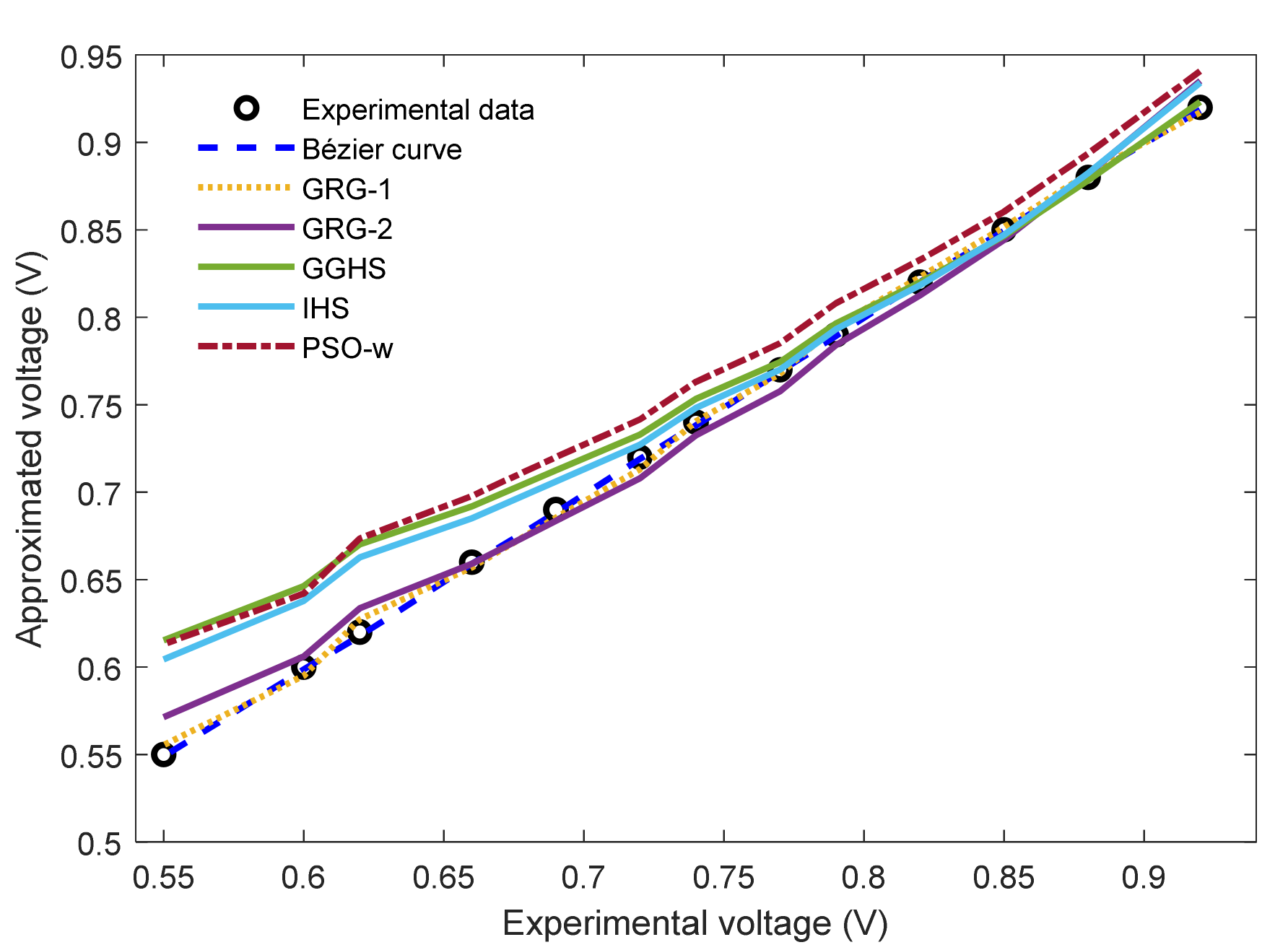
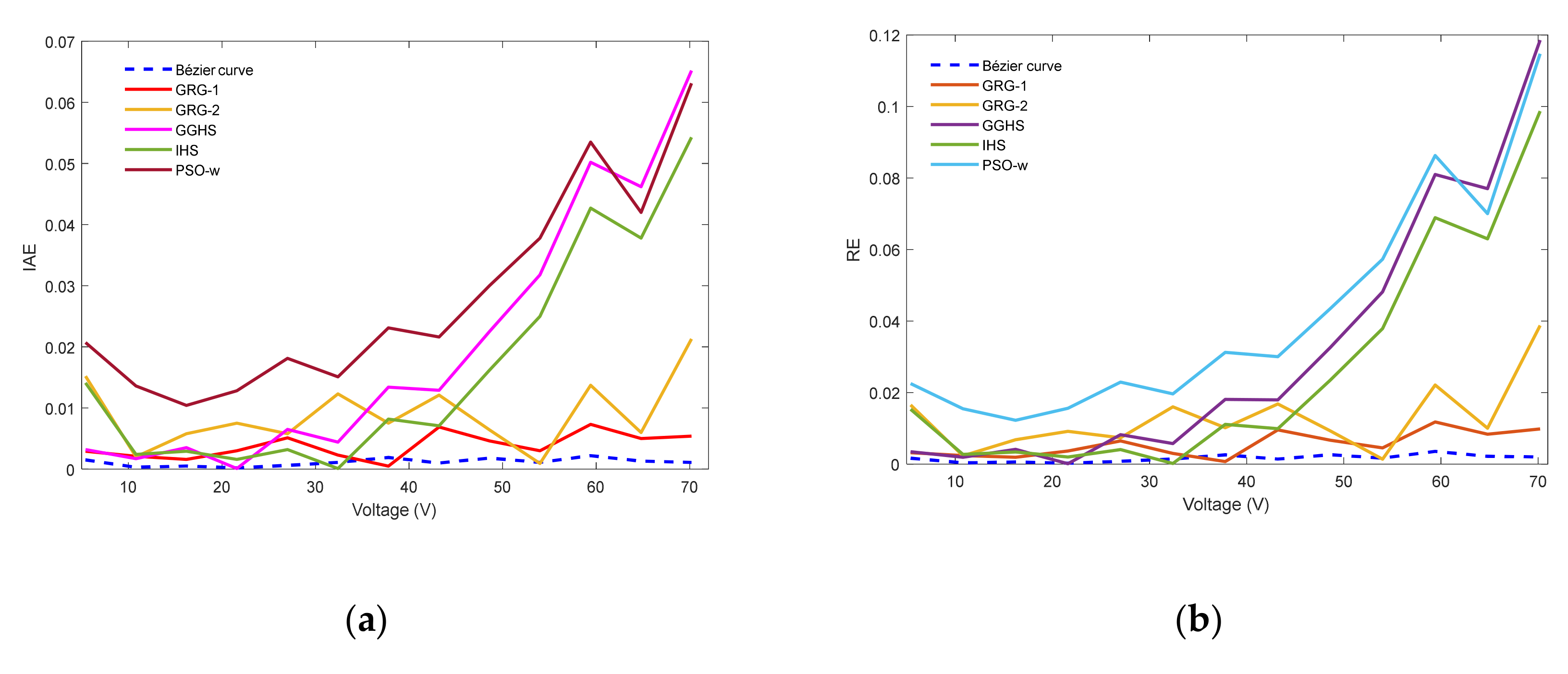
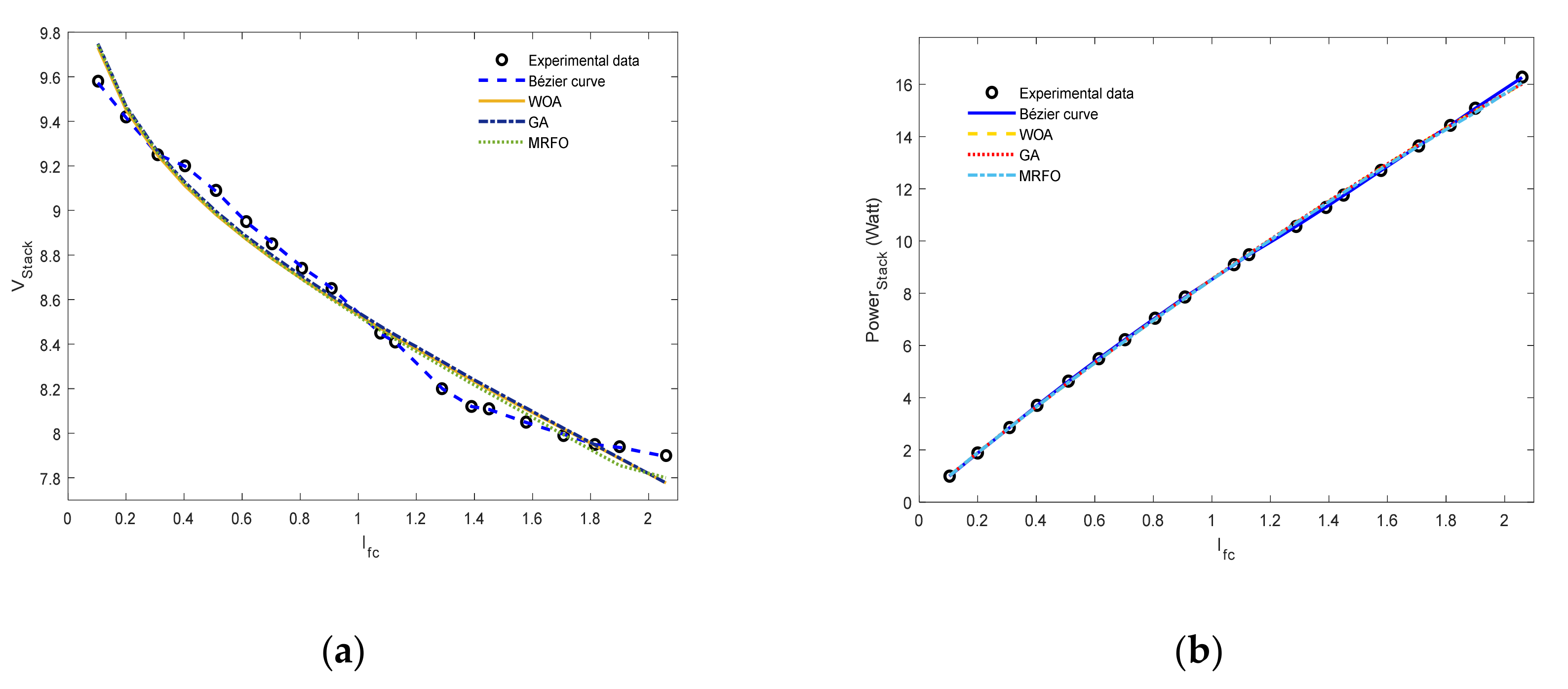
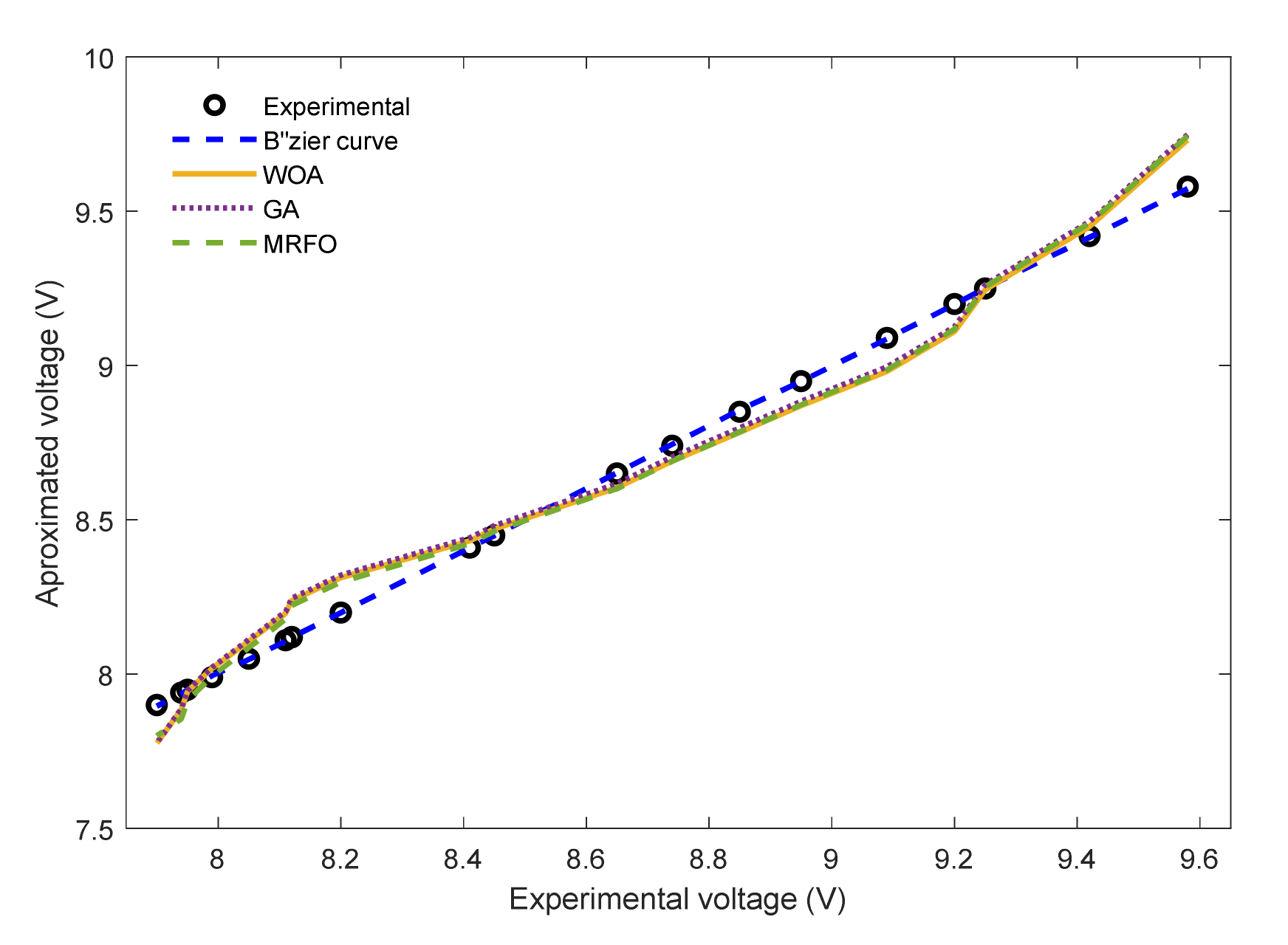
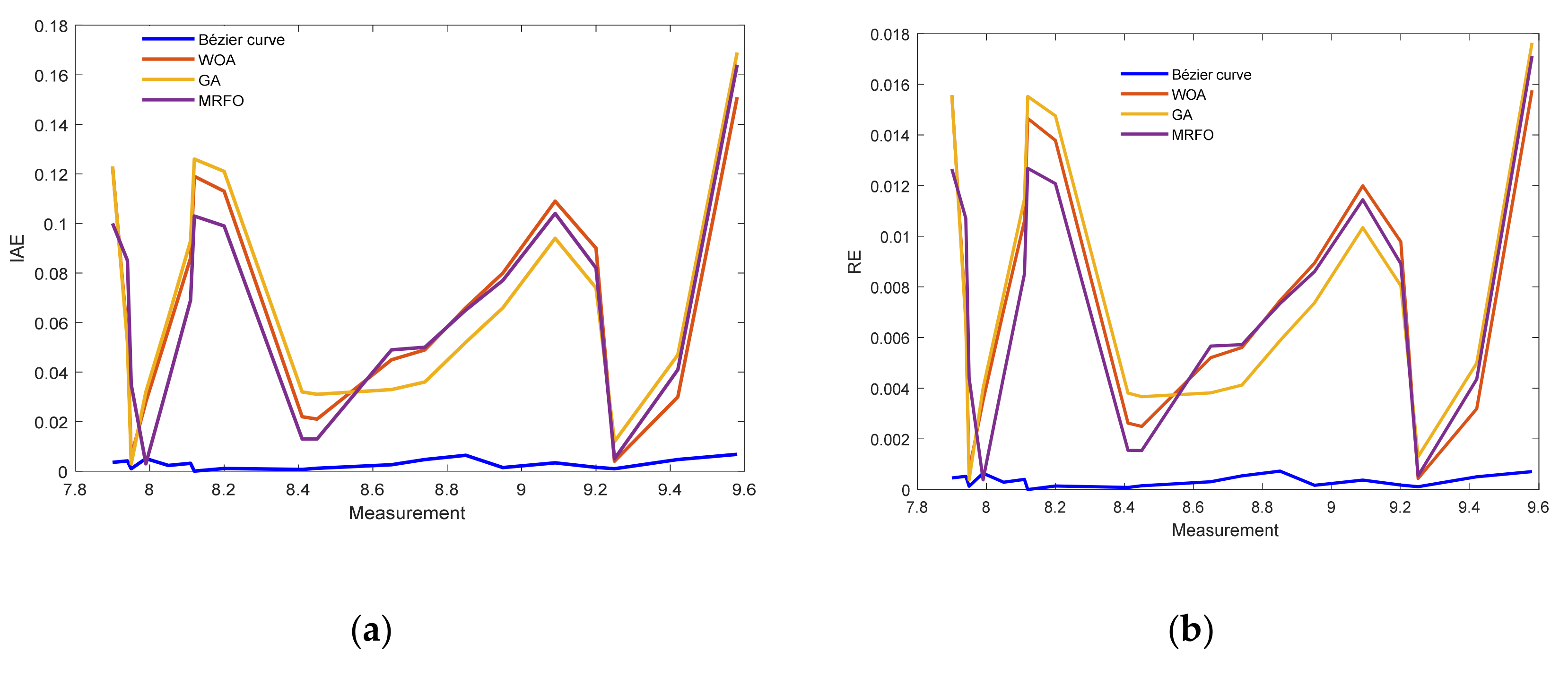
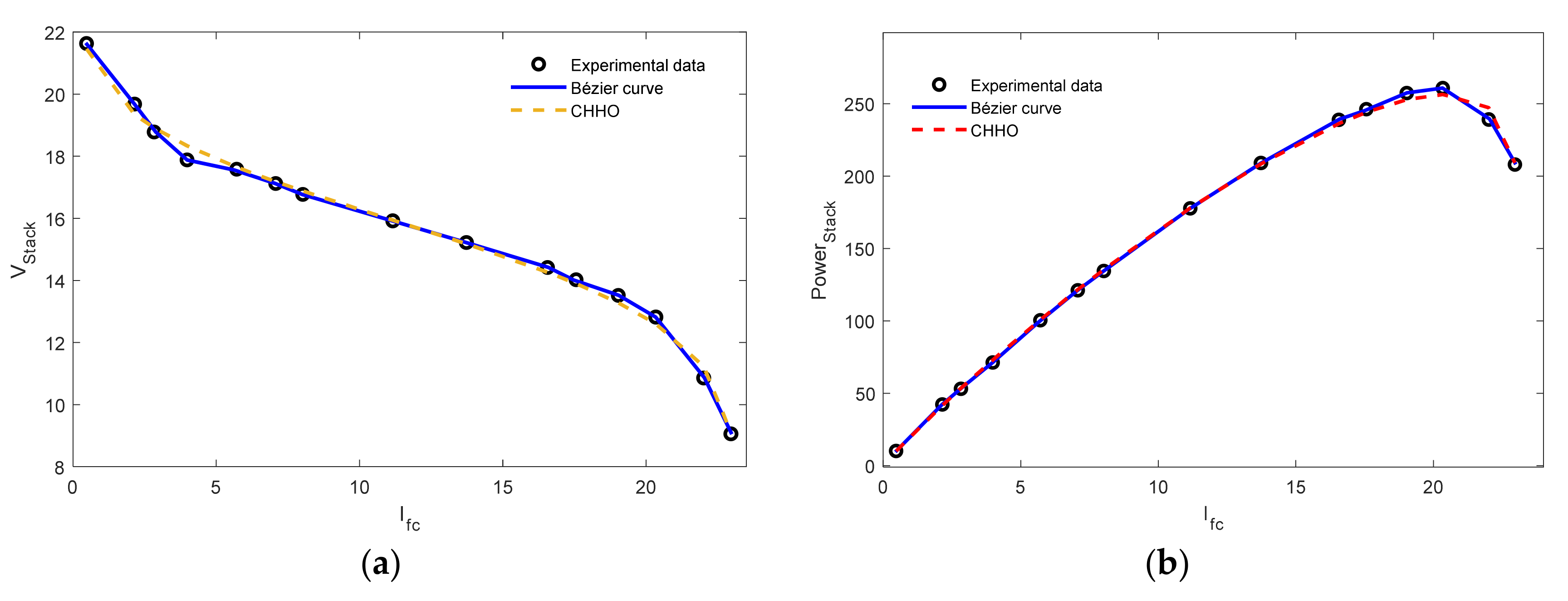
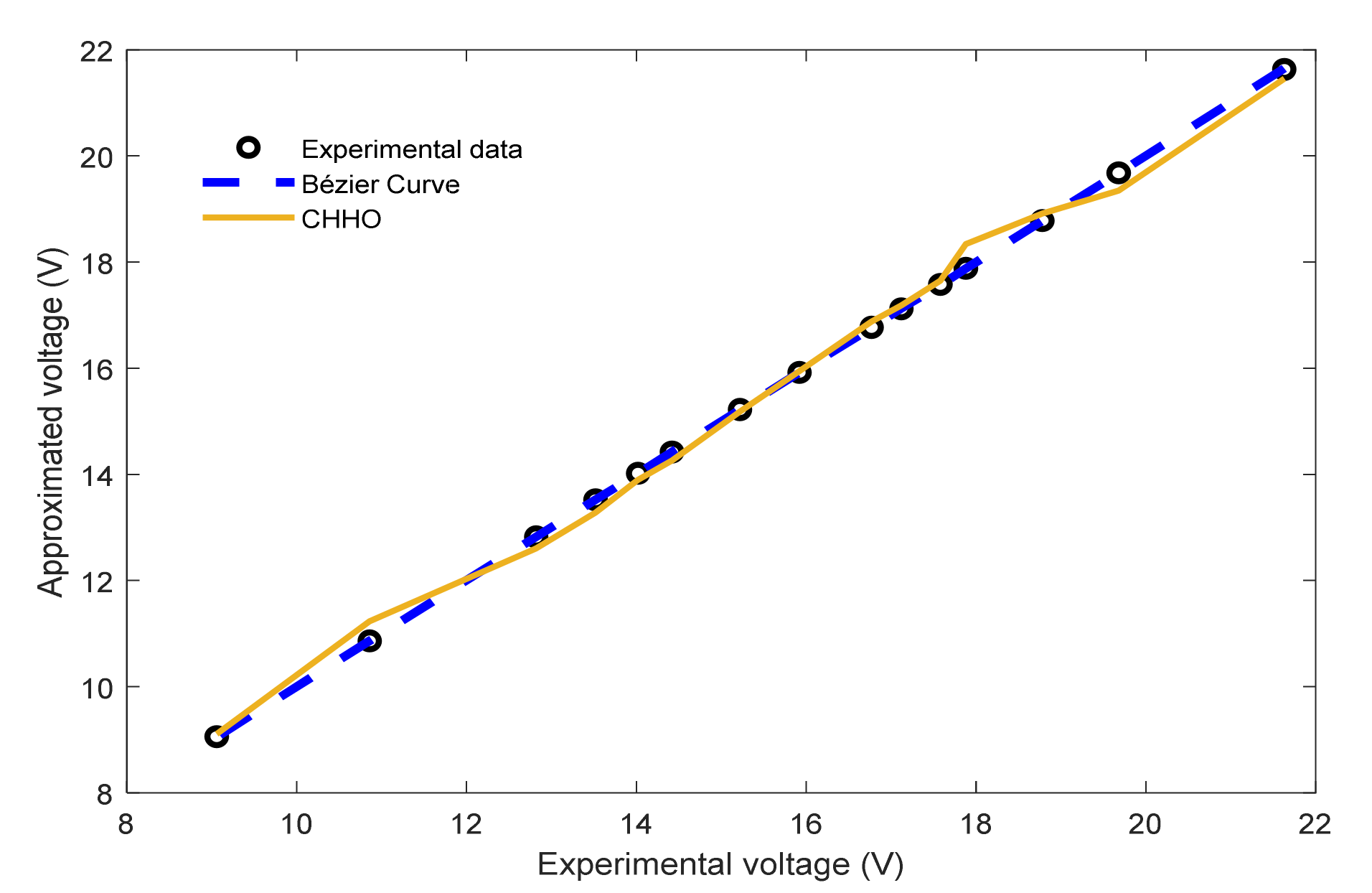
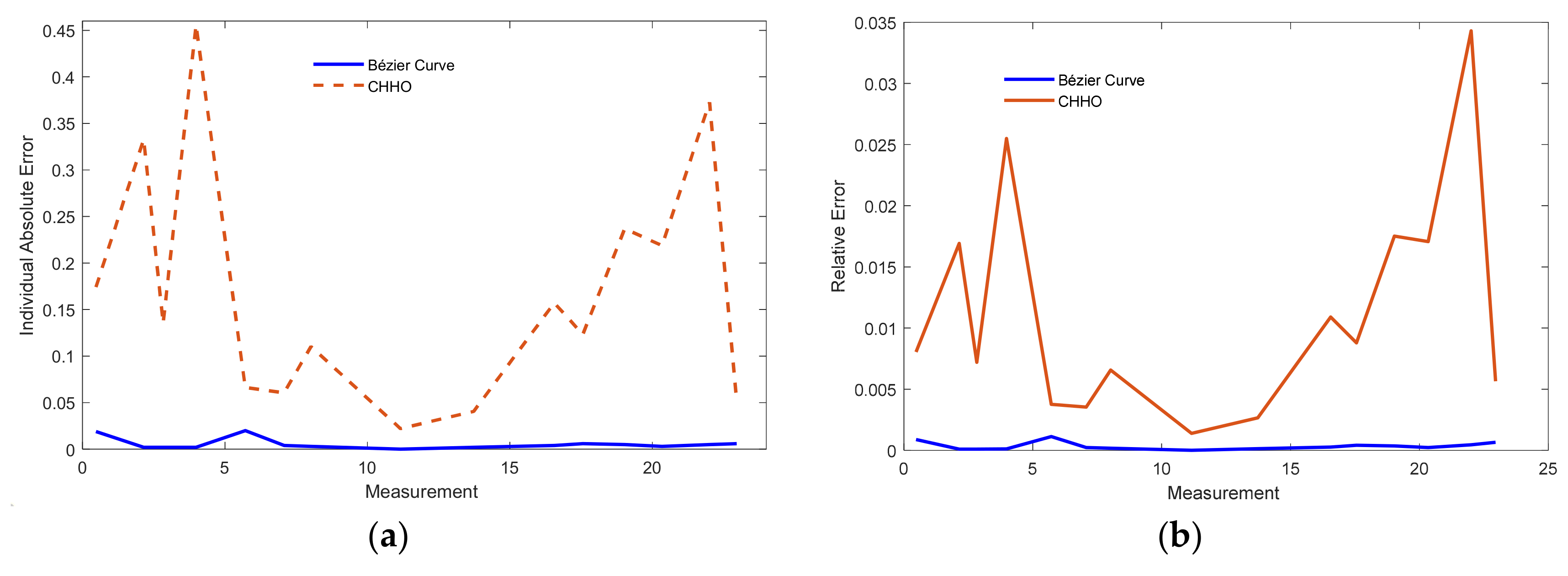
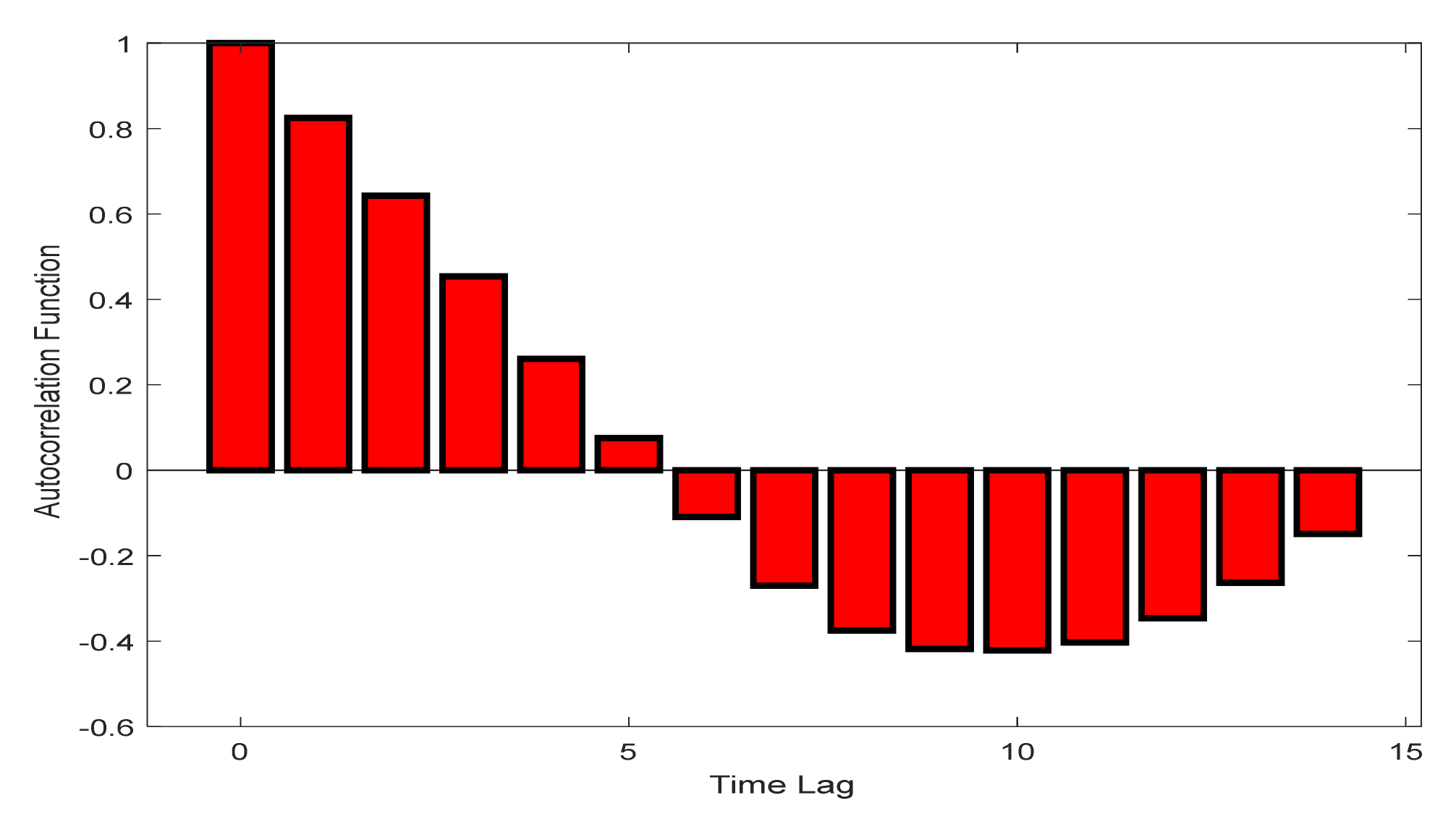
5.2. Case Study 2: Horizon H-12 W Stack
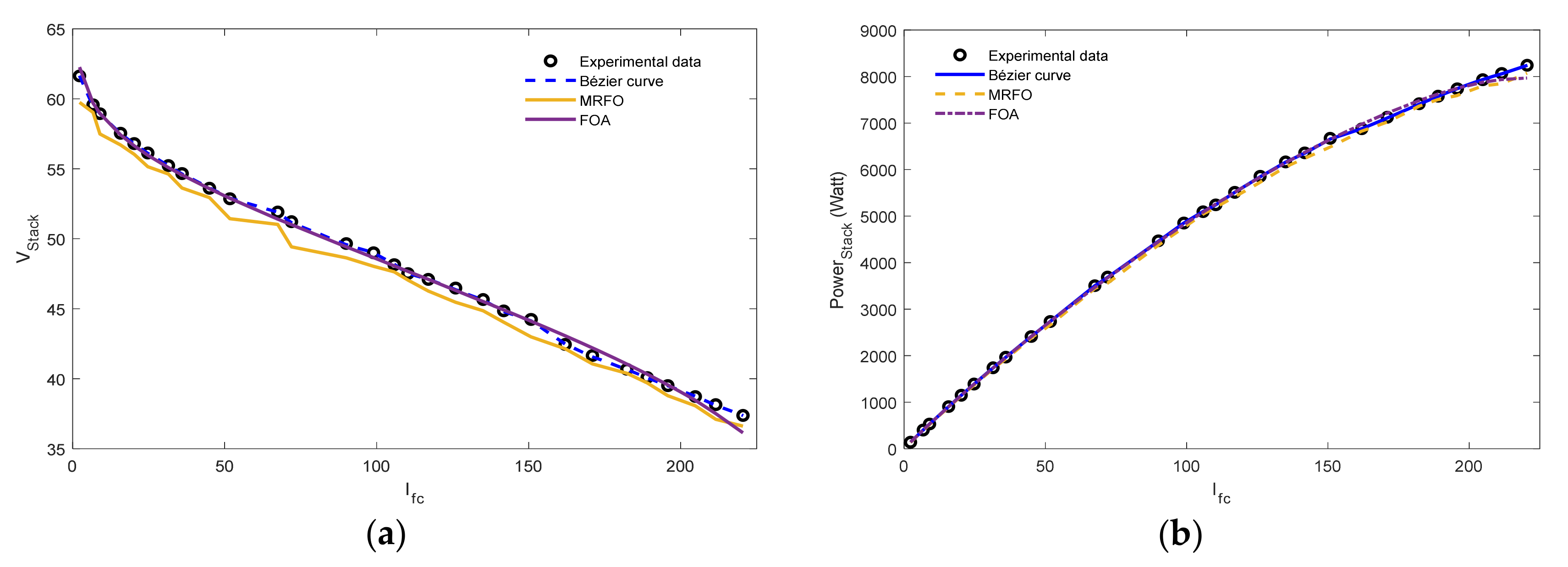
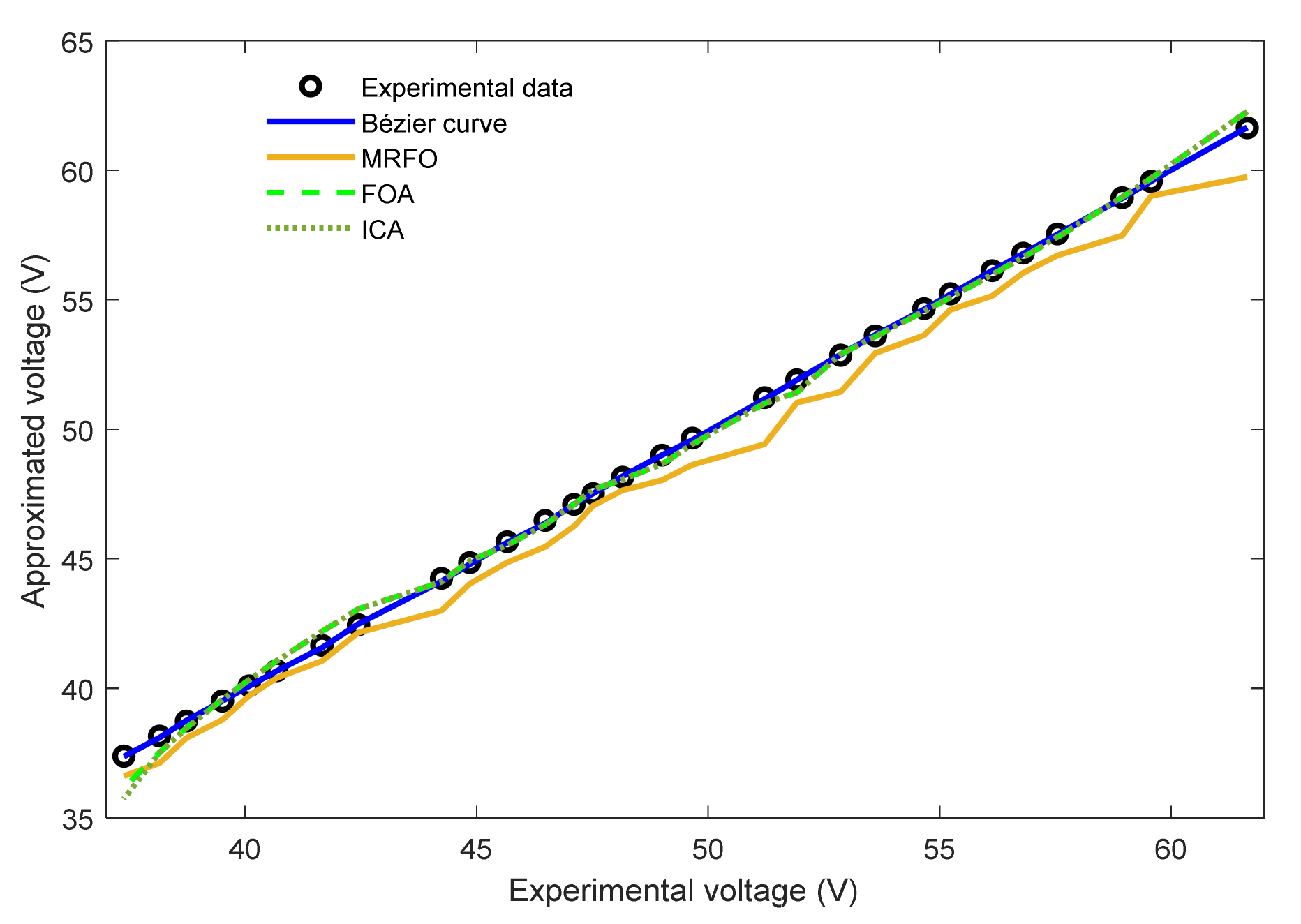
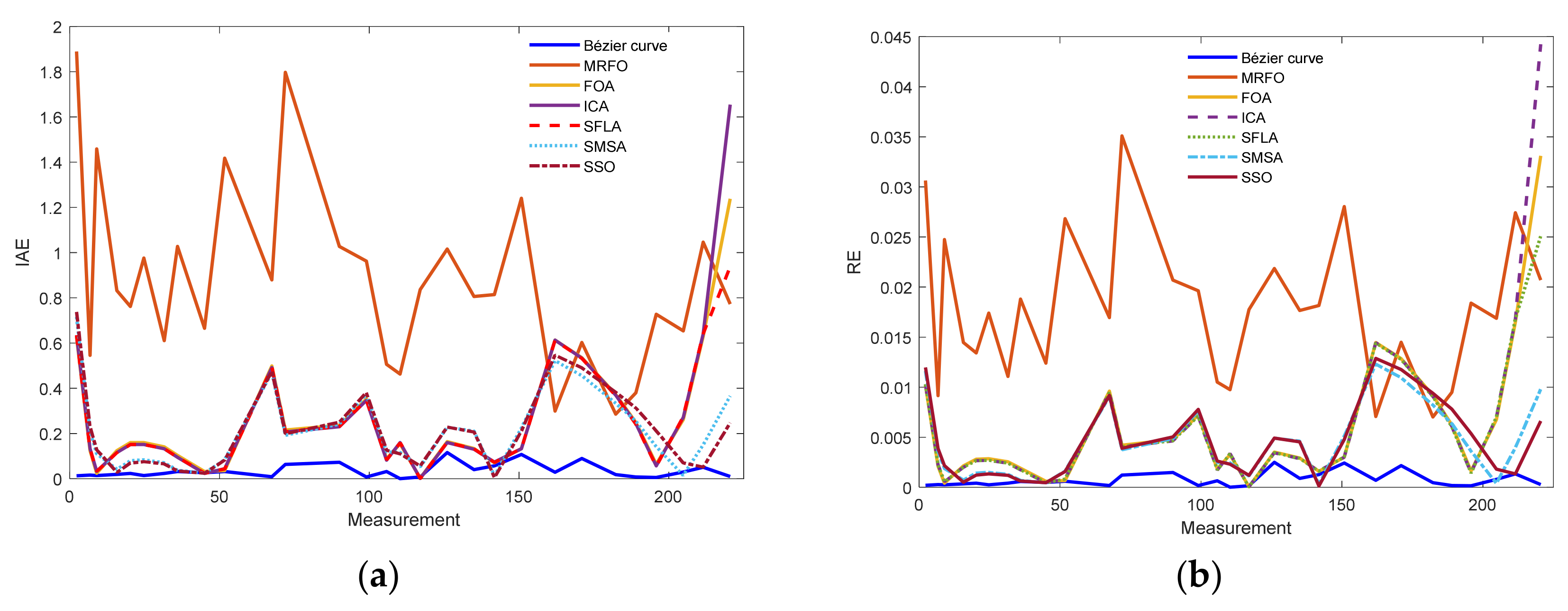
5.3. Case Study 3: NedStackPS6 PEMFC Stack
5.4. Case Study 4: 250 W PEMFC Stack
6. Analysis and Discussion
7. Conclusions
- Construction of a good fuel cell model device based on the approximated curves;
- Development of a new implicit model.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Staffell, I.; Scamman, D.; Velazquez-Abad, A.; Balcombe, P.; Dodds, P.E.; Ekins, P.; Shah, N.; Ward, K.R. The role of hydrogen and fuel cells in the global energy system. Energy Environ. Sci. 2019, 12, 463–491. [Google Scholar] [CrossRef]
- Ramadhani, F.; Hussain, M.A.; Mokhlis, H.; Hajimolana, S. Optimization strategies for solid oxide fuel cell (SOFC) application: A literature survey. Renew. Sustain. Energy Rev. 2017, 76, 460–484. [Google Scholar] [CrossRef]
- El-Hay, E.A.; El-Hameed, M.A.; El-Fergany, A.A. Optimized parameters of SOFC for steady state and transient simulations using interior search algorithm. Energy 2019, 166, 451–461. [Google Scholar] [CrossRef]
- Agwa, M.A.; El-Fergany, A.A.; Sarhan, M.G. Steady-state modeling of fuel cells based on atom search optimizer. Energies 2019, 12, 1884. [Google Scholar] [CrossRef]
- Shen, P.K. PEM fuel cell catalyst layers and MEAs. In PEM Fuel Cell Electrocatalysts and Catalyst Layers: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2008; pp. 355–380. [Google Scholar] [CrossRef]
- Wang, M.; Park, J.H.; Kabir, S.; Neyerlin, K.C.; Kariuki, N.N.; Lv, H.; Stamenkovic, V.R.; Myers, D.J.; Ulsh, M.; Mauger, S.A. Impact of catalyst ink dispersing methodology on fuel cell performance using in-situ X-ray scattering. ACS Appl. Energy Mater. 2019, 2, 6417–6427. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Y.; Wang, Z. Parameter estimation of proton exchange membrane fuel cells using eagle strategy based on JAYA algorithm and nelder-mead simplex method. Energy 2019, 173, 457–467. [Google Scholar] [CrossRef]
- Uzunoglu, M.; Alam, M.S. Fuel-cell systems for transportations. In Power Electronics Handbook, 4th ed.; Rashid, M.H., Ed.; Elisevier: Amsterdam, The Netherlands, 2018; pp. 1091–1112. [Google Scholar] [CrossRef]
- Chandan, A.; Hattenberger, M.; El-kharouf, A.; Du, S.; Dhir, A.; Self, V.; Pollet, B.G.; Ingram, A.; Bujalski, W. High temperature (HT) polymer electrolyte membrane fuel cells (PEMFC)-a review. J. Power Sources 2013, 231, 264–278. [Google Scholar] [CrossRef]
- Chen, F.; Yu, Y.; Gao, Y. Temperature control for proton exchange membrane fuel cell based on current constraint with consideration of limited cooling capacity. Fuel Cells 2017, 17, 662–670. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, X.; Lie, T.T.; Li, G. Mathematical modeling and simulation for external electrothermal characteristics of an alkaline water electrolyzer. Int. J. Energy Res. 2018, 42, 3899–3914. [Google Scholar] [CrossRef]
- Aouali, F.Z.; Becherif, M.; Ramadan, H.S.; Emziane, M.; Khellaf, A.; Mohammedi, K. Analytical modelling and experimental validation of proton exchange membrane electrolyser for hydrogen production. Int. J. Hydrogen Energy 2017, 42, 1366–1374. [Google Scholar] [CrossRef]
- Lee, W.-Y.; Park, G.-G.; Yang, T.-H.; Yoon, Y.-G.; Kim, C.-S. Empirical modeling of polymer electrolyte membrane fuel cell performance using artificial neural networks. Int. J. Hydrogen Energy 2004, 29, 961–966. [Google Scholar] [CrossRef]
- El-Fergany, A.A.; Hasanien, H.M.; Agwa, A.M. Semi-empirical PEM fuel cells model using whale optimization algorithm. Energy Convers. Manag. 2019, 201, 112197. [Google Scholar] [CrossRef]
- Gao, F.; Blunier, B.; Miraoui, A. Proton Exchange Membrane Fuel Cells Modeling; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Amphlett, C.; Mann, R.F.; Peppley, B.A.; Roberge, P.R.; Rodrigues, A. A model predicting transient responses of proton exchange membrane fuel cells. J. Power Sources 1996, 61, 183–188. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, N. Application of coRNA-GA based RBF-NN to model proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2018, 43, 329–340. [Google Scholar] [CrossRef]
- Priya, K.; Sathishkumar, K.; Rajasekar, N. A comprehensive review on parameter estimation techniques for proton exchange membrane fuel cell modelling. Renew. Sustain. Energy Rev. 2018, 93, 121–144. [Google Scholar] [CrossRef]
- Ritzberger, D.; Striednig, M.; Simon, C.; Hametner, C.; Jakubek, S. Online estimation of the electrochemical impedance of polymer electrolyte membrane fuel cells using broad-band current excitation. J. Power Sources 2018, 405, 150–161. [Google Scholar] [CrossRef]
- Taleb, M.A.; Béthoux, O.; Godoy, E. Identification of a PEMFC fractional order model. Int. J. Hydrogen Energy 2017, 42, 1499–1509. [Google Scholar] [CrossRef]
- Al-Baghdadi, M.A.R.S. Modelling of proton exchange membrane fuel cell performance based on semi-empirical equations. Renew. Energy 2005, 30, 1587–1599. [Google Scholar] [CrossRef]
- Geem, Z.W.; Noh, J.-S. Parameter estimation for a proton exchange membrane fuel cell model using GRG technique. Fuel Cells 2016, 16, 640–645. [Google Scholar] [CrossRef]
- Ye, M.; Wang, X.; Xu, Y. Parameter identification for proton exchange membrane fuel cell model using particle swarm optimization. Int. J. Hydrogen Energy 2009, 34, 981–989. [Google Scholar] [CrossRef]
- Bouaicha, A.; Allagui, H.; Aglzim, E.-H.; Rouane, A.; Mami, A. Validation of a methodology for determining the PEM fuel cell complex impedance modelling parameters. Int. J. Hydrogen Energy 2017, 42, 12738–12748. [Google Scholar] [CrossRef]
- Kandidayeni, M.; Macias, A.; Khalatbarisoltani-Boulon, A.L.; Kelouwani, S. Benchmark of proton exchange membrane fuel cell parameters extraction with metaheuristic optimization algorithms. Energy 2019, 183, 912–925. [Google Scholar] [CrossRef]
- Li, J.; Gao, X.; Cui, Y.; Hu, J.; Xu, G.; Zhang, Z. Accurate, efficient and reliable parameter extraction of PEM fuel cells using shuffled multi-simplexes search algorithm. Energy Convers. Manag. 2020, 206, 112501. [Google Scholar] [CrossRef]
- Miao, D.; Chen, W.; Zhao, W.; Demsas, T. Parameter estimation of PEM fuel cells employing the hybrid grey wolf optimization method. Energy 2020, 193, 116616. [Google Scholar] [CrossRef]
- Fathy, A.; Elaziz, M.A.; Alharbi, A.G. A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell. Renew. Energy 2020, 146, 1833–1845. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, N. Cuckoo search algorithm with explosion operator for modeling proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2019, 44, 3075–3087. [Google Scholar] [CrossRef]
- Fawzi, M.; El-Fergany, A.A.; Hasanien, H.M. Effective methodology based on neural network optimizer for extracting model parameters of PEM fuel cells. Int. J. Energy Res. 2019, 43, 8136–8147. [Google Scholar] [CrossRef]
- Rao, Y.; Shao, Z.; Ahangarnejad, A.H.; Gholamalizadeh, E.; Sobhani, B. Shark smell optimizer applied to identify the optimal parameters of the proton exchange membrane fuel cell model. Energy Convers. Manag. 2019, 182, 1–8. [Google Scholar] [CrossRef]
- El-Fergany, A.A. Extracting optimal parameters of PEM fuel cells using salp swarm optimizer. Renew. Energy 2018, 119, 641–648. [Google Scholar] [CrossRef]
- El-Fergany, A.A. Electrical characterisation of proton exchange membrane fuel cells stack using grasshopper optimizer. IET Renew. Power Gener. 2018, 12, 9–17. [Google Scholar] [CrossRef]
- Ali, M.; El-Hameed, M.A.; Farahat, M.A. Effective parameters’ identification for polymer electrolyte membrane fuel cell models using grey wolf optimizer. Renew. Energy 2017, 111, 455–462. [Google Scholar] [CrossRef]
- Turgut, O.E.; Coban, M.T. Optimal proton exchange membrane fuel cell modelling based on hybrid Teaching Learning Based Optimization-Differential Evolution algorithm. Ain Shams Eng. J. 2016, 7, 347–360. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, N.; Bi, Y.D. Srinivasan, parameter identification of PEMFC model based on hybrid adaptive differential evolution algorithm. Energy 2015, 90, 1334–1341. [Google Scholar] [CrossRef]
- Restrepo, C.; Konjedic, T.; Garces, A.; Calvente, J.; Giral, R. Identification of a proton-exchange membrane fuel cell’s model parameters by means of an evolution strategy. IEEE Trans. Ind. Inform. 2015, 11, 548–559. [Google Scholar] [CrossRef]
- Selem, S.I.; Hasanien, H.M.; El-Fergany, A.A. Parameters extraction of PEMFC’s model using manta rays foraging optimizer. Int. J. Energy Res. 2020, 44, 1–12. [Google Scholar] [CrossRef]
- Gong, W.; Yan, X.; Liu, X.; Cai, Z. Parameter extraction of different fuel cell models with transferred adaptive differential evolution. Energy 2015, 8, 139–151. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, G. Parameter fitting of PEMFC models based on adaptive differential evolution. Int. J. Electr. Power Energy Syst. 2014, 62, 189–198. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. An innovative global harmony search algorithm for parameter identification of a PEM fuel cell model. IEEE Trans. Ind. Electron. 2012, 59, 3473–3480. [Google Scholar] [CrossRef]
- Mohamed, N.; Majid, A.A.; Piah, A.R.M. Data fitting by G1 rational cubic Bézier curves using harmony search. Egypt. Inform. J. 2015, 16, 175–185. [Google Scholar] [CrossRef]
- Kawabata, K.; Ma, L.; Xue, J.; Zhu, C.; Zheng, N. A path generation for automated vehicle based on Bezier curve and via-points. Rob. Auton. Syst. 2015, 74, 243–252. [Google Scholar] [CrossRef]
- Huo, M.; Mengali, G.; Quarta, A.A.; Qi, N. Electric sail trajectory design with Bezier curve-based shaping approach. Aerosp. Sci. Technol. 2019, 88, 126–135. [Google Scholar] [CrossRef]
- Fürst, Y.; Brandt, S.; Kriegel, M. Thermal modelling of three-way mixing valves using Bézier curves for parameter estimation applications. J. Process. Control. 2020, 90, 56–62. [Google Scholar] [CrossRef]
- Susam, S.O.; Hudaverdi, U.B. A goodness-of-fit test based on Bézier curve estimation of Kendall distribution. J. Stat. Comput. Simul. 2020, 90, 1194–1215. [Google Scholar] [CrossRef]
- Ahn, Y.J. Circle approximation by G 2 Bézier curves of degree n with 2n−1 extreme points. J. Comput. Appl. Math. 2019, 358, 20–28. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, X.C. Approximation of conic section by quartic Bézier curve with endpoints continuity condition. Appl. Math. 2017, 32, 1–13. [Google Scholar] [CrossRef]
- Menesy, A.S.; Sultan, H.M.; Korashy, A.; Banakhr, F.A.; Ashmawy, M.G.; Kamel, S. Effective parameter extraction of different polymer electrolyte membrane fuel cell stack models using a modified artificial ecosystem optimization algorithm. IEEE Access 2020, 8, 31892–31909. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. A grouping-based global harmony search algorithm for modeling of proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2011, 36, 5047–5053. [Google Scholar] [CrossRef]
- Menesy, A.S.; Sultan, H.M.; Selim, A.; Ashmawy, M.G.; Kamel, S. Developing and applying chaotic harris hawks optimization technique for extracting parameters of several proton exchange membrane fuel cell stacks. IEEE Access 2020, 8, 1146–1159. [Google Scholar] [CrossRef]
- Outeiro, M.T.; Chibante, R.; Carvalho, A.S.; de Almeida, A.T. A new parameter extraction method for accurate modeling of PEM fuel cells. Int. J. Energy Res. 2009, 33, 978–988. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, Z.; Jiang, J. Fuel Cell Technology for Distributed Generation: An Overview; IEEE: Piscataway, NJ, USA, 2006; pp. 1613–1618. [Google Scholar] [CrossRef]
- Morin, G.; Goldman, R. A subdivision scheme for Poisson curves and surfaces. Comput. Aided Geom. Des. 2000, 17, 813–833. [Google Scholar] [CrossRef]
- Louzazni, M.; Khouya, A.; Amechnoue, K.; Mussetta, M.; Crăciunescu, A. Comparison and evaluation of statistical criteria in the solar cell and photovoltaic module parameters’ extraction. Int. J. Ambient Energy 2018, 41, 1–13. [Google Scholar] [CrossRef]
- Khandakar, A.; Chowdhury, M.E.H.; Kazi, M.K.; Benhmed, K.; Touati, F.; Al-Hitmi, M.; Gonzales, A.S.P.J. Machine learning based photovoltaics (PV) power prediction using different environmental parameters of Qatar. Energies 2019, 12, 2782. [Google Scholar] [CrossRef]
- Stacks, H.-S.F.C. H-12 PEM Fuel Cell 12W-Horizon Educational. Available online: https://www.horizoneducational.com/advancedproducts/h-12-pem-fuel-cell-12w/ (accessed on 12 September 2020).
| Fuel Cell | ncell | A(cm2) | l(μm) | PH2 (bar) | Po2 (bar) | T (K) | RHa, RHc |
|---|---|---|---|---|---|---|---|
| M/S Ballard [50] | 35 | 50.6 | 178 | 1 | 1 | 343 | 1 |
| Horizon H-12 [14,57] | 13 | 8.1 | 25 | 0.4935 | 1 | 302.15 | 1 |
| NedStack PS6 [25] | 65 | 240 | 178 | 0.5–5 | 0.5–5 | 343 | 1 |
| 250 W [49] | 24 | 27 | 178 | 1 | 0.2075 | 343.15–353.15 | 1 |
| Experimental | Bézier Curve | IAE | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Iex | Vex | Vb | Ib | Bézier Curve | GRG-1 [22] | GRG-2 [22] | GGHS [50] | IHS [50] | PSO-w [50] |
| 5.4 | 0.92 | 5.423 | 0.9185 | 1.50 × 10−3 | 2.9 × 10−3 | 1.52 × 10−2 | 3.2 × 10−3 | 1.41 × 10−2 | 2.07 × 10−2 |
| 10.8 | 0.88 | 10.8105 | 0.8803 | 3.00 × 10−4 | 2.1 × 10−3 | 2 × 10−3 | 1.7 × 10−3 | 2.4 × 10−3 | 1.36 × 10−2 |
| 16.2 | 0.85 | 16.1271 | 0.8495 | 5.00 × 10−4 | 1.6 × 10−3 | 5.8 × 10−3 | 3.5 × 10−3 | 2.9 × 10−3 | 1.04 × 10−2 |
| 21.6 | 0.82 | 21.5855 | 0.8202 | 2.00 × 10−4 | 3 × 10−3 | 7.5 × 10−3 | 1 × 10−4 | 1.6 × 10- | 1.28 × 10−2 |
| 27.0 | 0.79 | 27.044 | 0.7894 | 6.00 × 10−4 | 5.1 × 10−3 | 5.8 × 10−3 | 6.5 × 10−3 | 3.2 × 10−3 | 1.81 × 10−2 |
| 32.4 | 0.77 | 32.4315 | 0.7689 | 1.10 × 10−3 | 2.3 × 10−3 | 1.23 × 10−2 | 4.4 × 10−3 | 1 × 10−4 | 1.51 × 10−2 |
| 37.8 | 0.74 | 37.7481 | 0.7381 | 1.90 × 10−3 | 5 × 10−4 | 7.5 × 10−3 | 1.34 × 10−2 | 8.2 × 10−3 | 2.31 × 10−2 |
| 43.2 | 0.72 | 43.1356 | 0.719 | 1.00 × 10−3 | 6.9 × 10−3 | 1.21 × 10−2 | 1.29 × 10−2 | 7.1 × 10−3 | 2.16 × 10−2 |
| 48.6 | 0.69 | 48.5232 | 0.6882 | 1.80 × 10−3 | 4.6 × 10−3 | 6.4 × 10−3 | 2.25 × 10−2 | 1.62 × 10−2 | 3 × 10−2 |
| 54.0 | 0.66 | 53.9107 | 0.6589 | 1.10 × 10−3 | 3 × 10−3 | 9 × 10−4 | 3.18 × 10−2 | 2.5 × 10−2 | 3.78 × 10−2 |
| 59.4 | 0.62 | 59.3691 | 0.6178 | 2.20 × 10−3 | 7.3 × 10−3 | 1.37 × 10−2 | 5.02 × 10−2 | 4.27 × 10−2 | 5.35 × 10−2 |
| 64.8 | 0.60 | 64.8275 | 0.5987 | 1.30 × 10−3 | 5 × 10−3 | 6 × 10−3 | 4.62 × 10−2 | 3.78 × 10−2 | 4.2 × 10−2 |
| 70.2 | 0.55 | 70.1441 | 0.5489 | 1.10 × 10−3 | 5.4 × 10−3 | 2.13 × 10−2 | 6.52 × 10−2 | 5.43 × 10−2 | 6.31 × 10−2 |
| Experimental | Bézier Curve | IAE | |||||
|---|---|---|---|---|---|---|---|
| Iex | Vex | Ib | Vb | Bézier Curve | WOA [14] | GA [38] | MRFO [38] |
| 0.104 | 9.58 | 0.1032 | 9.5732 | 8.00 × 10−4 | 1.51 × 10−1 | 1.69 × 10−1 | 1.64 × 10−1 |
| 0.2 | 9.42 | 0.2010 | 9.4153 | 1.00 × 10−3 | 3.00 × 10−2 | 4.70 × 10−2 | 4.10 × 10−2 |
| 0.309 | 9.25 | 0.3097 | 9.2510 | 7.00 × 10−4 | 4.00 × 10−3 | 1.20 × 10−2 | 5.00 × 10−3 |
| 0.403 | 9.2 | 0.4032 | 9.1984 | 2.00 × 10−4 | 9.00 × 10−2 | 7.40 × 10−2 | 8.20 × 10−2 |
| 0.51 | 9.09 | 0.5097 | 9.0866 | 3.00 × 10−4 | 1.09 × 10−1 | 9.40 × 10−2 | 1.04 × 10−1 |
| 0.614 | 8.95 | 0.6141 | 8.9485 | 1.00 × 10−4 | 8.00 × 10−2 | 6.60 × 10−2 | 7.70 × 10−2 |
| 0.703 | 8.85 | 0.7032 | 8.8564 | 2.00 × 10−4 | 6.60 × 10−2 | 5.20 × 10−2 | 6.50 × 10−2 |
| 0.806 | 8.74 | 0.8076 | 8.7447 | 1.60 × 10−3 | 4.90 × 10−2 | 3.60 × 10−2 | 5.00 × 10−2 |
| 0.908 | 8.65 | 0.9076 | 8.6526 | 4.00 × 10−4 | 4.50 × 10−2 | 3.30 × 10−2 | 4.90 × 10−2 |
| 1.076 | 8.45 | 1.075 | 8.4488 | 1.00 × 10−3 | 2.10 × 10−2 | 3.10 × 10−2 | 1.30 × 10−2 |
| 1.127 | 8.41 | 1.1271 | 8.4093 | 1.00 × 10−4 | 2.20 × 10−2 | 3.20 × 10−2 | 1.30 × 10−2 |
| 1.288 | 8.2 | 1.2902 | 8.1989 | 2.20 × 10−3 | 1.13 × 10−1 | 1.21 × 10−1 | 9.90 × 10−2 |
| 1.39 | 8.12 | 1.3902 | 8.1200 | 2.00 × 10−4 | 1.19 × 10−1 | 1.26 × 10−1 | 1.03 × 10−1 |
| 1.45 | 8.11 | 1.4510 | 8.1068 | 1.00 × 10−3 | 8.60 × 10−2 | 9.30 × 10−2 | 6.90 × 10−2 |
| 1.578 | 8.05 | 1.5793 | 8.0477 | 1.30 × 10−3 | 5.70 × 10−2 | 6.20 × 10−2 | 3.60 × 10−2 |
| 1.707 | 7.99 | 1.7076 | 7.9951 | 6.00 × 10−4 | 2.80 × 10−2 | 3.20 × 10−2 | 3.00 × 10−3 |
| 1.815 | 7.95 | 1.8163 | 7.9490 | 1.30 × 10−3 | 6.00 × 10−3 | 3.00 × 10−3 | 3.50 × 10−2 |
| 1.9 | 7.94 | 1.9010 | 7.9359 | 1.00 × 10−3 | 5.40 × 10−2 | 5.20 × 10−2 | 8.50 × 10−2 |
| 2.06 | 7.9 | 2.0597 | 7.8964 | 3.00 × 10−4 | 1.23 × 10−1 | 1.23 × 10−1 | 1.00 × 10−1 |
| Experimental | Bézier Curve | IAE | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Iex | Vex | Ib | Vb | Bézier Curve | MRFO [38] | FOA [25] | ICA | SMSA [26] | SSO [32] |
| 2.25 | 61.64 | 2.2448 | 61.6528 | 1.28 × 10−2 | 1.889 | 0.6265 | 0.6347 | 0.7158 | 0.7381 |
| 6.75 | 59.57 | 6.4981 | 59.5867 | 1.67 × 10−2 | 0.546 | 0.1246 | 0.1328 | 0.2118 | 0.2305 |
| 9 | 58.94 | 9.0974 | 58.9256 | 1.44 × 10−2 | 1.458 | 0.0244 | 0.0326 | 0.1104 | 0.1276 |
| 15.75 | 57.54 | 15.714 | 57.5206 | 1.94 × 10−2 | 0.832 | 0.1239 | 0.1155 | 0.0418 | 0.0286 |
| 20.25 | 56.8 | 20.203 | 56.7768 | 2.32 × 10−2 | 0.762 | 0.1595 | 0.1511 | 0.0805 | 0.0698 |
| 24.75 | 56.13 | 24.693 | 56.1157 | 1.43 × 10−2 | 0.976 | 0.1595 | 0.1511 | 0.0838 | 0.0755 |
| 31.5 | 55.23 | 31.545 | 55.2066 | 2.34 × 10−2 | 0.611 | 0.1412 | 0.1328 | 0.0711 | 0.066 |
| 36 | 54.66 | 36.035 | 54.6280 | 3.20 × 10−2 | 1.027 | 0.1038 | 0.0954 | 0.0378 | 0.0346 |
| 45 | 53.61 | 45.014 | 53.6363 | 2.63 × 10−2 | 0.665 | 0.0325 | 0.0242 | 0.0245 | 0.0241 |
| 51.75 | 52.86 | 51.867 | 52.8925 | 3.25 × 10−2 | 1.418 | 0.0359 | 0.0441 | 0.0853 | 0.0826 |
| 67.5 | 51.91 | 67.462 | 51.9008 | 9.20 × 10−3 | 0.88 | 0.4989 | 0.4911 | 0.4697 | 0.4763 |
| 72 | 51.22 | 71.952 | 51.1570 | 6.30 × 10−2 | 1.797 | 0.2152 | 0.2076 | 0.1923 | 0.1997 |
| 90 | 49.66 | 89.910 | 49.5867 | 7.33 × 10−2 | 1.027 | 0.2369 | 0.2301 | 0.2416 | 0.2502 |
| 99 | 49 | 98.889 | 49.0082 | 8.20 × 10−3 | 0.962 | 0.3535 | 0.3472 | 0.373 | 0.381 |
| 105.8 | 48.15 | 105.74 | 48.1818 | 3.18 × 10−2 | 0.506 | 0.0882 | 0.0824 | 0.1192 | 0.1261 |
| 110.3 | 47.52 | 110.23 | 47.5206 | 6.00 × 10−4 | 0.463 | 0.1547 | 0.1602 | 0.1161 | 0.1102 |
| 117 | 47.1 | 117.08 | 47.1074 | 7.40 × 10−3 | 0.836 | 0.0029 | 0.002 | 0.0527 | 0.0567 |
| 126 | 46.48 | 126.06 | 46.3636 | 1.164 × 10−1 | 1.016 | 0.1638 | 0.1598 | 0.2279 | 0.2285 |
| 135 | 45.66 | 135.04 | 45.6198 | 4.02 × 10−2 | 0.806 | 0.1337 | 0.1306 | 0.2106 | 0.2067 |
| 141.8 | 44.85 | 141.9 | 44.7933 | 5.67 × 10−2 | 0.814 | 0.0712 | 0.0736 | 0.0136 | 0.0056 |
| 150.8 | 44.24 | 150.87 | 44.1322 | 1.078 × 10−1 | 1.24 | 0.1336 | 0.1324 | 0.2254 | 0.2108 |
| 162 | 42.45 | 161.98 | 42.4793 | 2.93 × 10−2 | 0.3 | 0.6136 | 0.6131 | 0.5221 | 0.5467 |
| 171 | 41.66 | 170.96 | 41.5702 | 8.98 × 10−2 | 0.603 | 0.5354 | 0.5334 | 0.4557 | 0.4901 |
| 182.3 | 40.68 | 182.3 | 40.6611 | 1.89 × 10−2 | 0.286 | 0.3733 | 0.3693 | 0.3337 | 0.3824 |
| 189 | 40.09 | 188.92 | 40.0826 | 7.40 × 10−3 | 0.38 | 0.2491 | 0.2437 | 0.2546 | 0.3131 |
| 195.8 | 39.51 | 195.77 | 39.5041 | 5.90 × 10−3 | 0.727 | 0.0644 | 0.0575 | 0.1426 | 0.212 |
| 204.8 | 38.73 | 204.75 | 38.7603 | 3.030 × 10−2 | 0.654 | 0.2618 | 0.2707 | 0.0151 | 0.0705 |
| 211.5 | 38.15 | 211.6 | 38.0991 | 5.09 × 10−2 | 1.046 | 0.6296 | 0.6403 | 0.1504 | 0.0514 |
| 220.5 | 37.38 | 220.58 | 37.37 | 1.00 × 10−2 | 0.773 | 1.2377 | 1.654 | 0.3661 | 0.2472 |
| Experimental | Bézier Curve | IAE | ||||
|---|---|---|---|---|---|---|
| Iex | Vex | Ib | Vb | Bézier Curve | MAEO [49] | CHHO [51] |
| 0.4717 | 21.63 | 0.44278 | 21.649 | 1.90 × 10−2 | 1.20 × 10−1 | 0.1741 |
| 2.149 | 19.68 | 2.1458 | 19.678 | 2.00 × 10−3 | 3.18 × 10−1 | 0.333 |
| 2.83 | 18.78 | 2.8951 | 18.778 | 2.00 × 10−3 | 1.45 × 10−1 | 0.1352 |
| 3.983 | 17.88 | 3.985 | 17.878 | 2.00 × 10−3 | 4.59 × 10−1 | 0.4558 |
| 5.713 | 17.58 | 5.6199 | 17.56 | 2.00 × 10−2 | 6.45 × 10−2 | 0.0662 |
| 7.075 | 17.12 | 7.0504 | 17.124 | 4.00 × 10−3 | 5.71 × 10−2 | 0.0606 |
| 8.019 | 16.77 | 8.0041 | 16.767 | 3.00 × 10−3 | 1.06 × 10−1 | 0.1103 |
| 11.16 | 15.92 | 11.138 | 15.92 | 2.20 × 10−2 | 1.85 × 10−2 | 0.022 |
| 13.73 | 15.22 | 13.726 | 15.218 | 2.00 × 10−3 | 4.25 × 10−2 | 0.0406 |
| 16.56 | 14.42 | 16.587 | 14.424 | 4.00 × 10−3 | 1.57 × 10−1 | 0.1572 |
| 17.56 | 14.02 | 17.473 | 14.014 | 6.00 × 10−3 | 1.23 × 10−1 | 0.1232 |
| 19.03 | 13.52 | 19.04 | 13.525 | 5.00 × 10−3 | 2.37 × 10−1 | 0.2368 |
| 20.34 | 12.82 | 20.334 | 12.823 | 3.00 × 10−3 | 2.21 × 10−1 | 0.2188 |
| 22.01 | 10.86 | 22.037 | 10.865 | 5.00 × 10−3 | 3.59 × 10−1 | 0.3726 |
| 22.96 | 9.058 | 22.99 | 9.052 | 6.00 × 10−3 | 1.01 × 10−2 | 0.0512 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Louzazni, M.; Al-Dahidi, S.; Mussetta, M. Fuel Cell Characteristic Curve Approximation Using the Bézier Curve Technique. Sustainability 2020, 12, 8127. https://doi.org/10.3390/su12198127
Louzazni M, Al-Dahidi S, Mussetta M. Fuel Cell Characteristic Curve Approximation Using the Bézier Curve Technique. Sustainability. 2020; 12(19):8127. https://doi.org/10.3390/su12198127
Chicago/Turabian StyleLouzazni, Mohamed, Sameer Al-Dahidi, and Marco Mussetta. 2020. "Fuel Cell Characteristic Curve Approximation Using the Bézier Curve Technique" Sustainability 12, no. 19: 8127. https://doi.org/10.3390/su12198127
APA StyleLouzazni, M., Al-Dahidi, S., & Mussetta, M. (2020). Fuel Cell Characteristic Curve Approximation Using the Bézier Curve Technique. Sustainability, 12(19), 8127. https://doi.org/10.3390/su12198127







