The Measurement of Social Cohesion at Province Level in Poland Using Metric and Interval-Valued Data

Abstract

The notion of social cohesion is increasingly used in the political, economic and academic debate. Due to its multidimensional, the assessment of social cohesion is not easy, especially if it is conducted at a lower than national level of aggregation. The aim of the study is to assess social cohesion in provinces of Poland in 2018 using the hybrid approach involving multidimensional scaling and linear ordering based on an aggregate measure. This type of study is usually conducted using classic metric data. However, the traditional approach does not account for the variation between lower level units (i.e., districts). The authors propose a methodology which makes this possible. Additionally the results of assessment of the multidimensional phenomenon can be presented in a two-dimensional space. Classic metric data and symbolic interval-valued data (three data types: min-max, 1st decile and 9th decile, 2nd decile and 8th decile) are jointly represented in a single diagram. The consistency of the research method ensures comparability of results of linear ordering. Two criteria were used in the comparative analysis of four rankings of social cohesion. The results of the study clearly showed that the current level of social cohesion at the provinces level is geographically and historically dependent.

1. Introduction and Motivation

The purpose of the study described in the article was to assess social cohesion of the provinces of Poland in 2018. The study was based on classic metric data and symbolic interval-valued data. Interval-valued variables describe objects of interest more precisely than classical metric variables. For classical metric data an observation on each variable in a data matrix is expressed as one real number (atomic approach). In contrast, for symbolic interval-valued data, observations on each variable are expressed as intervals $\left[x_{ij}^l,x_{ij}^u\right]$ $(x_{ij}^l\le x_{ij}^u$), where $x_{ij}^l$ denotes the lower bound and $x_{ij}^u$ the upper bound of the interval. Studies by [1,2] provide different examples of data that in real life are of interval type.

Social cohesion is often measured by means of various composite indicators. Duhaime et al. [3] make an attempt to measure the level of social cohesion in the Canadian Artic using six sets of indices: presence of social capital, demographic stability, social and economic inclusion, community quality of life, individual quality of life. Based on the definition of social cohesion by Bernard [4] and Chan et al. [5], the VALCOS (VALeurs et COhésion Sociale) index of social cohesion elaborated for European countries was developed [6]. It covers the political and socio-cultural domains of life in their formal and substantial relations. Langer et al. [7] developed two social cohesion indices: a national average SCI and a Social Cohesion Index Variance-Adjusted (SCIVA) to measure the national-level of social cohesion for 19 African countries in 2005, 2008 and 2012. The indices represent social cohesion as a triangle composed of the three components of societal relationships and attitudes: inequalities, trust, and identities. In the Polish literature, e.g., [8] analysed social cohesion in EU countries using a synthetic measure of development put forward by Z. Hellwig [9]. There are a number of other publications that have proposed composite indicators of social cohesion (i.e., [10,11]).

In some studies the index-based analysis is extended by the inclusion of additional statistical methods. Janmaat [12] considered 14 indicators describing 8 components of social cohesion and used exploratory factor analysis (EFA) to map 41 countries in the world in a two-dimensional space showing the relationship between two factors (solidarity, participation). In another study, Bottoni [13] used 24 indicators describing 7 dimensions of social cohesion for 29 European countries to build a multilevel CFA (confirmatory factor analysis) model of social cohesion. Dickes and Valentova [14] used multidimensional scaling (MDS) and a CFA model of social cohesion to map 47 European countries a two-dimensional MDS space. The results served as the basis for comparing levels of social cohesion in six broader geographical regions in Europe. An analogical study involving the same methods (MDS, CFA) for 33 European countries was described in Dickes et al. [15]. Using factor analysis and standardisation, Rajulton et al. [16] created an overall index of social cohesion across 49 Census Metropolitan Areas of Canada based on three dimensions: political (voting and volunteering), economic (occupation, income, labour force participation) and social (social interactions, informal volunteering). Lafuente et al. [17] make an attempt to assess the sustainability of social cohesion in the EU using nonlinear time-varying factor model and analyzing the level of convergence across EU countries.

In Dehnel et al. [18] the level of social cohesion was assessed using a hybrid approach combining multidimensional scaling and linear ordering, applied separately to classic metric data and symbolic interval-valued data (1st and 3rd quartile); the results were then compared.

The novelty of the study presented in this article consists in jointly mapping, by means of multidimensional scaling, classic metric data and symbolic interval-valued data (three data types: min-max, 1st decile and 9th decile, 2nd decile and 8th decile) in one chart. In the next step, all objects (districts) were ordered according to the level of social cohesion determined by means of an aggregate measure (composite indicator) based on the Euclidean distance from the pattern object. The application of a consistent research method ensures comparability of rankings of Poland’s provinces in terms of social cohesion. In the following step assessments of social cohesion based on 4 different types of data were compared using two criteria: results of cluster analysis involving a distance based on two correlation coefficients (Spearman’s $rho$ and Kendall’s $tau$) and the analysis of the degree of compatibility between rankings of districts based on individual variables and the overall ranking based on the aggregate measure.

It is worth noting that existing studies aimed at assessing the level of social cohesion are usually based on primary data, from a surveys. The use of these sources are associated with a certain limitation. Namely primary data do not allow for the inclusion for assessing the level of social cohesion in higher level territorial units (e.g., provinces) data for lower-level units (districts). Only secondary sources can provide this possibility by introducing interval-valued data into the analysis. The empirical study described in this article was based on secondary data from official statistical sources. They were obtained from the Local Data Bank (BDL) using the bdl R package [19] and API interface (Application Programming Interface). BDL is the Polish acronym of the Local Data Bank (Bank Danych Lokalnych).

2. Overview of Social Cohesion Concepts

Social cohesion is a concept which is frequently mentioned in various projects and analyses, both in research and in government policies. The measurement of social cohesion and comparative analyses of its level in different territorial units are far from easy. This is because no clear definition or conceptualization of social cohesion has been proposed so far. There is still no consensus on how to define values and factors related to the construct of social cohesion. The complexity of the concept of social cohesion can be illustrated by the variety of approaches that can be found in the literature [4,5,7,15,20,21,22,23,24,25,26,27]. All of them refer, to a varying degree, to six dimensions: social relations, identification, orientation towards the common good, shared values, quality of life, and (in)equality, though it is often indicated that the last three are antecedents or consequences of social cohesion rather than its core dimensions [28]. Although various approaches involve different areas of social cohesion, refer to different political views, are informed by different ideologies or concerns of policy makers, the majority of them overlap, covering similar dimensions [29] (p. 23). Nonetheless, each of the approaches proposed in the literature can be viewed as representing one of two discourses: the academic or the policy discourse [5].

The first category academic discourse is closely connected with social sciences, such as sociology and psychology. Studies referring to the academic discourse focus on processes of social integration and stability and social exclusion, while ignoring dilemmas associated with the definition of social cohesion [30,31,32].

The second category policy discourse refers to policies undertaken by governments and various national and international institutions (the European Union, Council of Europe, World Bank or OECD). In this case, social cohesion is viewed as a prerequisite of economic well-being. This goal can be achieved by overcoming numerous economic and social problems resulting from unequal income distribution, employment, housing issues, limited access to health care and education, participation in political and public life. Thus policy discourse can be described as problem-driven [5,15]. The list of major problems includes unemployment, poverty and social exclusion.

Policy-oriented studies are initiated and conducted by many national and international socio-political entities (governments, think tanks, foundations, organizations). Policy-makers usually address problems of social cohesion with a focus on their own concerns and from particular policy fields. Sometimes they even try to use the social cohesion term to promote their own agendas. As a result, policy-orientated analyses need to be treated with caution. For one thing, such studies often include too many social indicators, many of which do not properly capture components of social cohesion. Moreover, because territorial units face a complex mixture of socio-economic problems, every entity conducting research tends to create its own definition of social cohesion. Another problem is associated with the lack of distinction between factors affecting social cohesion and its actual components [5,13,15,28].

Both types of discourse on social cohesion described above are multi-faceted, but in each case the concept of social cohesion is different. The academic discourse is focused on a conceptual and analytic understanding of social cohesion. The policy discourse is rather social and economic problem-oriented. This is the main cause of existing discrepancies in measurement, and consequently in the assessment of the level of social cohesion. An additional difficulty of the academic approach is that it is largely based on subjective, qualitative assessments. The need to standardize the measurement method used to monitor the level and changes in social cohesion across time and societies is not new. However, the development of universal, assessable indicators would require the establishment of a single definitional framework of social cohesion. It should be based on the core elements of existing approaches to social cohesion presented and systematically mentioned in the literature of the past decades. Most approaches proposed so far refer to the policy discourse, which focuses on all types of social challenges faced by society [5,15,32]. A synthetic review of key approaches representing both the policy and academic discourse is presented below.

One of the first and most frequently cited concepts of social cohesion was formulated by Jane Jenson and was based on results of her own studies [20]. It represents the perspective found in the policy discourse. Rather than being a single definition, it consists of five dimensions:

• Belonging vs. isolation—which refers to the existence or lack of shared values and a sense of identity,
• Inclusion vs. exclusion—which refers to equal opportunities and citizens’ access to economic institutions and the market,
• Participation vs. non-involvement—which refers to political and social participation at various levels of government, especially the local level,
• Recognition vs. rejection—which refers to respect and tolerance of diversity in a diverse society,
• Legitimacy vs. illegitimacy—which addresses the question of respect for existing social norms and laws, the legitimacy of the main political and social institutions, especially the state, as mediators between different stakeholders.

Bernard [4] developed Jenson’s definition by adding another dimension—equality vs. inequality — as an important element of the economic sphere. He introduced a typology based on two aspects. The first one comprised spheres of activity undertaken by society (economic, political and socio-cultural, while the second referred to social relations in the strict sense [6]).

In 2002, Beauvais and Jenson [22], drawing on Jenson’s pluralistic approach [20], put forward a definition of social cohesion consisting of five elements: 1. Common values and a civic culture, 2. Social order and social control, 3. Social solidarity and reduction in wealth disparities, 4. Social networks and social capital, 5. Place attachment and identity [5]. The authors indicate that the way social cohesion is defined should depend on the main aspects investigated by the researcher, on a specific policy and should also address the most urgent social problems faced by territorial units, such as unemployment, poverty, discrimination, exclusion or any other problems that the researcher deems relevant [5].

In the literature a lot of attention has been paid to concepts of social cohesion are defined in terms of instruments enabling the achievement of cohesion, which is known as the means-end approach. In this case, the definition contains conditions that need to be met in order to ensure social cohesion [15]. Such concepts, representing the political approach, have been proposed, among others, by Berger-Schmitt [33,34] and Noll [35]. They demonstrated that social cohesion consists of two analytically different dimensions: inequality and social capital. The first refers to the question of promoting equal opportunities and reducing disparities and inequalities. The goal of the second one involves the strengthening of social relations, interactions and ties and comprises all aspects generally regarded as social capital [34]. The concepts have been criticized for being based on the definition of social cohesion defined in terms of conditions that can foster its development. An alternative proposal was advanced by Duhaime [5], who identified two components of social cohesion: access to formal economic and governmental institutions and access to family and community-based, face-to-face relations. Indicators identified in this concept (in line with the means-end approach), in many cases made reference to conditions favouring the development of social cohesion [3].

Another concept worth mentioning was formulated in 2006 by Chan et al. [5]. Following Bernard’s definition, social cohesion was described as “a state of affairs concerning both vertical and the horizontal interactions among members of society as characterized by a set of attitudes and norms that includes trust, sense of belongingness and the willingness to participate and help as well as their behavioural manifestations” [5]. While retaining the political and sociocultural sphere of social cohesion, the authors decided to exclude the economic dimension, arguing for a minimalist definition which ignores all characteristics regarded as factors or determinants of social cohesions, such as equality of opportunities, equality and social integration [6]. It should be emphasized that both Bernard [4] and Chan et al. [5] assert that social cohesion is a property of a group or society, not an individual. This means that even if it is measured at individual level, ultimately such data are aggregated and social cohesion is described at the level of different groups, regions or communities [15].

Following the studies of Bernard [4] and Chan et al. [5], Dickes et al. [15] and Dickes and Valentova [14] proposed their own definitions of social cohesion, which also did not account for the economic dimension. Four elements of social cohesion were distinguished: institutional trust (i.e., legitimacy vs. illegitimacy), solidarity and concern for the common good (i.e., acceptance vs. rejection), political participation and socio-cultural participation.

When one analyses the conceptualisation of social cohesion, it is possible to track the direction of changes which reflect the increasing role of socio-cultural and political indicators and the omission of the economic sphere. In contrast, a similar review of social cohesion research reveals that the emphasis is shifting towards spatial analysis of social cohesion, which takes into account not only the national but also regional and local level [36,37,38,39]. Moreover, a given society’s level of social cohesion can only be properly assessed when it can be compared across territorial units and over time. This can be achieved using methods of measuring social cohesion applied in the EU or proposed by OECD (Organisation for Economic Cooperation and Development). In the case of studies relating to countries and regions of the European Union, the EU regional Social Progress Index (EU-SPI) has been used since 2016 (https://ec.europa.eu/regional_policy/en/information/maps/social_progress). For purposes of the index, social progress is defined as “a society’s capacity to meet the basic human needs of its citizens, to establish the basis for people and communities to improve and sustain their quality of life and to create the conditions for people to reach their full potential” [40] (p. 91). The EU-SPI is calculated on the basis of variables representing the socio-cultural and political dimension. The economic dimension is deliberately excluded, which facilitates the assessment of the level of social cohesion, as economic indicators make it difficult to distinguish between causes and effects of this level in the final analysis. The EU-SPI is consistent with the overall framework of the global Social Progress Index and is based on fifty indicators, primarily from Eurostat. It covers three dimensions of social progress [41]:

• basic human needs (nutrition and basic medical care, water and sanitation, shelter housing, personal safety),
• foundations of well-being (access to basic knowledge, access to information and communication, health and wellness, environmental quality),
• opportunity (personal rights, personal freedom and choice, tolerance and inclusion, access to advanced education).

Given the nature of statistical (symbolic interval-valued) data used in the analysis, the empirical research described in the article was based on the approach adopted in studies conducted by EU countries using the EU-SPI. In our study this concept was applied at a lower level of spatial aggregation, namely at province level. These territorial units (Pol. województwo) vary considerably in economic and social terms, reflecting different historical developments in three parts of Poland annexed by three neighbouring countries in the 18th century. As a result, western provinces are generally characterised by a higher level of economic development than the ones in the eastern part of the country. The purpose of the analysis was to determine in this differentiation is reflected in the assessment of the level of social cohesion.

3. Research Methodology

The assessment of social cohesion in the provinces of Poland was performed using four datasets: classic metric data and interval-valued data (three types: min-max, 1st and 9th deciles, 2nd and 8th deciles) by applying a hybrid approach involving multidimensional scaling and linear ordering. Multidimensional scaling made it possible to map 4 datasets describing 16 provinces onto a two-dimensional space; and then results of linear ordering were used to compare rankings of provinces in terms of social cohesion.

The research methodology is a modified approach proposed by Walesiak [42] and Dehnel et al. [18]. The research procedure, which makes it possible to present four types of data in one study, consists of the following steps:

• Select a complex phenomenon that cannot be measured directly. In this study, it was the level of social cohesion.
• Select a set of objects and a set of variables closely related with the complex phenomenon of interest. The study involves measuring characteristics of $n$ objects ($i, k=1,\dots ,n; i, k$—object number) described by means of $m$ variables $(j=1,\dots ,m;j$—variable number). Collected information comprises classic metric data and three types of interval-valued data (min-max, 1st and 9th deciles, 2nd and 8th deciles). Metric data converted into interval-valued data are arranged in the form of data table $X_1={\left[x_{ij}^l,x_{ij}^u\right]}_{n\times m}$ ($x_{ij}^l=x_{ij}^u;i,k=1,\dots ,n;j=1,\dots ,m)$. The three types of interval-valued data min-max, 1st and 9th deciles, 2nd and 8th deciles are arranged in data tables $X_{\mathbf{2}}={\left[x_{ij}^l,x_{ij}^u\right]}_{n\times m}$ ($x_{ij}^l\le x_{ij}^u;i,k=n+1,\dots ,2n;j=1,\dots ,m$), $X_{\mathbf{3}}={\left[x_{ij}^l,x_{ij}^u\right]}_{n\times m}$ ($x_{ij}^l\le x_{ij}^u;i,k=2n+1,\dots ,3n; j=1,\dots ,m)$, $X_{\mathbf{4}}={\left[x_{ij}^l,x_{ij}^u\right]}_{n\times m}$ ($x_{ij}^l\le x_{ij}^u;i,k=3n+1,\dots ,4n; j=1,\dots ,m$).
• Combine the data in the form of a single data table $X^{\prime }={\left[x_{ij}^l,x_{ij}^u\right]}_{4n\times m}$ ($x_{ij}^l\le x_{ij}^u$) containing data tables $X_{\mathbf{1}}$, $X_{\mathbf{2}},$ $X_{\mathbf{3}}$ and $X_{\mathbf{4}}$.
• Add a pattern and anti-pattern object to the set of objects. Variables of interest can be divided into three types of preference variables: stimulants (where higher values are preferred), destimulants (where lower values are preferred), nominants (where the preferred value lies somewhere within the variable range). Formal definitions of stimulants, destimulants can be found in [43] (p. 48) while nominants are defined in [44] (p. 118). These definitions are also provided in [42]. Owing to the structure of the anti-pattern object nominants need to be converted into stimulants. Coordinates of the pattern object represent the most favourable values of preference variables (maximum values for stimulants and minimum values for destimulants). Coordinates of the anti-pattern object represent the least favourable values (minimum values for stimulants and maximum values for destimulants). In the case of symbolic interval-valued variables, coordinates area calculated separately for the lower and upper value of the interval. After including the pattern and anti-pattern object, the joint data table has the form $X={\left[x_{ij}^l,x_{ij}^u\right]}_{\left(4n+2\right)\times m}$ ($x_{ij}^l\le x_{ij}^u$).
• Normalise interval-valued variables and arrange the data in the form of a normalised data table $Z={\left[z_{ij}^l,z_{ij}^u\right]}_{\left(4n+2\right)\times m}$ ($z_{ij}^l\le z_{ij}^u$; $z_{ij}$ normalised observation) for symbolic interval-valued variables. The purpose of normalization is to ensure comparability of variables (cf. [45]). This is achieved by removing units from measurement results and standardizing their orders of magnitude. Symbolic interval-valued data require special normalization treatment. The lower and upper bound of the interval of the j-th variable for $4n+2$ objects ($n$ objects for 4 types of data, pattern and anti-pattern) are combined into one vector containing $2\left(4n+2\right)$ observations. This approach makes it possible to apply normalization methods used for classic metric data. Metric data were normalized using the interval_normalization function from the clusterSim package implemented in the R program [46].
  Normalisation methods can be represented by the following formula (cf. [47]):

  $$z_{ij}=\frac{x_{ij}-A_j}{B_j}$$

  (1)

  where:
  • $x_{ij}\left(z_{ij}\right)$ (normalised) value of j-th variable for i-th object,
  • $A_j$—shift parameter to arbitrary zero for j-th variable (see

    Table 1. Selected normalisation methods.

    Type	Method	Parameter
    		${\mathit{B}}_{\mathit{j}}$	${\mathit{A}}_{\mathit{j}}$
    n1	Standardisation	$s_j$	${\overline{x}}_j$
    n2	Positional standardisation	$ma{d}_j$	$me{d}_j$
    n3	Unitisation	$r_j$	${\overline{x}}_j$
    n3a	Positional unitisation	$r_j$	$me{d}_j$
    n5	Normalisation to $\left[-1;1\right]$ range	$\underset{i}{\max }\left|x_{ij}-{\overline{x}}_j\right|$	${\overline{x}}_j$
    n5a	Positional normalisation to $\left[-1;1\right]$ range	$\underset{i}{\max }\left|x_{ij}-me{d}_j\right|$	$me{d}_j$
    n12a	Positional normalisation	$\sqrt{{\displaystyle \sum }_{i=1}^n{\left(x_{ij}-me{d}_j\right)}^2}$	$me{d}_j$

    ${\overline{x}}_j$—mean for j-th variable, $s_j$—standard deviation for j-th variable $r_j$—range for j-th variable, $me{d}_j=\underset{i}{\mathrm{med}}\left(x_{ij}\right)$—median for j-th variable, $ma{d}_j=\underset{i}{\mathrm{mad}}\left(x_{ij}\right)$—median absolute deviation for j-th variable.

    ),
  • $B_j$—scaling parameter for the j-th variable (see Table 1).
• Select a measure of distance for symbolic interval-valued data (see

  Table 2. Distance measures for symbolic interval-valued data.

  Symbol	Name	Distance Measure ${\mathit{\delta }}_{\mathit{i}\mathit{k}}\left(\mathbf{Z}\right)$
  U_2_q1	Ichino-Yaguchi $q=1, \gamma =0.5$	${\displaystyle \sum }_{j=1}^m\phi \left(z_{ij},z_{kj}\right)$
  U_2_q2	Euclidean Ichino-Yaguchi $q=2, \gamma =0.5$	$\sqrt{{\displaystyle \sum }_{j=1}^m\phi {\left(z_{ij},z_{kj}\right)}^2}$
  H_q1	Hausdorff $q=1$	${\displaystyle \sum }_{j=1}^m\left[\max \left(\left|z_{ij}^l-z_{kj}^l\right|,\left|z_{ij}^u-z_{kj}^u\right|\right)\right]$
  H_q2	Euclidean Hausdorff $q=2$	${\left\{{\displaystyle \sum }_{j=1}^m{\left[\max \left(\left|z_{ij}^l-z_{kj}^l\right|,\left|z_{ij}^u-z_{kj}^u\right|\right)\right]}^2\right\}}^{1/2}$

  $z_{ij}=\left[z_{ij}^l,z_{ij}^u\right]$; $\phi \left(z_{ij},z_{kj}\right)=\left|z_{ij}\oplus z_{kj}\right|-\left|z_{ij}\otimes z_{kj}\right|+\gamma \left(2·\left|z_{ij}\otimes z_{kj}\right|-\left|z_{ij}\right|-\left|z_{kj}\right|\right)$; $| |$—interval length; $z_{ij}\oplus z_{kj}=z_{ij}{{\displaystyle \cup }}^{\text{}}{z}_{kj}$; $z_{ij}\otimes z_{kj}=z_{ij}{{\displaystyle \cup }}^{}{z}_{kj}$. Source: [48,49].

  ), calculate distances and arrange into a distance matrix $\delta ={\left[{\delta }_{ik}\left(Z\right)\right]}_{\left(4n+2\right)x\left(4n+2\right)}$.
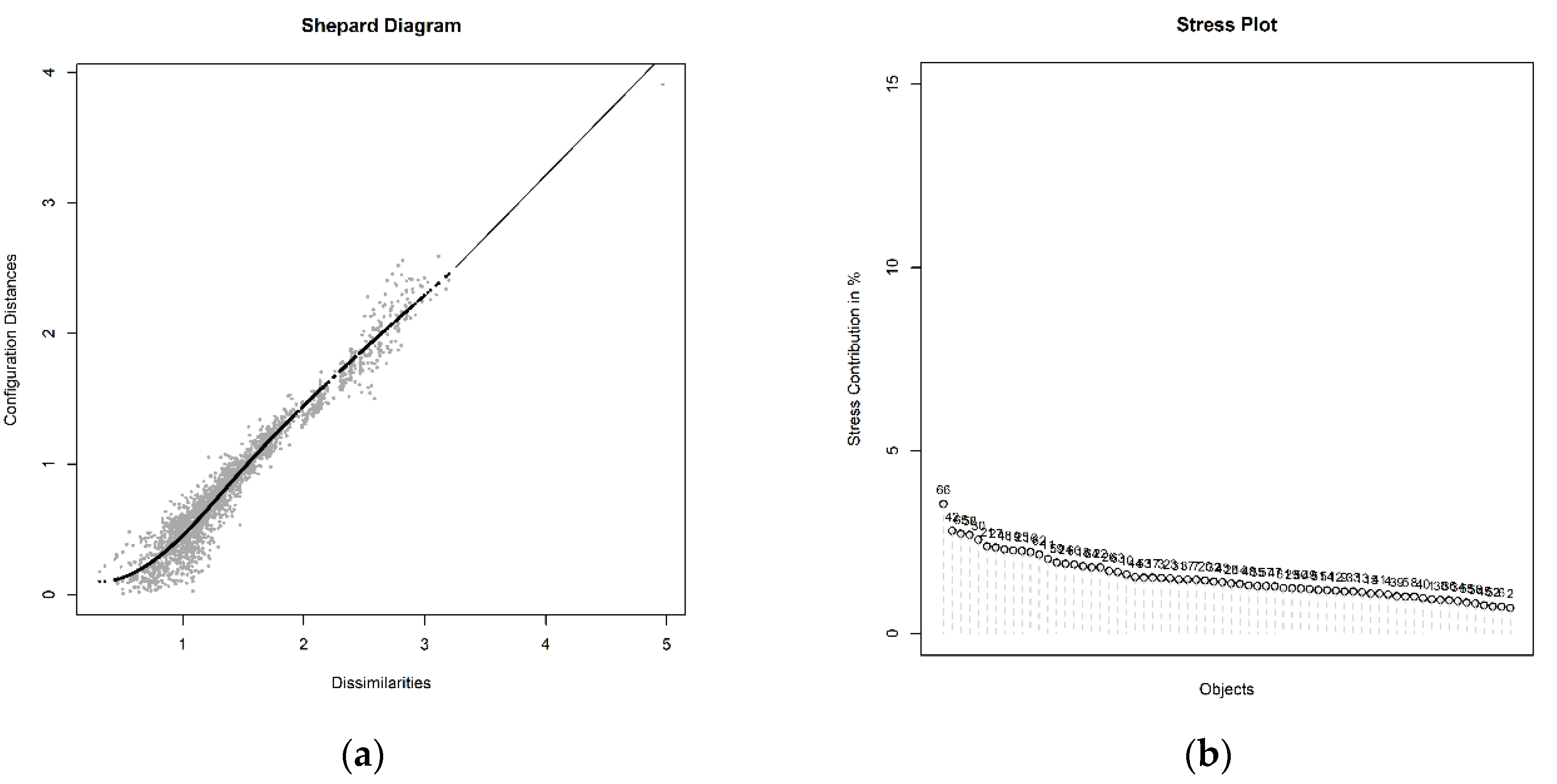
• Conduct multidimensional scaling (MDS): $f:{\delta }_{ik}\left(Z\right)\to d_{ik}\left(V\right)$ for all pairs $\left(i,k\right)$, where f denotes distance mapping from m-dimensional space ${\delta }_{ik}\left(Z\right)$ into corresponding distances $d_{ik}\left(V\right)$ in q-dimensional space ($q<m).$ To enable graphic presentation of results q is set to 2. Distances $d_{ik}\left(V\right)$ are unknown. The iterative procedure, implemented in the smacof algorithm, used to find configuration $V$ (given q dimensions) and calculate distance matrix $d_{ik}\left(V\right)$, is presented in [50] (pp. 204–205).

The solution used in the study makes it possible to select an optimal procedure of multidimensional scaling (MDS) for a given normalization method (Table 1), distance measure for symbolic interval-valued data (Table 2) and scaling models (ratio, interval, spline—polynomial function of second and third degree), available in the mdsOpt R package [46], which use the smacofSym function from the smacof package [51]. Two criteria were used to choose the optimal MDS procedure: the value of Kruskal’s $STRESS-1$ goodness-of-fit function and Hirschman-Herfindahl Index ($HHI$), calculated for percentage shares of objects in the value of the $STRESS-1$ function (stress per point). Out of MDS procedures for which $STRESS{-1}_p\le s$ ($s$—acceptable value of the goodness-of-fit measure), we select one for which $\underset{p}{\min }\left\{HH{I}_p\right\}$ ($p$—number of the MDS procedure). More information about the selection of the optimal MDS procedure can be found in the mdsOpt package vignette.

8.

In the end, as a result of applying multidimensional scaling, we obtain a two-dimensional data matrix $V={[v_{ij}]}_{\left(4n+2\right)xq}$ ($q=2$). Depending on the location of the pattern and anti-pattern object in the two-dimensional scaling space the coordinate system needs to be rotated by an angle of $\phi$ according to the formula:

$$\left[{v^{\prime }}_{ij}{]}_{\left(4n+2\right)x2}=\right[v_{ij}{]}_{\left(4n+2\right)x2}\times D$$

(2)

where:

• ${[{v^{\prime }}_{ij}]}_{\left(4n+2\right)x2}$—data matrix in a two-dimensional scaling space after rotating the coordinate system by an angle of $\phi$,
• $D=\left[\begin{array}{cc}cos\phi & -sin\phi \\ sin\phi & cos\phi \end{array}\right]$—rotation matrix.

The rotation does not change the arrangement of objects relative to one another but makes it possible to position the set axis connecting the pattern and anti-pattern along the identity line, which improves the visualization of results.

9.

Visualise and interpret the results (of multidimensional scaling) in a two-dimensional space. This is done by first joining two points, representing the anti-pattern and pattern, by a straight line to form the so-called set axis in the diagram. Then isoquants of development (curves of equal development) are drawn from the pattern point. Objects located between the isoquants represent a similar level of development. The same level can be achieved by objects located at different points along the same isoquant of development (due to a different configuration of variable values).

10.

Order objects according to the value of the aggregate measure $d_i$ based on the Euclidean distance from the pattern object [43]:

$$d_i=1-\sqrt{{\displaystyle \sum }_{j=1}^2{(v_{ij}-v_{+j})}^2}/\sqrt{{\displaystyle \sum }_{j=1}^2{(v_{+j}-v_{-j})}^2}$$

(3)

where: $v_{ij}$—j-th coordinate for i-th object in the two-dimensional MDS space, $v_{+j}\left(v_{-j}\right)$—j-th coordinate for the pattern (anti-pattern) object in the two-dimensional MDS space.

Values of the aggregate measure $d_i$ belong to the interval $\left[0;1\right]$. The higher the value of $d_i$, the higher the social cohesion of the objects. The objects are arranged according to descending values of the aggregate measure (3).

4. Data

Following the approach adopted in studies of social cohesion using the regional EU-SPI, three dimensions are considered: basic human needs, foundations of well-being and opportunities. Under this approach, the assessment of social cohesion in the provinces of Poland was carried out on the basis of 25 metric variables (see

Table 3. Variables applied in the assessment of social cohesion in the provinces of Poland.

Dimensions	Variables
Basic human needs	x1—mean gross monthly wage in PLN (Polish new zloty)
	x2—total unemployment rate in %
	x3—mean useful floor area of a dwelling per inhabitant in m2
	x4—average number of persons per room
	x5—length of the sewerage network in relation to the length of the water supply network in %
	x6 – number of doctors and dentists per 10,000 population
	x7—crimes reported (criminal offenses, against life and health, against property) per 10,000 population
	x8—road accidents per 100,000 population
Foundations	x9—users of water treatment services (% of total population)
of well-being	x10—percentage of all dwellings equipped with central heating
	x11—children enrolled in day-care centres per 1000 children up to the age of 3
	x12—children enrolled in nursery schools per 1000 children aged 3–5
	x13—students taking obligatory classes of English in primary and intermediate schools (% of all students)
	x14—members of sports clubs per 1,000 population
	x15—people participating in cultural events (organised by cultural centres and clubs) per 1000 population
	x16—area of public greenspace (parks, residential greenspace) per 10,000 population (in ha)
	x17—length of municipal and district improved hard surface roads per 10,000 population (in km)
	x18—death rate among persons below the age of 60
Opportunities	x19—dependency ratio (ratio of the dependent and elderly population per 100 working age population)
	$x{20}^N$—percentage share of women in the labour force
	x21—percentage share of young adults (up to the age of 25) among registered unemployed
	x22—percentage share of long-term unemployed (over 12 months) in the population of registered unemployed in %
	x23—places in stationary social welfare facilities per 10,000 population
	x24—voter turnout local elections (for municipal authorities and town councils with district rights) in 2018 in %
	x25—beneficiaries of social assistance at the place of residence (below the means test threshold) per 1000 population

).

Variables x1, x3, x5, x6, x9-x17, x23 and x24 represent stimulants (where higher values are more preferred), variables x2, x4, x7, x8, x18, x19, x21, x22 and x25 take the form of destimulants (where lower values are more preferred), and x20 is a nominant (with the nominal value of 50%). Statistical data for the 25 variables for 2018 come from the Local Data Bank maintained by Statistics Poland. The nominant variable $x{20}^N$ was converted into a stymulant according to the difference formula: $x20=\left|x{20}_{}^N-50\right|$.

5. Results of the Empirical Study

5.1. Results for Metric and Interval-Valued Data

In line with the procedure described in Section 3, four types of data—classic metric data and three types of symbolic interval-valued data (min-max, 1st and 9th deciles, 2nd and 8th deciles)—were mapped into a two-dimensional space and then rankings of provinces in Poland were compared in terms of social cohesion.

Data on social cohesion in the 16 provinces of Poland, described by 25 variables, were arranged in a data matrix $X_1^{\prime }={\left[x_{ij}\right]}_{16\times 25}$. Because the data were to be combined with symbolic interval-valued data, they had to be put in a data table $X_1={\left[x_{ij}^l,x_{ij}^u\right]}_{16\times 25}$ ($x_{ij}^l=x_{ij}^u;i,k=1,\dots ,16)$.

Poland has a three-tier system of administrative division, consisting of 16 provinces (Pol. województwo), 380 districts (Pol. powiat) and 2477 communes (Pol. gmina). In order to obtain symbolic interval-valued data, classic metric data on social cohesion in 380 districts described by 25 variables were aggregated at province level. The lower and upper bound of the interval for each variable in each province was obtained by calculating the minimum and maximum, 1st and 9th deciles, 2nd and 8th deciles, using district-level data. Interval-valued data (min-max, 1st and 9th deciles, 2nd and 8th deciles) were arranged in three data tables $X_2={\left[x_{ij}^l,x_{ij}^u\right]}_{16\times 25}$ ($x_{ij}^l\le x_{ij}^u;i,k=17,\dots ,32$), $X_3={\left[x_{ij}^l,x_{ij}^u\right]}_{16\times 25}$ ($x_{ij}^l\le x_{ij}^u;i,k=33,\dots ,48)$, $X_4={\left[x_{ij}^l,x_{ij}^u\right]}_{16\times 25}$ ($x_{ij}^l\le x_{ij}^u;i,k=49,\dots ,64$).

The data tables $X_1$, $X_2$, $X_3$ and $X_4$ were combined into one data table $X^{\prime }={\left[x_{ij}^l,x_{ij}^u\right]}_{64\times 25}$. After adding the pattern and anti-pattern object the final dataset was a data table $X={\left[x_{ij}^l,x_{ij}^u\right]}_{66\times 25}$ ($x_{ij}^l\le x_{ij}^u;i,k=1,\dots ,66$).

The optimal scaling procedure was selected after testing combinations of seven normalization methods (n1, n2, n3, n3a, n5, n5a, n12a—see Table 1), four distance measures for interval-valued data (Ichino-Yaguchi, Euclidean Ichino-Yaguchi, Hausdorff, Euclidean Hausdorff—see Table 2) and four MDS models (ratio, interval, polynomial function of second and third degree), yielding a total of 112 MDS procedures. Values of Kruskal’s STRESS-1 belong to the interval $\left[0.097572;0.183817\right]$. Of the MDS procedures for which $STRESS-1_p\le 0.120478$ (acceptable value of the goodness-of-fit measure calculated as a median), we selected the combination (using the optSmacofSymInterval function from the mdsOpt R package) for which $\underset{p}{\min }\left\{HH{I}_p\right\}=174.2$. This procedure involves normalisation n5 (normalisation to $\left[-1;1\right]$ range), the scaling model based on polynomial function of the 3^rd degree and the Euclidean Hausdorff distance. For this MDS procedure $STRESS-1=0.120065$.

The Shepard diagram (Figure 1a) and the Stress Plot (Figure 1b) confirm the correctness of the selected multidimensional scaling procedure.

Figure 2 shows results of multidimensional scaling of 16 provinces of Poland for four types of data according to the level of social cohesion in 2018. In the diagram the anti-pattern (AP) object and the pattern (P) object are connected by a straight line, known as the set axis. Six isoquants of development (curves of equal development) were arbitrarily identified, which divided the set axis into six equal parts. Isoquants located further away from the pattern object represent a lower level of social cohesion.

The results made it possible to assess the level of social cohesion in the provinces using four types of data simultaneously. One thing worth noting in Figure 2 is the arrangement of provinces in relation to the set axis $\mathrm{AP}-\mathrm{P}$. Sets of provinces based on symbolic interval-valued data are located increasingly further away from the set based on metric data ($x_{ij}^l=x_{ij}^u$), as the width of the interval for each set increases (2nd and 8th deciles, 1st and 9th deciles, minimum and maximum).

Table 4. Rankings of 16 provinces of Poland for four types of data according to the level of social cohesion in 2018 (value of measure $d_i$ ).

Province	no	Metric	Rank	d2-8	Rank	d1-9	Rank	Min-Max	Rank
Mazowieckie	16	0.5472	1	0.4348	10	0.4400	12	0.4161	13
Dolnośląskie	6	0.5229	2	0.5040	5	0.5316	4	0.5641	5
Śląskie	2	0.5042	3	0.5410	1	0.5450	3	0.5887	3
Opolskie	7	0.5035	4	0.5125	3	0.5283	5	0.6116	1
Lubuskie	3	0.4904	5	0.5204	2	0.5465	2	0.6048	2
Wielkopolskie	4	0.4832	6	0.4901	7	0.5177	7	0.5273	6
Pomorskie	9	0.4772	7	0.5113	4	0.5254	6	0.5203	7
Zachodniopomorskie	5	0.4765	8	0.5034	6	0.5473	1	0.5657	4
Małopolskie	1	0.4546	9	0.4578	8	0.4732	9	0.4413	10
Łódzkie	11	0.4431	10	0.4531	9	0.4684	10	0.4736	8
Podlaskie	15	0.4311	11	0.3786	16	0.4009	15	0.3727	15
Kujawsko-Pomorskie	8	0.4202	12	0.4121	13	0.4215	13	0.3805	14
Świętokrzyskie	12	0.4117	13	0.3933	14	0.3959	16	0.4268	12
Lubelskie	13	0.4058	14	0.4255	11	0.4529	11	0.3714	16
Warmińsko-Mazurskie	10	0.3874	15	0.3835	15	0.4010	14	0.4517	9
Podkarpackie	14	0.3849	16	0.4214	12	0.4746	8	0.4274	11
Parameters
Mean		0.4590		0.4589		0.4794		0.4840
Standard deviation		0.0477		0.0518		0.0543		0.0821
Median		0.4656		0.4555		0.4739		0.4627
Median absolute deviation		0.0568		0.0715		0.0792		0.1088

metric—metric data; d2-8—symbolic interval-valued data comprising 2nd and 8th decile (60% of observations), d1-9—symbolic interval-valued data comprising 1st and 9th decile (80% of observations); min-max—symbolic interval-valued data comprising minimum and maximum (100% of observations). Source: calculations made using R.

shows a ranking of 16 provinces for four types of data according to the level of social cohesion in 2018. Calculations were made using the clusterSim package.

Moreover, the dispersion of provinces, measured by the standard deviation and median absolute deviation (Table 4), increases as one moves from results based on metric data to those based on symbolic interval-valued data (with increasing interval width). The width of each set of provinces with respect to the set axis $\mathrm{AP}-\mathrm{P}$ increasing as the its interval width increases (it is the smallest for metric data, where $x_{ij}^l=x_{ij}^u$, and largest for symbolic interval-valued data comprising 100% observations, from minimum to maximum).

5.2. Comparative Analysis of the Results in the Assessment of Social Cohesion

The rankings of provinces of Poland according to the level of social cohesion were compared on the basis of the aggregate measure $d_i$ for four types of data (see Table 4): metric data, symbolic interval-valued data comprising 2nd and 8th decile (60% of observations), 1st and 9th decile (80% of observations) as well as minimum and maximum (100% of observations).

The results of the assessment of social cohesion were compared using two criteria. The first one was based on coefficients of correlation (Spearman’s $rho$ and Kendall’s $tau$) between aggregate measures $d_i$ for the four types of data in order to determine similarities and differences between different rankings of provinces according to social cohesion. The second criterion was the degree of compatibility between rankings of provinces based on individual variables and that based on the aggregate measure $d_i$ for the four types of data. The results of this comparison were used to choose the ranking providing the best reflection of the level of social cohesion in the provinces of Poland. This reason why this second criterion was used is that the overall ranking is the result of rankings obtained for individual variables.

Spearman’s $rho$ and Kendall’s $tau$ coefficients of correlation between aggregate measures $d_i$ calculated for the four types of data are shown in

Table 5. Spearman’s $rho$ and Kendall’s $tau$ coefficients of correlation between aggregate measures $d_i$ for 4 types of data.

Data	m	d2-8	d1-9	mm
m	1.000/1.000
d2-8	0.721/0.567	1.000/1.000
d1-9	0.629/0.417	0.969/0.750	1.000/1.000
mm	0.625/0.450	0.896/0.650	0.877/0.633	1.000/1.000

m—metric data; d2-8—symbolic interval-valued data comprising 2nd and 8th decile (60% of observations), d1-9—symbolic interval-valued data comprising 1st and 9th decile (80% of observations); mm—symbolic interval-valued data comprising minimum and maximum (100% of observations). Source: the authors’ tabulation.

.

For the purpose of cluster analysis, correlation coefficients were converted into distances: $d=\frac{1}{2}\left(1-rho\right)$ and $d=\frac{1}{2}\left(1-tau\right)$. Cluster analysis was used to identify similarities and differences in the rankings of provinces according to the level of social cohesion based on the aggregate measure $d_i$. The results were presented in the form of dendrites (Figure 3), following the Wrocław taxonomic method [52].

Results of the symbolic interval-valued approach differ considerably from the approach based on metric data. Assessments of social cohesion obtained using metric data are closest to results obtained for symbolic interval-valued data comprising 2nd and 8th decile.

The next step involved analysing the degree of compatibility between rankings of provinces based on individual variables and that based on the aggregate measure $d_i$ for the four types of data, using the following procedure:

• 16 provinces of Poland for 4 datasets (metric, min-max, 1st and 9th decile, 2nd and 8th decile) are linearly ordered according to a set of m variables to produce 4 rankings based on aggregate measures $d_i$ (see Table 4).
• For each variable ($j=1,\dots ,m$) a distance between each object and the pattern object is calculated according to the formula (the Ichino-Yaguchi distance for one variable):

  $$d_i^j=1-\left|\phi \left(x_{ij},x_{+j}\right)\right|/\phi \left(x_{+j},x_{-j}\right)$$

  (4)

  where: $x_{ij}=\left[x_{ij}^l,x_{ij}^u\right]$ ($x_{ij}^l\le x_{ij}^u$) interval ($x_{ij}^l=x_{ij}^u$, min-max, 1st and 9th decile, 2nd and 8th decile); $\phi \left(x_{ij},x_{+j}\right)=\left|x_{ij}\oplus x_{+j}\right|-\left|x_{ij}\otimes x_{+j}\right|+0.5\left(2·\left|x_{ij}\otimes x_{+j}\right|-\left|x_{ij}\right|-\left|x_{+j}\right|\right);$ $\left|\right|$ interval length; $x_{ij}\oplus x_{+j}=x_{ij}{{\displaystyle \cup }}^{\text{}}{x}_{+j}$; $x_{ij}\otimes x_{+j}=x_{ij}{{\displaystyle \cap }}^{\text{}}{x}_{+j}$; $x_{+j}$ ($x_{-j}$) interval of the pattern (anti-pattern) object for j-th variable.
  This yields m values of measures $d_i^1, d_i^2, \dots ,d_i^m.$
• The general rankings based on the aggregate measures $d_i$ (step 1) are compared with individual rankings based on measures $d_i^1, d_i^2, \dots ,d_i^m$ (step 2), separately for each data type using Spearman’s $rho$ and Kendall’s $tau$ correlation coefficients.
• For each data type, the median of results obtained in step 3 is calculated. A higher value of the median represents a higher degree of compatibility between rankings based on individual variables and the ranking based on the aggregate measure. The results are displayed in

  Table 6. The degree of compatibility between rankings of objects based on individual variables and the ranking based on the aggregate measure $d_i$.

  No.	Types of Data	Median Value
  		Spearman’s $\mathit{r}\mathit{h}\mathit{o}$	Rank	Kendall’s $\mathit{t}\mathit{a}\mathit{u}$	Rank
  1	Metric data	0.4176	3	0.2667	3
  2	Interval-valued (2nd and 8th deciles)	0.4371	1	0.3333	1
  3	Interval-valued (1st and 9th deciles)	0.4297	2	0.2833	2
  4	Interval-valued (min-max)	0.2676	4	0.1667	4

  Source: the authors’ tabulation.

  .

The greatest degree of compatibility between rankings of objects based on individual variables and the ranking created using the aggregate measure $d_i$ was obtained for intervals based on 2nd and 8th deciles. The use of deciles is an example of a robust approach (helps to eliminate the effect of outliers).

The ranking of provinces obtained on the basis of metric data does not account for the variation in the level of social cohesion between districts of a given province (lower level units). Mazowieckie (16) and Podlaskie (15) are characterised by a big disparity in the level of social cohesion between the leading district (Warsaw and Białystok, respectively) and the other ones. The leading districts have a strong impact on the overall level of variables at province level (metric data), and, consequently, on the more favourable assessment of social cohesion (see Table 4, columns 3 and 4). When metric data are replaced with symbolic interval-valued data, which account for the variation between districts with respect to the variables of interest, these two provinces are located much closer to the anti-pattern (see Figure 2). A switch from metric to interval-valued data comprising 2nd and 8th decile leads to the biggest decline in the values of measure $d_i$ for Mazowieckie ($-0.1124$) and Podlaskie ($-0.0525$). This is also reflected by the ranking drops registered by these provinces: down 9 places (Mazowieckie) and down 5 places (Podlaskie).

The results of the study indicate that the differences in the rankings depend on the degree of variation between districts within a given province. The biggest changes in the ranking of provinces after switching from metric to interval-valued data were observed for those objects (provinces) which were characterised by the relatively biggest variation among districts in terms of the study variables (see Figure 4). The use of interval-valued data comprising 2nd and 8th decile made it possible to eliminate the impact of outliers. Provinces in which districts were not very different from one another, in both cases occupied the same or similar position in the ranking (see Figure 5).

Figure 6 shows the spatial distribution of Polish provinces in 2018 in terms of the level of social cohesion based on values of measure $d_i$ for metric data and interval-valued data (the approach involving 2nd and 8th deciles). After applying another method of measurement the position of provinces has changed significantly. The provinces were not assessed merely on the basis of mean values, which can easily be affected by outliers, but also by accounting for how the variables varied across districts. In the case of provinces, districts classified as spatial poles of growth behave like extreme observations and can strongly influence the measurement for the entire province they belong to. This phenomenon is exemplified by measurements for the province of Mazowieckie, which are strongly affected by the district of Warsaw. The proposed modification of the method (using of interval-valued data) has made it possible to avoid this problem.

The assessment of the level of social cohesion across provinces on the basis of interval-valued data (the approach involving 2nd and 8th deciles) is clearly consistent with the assessment of the level of economic development. Provinces situated in Western Poland, characterised by a higher level of economic development, have also a higher level of social cohesion. It should be assumed that such a system of spatial differentiation results to a large extent from historical conditions, mainly related to the period of partitions (1795–1918) and changes after World War II.

6. Discussion and Conclusions

As a result of economic changes there is a growing demand for assessment of social cohesion. It plays an important role both in the economic and social sphere not only for the country as a whole but, more importantly, at the regional level. This is because there is a need to develop a methodology dedicated to this area of interest.

In the study the level of social cohesion in provinces of Poland in 2018 was assessed using a hybrid approach combining multidimensional scaling and linear ordering. The traditional approach is conducted using classic metric data and it does not account for the variation between lower level units (i.e., districts). The authors propose a methodology which makes this possible. The dataset containing the classic metric data was extended to symbolic interval-valued data (three data types: min-max, 1st decile and 9th decile, 2nd decile and 8th decile) and used in the analysis. In addition to producing a ranking of provinces according to the level of social cohesion, the results of assessment were presented in a two-dimensional space.

The results of the symbolic interval-valued approach differ considerably from those obtained using metric data (see Table 4 and dendrite diagrams in Figure 3). The differences become more evident, the wider the intervals are. The biggest degree of similarity between rankings of objects based on individual variables and the ranking based on the aggregate measure was obtained for intervals based on 2nd decile and 8th decile comprising 60% of observations at district level. In this case, social cohesion in the provinces was not assessed on the basis of atomic variable values, but using information from 60% of districts (the interval between 2nd and 8th decile). This approach made it possible to take into account the degree of variation in social cohesion between lower level units (districts) within a given province. The use of 2nd decile and 8th decile is an example of a robust approach, which is used for eliminating the effect of outliers.

The proposed modification makes it possible to assess social cohesion in provinces not only on the basis of a single real number (metric data), but also by taking into account characteristics of particular districts within each province (interval-valued data). It was found that the assessment of social cohesion in provinces based on interval-valued data is strongly affected by lower level units (districts). The overall assessment of a given province does not depend on one or two districts but on all of them. Decision makers at province level should therefore ensure that all districts develop more or less uniformly.

The novelty of the study presented in this article consists in jointly mapping, by means of a hybrid approach combining multidimensional scaling and linear ordering, classic metric data and symbolic interval-valued data (three data types: min-max, 1st decile and 9th decile, 2nd decile and 8th decile) in one chart. This approach makes it possible to take into account the degree of variation in social cohesion between lower level units (districts) within a given province.

It is worth adding that the method of assessing the level of social cohesion in territorial units proposed in the article does not require an additional survey, as it relies on secondary data sources. However, its application is limited by the availability of appropriate data. Not all phenomena associated with social cohesion are measured by official statistics. The situation looks different regarding the assessment of social cohesion based on primary data. In such cases, the researcher can include all dimensions of social cohesion when designing the survey questionnaire.

All calculations were performed using R scripts written by the authors.