Optimization of Remanufacturing Disassembly Line Balance Considering Multiple Failures and Material Hazards

Abstract

End-of-life (EOL) electromechanical products often have multiple failure characteristics and material hazard attributes. These factors create uncertain disassembly task sequences and affect the remanufacturing cost, environmental sustainability, and disassembly efficiency of the remanufacturing disassembly line system. To address this problem, a novel multi-constraint remanufacturing disassembly line balancing model (MC-RDLBM) is constructed in this article, which accounts for the failure characteristics of the parts and material hazard constraints. To assign the disassembly task reasonably, a disassembly priority decision-making model was presented to describe the relationship between the failure layer, the material hazards layer, and the economic feasibility layer. Furthermore, the multi-objective non-dominated sorting genetic algorithm II (NSGA-II) optimization for the MC-RDLBM is improved. To increase the convergence speed of the algorithm, an initial population construction method is designed, which includes the component failure and material hazards. Moreover, a novel genetic algorithm evolution rule with a Pareto non-dominant relation and crowded distance constraint is established, which expands the search scope of the chromosome’s autonomous evolution and avoids local convergence. Furthermore, a Pareto grade-based evaluation strategy for non-dominant solutions is proposed to eliminate the invalid remanufacturing disassembly task sequences. Finally, a case study verified the effectiveness and feasibility of the proposed method.

1. Introduction

Remanufacturing aims to recover the residual value of end-of-life (EOL) products. Disassembly is the key step of remanufacturing. The remanufacturing disassembly line is a standardized disassembly line for obtaining the batch remanufacturing cores. A reasonable remanufacturing disassembly line can improve the mass disassembly efficiency and reduce the remanufacturing cost.

At present, the study of the disassembly line balancing problem (DLBP) is attracting widespread attention. Based on Future Study Realization Analysis (FSRA) [1], the DLBP must be further studied in terms of various factors, including optimization efficiency, combination with the actual remanufacturing enterprises, and its environmental performance [2]. It is particularly important to establish a disassembly line system by combining aspects such as the disassembly task priority assignment method, the uncertainty of the disassembled parts, and the product conditions with the actual disassembly operation [3].

Unlike a traditional disassembly line, a remanufacturing disassembly line (RDL) aims to obtain remanufacturing cores with the minimum remanufacturing costs and environmental impact. The EOL electromechanical products often have a large number of uncertain failure modes and material hazard attributes, which are closely related to a product’s remanufacturability. The lower the degree of failure is, the better the remanufacturability is. Similarly, the higher the material hazards are, the greater the environmental impact is and the higher the disassembly priority of the remanufacturing disassembly line system becomes. Therefore, it is of great significance to study the RDLB under the influence of multiple failures and material hazards.

The remainder of this article is organized as follows. In Section 2, a literature review is presented and the motivation for this study is provided. In Section 3, the multi-constraint remanufacturing disassembly line balancing model (MC-RDLBM) considering failures and material hazards is constructed. The optimization of the MC-RDLBM based on the fast elitist non-dominated sorting genetic algorithm (ENSGA- II) is described in Section 4. In Section 5, the proposed model and method are validated with a case study. Concluding remarks are provided in Section 6.

2. Literature Review

2.1. Disassembly Line Balancing Problem

The classical DLBP methods include mathematical programming and heuristic and meta-heuristic optimization. Mathematical programming is an important branch of operations research, and its objective is numerical optimization. For example, Duta adopted the mathematical planning method to integrate constraints and used a heuristic method to obtain the optimal disassembly line scheduling scheme [4]. To solve the DLBP with uncertainty of the product life and supply quantity, a new mixed integer programming model was presented [5]. This method has the advantage of high solution precision. However, it is not suitable for solving the balance optimization problem of a largescale disassembly line.

Heuristic methods overcome the deficiencies of mathematical programming for solving largescale disassembly line problems. For example, an integer programming model based on an assumed cycle time for interval numbers was established by considering the uncertainty of the disassembly process [6]. Avikal et al. [7] used the Kano model, fuzzy analytic hierarchy process (AHP), and modified technique for Order Preference by Similarity to an Ideal Solution (M-TOPSIS) method to solve the DLBP. Ren et al. [8] proposed a disassembly line balanced multi-objective optimization method based on the 2-optimal algorithm and multi-criteria decision making (MCDM). The DLBP also can be solved based on Monte Carlo reinforcement learning methods [9]. The disassembly line model under a random working environment was proposed and solved using a genetic algorithm (GA) [10]. These methods are all heuristic methods, which greatly improve the solution speed. However, the solution quality is low because these methods become trapped in local optima.

At present, meta-heuristic algorithms, such as the multi-objective extremum GA, Pareto firefly algorithm, improved teaching learning-based optimization algorithm (ITLBO), discrete drosophila multi-objective optimization algorithm, and multi-objective genetic annealing algorithm, have been the main algorithms used to solve the DLBP [11]. For example, Gao et al. solved the DLBP of a typical drive system using the artificial bee colony algorithm, which can not only save energy and reduce consumption but also improve efficiency [12]. In addition, focusing on the uncertainty of the time between disassembly tasks and the NP (non-deterministic polynomial time) attribute of the disassembly line, some algorithms, such as the local iterative search algorithm [13], discrete flower pollination algorithm with four heuristic rules [14], triangular fuzzy number, and an artificial fish swarm algorithm [15], are proposed. These methods often need to combine multi-criteria decision-making methods to obtain the optimal result, which are complex processes. Therefore, when solving largescale DLBP problems, it is of great significance to explore and study new and efficient intelligent optimization methods, new coding methods, and efficient search strategies.

2.2. NSGA-II

As a result of its suitability for parallel computing and high robustness, genetic algorithms were widely used to solve the DLBP in the early stage [16]. When the processing time of the disassembly task is a triangular fuzzy number, the genetic algorithm has been proven to exhibit better solution performance [17]. However, the genetic algorithm cannot meet the new requirements of the DLBP, and the genetic algorithm integrated with Pareto screening technology and extreme value optimization (EO) has better solution performance [18]. To solve the multi-objective balance optimization problem, the GA has also developed into the non-dominated sorting genetic algorithm II (NSGA-II). Furthermore, it has been integrated with an elitist strategy to improve its computational efficiency [19]. For example, the NSGA-II was applied to solve the balancing problem of a double-sided assembly line by adding multi-criteria decision-making techniques to handle noninferior solution sets [20]. However, as the product complexity increased, the Pareto optimal set became larger when solving the multi-objective disassembly line problem based on the NSGA-II algorithm, which will introduce difficult choices for remanufacturing enterprises.

2.3. Study Motivation

The DLBP is a multi-objective NP-hard optimization problem, which has been studied from the aspects of economics [21,22,23,24], harmfulness [25], cost [26,27], efficiency [28,29,30,31], and energy consumption [32,33]. For example, Zhu et al. considered the hazards of the disassembly operation in the DLBP. Kazancoglu and Ozturkoglu proposed a matrix method for the quantification of the environmental hazard attributes of parts, and a disassembly line balance model was established [2].

The goal of the RDLB is to obtain the remanufacturing cores with the minimum remanufacturing cost and environmental impact. To simulate the actual working conditions, the parts with high remanufacturing value and containing materials that are hazardous to the environment should be given priority for disassembly. To our knowledge, the influence of the failure mode has rarely been considered in the DLBP. Thus, a multi-constraint remanufacturing disassembly line balance model (MC-RDLBM) considering multiple failures of parts and material hazards was constructed and optimized based on the improved NSGA-II algorithm in the study. To increase the computational efficiency, the ENSGA-II method was developed by integrating the multi-objective NSGA-II algorithm with the fast-elitist strategy to evaluate a non-dominated sorting method. Furthermore, MATLAB^® software has many new intelligent algorithm toolboxes and is widely used in engineering calculation and numerical analysis [27,34]. Thus, the prototype system of the multi-constraint remanufacturing disassembly line balance (MC-RDLB) was developed based on MATLAB^®.

3. Multi-constraint Remanufacturing Disassembly Line Balancing Model

A remanufacturing disassembly line of EOL electromechanical products aims to assign disassembly tasks properly to workstations based on factors such as the disassembly priority and remanufacturing cost. Theoretically, properties such as the materials hazard, failure mode, and failure degree of the parts will affect their remanufacturability and remanufacturing cost. The disassembly priority of the parts is decided by the assembly constraints between the parts and their own attributes, both of which have a master–slave relationship. The assembly constraints between the parts are the main conditions that cannot be violated. Their own attributes are constrained to be subordinate, including multiple failure modes and material hazards, which are independent of each other. The parts with better remanufacturability have higher disassembly priorities.

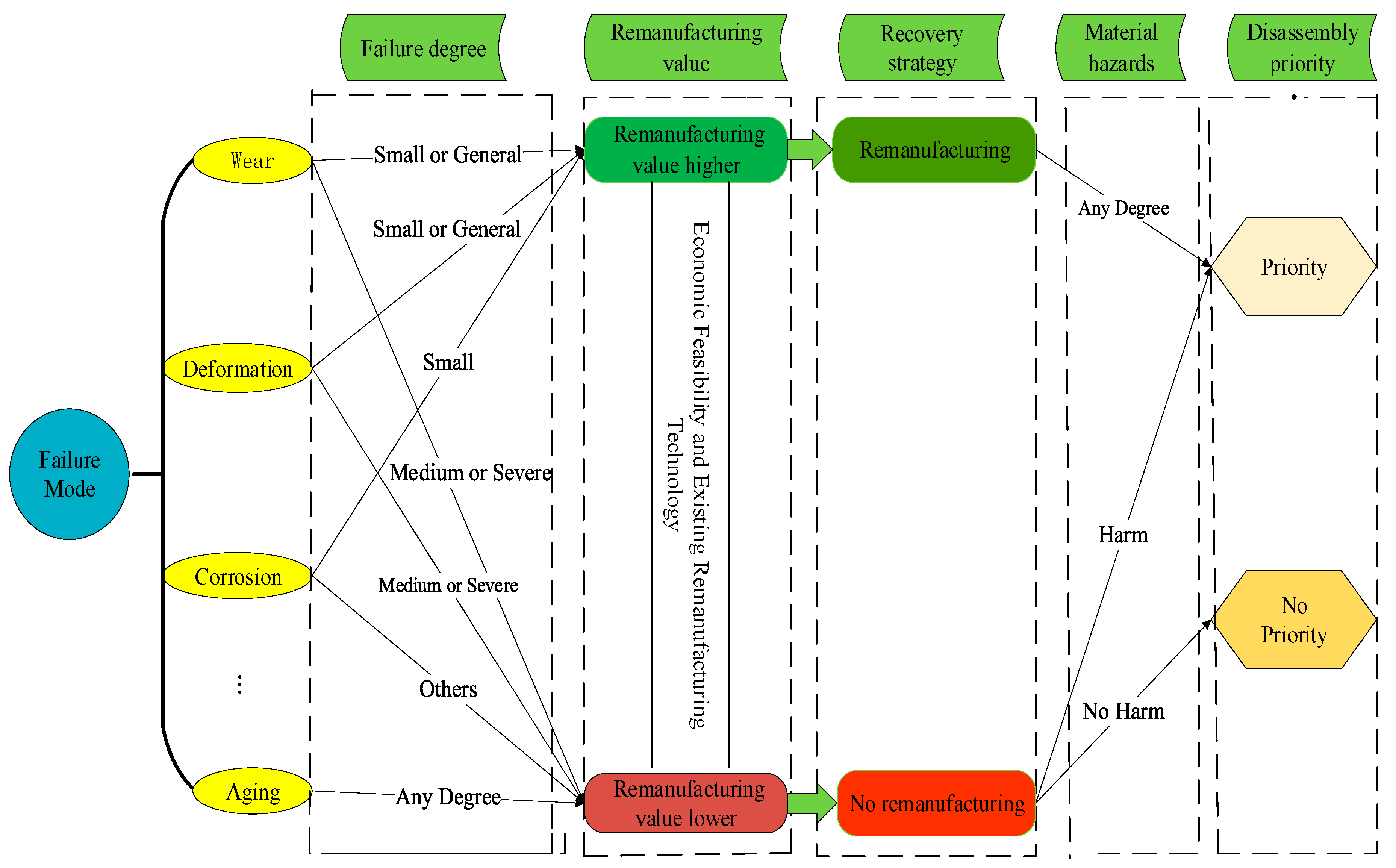
3.1. Remanufacturing Disassembly Priority Decision Based on Multiple Failures

EOL electromechanical products often have multiple failure modes, such as wear, deformation, corrosion, and aging. The failure degree is usually divided into small, general, medium, and severe failure [35]. The multiple failure characteristics of EOL products are judged by expert experience and inspection tools. The existing remanufacturing technology and remanufacturing costs are closely related to the remanufacturability of parts. In the remanufacturing disassembly line system, the parts with better remanufacturability should be disassembled as early as possible because of the intuitive remanufacturing benefits.

3.2. Remanufacturing Disassembly Priority Decision Based on Material Hazards

The material hazards of EOL products (e.g., laptop and mobile phone batteries) will create a health threat to the operators and environment pollution. The material hazard degree is generally divided into harmless and harmful. Based on the national standards of EOL product materials for personal safety and environmental pollution, when parts have higher material hazard degrees, they should have higher disassembly priority.

3.3. Remanufacturing Disassembly Priority Decision

To describe the relationship between the disassembly priority, failure modes, failure degree, and material hazards, a disassembly priority decision model was constructed, as shown in Figure 1.

An EOL electromechanical product with m parts is considered, and it is assigned N workstations. Figure 1 can be mapped into the following matrices:

(1)

Failure Mode Matrix C¹

$$C^1=\begin{array}{ccccc}\mathrm{Wear}& \mathrm{D}\mathrm{e}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}& \mathrm{Corrosion}& \mathrm{Aging}\cdots & \\ c^1{}_{11}& c^1{}_{12}& c^1{}_{13}& c^1{}_{14}\cdots & 1\\ c^1{}_{21}& c^1{}_{22}& c^1{}_{23}& c^1{}_{24}\cdots & 2\\ ⋮& ⋮& ⋮& \cdots & ⋮\\ c^1{}_{m1}& c^1{}_{m2}& c^1{}_{m3}& c^1{}_{m4}\cdots & m\end{array}$$

(1)

where $c^1{}_{ij}=\{\begin{array}{ll}0& otherswise\\ 1& \mathrm{part}i\mathrm{has}\mathrm{failure}\mathrm{mode}j\end{array}$.

(2)

Failure Degree Matrix C²

$$C^2=\begin{array}{ccccc}\mathrm{Samll}& \mathrm{General}& \mathrm{Medium}& \mathrm{Severe}& \\ c^2{}_{11}& c^2{}_{12}& c^2{}_{13}& c^2{}_{14}& 1\\ c^2{}_{21}& c^2{}_{22}& c^2{}_{23}& c^2{}_{24}& 2\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ c^2{}_{m1}& c^2{}_{m2}& c^2{}_{m3}& c^2{}_{m4}& m\end{array}$$

(2)

where $c^2{}_{ij}=\{\begin{array}{ll}0& otherswise\\ 1& \mathrm{part}i\mathrm{has}\mathrm{failure}\mathrm{degree}j\end{array}$

(3)

Economic Feasibility Matrix C³

$$C^3={\left\{e_{ij}\right\}}_{m\times 1}$$

(3)

where $e_{ij}=\{\begin{array}{ll}0& \mathrm{otherswise}\\ 1& \mathrm{part}i\mathrm{can}\mathrm{be}\mathrm{remanufactured}\end{array}$.

(4)

Hazard matrix C⁴

$$C^4={\left\{h_{ij}\right\}}_{m\times 1}$$

(4)

where $h_{ij}=\{\begin{array}{ll}0& \mathrm{otherswise}\\ 1& \mathrm{part}i\mathrm{has}\mathrm{material}\mathrm{hazards}\end{array}$.

Thus, the multivariate constraint matrix B can be deduced using the following equations:

$$C^1{}_{(m)}={\left[C^1\right]}^T\otimes C^2$$

(5)

$$C^2{}_{(m)}=C^1{}_{(m)}\times C^3$$

(6)

$$\mathbf{B}=C^2{}_{(m)}\times C^4$$

(7)

where $C_{\left(m\right)}^1$ represents the multiple failure modes and degrees of the parts, and $C_{\left(m\right)}^2$ represents the remanufacturability of parts with multiple failures. A = ${\left\{a_{ij}\right\}}_{m\times m}$ is the disassembly task priority relation matrix, where $a_{ij}\in \left\{0,1\right\}$ and $a_{ij}=1$ means that disassembly task i has priority over disassembly task j. B = ${\left\{b_{ij}\right\}}_{m\times m}$ is the multi-constraint matrix of the parts, where $b_{ij}\in \left\{0,1\right\}$ and $b_{ij}=1$ indicate that disassembly task i has multiple failure modes of components and material hazards, and thus, it should be assigned to the workstation in priority. When decision variable $x_{ir}$ = 1, the ith disassembly task is assigned to the rth workstation. S = ${\left\{s_{ij}\right\}}_{m\times m}$ is the comprehensive priority relation matrix of the disassembly task, where element $s_{ij}\in \left\{0,1,2\right\}$ and S = A + B.

3.4. Construction of Multi-Constraint Remanufacturing Disassembly Line Balance Mathematical Model

It is assumed that the disassembly time of each task is known and that each task is independent. The disassembly process of the EOL products cannot be interrupted, and each disassembly task can only be assigned to one workstation. The cycle time was not less than any disassembly task time, and all the disassembly tasks were executed in an ideal state. Aiming at minimizing the number of workstations and equilibrium rate of the remanufacturing disassembly line, and maximizing the remanufacturing cost, a mathematical model of multi-constraint remanufacturing disassembly line balance (MC-RDLB) optimization problem is presented with multiple constraints related to failures and material hazards. The model is as follows. The notation used in the formulations is listed in

Table 1. Symbol definition.

Symbol	Instructions
m	Number of disassembled parts
$N$	Number of disassembly workstations
CT	Cycle time
M	Number of disassembly tasks for a disassembly workstation
$t_i$	Time required for ith disassembly task
$x_{\mathit{ir}}$	ith disassembly task is assigned to workstation r
$P_i$	Remanufacturing value of disassembled parts in ith disassembly task
$P_i$	Disassembly task set in workstation r
Li	Position of part i in the configuration plan of disassembly line
$s_{ij}$	Disassembly task i takes precedence over disassembly task j
B	Multi-constraint matrix of waste mechanical and electrical products
A	Disassembly task priority relation matrix
S	Disassembly task comprehensive priority relation matrix

.

(1)

Objective functions

The number of disassembly workstations is minimized to reduce the cost of the disassembly line, and the objective function is expressed as follows:

$$\min f_1=N$$

(8)

The balance rate of the workstation represents the load condition of the disassembly line. When the balance rate of the workstation is the minimum, it means that the load of the disassembly line reaches the maximum and the efficiency of the disassembly line is improved. Thus, the objective function of minimizing the workstation equalization rate is defined as follows:

$$\min f_2=\sqrt{{\displaystyle \sum _{r=1}^N(CT-{\displaystyle \sum _{i=1}^M{t}_i\times x_{ir}{)}^2/N}}}$$

(9)

The remanufacturing value index represents the position of the parts in the configuration plan of the disassembly line. The remanufacturing value index is minimized to allow the parts with higher remanufacturing value to be disassembled earlier, which improves the remanufacturing value of the products. The objective function is expressed as follows:

$$\min f_3={\displaystyle \sum _{i=1}^M({\mathrm{L}}_i\times P_i)}$$

(10)

Therefore, the multi-objective function of the multi-constraint remanufacturing disassembly line balance is

$$\min F=(f_1,f_2,f_3)$$

(11)

(2)

Constraint conditions

$${\displaystyle \sum _{r=1}^N{x}_{ir}=1(i=1,2,3,\dots ,M)}$$

(12)

$${\displaystyle \underset{r=1}{\overset{N}{{\displaystyle \cup }}}{S}_r=M}$$

(13)

$${\displaystyle \sum _{i=1}^M{x}_{ir}=S_r,(r=1,2,3,\dots ,N)}$$

(14)

$${\displaystyle \sum _{i=1}^M{x}_{ir}\times t_i\le CT,r=(1,2,3,\dots ,N)}$$

(15)

$${\displaystyle \sum _{r=1}^N(r{x}_{mr}-r{x}_{nr})\ge 0,n=(1,2,3,\dots ,M-1)},m=(2,3,4,\dots ,M)$$

(16)

$$\frac{{\displaystyle \sum _{i=1}^M{t}_i}}{CT}\le N\le M$$

(17)

$${\displaystyle \sum _{j=1}^m{S}_{ij}=0}$$

(18)

In Equations (8)–(11), f₁ represents the number of dismantling workstations N, f₂ represents the equilibrium rate of the disassembly line, f₃ represents the remanufacturing value index of the parts, and f₄ is the multi-objective function.

The constraint sets given by Equations (12)–(16) represent precedence constraints of the disassembly [35]. Constraint set (12) requires that each disassembly task i is only assigned to one disassembly workstation. Constraint set (13) requires that all disassembly tasks in disassembly task set M are assigned. Constraint set (14) represents the number of disassembly tasks in the disassembly workstation r. Constraint set (15) prevents the total execution time $t_i$ of the disassembly task in the disassembly workstation r from exceeding the cycle time CT. Constraint set (16) states that the disassembly task priority relationship cannot be violated. Constraint set (17) requires the number of workstations N of the disassembly line to be within the limit range. Constraint set (18) represents the conditions under which the disassembly task j can be assigned to the disassembly workstation.

4. Optimization of Multi-Constraint Remanufacturing Disassembly Line Balance (MC-RDLB) Based on ENSGA-II

Multi-constraint remanufacturing disassembly line balance (MC-RDLB) is a multi-objective optimization problem (MOP). The dominant genetic algorithm (NSGA-II) is robust and can solve the MOP. Therefore, the ENSGA-II was developed by integrating the multi-objective NSGA-II algorithm with the fast-elitist evaluation non-dominated sorting method to solve the MC-RDLB.

4.1. Chromosome Encoding and Decoding

Based on the characteristics of the MC-RDLB, each feasible remanufacturing disassembly task and its optimization objective are mapped into a chromosome, which is encoded by the real number system.

The decoding aims to optimize the objective functions f₁, f₂, and f₃. The number of workstations f₁ can be determined as follows:

• Step 1. Set the cycle time CT, number of disassembled parts m, disassembly time of the ith task $t_i$, set I = 1 and N = 1.
• Step 2. Assign the ith disassembly task of feasible sequences to the Nth disassembly workstation and calculate the remaining disassembly time of workstation RT = CT − t_i. Let i = i + 1.
• Step 3. If i ≤ m, go to Step 4; otherwise, go to Step 5.
• Step 4. If t_i ≤ RT, go to Step 2; otherwise, N++.
• Step 5. Output workstation number N.

The workstation equilibrium rate f₂ for each feasible sequence can be calculated by the following steps:

• Step 1. Assign a disassembly task to the workstation and record the remaining time of the workstation.
• Step 2. Compare the remaining times of all the workstations for each task sequence. If the remaining time of the previous task is less than that of the next task, record it as the remaining time of the current workstation.
• Step 3. Calculate the workstation equilibrium rate using Equation (9).

The remanufacturing value index f₃ can be calculated using Equation (10).

4.2. Acquisition of Initial Population Considering Failure and Hazard Constraints

The initial population in the ENSGA-II is the set of feasible disassembly task sequences. The acquisition method of the initial population directly affects the convergence speed and optimal solution quality of the algorithm. To ensure that all chromosomes in the population are feasible solutions, a novel initial population construction method considering failure and material hazard constraints is designed, which is illustrated as follows:

• Step 1. According to the disassembly process plan of EOL products, construct the disassembly task priority matrix A and determine the novel multi-constraint matrix B using Equations (5)–(7). The comprehensive priority matrix S can then be derived. Define the initial population matrix as Q, which is the set of feasible disassembly sequences considering the failure and material hazards, and the disassembly task matrix G_m×m.
• Step 2. Let i = 1 and judge whether the matrix S is a zero matrix. If so, go to Step 3. If not, according to Equation (16), put the disassembling part into the disassembly task matrix G_m×m and update the matrix S.
• Step 3. Take out the ith row in G and randomly generate pop gene fragments, then store them in Q. Update the ith row in G at the same time and let i = i + 1.
• Step 4. Judge whether G is a zero matrix. If so, output Q; otherwise, go to Step 3.

The flow chart is shown in Figure 2.

4.3. Rules of Chromosome Evolution

Based on the Pareto non-dominant relationship and the crowding distance of chromosomes in the initial population Q, the elite chromosomes that must be retained in the parent population are determined. To obtain the optimum solution, the remaining chromosomes are mutated to generate the offspring population by crossover operators.

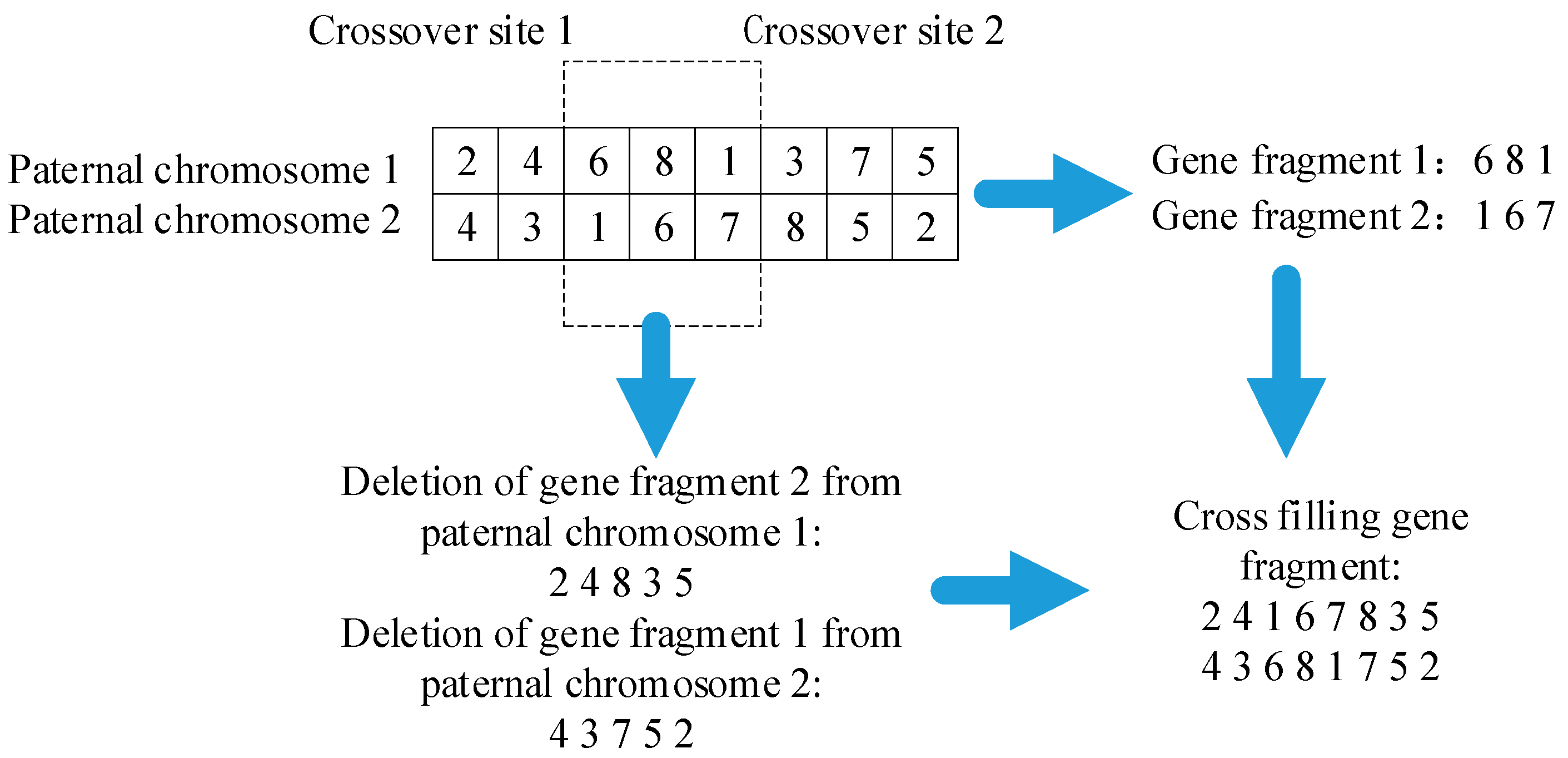
4.3.1. Crossover Operators

Two parent chromosomes 1 and 2 are randomly selected from the remaining population, and two crossing sites 1 and 2 on the parent chromosomes are determined randomly. The gene fragments between the two crossing sites are called fragment 1 and fragment 2. The genes in fragment 2 are deleted on parent chromosome 1. Meanwhile, the genes in fragment 1 are deleted on parent chromosome 2. Fragments 2 and 1 are filled into parent chromosomes 1 and 2, respectively, based on the crossing sites 1 and 2 to form the offspring chromosomes 1 and 2. The schematic diagram of the crossover is shown in Figure 3.

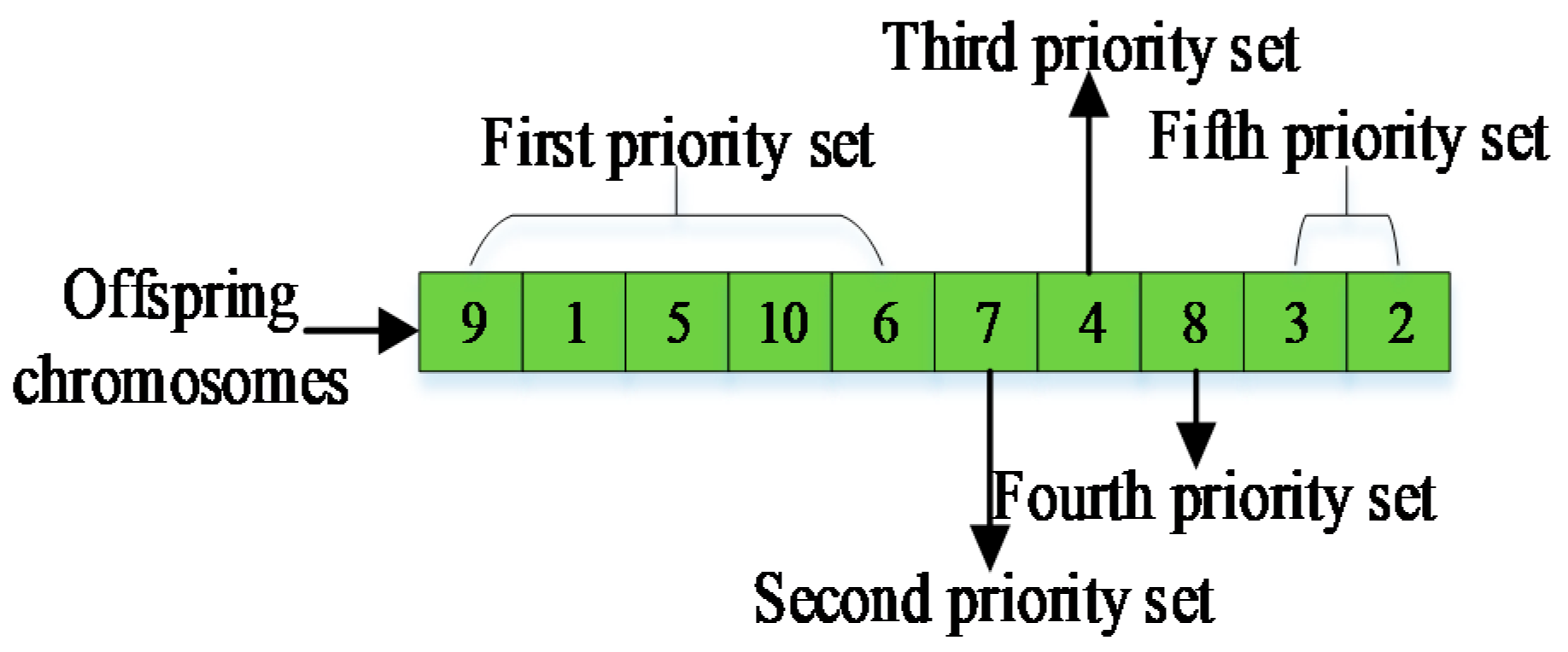
4.3.2. Chromosome Screening Mechanism

The disassembly task matrix obtained from the product disassembly process scheme is used as the judgment criterion in the screening operation. Thus, the disassembly tasks are ranked according to their priority in the G matrix, as shown in Figure 4.

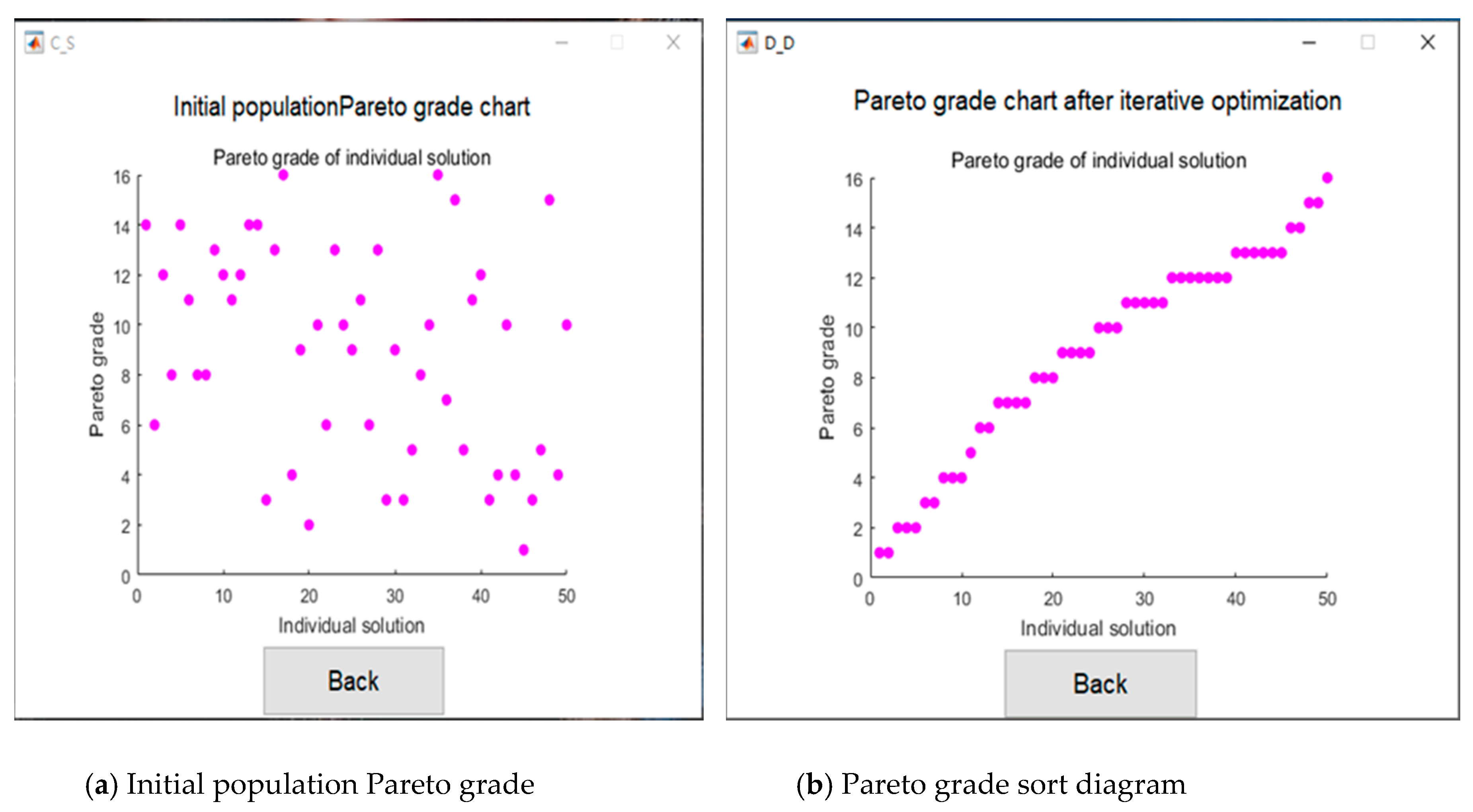
4.4. Evaluation of Non-Dominant Solution Based on Pareto Grade

To evaluate the non-dominant solution efficiently, a non-dominant solution evaluation method is proposed based on the Pareto grade. The non-dominant solutions are obtained based on the Pareto non-dominant relation from the initial population Q, which are defined as the first Pareto grade, and the residual solutions are defined as the second Pareto grade. Letting X_a and X_b represent any two chromosomes in the population, if the objective function f_i(X_a) ≤ f_i(X_b), then chromosome X_a is superior to X_b. Thus, based on the Pareto dominance relation, the third and fourth Pareto set can be deduced, and so on.

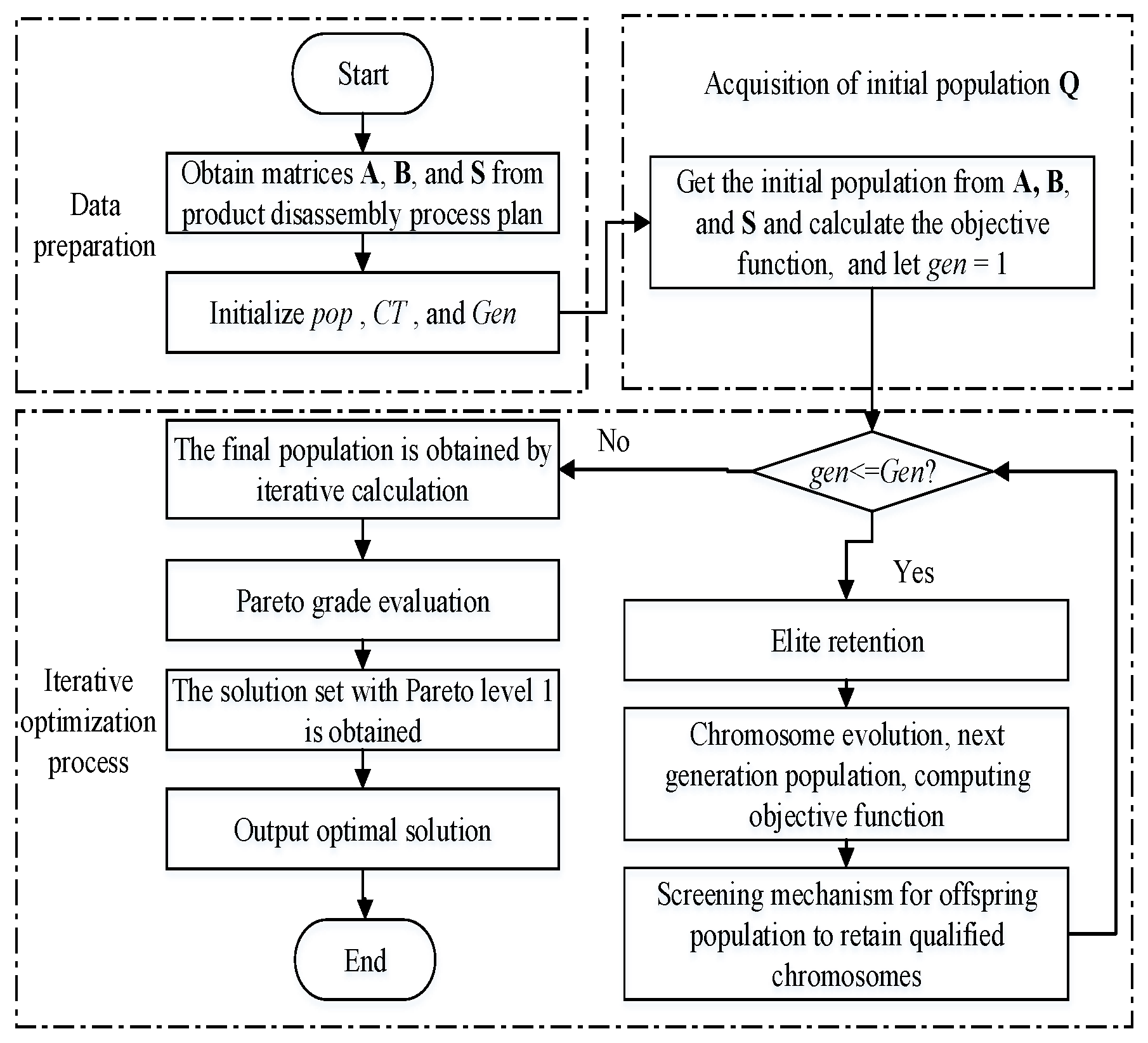
4.5. Solution Process of Remanufacturing Disassembly Line Balance Problem

The optimization of the RDLB aims to obtain a reasonable allocation of disassembly tasks with some constraints. It includes three stages.

• (1) Data preparation. The matrices A and B are constructed by analyzing the disassembly process scheme of the EOL product, and the comprehensive priority relation matrix S is derived. Initialize pop, CT, and Gen.
• (2) Acquisition of initial population Q.
• (3) Iterative optimization process. The initial population chromosomes are screened to obtain the non-dominant solutions using Equation (16). The optimal solution is obtained through evolution and iterative optimization.

The flow chart is illustrated in Figure 5.

5. Case Study

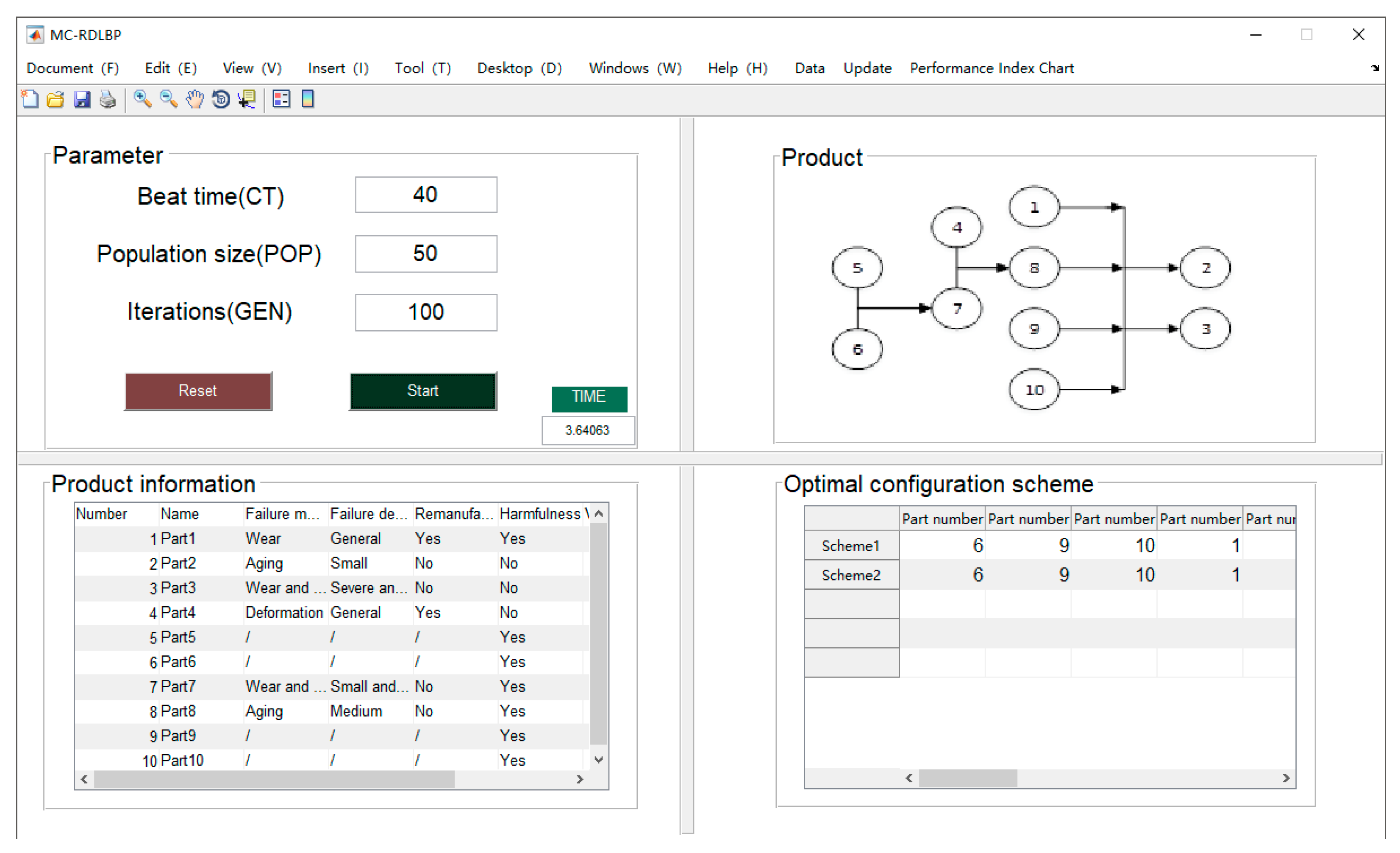
5.1. Verification

To verify the feasibility and effectiveness of this method, 10 disassembly tasks from the literature [35] were selected. The related information for 10 tasks is obtained and listed in

Table 2. Information list for the 10 tasks.

Part Number	Failure Mode	Failure Degree	Remanufacturing	Material Hazards	Remanufacturing Value (CNY)	Disassembly Time (s)
1	Wear	General	Yes	Yes	0	14
2	Aging	Small	No	No	500	10
3	Wear	Severe	No	No	0	12
	Corrosion	Small
4	Deformation	General	Yes	No	0	17
5	Null	Null	Null	Yes	0	23
6	Null	Null	Null	Yes	750	14
7	Deformation	Small	No	Yes	295	19
	Corrosion	General
8	Aging	Medium	No	Yes	0	36
9	Null	Null	Null	Yes	360	14
10	Null	Null	Null	Yes	0	10

. The related information is necessary to implement the proposed method, but it is time consuming. Future research should focus on RDLB with uncertain data and poor information.

In the optimization part of the computational analyses, the ENSGA-II algorithm program was developed in MATLAB R2016a, and the algorithm was implemented using a PC with a 2.30-GHz microprocessor with 4.00 GB of RAM. The prototype system of the multi-constraint remanufacturing disassembly line balance optimization (MC-RDLB) is shown in Figure 6.

Letting pop = 50, CT = 40 s, Gen = 100, the initial population Q and the Pareto grade can be obtained, which is shown in Figure 7a. The MC-RDLB is solved using the ENSGA-II algorithm, as shown in Figure 7b.

5.2. Algorithm Performance Analysis

Let pop = 50 and R = 10. The time complexity at a given scale of the proposed ENSGA-II algorithm mainly depends on the following components:

(1)

The complexity is $o\left(pop\times R^2\right)$ for the construction of the initial population Q.

(2)

The Pareto grade evaluation strategy requires the classification of S Pareto grades for pop chromosomes based on the non-dominant relationship, and the complexity is $o\left(po{p}^2\times S\right)$

(3)

The complexity is $o\left({\left(pop/2\right)}^2\times Q\right)$ to preserve the elitist solution, and we must screen Q chromosomes for pop/2 cross variants.

pop is the population size, R is the number of disassembly tasks, and Gen is the number of algorithm iterations, so the time complexity of the improved multi-objective GA algorithm is $T\left(\mathrm{ENSGA}\text{-}\mathrm{II}\right)=gen•o(pop\times S\times R^2)$. Based on the operation of the ENSGA-II algorithm, the number R of disassembly tasks has a great influence on the algorithm computation time.

To analyze the performance of the ENSGA-II algorithm, a numerical comparison of the three parts of the algorithm is shown in

Table 3. ENSGA-II experimental results.

Running Times	Optimal Solution/ns
	Pareto Grade Evaluation Strategy	Construct Initial Population Q	Screening Mechanisms
1	1.69	0.04	2.80
2	2.20	0.04	2.70
3	2.21	0.04	2.70
4	2.07	0.05	2.57
5	1.91	0.05	2.70
6	2.20	0.03	2.29
7	1.77	0.04	2.90
8	2.20	0.05	2.80
9	2.20	0.04	2.90
10	2.20	0.04	2.21
Minimum value	1.69	0.03	2.21
Average value	2.06	0.04	2.60
Maximum value	2.21	0.05	2.90

.

The main operation of the ENSGA-II algorithm was the Pareto grade evaluation strategy and screening mechanism. The termination condition of the algorithm for the given scale was nt × nt × 10 ms, where nt is the number of algorithm operations. This was compared with the GA and ITLBO [35], as shown in

Table 4. Comparison of algorithm performance.

Algorithm	Cycle Time/s	Minimum Values/ns	Average Values/ns	Maximum Values/ns
GA	40	5	5.3	6
ITLBO	40	5	5	5
ENSGA-II	40	3.924	4.7	5.15

.

The ENSGA-II algorithm has significant advantages in terms of the solution speed, and it could provide two optimal configuration schemes for the remanufacturing disassembly line. For convenience of comparison, the workstation balance rate f₂ and the remanufacturing value index f₃ were calculated using Equation (10) for the disassembly line configuration schemes in the literature [35], and the results are shown in

Table 5. Remanufacturing disassembly line configuration schemes comparison.

Algorithm	Remanufacture Disassembly Line Configuration Scheme	Workstation Number f1	Workstation Equilibrium Rate f2	Remanufacturing Value Index f3	Pareto Grade
GA	10, 6, 9, 4, 5, 7, 1, 8, 3, 2	5	8.865	9740	-
ITLBO	6, 9, 10, 1, 5, 7, 4, 8, 2, 3	5	8.59	7740	-
ENSGA-II	9, 6, 10, 1, 5, 7, 4, 8, 2, 3	5	4.02	7740	1
	10, 6, 9, 5, 1, 7, 4, 8, 3, 2	5	4.02	7740	1

.

Table 5 shows that the proposed ENSGA-II algorithm yielded better results than the GA in terms of the workstation balance rate and remanufacturing value index. The ENSGA-II algorithm was equivalent to the ITLBO algorithm in terms of the remanufacturing value index results, and the ENSGA-II improved the workstation balance rate by more than 50%. The workstation balance rate index aimed to measure the blocking of each workstation and to equalize each workstation of the remanufacturing disassembly line.

The experimental results of the above cases verified the effectiveness and feasibility of the proposed method. To analyze the influence of the number of iterations and the population size on the performance of the ENSGA-II algorithm, several experiments were conducted 11 times. The parameters were set as follows: Gen = 100–300, step size = 20, population size pop = 50, and CT = 40 runs.

The result shows that the number of non-dominant solutions decreased as the number of iterations increased, but the running time of the algorithm increased. The Pareto grade was the lowest when the number of iterations was around 200. Therefore, when pop and cycle time CT of the population size were given and the number of iterations Gen was 200, the algorithm exhibited good solution performances.

Next, the parameters were set as follows: pop = 50–110, step size = 10, number of iterations Gen = 200, and CT = 40, and the algorithm ran seven times.

The result shows that the number of non-dominated solutions and the running time of the algorithm increased with the increase in population size. The Pareto grade was the lowest when the population size was around 60. Therefore, when Gen = 200, CT = 40, and pop= 60, the algorithm exhibited better solution performance.

In summary, the population size and number of iterations should be reasonably selected based on the product complexity and the solution precision requirements of the enterprise.

6. Conclusions

A multi-constraint remanufacturing disassembly line balance model (MC-RDLBM) considering multiple failure and material hazard constraints was constructed, and the ENSGA-II algorithm was improved to solve the problem quickly. This approach could overcome the low efficiencies and complexities of the existing algorithms and an actual case was used to verify the proposed model and algorithm. The conclusions are as follows:

(1)

The multi-constraint remanufacturing disassembly line balance model (MC-RDLBM) takes into account constraints such as the assembly relationship of used mechanical and electrical products, multiple failure modes, failure degree, and material hazards, which is more in line with the engineering practice.

(2)

An initial population acquisition method considering multiple failure and material hazard constraints was proposed. The convergence speed of the algorithm was improved. The chromosome evolution rule was improved, which combined the Pareto dominance and crowding distance constraints to realize the autonomous evolution of chromosomes and expand the search scope simultaneously.

(3)

In this paper, 10 disassembly tasks from the literature [35] were selected to verify the proposed algorithm, and two optimal configuration schemes for the remanufacturing disassembly line were obtained. The results indicated that the ENSGA-II algorithm had significant advantages in terms of the solution speed, the remanufacturing value index, and the workstation balance rate.

Additionally, although this paper proposes a new solution to the remanufacturing disassembly line balancing problem considering multiple failure and material hazard constraints, which is of great significance in improving the mass disassembly efficiency and reducing the remanufacturing cost, the related information (shown in Table 2) is necessary to implement the proposed method. However, it is time-consuming. Future research should focus on RDLB with uncertain data and poor information.