1. Introduction
The rapidly growing demand of the fossil fuels, such as coal, crude oil, and natural gas, is substantially influencing the focus of researchers around the world towards the identification of an alternate source of energy in the recent decades. The clean, quiet, pollution-free, and low maintenance characteristics of solar photovoltaic (PV) systems has received more significant interest as an alternative source of energy [
1]. Solar energy has a great potential to meet global electricity demand considering its advantages concerning the environmental and economical aspects [
2]. However, when compared with other conventional energy generation sources, this on-demand source of energy has its drawbacks in terms of the low output efficiency and dependency of the output characteristics on stochastic weather conditions. A study conducted by Solangi et al. [
3] found that the contribution of PV systems in energy generation was about 14,000 MW in 2010 and this number is forecasted to reach 70,000 MW by 2020, illustrating the broader adaptation of the renewable energy-based systems. In an Australia context, renewable energy has increased from 10,650 MW to 19,700 MW from 2001 to 2012. Australia, being characterized with ideal hot weather patterns, it is highly beneficial for employing solar energy as an alternate option that accounts for about 20% of the RE target for electricity supply by 2020 [
4]. However, as mentioned earlier, one of the most significant challenges with PV systems is the cost that is associated with it. In addition to the material cost of the PV module, the damage incurred for the control system has a significant impact on the overall price of the PV system. Besides this, the control system also has a substantial effect on the performance and efficiency of the system, which indirectly contributes to the cost associated with the system. Accordingly, it is essential to have a proper control system integrated with the PV system. One of the critical challenges that affect the efficiency of the PV system is the dependency of the PV systems output power on the performance and reliability of the control strategy incorporated into the system, especially under partial shading conditions (PSC). An unreliable control strategy may result in a substantial loss of the potential PV energy generated under PSC or sudden environmental changes. Therefore, a sophisticated control strategy is incorporated into the PV system configuration for improved performance. The time taken to pay off the system when controlled by an improper control technique or devices can be very high, which affects the economic prospects of the system. Consequently, a proper control strategy implied the PV system has a substantial impact on the investment and running cost of the PV system.
The investment cost is affected by the type of controller, sensors, and other associated auxiliary circuits in the system. Moreover, the running cost is influenced by the efficiency and reliability of the control unit designed for tracking of maximum power point (MPP). Different aspects of PV system, such as the efficiency of the material used, configuration or architecture of the system, and efficient MPPT scheme, are considered as the key factors that influence the reduction of the cost. As a result, the importance of the control scheme used in the MPPT controller concerning the efficiency of the PV system is explored in numerous studies. These studies were aimed towards designing a simple and fast MPP tracking method for PV system under uniform irradiance levels. However, with the emergence of a bypass diode in the PV module configuration, most of the conventional approaches are subjected to failure under PSC [
5]. Numerous attempts have been made to design an appropriate MPPT control scheme in order to minimize the impacts of the PSC. Soft computational algorithms and evolution-based techniques, such as ant colony optimization (ACO), fuzzy logic control (FLC), artificial neural networks (ANNs), particle swarm optimization (PSO), and differential evolution (DE) based techniques have been used by several researchers to increase the performance of the system.
Observations form the initial review of the existing literature highlighted that a hybrid combination of an efficient system architecture and a MPPT control strategy is required for an efficient PV system. In order to carry out a detailed performance evaluation of the PV systems characteristics, a proper mathematical model of the system is developed [
6].
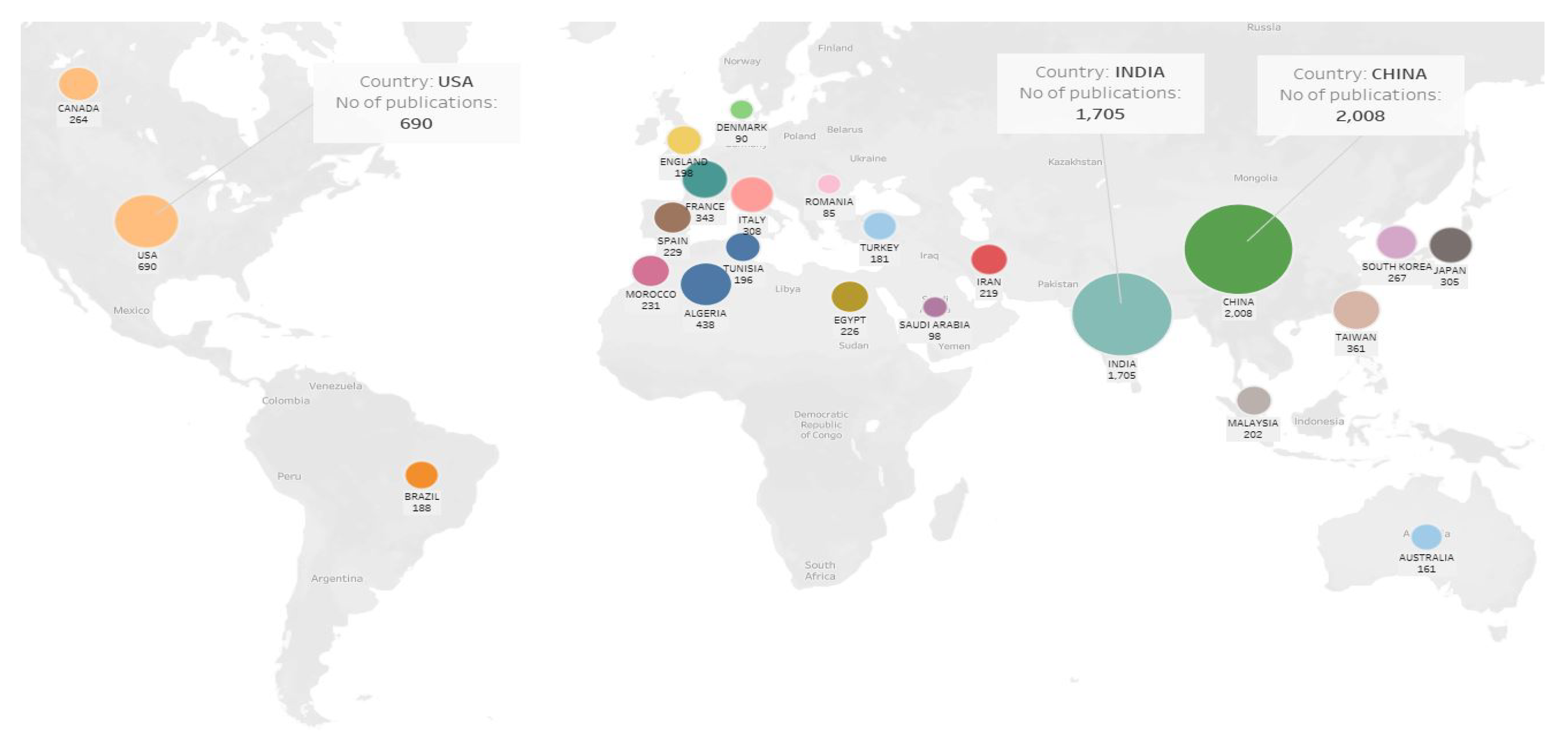
Figure 1 shows the distribution of research carried out in the world focusing on the MPPT of PV systems, created using the web of science database. Seyedmahmoudian et al., presented a critical review on the state of the art MPPT optimization approaches using artificial intelligence methods by evaluating the advantages and limitations of the approaches [
7]. Ahmed et al. [
8] proposed a method that can track the global MPP in most cases by doing a comprehensive range search and using this technique, and it was observed that more power could be generated using the proposed method under PSC. An MPPT controller uses hill-climbing search method by fuzzifying the rules to offer a faster and accurate MPPT technique under steady-state and dynamic weather conditions [
9]. A Novel mathematical model of a PV system characteristics under PSC is considered as one of the highlights of this research. The proposed fuzzy logic-based controller exhibits a fast converging rate with minimal oscillations around the global MPP under steady-state conditions [
10]. A two-stage MPPT technique which is very competitive, accurate and fast in tracking the global MPP under PSC using a P&O based MPPT technique specifically with an efficiency of 95% and significantly high converging speed is presented in [
11,
12].
An effective RMO-based MPPT technique for detecting the GMPP under PSC with improved convergence speed, efficiency, stability, and reduced computation cost is presented in [
13]. A comparative study on the nature inspired MPPT algorithm for PSC conducted by Pathy et al. clearly illustrated the importance of having a powerful MPPT control algorithm [
14]. Islam et al. [
15] discussed the results obtained from the performance evaluation carried out on different MPPT techniques providing a good reference for future researchers to identify the best suited MPPT technique without any complications. A detailed comparison of the impact of the performance of the MPPT techniques in terms of the accuracy and speed concerning the amount of energy produced is clearly expressed in [
16]. An extension theory-based MPPT control algorithm that can automatically adjust the step size of the search to track the MPP accurately and faster is presented in [
17]. Besides, the proposed technique simultaneously improves the dynamic and steady-state performance of the PV systems MPP tracking. In [
18], a power incremental aided incremental conductance-based MPPT technique that performs either variable frequency constant duty cycle or constant frequency variable duty cycle.
Two-stage MPPT of a PV system under PSC was simulated using PSIM software and experimentally evaluated using instant online measurement using actual size equipment [
19,
20]. A novel incremental conductance (InC)-based MPPT algorithm that modulates the duty cycle of the MPPT converter to increase the tracking speed, which reduces the power losses is presented in this research [
21]. Sequential extremum seeking control based global MPP tracking control strategy under PSC was proposed in this research [
22]. A DEPSO based mathematical MPPT forecasting model of a PV system equipped with a hybrid self-energized weather data logging system is performed to improve the performance and tracking accuracy and speed of the system [
23]. A BAT based mathematical MPPT forecasting model of a PV system equipped with a hybrid self-energized weather data logging system is presented to improve the performance and tracking accuracy and speed of the system [
24]. Stochastic nature of the PSO based MPPT control technique was evaluated under different PSC that improved the performance and tracking rate of the system [
25]. A genetic algorithm-based MPPT optimization of a PV system under PSC was evaluated using MATLAB SIMULINK was presented in [
26]. Additionally, a differential evolution based MPPT optimization of a PV system under PSC was evaluated using MATLAB SIMULINK was explored in [
27]. A low-cost microcontroller that can overcome the weakness of the searching problem for the global MPP of the PV system characteristics is presented [
28]. An advanced PSO based MPPT controller is used to validate a 500 W photovoltaic system by demonstrating an effective and efficient tracking algorithm [
29]. Therefore, the different control strategies that where proposed to reduce the cost and increase the efficiency of the PV system operation and a comprehended review is presented in
Table 1.
There exists a lot of local maximum power points (LMPP) in the solution space, and it is essential and challenging to track the global maximum power point (GMPP) at the output of PV systems under PSC because of the multi-dimensional characteristics of the output of the PV system. When considering the capabilities of the stochastic objective functions used in the optimization in terms of the ability to track GMPP, the use of the PSO technique is universal. For example, a standard PSO based MPPT technique is used to track the GMPP of the partially shaded PV system in [
29,
30]. Despite the higher usage of the PSO technique in MPPT analysis, it has some drawbacks associated with it in terms of low convergence speed, the dependency of the random coefficients used in computation, and high computational expense.
The MPPT schemes with these advanced techniques require a microcontroller with ample memory in order to effectively process the algorithms. The accurate and reliable performance of such methods has significantly helped in reducing the running cost of the PV system, along with higher efficiency under partial shading conditions. However, the performance of these methods is only satisfactory for a small and medium-sized PV system with standard configurations. However, in general, most of the PV systems (BIPV) suffer from high complexity, high computational cost, and frequent fluctuations during the tracking period. This limitation has encouraged researchers to explore more on effective MPPT schemes for target PV systems with standard system architecture that is also known as decentralized architecture. In the decentralized architecture of PV systems, each PV array is connected to an individual DC-DC converter. Decentralized or conventional system architecture enables the accurate tracking of MPPT at the output characteristics under a partially shaded PV system. However, the decentralized system architecture requires a higher number of DC-DC converters and sensors, which significantly adds to the overall investment cost of a PV system. In general, the architecture of the PV system has a substantial impact on the initial cost of the PV system, especially the control system incorporated. One of the critical problems associated with large scale series-parallel-configured PV systems is the expensive control system integrated into the system, which is mostly related to a large number of voltage and current sensors used [
31]. Therefore, any reduction in the total number of sensors used in the control system will reduce the total cost of the PV system. However, it should be remembered that the architecture of the PV system will directly alter the output characteristics measured by the control system [
32]. Any change made to the PV system configuration should be compatible with the capability and appropriateness of applying the MPPT control scheme. An evaluation of a distributed PV system architecture using different MPPT algorithms was analysed by Chao et al. [
33]. In this paper, a new distributed architecture of the PV module which could be used as a building integrated PV (BIPV) systems is proposed and validated using RMO based MPPT techniques. The proposed methodology is evaluated with different PSC scenarios which illustrate the improved performance in tracking the MPP and the reduction in the total investment and running cost of the PV system.
2. Distributed Photovoltaic Configuration
The type of control system architecture and the MPPT technique used in the solar PV systems have a substantial impact on the initial and running cost. This study aims at designing a reliable, robust, and efficient control system architecture integrated with a powerful MPPT technique that reduces the total cost of the system. A brief explanation of the conventional control system architecture of PV systems is explained by highlighting the advantages and disadvantages in detail in this section below. Followed by which a novel distributed control system architecture of a solar PV system is proposed. The proposed distributed control system architecture of solar PV systems is considered to be more effective and efficient. In addition, it also consists of a smaller number of sensors used for tracking of MPP, which substantially reduces the total cost of the PV architecture.
In general, because of the low power rating of PV module, they are generally connected in the series-parallel configuration for improved performance based on the application. With standalone series or parallel configurations of the PV system, the load current or voltage requirements are not generally met. Accordingly, a hybrid combination of both series and parallel configuration is ideally preferred. In the presence of multiple arrays in the series-parallel configurations, two general control system architectures are considered:
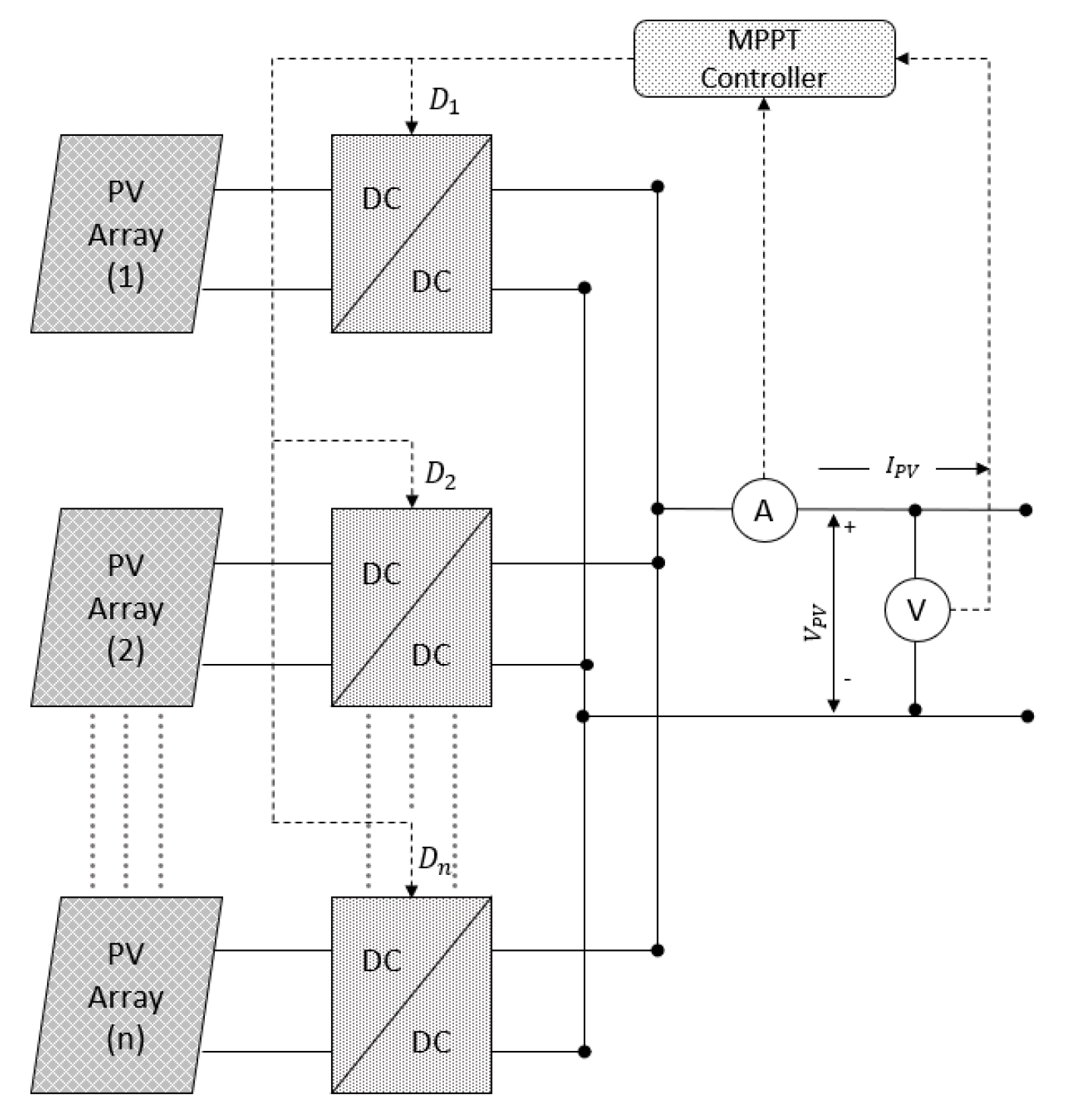
The decentralized architecture of the PV system is divided into multiple subsystems, each individual subsystem is connected to a converter and controlled by a set of sensors and controllers. The block diagram for this system architecture is shown in
Figure 2a.
The centralized architecture of PV system consists of multiple subsystems connected to a single converter and controlled by a centralized controller.
Figure 2b shows the block diagram for this centralized architecture.
The advantages and disadvantages of the centralized and the decentralized PV system architectures is explained below: in the former scheme, the PSC problems can be dealt more appropriately and the proportion of power loss due to this mismatching condition is reduced. However, this architecture results in a more complex and expensive PV system, as it requires a separate control system for each subsystem. Therefore, the final cost of the control system is substantially increased. In the latter scheme, the series of parallel-connected PV modules are connected to a single DC-DC converter and controlled by a single controller. Thus, avoiding additional controllers and sensors reduces the total cost of the system. However, this scheme greatly reduces the efficiency of the control unit under PS conditions, which increase the energy loss over time. In a nutshell, the comparison between the two conventional techniques is explained in
Table 2 below.
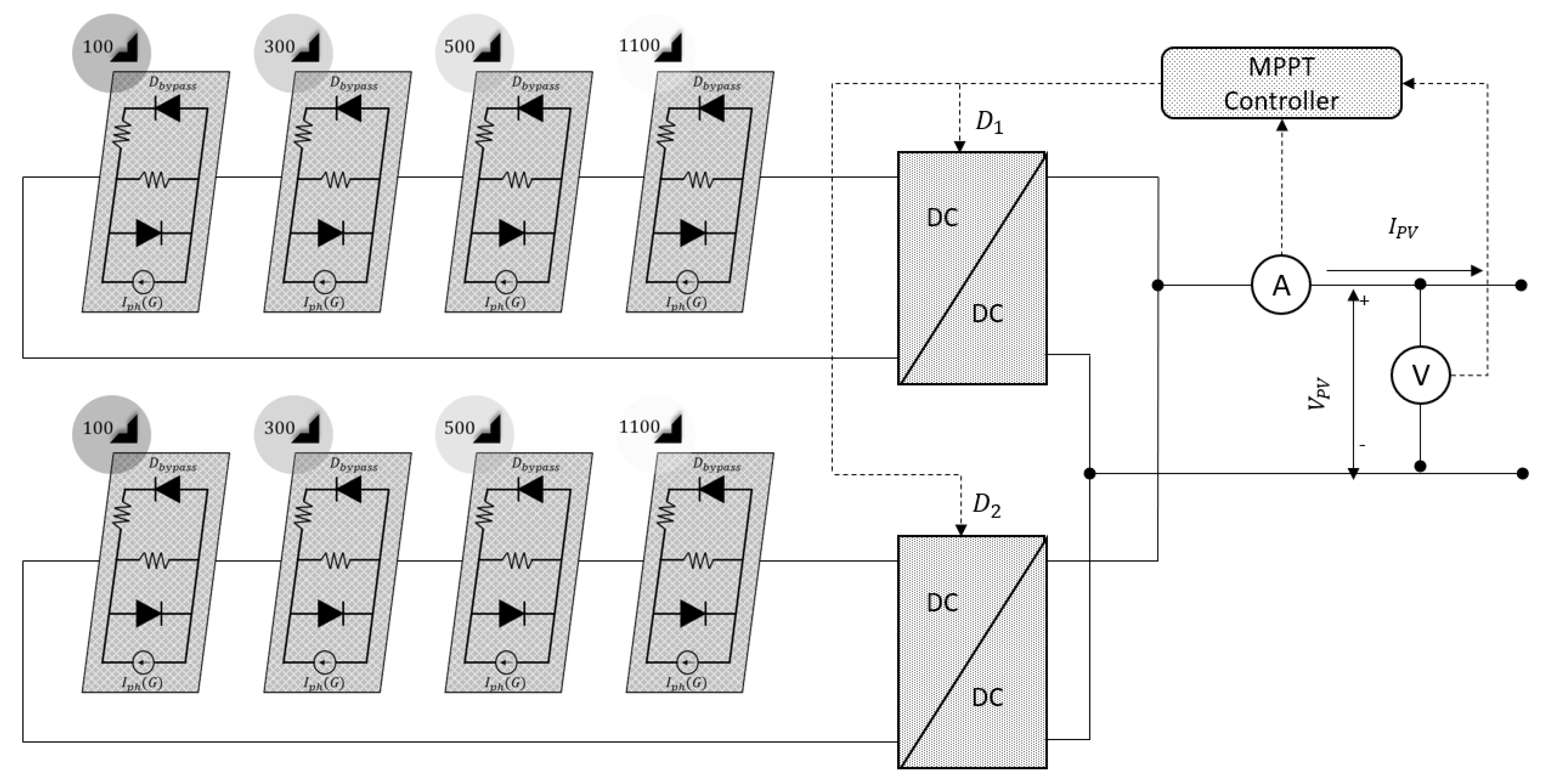
Figure 3 illustrated the proposed distributed architecture with the combination of both centralized and decentralized architectures, as shown in
Figure 2. The proposed architecture aimed to overcome the problem associated with the configurations mentioned above. This structure not only reduces the detrimental effects of PSC but also adds no additional cost to the system, as only one pair of sensors is required for each PV module. A centralized controller is present in the distributed architecture, which is used for tracking the PV systems output’s maximum power point (MPP). However, the solar PV systems multidimensional characteristics in terms of the control system require a very sophisticated MPPT controller. Despite the intensive mathematical computational requirements of the conventional MPPT techniques, it is unable to accurately find the MPP under PSC. A robust, efficient, and mathematically less computational algorithm, like RMO, is selected and evaluated in the following sections of the paper when considering the above-mentioned limitations.
3. Radial Movement Optimization
The identification of the best-suited solution for a given problem within the given constraints is called optimization. Radial movement optimization (RMO) is a population-based stochastic metaheuristic global optimization technique that is used to optimize nonlinear and non-differentiable problems in a continuous domain. RMO is substantially similar to the other swarm-based evolutionary techniques, like differential evolution (DE) and particle swarm optimization (PSO) [
34]. RMO is consistent in obtaining optimal solutions in a short time, and it is accurate in the identification of global optima of the solution space. The RMO technique starts with the process of randomly initializing the particles around the centre of the radial orbit of the RMO, which is then updated every step in the vector search space. Each scattered particle in the search space is considered as a vector representing the possible solution of the optimized problem. The movement of particles at different velocities in the multi-dimensional search space is distributed along the fixed radii of a sphere. The movement vector of the particles is determined by considering the best two fitness values and the randomized vector used in the optimization. The movement of the particles in a radial pattern increases the ability to explore and exploit larger three-dimensional (3D) vector search space in an optimal manner. RMO requires less memory and it produces a more optimized and denser searching pattern, as it does not transfer the location and the velocity of the particle in each iteration. Instead, the particles start to move from the updated centre point in the next generation at random velocity. Additionally, in RMO, the global best solution is stored as a global reference vector, which helps the algorithm in avoiding the process of being trapped at the local optima.
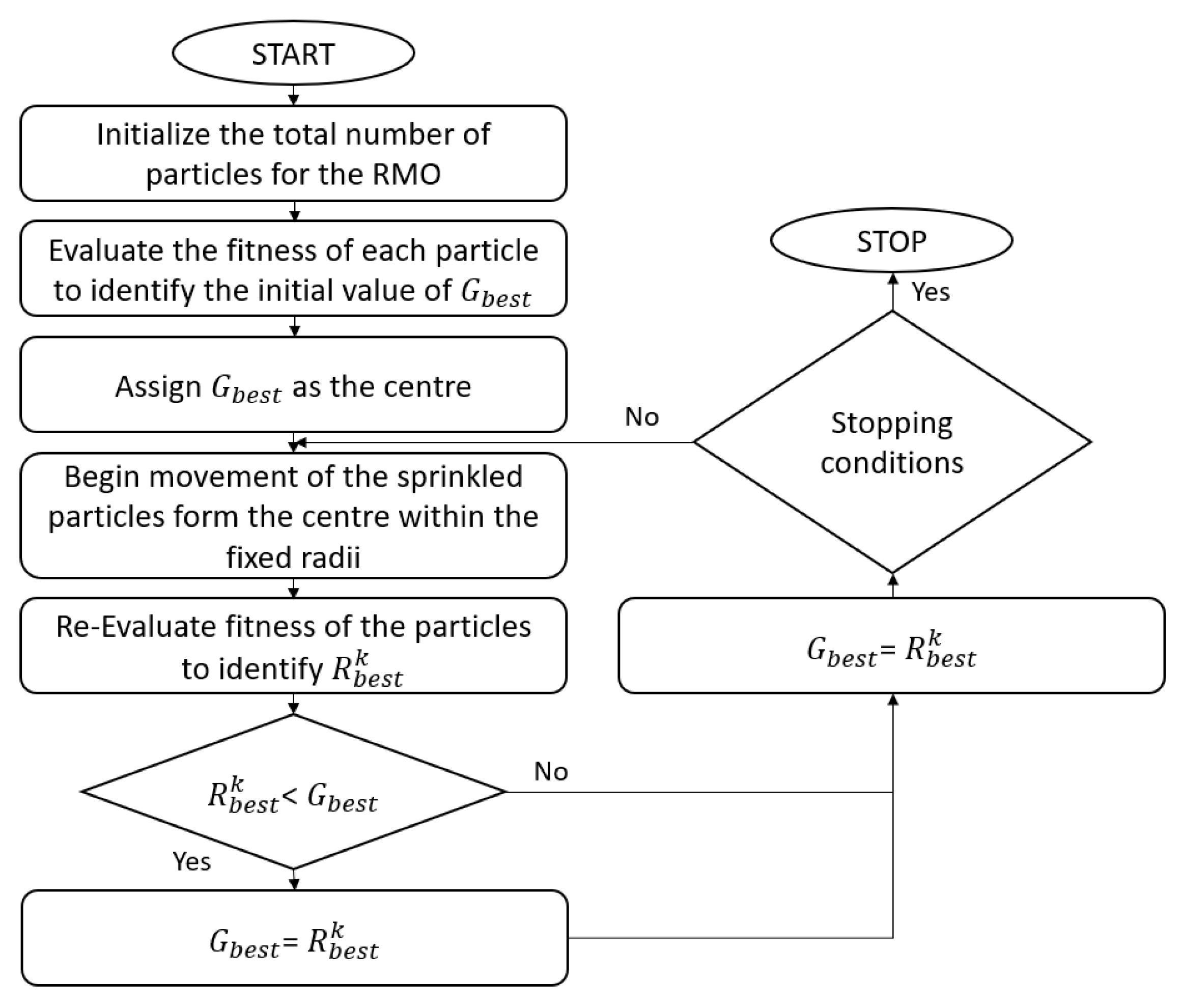
Figure 4 shows the operational flow of the RMO algorithm. The fitness of each particle in the search space is evaluated while using the user-defined objective function from which the best fitness value of each generation step is assigned as the radial best solution (
). Followed by which the best
among all the generations so far is stored as the global best (
). The optimization process stops when it reaches the stopping condition of either the maximum number of generations or value of
getting closer to the desired value occurs. The two main stages of the RMO-based optimization technique are explained, as follows:
3.1. Random Initialization of the Search Space
The RMO algorithm starts with the initialization process, just like the other optimization techniques. The location of each particle within the search space is distributed uniformly, and it is represented by the matrix of size
, as expressed in Equation (
1). The
represents the number of particles assumed for the optimization task that is determined by the user, and
the number of dimensions represents the total number of variables considered in the optimization. The values of
and
do not change during each trial of the optimization process.
The initial location of the particles within the search space is randomly assigned. Equation (
2), expressed below, indicates the mathematical representation of the particles random initialization in the search space that was considered for this study.
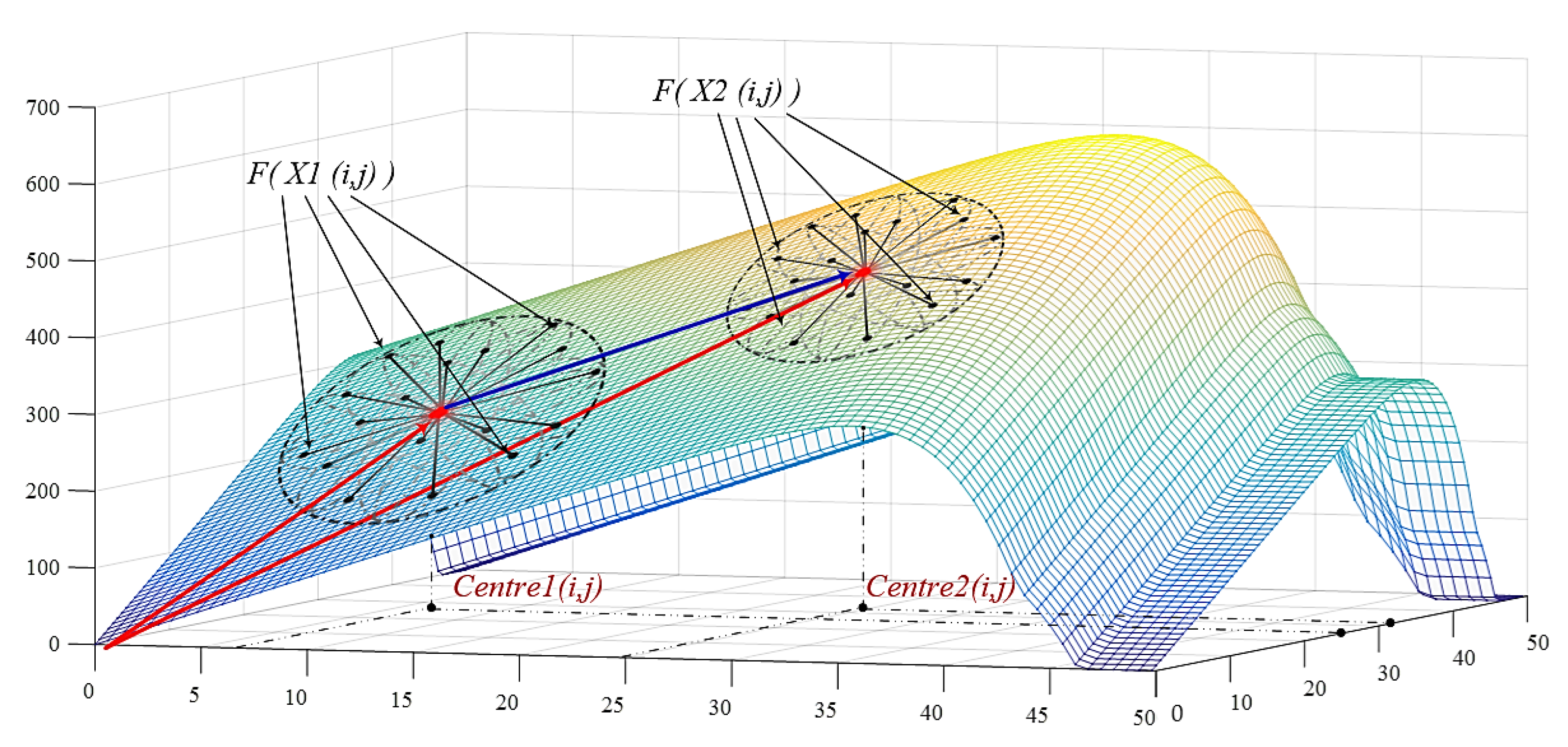
The dimension constraints are represented as and . Along with this, a normally distributed randomness is added in the form of a Gaussian distribution expressed in between 0 and 1 as rand (0,1). After the initialization process, the distribution of the particles along the jth dimension is carried out uniformly. This distribution is based on the proposition of the length of the dimension and . The center point is obtained after uniform evaluation of the fitness of every particle in the search space and this point is considered as the location from which particles starts to move around a fixed radius in the next generation.
3.2. Exploration Pattern of the Particles
In the second phase of the RMO technique, the sprinkling of the particles along the radii in a straight-line path that is based on the vector
around the recognised centre point in the search space is carried out.
is a random vector of size
and
k is a positive integer judiciously chosen by the user. From the inferences obtained from the trails, the value of
k for the ideal performance of the optimization techniques is found to be in the range of 2 to 5. However, the results are also based on other parameters that are involved in the optimizer, such as the limitation of the solution search space and the type of objective function chosen. The value of 2 is assumed for the constant
k in the optimization highlighted in this paper. In conventional approaches, like PSO, an inertia weight parameter is considered for determining the rate of convergence of the algorithm.
represents the inertia weight, and it tends to be a descending value for the number of generations. The relationship between
and the total generation steps run is expressed in Equation (
5).
In RMO, a constant value is considered for the
, which is in the range of 0–1 in the initial ten iterations and then it is updated based on the relationship expressed in Equation (
5). Where the values of
and
is assumed to be 1 and 0.
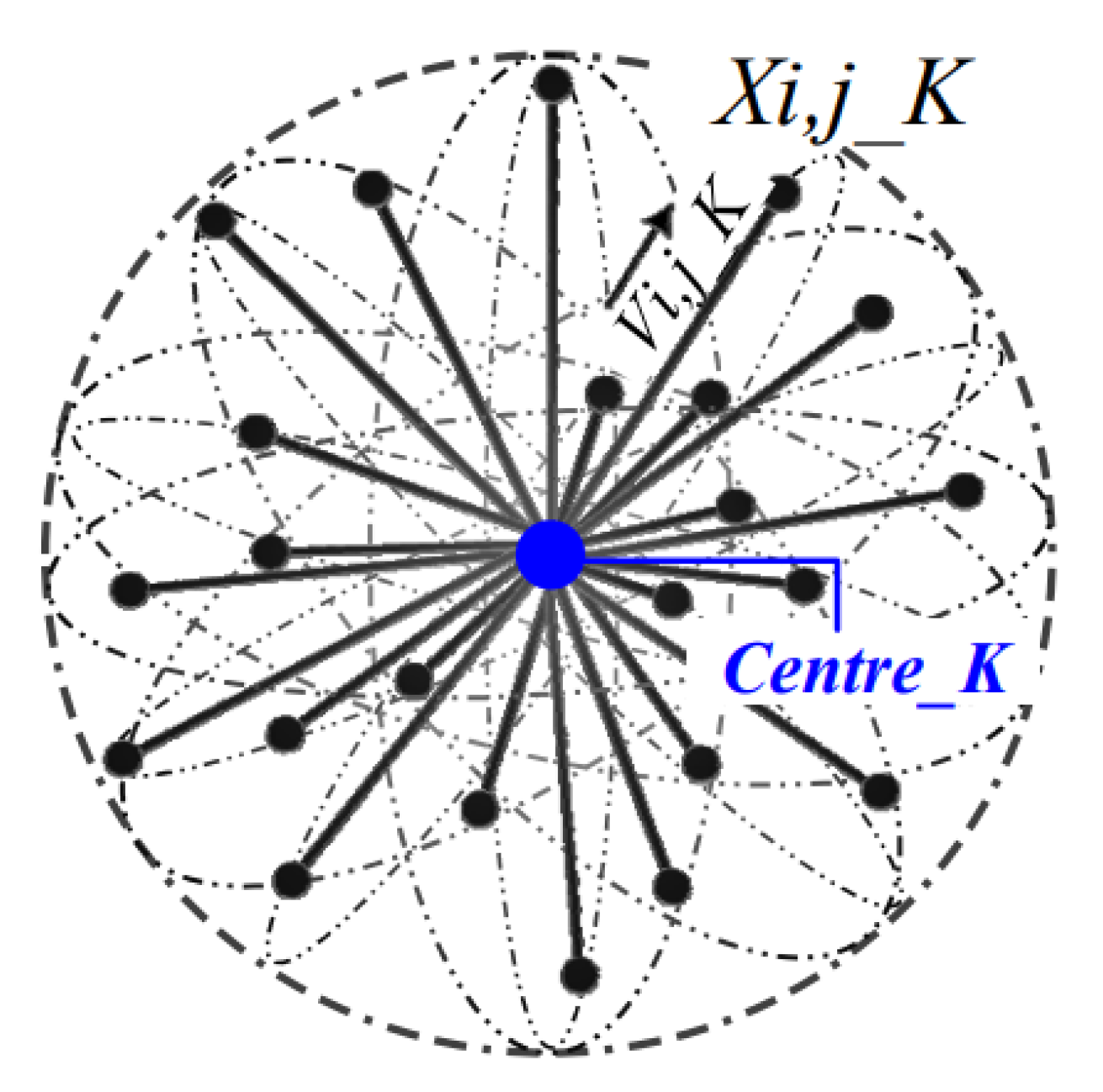
Figure 5 highlights the pictorial representation of the way that the particles are sprinkled from the centre point with a max radius of
in the RMO technique.
After the particles getting distributed across the search space, each particles fitness value is evaluated while using the objective function of the optimizer. In each generation, the particle with the optimal fitness value is considered as the radial best (
) particle. The locations of
and
are considered for finding out the updated centre point every generation based on the following expression highlighted in Equation (
6).
and
are the coefficients set by the user at the start of the optimization process.
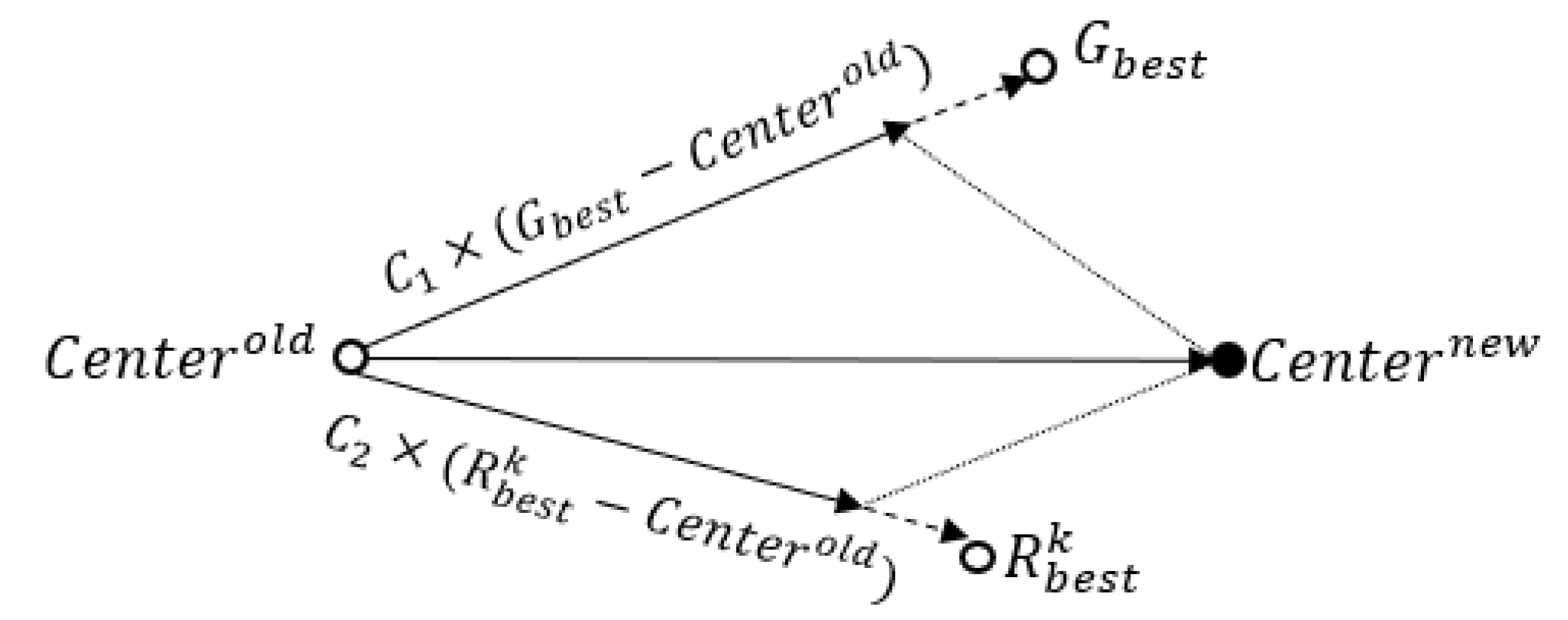
Figure 6 indicates the vector diagram representing the centre update process.
In the next generation, followed by the update of the centre point location, the particles start scattering from the updated centre point. The
solution is compared with
solution to identify whether
indicates a fitter solution than
or not. If
is fitter than
, then the
value is updated with the current
value. This process is repeated until the stopping conditions of
equaling the targeted value or maximum generation value.
Figure 7 depicts how the centre point gets updated in between two successive generations in a 3D solution search space.
In contrast to the conventional algorithms, like differential evolution (DE) and particle swarm optimization (PSO), in RMO, the particles do not travel all over the solution space. Therefore, the need for saving all of the current particle locations to be carried over to the next step is excluded. The reduction of the total memory needed for performing the optimization is evident from this process. The following section clearly explains how the RMO technique is used for the proposed application of identifying the MPPT of the PV system.
6. Results and Discussion
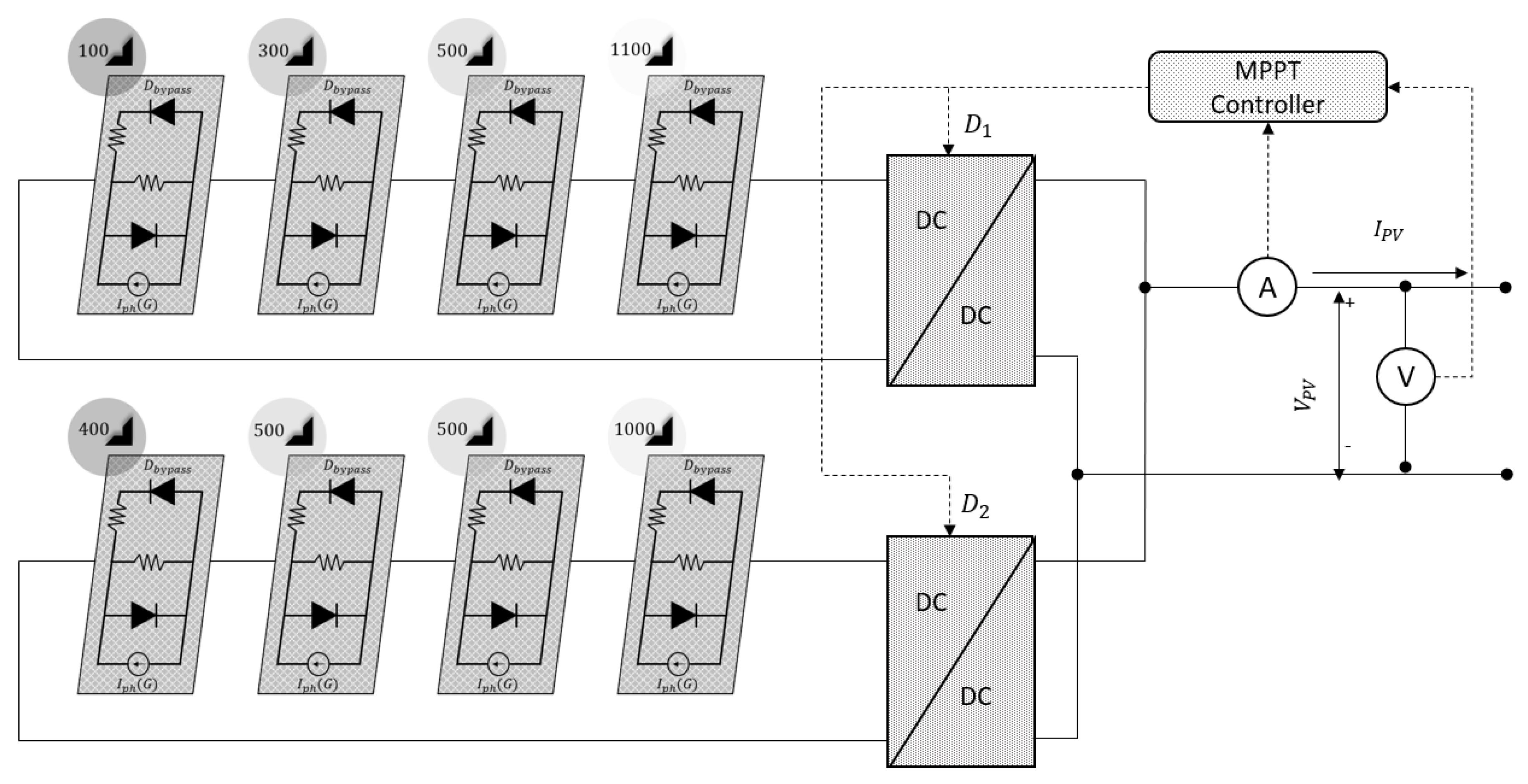
In this section, the performance of the RMO-based MPPT technique is evaluated with the proposed distributed architecture of the PV module configuration under five different PSC scenarios. Partial shading patterns are stochastic in nature and innumerable possibilities of weather patterns are possible. Accordingly, it is essential to validate the performance of the system under different scenarios to validate its reliability. For simplicity, in the first three scenarios considered for evaluation, a smaller PV system which results in a three-dimensional output P–V characteristics are evaluated. Followed by this, two scenarios are considered to have larger and more complicated systems. In the first three scenarios, the PV system consists of two subsets, each with four series-connected PV modules evaluated under different PSC. In scenarios four and five, a similar setup is considered, but, instead of two subsets, we have four subsets of four PV modules connected to the distributed architecture of control system. In the testing scenario 1, the PV modules in both the subsets of distributed architecture receive solar irradiance of
,
,
and
as illustrated in
Figure 9.
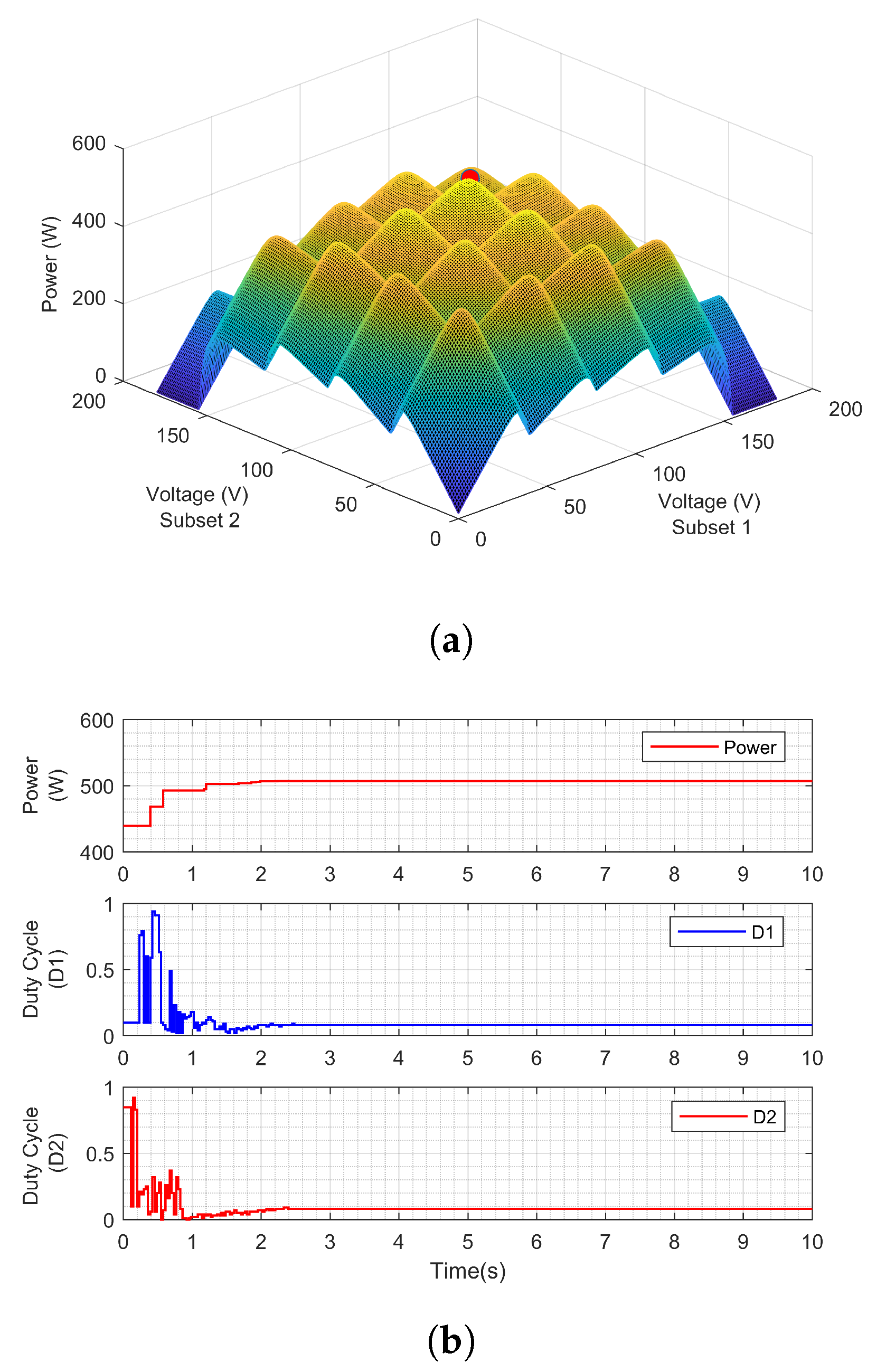
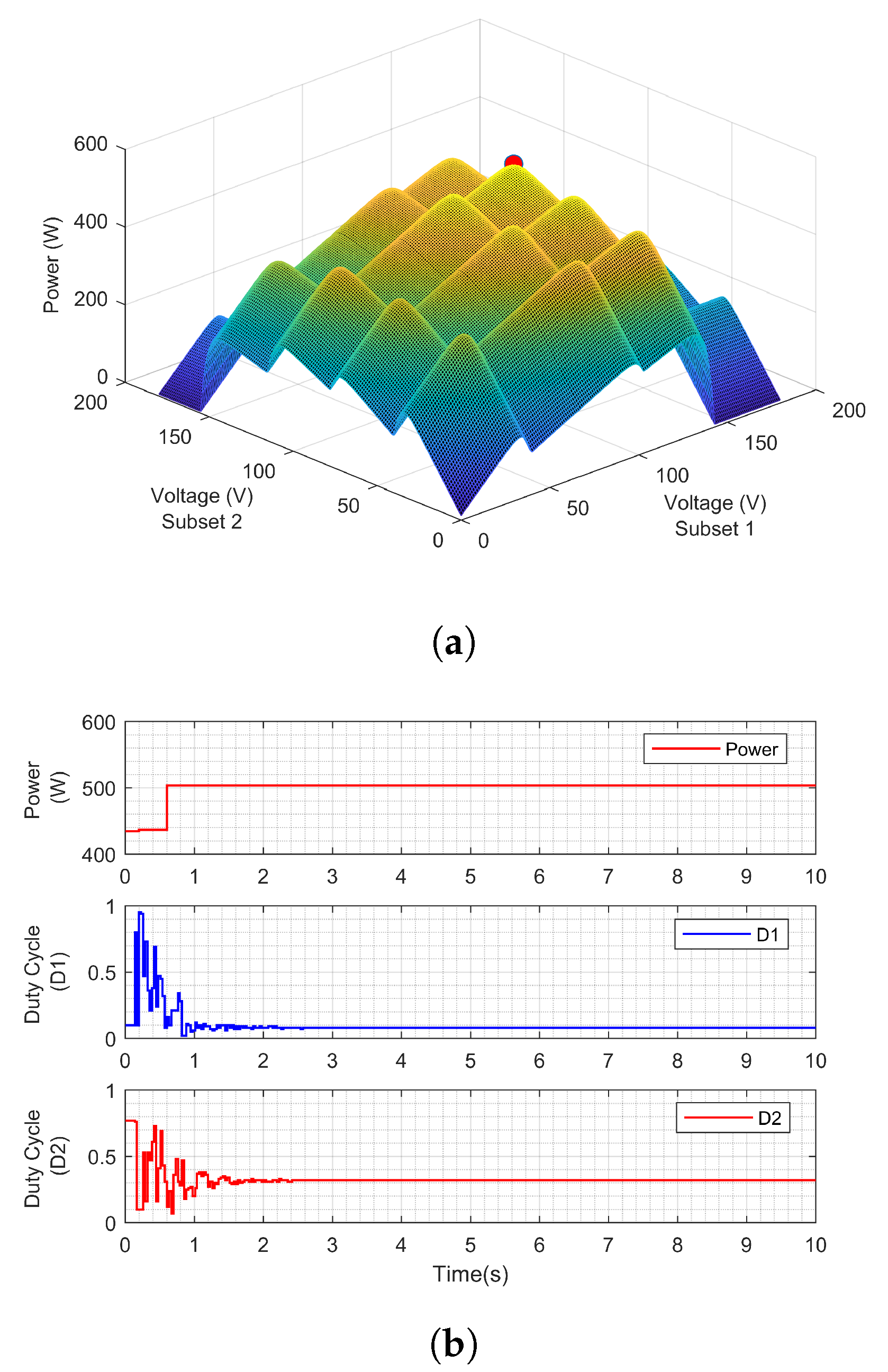
The power–voltage relationship of the proposed PV system architecture with the RMO based MPPT controller will result in a three-dimensional characteristic response. Assuming a similar PSC pattern for both subsets, the relationship between the modules’ voltage and the generating power for this PV architecture under the testing scenario. The consequent characteristic has a similar shape of the Rastrigin function, which is one of the most commonly used functions for evaluating the strength of soft computing methods. These characteristics will allow precise evaluation of the reliability, accuracy and convergence speed of the selected MPPT technique. The output performance of the RMO based MPPT technique and the three-dimensional power-voltage characteristics under the testing scenario 1 is illustrated in
Figure 10. The two separate duty cycles were sent to the connected converters for the improved performance of the PV system, as shown in the figure. Regardless of the shape of the PS pattern, the RMO-based MPPT tracks the GMPP in 2 s, which illustrates the fast-tracking speed for the proposed technique. The results also indicate that the proposed RMO based MPPT technique performs better for the distributed architecture PV system that is considered for evaluation in this paper. In the testing scenario 2, the modules in the first subset receive solar irradiance of
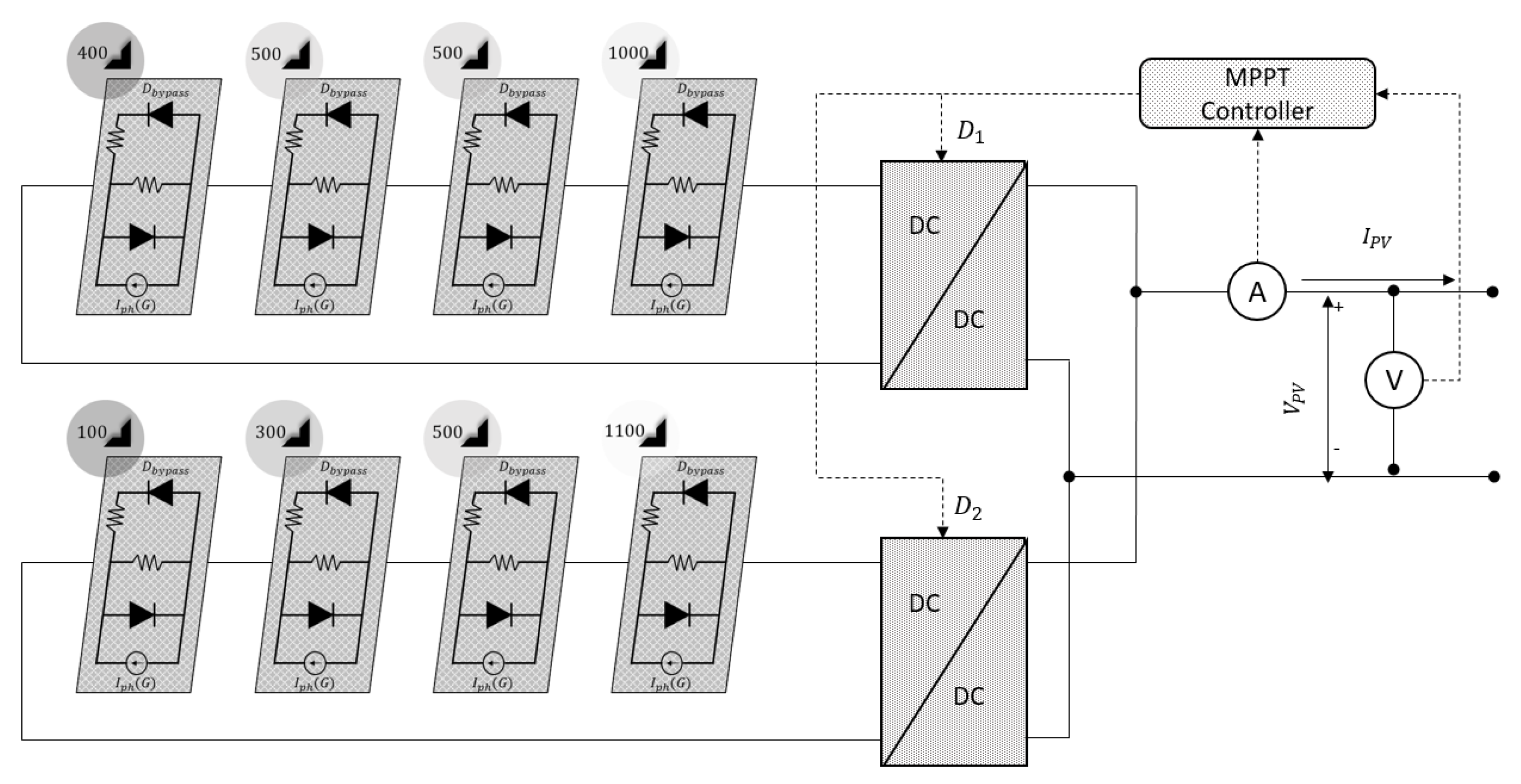
,
,
and
, and the modules in the second subset receive
,
and
, as illustrated in
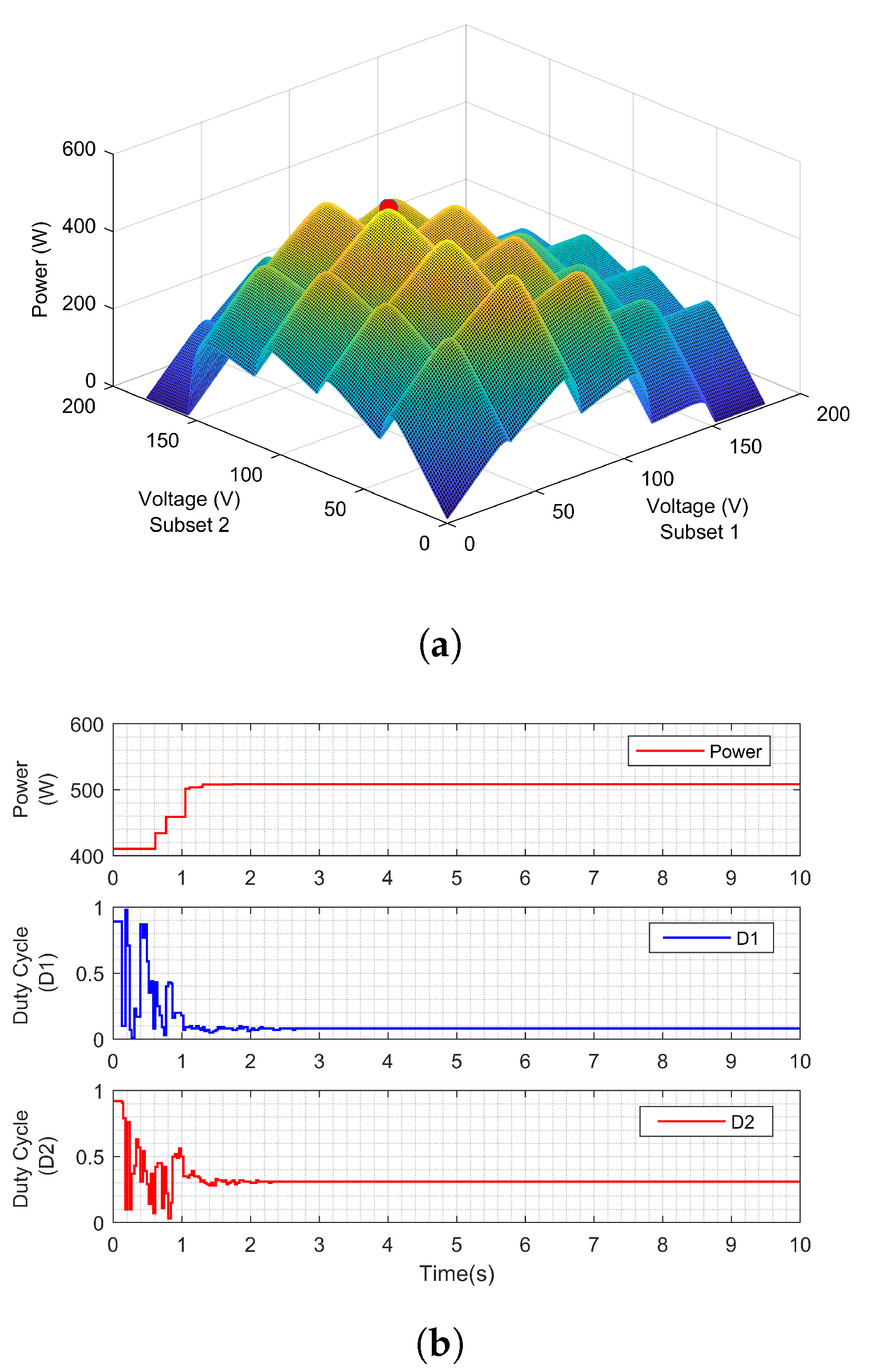
Figure 11. This arrangement creates four peaks at the output of PV Subset 1 and three peaks at the output of PV Subset 2. The consequent characteristics of the PV system in terms of output performance of the RMO based MPPT along with the three-dimensional power-voltage characteristics under the testing scenario 2 is illustrated in
Figure 12. It is clear that the proposed MPPT method exhibits satisfactory performance under this condition. After the initial explorations throughout the search space, the GMPP is successfully tracked at around
s, which demonstrates the fast-tracking capabilities of the proposed method. The results also indicate that there is no steady state oscillation at the output curve after the tracking is finalized.
In testing scenario 3, there is a minor difference between the values of GMPP and the other peaks (LMPP) in the output characteristics of the partially shaded PV system. The modules in the first subset receive irradiance of
,
and
and the modules in the second subset receive irradiance of
,
,
and
, as illustrated
Figure 13. The output characteristics of the PV system and the power-voltage characteristics of the distributed architecture under the testing condition three is highlighted in
Figure 14. It is evident from the output response that there is a very slight difference between the GMPP and the surrounding peaks. The difference between the power values of GMPP and the largest LMPP is less than
, which makes it more difficult for the control scheme to differentiate the actual GMPP and accurately identify it.
The results show that, within the initial iterations, the MPPT controller explores a large range of search space rapidly and accurately identifies the MPP. The duty cycle variation shows that at s, the operating point oscillates within a small portion of search space, and the operating power gradually approaches the maximum power and tracks the actual GMPP at s, illustrating the short tracking period requirement of the proposed scheme for the simulated PS conditions. There is no oscillation in the output of the PV system once the output signal is determined. This characteristic is significant for illustrating the stability of the overall system.
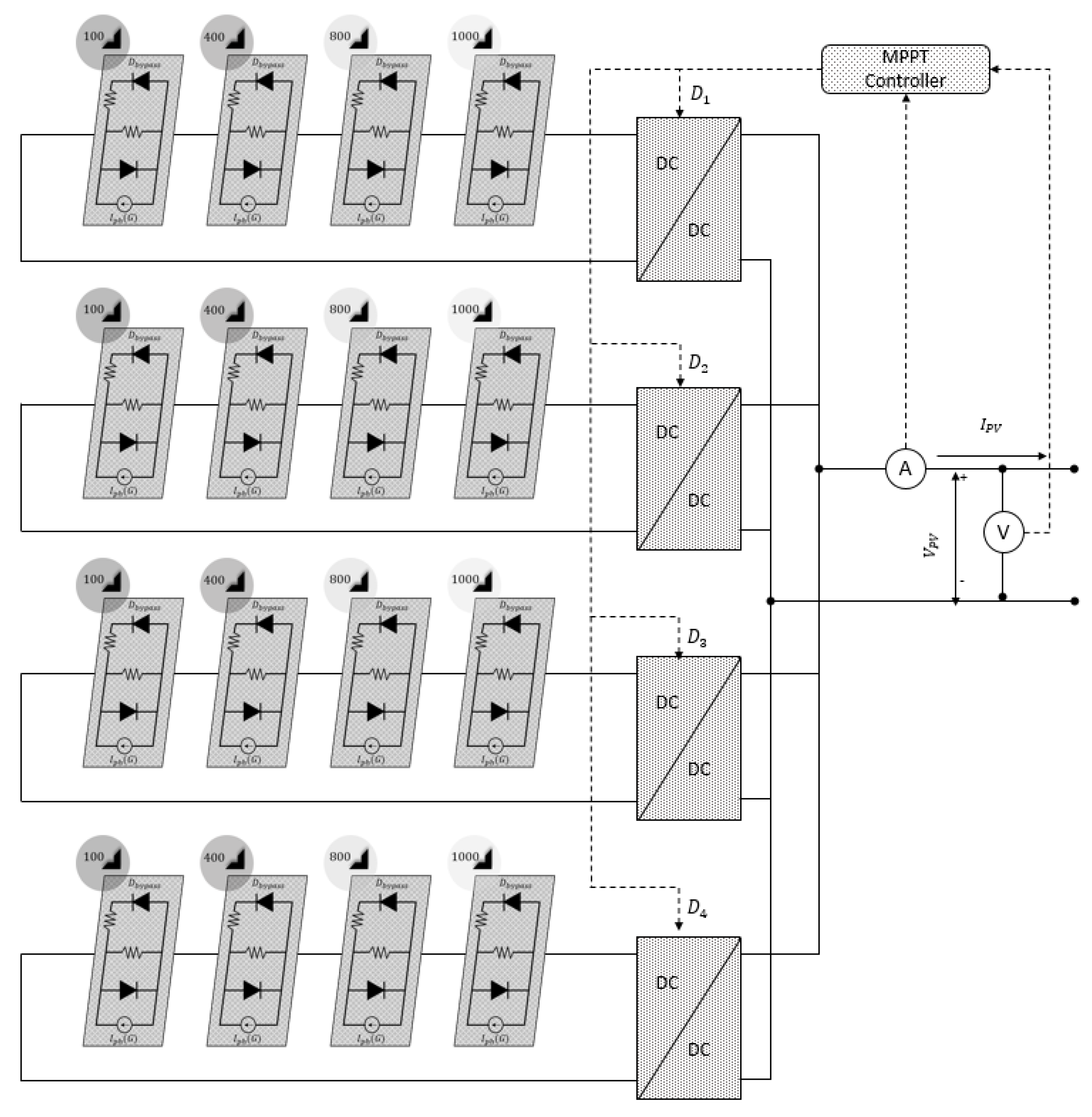
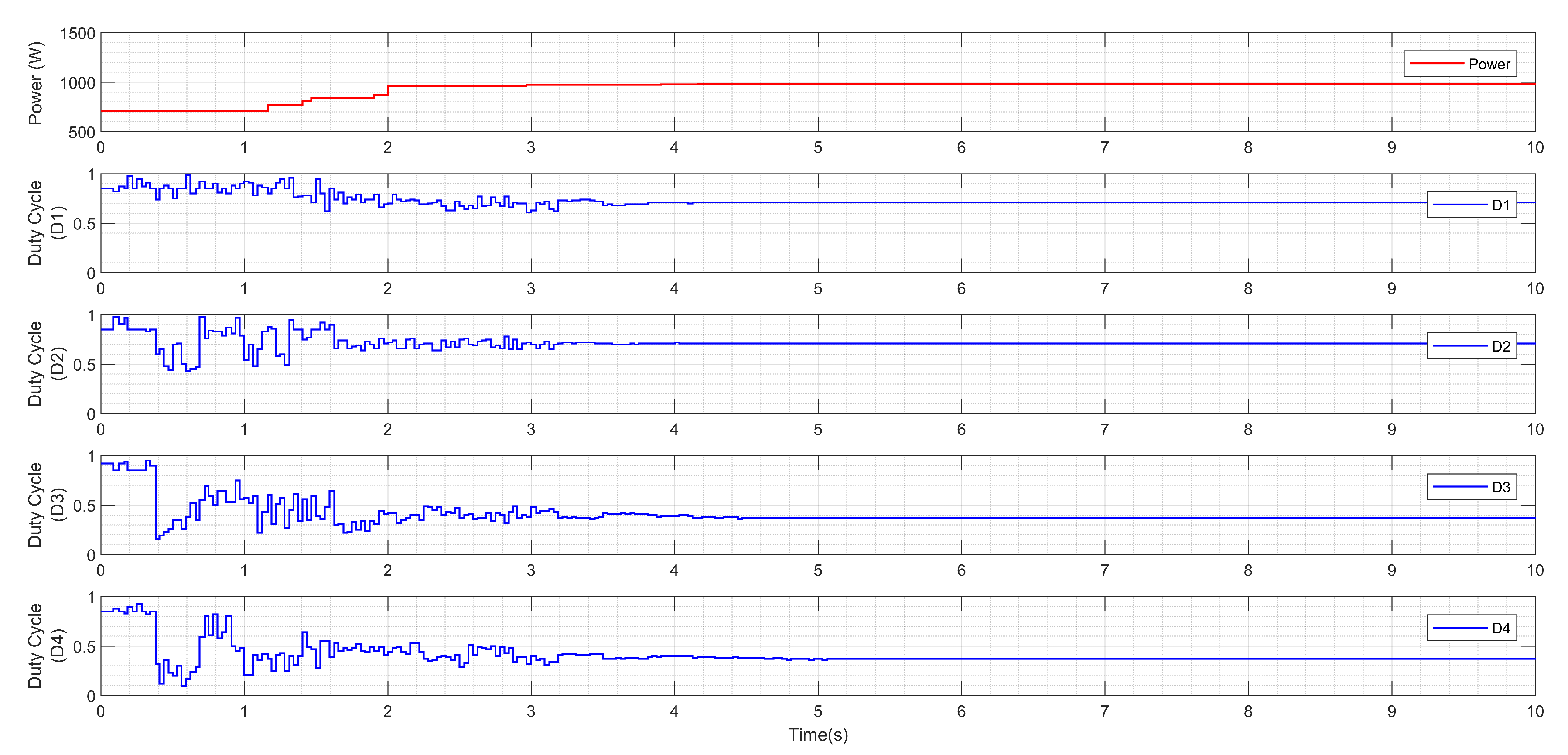
In the next couple of testing scenarios, the proposed RMO based technique applied to the distributed architecture PV system is evaluated on a larger-scale PV system with a larger number of subsets. A PV system with a distributed architecture consisting of four subsets is validated under testing scenarios 4 and 5 to demonstrate the effectiveness of the proposed technique used in a larger system. The modules in each subset receive irradiance levels of
,
,
and
for scenario 4, as illustrated in
Figure 15. The PV characteristics of these proposed scenarios have five dimensions from the perspective of the controller, so the controller needs to search a four-dimensional duty cycle search space to find the GMPP. It is not possible to show these characteristics with a basic visualization.
Figure 16 highlights the output performance of the proposed RMO-based MPPT technique applied under the testing scenario four.
From the results highlighted, the proposed MPPT control algorithm explores the search space in a meta-heuristic fashion and finds the GMPP at s. The sampling time considered for this analysis is 50 ms, which can be modified based on the capabilities of the type of controller used. The proposed RMO based MPPT technique is fast in converging to the global minimum when compared to the other MPPT techniques used in general. The exploration trajectory for each duty cycle is assumed to be different, as the centralized controller aims in searching the four-dimensional solution space in order to accurately track the GMPP, which then maximizes the output of the PV systems (DC-DC converters).
As mentioned earlier, the PS patterns for all subsets in the PV system under the shading scenario 4 are the same. Therefore, after the initial explorations, the final duty cycles will reach an identical value, as illustrated in the output response that is shown in
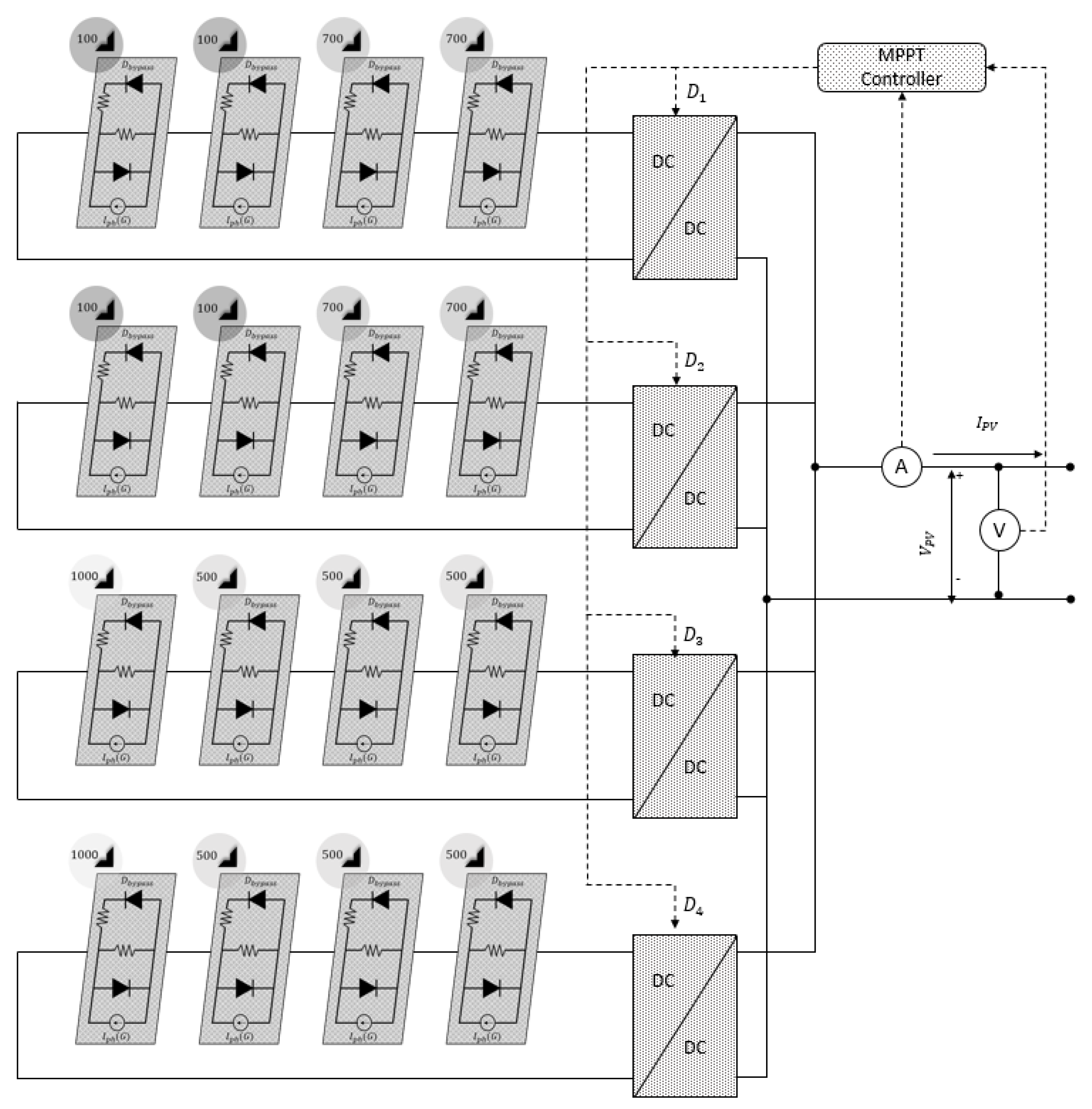
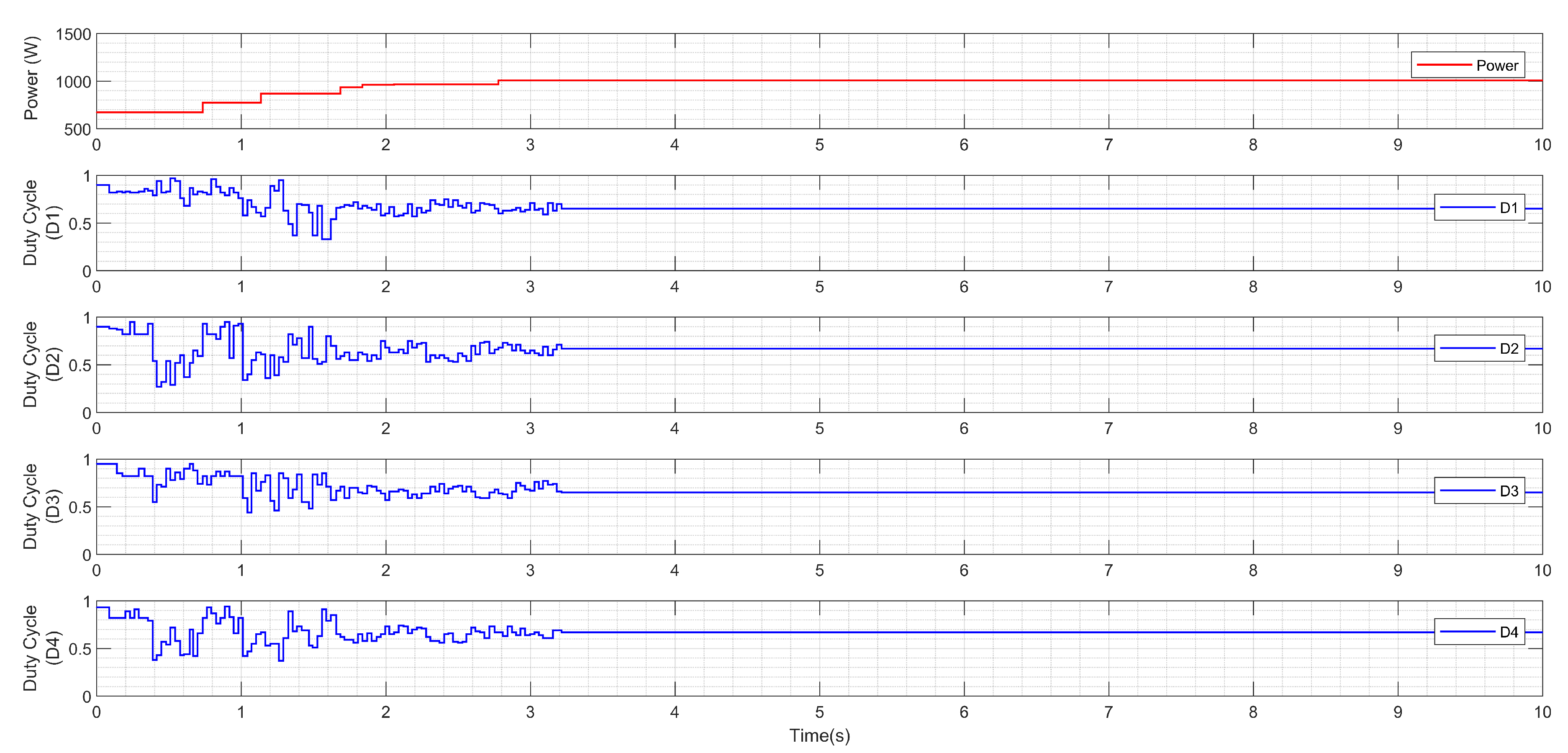
Figure 16. In testing scenario 5, a PV system with four subset configuration similar to scenario four is considered. However, in contrast with previous scenarios, the shading patterns of the four subsets are not identical in this scenario. Therefore, the final output signals are not identical. Under this scenario, the modules in subset 1 and subset 2 receive an irradiance of
and
. The modules in subset 3 and subset 4 receive an irradiance of
and
, as illustrated in
Figure 17. Due to the large size of this system and a large number of dimensions, it is not possible to visualize the PV characteristics from the control unit perspective to illustrate where the GMPP is exactly located in the PV characteristic response. The output performance of the proposed RMO–MPPT technique under this testing scenario is shown in
Figure 18. It is apparent that the duty cycles representing the maximum power for each PV subset depend on the pattern of PS. Having said that, Subsets 1 and 2 receive similar irradiance levels, and their operating points converge towards similar duty cycle values:
. A similar scenario occurs for the other two PV subsets; their final duty cycles are
, as shown in
Figure 18. Note that the size of the search space increases substantially as the number of subsets increases. Under the current and previous scenarios, the search space has 40 million data points in the solution space, which illustrates the performance of the proposed MPPT technique aimed at accurately finding the unique GMPP.
It was evident from the simulation results that tracking of a GMPP in such a large search space requires a compelling MPPT technique, like RMO. Additionally, the proposed distributed architecture gives way for the implementation of two or more sensor nodes along with the controller, which can detect the MPPT accurately and consistently at low cost. The results illustrated that the proposed RMO based MPPT technique is a viable solution to be employed as an MPPT controller scheme in the distributed PV system. The proposed distributed architectures comparison with the conventional centralized and decentralized architecture of the PV modules in terms of cost, efficiency, MPPT tracking capabilities under PSC, reliability, and scalability of the system, as illustrated in
Table 3.
Figure 19 depicted the inferences obtained from the comparison study highlighted in
Table 3. The proposed RMO based MPPT technique is compared with the other commonly used MPPT techniques, like InC, PSO, MPSO and GWO with respect to the MPPT tracking capabilities, simplicity, efficiency, reliability, initial location dependency, tracking speed, and stead state oscillation, as shown in
Table 4.