1. Introduction
Industry 4.0 and the digitization of the manufacturing sectors were once considered as future trends [
1,
2]. Nowadays, Industry 4.0 and the transformation of manufacturing strategies for a more customer-oriented implication of mass customization are strategic priorities for manufacturers who seek sustainable competitiveness [
3]. Modern manufacturers, therefore, are required to alter their existing linear and rigid production models and develop a more flexible and modular production system that effectively addresses the ever-changing customer demands and market circumstances within the Industry 4.0 environment [
4]. Customer-oriented mass customization is among many competitiveness strategies that are linked tightly to the concept of manufacturing sustainability within the Industry 4.0 literature [
5,
6], particularly in the sense that manufacturers commonly struggle with meeting the micro-economic sustainability criteria while transitioning into the more customer-oriented mass customization of products under the umbrella of Industry 4.0 [
7]. As a common strategy for staying economically sustainable in the current competitive market, manufacturers aiming for mass customization strategies are interested in producing different models of their products while undergoing the smallest change in costs in terms of tools and facilities [
8]. In such circumstances, among many manufacturing configurations, mixed-model assembly lines are widely used, as they enable manufacturers to produce different models of a basic product model in the same line without incurring a high cost [
9]. In general, the use of a mixed-model assembly line enables the production of various versions of a base product with some differences from the base product [
10,
11]. The mixed-model assembly line has several advantages, such as quick response to customer demands, fewer expenses to produce the new models of a given base model by using the same facilities, and more production flexibility [
12,
13]. In other words, the mixed-model assembly line is an essential factor for today’s manufacturers to overcome the recent challenges associated with operating in the Industry 4.0 environment, particularly regarding the diversity of products, as well as the rapid response to ever-changing customer expectations and demands [
14]. Despite many advantages of mixed-model assembly lines, supplying these high-variant mixed-model lines with the required material is a challenging task. In reality, a massive number of parts/materials must be transferred to a location near the production line (at stations), and any shortage of parts results in the line stopping and interruption of production [
15].
Moreover, modern manufacturers’ decision to apply various Just-In-Time (JIT) principles to minimize the inventory near the line while avoiding shortages imposes another significant difficulty to the material supply [
16]. To cope with this problem and to increase the reliability and flexibility of the part feeding process, it is a common practice for world-class manufacturers to implement and benefit from the supermarket concept. The supermarket is a decentralized logistic area near the assembly line where all parts/materials are sorted nearby the assembly line. This in-plant decentralized logistic area (supermarket) enables the manufacturers, especially those who are dealing with high-volume of production, to massively take advantage of a reliable and frequent small-lot JIT part delivery [
17,
18]. Typically, parts in supermarkets are transported to the shop floor according to the predefined production sequence in small bins and utilizing tugger trains, which are either automatically guided or human-driven vehicles [
19]. Applying the supermarket concept has several advantages. Nonetheless, planning and control of these in-plant logistics areas is a considerably complex problem that requires careful optimization [
20,
21]. Two crucial decisions immensely affect the performance of the in-plant material supply process when it comes to using the supermarket concept, including (1) the decision on a delivery schedule for each tugger train, and (2) the decision on the quantity of each material that should be loaded on each tugger train during each line visit.
It is worth mentioning that the in-plant material supply problem is an extensive research area that covers many sub-areas, such as transport of parts, storage of parts, and parts feeding policy, among many others. Each of the areas mentioned contains several operational, tactical, and strategic problems to be solved. For instance, targeting the transport of parts, material handling equipment selection, loading, scheduling, and routing are among the optimization problems that should be addressed [
22,
23].
The present study concerns planning the frequent small-lot deliveries from a decentralized storage area and utilizing tugger trains. In particular, this study addresses the Tugger Train Loading (TTL) and Delivery Schedule (DS) problems, where the material types and their quantity, as well as the best sequence of materials that should be delivered to each assembly station at each time, should be decided to minimize the total cost associated with transportation and material holding at assembly stations. In this regard and borrowing from the computer science field, a two-stage heuristic algorithm is developed based on the concept of the multilevel queue scheduling algorithm.
The remainder of the paper is structured as follows.
Section 2 provides a brief review of the literature and related studies.
Section 3 discusses the material supply problem at assembly lines by highlighting the specific problem under study. A quantitative analysis of the problem in the form of a mathematical model is presented in
Section 4. The two-stage heuristic algorithm is presented in
Section 5, and the results of the computational study for testing the heuristic algorithm is reported in
Section 6. Finally,
Section 7 discusses the concluding remarks and future research directions.
2. Literature Review
The in-plant material supply problem contains different aspects and requires solving various decision problems that may not be in the scope of this study. Therefore, this review is merely limited to the previous studies that addressed the transport of parts to assembly lines and considered the application of the supermarket concept and the utilization of tugger trains for material delivery.
Emde et al. [
24] addressed the tugger train loading problem by proposing a polynomial-time solution procedure. The authors tried to minimize the sum and maximum inventories at the assembly stations by determining an optimum loading plan for tugger trains in successive tours. Golz et al. [
15] introduced a new heuristic to cope with the routing, scheduling, and loading problems of tugger trains simultaneously. Their study attempted to minimize the number of tugger trains (equivalently minimize the drivers) used for part delivery purposes at the assembly lines while the stock-outs at the stations were not allowed. Moreover, the decision on the routes was limited to choosing a path from a set of predetermined delivery paths. Emde and Boysen [
25] presented nested dynamic programming (DP) to deal with tugger train routing and scheduling problems. They tried to find fixed routs for tugger trains as well as cyclic and non-cyclic schedules. Emde and Boysen’s [
25] study showed that the level of inventory at stations in a non-cyclic delivery schedule is considerably lower than the cyclic tours. Rao et al. [
26] introduced a model to optimally schedule the single-vehicle (tugger train equivalent) part delivery problem within which parts were delivered from the storage center to the workstations in a mixed-model assembly line. To minimally reduce the total inventory holding and travel costs, these authors tried to develop a detailed specification of the destination workstation and the part quantity along with the departure time of each particular delivery. In doing so, Rao et al. [
26] introduced a hybrid genetic algorithm and simulated annealing (GASA) and implemented a backward-backtracking approach. These authors tested both approaches on a series of real-world data collected from an automobile manufacturer in China. The results showed that although the backward-back tracking approach was not able to solve the large-size problems, the GASA approach could efficiently solve all the test problems.
Faccio et al. [
27] presented a simulation model of an assembly line feeding system based on a real case study in an Italian automotive manufacturer. They tried to cope with the problems of scheduling and loading of tugger trains while considering a kanban-controlled production system and stochastic demand. Different scenarios by considering four critical parameters, namely the number of tugger trains, service level, tour frequency, and tugger train capacity, were analyzed. The performance of solutions related to each scenario was investigated based on six production factors, and the effect of each parameter on the solution was examined.
Fathi et al. [
28] tackled the part feeding problem at the assembly line by proposing a mathematical model and an ant colony optimization algorithm (ACO). The study attempted to find the best sequence and quantity of parts to be loaded on tugger trains on fixed routes and with cyclic delivery trips. Fathi et al. [
29] addressed the part delivery scheduling problem by presenting a mathematical model and simulated annealing (SA) algorithm. The authors tried to plan the tugger train delivery to minimize the total number of deliveries as well as the inventory levels at assembly stations. Muguerza et al. [
30] studied the material supply problem at assembly lines with an emphasis on energy efficiency. Their study aimed to define the sequence of assembly stations that are to be visited by the tugger train at each delivery trip as well as the number of pallets to be delivered at each visit. Muguerza et al. [
30] presented an analytical approach in the form of a mathematical model as the solution method. The ultimate goal of the model was to minimize the energy consumption of the supplying strategy. Fathi et al. [
31] tried to solve the part delivery problem at assembly lines by suggesting a modified particle swarm optimization (PSO) algorithm. The study aimed to optimally schedule the part delivery to assembly stations via tugger trains to minimize the total number of delivery trips and the sum of inventory. A mathematical model and complexity analysis of the problem were also provided in this study.
Emde and Schneider [
32] addressed the Vehicle Routing problem for JIT part delivery to assembly lines. The authors proposed a mathematical formulation of the problem and developed a large neighborhood search algorithm (NSA) to solve it. The optimization objectives in their study were to minimize the number of transport vehicles as well as the total route duration, while considering the limited storage capacity at assembly stations. This study also investigated the effect of the inconsistency of the demand rates on the part feeding system. Peng and Zhou [
33] made an effort to facilitate the material supply process in automobile assembly lines through solving the multiple server scheduling problems. Peng and Zhou [
33] proposed a mathematical optimization model as well as a hybrid ant colony optimization (HACO) algorithm to find an optimum schedule for sequencing and loading the materials on servers. The optimization objective considered in this study was to minimize the line-side inventory while relaxing some critical assumptions, such as stock-out occurrence and line-side storage limitation. Zhou and Shen [
9] addressed the material supply problem at the assembly line by proposing a multi-objective hybrid Tabu search and particle swarm optimization (TSPSO) algorithms. The optimization objectives considered were to minimize the total weighted tardiness and energy consumption. The authors also presented a mathematical formulation of the problem. The results of the study showed that energy consumption could be reduced significantly by following an optimal delivery schedule. Zhou and Peng [
34] assumed that several parallel machines could be used for material delivery to workstations at assembly lines. Therefore, the authors studied the parallel machine scheduling problem to find a good schedule for loading the machines with materials to minimize the line-side inventory. An exact algorithm was developed based on the problem properties capable of solving small size problems. To cope with large-scale problems, the authors proposed a hybrid teaching–learning-based optimization algorithm.
In conclusion, the existing academic contributions by prior scholars have significantly advanced the current understanding of supermarket-based in-plant material supplying optimization and, in particular, transport of parts to assembly lines. A summary of the studies reviewed, including the solution methods used and the decision problem addressed, is presented in
Table 1.
The review of the literature shows the importance of Tugger Train Loading (TTL) and Delivery Schedule (DS) problems, as most of the previous studies targeted at solving these two. Moreover, it can be seen that although a mathematical model was presented in almost all of the earlier studies, the authors resorted to heuristic algorithms due to the complex nature of the problem.
Most of the algorithms proposed in the previous studies are complicated and hard to understand and use by logistics operators in the real-world industry, specifically by small- and medium-sized enterprises. In such circumstances, the current study aims at proposing a simple, yet effective, solution method based on some rule of thumbs that can be efficiently used in the shop floor with little to no prior knowledge in programming and optimization. In terms of the problem specification, this study differs from the previous ones by allowing the delivery on specific paths available to the tugger trains and imposing restriction on making shortcuts. These restrictions are applied based on the observations in real-world shop floors and to address the issue of space scarcity near the stations in the assembly lines, as well as to avoid any disorder on the shop floor. Additionally, this study also assumes that only a single supermarket can support each assembly line. This assumption ensures that deliveries, as well as the part requests, are all managed entirely at a single location close to the assembly line (i.e., supermarket).
3. Problem Description
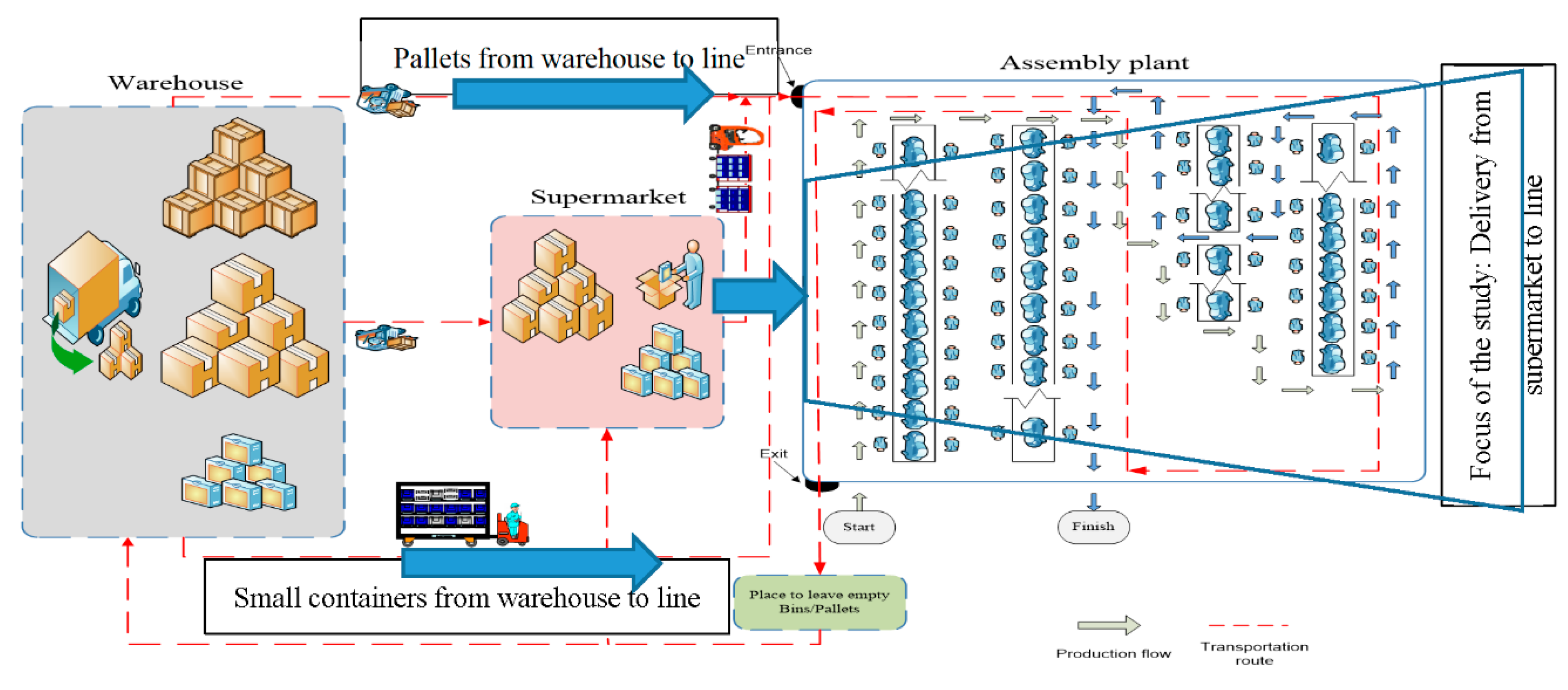
In general, most manufacturing companies have the main central warehouse to receive and store goods, which is far from the assembly line and a supermarket that is close to the shop floor/assembly line. Companies follow different strategies for supplying materials to the production lines. The main supply strategies are (1) direct transportation of the parts from the warehouse to the assembly line in pallets, (2) direct transportation of the materials in small containers from the warehouse to the assembly line in case no pre-assembly or excessive operation is needed, and (3) transportation of the parts to the supermarket, i.e., the parts that are received in pallets from the supplier, but have to be delivered more frequently to the stations in small containers.
This study is focused on the assembly line part feeding from the supermarket, utilizing tugger trains and in small identical standardized shapes and size bins, which is a requirement for the shooter racks [
20]. A tugger train consists of a towing vehicle, operated by a driver, which is connected to a few wagons. First, bins are loaded into wagons at the supermarket. Consequently, the supermarket will be a starting point for tugger trains to commute to the assembly plant based on a predetermined schedule to deliver the bins full of parts to the corresponding stations while collecting the empty bins. This means that at each stopover in the assembly line, full bins are unloaded in the respective stations, and the empty bins are loaded to return. Finally, the empty tugger train returns to the supermarket to be reloaded for the next tour. The tours are frequently done in each working shift due to the JIT philosophy to reduce the inventory level in the shop floor by frequent small-lot deliveries, as well as space scarcity near the stations in the assembly lines. The tugger trains are only authorized to travel on predefined paths through the assembly plant due to safety reasons.
To better understand the material supplying process explained above, a graphical view of the process is depicted in
Figure 1. As shown in this figure, the focus of the study is on material delivery from the supermarket to the assembly line.
Despite the advantages of applying the concept of small-lot deliveries, it needs an accurate plan to avoid any material shortage at the workstations and requires the solving of the Tugger Train Loading (TTL) and Delivery Schedule (DS) problems. The DS aims to find the best sequence of stations to be visited, which will further lead to the improvement of some criteria, such as lead time, inventory level, and number of line visits. Moreover, the TTL aims to find the best order and quantity of bins to be loaded in a tugger train, which also results in the use of fewer transport vehicles as well as the number of line visits.
The main assumptions and characteristics of the in-plant material supply process are presented below.
Only one supermarket is available to serve the stations on each assembly line;
The traveling path, location of the stations, and the supermarket on the shop floor are given;
The storage capacity in each station is limited and known;
Tugger trains are only allowed to travel on predefined paths;
There is no more than one tugger on the same path, and tuggers do not block each other during a tour;
All tugger trains are identical in terms of speed and loading capacity;
Parts are supplied only in small containers with a given capacity for each part type, and only fully loaded bins are delivered, and empty bins are collected at each station;
The assembly line is assumed to be straight; therefore, there is no restriction to visit the stations, because all the stations have to be passed by on each line visit;
Tugger trains can only enter and leave the assembly plant at specific points, and no shortcut is allowed;
There is no restriction on the number of stations that can be supplied on each line visit;
Containers have identical and standardized shapes and sizes;
The production sequence is known within the planning horizon;
A limitation of tugger wagons per tugger trains is applied due to the difficulty in sharp turns on the shop floor;
Each container only contains one specific part;
Each wagon can be loaded with different containers in terms of content;
The weight restriction is not considered, as tuggers are adequately powerful;
There is a capacity limitation for each tugger;
All the time interval between line visits are identical and known in advance;
The shortage is not allowed throughout the entire planning horizon.
4. Problem Formulation
To better understand the problem, including the underlying assumption and constraints, a mathematical model of the problem is presented. The assumptions and constants of the model are the same as those found in Fathi et al. [
29]. The model presented is a mixed-integer linear programming (MILP) model. The MILP model is an optimization model for optimally loading tugger trains and scheduling the deliveries. The objective of the optimization is to minimize the total martial supply cost, including the cost of line visits and material storage at the stations.
The notation used in the MILP model, including indices, parameters, and decision variables are as follows.
Indices:
I: Set of material types;
i: Index of material type (i ∈ I);
C: Set of cycles;
c: Index of cycles (c ∈ Cmax).
Parameters:
: Inventory level of material type i at the beginning of the production;
Loading capacity of tugger train;
The storage capacity at the line for material type i;
Demand of material type i on cycle c;
n: Total number of material types;
Cmax: maximum number of cycles;
DC: Delivery cost;
IC: Inventory cost.
Decision variables:
Amount of material type i delivered in cycle c;
Inventory level of material i in cycle c;
: Equals one if delivery is planned at cycle c is, otherwise equals 0.
Equation (1) represents the objective function, that consists of the cost of line visits and the cost of holding inventory at stations. Equation (2) ensures that the total amount of each material that is delivered in all cycles satisfies the total demand of that specific material. Equation (3) ensures that no shortage of material will happen in any cycle. Equation (4) ensures that the transport vehicle (i.e., in this case, tugger train) is not overloaded, while ensuring that any material is delivered unless a tugger train is assigned for the line visit. Equation (5) ensures that the storage capacity for each specific type of material is not overloaded. Equations (6)–(8) define the domain of the variables and enforcing that only full containers can be delivered, no backlog of material orders can happen, and no material can be delivered if no tugger train is available for the line visit, respectively.
subject to:
5. Proposed Heuristic Algorithm
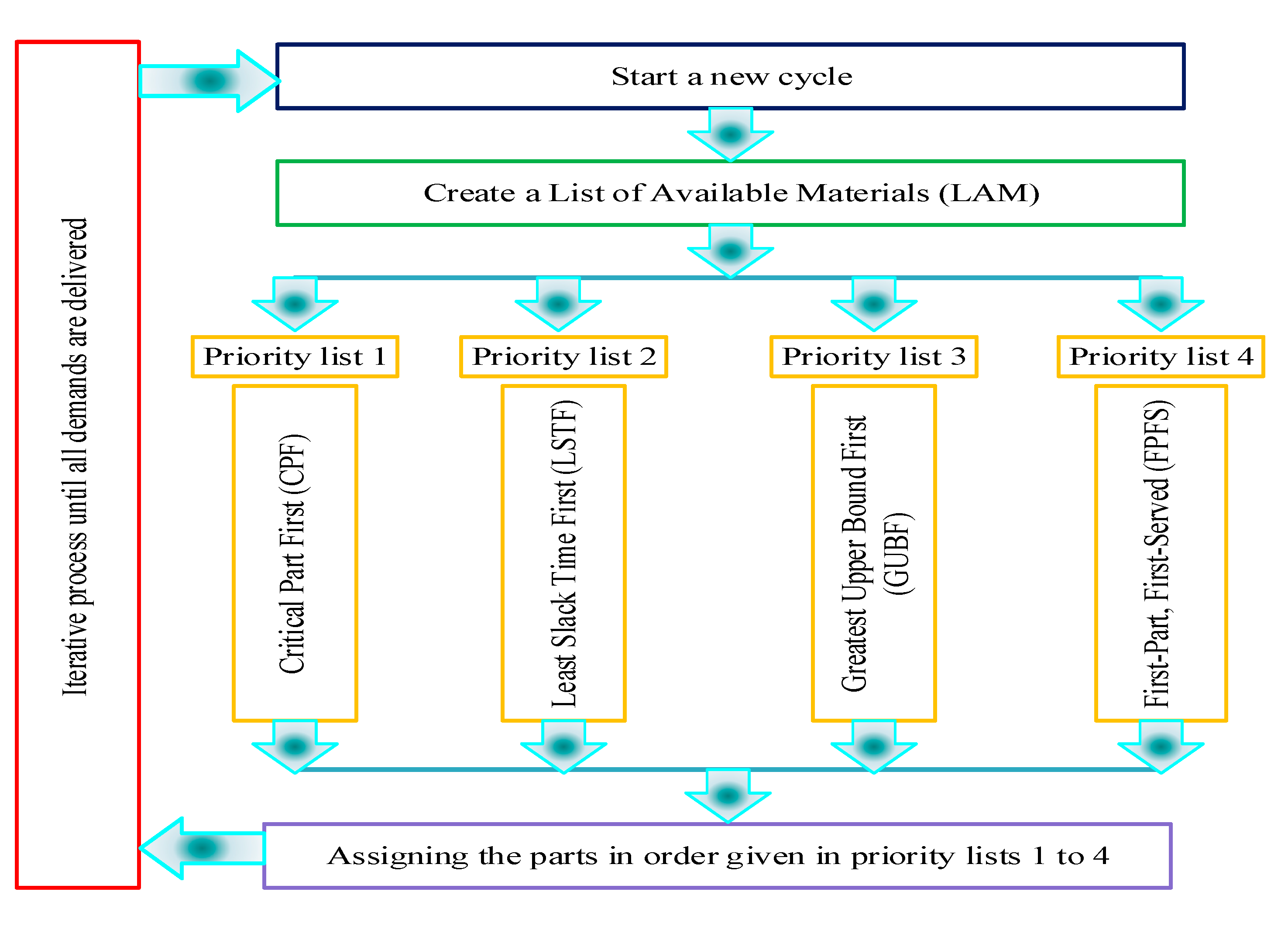
The algorithm proposed in this study is a two-stage heuristic that was developed based on the well-known concept of multilevel queue scheduling in the computer science field. The multilevel queue scheduling algorithm suggests that processes should be divided into groups based on their specific properties. Then, a certain number of queues should be created where the total number of queues is equal to the groups the processes are divided into. Each queue has a particular priority and applies its scheduling algorithm. The processes in a queue can only be executed if all the queues with a higher priority are empty. In other words, the process in higher priority queues must be completed before executing the process in a lower priority queue. There are several advantages to using multilevel queues. Some of these advantages are: (1) flexibility in implementation, (2) shorter execution time due to prioritizing the process, and (3) possibility of applying the preemptive or non-preemptive concept.
Following the main idea and reasoning behind the multilevel queue scheduling algorithm, the proposed heuristic algorithm for material supply consists of four queues with different priority levels. The introduction of priority levels is necessary because in material supply using tugger trains, not all the materials can be delivered at once due to the limited capacity of the trains as well as the space limitation at the stations. Therefore, material delivery to stations should be gradual, meaning having a priority plan is crucial to avoid a shortage or over-delivery. In this regard, a particular priority rule is suggested for each queue to load the tugger trains with materials and deliver them to stations. The proposed priority rules are named Critical Part First (CPF), Least Slack Time First (LSTF), Greatest Upper Bound First (GUBF), and First-Part, First Served (FPFS).
The CPF aims to rank the materials based on their urgency for the production. To decide on the level of urgency of each specific material, a criticality number is calculated for each material type using Equation (9):
where
CN(
i) is the criticality number of material type
i,
is the demand for material type
i in cycle
c, and
is the amount of material type
i already delivered to stations in cycle
c.The LSTF assigns a priority value to each material type by following this principle that the less the material is available at a station concerning the demand of the station, the higher the material priority. In other words, the shorter the slack time (i.e., the maximum time allowed to the next delivery) of a material type, the higher the priority value of that material. The priority value is calculated using Equation (10). The higher the priority value, the higher the delivery priority:
where
is the priority value for material type
i,
and
are the demand and the available inventory at stations for material type
i in cycle
c.The GUBF refers to the unused storage capacity at stations and suggests that higher priority should be assigned to materials that have more space left for storage. An upper bound value can be calculated using Equation (11), where a higher value proposes higher property for delivery:
where
is the upper bound value for material type
i,
is the total storage capacity at stations for material type
i, and
the available inventory at stations for material type
i in cycle
c.The FPFS is a simple rule of thumb that suggests delivering the materials according to their reference number. It means that a material with a smaller reference should be delivered before a material with a greater number.
Given the above-proposed priority rules, materials are sorted according to their given priority in four different priority lists and are located in their specified queue in each cycle. Then, starting from the first queue, materials are chosen for delivery based on their given priority while satisfying all the constraints, e.g., storage capacity at stations and tugger tarins. The process is continued until all the demands are delivered to stations.
Figure 2 depicts the proposed solution methodology.
As mentioned before, the proposed algorithm has two stages. The first stage aims to reduce the total cost of the line visit by minimizing the number of visits, and the second stage aims to minimize the material holding cost by reducing the inventory level at stations. In the first stage of the algorithm, based on the maximum possible number of line visits (e.g., the maximum number of cycles) that is assumed to have the same time interval, material containers are loaded onto the tugger trains on each cycle according to the methodology presented in
Figure 2. This stage of the algorithm is summarized as Algorithm 1.
| Algorithm 1 First stage: minimizing the number of line visits. |
While all demands are not delivered, start a new cycle and create the according to Equation (12)
If LAM is not empty, create priority lists 1 to 4 as presented in Figure 2. While priority list 1 is not empty, select a material type from priority list 1 that has the highest . If there are one or more material types with the same as the selected material, choose a material type from list 2 to 4, respectively End if Assign the exact amount of containers needed from the selected material to satisfy its demand in the current cycle. Remove the selected material type from . End while While there is any free space on the tugger train, create the list of extra material (LEM) according to Equation (13) If LEM is not empty, create priority lists 1 to 4 Assign only one container of the material type that has higher priority in list 1 (If there are one or more material types with the same , choose a material type from list 2 to 4, respectively) to the tugger train and update the capacity of the tugger train. End if Update all the information and terminate the assigning process in the current cycle. End while Else Leave the current cycle without assigning any material and update all the information to start the next cycle. End if End while Return to the solution.
|
Consistent with the JIT philosophy, the second stage in the execution of the algorithm involves the heuristic aiming for the reduction of the inventory level at stations. Using the solution obtained from the first stage as the starting point, the algorithm in the second stage tries to reduce the inventory at stations. In doing so, it will attempt to re-schedule the deliveries so that only the most necessary materials will be delivered on the active cycles identified in the first stage. In other words, without adding any new cycle, the second stage of the algorithm rearranges the deliveries to delay the delivery of material to the latest possible time. An algorithmic description of this stage is given as Algorithm 2.
| Algorithm 2 Second stage: minimizing the inventory level. |
Create the set of available cycles (i.e., the cycles that are not removed in the first stage) AC, according to Equation (14).
While AC is not empty Select the first possible cycle (which is in the AC) and find the number of the consecutive removed cycles (RC) after the selected cycle, according to Equation (15). Keep the required amount of all material types to meet the demand of the current cycle and all the consecutive removed cycles after the current cycle and transfer the extra containers to the next available cycle. Remove the selected cycle from AC. End while For all available cycles in the AC, from the last to the first (recursive process) If the number of assigned containers to the tugger train in the current cycle exceeds the capacity of the tugger train While the number of containers is more than the capacity of the tugger train Create a new candidate list (NCL), according to Equation (16). If NCL is not empty, create priority lists 1 to 4, as presented in Figure 2 Transfer only one container of the material type that has higher priority in list 1 (If there are one or more material types with the same , choose a material type from list 2 to 4, respectively) to the first available cycle before the current tour. Update the information concerning the current cycle as well as the cycle that received the selected material. End if End while End if End for Return the solution.
|
6. Computational Results
A set of instances taken from the literature (i.e., [
29]) that included nine different problems with different sizes (small, medium, and large) were solved to allow for a more detailed assessment of the efficiency and effectiveness of the heuristic proposed. The loading capacity of the tugger train (LC) was set to be between 50 and 150 containers, depending on the number of wagons attached to each tugger train (i.e., 50 containers per wagon and the maximum of 3 wagons per tugger train). All the instances were solved considering three different maximum allowed number of line visits. In total, 27 instances were solved by the proposed heuristic, and the results obtained were compared against the best solution found by a well-known commercial solver, i.e., CPLEX. The proposed heuristic was coded in MATLAB R2019b and run on a personal computer with Intel Core i5, with 2.4 GHz CPU and 8 GB of RAM.
To evaluate the performance of the heuristic, the results achieved from the heuristic and the MILP model solved by CPLEX were compared concerning the cost of line visits (CLV), cost of holding inventory (CHI) at stations, and the total cost including the CLV and CHI. It is worth noting that comparison of the inventory holding cost can only be made if the number of line visits is the same, because it is not unexpected to have less inventory when having more line visits.
The computational results for both the proposed heuristic and the CPLEX are given in
Table 2. To facilitate the comparison, the worst and best results obtained by the heuristic in comparison with the results achieved from CPLEX are shown in bold numbers and marked with “*”, respectively.
The analysis of the results listed in
Table 2 shows that the proposed heuristic found a solution with the same or lower cost for line visits (i.e., lower cost in two instances, as shown with “*”) as compared to the solution obtained by CPLEX during the limited 2-h time. Moreover, the heuristic algorithm successfully found the same amount of inventory holding cost for 25 instances out of 29. Moreover, it was observed that CPLEX was not able to find the optimum solution during the predetermined computation time (2 h) for 11 instances (mostly comprised of large-scale problems). Nevertheless, the heuristic algorithm proposed managed to find an optimum or near-optimum solution in the majority of the instances solved within a minimal computational time.
Table 2 lists the percentage error of the heuristic algorithm from CPLEX regarding the cost of holding inventory to facilitate the necessary comparisons. The assessment of the percentage error value revealed that in close to 86% of the solved instances, the heuristic algorithm found the same cost for holding inventory as compared to the MILP model solved by CPLEX.
Regarding the total cost, the heuristic algorithm found the same solution in 19 out of 27 (almost 70%) of the solved instances and a better solution in four problems as compared to the MILP model.
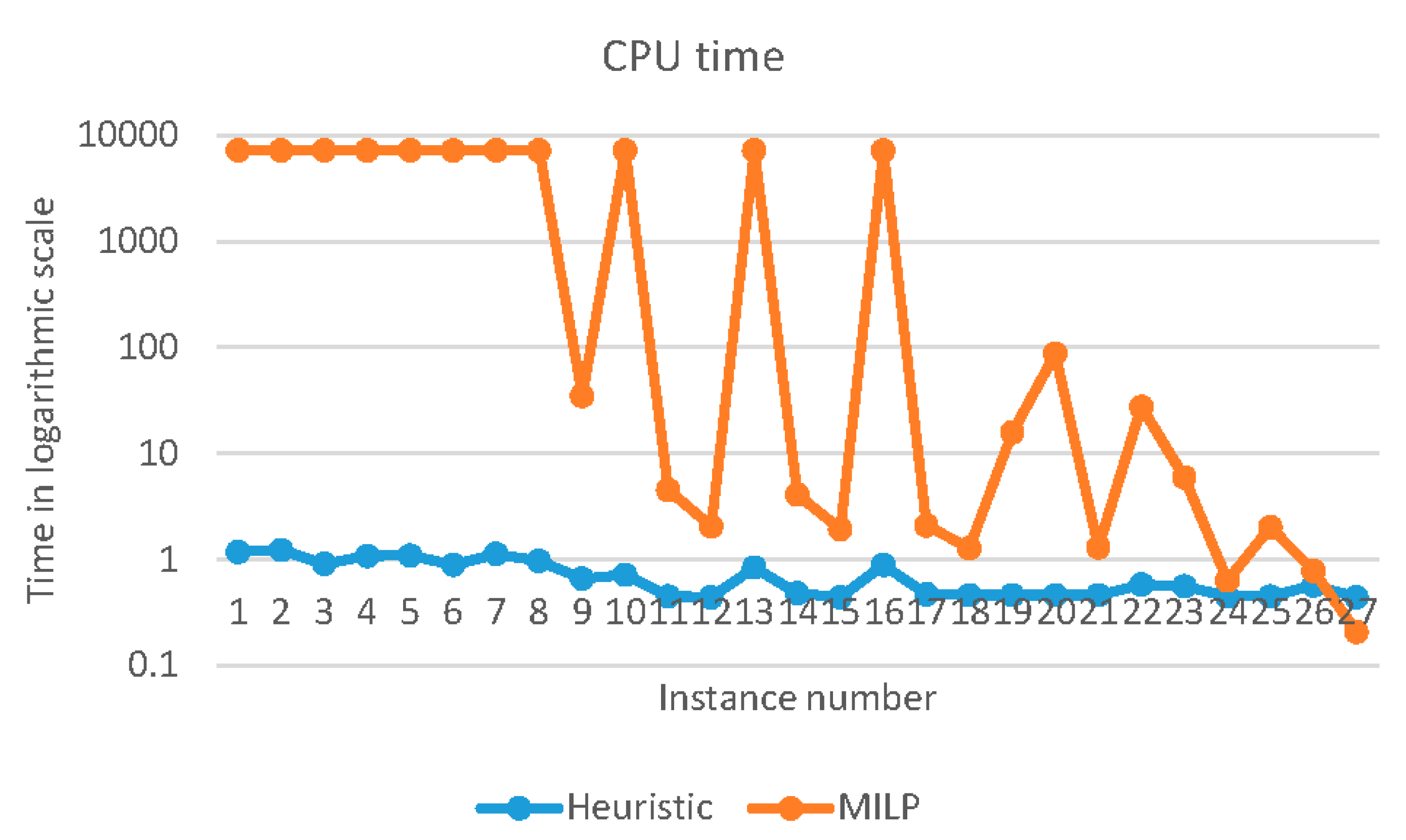
Figure 3 shows a comparison of the solution time for each problem by the proposed algorithm and the MILP. As can be observed, the proposed algorithm was extremely fast in finding a good and feasible solution to the problems solved in a fraction of time. The results also show that the MILP can solve the small and medium-size problems in a reasonable amount of time, but the computation time severely increases as the problem size increases.
7. Concluding Remarks and Future Directions
For decades, mass-production and the underlying goals of cost-saving and higher productivity have been the leading business strategy across the manufacturing Industry. With the advent of digital transformation and the progression of Industry 4.0, more customer-focused goals are an integral part of the business strategy across various industrial sectors. Since some degree of product personalization and manufacturing modularity is a necessary response to the market turbulence, manufacturers nowadays are increasingly concerned with reshaping their strategies from mass production to mass customization as the manufacturing sector revolution under the umbrella of Industry 4.0 grows. To meet the micro-economic sustainability criteria while altering the preexisting production models consistent with the customer-oriented mass customization philosophy, manufacturers need to minimize changes to the production layout, machinery, processes, and facilities, while improving the overall production modularity and agility. To meet both customer orientation and manufacturing sustainability criteria simultaneously, contemporary manufacturers are striving to implement mixed-model assembly lines to produce a wide variety of basic products, while minimizing the machinery and production line reconfiguration costs. To enable manufacturers to take greater advantage of mixed-model assembly lines, the present study addressed the issue of the material supply problem at a mixed-model assembly line while considering the use of the supermarket concept. A two-stage heuristic algorithm was proposed as the solution approach. The proposed heuristic was designed based on the central concept of the multilevel queue scheduling algorithm. As part of the heuristic, four priority rules were presented with specific formulas enabling the prioritization of the materials to be chosen for delivery in each line visit. The main decision problems considered in this study were the tugger train loading and material delivery scheduling. The main optimization objective was defined as minimizing the total cost material delivery cost, including the cost of the line visits and inventory holding at stations.
The performance of the heuristic algorithm proposed was tested by solving a set of problem instances taken from the literature. To illustrate the efficiency of the proposed algorithm, the results achieved by the heuristic algorithm were compared against the solutions obtained by solving the related MILP model. Comparisons performed, collectively, demonstrated that the heuristic proposed offers a satisfying level of efficiency, as it successfully found ‘good’ results in the majority of the cases. More precisely, the heuristic found the same or lower line visits cost as compared to the MILP across all the instances solved. Moreover, and in comparison to the solution provided by the MILP model, the algorithm also found the same results for close to 86% of the problems solved in terms of inventory holding cost. Moreover, it is worth mentioning that while the computational time for solving the MILP model by CPLEX was significantly high and in 11 out of 27 instances, no optimal solution could be found during the 2-h time limit; however, the heuristic proposed in this study managed to successfully find a ‘good’ solution for the majority of the solved instances in one minute or less. Overall, the present study contributed to the issue of micro-economic sustainability of manufacturers by enabling factories to reduce the overall production costs thanks to the optimization of line visits and inventory holding costs across the production lines, favorable conditions that offer an indirect contribution to the plant-level energy sustainability as well.
For future works, the proposed heuristic can be adapted to cope with the material supply problem considering another type of assembly line, e.g., U-shaped and parallel. Moreover, stochastic material demand might also be considered as an extension of the current study. Furthermore, the performance of the proposed heuristic can also be benchmarked against metaheuristic algorithms, such as Tabu Search and Genetic Algorithm. Considering the satisfying performance of the proposed algorithm, the concept of multilevel queue scheduling can also be adapted to design algorithms for other types of production and logistics problems. Additionally, the performance of each priority rules proposed in this study can be tested in dealing with other similar problems.