A Multi-Objective Model for Sustainable Perishable Food Distribution Considering the Impact of Temperature on Vehicle Emissions and Product Shelf Life
Abstract
1. Introduction
2. Literature Review
3. Problem Statement and Model Formulation
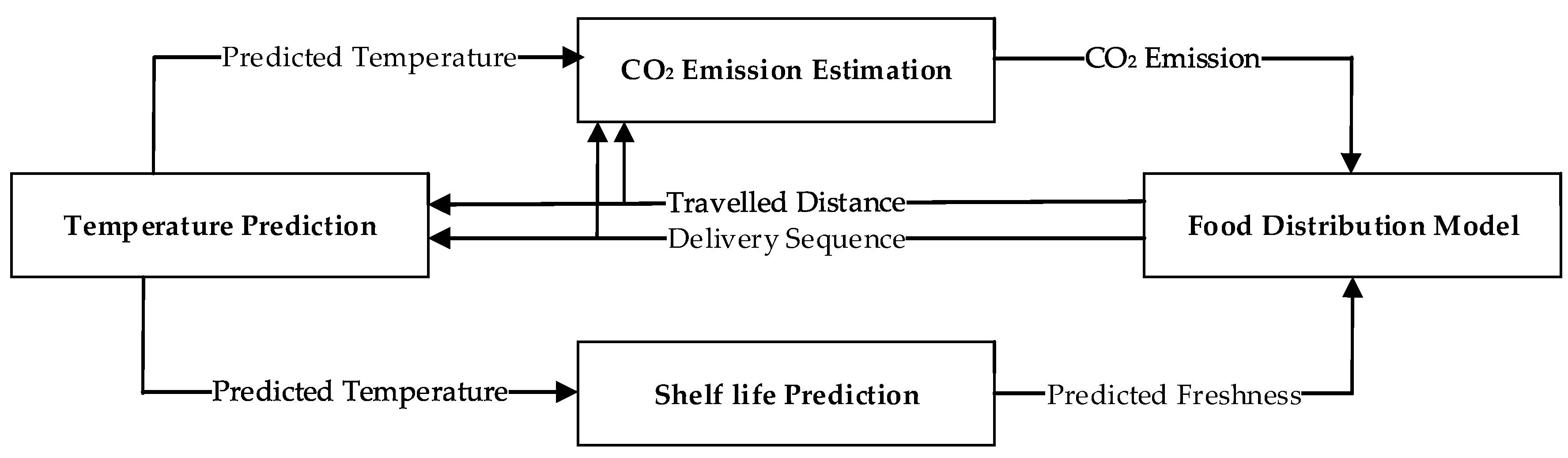
3.1. Temperature Prediction Based on Heat Transfer
3.1.1. Temperature Prediction during Unloading
3.1.2. Temperature Prediction during Transportation
3.2. CO2 Emissions
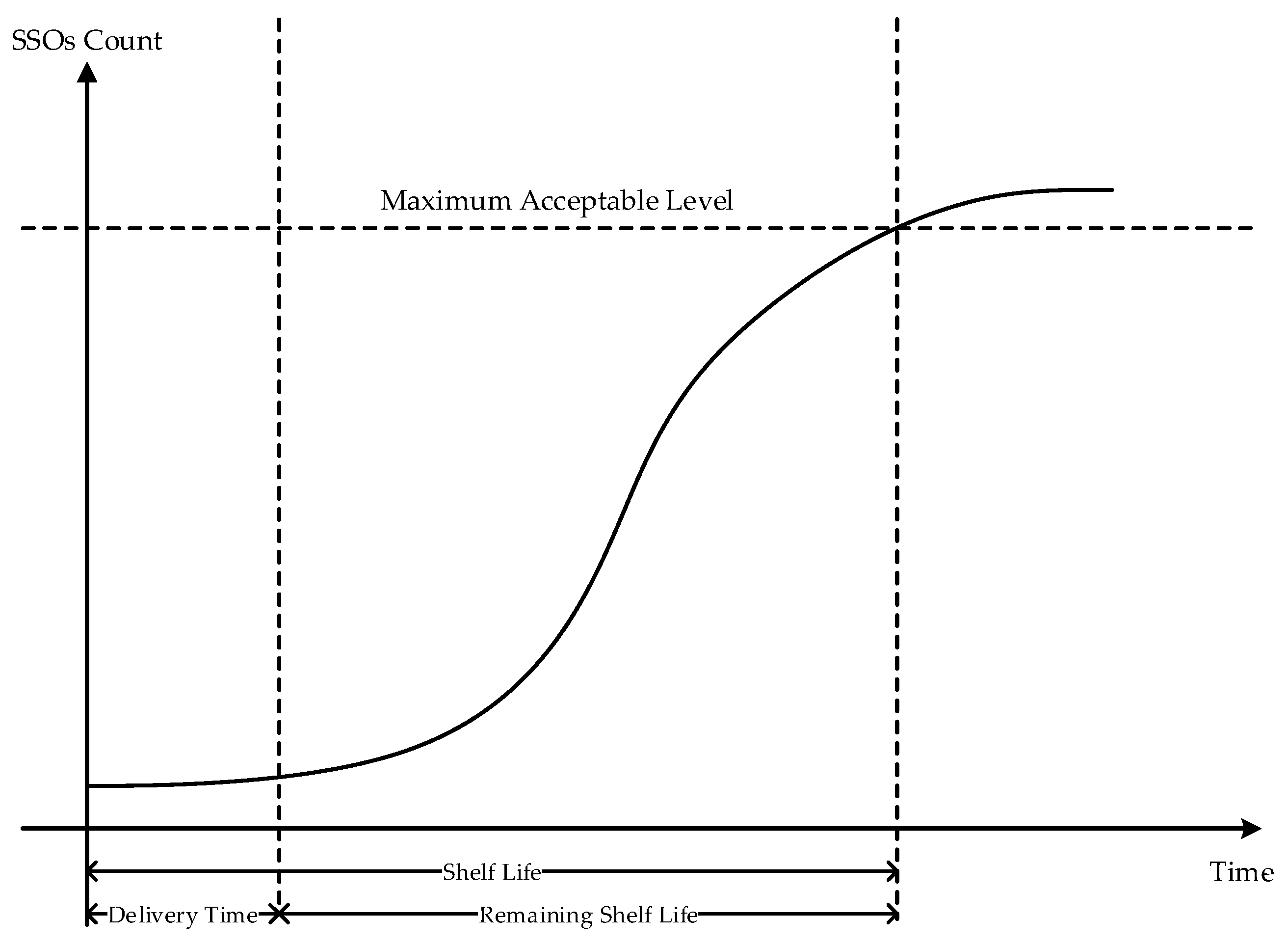
3.3. Food Product Freshness Based on Shelf Life Prediction
3.4. Mathematical Model
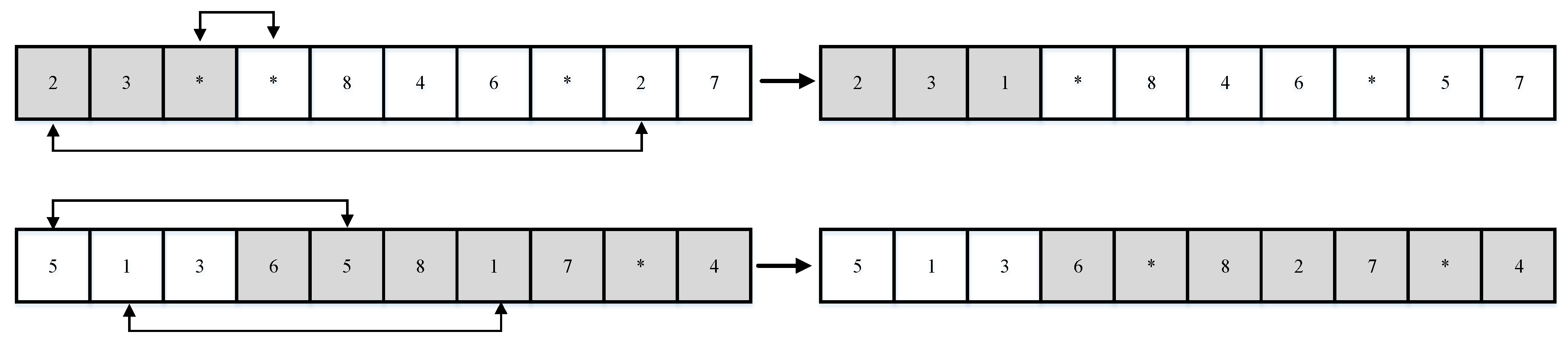
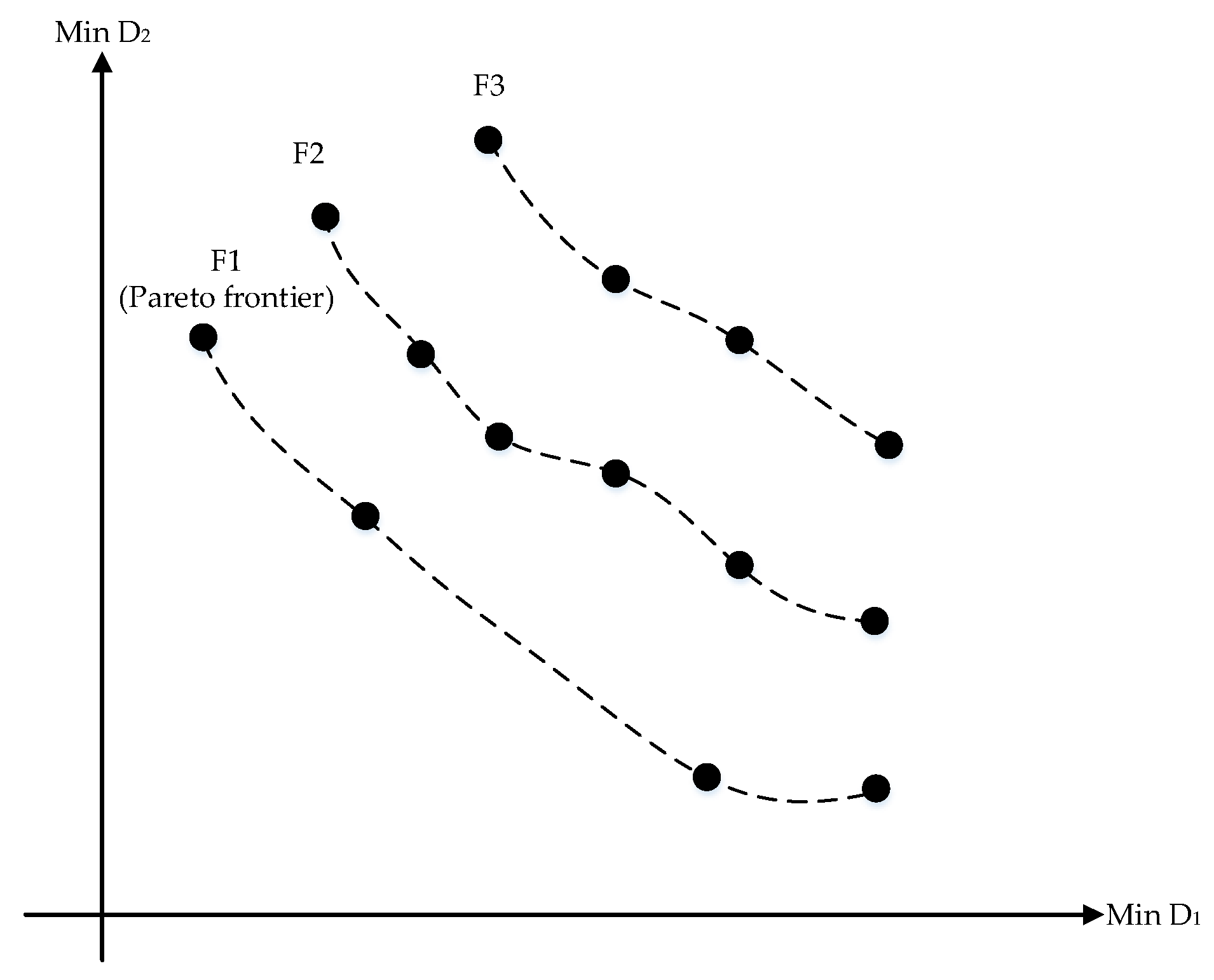
4. Solution Procedure
| Algorithm 1 NSGA-II main loop pseudocode |
| p = population of randomly generated chromosomes with size pops for i = 1 to Max number of iterations do for j =1 to (pc ÷ 2) do c1 = 1st randomly chosen parent chromosome c2 = 2nd randomly selected parent chromosome popc = append crossover (c1, c2) for k = 1 to pm do m = a randomly chosen parent chromosome popm = append mutate (m) pop = merge (p, popc, popm) function (non-dominated sorting (input: pop)) return: Rank of chromosomes function (crowding distance (input: pop, rank)) return: crowding distance value for each chromosome function (sort population (input: pop, rank, crowding distance)) return: sorted pop based on 1) rank, 2) crowding distance pop = store only the top pop and truncate the others function (non-dominated sorting (input: pop)) return: Rank of chromosomes function (crowding distance (input: pop, rank)) return: crowding distance value for each chromosome function (sort population (input: pop, rank, crowding distance)) return: sorted pop based on 1) rank, 2) crowding distance Pareto_frontier = chromosomes with rank 1 Go to the next iteration if the stopping criteria are not met |
5. Computational Results and Discussion
5.1. Performance of the Solution Method
5.2. Optimality Analysis
5.3. Sensitivity to Shelf Life
5.4. Sensitivity to Temperature Setting
6. Conclusions and Future Research
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Todorovic, V.; Maslaric, M.; Bojic, S.; Jokic, M.; Mircetic, D.; Nikolicic, S. Solutions for more sustainable distribution in the short food supply chains. Sustainability 2018, 10, 3481. [Google Scholar] [CrossRef]
- James, S.J.; James, C.; Evans, J.A. Modelling of food transportation systems—A review. Int. J. Refrig. 2006, 29, 947–957. [Google Scholar] [CrossRef]
- Tarantilis, C.D.; Kiranoudis, C.T. Distribution of fresh meat. J. Food Eng. 2002, 51, 85–91. [Google Scholar] [CrossRef]
- Yang, S.; Xiao, Y.; Zheng, Y.; Liu, Y. The Green Supply Chain Design and Marketing Strategy for Perishable Food Based on Temperature Control. Sustainability 2017, 9, 1511. [Google Scholar] [CrossRef]
- Bruckner, S.; Albrecht, A.; Petersen, B.; Kreyenschmidt, J. A predictive shelf life model as a tool for the improvement of quality management in pork and poultry chains. Food Control. 2013, 29, 451–460. [Google Scholar] [CrossRef]
- Gharehyakheh, A.; Krejci, C.; Cantu, J.; Rogers, J. Dynamic Shelf-Life Prediction System to Improve Sustainability in Food Banks. In Proceedings of the 2019 IISE Annual Conference, Orlando, FL, USA, 18–21 May 2019. [Google Scholar]
- Göransson, M.; Jevinger, A.; Nilsson, J. Shelf-life variations in pallet unit loads during perishable food supply chain distribution. Food Control. 2018, 84, 552–560. [Google Scholar] [CrossRef]
- Kreyenschmidt, J.; Hübner, A.; Beierle, E.; Chonsch, L.; Scherer, A.; Petersen, B. Determination of the shelf life of sliced cooked ham based on the growth of lactic acid bacteria in different steps of the chain. J. Appl. Microbiol. 2010, 108, 510–520. [Google Scholar] [CrossRef]
- Novaes, A.G.N.; Lima, O.F., Jr.; de Carvalho, C.C.; Bez, E.T. Thermal performance of refrigerated vehicles in the distribution of perishable food. Pesqui. Oper. 2015, 35, 251–284. [Google Scholar] [CrossRef]
- Osvald, A.; Stirn, L.Z. A vehicle routing algorithm for the distribution of fresh vegetables and similar perishable food. J. Food Eng. 2008, 85, 285–295. [Google Scholar] [CrossRef]
- Mercier, S.; Villeneuve, S.; Mondor, M.; Uysal, I. Time–Temperature Management Along the Food Cold Chain: A Review of Recent Developments. Compr. Rev. Food Sci. Food Saf. 2017, 16, 647–667. [Google Scholar] [CrossRef]
- Food Waste and Loss. United States Department of Agriculture. 2015. Available online: https://www.fda.gov/food/consumers/food-waste-and-loss (accessed on 9 February 2020).
- Gustavsson, J.; Cederberg, C.; Sonesson, U.; van Otterdijk, R.; Meybeck, A. Global Food Losses and Food Waste: Extent, Causes and Prevention; Swedish Institute for Food and Biotechnology (SIK): Gothenburg, Sweden, 2011. [Google Scholar]
- Young, L. Our Biggest Problem? We’re Wasting Food. Can. Grocer 2012. Available online: http://www.canadiangrocer.com/top-stories/what-a-waste-19736 (accessed on 6 April 2020).
- Scharff, R.L. Economic burden from health losses due to foodborne illness in the united states. J. Food Prot. 2012, 75, 123–131. [Google Scholar] [CrossRef] [PubMed]
- CDC. Burden of Foodborne Illness: Findings. In Centers for Disease Control and Prevention; 2011. Available online: https://www.cdc.gov/foodborneburden/2011-foodborne-estimates.html (accessed on 10 April 2020).
- Stellingwerf, H.M.; Kanellopoulos, A.; van der Vorst, J.G.A.J.; Bloemhof, J.M. Reducing CO2 emissions in temperature-controlled road transportation using the LDVRP model. Transp. Res. Part D Transp. Environ. 2018, 58, 80–93. [Google Scholar] [CrossRef]
- Adekomaya, O.; Jamiru, T.; Sadiku, R.; Huan, Z. Sustaining the shelf life of fresh food in cold chain–A burden on the environment. Alex. Eng. J. 2016, 55, 1359–1365. [Google Scholar] [CrossRef]
- Ketzenberg, M.; Bloemhof, J.; Gaukler, G. Managing Perishables with Time and Temperature History. Prod. Oper. Manag. 2015, 24, 54–70. [Google Scholar] [CrossRef]
- Gharehyakheh, A.; Cantu, J.; Krejci, C.; Rogers, J. Sustainable delivery system in a temperature controlled supply chain. In Proceedings of the IISE Annual Conference and Expo 2018, Orlando, FL, USA, 19–22 May 2018; pp. 1534–1539. [Google Scholar]
- Tassou, S.A.; De-Lille, G.; Ge, Y.T. Food transport refrigeration–Approaches to reduce energy consumption and environmental impacts of road transport. Appl. Therm. Eng. 2009, 29, 1467–1477. [Google Scholar] [CrossRef]
- Wang, X.; Wang, M.; Ruan, J.; Zhan, H. The Multi-objective Optimization for Perishable Food Distribution Route Considering Temporal-spatial Distance. Procedia Comput. Sci. 2016, 96, 1211–1220. [Google Scholar] [CrossRef]
- Rahbari, A.; Nasiri, M.M.; Werner, F.; Musavi, M.; Jolai, F. The vehicle routing and scheduling problem with cross-docking for perishable products under uncertainty: Two robust bi-objective models. Appl. Math. Model. 2019, 70, 605–625. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, Q.; Kaku, I.; Xu, Y. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 1419–1431. [Google Scholar] [CrossRef]
- Musavi, M.M.; Bozorgi-Amiri, A. A multi-objective sustainable hub location-scheduling problem for perishable food supply chain. Comput. Ind. Eng. 2017, 113, 766–778. [Google Scholar] [CrossRef]
- Chen, H.K.; Hsueh, C.F.; Chang, M.S. Production scheduling and vehicle routing with time windows for perishable food products. Comput. Oper. Res. 2009, 36, 2311–2319. [Google Scholar] [CrossRef]
- Ghezavati, V.R.; Hooshyar, S.; Tavakkoli-Moghaddam, R. A Benders’ decomposition algorithm for optimizing distribution of perishable products considering postharvest biological behavior in agri-food supply chain: A case study of tomato. Cent. Eur. J. Oper. Res. 2017, 25, 29–54. [Google Scholar] [CrossRef]
- Albrecht, W.; Steinrücke, M. Coordinating continuous-time distribution and sales planning of perishable goods with quality grades. Int. J. Prod. Res. 2018, 56, 2646–2665. [Google Scholar] [CrossRef]
- Ahumada, O.; Villalobos, J. A tactical model for planning the production and distribution of fresh produce. Ann. Oper. Res. 2011, 190, 339–358. [Google Scholar] [CrossRef]
- Farahani, P.; Grunow, M.; Günther, H.O. Integrated production and distribution planning for perishable food products. Flex. Serv. Manuf. J. 2012, 24, 28–51. [Google Scholar] [CrossRef]
- Hsu, C.I.; Hung, S.F.; Li, H.C. Vehicle routing problem with time-windows for perishable food delivery. J. Food Eng. 2007, 80, 465–475. [Google Scholar] [CrossRef]
- Bortolini, M.; Faccio, M.; Ferrari, E.; Gamberi, M.; Pilati, F. Fresh food sustainable distribution: Cost, delivery time and carbon footprint three-objective optimization. J. Food Eng. 2016, 174, 56–67. [Google Scholar] [CrossRef]
- Amorim, P.; Almada-Lobo, B. The impact of food perishability issues in the vehicle routing problem. Comput. Ind. Eng. 2014, 67, 223–233. [Google Scholar] [CrossRef]
- Amorim, P.; Günther, H.O.; Almada-Lobo, B. Multi-objective integrated production and distribution planning of perishable products. Int. J. Prod. Econ. 2012, 138, 89–101. [Google Scholar] [CrossRef]
- Hsu, C.I.; Chen, W.T.; Wu, W.J. Optimal delivery cycles for joint distribution of multi-temperature food. Food Control. 2013, 34, 106–114. [Google Scholar] [CrossRef]
- Hsiao, Y.-H.; Chen, M.-C.; Chin, C.-L. Distribution planning for perishable foods in cold chains with quality concerns: Formulation and solution procedure. Trends Food Sci. Technol. 2017, 61, 80–93. [Google Scholar] [CrossRef]
- Gallo, A.; Accorsi, R.; Baruffaldi, G.; Manzini, R. Designing sustainable cold chains for long-range food distribution: Energy-effective corridors on the Silk Road Belt. Sustainability 2017, 9, 2044. [Google Scholar] [CrossRef]
- Wang, S.; Tao, F.; Shi, Y. Optimization of Location-Routing Problem for Cold Chain Logistics Considering Carbon Footprint. Int. J. Environ. Res. Public Health 2018, 15, 86. [Google Scholar] [CrossRef]
- Bektaş, T.; Laporte, G. The pollution-routing problem. Transp. Res. Part B Methodol. 2011, 45, 1232–1250. [Google Scholar] [CrossRef]
- Accorsi, R.; Gallo, A.; Manzini, R. A climate driven decision-support model for the distribution of perishable products. J. Clean. Prod. 2017, 165, 917–929. [Google Scholar] [CrossRef]
- Govindan, K.; Jafarian, A.; Khodaverdi, R.; Devika, K. Two-echelon multiple-vehicle location-routing problem with time windows for optimization of sustainable supply chain network of perishable food. Int. J. Prod. Econ. 2014, 152, 9–28. [Google Scholar] [CrossRef]
- Molina, J.C.; Eguia, I.; Racero, J.; Guerrero, F. Multi-objective Vehicle Routing Problem with Cost and Emission Functions. Procedia Soc. Behav. Sci. 2014, 160, 254–263. [Google Scholar] [CrossRef]
- Wang, F.; Lai, X.; Shi, N. A multi-objective optimization for green supply chain network design. Decis. Support Syst. 2011, 51, 262–269. [Google Scholar] [CrossRef]
- Devapriya, P.; Ferrell, W.; Geismar, N. Integrated production and distribution scheduling with a perishable product. Eur. J. Oper. Res. 2017, 259, 906–916. [Google Scholar] [CrossRef]
- Khalili-Damghani, K.; Abtahi, A.R.; Ghasemi, A. A New Bi-objective Location-routing Problem for Distribution of Perishable Products: Evolutionary Computation Approach. J. Math. Model. Algorithms Oper. Res. 2015, 14, 287–312. [Google Scholar] [CrossRef]
- Nakandala, D.; Lau, H.; Zhang, J. Cost-optimization modelling for fresh food quality and transportation. Ind. Manag. Data Syst. 2016, 116, 564–583. [Google Scholar] [CrossRef]
- Soysal, M.; Bloemhof-Ruwaard, J.M.; van der Vorst, J.G.A.J. Modelling food logistics networks with emission considerations: The case of an international beef supply chain. Int. J. Prod. Econ. 2014, 152, 57–70. [Google Scholar] [CrossRef]
- Validi, S.; Bhattacharya, A.; Byrne, P.J. A case analysis of a sustainable food supply chain distribution system—A multi-objective approach. Int. J. Prod. Econ. 2014, 152, 71–87. [Google Scholar] [CrossRef]
- Accorsi, R.; Baruffaldi, G.; Manzini, R. Picking efficiency and stock safety: A bi-objective storage assignment policy for temperature-sensitive products. Comput. Ind. Eng. 2018, 115, 240–252. [Google Scholar] [CrossRef]
- Gharehyakheh, A.; Tavakkoli-Moghaddam, R. A fuzzy solution approach for a multi-objective integrated production-distribution model with multi products and multi periods under uncertainty. Manag. Sci. Lett. 2012, 2, 2425–2434. [Google Scholar] [CrossRef]
- Holdsworth, S.D.; Simpson, R. Thermal Processing of Packaged Foods; Springer: Cham, Germany, 2016; Volume 284. [Google Scholar]
- Gibson, A.M.; Bratchell, N.; Roberts, T.A. The effect of sodium chloride and temperature on the rate and extent of growth of Clostridium botulinum type A in pasteurized pork slurry. J. Appl. Bacteriol. 1987, 62, 479–490. [Google Scholar] [CrossRef]
- Arrhenius, S. Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren. Z. Phys. Chem. 1889, 4, 226–248. [Google Scholar]
- Savelsbergh, M.W.P. Local search in routing problems with time windows. Ann. Oper. Res. 1985, 4, 285–305. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Solomon, M.M. Vehicle Routing and Scheduling with Time Windows Constraints: Models and Algorithms. Ph.D. Thesis, University of Pennsylvania, Philadelphia, PA, USA, 1984. [Google Scholar]



| Literature | Quality Degradation Changes | Method of Addressing Perishability | Objectives | Temperature Effect on Quality | Emission | Temperature Effect on Emissions | Temperature Prediction | Solution Method | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Linear over Time | Linear over Temperature | Nonlinear over Time | Nonlinear over Temperature | Economic | Perishability | Emissions | Transportation | Refrigeration | Exact | Heuristic | Metaheuristic | |||||
| Hsu et al. [31] | x | The predicted amount of spoiled products are added to the shipment to ensure orders are filled | x | x | x | x | x | |||||||||
| Osvald & Stirn [10] | x | Minimize delivery time | x | x | ||||||||||||
| Chen et al. [26] | x | Minimize product deterioration, assuming a constant rate | x | x | ||||||||||||
| Wang et al. [43] | Does not address perishability | x | x | x | x | |||||||||||
| Ahumada & Villalobos [29] | x | Minimize product decay | x | x | ||||||||||||
| Farahani et al. [30] | x | Minimize time between production and delivery | x | x | ||||||||||||
| Amorim et al. [34] | x | x | Maximize fractional remaining shelf life | x | x | x | ||||||||||
| Hsu et al. [35] | Does not address perishability | x | x | x | ||||||||||||
| Govindan et al. [41] | Does not address perishability | x | x | x | x | |||||||||||
| Molina et al. [42] | Does not address perishability | x | x | x | x | |||||||||||
| Amorim & Almada-Lobo [33] | x | Maximize average freshness | x | x | x | x | ||||||||||
| Khalili-Damghani et al. [45] | x | Constrain delivery of products to occur before they expire | x | x | x | |||||||||||
| Bortolini et al. [32] | x | Minimize delivery time | x | x | x | x | x | |||||||||
| Wang et al. [22] | x | x | Maximize freshness | x | x | x | ||||||||||
| Ghezavati et al. [27] | x | Minimize quality degradation and disposal costs | x | x | ||||||||||||
| Devapriya et al. [44] | x | Constrain delivery of products to occur before they expire | x | x | ||||||||||||
| Hsiao et al. [36] | x | x | Minimize loss in shelf life as product-related costs | x | x | |||||||||||
| Gallo et al. [37] | x | x | Minimize energy consumed to cool down products spoiled in transportation | x | x | x | x | |||||||||
| Musavi & Bozorgi-Amiri [25] | x | Maximize purchase probability | x | x | x | x | x | |||||||||
| Albrecht & Steinrücke [28] | x | Maximize revenue from the grade of quality | x | x | ||||||||||||
| Wang et al. [38] | x | Minimize product damage costs in the objective function | x | x | x | x | ||||||||||
| Stellingwerf et al. [17] | Does not address perishability | x | x | x | x | x | ||||||||||
| Rahbari et al. [23] | x | Maximize freshness | x | x | x | |||||||||||
| This research | x | x | Maximize average freshness | x | x | x | x | x | x | x | x | x | ||||
| Sets: |
| C = {1, …, n}: set of customers |
| V = {1, …, v}: set of vehicles |
| N = {0} C: set of depot and customers |
| A = {(i, j): i, j N, and i ≠ j}: set of paths from node i to node j |
| Parameters: |
| cij: cost of traveling from node i to node j |
| tij: travel time from node i to node j |
| F: fixed dispatching cost |
| Q: vehicle capacity |
| di: customer i demand |
| [ai, bi]: required time window for delivery to customer i |
| ut: average unloading time for one unit of product |
| ui: unloading time at customer i, where = and ui ≤ bi − ai |
| Decision variables: |
| : time that vehicle k arrives at node i |
| : equals 1 if vehicle k travels from node i to node j, 0 otherwise |
| : units of product carried by vehicle k between nodes i and j |
| w-SA Parameters | Value | NSGA-II Parameters | Value | Test Problem Parameters | Value |
|---|---|---|---|---|---|
| Initial temperature | 20 | Population size | 30 | Vehicle speed (km h−1) | 15 |
| Damping rate | 0.99 | Crossover rate | 0.7 | Product shelf life (h) | 2880 |
| Mutation rate | 0.4 | Fixed cost per vehicle ($) | 1000 | ||
| Transportation cost ($ km−1) | 1.5 | ||||
| Service time (minute) | 10 * 90 ** | ||||
| Vehicle capacity (kg) | 200 |
| Test Problem | w-SA | NSGA-II | Gap | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Costs ($) | Freshness (%) | CO2 (lbs × 103) | Costs ($) | Freshness (%) | CO2 (lbs × 103) | Costs ($) | Freshness (%) | CO2 (lbs × 103) | |
| R101 (25) | 5233 | 89% | 4164 | 4,886 | 95% | 3848 | 6.6% | 4.8% | 17.5% |
| R101 (100) | 13,450 | 90% | 48,042 | 12,356 | 94% | 45,026 | 8.1% | 2.3% | 6.3% |
| C101 (25) | 3065 | 90% | 2452 | 2761 | 96% | 2305 | 9.9% | 6.7% | 6.0% |
| C101 (100) | 10,655 | 92% | 39,787 | 9452 | 94% | 38,564 | 11.3% | 2.2% | 3.1% |
| RC101 (25) | 3318 | 90% | 3,075 | 3027 | 92% | 2684 | 8.8% | 4.6% | 12.7% |
| RC101 (100) | 11,569 | 91% | 47,666 | 10,335 | 93% | 42,597 | 10.7% | 4.5% | 2.4% |
| Optimality | No. of Vehicles | Costs ($) | Freshness (%) | CO2 (lbs × 103) |
|---|---|---|---|---|
| Cost | 7 | 4886 (*) | 55% (42% gap) | 3997 (4% gap) |
| Freshness | 8 | 112,123 (95% gap) | 95% (*) | 66,413 (94% gap) |
| Emission | 7 | 5723 (14% gap) | 56% (41% gap) | 3848 (*) |
| Final solution | 7 | 10,213 (52% gap) | 75% (21% gap) | 8892 (57% gap) |
| Shelf Life (h) | Costs ($) | Freshness (%) | CO2 (lbs × 103) |
|---|---|---|---|
| 168 | 13,522 | 62% | 12,916 |
| 1440 | 11,390 | 71% | 10,662 |
| 2880 | 10,213 | 75% | 8892 |
| Temperature (°K) | Costs ($) | Freshness (%) | CO2 (lbs × 103) |
|---|---|---|---|
| 263 | 10,213 | 75% | 8892 |
| 265 | 10,526 | 72% | 8556 |
| 267 | 11,013 | 68% | 8436 |
| 269 | 11,596 | 60% | 8301 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gharehyakheh, A.; Krejci, C.C.; Cantu, J.; Rogers, K.J. A Multi-Objective Model for Sustainable Perishable Food Distribution Considering the Impact of Temperature on Vehicle Emissions and Product Shelf Life. Sustainability 2020, 12, 6668. https://doi.org/10.3390/su12166668
Gharehyakheh A, Krejci CC, Cantu J, Rogers KJ. A Multi-Objective Model for Sustainable Perishable Food Distribution Considering the Impact of Temperature on Vehicle Emissions and Product Shelf Life. Sustainability. 2020; 12(16):6668. https://doi.org/10.3390/su12166668
Chicago/Turabian StyleGharehyakheh, Amin, Caroline C. Krejci, Jaime Cantu, and K. Jamie Rogers. 2020. "A Multi-Objective Model for Sustainable Perishable Food Distribution Considering the Impact of Temperature on Vehicle Emissions and Product Shelf Life" Sustainability 12, no. 16: 6668. https://doi.org/10.3390/su12166668
APA StyleGharehyakheh, A., Krejci, C. C., Cantu, J., & Rogers, K. J. (2020). A Multi-Objective Model for Sustainable Perishable Food Distribution Considering the Impact of Temperature on Vehicle Emissions and Product Shelf Life. Sustainability, 12(16), 6668. https://doi.org/10.3390/su12166668






