Trip Chaining Model with Classification and Optimization Parameters
Abstract
1. Introduction
- To provide a detailed classification of parameters related to trip chaining.
- To identify the types, potential values, and data sources of the parameters.
- To aggregate weights related to parameters, so that user settings can be easier.
- To create a utility function for the activity chain optimization.
2. Literature Review
3. Definition of Classification and Optimization Parameters
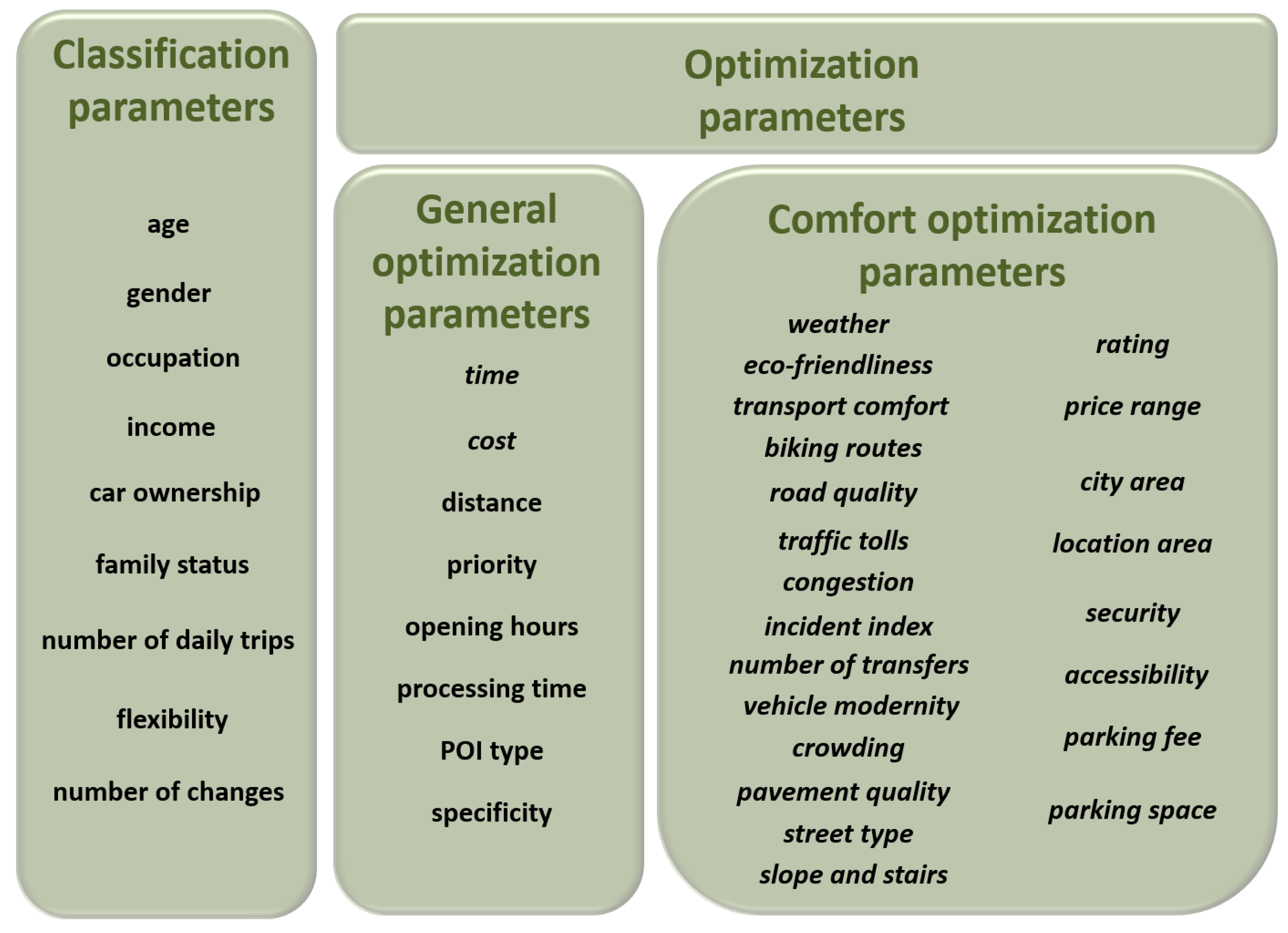
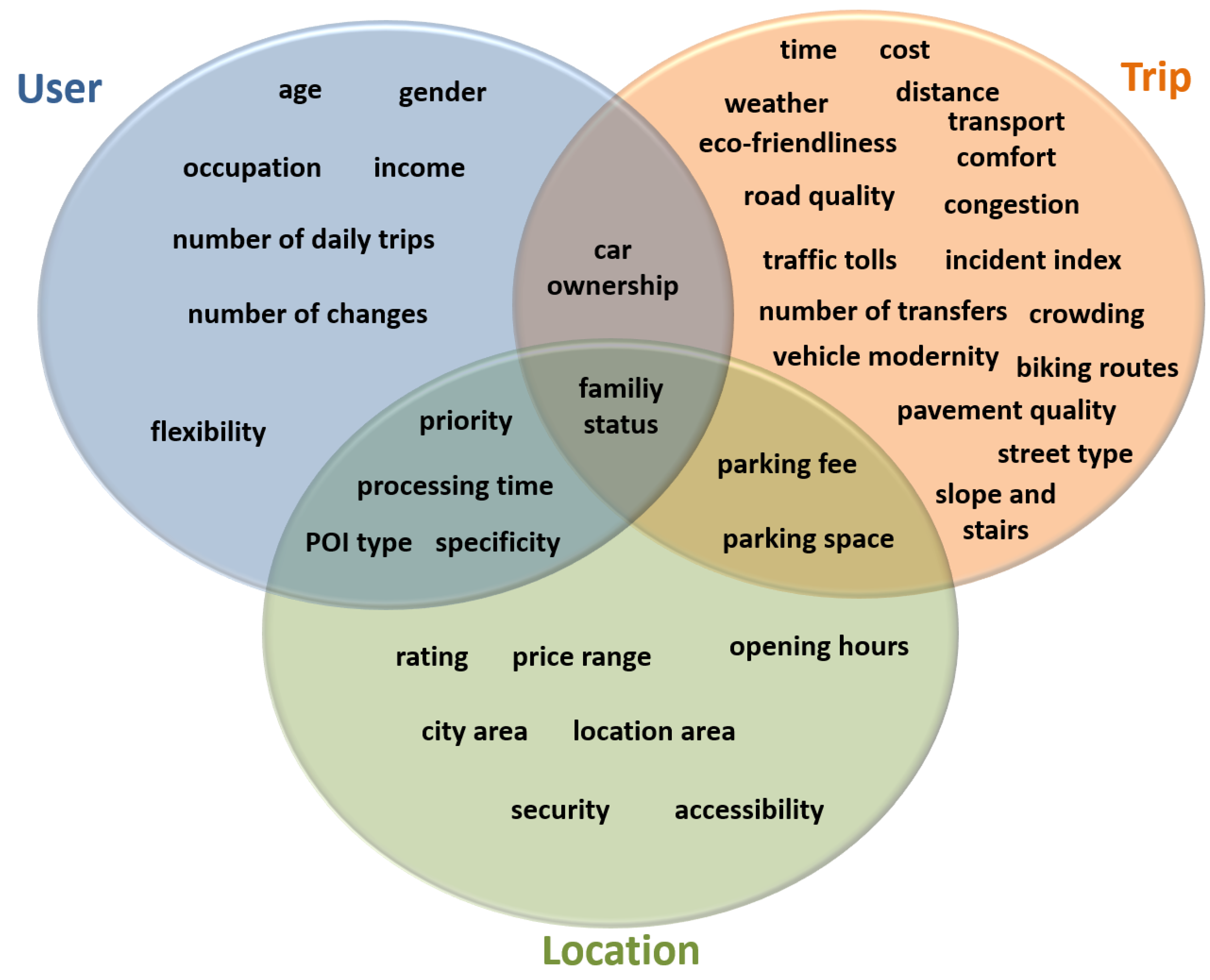
3.1. Classification Parameters
- Age, gender, occupation, income, car ownership, family status: The basic socio-economic data, which are required to categorize users into user groups.
- Number of daily trips: Average number of trips during a day (e.g., users with family tend to make more daily trips, while pensioners probably make fewer daily trips).
- Flexibility: Average number of flexible activities during a day (e.g., users with flexible working hours and students tend to have more flexible activities).
- Number of changes: Average number of changes in daily activity plans (e.g., younger people tend to change their mind and have new unplanned events during the day).
3.2. General Optimization Parameters
- Time (p1): Total travel time spent during a trip (e.g., driving time is calculated from the distance, public transport time is calculated from the timetable information).
- Cost (p2): Price to be paid for the chosen trip for different transportation modes (e.g., driving cost is calculated from the distance, public transport cost is calculated from the number of needed tickets).
- Distance (p3): Defines locations and distances, so that trip times can be calculated.
- Priority (p4): The priority of the actual activity that can be processed in the given location (e.g., fix or flexible).
- Opening hours (p5): Time interval between the opening time and closing time of the given location.
- Processing time (p6): Time spent by the user at the given location [minutes].
- POI type (p7): The type of the location regarding the point of interest typology (e.g., restaurant, post office).
- Specificity (p8): Defines whether one brand is searched by the user or more brands of the same POI type are possible solutions.
3.3. Comfort Optimization Parameters
- Weather (p9): Measure for the actual daily average weather situation measured by the temperature and the humidity (e.g., rainy, windy).
- Eco-friendliness (p10): Measure for environmental classification of different transportation modes measured by their average CO2 emission (e.g., biking is very eco-friendly as it produces no emissions).
- Transport comfort (p11): Measure for the comfort level generally provided by transportation modes measured by social norms (e.g., cars considered comfortable).
- Biking routes (p12): Type of roads used by bikers, if during a trip more types are present, then their average value regarding the length has to be taken into account.
- Road quality (p13): Measure for the quality of roads.
- Traffic tolls (p14): Average price to be paid on certain roads.
- Congestion (p15): Average percentage of congestion on a certain trip during a day.
- Incidents index (p16): Number of yearly incidents along a chosen trip per average hourly traffic volume.
- Number of transfers (p17): Number of transfers between two consecutive activities.
- Vehicle modernity (p18): Age of the used vehicle during a trip.
- Crowding (p19): Percentage of passengers per capacity in the vehicle.
- Pavement quality (p20): Measure for the quality of pavements.
- Street type (p21): Type of streets (e.g., main road, park, alley).
- Slope and stairs (p22): Measure for the steepness of the streets and existence of stairs during the trip (e.g., locations in hilly areas are harder to access for elderly people).
- Rating (p23): Average value calculated from reviews of the location by other users.
- Price range (p24): Average prices of typical services in the given location.
- City area (p25): Type of the far environment (e.g., district), where the place is located.
- Location area (p26): Type of the close environment (e.g., main road, park, alley).
- Security (p27): Number of yearly crimes in the city area, where the place is located.
- Accessibility (p28): Measure for the easiness to access the location (with wheelchair).
- Parking fees (p29): Average price of parking fees in the area of the location.
- Parking space (p30): Number of free parking spaces in the area of the location.
4. Elaboration of the Method
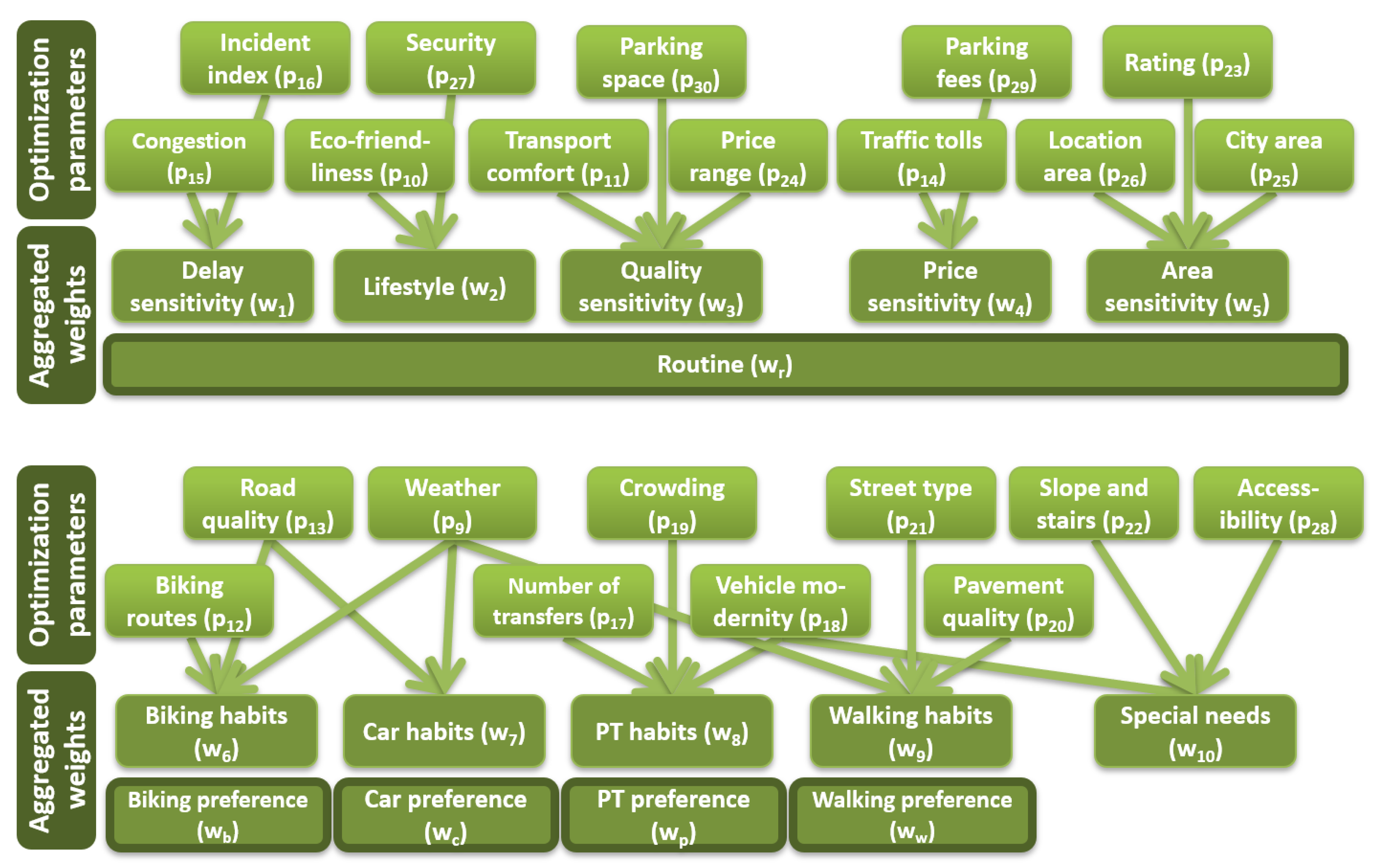
4.1. Aggregated Weights
- Routine (wr): Measure of willingness to differ from well-known routes; this weight has a general effect on several parameters (e.g., willingness to make detours, if it is beneficial), is a super aggregation with an effect on delay sensitivity, lifestyle, quality sensitivity, price sensitivity, and area sensitivity.
- Delay sensitivity (w1): Average delay tolerated by the user, which depends on the congestion and the incident probability of the chosen trip (e.g., users with high delay sensitivity should avoid congested routes).
- Lifestyle (w2): Measure for environmental consciousness and security features (e.g., rather using more eco-friendly transportation modes and avoiding dangerous areas).
- Quality sensitivity (w3): Measure for taking comfort features, price ranges, and parking space into account (e.g., businessmen tend to use cars and visit places with higher prices).
- Price sensitivity (w4): Willingness to pay for a certain trip, which includes traffic tolls and parking fees (e.g., workers may travel longer distances, where no traffic toll has to be paid).
- Area sensitivity (w5): Measure for taking features regarding ratings and the area of the location into account such as the city area and location area (e.g., users tend to visit restaurants in the city center, but a recreational activity rather close to a park).
- Biking preference (wb): Measure of the willingness of using a bike during trips (e.g., students tend to bike more often); this weight has a general effect on biking related parameters,
- Biking habits (w6): requirements of the users regarding road quality, biking routes, and weather (e.g., many users prefer built roads and good weather).
- Car preference (wc): Measure of the willingness of using a car during trips (e.g., businessmen tend to use their own cars more often); this weight has a general effect on car related parameters.
- Car habits (w7): Requirements of the users regarding road quality and weather (e.g., certain users do not use their cars in winter).
- PT preference (wp): Measure of the willingness of using PT during trips (e.g., younger people prefer public transportation, because they can utilize their time more efficiently by reading on the vehicles); this weight has a general effect on PT related parameters.
- PT habits (w8): Requirements of the users regarding number of transfers, crowding, and vehicle types including cleanliness, comfortable seats, heating and air conditioning (e.g., users do not prefer old vehicles without air conditioning during the summer).
- Walking preference (ww): Measure of the willingness to walk during trips (e.g., young people tend to walk more); this weight has a general effect on walking related parameters.
- Walking habits (w9): Requirements of users regarding pavement quality, street type, and weather (e.g., certain users prefer nice road with trees and good weather).
- Special needs (w10): The need for special services such as modern low floor vehicles, need to avoid stairs or slopes and accessibility of locations (e.g., users with wheelchairs do not like to visit places without ramps).
4.2. Utility Function
- p—Optimization parameters.
- w—Weights (including aggregated weights).
- u(p,w)—Main utility function.
- ptime—Value of time optimization parameter.
- wtime—Weight of time optimization parameter.
- pcost—Value of cost optimization parameter.
- wcost—Weight of cost optimization parameter.
- ui(p,w)—Utility function regarding comfort optimization parameters, i = 1,..,m.
- m—Number of utility functions regarding comfort optimization parameters.
4.3. Optimization Algorithm
- Data input: This part is especially supported by the classification and optimization parameters, which were discussed in detail in Section 3. They provide the main input for the optimization algorithm. During the creation of activity chains, it is assumed that the user is already aware of the activities and other parameters, which are provided to the algorithm in advance.
- Creation of alternatives: Priority is one of the most important optimization parameters. Based on its value, if an activity is flexible, then the demanded service may be available in more places. The algorithm has to find these alternative locations, so that better alternatives can replace the original activity locations. However, if an activity is fixed, then the activity location cannot be changed and thus optimization cannot be performed for this activity.
- Calculation of the utility function: With the original and alternative locations of activities, the utilities between the activity locations can be calculated. The utility function was discussed in detail in Section 4.1 and Section 4.2, which provides the ranking of different alternatives.
- Optimization algorithm: The GA calculates based on the provided utility function of the best scenarios, which results in an optimized set of activity locations based on the provided classification and optimization parameters. The GA framework runs several times to find possible solutions. It is not ensured that the global optimum will be reached, however, with good parameter settings, the solution can be quite close.
- Visualization: The proposed activity chain has to be shown on a map, where the optimal activity locations are present, and the daily route is available.
5. Discussion
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Bhat, C.R.; Singh, S.K. A comprehensive daily activity-travel generation model system for workers. Transp. Res. Part A Policy Pract. 2000, 34, 1–22. [Google Scholar] [CrossRef]
- Wen, C.-H.; Koppelman, F.S. A conceptual and methdological framework for the generation of activity-travel patterns. Transportation 2000, 27, 5–23. [Google Scholar] [CrossRef]
- Bowman, J.L.; Ben-Akiva, M.E. Activity-based disaggregate travel demand model system with activity schedules. Transp. Res. Part A Policy Pract. 2001, 35, 1–28. [Google Scholar] [CrossRef]
- Islam, M.T.; Habib, K.M.N. Unraveling the relationship between trip chaining and mode choice: Evidence from a multi-week travel diary. Transp. Plan. Technol. 2012, 35, 409–426. [Google Scholar] [CrossRef]
- McGuckin, N.; Murakami, E. Examining Trip-Chaining Behavior: Comparison of Travel by Men and Women. Transp. Res. Rec. J. Transp. Res. Board 1999, 1693, 79–85. [Google Scholar] [CrossRef]
- Subbarao, S.S.V.; Krishna Rao, K.V. Trip chaining behavior in developing countries: A study of Mumbai Metropolitan Region, India. Eur. Transp. 2013, 53, 1–7. [Google Scholar]
- Golob, T.F.; Hensher, D.A. The trip chaining activity of Sydney residents: A cross-section assessment by age group with a focus on seniors. J. Transp. Geogr. 2007, 15, 298–312. [Google Scholar] [CrossRef]
- Kotoula, K.; Sialdas, A.; Botzoris, G.; Chaniotakis, E.; Grau, J.M. Exploring the Effects of University Campus Decentralization to Students’ Mode Choice. Period. Polytech. Transp. Eng. 2018, 46, 207–214. [Google Scholar] [CrossRef]
- Mazzulla, G. An activity-based system of models for student mobility simulation. Eur. Transp. Res. Rev. 2009, 1, 163–174. [Google Scholar] [CrossRef][Green Version]
- Pronello, C.; Camusso, C. Travellers’ profiles definition using statistical multivariate analysis of attitudinal variables. J. Transp. Geogr. 2011, 19, 1294–1308. [Google Scholar] [CrossRef]
- Prillwitz, J.; Barr, S. Moving towards sustainability? Mobility styles, attitudes and individual travel behavior. J. Transp. Geogr. 2011, 19, 1590–1600. [Google Scholar] [CrossRef]
- Haustein, S.; Hunecke, M. Identifying target groups for environmentally sustainable transport: Assessment of different segmentation approaches. Curr. Opin. Environ. Sustain. 2013, 5, 197–204. [Google Scholar] [CrossRef]
- Timmermans, H.J.; Van Der Waerden, P.; Alves, M.; Polak, J.W.; Ellis, S.; Harvey, A.S.; Kurose, S.; Zandee, R. Spatial context and the complexity of daily travel patterns: An international comparison. J. Transp. Geogr. 2003, 11, 37–46. [Google Scholar] [CrossRef]
- Liao, F.; Arentze, T.A.; Timmermans, H. Incorporating space–time constraints and activity-travel time profiles in a multi-state supernetwork approach to individual activity-travel scheduling. Transp. Res. Part B Methodol. 2013, 55, 41–58. [Google Scholar] [CrossRef]
- Buliung, R.N.; Roorda, M.J.; Remmel, T.K. Exploring spatial variety in patterns of activity-travel behaviour: Initial results from the Toronto Travel-Activity Panel Survey (TTAPS). Transportation 2008, 35, 697–722. [Google Scholar] [CrossRef]
- Balaji, M.; Santhanakrishnan, S.; Dinesh, S.N. An Application of Analytic Hierarchy Process in Vehicle Routing Problem. Period. Polytech. Transp. Eng. 2019, 47, 196–205. [Google Scholar] [CrossRef]
- Hafezi, M.H.; Liu, K.; Millward, H. Learning Daily Activity Sequences of Population Groups using Random Forest Theory. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 194–207. [Google Scholar] [CrossRef]
- Kang, J.E.; Recker, W.W. The location selection problem for the household activity pattern problem. Transp. Res. Part B Methodol. 2013, 55, 75–97. [Google Scholar] [CrossRef]
- Hilgert, T.; Kagerbauer, M.; Schuster, T.; Becker, C. Optimization of Individual Travel Behavior through Customized Mobility Services and their Effects on Travel Demand and Transportation Systems. Transp. Res. Procedia 2016, 19, 58–69. [Google Scholar] [CrossRef]
- Juhasz, M.; Mátrai, T.; Kerényi, L.S. Changes in Travel Demand in Budapest during the Last 10 Years. Transp. Res. Procedia 2014, 1, 154–164. [Google Scholar] [CrossRef]
- Prelipcean, A.C.; Gidofalvi, G.; Susilo, Y.C.P.A. Comparative framework for activity-travel diary collection systems. In Proceedings of the 2015 International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Budapest, Hungary, 3–5 June 2015; pp. 251–258. [Google Scholar]
- Duleba, S.; Mishina, T.; Shimazaki, Y. A dynamic analysis on public bus transport’s supply quality by using ahp. Transportation 2012, 27, 268–275. [Google Scholar] [CrossRef]
- Sierpiński, G.; Staniek, M.; Celiński, I. Travel Behavior Profiling Using a Trip Planner. Transp. Res. Procedia 2016, 14, 1743–1752. [Google Scholar] [CrossRef]
- Lawton, T.K. Activity and time use data for activity-based forecasting. In Proceedings of the Activity-Based Travel Forecasting Conference, New Orleans, LA, USA, 2–5 June 1996; pp. 103–118. [Google Scholar]
- Frignani, M.Z.; Auld, J.A.K.C.; Nelson, P. Urban Travel Route and Activity Choice Survey: Internet-Based Prompted-Recall Activity Travel Survey Using Global Positioning System Data. Transp. Res. Rec. J. Transp. Res. Board 2010, 2183, 19–28. [Google Scholar] [CrossRef]
- Arentze, T.; Kemperman, A.; Aksenov, P. Estimating a latent-class user model for travel recommender systems. Inf. Technol. Tour. 2018, 19, 61–82. [Google Scholar] [CrossRef]
- Arentze, T.A. Adaptive Personalized Travel Information Systems: A Bayesian Method to Learn Users’ Personal Preferences in Multimodal Transport Networks. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1957–1966. [Google Scholar] [CrossRef]
- Nijland, L.; Arentze, T.; Timmermans, H. Incorporating planned activities and events in a dynamic multi-day activity agenda generator. Transportation 2012, 39, 791–806. [Google Scholar] [CrossRef]
- Miller, E.J.; Roorda, M.J. Prototype Model of Household Activity-Travel Scheduling. Transp. Res. Rec. J. Transp. Res. Board 2003, 1831, 114–121. [Google Scholar] [CrossRef]
- Chowdhury, T.; Scott, D.M. Role of the built environment on trip-chaining behavior: An investigation of workers and non-workers in Halifax, Nova Scotia. Transportation 2018, 47, 737–761. [Google Scholar] [CrossRef]
- Dib, O.; Manier, M.-A.; Caminada, A. Memetic Algorithm for Computing Shortest Paths in Multimodal Transportation Networks. Transp. Res. Procedia 2015, 10, 745–755. [Google Scholar] [CrossRef]
- Ghiani, G.; Manni, E.; Thomas, B.W. A Comparison of Anticipatory Algorithms for the Dynamic and Stochastic Traveling Salesman Problem. Transp. Sci. 2012, 46, 374–387. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Comi, A. Individual utility-based path suggestions in transit trip planners. IET Intell. Transp. Syst. 2016, 10, 219–226. [Google Scholar] [CrossRef]
- Västberg, O.B.; Karlström, A.; Jonsson, D.; Sundberg, M. A Dynamic Discrete Choice Activity-Based Travel Demand Model. Transp. Sci. 2019, 54, 1–21. [Google Scholar] [CrossRef]
- Pougala, J.; Hillel, T.; Bierlaire, M. Scheduling of daily activities: An optimization approach. In Proceedings of the 20th Swiss Transport Research Conference (STRC), Lausanne, Switzerland, 13–14 May 2020. [Google Scholar]
- Malik, S.; Kim, D. Optimal Travel Route Recommendation Mechanism Based on Neural Networks and Particle Swarm Optimization for Efficient Tourism Using Tourist Vehicular Data. Sustainability 2019, 11, 3357. [Google Scholar] [CrossRef]
- Charypar, D.; Nagel, K. Generating complete all-day activity plans with genetic algorithms. Transportation 2005, 32, 369–397. [Google Scholar] [CrossRef]
- Saharidis, G.K.D.; Rizopoulos, D.; Fragkogios, A.; Chatzigeorgiou, C. A hybrid approach to the problem of journey planning with the use of mathematical programming and modern techniques. Transp. Res. Procedia 2017, 24, 401–409. [Google Scholar] [CrossRef]
- Aifadopoulou, G.; Ziliaskopoulos, A.; Chrisohoou, E. Multiobjective Optimum Path Algorithm for Passenger Pretrip Planning in Multimodal Transportation Networks. Transp. Res. Rec. J. Transp. Res. Board 2007, 2032, 26–34. [Google Scholar] [CrossRef]
- Delling, D.; Dibbelt, J.; Pajor, T.; Wagner, D.; Werneck, R.F. Computing Multimodal Journeys in Practice. Comput. Vis. 2013, 7933, 260–271. [Google Scholar] [CrossRef]
- Freisleben, B.; Merz, P. A genetic local search algorithm for solving symmetric and asymmetric traveling salesman problems. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 616–621. [Google Scholar]
- Nygard, K.E.; Yang, C.H. Genetic Algorithms for the Traveling Salesman Problem with Time Windows. In Computer Science and Operations Research; Elsevier: Amsterdam, The Netherlands, 1992; pp. 411–423. [Google Scholar] [CrossRef]
- Hwang, H.-S. An improved model for vehicle routing problem with time constraint based on genetic algorithm. Comput. Ind. Eng. 2002, 42, 361–369. [Google Scholar] [CrossRef]
- Archetti, C.; Feillet, D.; Gendreau, M.; Speranza, M.G. Complexity of the VRP and SDVRP. Transp. Res. Part C Emerg. Technol. 2011, 19, 741–750. [Google Scholar] [CrossRef]
| Author | Topic | Modelling | Algorithm | Multimodal | Activity Types | Optimization | Utility Function | Classification Parameters | Optimization Parameters |
|---|---|---|---|---|---|---|---|---|---|
| Artenze (2013) [27] | Personalized advice based on travel choices | x | x | x | |||||
| Nijland et al. (2012) [28] | Effects of planned activities on the activity schedule | x | x | ||||||
| Miller and Roorda (2003) [29] | Activity schedules and travel patterns | x | x | ||||||
| Chowdhury and Scott (2020) [30] | Built environment with personal parameters | x | x | x | |||||
| Dib et al. (2015) [31] | Route planning using genetic algorithm | x | x | x | x | ||||
| Ghiani (2011) [32] | Traveling Salesman Problem with heuristic algorithm | x | x | x | |||||
| Nuzzolo and Comi (2016) [33] | Route suggestions based on individual utility function | x | x | x | x | x | |||
| Västberg et al. (2019) [34] | Dynamic activity travel planning | x | x | x | x | x | x | ||
| Pougala et al. (2020) [35] | Scheduling of daily activities | x | x | x | x | x | x | ||
| Malik and Kim (2019) [36] | Optimal Travel Route Recommendation | x | x | x | x | x | x | ||
| Charypar and Nagel (2005) [37] | Scheduling with multi-agent simulation model | x | x | x | x | x | x | ||
| proposed | Activity chain optimization | x | x | x | x | x | x | x | x |
| Parameter Type | Component Type | Values | Data Source | |
|---|---|---|---|---|
| age | classification | user | 1 (0–20) 2 (21–30) 3 (31–40) 4 (40–60) 5 (more than 60) | user |
| gender | classification | user | 1 (male) 2 (female) | user |
| occupation | classification | user | 1 (student) 2 (worker) 3 (pensioner) | user |
| income | classification | user | 1 (0–500) 2 (500–1000) 3 (1000–2000) 4 (2000–3000) 5 (more than 3000 Euro) | user |
| car ownership | classification | user/trip | 1 (no car) 2 (one car) 3 (more cars) | user |
| family status | classification | user/trip/location | 1 (single) 2 (married) 3 (has children) | user |
| number of daily trips | classification | user | 1 (0–1) 2 (2–3) 3 (more than 3) | user/application |
| flexibility | classification | user | 1 (0–1) 2 (2–3) 3 (more than 3) | user/application |
| number of changes | classification | user | 1 (0–1) 2 (2–3) 3 (more than 3) | user/application |
| Parameter Type | Component Type | Values | Data Source | |
|---|---|---|---|---|
| time | with weight | trip | 0–1000 min | map provider/transport operator |
| cost | with weight | trip | 0–1000 Euro | map provider/transport operator |
| distance | without weight | trip | 0–10.000 m | map provider |
| priority | without weight | user/location | 1 (fix) 2 (temporally flexible) 3 (spatially flexible) 4 (totally flexible) | user |
| opening hours | without weight | location | 0–24 h | POI database |
| processing time | without weight | user/location | 0–1000 min | user |
| POI type | without weight | user/location | several types (e.g., restaurant, post office) | user/POI database |
| specificity | without weight | user/location | special brands under POI type | user/POI database |
| Parameter Type | Component Type | Low Value | Middle Value | High Value | Data Source | |
|---|---|---|---|---|---|---|
| weather | biking, car, PT habits | trip | good weather | windy, rainy, cold | heavy rain or snow | meteorology |
| eco-friendliness | lifestyle | trip | biking, walking | public transport | car | operator/ municipality |
| transport comfort | social status | trip | car | public transport | biking, walking | society |
| biking routes | biking habits | trip (bike) | bike lane | average road | off-road | municipality |
| road quality | biking, car habits | trip (car) | perfect | average | bad | road network operator |
| traffic tolls | price sensitivity | trip (car) | 0–1 Euro | 2–3 Euro | more than 3 Euro | road network operator |
| congestion | delay sensitivity | trip (car) | free flow | normal traffic | congested | traffic information |
| incident index | delay sensitivity | trip (car) | 0–0,1 | 0.2–0.3 | more than 0.3 | national office |
| number of transfers | PT habits | trip (PT) | 0–1 | 2–3 | more than 3 | transport operator |
| vehicle modernity | PT habits | trip (PT) | 0–5 | 6–10 | more than 10 years old | transport operator |
| crowding | PT habits | trip (PT) | 0–30% | 31–60% | 61–100% | transport operator |
| pavement quality | walking habits | trip (walking) | perfect | average | bad | road network operator |
| street type | walking habits | trip (walking) | alley, park | street, avenue | highway, main street | municipality |
| slope and stairs | special needs | trip (walking) | straight | hilly | steep or many stairs | municipality |
| Parameter Type | Component Type | Low Value | Middle Value | High Value | Data Source | |
|---|---|---|---|---|---|---|
| rating | area sensitivity | location | 4–5 | 3 | 1–2 | social media |
| price range | social status | location | 4–5 | 3 | 1–2 | social media |
| city area | area sensitivity | location | city center | suburbs | industrial area | municipality |
| location area | area sensitivity | location | alley, park | street, avenue | highway, main street | municipality |
| security | lifestyle | location | 0–10 | 10–30 | more than 30 crimes | national office |
| accessibility | special needs | location | fully accessible | difficultly accessible | not accessible | POI database |
| parking fees | price sensitivity | location | 0–1 | 2–3 | more than 3 Euro | road network operator |
| parking space | social status | location | 0–10 | 11–20 | more than 20 spaces | traffic information |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esztergár-Kiss, D. Trip Chaining Model with Classification and Optimization Parameters. Sustainability 2020, 12, 6422. https://doi.org/10.3390/su12166422
Esztergár-Kiss D. Trip Chaining Model with Classification and Optimization Parameters. Sustainability. 2020; 12(16):6422. https://doi.org/10.3390/su12166422
Chicago/Turabian StyleEsztergár-Kiss, Domokos. 2020. "Trip Chaining Model with Classification and Optimization Parameters" Sustainability 12, no. 16: 6422. https://doi.org/10.3390/su12166422
APA StyleEsztergár-Kiss, D. (2020). Trip Chaining Model with Classification and Optimization Parameters. Sustainability, 12(16), 6422. https://doi.org/10.3390/su12166422





