Cluster Analysis of Public Bike Sharing Systems for Categorization
Abstract
1. Introduction
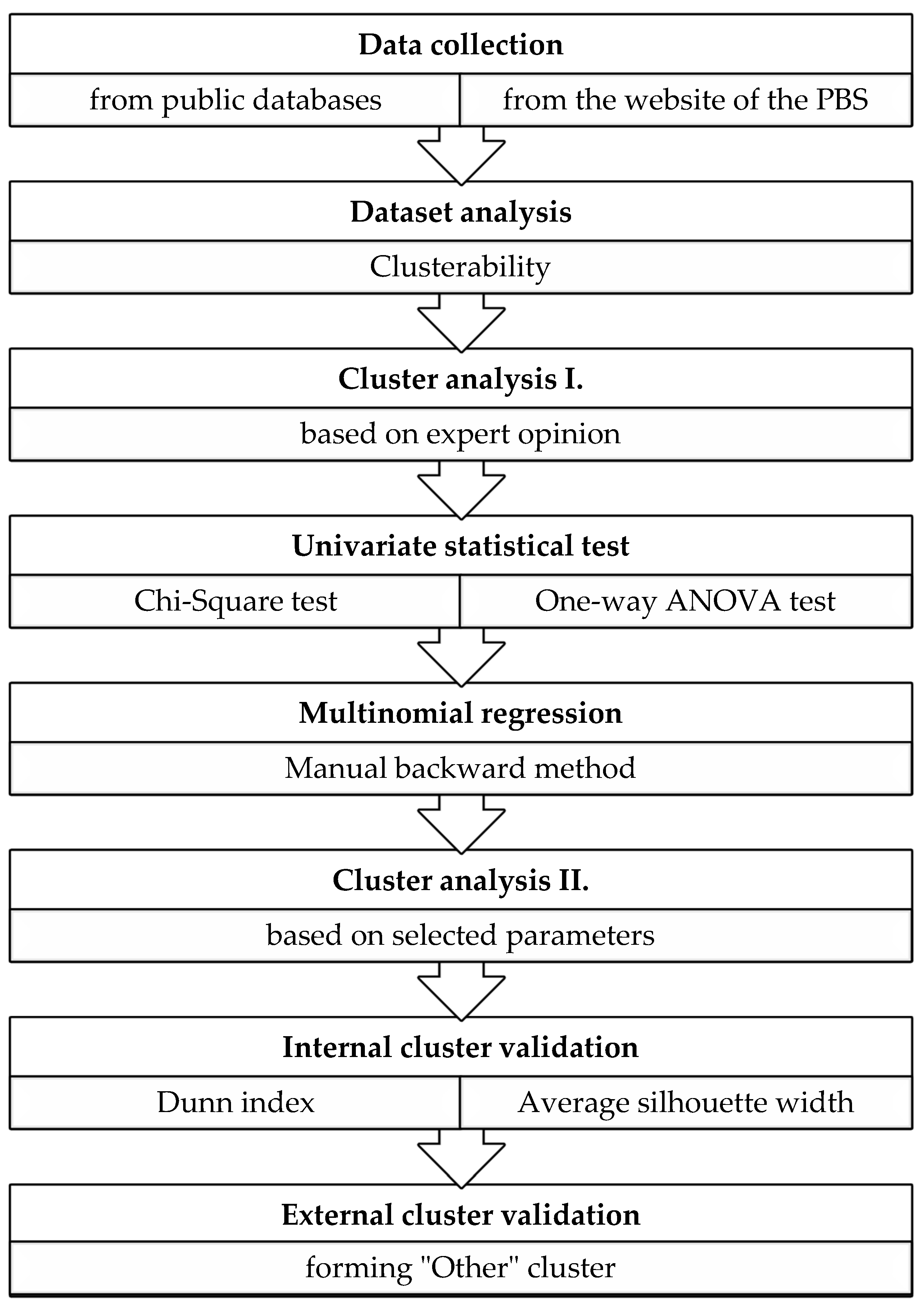
2. Methodology
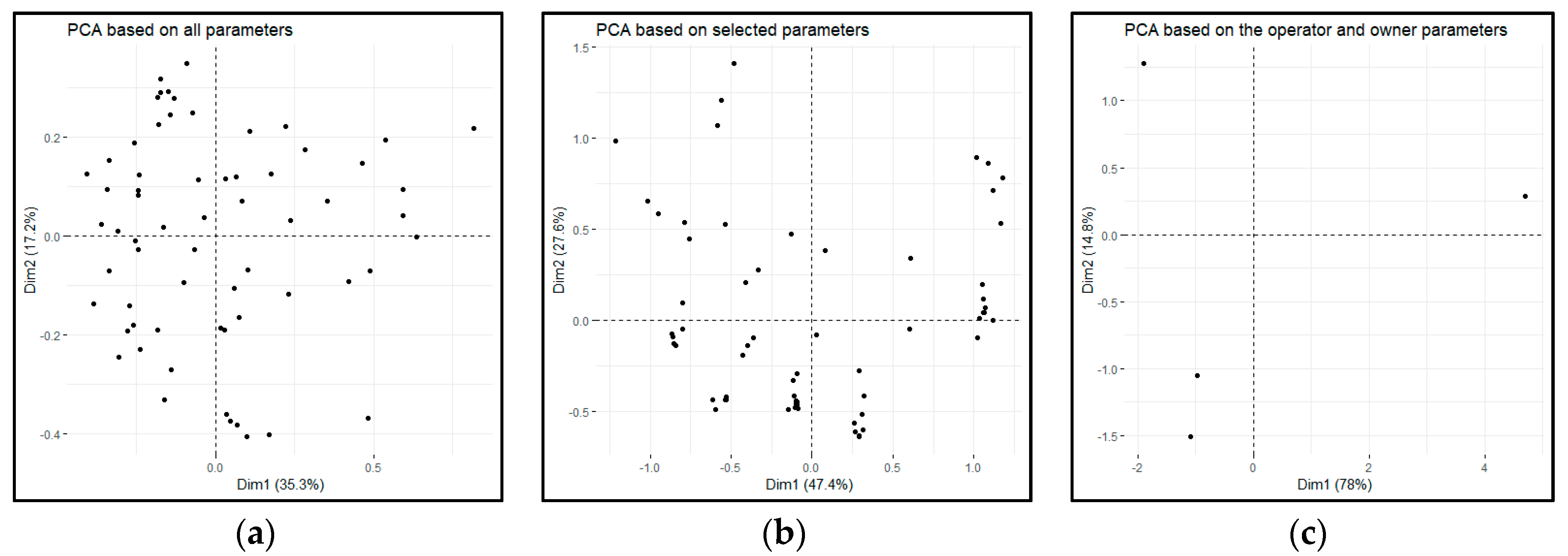
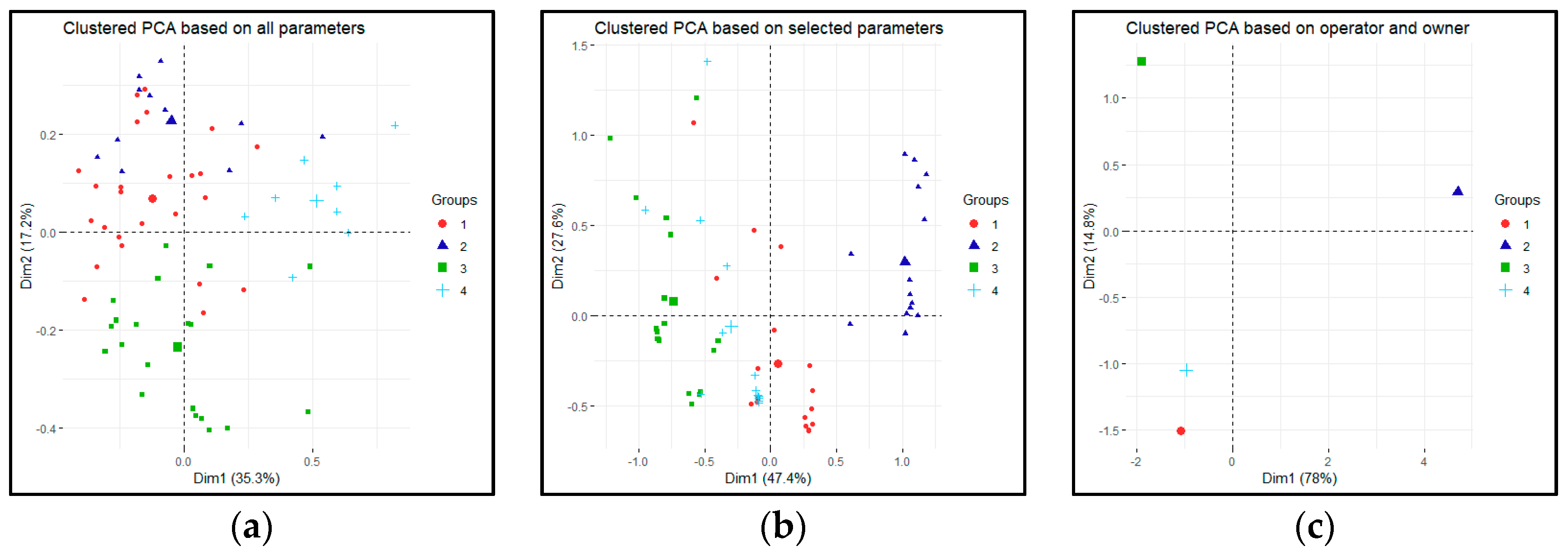
- The entire dataset (all collected 64 parameters),
- Selected parameters based on multinomial regression,
- Only operator and owner parameters.
2.1. Data Collection, Database
- 50 systems from Europe, 50 systems from Asia, 5 systems from Australia and New Zealand, and 20 systems from the Americas,
- 3/4 should be docked systems, while the remaining 1/4 is dockless.
- Location of the systems (Continent, Country, City, etc.),
- Contextual data (climate, start year of operation, size of the city, size of the service area, population, income, topology of the city, etc.),
- Data about the system (owner, operator, number of bikes, number of stations, etc.),
- Fare system (access fee, usage fee, deposit etc.),
- Data related to the system operations (when it is closed, how a bike can be hired, etc.),
- Derived data (bike density, station density, etc.).
2.2. Dataset Analysis
- Compute the dissimilarity matrix for the data set using Gower distance.
- Reorder the dissimilarity matrix so that similar objects get close to one another, which results in an ordered dissimilarity matrix.
- The ordered dissimilarity matrix is converted into an image for visual inspection.
- Get a random sample from the original real dataset.
- Compute a distance from each point to each nearest neighbor of the original real dataset.
- Generate a random dataset based on uniform distribution with the same variation as the original real dataset.
- Compute a distance from each point to each nearest neighbor of the random dataset.
- Calculate the Hopkins statistics (H) as the mean nearest neighbor distance in the random dataset divided by the sum of the mean nearest neighbor distance in the original real and the random dataset.
2.3. Clustering Based on Expert Opinion
2.4. Univariate Statistical Tests
2.5. Multinomial Regression
- The dependent variable is a nominal one and should be mutually exclusive.
- There are two or more independent nominal or continuous variables.
- There should be no multicollinearity.
- There need to be a relationship between any continuous independent variable and the logit transformation of the dependent one.
- There should be no outliers.
2.6. Cluster Analysis for Selected Parameters
2.7. Internal Cluster Validation
- The average distance between clusters measures the separation of clusters; as the average distance increases, so does the separation.
- The average distance within cluster objects measures the compactness of the clusters; as it decreases, the compactness increases.
- The average silhouette width also measures the separation between clusters. Each silhouette width coefficient is close to 1 if the object is in the right cluster, 0 means that the object is between clusters and −1 means that the object is entirely in the wrong cluster. So, we want the average to be as close to 1 as possible.
- The Pearson Gamma or normalized gamma coefficient shows the correlation between distances and a 01-vector where 0 means same cluster and 1 means different clusters.
- The Dunn index may be calculated in two ways, but in both cases, the Dunn index should be maximized: In the first version, the minimum separation divided by the maximum diameter; in the second way, the minimum average dissimilarity between two cluster divided by the maximum average within cluster dissimilarity.
2.8. External Cluster Validation
3. Results and Discussion
- Factor: Int_PT_fare, Int_user_card, Wout_registration, Deposit_short, Mobile_station.
- Continuous: First_30, Agglo_coverage, Station_density, Long_aff, E_bike_density, Bikes.
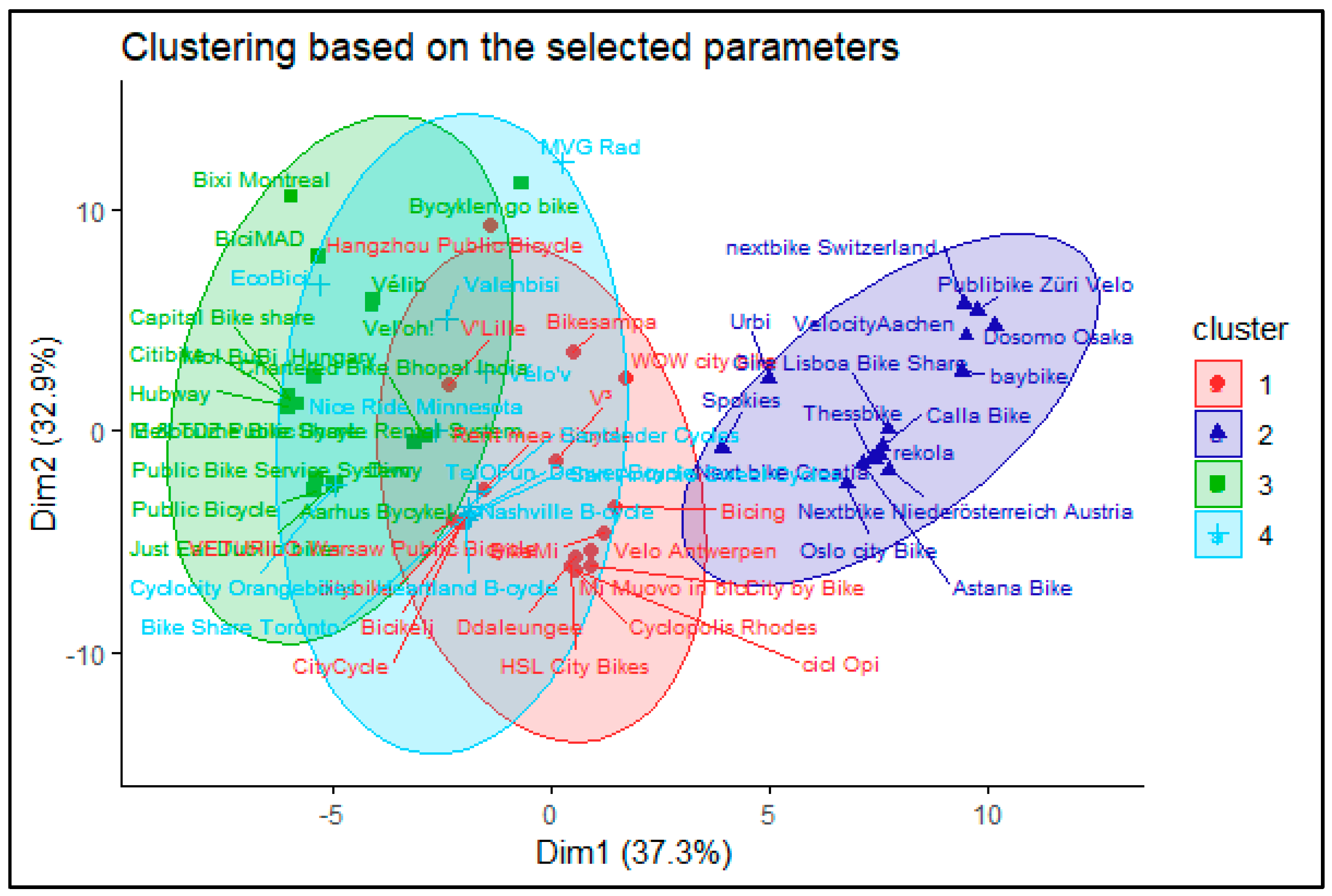
- Cluster 1 (Public systems): Both the operator and owner of the system are public institutions. The owner is usually a city or one of its companies. The operator can be the same organization or a new one created for this specific purpose. The income is coming directly from the user fees, but usually it requires subsidization. The goal of such a scheme usually is to provide an alternative transport mode or educate the citizens rather than profit making. Typical example: MVG Rad (Munich).
- Cluster 2 (Private systems): Both the operator and owner of the system are private companies, usually the same one. The income is coming from the user fees as well as advertisements. The goal here is clearly profit making, therefore a more cost-efficient operation is envisaged. Furthermore, some limitation related to the network or the users can be applied. Typical example: NextBike Croatia.
- Cluster 3 (Mixed systems): The owner of the system is a public entity (usually a city or a transport operator), while the operator is a private company. The goal of the owner is usually to provide wider transport choices to citizens, while a private company is providing a service. There are two distinct business models for the private company based on the main source of income. In both cases, the user fees are collected for the owner, hence the financial risk from the usage is on the owner side. In the first type, the service provider gets a service fee (availability payment) based on a service level agreement. In the second type, the operator can use different advertising spaces around the city to cover the expenses of the system operation. However, from the system point of view, there are not enough distinct features of these two subtypes to cluster them separately. Typical example: MOL-Bubi (Budapest-subtype 1); Velib (Paris-subtype 2).
- Cluster 4 (other systems): There are several systems that can be categorized by an unsupervised algorithm to one of the above clusters based on the expert knowledge of the authors cannot fit well with them. The reasons are usually hard to spot, but for instance, it can be that a public company design a system with clear profit-making goals, or a private company acts similarly towards a public entity. There are especially some outliers in the Chinese systems, due to the specificities of the country political structure.
4. Conclusions
- Data collection,
- Dataset analysis,
- Cluster analysis I.,
- Univariate statistical tests,
- Multinomial regression,
- Cluster analysis II.,
- Internal cluster validation,
- External cluster validation.
Author Contributions
Funding
Conflicts of Interest
References
- United Nations, Department of Economic and Social Affairs Population Division. World Population Prospects The 2012 Revision Volume I: Comprehensive Tables; (ST/ESA/SER.A/336); United Nations, Department of Economic and Social Affairs: New York, NY, USA, 2013. [Google Scholar]
- United Nations, Department of Economic and Social Affairs; Population Division. World Urbanization Prospects: The 2018 Revision; (ST/ESA/SER.A/420); United Nations, Department of Economic and Social Affairs: New York, NY, USA, 2019. [Google Scholar]
- Fenton, B.; Nash, A.; Wedderburn, M. Walking, Cycling and Congestion—Implementer’s Guide to Using the FLOW Tools for Multimodal Assessments; FLOW Consortium: Brussels, Belgium, 2018. [Google Scholar]
- Rudolph, F.; Mátrai, T. Congestion from a Multimodal Perspective. Period. Polytech. Transp. Eng. 2018, 46, 215–221. [Google Scholar] [CrossRef]
- Szabó, Z.; Török, Á. Spatial Econometrics—Usage in Transportation Sciences: A Review Article. Period. Polytech. Transp. Eng. 2019. [Google Scholar] [CrossRef]
- Pupavac, D.; Maršanić, R.; Krpan, L. Elasticity of Demand in Urban Traffic Case Study: City of Rijeka. Period. Polytech. Transp. Eng. 2019. [Google Scholar] [CrossRef]
- Garrard, J. Active Transport: Children and Young People, An Overview of Recent Evidence; Vic Health: Melbourne, VI, Australia, 2009.
- World Health Organization. Global Health Risks: Mortality and Burden of Disease Attributable to Selected Major Risks; World Health Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Department for City Planning New York. Bike-Share—Opportunities in New York City; Department for City Planning New York: New York, NY, USA, 2009.
- Shaheen, S.; Guzman, S.; Zhang, H. Bikesharing in Europe, the Americas, and Asia: Past, Present, and Future. Transp. Res. Rec. J. Transp. Res. Board 2010, 2143, 159–167. [Google Scholar] [CrossRef]
- Luo, H.; Kou, Z.; Zhao, F.; Cai, H. Comparative life cycle assessment of station-based and dock-less bike sharing systems. Resour. Conserv. Recycl. 2019. [Google Scholar] [CrossRef]
- Fishman, E. Bikeshare: A Review of Recent Literature. Transp. Rev. 2016, 36, 92–113. [Google Scholar] [CrossRef]
- Shaheen, S.A.; Martin, E.W.; Chan, N.D. Public Bikesharing in North America: Early Operator and User Understanding, MTI Report 11-19. Mineta Transp. Inst. Publ. 2012. [Google Scholar] [CrossRef]
- Fishman, E.; Washington, S.; Haworth, N. Barriers and facilitators to public bicycle scheme use: A qualitative approach. Transp. Res. Part F Traffic Psychol. Behav. 2012, 15, 686–698. [Google Scholar] [CrossRef]
- Fishman, E.; Washington, S.; Haworth, N. Bike Share: A Synthesis of the Literature. Transp. Rev. 2013, 33, 148–165. [Google Scholar] [CrossRef]
- DeMaio, P. Bike-Sharing: History, Impacts, Models of Provision, and Future. J. Publ. Transp. 2009, 12, 41–56. [Google Scholar] [CrossRef]
- Wu, G.; Si, H.; Chen, J.; Shi, J.; Zhao, X. Mapping the bike sharing research published from 2010 to 2018: A scientometric review. J. Clean. Prod. 2018, 213, 415–427. [Google Scholar] [CrossRef]
- Mátrai, T.; Tóth, J. Comparative Assessment of Public Bike Sharing Systems. Transp. Res. Procedia 2016, 14, 2344–2351. [Google Scholar] [CrossRef]
- Tóth, J.; Mátrai, T. Újszerű, nem motorizált közlekedési megoldások. In Proceedings of the Közlekedéstudományi Konferencia, Győr, Hungary, 26–27 March 2015. [Google Scholar]
- Mátrai, T.; Mándoki, P.; Tóth, J. Benchmarking tool for bike sharing systems. In Proceedings of the Third International Conference On Traffic And Transport Engineering (ICTTE), Belgrade, Serbia, 24–25 November 2016; Cokorilo, O., Ed.; Scientific Research Center Ltd.: Belgrade, Serbia; pp. 550–558.
- Mátrai, T.; Tóth, J. Categorization of bike sharing systems: A case study from Budapest. In Proceedings of the European Conference on Mobility Management, Athens, Greece, 1–3 June 2016. [Google Scholar]
- Médard de Chardon, C. The contradictions of bike-share benefits, purposes and outcomes. Transp. Res. Part A Policy Pract. 2019, 121, 401–419. [Google Scholar] [CrossRef]
- Ricci, M. Bike sharing: A review of evidence on impacts and processes of implementation and operation. Res. Transp. Bus. Manag. 2015, 15, 28–38. [Google Scholar] [CrossRef]
- Winslow, J.; Mont, O. Bicycle Sharing: Sustainable Value Creation and Institutionalisation Strategies in Barcelona. Sustainability 2019, 11, 728. [Google Scholar] [CrossRef]
- Cohen, B.; Kietzmann, J. Ride On! Mobility Business Models for the Sharing Economy. Organiz. Environ. 2014, 27, 279–296. [Google Scholar] [CrossRef]
- Hamidi, Z.; Camporeale, R.; Caggiani, L. Inequalities in access to bike-and-ride opportunities: Findings for the city of Malmö. Transp. Res. Part A Policy Pract. 2019, 130, 673–688. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.; Duan, Z.; Bryde, D. Sustainable bike-sharing systems: Characteristics and commonalities across cases in urban China. J. Clean. Prod. 2015, 97, 124–133. [Google Scholar] [CrossRef]
- Van Waes, A.; Farla, J.; Frenken, K.; de Jong, J.P.J.; Raven, R. Business model innovation and socio-technical transitions. A new prospective framework with an application to bike sharing. J. Clean. Prod. 2018, 195, 1300–1312. [Google Scholar] [CrossRef]
- Gao, P.; Li, J. Understanding sustainable business model: A framework and a case study of the bike-sharing industry. J. Clean. Prod. 2020, 267, 122229. [Google Scholar] [CrossRef]
- Osterwalder, A.; Pigneur, Y.; Tucci, C.L. Clarifying Business Models: Origins, Present, and Future of the Concept. Commun. Assoc. Inform. Syst. 2005, 16, 1. [Google Scholar] [CrossRef]
- Claudio-González, M.G.; Martín-Baranera, M.; Villarroya, A. A cluster analysis of the business models of Spanish journals. Learn. Publ. 2016, 29, 239–248. [Google Scholar] [CrossRef]
- Engel, C.; Haude, J.; Kühl, N. Business Model Clustering: A network-based approach in the field of e-mobility services. In Proceedings of the 2nd Karlsruhe Service Summit, Karlsruhe, Germany, 25–26 February 2016; pp. 11–25. [Google Scholar]
- Kassambara, A. Practical Guide to Cluster Analysis in R: Unsupervised Machine Learning, 1st ed.; STHDA: Marseille, France, 2017; ISBN 1542462703. [Google Scholar]
- Boufidis, N.; Nikiforiadis, A.; Chrysostomou, K.; Aifadopoulou, G. Development of a station-level demand prediction and visualization tool to support bike-sharing systems’ operators. Transp. Res. Procedia 2020, 47, 51–58. [Google Scholar] [CrossRef]
- Wei, X.; Luo, S.; Nie, Y.M. Diffusion behavior in a docked bike-sharing system. Transp. Res. Part C Emerg. Technol. 2019, 107, 510–524. [Google Scholar] [CrossRef]
- Jia, W.; Tan, Y.; Liu, L.; Li, J.; Zhang, H.; Zhao, K. Hierarchical prediction based on two-level Gaussian mixture model clustering for bike-sharing system. Knowl. Based Syst. 2019, 178, 84–97. [Google Scholar] [CrossRef]
- Kou, Z.; Cai, H. Understanding bike sharing travel patterns: An analysis of trip data from eight cities. Phys. A Stat. Mech. Appl. 2019. [Google Scholar] [CrossRef]
- Meddin, R. Bike Sharing Map. Available online: www.bikesharingmap.com (accessed on 28 February 2020).
- Gower, J.C. A General Coefficient of Similarity and Some of Its Properties. Biometrics 1971, 27, 857. [Google Scholar] [CrossRef]
- Maechler, M.; Rousseeuw, P.; Struyf, A.; Hubert, M.; Hornik, K. Cluster: Cluster Analysis Basics and Extensions, R Package version 2.0.8; R Core Team: Vienna, Austria, 2019. [Google Scholar]
- Bezdek, J.C.; Hathaway, R.J. VAT: A tool for visual assessment of (cluster) tendency. In Proceedings of the International Joint Conference on Neural Networks, Honolulu, HI, USA, 12–17 May 2002; pp. 2225–2230. [Google Scholar] [CrossRef]
- Bursac, Z.; Gauss, C.H.; Williams, D.K.; Hosmer, D.W. Purposeful selection of variables in logistic regression. Sour. Code Biol. Med. 2008, 3. [Google Scholar] [CrossRef]
- Yeager, K. SPSS Tutorials: Chi-Square Test of Independence. Available online: https://libguides.library.kent.edu/SPSS/ChiSquare (accessed on 31 August 2019).
- Yeager, K. SPSS Tutorials: One-Way ANOVA. Available online: https://libguides.library.kent.edu/spss/onewayanova (accessed on 31 August 2019).
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; Wiley Series in Probability and Statistics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1990; ISBN 9780470316801. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2017. [Google Scholar]
- Kassambara, A.; Fabian, M. Factoextra: Extract and Visualize the Results of Multivariate Data Analyses; STHDA: Marseille, France, 2017. [Google Scholar]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. On clustering validation techniques. J. Intel. Inform. Syst. 2001, 17, 107–145. [Google Scholar] [CrossRef]
- Gordon, A.D. Classification; Chapman and Hall: London, UK; CRC: Boca Raton, FL, USA, 1999; ISBN 9780367805302. [Google Scholar]
- Meilǎ, M. Comparing clusterings-an information based distance. J. Multivar. Anal. 2007, 98, 873–895. [Google Scholar] [CrossRef]
- Mátrai, T. Public bike sharing systems database. Mendeley Data 2019. [Google Scholar] [CrossRef]
- Caggiani, L.; Camporeale, R.; Ottomanelli, M.; Szeto, W.Y. A modeling framework for the dynamic management of free-floating bike-sharing systems. Transp. Res. Part C Emerg. Technol. 2018, 87, 159–182. [Google Scholar] [CrossRef]
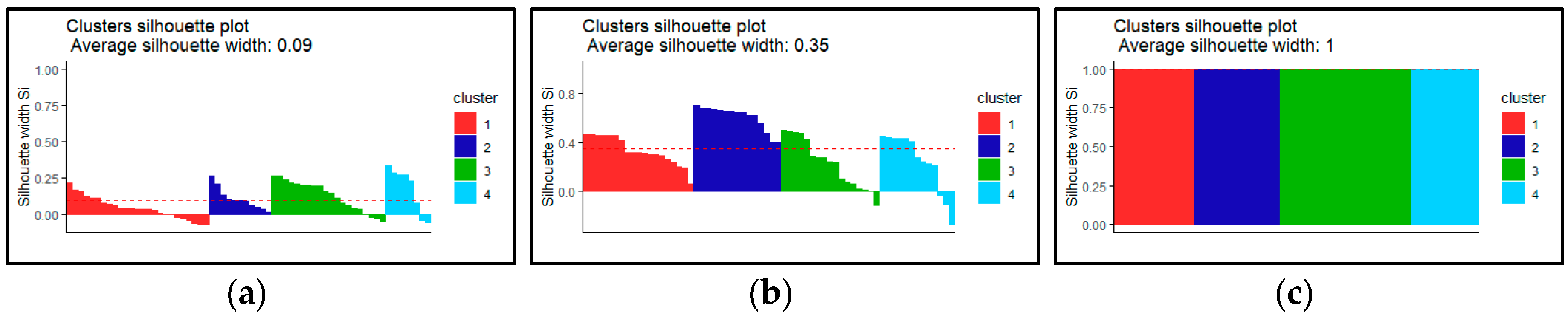
| Cluster Number | Owner | Operator | Comment |
|---|---|---|---|
| 1 | Public | Advertising company | An advertising company provides services to a public institution, the income for the advertising company might not be realized from the direct user fees, but from some advertising spaces around the city |
| 3 | Public | Service provider | A service provider operates a system on behalf of the public institution, the income for these service providers can be an availability payment. |
| 4 | Public | Public | A public institution operates the system or sets up a public company for operation, the income is directly from the user fees. |
| 2 | Private | Private company | The owner of the system is the same private company as the operator, the incomes are from the user fees and from the advertisements. |
| Parameter | Value | Asymptotic Significance (2-Sided) |
|---|---|---|
| Owner | 63.574 | 0.000 |
| Operator | 183.798 | 0.000 |
| User_card_dock | 15.654 | 0.001 |
| Wout_registration | 12.026 | 0.007 |
| User_card_terminal | 11.718 | 0.008 |
| Int_user_card | 11.156 | 0.011 |
| Deposit_short | 11.148 | 0.011 |
| Continent | 19.562 | 0.021 |
| Credit_card_terminal | 9.109 | 0.028 |
| Mobile_station | 8.045 | 0.045 |
| App_bike | 7.999 | 0.046 |
| Country | 126.487 | 0.051 |
| Hour_closed | 6.995 | 0.072 |
| Diff_station | 19.487 | 0.077 |
| Code_dock | 6.133 | 0.105 |
| Code_terminal | 6.106 | 0.107 |
| Diff_renting_option | 25.603 | 0.109 |
| Deposit_long | 6.050 | 0.109 |
| Int_PT_Fare | 5.415 | 0.144 |
| Code_bike | 4.287 | 0.232 |
| Parameter | F | Significance |
|---|---|---|
| Operation | 13.773 | 0.000 |
| Deposit_short_EUR | 4.367 | 0.007 |
| Service_area | 3.877 | 0.013 |
| Deposit_long_EUR | 3.793 | 0.014 |
| E_bikes_dens | 3.686 | 0.016 |
| Station | 3.433 | 0.022 |
| Bikes | 3.365 | 0.024 |
| Docks | 3.141 | 0.031 |
| City_size | 2.337 | 0.082 |
| Population | 2.096 | 0.109 |
| Long_att | 1.884 | 0.142 |
| Long_aff | 1.818 | 0.154 |
| First_30 | 1.776 | 0.160 |
| Agglo_coverage | 1.555 | 0.209 |
| Station_density | 1.449 | 0.237 |
| Cluster Id. | Based on All Parameters | Based on the Selected Parameters | Based on the Operator and Owner Parameters | |||
|---|---|---|---|---|---|---|
| Cluster Size | Average Silhouette Width | Cluster Size | Average Silhouette Width | Cluster Size | Average Silhouette Width | |
| 1 | 25 | 0.04 | 19 | 0.33 | 14 | 1 |
| 2 | 11 | 0.10 | 15 | 0.60 | 15 | 1 |
| 3 | 20 | 0.12 | 17 | 0.22 | 23 | 1 |
| 4 | 8 | 0.17 | 13 | 0.24 | 12 | 1 |
| Based on All Parameters | Based on the Selected Parameters | Based on the Operator and Owner Parameters | |
|---|---|---|---|
| Number of observations | 64 | 64 | 64 |
| Average distance between clusters | 0.2543182 | 0.330922 | 0.7448368 |
| Average distance within cluster | 0.2315138 | 0.1898745 | 0 |
| Average silhouette width | 0.01317239 | 0.356468 | 1 |
| Pearson Gamma coefficient | 0.1585032 | 0.4660481 | 0.8330978 |
| Dunn index, first version | 0.2005322 | 0.1838311 | ∞ |
| Dunn index, second version | 0.8049529 | 1.323103 | ∞ |
| Based on All Parameters | Based on the Selected Parameters | Based on the Operator and Owner Parameters | |
|---|---|---|---|
| Corrected Rand index | 0.07757761 | 0.4368271 | 1 |
| Variation Index | 2.22212 | 1.217804 | 4.440892 × 10−16 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mátrai, T.; Tóth, J. Cluster Analysis of Public Bike Sharing Systems for Categorization. Sustainability 2020, 12, 5501. https://doi.org/10.3390/su12145501
Mátrai T, Tóth J. Cluster Analysis of Public Bike Sharing Systems for Categorization. Sustainability. 2020; 12(14):5501. https://doi.org/10.3390/su12145501
Chicago/Turabian StyleMátrai, Tamás, and János Tóth. 2020. "Cluster Analysis of Public Bike Sharing Systems for Categorization" Sustainability 12, no. 14: 5501. https://doi.org/10.3390/su12145501
APA StyleMátrai, T., & Tóth, J. (2020). Cluster Analysis of Public Bike Sharing Systems for Categorization. Sustainability, 12(14), 5501. https://doi.org/10.3390/su12145501





