Energy Efficiency: Indicator, Estimation, and a New Idea
Abstract
:1. Introduction
2. The Measurements of Energy Efficiency
2.1. Common Measurements
2.1.1. Energy-Consumption-Efficacy-Indicator
2.1.2. Energy-Economic-Efficiency-Estimate
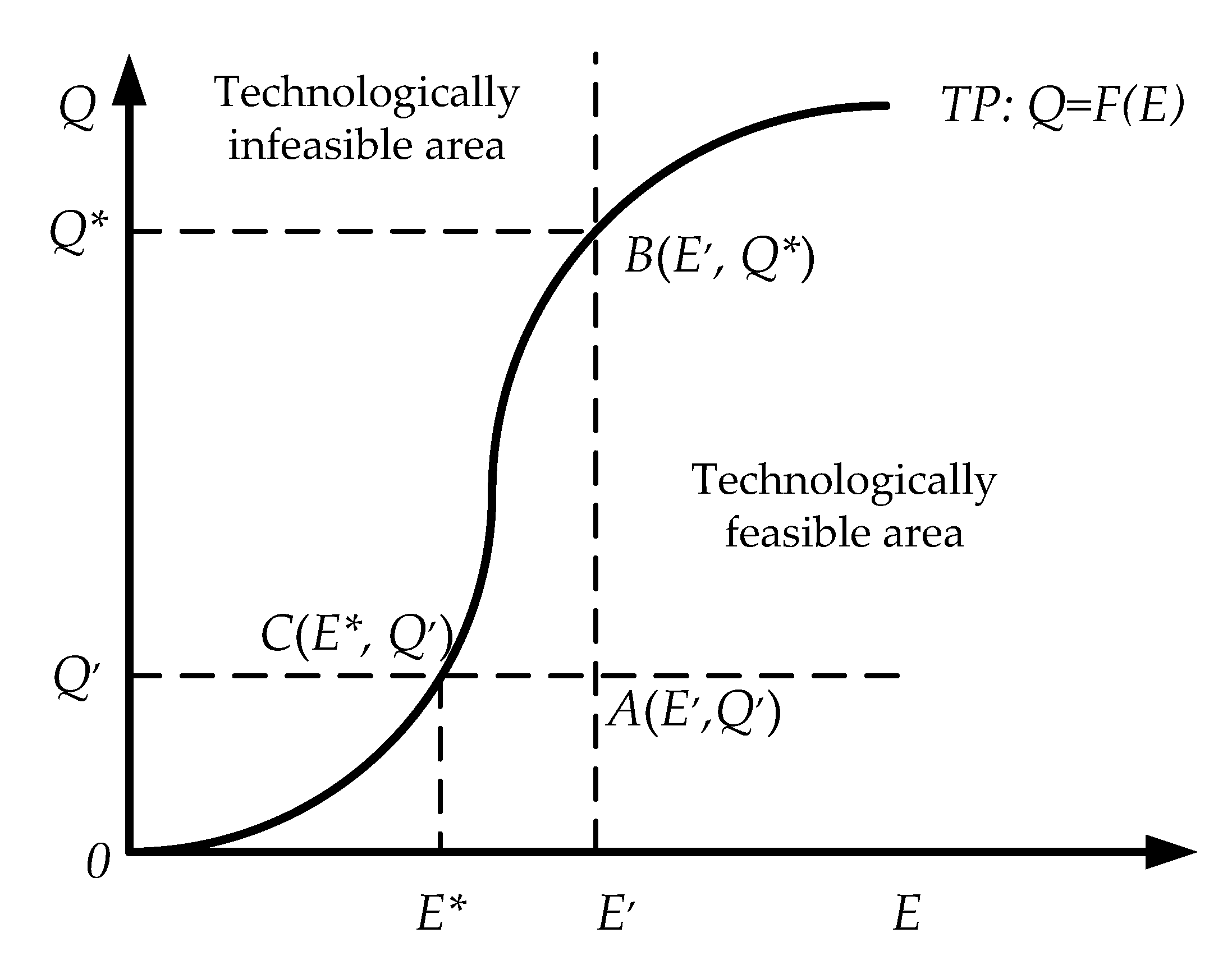
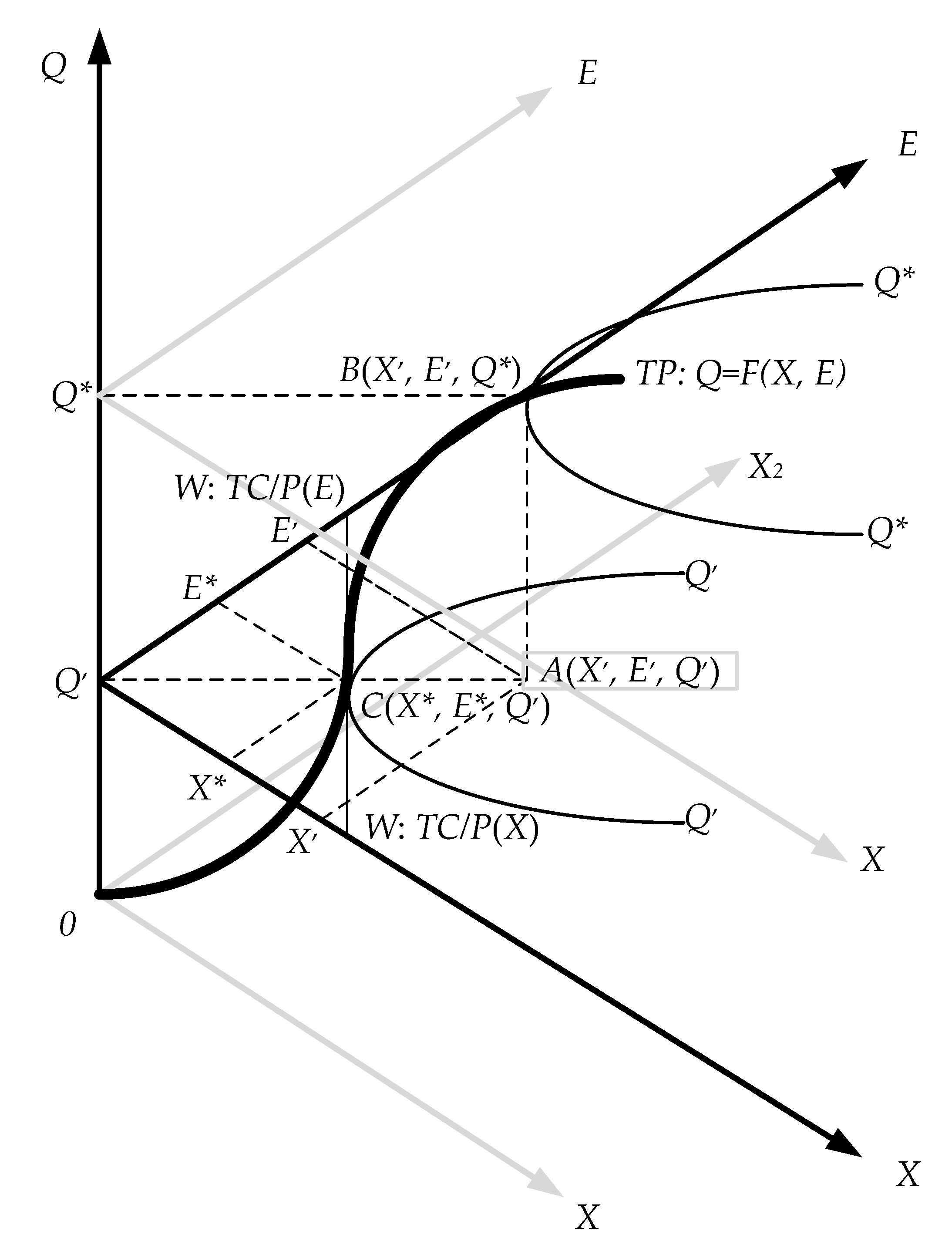
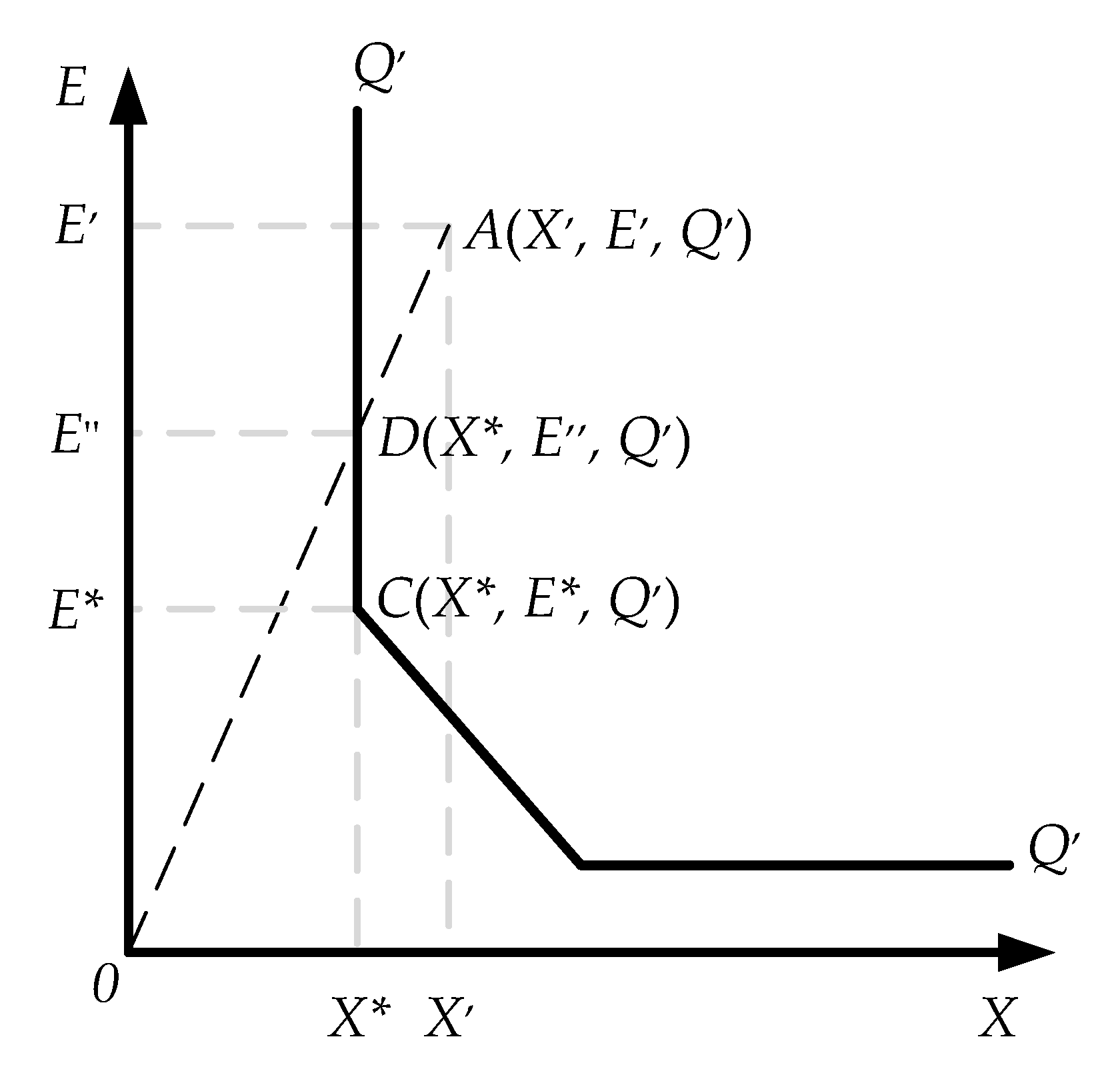
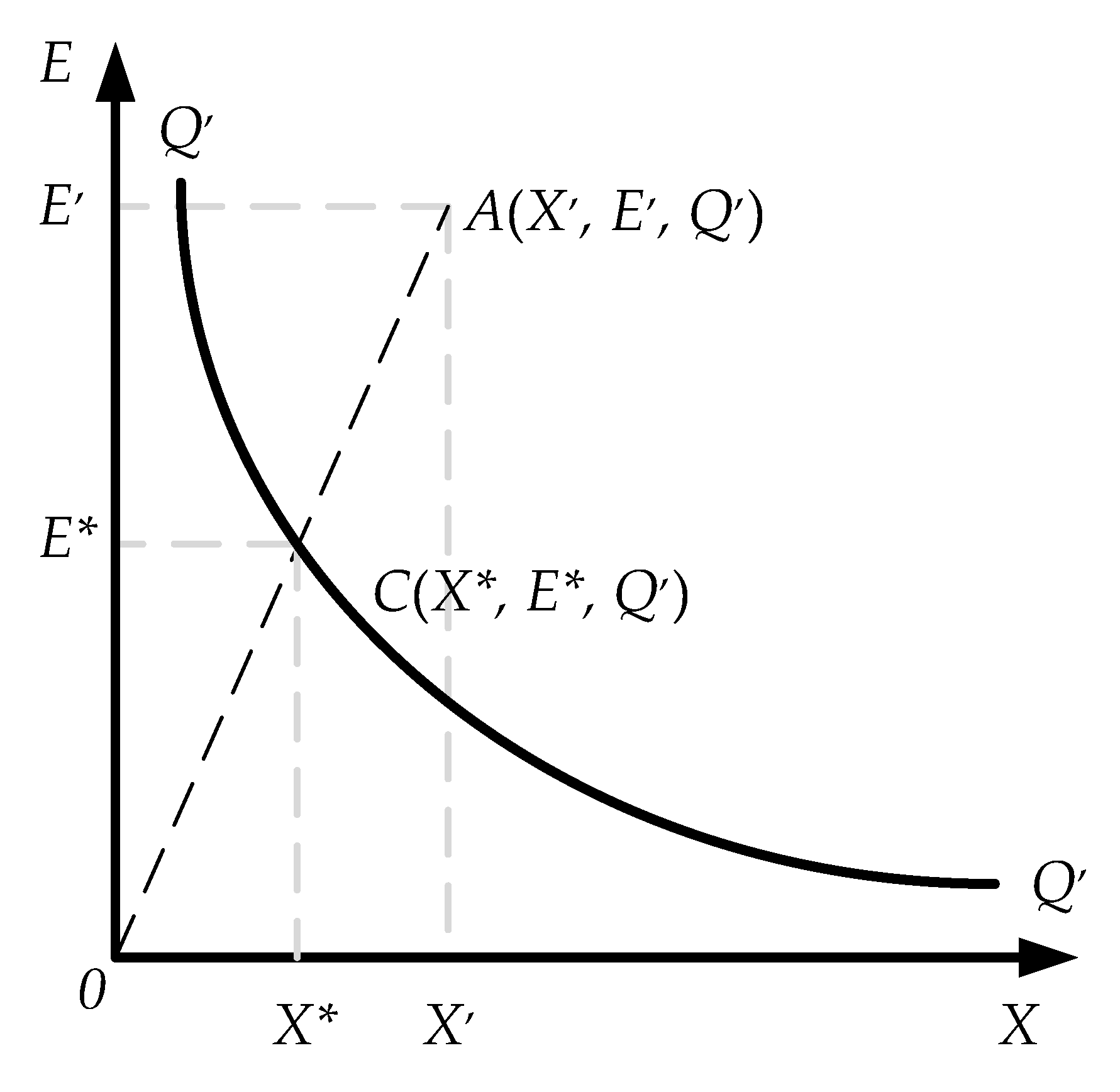
2.2. A New Approach
3. Empirical Applications
3.1. Data Collections and Preliminary Summaries
3.2. Specifications and Estimation Results
3.3. Further Comparisons
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Melo, C.A.; Jannuzzi, G.M. Energy Efficiency Standards for Refrigerators in Brazil: A Methodology for Impact Evaluation. Energy Policy 2010, 38, 6545–6550. [Google Scholar] [CrossRef]
- Miketa, A.; Mulder, P. Energy Productivity across Developed and Developing Countries in 10 Manufacturing Sectors: Patterns of Growth and Convergence. Energy Econ. 2005, 27, 429–453. [Google Scholar] [CrossRef]
- Landi, D.; Capitanelli, A.; Germani, M. Ecodesign and Energy Labelling: The Role of Virtual Prototyping. Procedia Cirp 2017, 61, 87–92. [Google Scholar] [CrossRef]
- Germani, M.; Landi, D.; Rossi, M. Efficiency and Environmental Analysis of A System for Renewable Electricity Generation and Electrochemical Storage of Residential Buildings. Procedia Cirp 2015, 29, 839–844. [Google Scholar] [CrossRef]
- Landi, D.; Castorani, V.; Germani, M. Interactive Energetic, Environmental and Economic Analysis of Renewable Hybrid Energy System. Int. J. Interact. Des. Manuf. 2019, 13, 885–899. [Google Scholar] [CrossRef]
- Capitanelli, A.; Germani, M.; Landi, D.; Papetti, A. A Methodology to Design A Knowledge-based Tool for Residential Buildings Simulation. ASME 2015 International Mechanical Engineering Congress and Exposition. Am. Soc. Mech. Eng. Digit. Collect. 2015. [Google Scholar] [CrossRef]
- Tahir, Y.; Nadeem, M.F.; Ahmed, A.; Khan, I.A.; Qamar, F. A Review on Hybrid Energy Storage Systems in Microgrids. In Proceedings of the 2020 3rd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 29–30 January 2020; pp. 1–7. [Google Scholar]
- Hardisty, D.J.; Shim, Y.; Sun, D.; Griffin, D.W. Encouraging Energy Efficiency: Product Labels Activate Temporal Tradeoffs 2020. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3576266 (accessed on 31 May 2020).
- Chen, K.H.; Yang, H.Y.; Lee, J.M.; Chi, C.F. The Impact of Energy Prices on Energy Consumption, and Energy Efficiency: Evidence from Taiwan. Energy Effic. 2016, 9, 1329–1349. [Google Scholar] [CrossRef]
- Shove, E. What Is Wrong with Energy Efficiency. Build. Res. Inf. 2018, 46, 779–789. [Google Scholar] [CrossRef]
- Merriam-Webster Dictionary. Available online: https://www.merriam-webster.com/dictionary/efficiency (accessed on 11 October 2018).
- International Energy Agency. Energy Efficiency Indicators: Essential for Policy Making 2014. Available online: https://www.iea.org/publications/freepublications/ (accessed on 23 February 2020).
- Hu, J.L.; Wang, S.C. Total-factor Energy Efficiency of Regions in China. Energy Policy 2006, 34, 3026–3217. [Google Scholar] [CrossRef]
- Atakhanova, Z.; Howie, P. Electricity Demand in Kazakhstan. Energy Policy 2007, 35, 3729–3743. [Google Scholar] [CrossRef]
- Patterson, M.G. What is Energy Efficiency? Concepts, Indicators, and Methodological Issues. Energy Policy 1996, 24, 377–390. [Google Scholar] [CrossRef]
- Bakar, N.N.A.; Hassan, M.Y.; Abdullah, H.; Rahman, H.A.; Abdullah, M.P.; Hussin, F.; Bandi, M. Energy Efficiency Index as An Indicator for Measuring Building Energy Performance: A review. Renew. Sustain. Energy Rev. 2015, 44, 1–11. [Google Scholar] [CrossRef]
- Cai, W.; Liu, F.; Dinolov, O.; Xie, J.; Liu, P.; Tuo, J. Energy Benchmarking Rules in Machining Systems. Energy 2018, 142, 258–263. [Google Scholar] [CrossRef]
- Farla, J.C.; Blok, K. The Use of Physical Indicators for the Monitoring of Energy Intensity Developments in the Netherlands, 1980–1995. Energy 2000, 25, 609–638. [Google Scholar] [CrossRef]
- Heiple, S.; Sailor, D.J. Using Building Energy Simulation and Geospatial Modeling Techniques to Determine High Resolution Building Sector Energy Consumption Profiles. Energy Build. 2008, 40, 1426–1436. [Google Scholar] [CrossRef] [Green Version]
- Sheng, Y.; Miao, Z.; Zhang, J.; Lin, X.; Ma, H. Energy Consumption Model and Energy Benchmarks of Five-star Hotels in China. Energy Build. 2018, 165, 286–292. [Google Scholar] [CrossRef]
- Farrell, M.J. The Measurement of Productive Efficiency. J. R. Stat. Soc. 1957, 120, 253–290. [Google Scholar] [CrossRef]
- Hu, J.L.; Kao, C.H. Efficient Energy-saving Targets for APEC Economies. Energy Policy 2007, 35, 373–382. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the Efficiency of Decision Making Units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Bi, G.B.; Song, W.; Zhou, P.; Liang, L. Does Environmental Regulation Affect Energy Efficiency in China's Thermal Power Generation? Empirical Evidence from A Slacks-based DEA Model. Energy Policy 2014, 66, 537–546. [Google Scholar] [CrossRef]
- Wu, A.H.; Cao, Y.Y.; Liu, B. Energy Efficiency Evaluation for Regions in China: An Application of DEA and Malmquist Indices. Energy Effic. 2014, 7, 429–439. [Google Scholar] [CrossRef]
- Li, K.; Lin, B. Metafrontier Energy Efficiency with CO2 Emissions and Its Convergence Analysis for China. Energy Econ. 2015, 48, 230–241. [Google Scholar] [CrossRef]
- Li, M.J.; Tao, W.Q. Review of Methodologies and Polices for Evaluation of Energy Efficiency in High Energy-Consuming Industry. Appl. Energy 2017, 187, 203–215. [Google Scholar] [CrossRef]
- Shi, S.A.; Xia, L.; Meng, M. Energy Efficiency and Its Driving Factors in China’s Three Economic Regions. Sustainability 2017, 9, 2059. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Gao, Y.; An, Q.; Wang, Z.; Neralić, L. Energy Efficiency Measurement of Chinese Yangtze River Delta’s Cities Transportation: A DEA Window Analysis Approach. Energy Effic. 2018, 11, 1941–1953. [Google Scholar] [CrossRef]
- Tian, P.; Lin, B. Regional Technology Gap in Energy Utilization in China's Light Industry Sector: Non-parametric Meta-frontier and Sequential DEA Methods. J. Clean. Prod. 2018, 178, 880–889. [Google Scholar] [CrossRef]
- Feijoó, M.L.; France, J.F.; Hernández, J.M. Global Warming and the Energy Efficiency of Spanish Industry. Energy Econ. 2002, 24, 405–423. [Google Scholar] [CrossRef]
- Aigner, D.J.; Lovell, C.A.K.; Schmidt, P. Formulation and Estimation of Stochastic Frontier Production Function Models. J. Econom. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Meeusen, W.; van Den Broeck, J. Efficiency Estimation from Cobb–Douglas Production Functions with Composed Error. Int. Econ. Rev. 1977, 18, 435–444. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W.; Zhou, D.Q. “Measuring Economy-wide Energy Efficiency Performance: A Parametric Frontier Approach. Appl. Energy 2012, 90, 196–200. [Google Scholar] [CrossRef]
- Filippini, M.; Zhang, L. Estimation of the Energy Efficiency in Chinese Provinces. Energy Effic. 2016, 9, 1315–1328. [Google Scholar] [CrossRef]


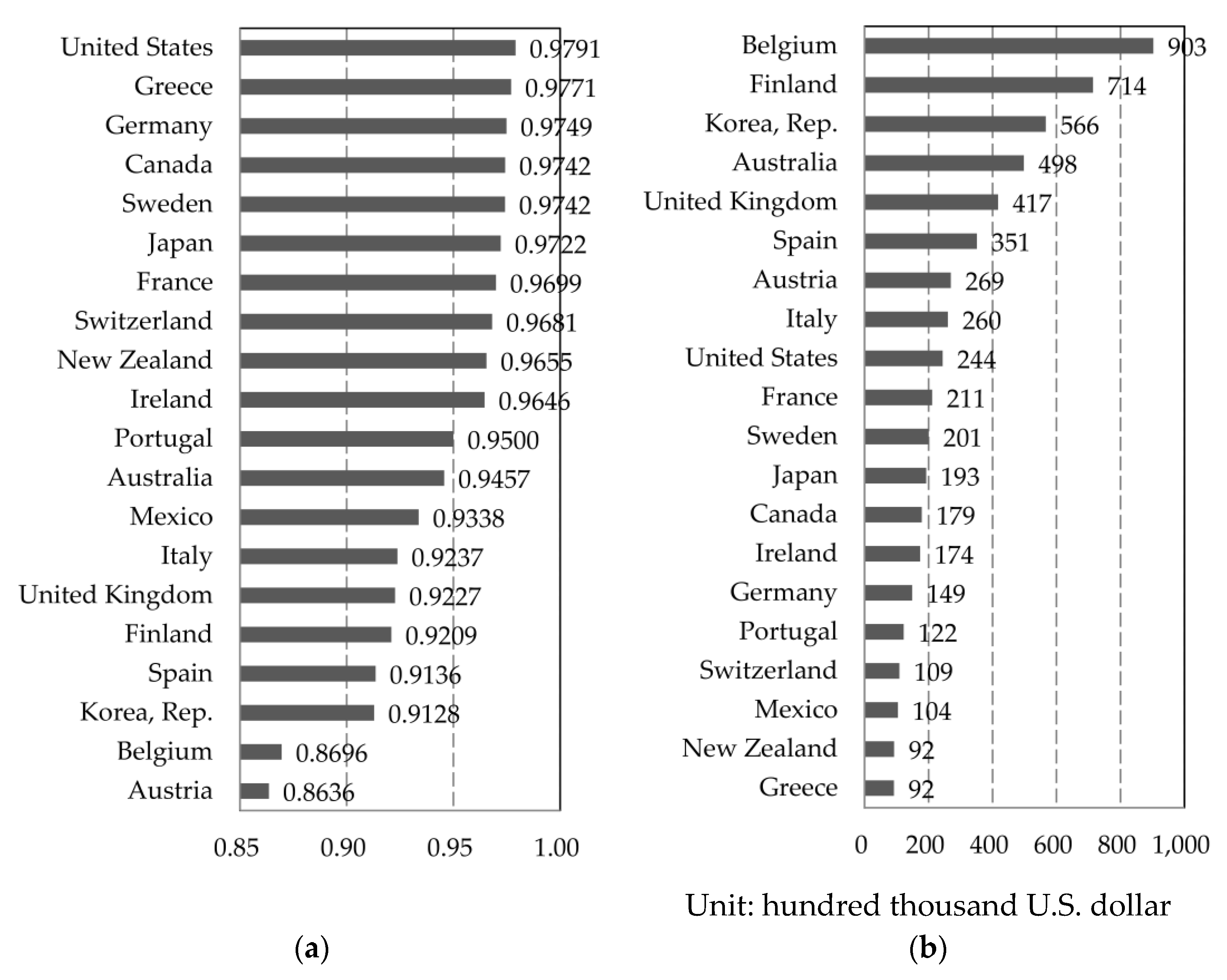
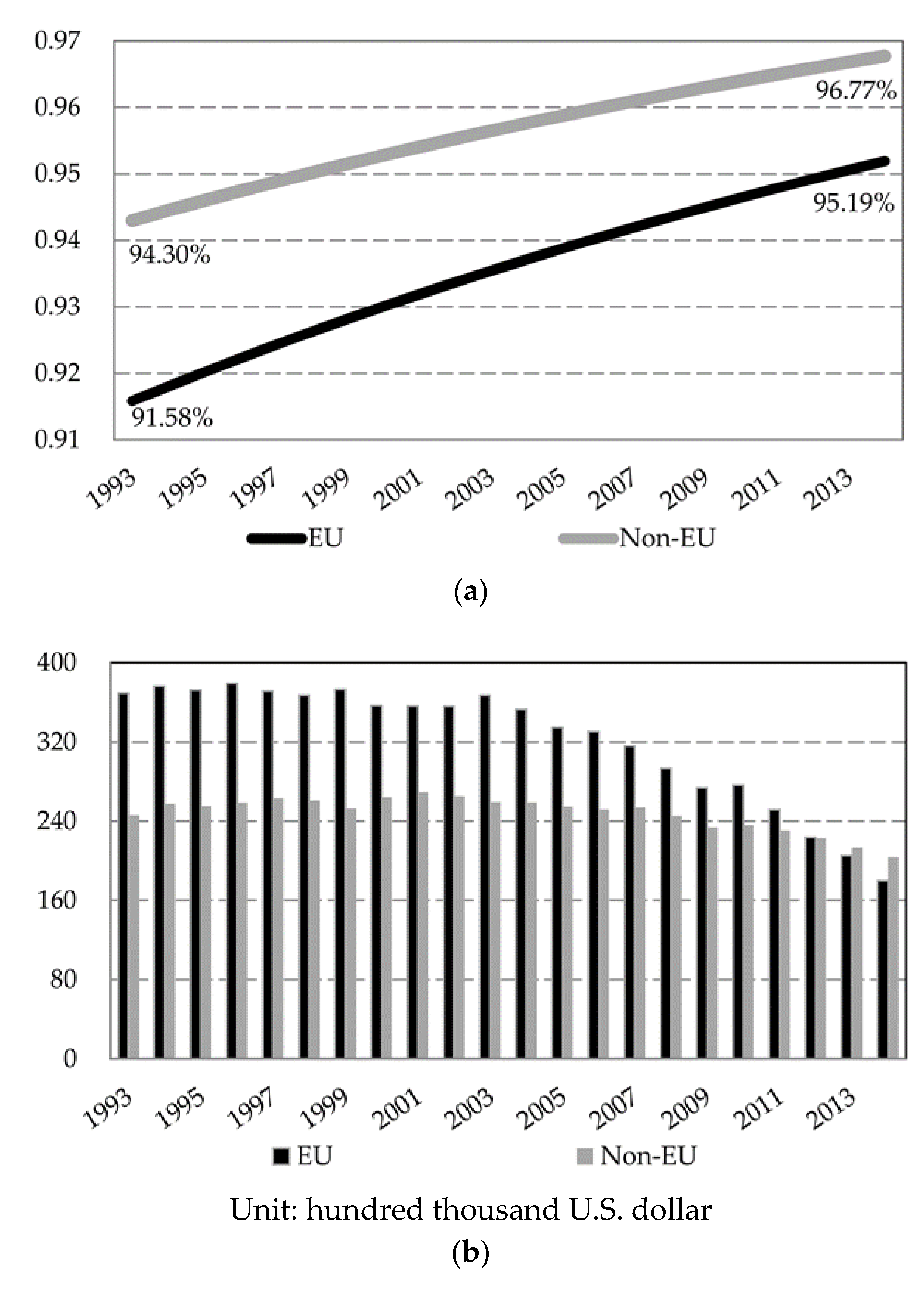
| Countries/Variables | Annual Real GDP (Y) | Energy Input (E) | ||
|---|---|---|---|---|
| Australia | 759,560.49 | (175,281.54) | 9165.18 | (807.55) |
| Austria | 309,220.85 | (56,641.41) | 1955.71 | (363.62) |
| Belgium | 376,454.54 | (67,298.53) | 6873.83 | (658.86) |
| Canada | 1,201,127.99 | (209,265.47) | 6890.83 | (371.59) |
| Finland | 175,925.26 | (37,793.12) | 8936.78 | (1185.88) |
| France | 2,053,349.04 | (354,517.80) | 7012.62 | (421.088) |
| Germany | 2,912,371.78 | (422,470.86) | 5895.23 | (304.03) |
| Greece | 276,505.40 | (51,521.54) | 4000.78 | (551.46) |
| Ireland | 155,637.13 | (53,521.13) | 4872.44 | (588.88) |
| Italy | 1,911,839.25 | (215,882.75) | 3397.29 | (457.09) |
| Japan | 4,233,242.28 | (231,577.82) | 6910.15 | (379.08) |
| Korea, Rep. | 1,211,316.10 | (343,360.55) | 6680.78 | (2334.85) |
| Mexico | 1,391,473.43 | (352,353.99) | 1593.64 | (299.30) |
| New Zealand | 114,982.99 | (23,353.74) | 2693.54 | (530.81) |
| Portugal | 238,144.89 | (46,207.78) | 2450.33 | (481.05) |
| Spain | 1,224,794.42 | (307,470.61) | 4074.65 | (694.89) |
| Sweden | 335,742.70 | (62,579.79) | 7652.06 | (932.18) |
| Switzerland | 338,275.48 | (74,689.45) | 3403.52 | (180.23) |
| United Kingdom | 2,095,952.86 | (359,169.68) | 5347.64 | (545.83) |
| United States | 13,581,642.44 | (2,235,112.17) | 11,674.81 | (562.09) |
| Variables | Coefficient | Std. Err. | |
|---|---|---|---|
| α0 | 0.032 | (0.015) | *** |
| α1 | 0.042 | (0.040) | |
| α2 | 0.150 | (0.036) | *** |
| α3 | 0.138 | (0.044) | *** |
| α4 | 0.012 | (0.030) | |
| α5 | 0.071 | (0.031) | *** |
| α6 | 0.0061 | (0.0321) | |
| α7 | 0.011 | (0.026) | |
| α8 | −0.0077 | (0.0265) | |
| α9 | 0.041 | (0.032) | |
| α10 | 0.061 | (0.040) | |
| α11 | −0.0014 | (0.0235) | |
| α12 | 0.043 | (0.073) | |
| α13 | 0.022 | (0.067) | |
| α14 | 0.035 | (0.021) | * |
| α15 | 0.040 | (0.021) | ** |
| α16 | 0.072 | (0.034) | *** |
| α17 | 0.017 | (0.028) | |
| α18 | 0.013 | (0.038) | |
| α19 | 0.080 | (0.027) | *** |
| σ2 | 0.0320 | (0.0031) | *** |
| κ | 0.803 | (0.018) | *** |
| μ | −0.321 | (0.079) | ** |
| η | 0.0280 | (0.0051) | *** |
| Log-likelihood ratio | 460.0048 | ||
| No. of observations | 20 | ||
| No. of periods | 22 | ||
| No. of samples | 440 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.-H.; Cheng, J.-C.; Lee, J.-M.; Li, L.-Y.; Peng, S.-Y. Energy Efficiency: Indicator, Estimation, and a New Idea. Sustainability 2020, 12, 4944. https://doi.org/10.3390/su12124944
Chen K-H, Cheng J-C, Lee J-M, Li L-Y, Peng S-Y. Energy Efficiency: Indicator, Estimation, and a New Idea. Sustainability. 2020; 12(12):4944. https://doi.org/10.3390/su12124944
Chicago/Turabian StyleChen, Ku-Hsieh, Jen-Chi Cheng, Joe-Ming Lee, Liou-Yuan Li, and Sheng-Yu Peng. 2020. "Energy Efficiency: Indicator, Estimation, and a New Idea" Sustainability 12, no. 12: 4944. https://doi.org/10.3390/su12124944
APA StyleChen, K.-H., Cheng, J.-C., Lee, J.-M., Li, L.-Y., & Peng, S.-Y. (2020). Energy Efficiency: Indicator, Estimation, and a New Idea. Sustainability, 12(12), 4944. https://doi.org/10.3390/su12124944





