Analysis of Run-Off-Road Accidents by Association Rule Mining and Geographic Information System Techniques on Imbalanced Datasets
Abstract
1. Introduction
- Few studies were conducted to analyze ROR accidents, which cause most fatalities on roads. This paper is one of the few studies to explore the key factors associated with the accident severity of ROR accidents, especially the key factors related to fatal accidents.
- Datasets of ROR accidents are extremely imbalanced, in which FA are much less than NFA. Data mining methods on such extremely imbalanced datasets make the results deteriorated or biased. This study proposes a novel method to address the imbalance problem in ROR accidents. The proposed method can avoid the randomness caused by sampling methods and improve the robustness and reliability of the results on imbalanced datasets.
- This study applies ARM for the severity analysis of ROR accidents. It can not only explore individual key factors associated with injury severity but also identify the interactive relationship between multiple factors in ROR accidents.
- This is one of the few papers to conduct spatial analysis of ROR accidents by GIS technology. The hot spots of ROR accidents associated with key factors can be presented in GIS maps. Policymakers can refer to these maps when making decisions.
2. Methodology
2.1. BRDB Method
2.1.1. Bootstrap Resampling Method
2.1.2. Process of BRDB Method
2.2. ARM
2.3. Ensemble Method
2.4. GIS Analysis
3. Case Study
- (1)
- Road characteristics: Five variables are collected to describe the roads on which ROR accidents occur, including “Road Geometry,” “Speed Limitation,” “Road Surface Type,” “Road Type,” and “Road Surface Condition.”
- (2)
- Crash characteristics: Ten variables are collected to indicate the details of ROR accidents, including “Time of Day,” “Day Type,” “Accident Type,” “Types of ROR Accidents,” “Number of Vehicles involved,” “Number of Persons involved,” “Motorcycle/Bicycle Involved,” “Trucks Involved,” “Pedestrian Involved,” and “Vehicle Used for Years.”
- (3)
- Human characteristics: Three variables are collected to describe the details of drivers, including “Driver Sex,” “Driver Age,” and “Helmet/Belt Worn.”
- (4)
- Environmental information: Four variables are collected to indicate the environmental conditions when ROR accidents occur, including “Light Condition,” “Traffic Control,” “Atmospheric Condition,” and “Urbanization Class.”
4. Results
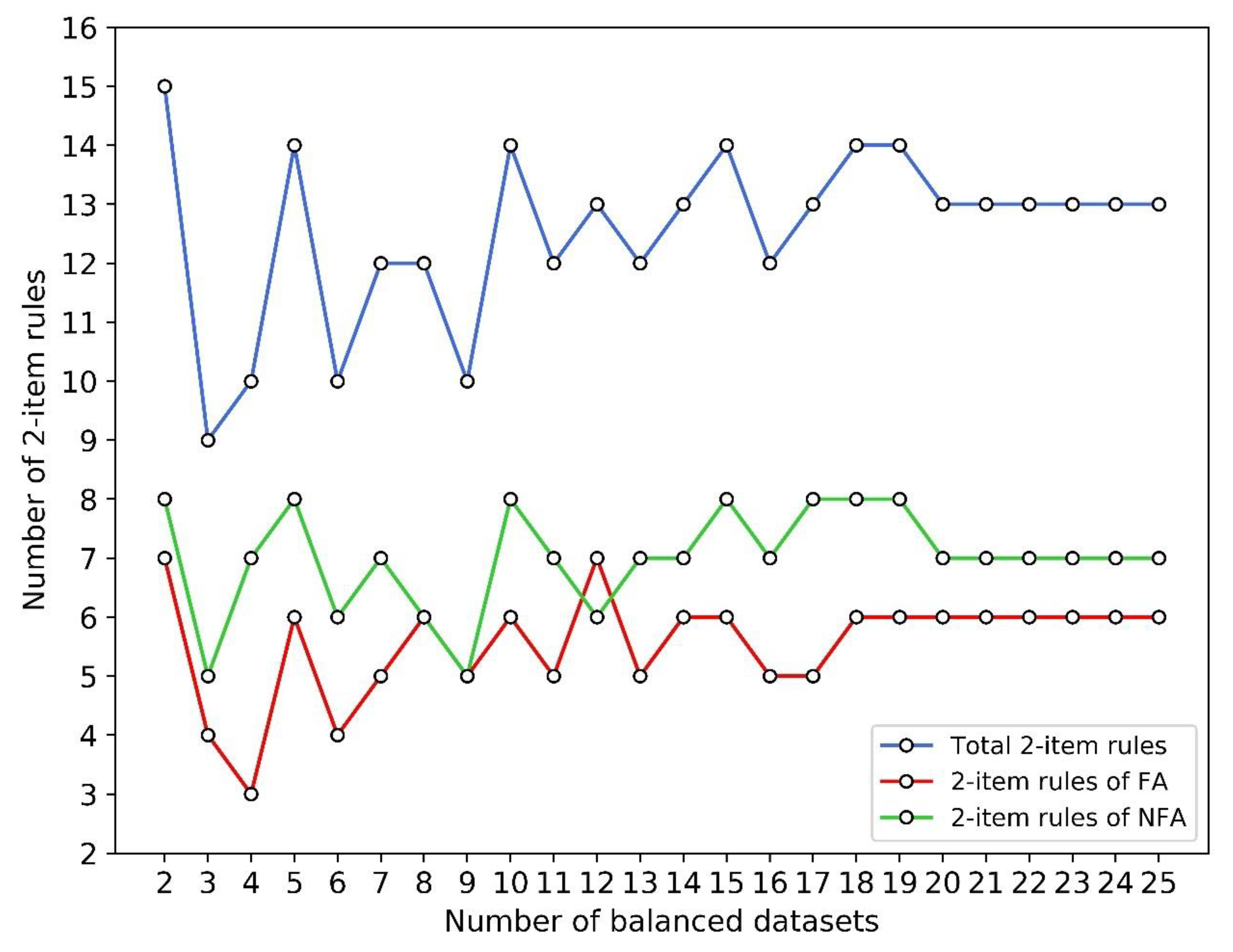
4.1. Parameter Optimization: The Number of Balanced Datasets
4.2. Analysis of Two-Item Rules
4.3. Analysis of Three-Item Rules
4.3.1. An Overall Analysis of Three-Item Rules
4.3.2. Comparison between Two-Item and Three-Item Rules
5. Discussions
5.1. GIS Analysis
5.1.1. GIS Analysis of Overall Density Distribution
5.1.2. GIS Analysis of ROR Accidents Related to Individual Key Factors
- ‘Helmet/Belt Worn = No’: This factor has the highest confidence and lift level among all the factors of FA. This is because the use of helmets and seat belts can significantly reduce impact force to victims in traffic accidents. Without this protection, victims are more likely to get a fatal injury. Effective measures for hot spots in Figure 17A: (1) Traffic authority needs to enforce the use of helmet and seat belt (e.g., policy publicity, violation penalty); (2) drivers and occupants should consciously use helmets and seat belts for safety consideration.
- ‘Light Condition = Dark street with no lights’: Dark condition reduces drivers’ visibility range. Drivers in darkness are more likely to encounter unexpected situations and need more reaction time to control vehicles. These reasons increase the impact force on victims and also increase the likelihood of fatalities in ROR accidents. Effective measures for hot spots in Figure 17B: (1) Traffic authority should install more streetlights for drivers in the case of sufficient funds; (2) drivers should drive more cautiously in dark conditions.
- ‘Types of ROR Accidents = 8 (Off Left Bend into Object)’: This type of accident is left-curve driving that collides with fixed objects, which is shown in Figure 4. Curve driving reduced drivers’ visibility and maneuverability to control vehicles [51]. Besides, drivers sit on the right side of vehicles in Victoria. This obstructs drivers’ visibility when driving on a left curve. Also, vehicles colliding into fixed objects yield huge impact force to victims. These reasons increase the likelihood of fatalities in ROR accidents. Effective measures for hot spots in Figure 17C: (1) Traffic authority should install more signboards and warning lights on curved roads; (2) more rumble strips and monitoring cameras need to be installed on curved roads to control vehicle speeds; (3) drivers should drive more carefully on left-curve roads.
- ‘Speed Limit = 100–110’: The reason is that drivers drive very fast on roads with a high-speed limit. They have less time to control vehicles and therefore have a huge impact force in an emergency. This increases the likelihood of fatalities in ROR accidents. Effective measures for hot spots in Figure 17D: (1) Traffic authority should reduce the speed limit of some roads with high frequency of FA; (2) drivers should drive more cautiously on high-speed roads.
- ‘Time of Day = Late in night (23 p.m. or 0–4 a.m.)’: Drivers drive very fast due to low traffic flow late at night. Collisions with high speed impose huge impact force on victims. Besides, tiredness and poor visibility also increase the possibility of fatalities in ROR accidents. Effective measures for hot spots in Figure 17E: (1) Traffic authority should install more signboards and warning lights to remind drivers to be vigilant late at night; (2) drivers try not to drive late at night. If they must drive, they should beware of driving fatigue.
- ‘Driver Age >= 65’: The reason may be that old drivers need more reaction time in an emergency. Besides, their physical conditions increase the probability of fatalities in ROR accidents. Effective measures for hot spots in Figure 17F: (1) Traffic authority may consider setting an upper age limit for drivers; (2) old drivers should drive slowly and keep particularly cautious on roads.
5.2. The Necessity to Balance Data Distribution
5.3. Comparison with Traditional Data-Balancing Methods
- (1)
- Unlike traditional data-balancing methods with one randomly sampling dataset, the proposed methodology transfers an imbalanced dataset into multiple balanced datasets. If enough balanced datasets are provided, the randomness caused by sampling methods can be avoided in the proposed methodology. Therefore, the proposed methodology can improve the robustness and reliability of the results on imbalanced datasets.
- (2)
- Two kinds of criteria are adopted to select ensemble rules: The mean values (, and ) and the lower limit of 95% (, and ). The mean values can reflect the central tendency of the parameters (i.e., support, confidence, and lift) of ensemble rules. The lower limit of 95% can ensure that the true values of parameters (i.e., support, confidence, and lift) of ensemble rules are larger than the specified level. These criteria can ensure the quality of the ensemble rules, which can improve the reliability of the results from imbalanced datasets.
6. Conclusions
- (1)
- Six individual key factors are identified to be closely associated with fatal ROR accidents, including ‘Helmet/Belt Worn = No,’ ‘Light Condition = Dark street with no lights,’ ‘Types of Off-path Accidents = 8,’ ‘Speed Limit = 100/110,’ ‘Time of Day = Late in night,’ and ‘Driver Age >= 65.’ Hot spots of ROR accidents related to these factors are presented by GIS technology. Effective measures are accordingly proposed to reduce ROR accidents in hot spots and improve road safety.
- (2)
- The results indicate that three-item rules have higher confidence and lift levels than two-item rules, but lower support level. The higher confidence and lift levels imply that factors acting interactively increase the likelihood of FA or NFA.
- (3)
- ARM method tends to extract enormous meaningless rules of NFA with few valuable rules of FA on imbalanced datasets. Therefore, it is necessary to apply a data-balancing method on imbalanced datasets to extract meaningful rules associated with accident severity.
- (4)
- Compared with traditional data-balancing methods, the proposed framework has been validated to provide more robust and reliable results on imbalanced datasets. It is worth noting that the proposed framework can identify more factors of FA; therefore, more effective measures can be proposed to reduce fatalities and improve road safety.
- (5)
- Imbalance problems exist in various fields, for example, traffic accidents, credit scoring, machinery fault diagnosis, occupational accidents in construction industry, and diagnosis of rare diseases [24,52,53,54,55,56]. The proposed framework can be applied to address the imbalance problem in various applications and improve the analysis performance of the results.
Author Contributions
Funding
Conflicts of Interest
References
- Hong, J.; Tamakloe, R.; Park, D. A Comprehensive Analysis of Multi-Vehicle Crashes on Expressways: A Double Hurdle Approach. Sustainability 2019, 11, 2782. [Google Scholar] [CrossRef]
- Casado-Sanz, N.; Guirao, B.; Attard, M. Analysis of the Risk Factors Affecting the Severity of Traffic Accidents on Spanish Crosstown Roads: The Driver’s Perspective. Sustainability 2020, 12, 2237. [Google Scholar] [CrossRef]
- Jou, R.-C.; Chen, T.-Y. External Costs to Parties Involved in Highway Traffic Accidents: The Perspective of Highway Users. Sustainability 2015, 7, 7310–7332. [Google Scholar] [CrossRef]
- Wang, J.; Lu, H.; Sun, Z.; Wang, T.; Wang, K. Investigating the Impact of Various Risk Factors on Victims of Traffic Accidents. Sustainability 2020, 12, 3934. [Google Scholar] [CrossRef]
- WHO. Global Status Report on Road Safety 2018 (World Health Organization (WHO). 2018. Available online: http://www.who.int/violence_injury_prevention/road_safety_status/2018/en/ (accessed on 13 June 2020).
- Al-Bdairi, N.S.S.; Hernandez, S. An empirical analysis of run-off-road injury severity crashes involving large trucks. Accid. Anal. Prev. 2017, 102, 93–100. [Google Scholar] [CrossRef]
- Dirnbach, I.; Kubjatko, T.; Kolla, E.; Ondruš, J.; Šarić, Ž. Methodology Designed to Evaluate Accidents at Intersection Crossings with Respect to Forensic Purposes and Transport Sustainability. Sustainability 2020, 12, 1972. [Google Scholar] [CrossRef]
- Griselda, L.; Juan, D.O.; Joaquín, A. Using Decision Trees to Extract Decision Rules from Police Reports on Road Accidents. Procedia—Soc. Behav. Sci. 2012, 53, 106–114. [Google Scholar] [CrossRef]
- Eboli, L.; Forciniti, C. The Severity of Traffic Crashes in Italy: An Explorative Analysis among Different Driving Circumstances. Sustainability 2020, 12, 856. [Google Scholar] [CrossRef]
- Gong, L.; Fan, W. (David). Modeling single-vehicle run-off-road crash severity in rural areas: Accounting for unobserved heterogeneity and age difference. Accid. Anal. Prev. 2017, 101, 124–134. [Google Scholar] [CrossRef]
- Cheng, J.C.P.; Ma, L.J. A data-driven study of important climate factors on the achievement of LEED-EB credits. Build. Environ. 2015, 90, 232–244. [Google Scholar] [CrossRef]
- Cheng, J.C.P.; Ma, L.J. A non-linear case-based reasoning approach for retrieval of similar cases and selection of target credits in LEED projects. Build. Environ. 2015, 93, 349–361. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, J.C.P. Data-driven study on the achievement of LEED credits using percentage of average score and association rule analysis. Build. Environ. 2016, 98, 121–132. [Google Scholar] [CrossRef]
- Lee, S.; Cha, Y.; Han, S.; Hyun, C. Application of Association Rule Mining and Social Network Analysis for Understanding Causality of Construction Defects. Sustainability 2019, 11, 618. [Google Scholar] [CrossRef]
- Arreeras, T.; Arimura, M.; Asada, T.; Arreeras, S. Association Rule Mining Tourist-Attractive Destinations for the Sustainable Development of a Large Tourism Area in Hokkaido Using Wi-Fi Tracking Data. Sustainability 2019, 11, 3967. [Google Scholar] [CrossRef]
- Park, J.; Cha, Y.; Al Jassmi, H.; Han, S.; Hyun, C. Identification of Defect Generation Rules among Defects in Construction Projects Using Association Rule Mining. Sustainability 2020, 12, 3875. [Google Scholar] [CrossRef]
- Ma, J.; Ding, Y.; Cheng, J.C.P.; Jiang, F.; Wan, Z. A temporal-spatial interpolation and extrapolation method based on geographic Long Short-Term Memory neural network for PM2.5. J. Clean. Prod. 2019, 237, 117729. [Google Scholar] [CrossRef]
- Lee, H.K.; Kim, S.B. An overlap-sensitive margin classifier for imbalanced and overlapping data. Expert Syst. Appl. 2018, 98, 72–83. [Google Scholar] [CrossRef]
- Ma, J.; Ding, Y.; Cheng, J.C.P.; Jiang, F.; Xu, Z. Soft detection of 5-day BOD with sparse matrix in city harbor water using deep learning techniques. Water Res. 2020, 170, 115350. [Google Scholar] [CrossRef]
- Taamneh, M. Investigating the role of socio-economic factors in comprehension of traffic signs using decision tree algorithm. J. Saf. Res. 2018. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, J.; Li, W.; Gu, T.; Shi, W. Exploring traffic congestion correlation from multiple data sources. Pervasive Mob. Comput. 2017, 41, 470–483. [Google Scholar] [CrossRef]
- Thabtah, F. A review of associative classification mining. Knowl. Eng. Rev. 2007, 22, 37–65. [Google Scholar] [CrossRef]
- Liu, B.; Ma, Y.; Wong, C.-K. Classification Using Association Rules: Weaknesses and Enhancements. In Data Mining for Scientific and Engineering Applications; Massive Computing; Springer: Boston, MA, USA, 2001; pp. 591–605. ISBN 978-1-4020-0114-7. [Google Scholar]
- Mujalli, R.O.; López, G.; Garach, L. Bayes classifiers for imbalanced traffic accidents datasets. Accid. Anal. Prev. 2016, 88, 37–51. [Google Scholar] [CrossRef] [PubMed]
- Thammasiri, D.; Delen, D.; Meesad, P.; Kasap, N. A critical assessment of imbalanced class distribution problem: The case of predicting freshmen student attrition. Expert Syst. Appl. 2014, 41, 321–330. [Google Scholar] [CrossRef]
- Longadge, R.; Dongre, S.S.; Malik, L. Class Imbalance Problem in Data Mining: Review. Int. J. Comput. Sci. Netw. 2013, 2, 6. [Google Scholar]
- Ma, J.; Ding, Y.; Cheng, J.C.P.; Tan, Y.; Gan, V.J.L.; Zhang, J. Analyzing the Leading Causes of Traffic Fatalities Using XGBoost and Grid-Based Analysis: A City Management Perspective. IEEE Access 2019, 7, 148059–148072. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, J.C.P. Estimation of the building energy use intensity in the urban scale by integrating GIS and big data technology. Appl. Energy 2016, 183, 182–192. [Google Scholar] [CrossRef]
- Ma, J.; Ding, Y.; Cheng, J.C.P.; Jiang, F.; Tan, Y.; Gan, V.J.L.; Wan, Z. Identification of high impact factors of air quality on a national scale using big data and machine learning techniques. J. Clean. Prod. 2020, 244, 118955. [Google Scholar] [CrossRef]
- Macharia, D.; Kaijage, E.; Kindberg, L.; Koech, G.; Ndungu, L.; Wahome, A.; Mugo, R. Mapping Climate Vulnerability of River Basin Communities in Tanzania to Inform Resilience Interventions. Sustainability 2020, 12, 4102. [Google Scholar] [CrossRef]
- Wang, S.W.; Gebru, B.M.; Lamchin, M.; Kayastha, R.B.; Lee, W.-K. Land Use and Land Cover Change Detection and Prediction in the Kathmandu District of Nepal Using Remote Sensing and GIS. Sustainability 2020, 12, 3925. [Google Scholar] [CrossRef]
- Li, K.; Wang, R.; Lei, H.; Zhang, T.; Liu, Y.; Zheng, X. Interval prediction of solar power using an Improved Bootstrap method. Sol. Energy 2018, 159, 97–112. [Google Scholar] [CrossRef]
- Matsuyama, T. An application of bootstrap method for analysis of particle size distribution. Adv. Powder Technol. 2018, 29, 1404–1408. [Google Scholar] [CrossRef]
- Beyaztas, U.; Bickici Arikan, B.; Beyaztas, B.H.; Kahya, E. Construction of prediction intervals for Palmer Drought Severity Index using bootstrap. J. Hydrol. 2018, 559, 461–470. [Google Scholar] [CrossRef]
- Noh, B.; Son, J.; Park, H.; Chang, S. In-Depth Analysis of Energy Efficiency Related Factors in Commercial Buildings Using Data Cube and Association Rule Mining. Sustainability 2017, 9, 2119. [Google Scholar] [CrossRef]
- Li, Y.; Yamamoto, T.; Zhang, G. Understanding factors associated with misclassification of fatigue-related accidents in police record. J. Saf. Res. 2018, 64, 155–162. [Google Scholar] [CrossRef] [PubMed]
- Montella, A. Identifying crash contributory factors at urban roundabouts and using association rules to explore their relationships to different crash types. Accid. Anal. Prev. 2011, 43, 1451–1463. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Bao, J.; Wang, C.; Liu, P. Association rule analysis of factors contributing to extraordinarily severe traffic crashes in China. J. Saf. Res. 2018, 67, 65–75. [Google Scholar] [CrossRef]
- Verma, A.; Khan, S.D.; Maiti, J.; Krishna, O.B. Identifying patterns of safety related incidents in a steel plant using association rule mining of incident investigation reports. Saf. Sci. 2014, 70, 89–98. [Google Scholar] [CrossRef]
- Pai, C.-W.; Saleh, W. Modelling motorcyclist injury severity by various crash types at T-junctions in the UK. Saf. Sci. 2008, 46, 1234–1247. [Google Scholar] [CrossRef]
- Abrari Vajari, M.; Aghabayk, K.; Sadeghian, M.; Shiwakoti, N. A multinomial logit model of motorcycle crash severity at Australian intersections. J. Saf. Res. 2020, 73, 17–24. [Google Scholar] [CrossRef]
- Yannis, G.; Laiou, A.; Papantoniou, P.; Christoforou, C. Impact of texting on young drivers’ behavior and safety on urban and rural roads through a simulation experiment. J. Saf. Res. 2014, 49, 25.e1–31. [Google Scholar] [CrossRef]
- Waseem, M.; Ahmed, A.; Saeed, T.U. Factors affecting motorcyclists’ injury severities: An empirical assessment using random parameters logit model with heterogeneity in means and variances. Accid. Anal. Prev. 2019, 123, 12–19. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.S.; Kim, H.J.; Son, B. Factors associated with automobile accidents and survival. Accid. Anal. Prev. 2006, 38, 981–987. [Google Scholar] [CrossRef] [PubMed]
- Morgan, A.; Mannering, F.L. The effects of road-surface conditions, age, and gender on driver-injury severities. Accid. Anal. Prev. 2011, 43, 1852–1863. [Google Scholar] [CrossRef] [PubMed]
- Yau, K.K.W.; Lo, H.P.; Fung, S.H.H. Multiple-vehicle traffic accidents in Hong Kong. Accid. Anal. Prev. 2006, 38, 1157–1161. [Google Scholar] [CrossRef]
- Weng, J.; Zhu, J.-Z.; Yan, X.; Liu, Z. Investigation of work zone crash casualty patterns using association rules. Accid. Anal. Prev. 2016, 92, 43–52. [Google Scholar] [CrossRef]
- Kumar, S.; Toshniwal, D. A data mining approach to characterize road accident locations. J. Mod. Transp. 2016, 24, 62–72. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Chung, J.-H.; Son, B. Analysis of traffic accident size for Korean highway using structural equation models. Accid. Anal. Prev. 2008, 40, 1955–1963. [Google Scholar] [CrossRef]
- Pande, A.; Abdel-Aty, M. Market basket analysis of crash data from large jurisdictions and its potential as a decision support tool. Saf. Sci. 2009, 47, 145–154. [Google Scholar] [CrossRef]
- Kim, J.-K.; Kim, S.; Ulfarsson, G.F.; Porrello, L.A. Bicyclist injury severities in bicycle–motor vehicle accidents. Accid. Anal. Prev. 2007, 39, 238–251. [Google Scholar] [CrossRef]
- Brown, I.; Mues, C. An experimental comparison of classification algorithms for imbalanced credit scoring data sets. Expert Syst. Appl. 2012, 39, 3446–3453. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, D.; Han, T.; Wang, N.; Yang, W.; Yang, Y. Rotating Machinery Fault Diagnosis for Imbalanced Data Based on Fast Clustering Algorithm and Support Vector Machine. J. Sens. 2017, 2017, 8092691. [Google Scholar] [CrossRef]
- Cheng, C.-W.; Lin, C.-C.; Leu, S.-S. Use of association rules to explore cause–effect relationships in occupational accidents in the Taiwan construction industry. Saf. Sci. 2010, 48, 436–444. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, X. A New Over-Sampling Approach: Random-SMOTE for Learning from Imbalanced Data Sets. In Proceedings of the Knowledge Science, Engineering and Management, Irvine, CA, USA, 12–14 December 2011; Xiong, H., Lee, W.B., Eds.; Springer: Berlin, Heidelberg, Germany, 2011; pp. 343–352. [Google Scholar]
- Jiang, F.; Yuen, K.K.R.; Lee, E.W.M. A long short-term memory-based framework for crash detection on freeways with traffic data of different temporal resolutions. Accid. Anal. Prev. 2020, 141, 105520. [Google Scholar] [CrossRef] [PubMed]

















| No. | Variable | Categories | Number of Cases | Severity | |
|---|---|---|---|---|---|
| FA (%) | NFA (%) | ||||
| (1) Road characteristics | |||||
| 1 | Road Geometry | Cross intersection | 1924 | 1.72 | 98.28 |
| T’ intersection | 3961 | 2.73 | 97.27 | ||
| Y’ intersection | 77 | 1.30 | 98.70 | ||
| Multiple intersections | 350 | 2.57 | 97.43 | ||
| Not at intersection | 25,542 | 4.20 | 95.80 | ||
| Others | 86 | 1.16 | 98.84 | ||
| 2 | Speed Limitation | 30–50 | 4571 | 1.73 | 98.27 |
| 60–75 | 8294 | 2.65 | 97.35 | ||
| 80–90 | 4852 | 3.28 | 96.72 | ||
| 100–110 | 13,100 | 5.79 | 94.21 | ||
| Unknown | 1123 | 0.62 | 99.38 | ||
| 3 | Road Surface Type | Paved | 28,081 | 4.02 | 95.98 |
| Unpaved | 3747 | 2.54 | 97.46 | ||
| Unknown | 112 | 0.89 | 99.11 | ||
| 4 | Road Type | Highways | 6867 | 4.81 | 95.19 |
| Forest roads | 46 | 4.35 | 95.65 | ||
| Tourist roads | 992 | 4.74 | 95.26 | ||
| Main roads | 9089 | 3.91 | 96.09 | ||
| Freeway ramps | 408 | 1.72 | 98.28 | ||
| Unclassified roads | 14,538 | 3.32 | 96.68 | ||
| 5 | Road Surface Condition | Dry | 23,325 | 4.21 | 95.79 |
| Not dry | 7902 | 2.75 | 97.25 | ||
| Unknown | 713 | 3.65 | 96.35 | ||
| (2) Crash characteristics | |||||
| 6 | Time of Day | Peak time | 6278 | 3.33 | 96.67 |
| Day time off-peak | 16,179 | 3.28 | 96.72 | ||
| Night time off-peak | 3619 | 4.28 | 95.72 | ||
| Late in night (23 p.m. or 0–4 a.m.) | 5864 | 5.61 | 94.39 | ||
| 7 | Day Type | Weekend | 11,035 | 4.30 | 95.70 |
| Weekday | 30,905 | 2.43 | 97.57 | ||
| 8 | Accident Type | Collision with vehicle | 519 | 1.35 | 98.65 |
| Struck pedestrian | 0 | -- | -- | ||
| Struck animal | 7 | 0.00 | 100 | ||
| Collision with a fixed object | 25,001 | 4.39 | 95.61 | ||
| Collision with some other object | 174 | 2.87 | 97.13 | ||
| Vehicle overturned (no collision) | 4139 | 2.46 | 97.54 | ||
| Fall from or in moving vehicle | 10 | 10.00 | 90.00 | ||
| No collision and no object struck | 2086 | 0.58 | 99.42 | ||
| Other accident | 4 | 0.00 | 100 | ||
| 9 | Types of ROR Accidents | 1 Off carriageway to Left | 2281 | 1.62 | 98.38 |
| 2 Left off carriageway into object | 10,594 | 3.40 | 96.60 | ||
| 3 Off carriageway to right | 1292 | 2.24 | 97.76 | ||
| 4 Right off carriageway into object | 7676 | 4.46 | 95.54 | ||
| 5 Off carriageway right bend | 1662 | 1.68 | 98.32 | ||
| 6 Off right bend into object | 4348 | 5.20 | 94.80 | ||
| 7 Off carriageway left bend | 993 | 2.01 | 97.99 | ||
| 8 Off left bend into object | 3094 | 5.88 | 94.12 | ||
| 10 | Number of Vehicles involved | 1 | 29,609 | 3.89 | 96.11 |
| 2 | 1974 | 2.99 | 97.01 | ||
| >=3 | 357 | 3.36 | 96.64 | ||
| 11 | Number of Persons involved | 1 | 21,719 | 3.61 | 96.39 |
| 2 | 6368 | 3.85 | 96.15 | ||
| >=3 | 3853 | 5.04 | 94.96 | ||
| 12 | Motorcycle/Bicycle Involved | Yes | 4373 | 3.52 | 96.48 |
| No | 27,567 | 3.88 | 96.12 | ||
| 13 | Trucks Involved | Yes | 1301 | 4.30 | 95.70 |
| No | 30,639 | 3.81 | 96.19 | ||
| 14 | Pedestrian Involved | Yes | 146 | 3.42 | 96.58 |
| No | 31,794 | 3.83 | 96.17 | ||
| 15 | Vehicle Used for Years | >=5 | 25,116 | 3.88 | 96.12 |
| <5 | 6824 | 3.66 | 96.34 | ||
| (3) Human characteristics | |||||
| 16 | Driver Sex | Male | 21,677 | 4.46 | 95.54 |
| Not male | 10,263 | 2.51 | 97.49 | ||
| 17 | Driver Age | >=65 | 2460 | 5.53 | 94.47 |
| <65 | 29,480 | 3.69 | 96.31 | ||
| 18 | Helmet/Belt Worn | Yes | 29,564 | 3.14 | 96.86 |
| No | 2376 | 12.50 | 87.50 | ||
| (4) Environmental information | |||||
| 19 | Light Condition | Dark street with no lights | 5230 | 6.37 | 93.63 |
| Dark street with lights on | 5838 | 3.55 | 96.45 | ||
| Day light | 20,397 | 3.26 | 96.74 | ||
| Unknown | 475 | 4.00 | 96.00 | ||
| 20 | Traffic Control | Yes | 3241 | 2.07 | 97.93 |
| No | 28,699 | 4.03 | 95.97 | ||
| 21 | Atmospheric Condition | Clear | 24,840 | 4.03 | 95.97 |
| Not clear | 5961 | 3.07 | 96.93 | ||
| Unknown | 1139 | 3.42 | 96.58 | ||
| 22 | Urbanization Class | Large provincial cities | 1157 | 2.25 | 97.75 |
| Melbourne urban | 11,881 | 2.42 | 97.58 | ||
| Melbourne CBD | 53 | 0.00 | 100 | ||
| Rural Victoria | 15,910 | 5.15 | 94.85 | ||
| Small cities | 1285 | 2.80 | 97.20 | ||
| Small towns | 436 | 4.36 | 95.64 | ||
| Towns | 967 | 3.62 | 96.38 | ||
| Unknown | 251 | 0.00 | 100 | ||
| No. | Antecedents | Consequents | Support | Confidence | Lift | |||
|---|---|---|---|---|---|---|---|---|
| Mean % | 95% CI | Mean % | 95% CI | Mean % | 95% CI | |||
| #1 | Helmet/Belt Worn = No | FA | 12.13 | -- | 78.41 | (77.70,79.11) | 1.57 | (1.55,1.58) |
| #2 | Light Condition = Dark street with no lights | FA | 13.60 | -- | 63.77 | (63.25,64.29) | 1.28 | (1.27, 1.29) |
| #3 | Types of ROR Accidents = 8 | FA | 7.43 | -- | 61.81 | (60.88,62.74) | 1.24 | (1.22,1.25) |
| #4 | Speed Limit = 100/110 | FA | 31.00 | -- | 61.05 | (60.67,61.43) | 1.22 | (1.21,1.23) |
| #5 | Time of Day = Late in night (23 p.m. or 0–4 a.m.) | FA | 13.44 | -- | 59.57 | (58.87,60.27) | 1.19 | (1.18,1.21) |
| #6 | Driver Age >=65 | FA | 5.56 | -- | 59.51 | (58.37,60.64) | 1.19 | (1.17,1.21) |
| #7 | Speed Limit = 30/40/50 | NFA | 7.28 | (7.08, 7.48) | 69.22 | (68.63,69.8) | 1.38 | (1.37,1.40) |
| #8 | Traffic Control = Yes | NFA | 5.26 | (5.12, 5.41) | 65.72 | (65.11,66.32) | 1.31 | (1.30,1.33) |
| #9 | Urbanization Class = Melbourne urban | NFA | 19.00 | (18.72,19.28) | 61.73 | (61.38,62.09) | 1.23 | (1.23,1.24) |
| #10 | ACCIDENT TYPE = Vehicle overturned (no collision) | NFA | 6.58 | (6.41, 6.75) | 61.16 | (60.55,61.77) | 1.22 | (1.21,1.24) |
| #11 | Driver Sex = Not male | NFA | 16.37 | (16.10,16.65) | 60.81 | (60.41,61.21) | 1.22 | (1.21,1.22) |
| #12 | Road Surface Type = Unpaved | NFA | 5.94 | (5.76, 6.11) | 60.39 | (59.68,61.10) | 1.21 | (1.19,1.22) |
| #13 | Speed Limitation = 60/75 | NFA | 13.36 | (13.16,13.56) | 59.76 | (59.40,60.13) | 1.20 | (1.19,1.21) |
| No. | Antecedents | Consequents | Support | Confidence | Lift | |||
|---|---|---|---|---|---|---|---|---|
| Mean % | 95% CI | Mean % | 95% CI | Mean % | 95% CI | |||
| *1 | Helmet/Belt Worn = No and Speed Limit = 100–110 | FA | 7.11 | -- | 86.80 | (85.69,87.90) | 1.74 | (1.71,1.76) |
| *2 | Light Condition = Dark street with no lights and Speed Limit = 100–110 | FA | 10.09 | -- | 68.09 | (67.43,68.76) | 1.36 | (1.35,1.38) |
| *3 | Types of Off-path Accidents = 8 and Driver Sex = Male | FA | 5.96 | -- | 64.24 | (63.46,65.03) | 1.28 | (1.27,1.30) |
| *4 | Speed Limit = 100–110 and Helmet/Belt Worn = No | FA | 7.11 | -- | 86.80 | (85.69,87.90) | 1.74 | (1.71,1.76) |
| *5 | Time of Day = Late in Night and Urbanization Class = Rural Victoria | FA | 6.82 | -- | 69.75 | (68.92,70.58) | 1.40 | (1.38,1.41) |
| *6 | Driver Age >=65 and Accident Type = Collision with a fixed object | FA | 5.11 | -- | 62.81 | (61.86,63.76) | 1.26 | (1.24,1.28) |
| *7 | Speed Limit = 30/40/50 and Helmet/Belt Worn = Yes | NFA | 6.57 | (6.40,6.74) | 75.50 | (75.01,75.99) | 1.51 | (1.50,1.52) |
| *8 | Traffic Control = Yes and Pedestrian Involved = No | NFA | 5.17 | (5.01,5.33) | 65.64 | (64.95,66.33) | 1.31 | (1.30,1.33) |
| *9 | Urbanization Class = Melbourne Urban and Driver Sex = Not Male | NFA | 5.66 | (5.50,5.81) | 80.22 | (79.78,80.66) | 1.60 | (1.59,1.61) |
| *10 | Accident Type = Vehicle overturned (no collision) and Helmet/Belt Worn = Yes | NFA | 6.17 | (5.96,6.37) | 72.82 | (72.12,73.53) | 1.46 | (1.44,1.47) |
| *11 | Driver Sex = Not Male and Urbanization Class = Melbourne Urban | NFA | 5.66 | (5.50,5.81) | 80.22 | (79.78,80.66) | 1.60 | (1.59,1.61) |
| *12 | Road Surface Type = Unpaved and Helmet/Belt Worn = Yes | NFA | 5.57 | (5.38,5.75) | 70.03 | (69.33,70.74) | 1.40 | (1.39,1.41) |
| *13 | Speed Limitation = 60–75 and Light Condition = Day light | NFA | 7.17 | (6.95,7.40) | 71.11 | (70.46,71.77) | 1.42 | (1.41,1.44) |
| Dataset | Support | Confidence | Lift | Factors (FA) | Factors (NFA) | Total Factors |
|---|---|---|---|---|---|---|
| Balanced dataset with the proposed methodology | 5.00% | 59% | 1.15 | 6 | 7 | 13 |
| Original imbalanced dataset (FA: NFA = 4%: 96%) | 5.00% | 59% | 1.15 | 0 | 0 | 0 |
| 5.00% | 10% | 1 | 0 | 29 | 29 | |
| 5.00% | 5% | 1 | 0 | 29 | 29 | |
| 5.00% | 1% | 1 | 0 | 29 | 29 | |
| 1.00% | 10% | 1 | 0 | 41 | 41 | |
| 1.00% | 5% | 1 | 4 | 41 | 45 | |
| 1.00% | 1% | 1 | 19 | 41 | 60 | |
| 0.50% | 10% | 1 | 1 | 43 | 44 | |
| 0.50% | 5% | 1 | 8 | 43 | 51 | |
| 0.50% | 1% | 1 | 23 | 43 | 66 | |
| 0.10% | 10% | 1 | 1 | 48 | 49 | |
| 0.10% | 5% | 1 | 9 | 48 | 57 | |
| 0.10% | 1% | 1 | 28 | 48 | 76 |
| Data-Balancing Methods | Tests | Number of Balanced Datasets in Each Test | Number of Total Accidents in Each Test | Number of FA in Each Test | Number of NFA in Each Test |
|---|---|---|---|---|---|
| Original dataset | / | / | 31,940 | 1224 | 30,716 |
| Under-sampling | 10 | 1 | 2448 | 1224 | 1224 |
| Over-sampling | 10 | 1 | 61,432 | 30,716 | 30,716 |
| Mix-sampling | 10 | 1 | 24,480 | 12,240 | 12,240 |
| The proposed methodology | 10 | 25 | 31,824 | 1224 | 30,600 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, F.; Yuen, K.K.R.; Lee, E.W.M.; Ma, J. Analysis of Run-Off-Road Accidents by Association Rule Mining and Geographic Information System Techniques on Imbalanced Datasets. Sustainability 2020, 12, 4882. https://doi.org/10.3390/su12124882
Jiang F, Yuen KKR, Lee EWM, Ma J. Analysis of Run-Off-Road Accidents by Association Rule Mining and Geographic Information System Techniques on Imbalanced Datasets. Sustainability. 2020; 12(12):4882. https://doi.org/10.3390/su12124882
Chicago/Turabian StyleJiang, Feifeng, Kwok Kit Richard Yuen, Eric Wai Ming Lee, and Jun Ma. 2020. "Analysis of Run-Off-Road Accidents by Association Rule Mining and Geographic Information System Techniques on Imbalanced Datasets" Sustainability 12, no. 12: 4882. https://doi.org/10.3390/su12124882
APA StyleJiang, F., Yuen, K. K. R., Lee, E. W. M., & Ma, J. (2020). Analysis of Run-Off-Road Accidents by Association Rule Mining and Geographic Information System Techniques on Imbalanced Datasets. Sustainability, 12(12), 4882. https://doi.org/10.3390/su12124882






