Development and Predictive Validity of the Computational Thinking Disposition Questionnaire

Abstract

Providing humans with quality education is regarded as one of the core pillars supporting the sustainable development of the world. The idea of computational thinking (CT) brings an innovative inspiration for people to adapt to our intelligent, changing society. It has been globally viewed as crucial that 21st-century learners should acquire the necessary skills to solve real-world problems effectively and efficiently. Recent studies have revealed that the nurture of CT should not only focus on thinking skills, but also on dispositions. Fostering students’ CT dispositions requires the cultivation of their confidence and persistence in dealing with complex problems. However, most of the existing measurement methods related to CT pivot on gauging thinking skills rather than dispositions. The framework of the CT disposition measurement model proposed in this paper was developed based on three theoretical features of thinking dispositions: Inclination, capability, and sensitivity. A two-phase analysis was conducted in this study. With the participation of 640 Grade 5 students in Hong Kong, a three-dimensional construct of the measurement model was extracted via exploratory factor analysis (16 items). The measurement model was further validated with another group of 904 Grade 5 students by confirmative factor analysis and structural equation modeling. The results align with the theoretical foundation of thinking dispositions. In addition, a CT knowledge test was introduced to explore the influences between students’ CT dispositions and their CT knowledge understanding.

1. Introduction

The 2019 Sustainable Development Goals (SDGs) [1] reports highlighted increasing inequality among and within countries, something that requires urgent attention. Regarding Goal 4 of the SDGs, all individuals should have the same opportunities to develop their skills and knowledge [2]. However, this increasing inequality in obtaining a quality education will become more challenging in the new Intelligence Era. In the study of [3], it is pointed out that knowledge capital will be the tipping point of future economic development. The focus of new technology is on creating and developing knowledge. The biggest difference between the new era and the agricultural and industrial society of old is that the former is no longer dominated by physical and mechanical energy; rather, mainly by intelligence. Those 265 million children currently out of school (22% of them are of primary school age [1]) lack basic skills not only including reading and computing, but also constructing knowledge, which is important in adapting to a changing and intelligent world. Computational thinking (CT) brings an innovative solution and has been globally viewed as a crucial skill that 21st-century learners should acquire to solve real-world problems effectively and efficiently [4]. Over the past few decades, research in Computational Thinking (CT) has been burgeoning [5]. CT represents a way of thinking that is in line with many 21st century skills, such as problem-solving, creativity, and critical thinking [6]. More importantly, CT is a form of thinking that is crucial for a society with sustained economic and technological developments closely intertwined with the general wellbeing of the society. In today’s world, where most problems and emerging issues are studied with data sciences and resolved through computer-based solutions, cultivating the young with CT has been recognized as an important goal by many education ministries.

In education, CT promotes students’ cognitive understanding and problem-solving capabilities in a wide range of learning contexts [7]. CT education is popularly embedded in interdisciplinary science, technology, engineering, and mathematics (STEM) projects in K–12 education [8,9]. In recent years, CT has been introduced to K–12 students in 13 European countries, with an aim of nurturing students’ problem-solving skills and creativity in a rapidly changing world [10]. In Hong Kong and China, CT has been incorporated as part of the STEM curriculum in schools [11].

While some researchers view CT simply as an additional form of thinking skills needed in today’s society [12], the complex nature of CT prompts others to dig deeper, suggesting an extended understanding of CT as disposition [13]. Nurturing students to be self-driven problem-solvers in the digital world and equipping them with CT skills and knowledge may not be enough. CT uses knowledge of coding to solve problems; however, it does not account for the volition to employ these competencies to solve relevant problems. Thus, researchers argue for the need for CT dispositions as a source of motivation to persistently dissect complex real-world problems and seek efficient solutions through coding [14,15]. In other words, the notion of CT disposition accounts for both the psychological and cognitive aspects of computational problem-solving. Existing research indicates that specific thinking skills are positively correlated with an internal motivation to think and are the constituents of specific thinking dispositions [16]. Therefore, good thinkers tend to have both thinking skills and a thinking disposition [17]. Although it has been suggested that CT is integrated into K–12 classrooms to foster students’ dispositions in CT, a validated measurement of CT dispositions seems to be lacking. The aims of this study are to propose and validate a measurement instrument of CT knowledge and CT dispositions.

2. Literature Review

2.1. Computational Thinking

CT is regarded as a specific form of thinking that conceptually stems from the domain of computer sciences, involving problem-solving, system design, and an understanding of people’s behavior [18]. Building up from Wing’s work, the Computer Science Teachers Association (CSTA) [19] set up a task force to develop the CSTA K–12 Computer Science Standards, which underline “abstraction”, “automation”, and “analysis” as the core elements of CT. Lee et al. [20] and Csizmadia et al. [21] further delineated that CT skills should include abstraction, algorithmic thinking, decomposition, debugging, generalization, and automation. Operationally, CT should be composed of the key concepts of problem-solving, including defining the problem and breaking the problem down into smaller parts, constructing algorithms with computational concepts, such as sequences, operators, and conditionals, and iterative testing of solutions [16]. Wing advocated the infusion of CT-related learning into K–12 education [18]. Although CT is the basis of computer science, the potential learning impacts that CT concepts can bring to students are cross-disciplinary and favorable for various learning contexts [13].

2.2. Computational Thinking Dispositions

While CT is most often regarded as a problem-solving process that emphasizes one’s cognitive process and thinking skills [20,22], more attention should be paid to the dispositions that students develop in CT education. CT dispositions refer to people’s psychological status or attitudes when they are engaged in CT development [23]. CT dispositions have recently been referred to as “confidence in dealing with complexity, a persistent working with difficulties, an ability to handle open-ended problems” [20,24,25]. Ryle defined thinking dispositions [26] as “not to be in a particular state, or to undergo a particular change”, but “to be bound or liable to be in a particular state, or undergo a particular change when a particular condition is realized” (p. 31). Prolonged engagement in computational practices with an emphasis on the CT process and ample learning opportunities in a motivating environment are the necessary conditions to cultivate CT dispositions [22].

2.3. Three Common Features of Computational Thinking Dispositions

While dispositions have long been recognized as a psychological construct, the definition of thinking dispositions remains largely unclear owing to the different schools of interpretation (see below). Thus, to investigate students’ learning outcomes from the perspective of CT dispositions, it is crucial to clarify the definitions, identify the conceptual features, and construct a validated measurement framework.

Social psychologists commonly classify a disposition as “an attitudinal tendency” [27,28]. Facione et al. delineated a thinking disposition as a set of attitudes [29]. A disposition is a person’s consistent internal motivation to act toward, or to respond to, persons, events, or circumstances in habitual, yet potentially malleable ways [19]. Disposition is regarded as a “collection” of preferences, attitudes, and intentions, as well as a number of capabilities [30] akin to the definition that [29] defined, but the study went on to highlight those capabilities that undergird the proponents to act upon situations. Perkins et al. further elaborated that a thinking disposition is a “triadic conception”, including sensitivity, inclination, and ability [31]. McCune et al. suggested the features of thinking dispositions, such as ability, willingness (akin to attitude), awareness of the process, and sensitivity to context, all of which denoted a situational readiness that can induce the inclination and capabilities to solve problems through CT [32]. Building on their works, we summarized the three common conceptual features of a thinking disposition—inclination, capability, and sensitivity towards CT.

Inclination is the impetus felt towards behavior [31], and is composed of students’ psychological preferences, motivational beliefs, and intentional tendencies [33] towards learning coding and CT. In other words, it means students’ positive attitudes and intentions [30,31], or continuing desires and willingness, to adopt effortful, deep approaches [32] to problem-solving by way of coding.

Capability refers to students’ belief in their self-efficacy to successfully achieve learning outcomes in coding education (i.e., to acquire CT skills). Self-efficacy is based on an individual’s perceived capability [34]. It plays a critical role in enhancing self-motivation to acquire CT skills. The capabilities are also intellectual and allow for the basic capacity to follow through with such behavior [35]. It may also refer to beliefs in one’s capabilities to organize and execute the learning tasks [36].

Sensitivity is defined as students’ alertness to occasions, allowing for the development of new understanding and applying it across a wide range of contexts [31,32]. Sensitivity is one of the most important manifestations of disposition. Disposition is not simply a desire, but a habit of mind [37]; it is an intellectual virtue [31] that needs to be exercised repeatedly in order to form [38]. Habits of mind in the CT context indicate whether learners can think computationally. Meanwhile, dealing with complexity and handling open-ended problems are considered as important computational perspectives [7]. As a summary, students’ sensitivity is required for them to deal with complex real-world problems by drawing from their CT. It refers to how flexibly a coder can recast a problem in the computational framework and make use of their coding knowledge and CT skills to tackle problems.

3. Research Motivation and Objectives

3.1. Research Motivation

More recently, quantitative research on the acquisition of CT skills through coding education has moved towards investigating the relationships of the variables of CT skills [39]. Durak and Saritepeci tested a wide range of variables through structural equation modeling (SEM) and found that CT skills were highly predicable by legislative, executive, and judicial thinking styles [40]. Furthermore, to identify a validated CT measurement method from cognitive perspectives, a cognitive measurement method with five dimensions was proposed, one including creativity, algorithmic thinking, cooperation, critical thinking, and problem-solving [41]. In addition, an SEM model was established with six influential factors, including interest, collaboration, meaningfulness, impact, creative self-efficacy, and programming self-efficacy [42]. While there is a growing interest in investigating the cognitive aspect of CT, the field has yet to fully explore a validated measurement method for measuring CT dispositions.

3.2. Research Questions

To address the current gaps in the measurement of CT dispositions, the following research questions need to be solved:

(1)

Can the three factors (inclination, capability, and sensitivity) of CT disposition be extracted through exploratory factor analysis (EFA)?

(2)

Can the three factors of CT disposition be confirmed through confirmatory factor analysis (CFA)?

(3)

Can the three factors predict students’ CT knowledge understanding results?

4. Instrument Design

To measure thinking dispositions, past research mainly employed two approaches [35]: A self-rating approach (e.g., [43,44,45]) and a behavioral approach (e.g., [37]). In this study, a self-rating approach was applied. According to the three common conceptual features of thinking dispositions and CT-related concepts, a measurement with three distinctive dimensions, including inclination, capability, and sensitivity, was proposed.

4.1. First Dimension: “Inclination”

Inclination assesses students’ attitudes, psychological preferences, and motivational beliefs towards coding and CT. Attitudinal processes are composed of some intrinsic structures that offer learners both/either positive and/or negative direction for setting their learning goals [46,47,48,49]. They also bear relations with motivational aspects [50,51,52,53]. Intrinsic motivation is defined as a hierarchy of needs and is a set of reasons for people to behave in the ways that they do [54].

In 1991, Pintrich et al. developed the Motivated Strategies for Learning Questionnaire (MSLQ) to explain students’ intrinsic values towards their learning experiences [55]. Credé and Phillips conducted a meta-analytic review of the MSLQ, identifying three theoretical components consisting of motivational orientations toward a course: Value beliefs, expectancy, and affectiveness [56]. However, the authors of [57] applied the motivational part of the questionnaire (MSLQ-A) in an online learning context. The study concluded that only test anxiety, self-efficacy, and extrinsic goal orientation were loaded as the original subscales. The results were similar to those of [58], which proposed two-factor structures (task value and self-efficacy), such as the Online Learning Value and Self-Efficacy Scale (OLVSES).

The Colorado Learning Attitudes about Science Survey (CLASS) provided an example of attitude measurement with eight dimensions [59]. However, the authors of [60] argued that most of the current attitude measures (including CLASS) might not be able to measure the right kinds of attitudes and beliefs. An effective attitude measure should be developed with a higher correlation with students’ practical epistemology.

Overall, to measure students’ inclination of acquiring CT through a coding course, we mainly adopted the MSLQ-A part, the OLVSES, and students’ practical epistemology. Eight items were developed from the aspects of students’ value beliefs, expectancy, and affectiveness towards CT, coding, and problem-solving (see Table 1).

Table 1. Designed items for the inclination measure.

ID	Items
t1	I want to enhance my learning ability via Scratch.
t2	I want to acquire coding knowledge via Scratch.
t3	I want to learn coding more effectively via Scratch.
t4	I want to learn coding because it is important.
t5	I want to learn coding because it is interesting.
t6	I want to learn more coding knowledge and skills.
t7	I want to express my ideas with coding.
t8	I want to solve more problems by coding.

4.2. Second Dimension: “Capability”

Capability measures students’ perceived self-efficacy in acquiring CT skills through coding classes. In the study of [61], Bandura investigated how perceived self-efficacy facilitated cognitive development, and concluded that perceived efficacy is positively correlated with students’ cognitive capabilities. By understanding students’ self-efficacy in CT developed through coding education, we can have a grasp of their beliefs about their personal competence, adaptation, and confidence. Students’ competence beliefs, including their academic self-concept and self-efficacy, are positively related to their desirable learning achievements [36].

Past studies on the self-efficacy measurement are wide-ranged (e.g., [34,62,63]). A notable instrument is a 32 item Computer Self-Efficacy Scale by Murphy et al. [64], which focused on different levels of computer skills [65,66]. As the “one-measure-fits-all” approach usually has limitations, the authors of [34] provided a guideline for constructing self-efficacy scales.

Therefore, to measure students’ capability in acquiring CT through a coding course, we adopted the guideline from [34] and students’ practical epistemology. Ten items were proposed from the aspects of students’ perceived self-efficacy towards CT, coding, and problem-solving (see Table 2).

Table 2. Designed items for the capability measure.

ID	Items
t9	Learning coding is easy with Scratch.
t10	I can use Scratch to code easily and independently.
t11	I can easily learn how to operate Scratch.
t12	I know how to code.
t13	To me, coding is not difficult.
t14	I will insist on my own coding plan despite criticism.
t15	I have confidence in handling any problems in coding.
t16	I have confidence in designing good programs.
t17	I hope that teachers will design more challenging coding tasks for me.
t18	I can use computational thinking to understand problems in the real world.

4.3. Third Dimension: “Sensitivity”

Sensitivity measures students’ potentials to evaluate, manage, and improve their thinking skills in dealing with complex real-world problems. The more learners are aware of their learning processes, the more they can control their thinking processes for problem-solving [16]. When it comes to dealing with complexity, good thinkers tend to be able to create new ideas in different contexts [66]. With an open-minded attitude, they can more easily cultivate an awareness of multi-perspective thinking to solve complicated problems. Based on the above notions, ten items were proposed (see Table 3).

Table 3. Designed items for the sensitivity measure.

ID	Items
t19	I know adding existing programs to my Scratch can help me design more complex things.
t20	I understand programs as an integral structure in which a small change will affect the whole program design.
t21	I know a program design includes planning and the steps and instructions for solving problems.
t22	I know how to connect new problems with acquired coding knowledge.
t23	I know successful coding requires several rounds of debugging.
t24	I know it is important to find out the information that can solve the main problem.
t25	I know it is important to look for commonalities or similarities (or common features) among questions while coding.
t26	I know it will be easier to understand and handle a problem when it is broken down into smaller ones.
t27	I know it is important to learn from failures.
t28	I know it is important to find a suitable solution based on the previous experience.

A measurement model with 28 items was initially developed. The items were first tested by two participating primary school teachers and two training project designers. Furthermore, two professors in the relevant research domain helped to review the designed items.

5. Research Methods

5.1. Framework of Research Implementation

To develop a scientific measurement instrument, a two-phase study was designed:

-

In Phase 1, EFA was conducted to establish a measurement instrument based on the theoretical framework in Section 2.

-

In Phase 2, CFA was performed to validate the measurement instrument with the goodness of model fit, as well as the construct reliability and the convergent and discriminant validity (see Figure 1).

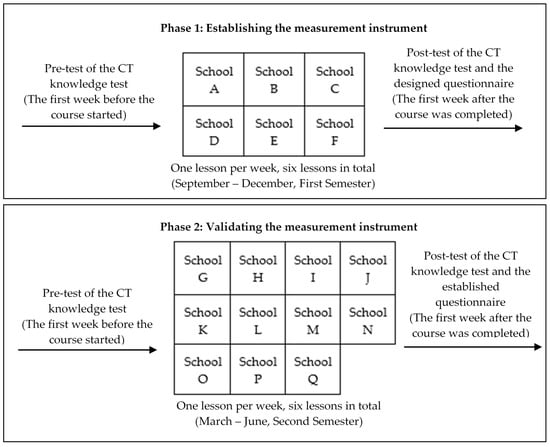Figure 1. Framework of research implementation.

The participants were all Grade 5 primary students who joined a coding course. In Phase 1, data were collected from the first six primary schools that conducted the coding course in the first semester. In Phase 2, data were collected from an alternative eleven primary schools that ran the coding course in the second semester.

Before the course started, a pre-test had been administered to understand students’ knowledge levels of the seven CT concepts [22], which were the core learning content of the coding course (see Table 4).

Table 4. Perceived knowledge understanding (KU) about the seven computational thinking (CT) concepts.

ID	Items
KU1	Data are functional when they are stored, read, and updated.
KU2	Operators provide functional support from mathematics, logics, and strings.
KU3	Conditionals mean that the program has a corresponding operating result under certain conditions.
KU4	Parallelism is running multiple instructions at the same time.
KU5	Events describe things that cause others to happen.
KU6	Loops repeatedly run a series of programs in the same order.
KU7	Sequences are a series of steps that enable the program to perform a task.

After the coding course, a post-test of the CT knowledge understanding test and the designed CT disposition questionnaire were administered.

5.2. Implementation of the Coding Course

The research was carried out in a “Learn-to-code” education project in Hong Kong. It involved seventeen primary schools, among which six schools with 640 Grade 5 students (aged 10.2 on average) participated in Phase 1, and eleven schools with 907 Grade 5 students (aged 10.4 on average) participated in Phase 2.

Scratch was the coding environment used in the project. The students learned to create four mini-games (see Figure 2) within six lessons (one lesson per week, 140 min per lesson). The major aim of the project was to equip the participating students with CT concepts (sequences, loops, parallelism, events, conditionals, operators, and data) and CT skills (abstraction, algorithmic thinking, decomposition, evaluation, and generalization).

Figure 2. “Learn-to-code” education project. (a) The mini-game: “Maze”; (b) the mini-game: “Golden Coin”; (c) the mini-game: “Shooting Game”; (d) the mini-game: “Flying Cat”; (e) the classroom context.

5.3. Data Collection

Table 5 shows the demographic information of the participants.

Table 5. Participants’ demographic information.

Category		Phase 1		Phase 2
		Count	Percentage	Count	Percentage
Gender	Female	309	48.3%	454	50.1%
	Male	327	51.1%	452	49.8%
	Missing	4	0.6%	1	0.1%
Coding Experience	Enriched	58	9.1%	62	6.8%
	Basic	234	36.6%	347	38.3%
	A little	190	29.7%	244	26.9%
	N.E.	158	24.6%	253	28%

(1) In Phase 1, gender was well distributed. Among the 640 students, 36.6% had “basic” coding experience; 29.7%, “a little experience”; 24.6%, “no experience”. In total, 90.9% of them did not have an “enriched” coding experience.

(2) In Phase 2, gender was also well distributed. Among the 907 students, 38.3% had “basic” coding experience; 26.9%, “a little experience”; 27.7%, “no experience”. In total, 93.2% of them did not have an “enriched” coding experience.

5.4. Data Analysis

5.4.1. Independent t-Test

To avoid the biased results caused by students’ different knowledge levels in Phase 1 and Phase 2, independent t-tests were conducted to test the samples’ homogeneity of CT knowledge levels before joining the coding course.

5.4.2. Exploratory Factor Analysis (EFA)

The questionnaire adopted the five-point Likert scale with anchors ranging from 1 = “strongly disagree” to 5 = “strongly agree”. First, common factors were extracted from the post-test data of Phase 1 by EFA to establish the measurement model. Furthermore, whether or not the factors derived from EFA aligned with the three common features discussed in Section 2.3 was tested.

5.4.3. Confirmative Factor Analysis (CFA)

CFA was employed to validate the measurement model. The factor loadings (>0.7), composite reliability (CR > 0.7), the Cronbach’s alpha coefficients (>0.7), and average variance extracted (AVE > 0.5) were computed to provide indexes for the assessment of the construct reliability and the convergent and discriminant validity [67].

5.4.4. Structural Equation Modeling (SEM)

SEM [68] first tested the model fit goodness of the established measurement model. Secondly, it also explored the path model to investigate the direct and total effects among variables (e.g., inclination, capability, sensitivity, and students’ CT knowledge understanding). Indicators such as χ2/df (<3 is perfect fitting; <5 is acceptable), Normed Fix Index (NFI), Incremental Fit Index (IFI), Tucker Lewis Index (TLI), Comparative Fit Index (CFI) (>0.9 is perfect fitting; >0.8 is reasonable), and Root Mean Square Error of Approximation (RMSEA) (<0.05 is perfect fitting; <0.08 is acceptable) were tested to validate the goodness of the model fit.

5.4.5. Linear Regression Analysis

Linear Regression Analysis predicts whether students’ CT dispositions (inclination, capability, and sensitivity; independent variables) contribute statistically significantly to their CT knowledge understanding (the dependent variable). The multiple correlation coefficient (R) and the determination coefficient (R²) explored whether these variables are suitable for linear regression analysis. Analysis of variance (ANOVA) reports how well the regression equation fits the data (p < 0.05). The coefficients (B values) determine the relationship between students’ CT dispositions and their perceived CT knowledge understanding by forming a regression equation.

6. Results

6.1. Homogeneity of the Sample

To avoid the biased results caused by students’ different knowledge levels of CT, independent t-tests were administered to check the homogeneity of all samples (Phase 1 and Phase 2) by using the pre-test of CT knowledge understanding test (see Table 4). Since all significance values of Levene’s Test for Equality of Variances from KU1–KU7 are less than 0.0005, t values of equal variances not assumed were taken. No significant difference (sig. > 0.05) between Phase 1 and Phase 2 responses (KU1–KU7) was found (see Table 6). Therefore, Phase 1 and Phase 2 students had homogenous CT knowledge understanding levels before attending the coding course.

Table 6. Independent t-test for testing samples’ homogeneity.

Item ID	t-Test for Equality of Means
	t	Sig. (2-Tailed)	Mean Difference	Std. Error Difference
KU1	−0.16	0.87	−0.01	0.06
KU2	−1.65	0.10	−0.10	0.06
KU3	−1.28	0.20	−0.07	0.06
KU4	0.62	0.54	0.03	0.06
KU5	−0.83	0.41	−0.04	0.05
KU6	−1.61	0.11	−0.09	0.06
KU7	−0.78	0.44	−0.04	0.05

6.2. Research Phase 1: Establishing the Measurement Instrument

Data collected from Phase 1 (640 students in the first semester) were analyzed for establishing the measurement instrument. The Kaiser-Meyer-Olkin (KMO) value (0.976) and Bartlett’s test (p-value is 0.000***) indicated that the measurement model was suitable for EFA. A Principal Component Analysis (PCA) was used as the extraction method. Rotation converged in nine iterations by Varimax with Kaiser Normalization rotation. As a result, twelve items were removed: (1) Items that loaded on two or more dimensions were removed, since these items may have negative influences on discriminant validity. Thus, t2, t15, and t16 were excluded. (2) Items with factor loadings below 0.5 were removed, since they failed to reach the acceptable benchmark line. Thus, t3, t5, and t14 were excluded, since they failed to reach the acceptable benchmark line. (3) Items that could not properly match to the corresponding extracted dimension were also removed. Thus, t25 and t26 were excluded.

At this stage, the initial measurement model was first established (see Table 7). The extracted dimensions (inclination, capability, and sensitivity) aligned with the three common features found in the reviewed literature on thinking dispositions (e.g., [32,33,35]).

Table 7. Exploratory factor analysis and rotated component matrix.

Dimensions and Operational Definitions		Items	Component
			1	2	3
Inclination	The attitudinal processes imply one’s intrinsic beliefs, expectancy, and affectiveness on learning to code and obtaining CT skills in a specific learning context.	t1	0.69
		t4	0.56
		t7	0.66
		t8	0.75
Capability	One’s perceived efficacy is a judgment of his or her capabilities to bring about desired outcomes (e.g., CT skills, problem-solving skills) through the coding course.	t10		0.75
		t11		0.77
		t12		0.66
		t13		0.78
		t17		0.63
		t18		0.58
Sensitivity	Habits of mind express whether learners can think computationally. The more learners are aware of their learning process, the more they can control their thinking process when it comes to problem-solving and CT.	t19			0.54
		t20			0.68
		t21			0.58
		t23			0.72
		t24			0.60
		t27			0.64

6.3. Research Phase 2: Validating the Measurement Instrument

Data collected from Phase 2 (907 students in the second semester) were analyzed with IBM^® Amos 23.0.0 software. SEM was used to validate the measurement model. The maximum likelihood estimation method was applied considering a large number of samples (above 500). Therefore, the goodness of model fit was obtained: χ2/df = 3.577, NFI = 0.949, IFI = 0.963, TLI = 0.956, CFI = 0.963, and RMSEA = 0.053 (see Figure 3).

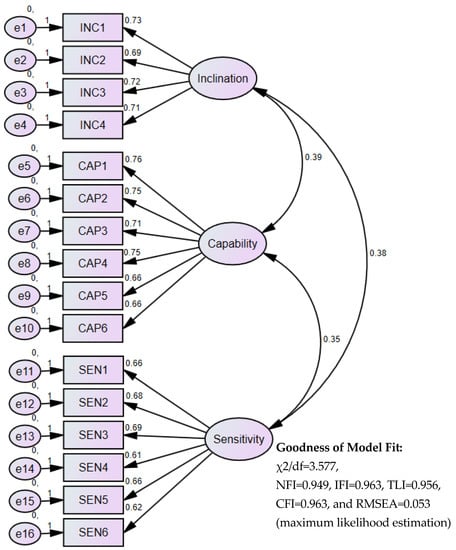
Figure 3. Structural equation model for validating the measurement model.

Furthermore, the construct reliability validity and the convergent and discriminant validity were all analyzed with IBM^® SPSS 22, resulting in: (i) All factor loadings being significant and greater than 0.7; (ii) in all dimensions, both CR and the Cronbach’s alpha coefficients were greater than 0.7, with AVE greater than 0.5; and (iii) the square root of AVE of each construct was higher than the correlation between it and any other constructs in the model (see Table 8 and Table 9).

Table 8. Construct reliability validity and convergent validity.

Items			Factor Loading a	CR	AVE	Cronbach’s Alpha
Inclination	INC1	I want to enhance my learning ability via Scratch.	0.82	0.88	0.65	0.82
	INC2	I want to learn coding because it is important.	0.79
	INC3	I want to express my ideas with coding.	0.82
	INC4	I want to solve more problems by coding.	0.79
Capability	CAP1	I can use Scratch to code easily and independently.	0.85	0.91	0.63	0.88
	CAP2	I can easily learn how to operate Scratch.	0.82
	CAP3	I know how to code.	0.79
	CAP4	To me, coding is not difficult.	0.83
	CAP5	I hope that teachers will design more challenging coding tasks for me.	0.75
	CAP6	I can use computational thinking to understand the problems in the real world.	0.74
Sensitivity	SEN1	I know adding existing programs to my Scratch can help me design more complex things.	0.74	0.88	0.55	0.84
	SEN2	I understand programs as integral structures in which a small change will affect the whole program design.	0.77
	SEN3	I know a program design includes planning and the steps and instructions for solving problems.	0.76
	SEN4	I know successful coding requires several rounds of debugging.	0.74
	SEN5	I know it is important to find out the information that can solve the main problem.	0.73
	SEN6	I know it is important to learn from failing experiences.	0.72

^a Factor Loadings were extracted via the Principal Component Analysis in the SPSS context.

Table 9. Discriminant analysis.

Dimensions	Inclination	Capability	Sensitivity
Inclination	0.81
Capability	0.668 **	0.80
Sensitivity	0.647 **	0.682 **	0.74

** Correlation is significant at the 0.01 level (two-tailed; Pearson correlation method).

6.4. Relationship between CT Dispositions and CT Knowledge Understanding

6.4.1. Contributions of CT Dispositions to CT Knowledge Understanding

Linear Regression Analysis predicts the contributions of students’ CT dispositions to their CT knowledge understanding. The value of R is 0.845, which indicates a high degree of correlation. The R² value (0.714) indicates that 71.4% of the total variation in the dependent variable (CT knowledge understanding) can be explained by the independent variable (inclination, capability, and sensitivity), which is very large. The ANOVA result indicates that the regression model predicts the dependent variable significantly well, since the p-value in the “Regression” row is less than 0.001 (as it is a good fit for the data).

Table 10 shows the coefficient table, which predicts students’ CT knowledge understanding from their CT dispositions. From the coefficient table, students’ CT dispositions (inclination, capability, and sensitivity) contribute statistically significantly to the model (all p values < 0.001). Furthermore, the coefficients (B values) show the contributions of students’ CT dispositions to their CT knowledge understanding by forming the regression equation:

CT knowledge understanding = 0.596 + 0.177 (Inclination) + 0.2 (Capability) + 0.471 (Sensitivity).

(1)

Table 10. Coefficients ^a.

Model	Unstandardized Coefficients		Standardized Coefficients	t	Sig.
	B	Std. Error	Beta
1 (Constant)	0.596	0.069		8.638	0.000
Inclination	0.177	0.021	0.214	8.370	0.000
Capability	0.200	0.022	0.245	9.184	0.000
Sensitivity	0.471	0.025	0.489	18.799	0.000

^a Dependent variable: CT knowledge understanding (KU).

6.4.2. Estimating Direct and Total Effects via the Path Model

SEM explored a path model to investigate direct and total effects between students’ CT dispositions and their CT knowledge understanding. The model fit goodness of the model is at the acceptable level (maximum likelihood estimation): χ2/df = 3.757, NFI = 0.925, IFI = 0.944, TLI = 0.937, CFI = 0.944, and RMSEA = 0.055 (see Figure 4).

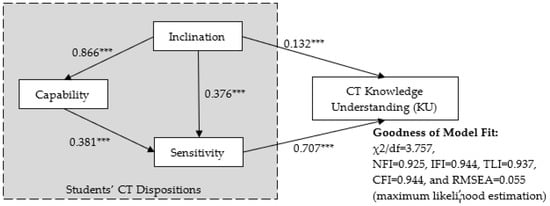
Figure 4. The path model (direct effects, *** p < 0.001).

Regarding the direct effects among all variables: (1) Inclination has significant influences on capability (the path coefficient of 0.866), sensitivity (the path coefficient of 0.376), and CT knowledge understanding (the path coefficient of 0.132). (2) Capability has significant influences on sensitivity (the path coefficient of 0.381). (3) Sensitivity has significant influences on CT knowledge understanding (the path coefficient of 0.707).

Table 11 shows the total effects among all variables: (1) All factors of CT dispositions (inclination, capability, and sensitivity) have total effects on CT knowledge understanding with the values of 0.632, 0.27, and 0.707, respectively. (2) Among three factors of CT dispositions, inclination and capability have total effects on sensitivity with values of 0.706 and 0.381. Other than that, inclination has a total effect on capability with a value of 0.866.

Table 11. Total effects in the path model.

Total Effects	CT Dispositions			CT Knowledge Understanding (KU)
	Inclination	Capability	Sensitivity
Capability	0.866	0.000	0.000	0.000
Sensitivity	0.706	0.381	0.000	0.000
CT Knowledge Understanding (KU)	0.632	0.270	0.707	0.000

7. Discussions and Conclusions

7.1. Instrument Development

Past studies on thinking dispositions (e.g., [35,45]) and CT measurements (e.g., [22,41]) have laid an important foundation for designing a cognitive measurement model. Our proposed measurement framework was constructed based on the three common conceptual features of thinking dispositions in the literature review: Inclination, capability, and sensitivity. Overall, the study contributes to the current interest in CT [18] by creating a valid and reliable instrument from the perspective of disposition.

A two-phase research framework was designed: (1) In Phase 1, with the participation of 640 Grade 5 students in Hong Kong, the constructs of the measurement model were initially developed via EFA. (2) In Phase 2, another group of 907 Grade 5 students joined the same coding course. The predictive validation was performed, and the measurement model was validated by SEM. The construct reliability, convergent validity, and discriminant validity were evaluated. As a result, a validated measurement model with three dimensions (i.e., inclination, capability, and sensitivity) (16 items) was established to delineate students’ CT dispositions in K–12 education. The instrument also provided an alternative perspective to assess students’ learning performance in the coding course.

7.2. Influence of CT Dispositions on CT Knowledge Understanding

Regarding the regression equation, sensitivity contributes the most (B = 0.471) to students’ knowledge understanding (KU1–KU7), followed by capability (B = 0.2) and inclination (B = 0.177). Regression analysis also indicated that students’ CT dispositions (inclination, capability, and sensitivity) contribute statistically significantly to their CT knowledge understanding.

Furthermore, to estimate direct effects among all variables, a path model has been established (Figure 4). It revealed the relationship between students’ CT dispositions and their CT knowledge understanding:

(1) Both inclination and sensitivity (two key factors of CT dispositions) have direct effects on CT knowledge understanding. Sensitivity influences CT knowledge understanding the most (0.707), followed by inclination (0.132), indicating that students’ habits of mind (their thinking computationally) highly influence their knowledge understanding.

(2) However, there is no direct effect from capability on students’ CT knowledge understanding. This indicated that only students’ perceived capability of having CT could not represent their knowledge achievements.

(3) Among the three factors of CT dispositions, sensitivity can be significantly influenced by inclination (0.376) and capability (0.381). Since sensitivity has a significant direct effect on CT knowledge understanding, this indicates that inclination and capability shall have indirect effects on CT knowledge understanding.

Regarding the total effects among all variables: (1) All factors of CT dispositions (inclination, capability, and sensitivity) have total effects on CT knowledge understanding, while inclination and sensitivity are key factors with the greatest total effects (0.632 and 0.707). (2) Among the three factors of CT dispositions, both inclination and capability have total effects on sensitivity. Moreover, inclination again contributes most of the total effects on sensitivity.

7.3. Limitations

Given the complex and diverse perspectives from the researchers regarding thinking dispositions and CT dispositions, this study piloted a questionnaire to measure CT dispositions among primary school students who acquired some CT knowledge and skills. Nevertheless, this questionnaire has yet to include all dimensions discussed in the literature and may have missed out on some related aspects. Future research can deepen the current study by investigating other possible dimensions of CT dispositions. In addition, a further CFA is needed to evaluate how well the proposed measurement model can be adopted in other online learning contexts.