Pythagorean Fuzzy SWARA–VIKOR Framework for Performance Evaluation of Solar Panel Selection
Abstract
1. Introduction
- (a)
- An integrated Pythagorean fuzzy–SWARA–VIKOR (PF–SWARA–VIKOR) framework is proposed.
- (b)
- The PFS-based SWARA method is utilized to assess the criteria weights.
- (c)
- A problem regarding the selection of solar panels is presented and evaluated by utilizing the proposed PF–SWARA–VIKOR method, which reveals the applicability of the introduced approach.
- (d)
- A comparative study and sensitivity analysis are also discussed to show the usefulness of the introduced approach.
2. Preliminaries
3. Proposed Pythagorean Fuzzy–SWARA–VIKOR Method
4. An Empirical Study: Performance Evaluation of Solar Panel Selection
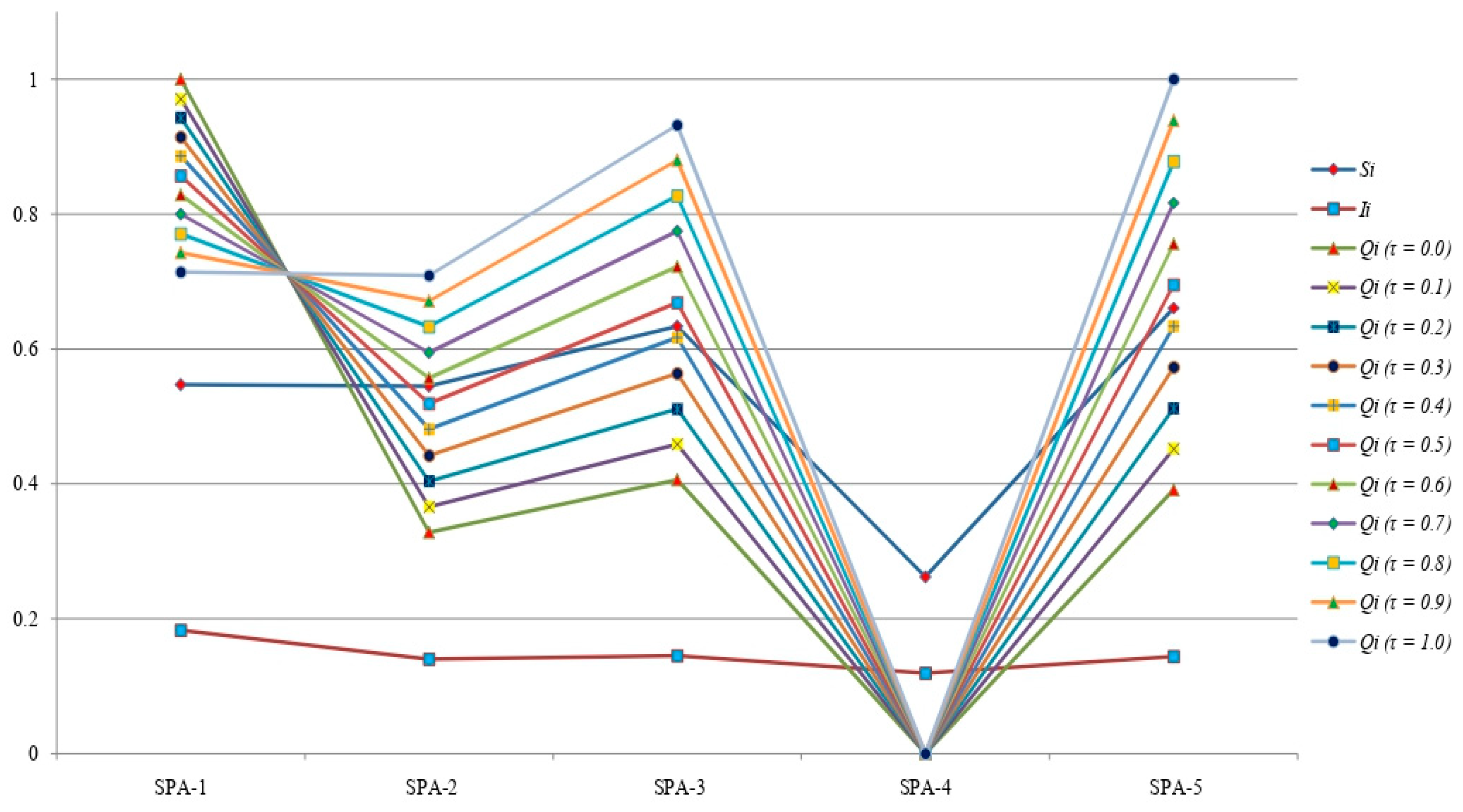
4.1. Sensitivity Analysis
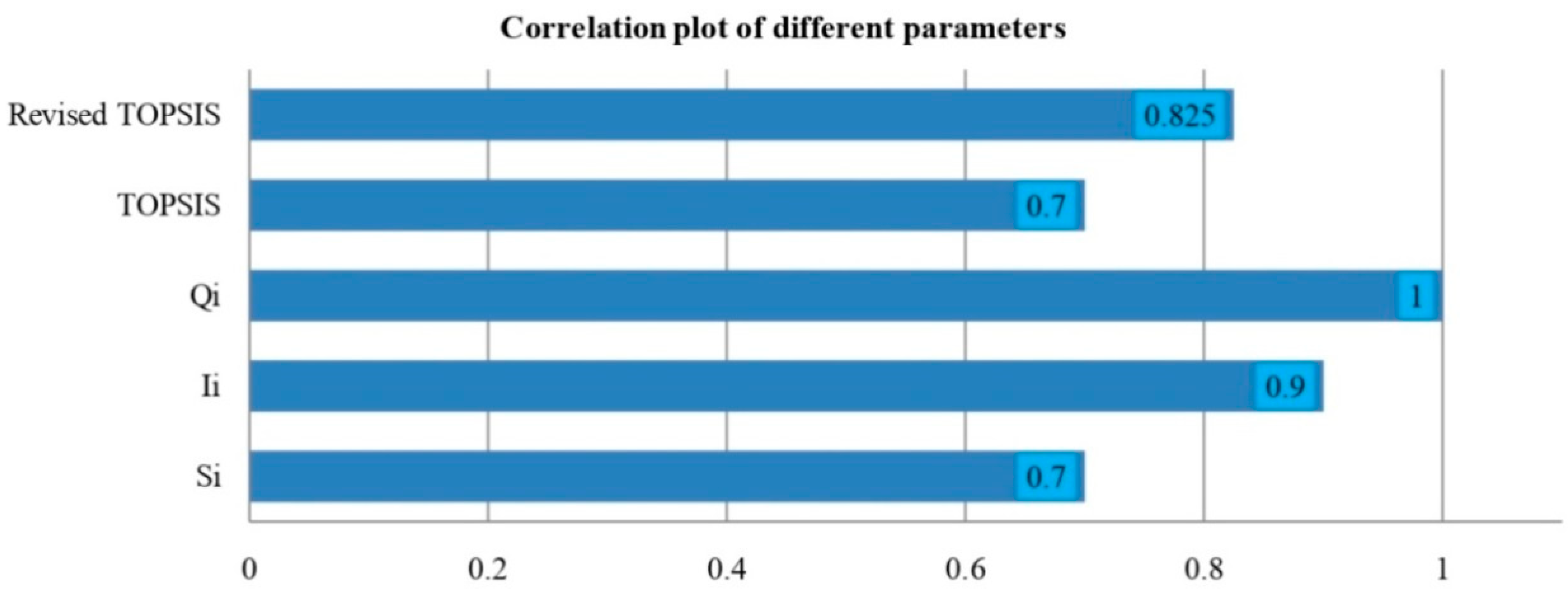
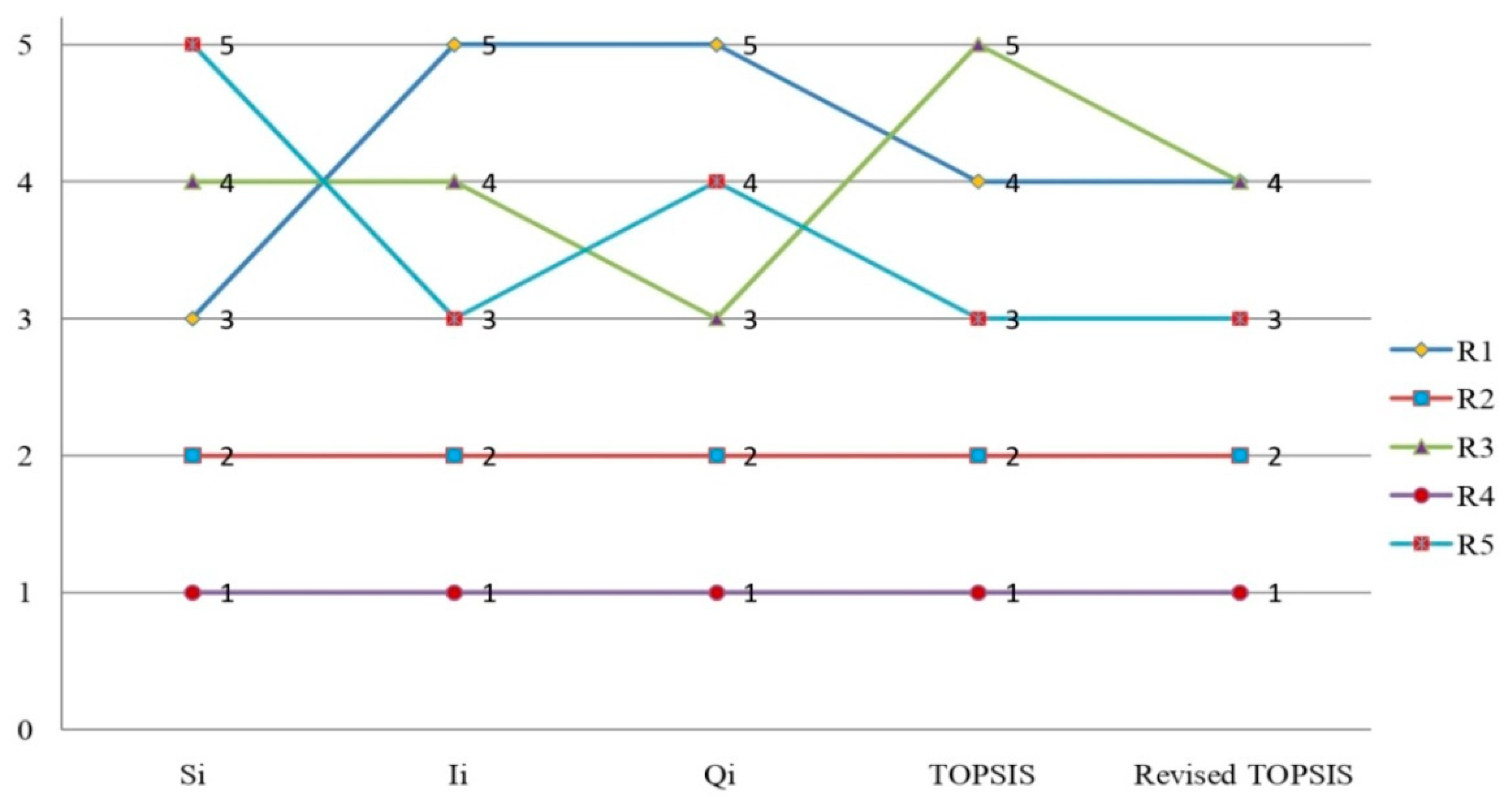
4.2. Comparative Study
PF-TOPSIS Method
- (a)
- The PF–SWARA–VIKOR method represents the Pythagorean fuzzy information, which can depict the MD, ND, and hesitation degree with an effortless mathematical description. Based on it, we can determine the significance degree of the DEs without any modification and, therefore, the developed method can successfully avoid the loss of information.
- (b)
- As some of the previous measures under the PFSs [33] have been incapable of providing the preference order of the alternatives accurately, thus, their consequent methods may not present relevant outcomes. Alternatively, the proposed approach has the capability to prevail over their limitations and is therefore able to order the alternatives appropriately, which makes it a more desirable approach to solving MCDM problems.
- (c)
- The SWARA approach is utilized to compute the subjective weights of criteria in the process of performance evaluation of solar panels, which makes the developed PF–SWARA–VIKOR approach more sensible, flexible, and efficient.
- (d)
- The developed framework has the following benefits when choosing solar panels:
- An innovative procedure is utilized to enumerate tangible sub-criteria successfully.
- The integrated approach eradicates the subjective estimation of indistinct sub-criteria.
- Pythagorean fuzzy SWARA is used to achieve appropriate harmonizing of criteria.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Streimikiene, D.; Balezentis, T.; Krisciukaitiene, I.; Balezentis, A. Prioritizing sustainable electricity production technologies: MCDM approach. Renew. Sustain. Energy Rev. 2012, 16, 3302–3311. [Google Scholar] [CrossRef]
- Dehghani, E.; Jabalameli, M.S.; Jabbarzadeh, A. Robust design and optimization of solar photovoltaic supply chain in an uncertain environment. Energy 2018, 142, 139–156. [Google Scholar] [CrossRef]
- Alblawi, A.; Elkholy, M.H.; Talaat, M. ANN for assessment of energy consumption of 4 kW PV modules over a year considering the impacts of temperature and irradiance. Sustainability 2019, 11, 6802. [Google Scholar] [CrossRef]
- Wang, T.-C.; Tsai, S.-Y. Solar Panel Supplier Selection for the Photovoltaic System Design by Using Fuzzy Multi-Criteria Decision Making (MCDM) Approaches. Energies 2018, 11, 1989. [Google Scholar] [CrossRef]
- Ramachandra, T.V.; Jha, R.K.; Vamsee Krishna, S.; Shruthi, B.V. Solar energy decision support system. Int. J. Sustain. Energy 2005, 24, 207–224. [Google Scholar] [CrossRef]
- Charabi, Y.; Gastli, A. GIS assessment of large CSP plant in Duqum, Oman. Renew. Sustain. Energy Rev. 2010, 14, 835–841. [Google Scholar] [CrossRef]
- Cavallaro, F. Fuzzy TOPSIS approach for assessing thermal-energy storage in concentrated solar power (CSP) systems. Appl. Energy 2010, 87, 496–503. [Google Scholar] [CrossRef]
- Beltran, P. An AHP (analytic hierarchy process)/ANP (analytic network process)-based multi-criteria decision approach for the selection of solar-thermal power plant investment project. Energy 2013, 17, 645–658. [Google Scholar]
- Khan, G.; Rathi, S. Optimal site selection for solar PV power plant in an Indian state using geographical information system (GIS). Int. J. Emerg. Eng. Res. Technol. 2014, 2, 260–266. [Google Scholar]
- Kowalski, K.; Stagl, S.; Madlener, R.; Omann, I. Sustainable energy futures: Methodological challenges in combining scenarios and participatory multi-criteria analysis. Eur. J. Oper. Res. 2017, 197, 1063–1074. [Google Scholar] [CrossRef]
- Tavana, M.; Arteaga, F.J.S.; Mohammadi, S.; Alimohammadi, M. A fuzzy multi-criteria spatial decision support system for solar farm location planning. Energy Strategy Rev 2017, 18, 93–105. [Google Scholar] [CrossRef]
- Ozdemir, S.; Sahin, G. Multi-criteria decision-making in the Location Selection for a Solar PV Power Plant using AHP. Measurement 2018, 129, 218–226. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, V.T.; Thai, H.T.N.; Duong, D.H. Multi-Criteria Decision Making (MCDM) Approaches for Solar Power Plant Location Selection in Viet Nam. Energies 2018, 11, 1504. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Kengpol, A.; Rontlaong, P.; Tuominen, M. A decision support system for selection of solar power plant locations by applying fuzzy AHP and TOPSIS: An empirical study. J. Softw. Eng. Appl. 2013, 6, 470–481. [Google Scholar] [CrossRef]
- Sindhu, S.; Nehra, V.; Luthra, S. Investigation of feasibility study of solar farms deployment using hybrid AHP-TOPSIS analysis: Case study of India. Renew. Sustain. Energy Rev. 2017, 73, 496–511. [Google Scholar] [CrossRef]
- Sasikumar, G.; Ayyappan, S. Multi-criteria Decision Making for Solar Panel Selection Using Fuzzy Analytical Hierarchy Process and Technique for Order Preference by Similarity to ideal Solution (TOPSIS): An Empirical Study. J. Inst. Eng. (India) Ser. C 2019, 100, 707–715. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Xia, M.; Xu, Z.S. Entropy/cross entropy-based group decision making under intuitionistic fuzzy environment. Inf. Fusion 2012, 13, 31–47. [Google Scholar] [CrossRef]
- Mishra, A.R. Intuitionistic fuzzy information with application in rating of township development. Iran. J. Fuzzy Syst. 2016, 13, 49–70. [Google Scholar]
- Mishra, A.R.; Rani, P. Shapley divergence measures with VIKOR method for multi-attribute decision-making problems. Neural Comput. Appl. 2019, 31, 1299–1316. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Gumus, S.; Bali, O. Dynamic Aggregation Operators Based on Intuitionistic Fuzzy Tools and Einstein Operations. Fuzzy Inf. Eng. 2017, 9, 45–65. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. Some Generalized Complex Intuitionistic Fuzzy Aggregation Operators and Their Application to Multicriteria Decision-Making Process. Arab. J. Sci. Eng. 2019, 44, 2679–2698. [Google Scholar] [CrossRef]
- Dhivya, J.; Sridevi, B. A novel similarity measure between intuitionistic fuzzy sets based on the mid points of transformed triangular fuzzy numbers with applications to pattern recognition and medical diagnosis. Appl. Math. —A J. Chin. Univ. 2019, 34, 229–252. [Google Scholar] [CrossRef]
- Dutta, P.; Goala, S. Fuzzy decision making in medical diagnosis using an advanced distance measure on intuitionistic fuzzy sets. Open Cybern. Syst. J. 2018, 12, 136–149. [Google Scholar] [CrossRef]
- Yu, H.; Fan, J. A novel segmentation method for uneven lighting image with noise injection based on non-local spatial information and intuitionistic fuzzy entropy. Eurasip J. Adv. Signal Process. 2017. [Google Scholar] [CrossRef]
- Ansari, M.D.; Mishra, A.R.; Ansari, F.T. New divergence and entropy measures for intuitionistic fuzzy sets on edge detection. Int. J. Fuzzy Syst. 2018, 20, 474–487. [Google Scholar] [CrossRef]
- Mishra, A.R.; Kumari, R. Multi-criteria COPRAS Method Based on Parametric Measures for Intuitionistic Fuzzy Sets: Application of Green Supplier Selection. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean Fuzzy Subsets. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting, Edmonton, AB, Canada, 24–28 June 2013; pp. 57–61. [Google Scholar]
- Yager, R.R. Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Yager, R.R.; Abbasov, A.M. Pythagorean membership grades, complex numbers and decision making. Int. J. Intell. Syst. 2013, 28, 436–452. [Google Scholar] [CrossRef]
- Zhang, X.L.; Xu, Z.S. Extension of TOPSIS to Multicriteria Decision Making with Pythagorean Fuzzy Sets. Int. J. Intell. Syst. 2014, 29, 1061–1078. [Google Scholar] [CrossRef]
- Gou, X.; Xu, Z.S.; Ren, P. The Properties of Continuous Pythagorean Fuzzy Information. Int. J. Intell. Syst. 2016, 31, 401–424. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Razaei, G.; Liao, H.; Mardani, A. Extended Pythagorean Fuzzy TOPSIS Method Based on Similarity Measure for Sustainable Recycling Partner Selection. Int. J. Fuzzy Syst. 2019. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Pardasani, K.R. A novel WASPAS approach for multi-criteria physician selection problem with intuitionistic fuzzy type-2 sets. Soft Comput. 2020, 24, 2355–2367. [Google Scholar] [CrossRef]
- Ma, Z.M.; Xu, Z.S. Symmetric Pythagorean Fuzzy Weighted Geometric/Averaging Operators and Their Application in Multicriteria Decision-Making Problems. Int. J. Intell. Syst. 2016, 31, 1198–1219. [Google Scholar] [CrossRef]
- Khan, A.A.; Ashraf, S.; Abdullah, S.; Qiyas, M.; Luo, J.; Khan, S.U. Pythagorean fuzzy Dombi aggregation operators and their application in decision support system. Symmetry 2019, 11, 383. [Google Scholar] [CrossRef]
- Liu, J.; Liu, P.; Liu, S.F.; Zhou, X.Z.; Zhang, T. A study of decision process in MCDM problems with large number of criteria. Int. Trans. Oper. Res. 2015, 22, 237–264. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The CRITIC method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Podvezko, V. Integrated determination of objective criteria weights in MCDM. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 267–283. [Google Scholar] [CrossRef]
- Mishra, A.R.; Rani, P.; Pardasani, K.R.; Mardani, A. A Novel Hesitant Fuzzy WASPAS Method for Assessment of Green Supplier Problem Based on Exponential Information Measures. J. Clean. Prod. 2019. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Pardasani, K.R.; Mardani, A.; Liao, H.; Streimikiene, D. A novel VIKOR approach based on entropy and divergence measures of Pythagorean fuzzy sets to evaluate renewable energy technologies in India. J. Clean. Prod. 2019, 238. in press. [Google Scholar] [CrossRef]
- Kersuliene, V.; Zavadskas, E.K.; Turskis, Z. Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA). J. Bus. Econ. Manag. 2010, 11, 243–258. [Google Scholar] [CrossRef]
- Karabasevic, D.; Paunkovic, J.; Stanujkic, D. Ranking of companies according to the indicators of corporate social responsibility based on SWARA and ARAS methods. Serb. J. Manag. 2016, 11, 43–53. [Google Scholar] [CrossRef]
- Mardani, A.; Nilashi, M.; Zakuan, N.; Loganathan, N.; Soheilirad, S.; Saman, M.Z.M.; Ibrahim, O. A systematic review and meta-analysis of SWARA and WASPAS methods: Theory and applications with recent fuzzy developments. Appl. Soft Comput. 2017, 57, 265–292. [Google Scholar] [CrossRef]
- Maghsoodi, A.I.; Maghsoodi, A.I.; Mosavi, A.; Rabczuk, T.; Zavadskas, E.K. Renewable Energy Technology Selection Problem Using Integrated H-SWARA-MULTIMOORA approach. Sustainability 2018, 10, 4481. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antuchevicience, J. An extended step-wise weight assessment ratio analysis with symmetric interval type-2 fuzzy sets for determining the subjective weights of criteria in multi-criteria decision-making problems. Symmetry 2018, 10, 91. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R. Single-valued neutrosophic SWARA-VIKOR framework for performance assessment of eco-industrial thermal power plants. ICSES Trans. Neural Fuzzy Comput. 2020, 3, 1–9. [Google Scholar]
- Opricovic, S. Multicriteria optimization of civil engineering systems. Fac. Civ. Eng. Belgrade 1998, 2, 5–21. [Google Scholar]
- Opricovic, S.; Tzeng, G.H. Multicriteria planning of post-earthquake sustainable reconstruction. Comput Aided Civ. Infrastruct. Eng 2002, 17, 211–220. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Tzeng, G.H.; Lin, C.W.; Opricovic, S. Multi-criteria analysis of alternative-fuel buses for public transportation. Energy Policy 2005, 33, 1373–1383. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Govindan, K.; Senin, A.A.; Jusoh, A. VIKOR Technique: A Systematic Review of the State of the Art Literature on Methodologies and Applications. Sustainability 2016, 8, 37. [Google Scholar] [CrossRef]
- Zhang, X.; Xing, X. Probabilistic linguistic VIKOR method to evaluate green supply chain initiatives. Sustainability 2017, 9, 1231. [Google Scholar] [CrossRef]
- Suh, Y.; Park, Y.; Kang, D. Evaluating mobile services using integrated weighting approach and fuzzy VIKOR. PloS ONE 2019, 14, e0222312. [Google Scholar]
- Krishankumar, R.; Premaladha, J.; Ravichandran, K.S.; Sekar, K.R.; Manikandan, R.; Gao, X.Z. A novel extension to VIKOR method under intuitionistic fuzzy context for solving personnel selection problem. Soft Comput. 2020, 24, 1063–1081. [Google Scholar] [CrossRef]
- Phochanikorn, P.; Tan, C. A new extension to a multi-criteria decision-making model for sustainable supplier selection under an intuitionistic fuzzy environment. Sustainability 2019, 11, 5413. [Google Scholar] [CrossRef]
- Salimi, A.H.; Noori, A.; Bonakdari, H.; Samakosh, J.M.; Sharifi, E.; Hassanvand, M.; Gharabaghi, B.; Agharazi, M. Exploring the Role of Advertising Types on Improving the Water Consumption Behavior: An Application of Integrated Fuzzy AHP and Fuzzy VIKOR Method. Sustainability 2020, 12, 1232. [Google Scholar] [CrossRef]
- Taylan, O.; Alamoudi, R.; Kabli, M.; AlJifri, A.; Ramzi, F.; Herrera-Viedma, E. Assessment of energy systems using extended fuzzy AHP, fuzzy VIKOR, and TOPSIS approaches to manage non-cooperative opinions. Sustainability 2020, 12, 2745. [Google Scholar] [CrossRef]
- Chen, T.-Y. A novel VIKOR method with an application to multiple criteria decision analysis for hospital-based post-acute care within a highly complex uncertain environment. Neural Comput. Appl. 2019, 31, 3969–3999. [Google Scholar] [CrossRef]
- Rani, P.; Jain, D. Information measures-based multi-criteria decision-making problems for interval-valued intuitionistic fuzzy environment. Proc. Natl. Acad. Sci. India Sect. A: Phys. Sci. 2019, in press. [Google Scholar] [CrossRef]
- Pérez-Velázquez, A.; Oro-Carralero, L.L.; Moya-Rodríguez, J.L. Supplier selection for photovoltaic module installation utilizing fuzzy inference and the VIKOR method: A green approach. Sustainability 2020, 12, 2242. [Google Scholar] [CrossRef]
- Hadi-Vencheh, A.; Mirjaberi, M. Fuzzy inferior ratio method for multiple attribute decision making problems. Inf. Sci. 2014, 277, 263–272. [Google Scholar] [CrossRef]
- Cavallaro, F.; Marino, D.; Streimikiene, D. Environmental Assessment of a Solar Tower Using the Life Cycle Assessment (Lca); Springer International Publishing: Cham, Switzerland, 2019; pp. 621–628. [Google Scholar]
- Cavallaro, F.; Zavadskas, E.K.; Streimikiene, D. Concentrated solar power (csp) hybridized systems. Ranking based on an intuitionistic fuzzy multi-criteria algorithm. J. Clean. Prod. 2018, 179, 407–416. [Google Scholar] [CrossRef]
- Cavallaro, F.; Zavadskas, E.K.; Streimikiene, D.; Mardani, A. Assessment of concentrated solar power (csp) technologies based on a modified intuitionistic fuzzy topsis and trigonometric entropy weights. Technol. Forecast. Soc. Chang. 2019, 140, 258–270. [Google Scholar] [CrossRef]
- Cavallaro, F.; Ciraolo, L. Sustainability Assessment of Solar Technologies Based on Linguistic Information. In Assessment and Simulation Tools for Sustainable Energy Systems. Theory and Application; Green Energy and Technology; Cavallaro, F., Ed.; Springer: London, UK, 2013; pp. 3–25. [Google Scholar]
| Criteria | Descriptions | Type |
|---|---|---|
| Peak power rating (T1) | Refers to the maximum output (in Watts) under standard test conditions | Benefit |
| Peak efficiency (T2) | Refers to the high peak efficiency | Benefit |
| Maximum power current (T3) | Refers to the high value of current | Benefit |
| Maximum power voltage (T4) | Refers to the high value of power current | Benefit |
| Weight (T5) | Prefers to the solar panel with less weight | Cost |
| Price (T6) | Considers the price of solar panels | |
| Reliability (T7) | Measures the reliability of the solar panel | Benefit |
| Spare parts availability (T8) | The availability of solar panel (SP) spare parts is one of the factors deciding customer fulfillment | Benefit |
| R1 | R2 | R3 | R4 | R5 | |
|---|---|---|---|---|---|
| T1 | E1: (0.29, 0.75) E2: (0.40, 0.70) E3: (0.45, 0.65) | E1: (0.70, 0.45) E2: (0.72, 0.50) E3: (0.65, 0.50) | E1: (0.58, 0.55) E2: (0.55, 0.60) E3: (0.60, 0.55) | E1: (0.55, 0.65) E2: (0.52, 0.66) E3: (0.60, 0.55) | E1: (0.60, 0.55) E2: (0.70, 0.45) E3: (0.65, 0.50) |
| T2 | E1: (0.63, 0.40,) E2: (0.55, 0.60) E3: (0.68, 0.35) | E1: (0.63, 0.45) E2: (0.60, 0.50) E3: (0.55, 0.60) | E1: (0.60, 0.45) E2: (0.65, 0.50) E3: (0.58, 0.44) | E1: (0.60, 0.57) E2: (0.55, 0.60) E3: (0.50, 0.60) | E1: (0.60, 0.50) E2: (0.55, 0.60) E3: (0.55, 0.50) |
| T3 | E1: (0.55, 0.65) E2: (0.60, 0.70) E3: (0.50, 0.70) | E1: (0.70, 0.45) E2: (0.70, 0.50) E3: (0.68, 0.45) | E1: (0.64, 0.55) E2: (0.55, 0.57) E3: (0.60, 0.55) | E1: (0.60, 0.55) E2: (0.70, 0.50) E3: (0.65, 0.55) | E1: (0.70, 0.50) E2: (0.65, 0.50) E3: (0.68, 0.50) |
| T4 | E1: (0.55, 0.60) E2: (0.59, 0.45) E3: (0.60, 0.50) | E1: (0.55, 0.65) E2: (0.50, 0.65) E3: (0.55, 0.60) | E1: (0.50, 0.60) E2: (0.55, 0.60) E3: (0.45, 0.65) | E1: (0.55, 0.65) E2: (0.63, 0.42) E3: (0.60, 0.50) | E1: (0.55, 0.50) E2: (0.60, 0.50) E3: (0.45, 0.65) |
| T5 | E1: (0.51, 0.55) E2: (0.60, 0.50) E3: (0.60, 0.55) | E1: (0.65, 0.48) E2: (0.60, 0.55) E3: (0.66, 0.47) | E1: (0.60, 0.45) E2: (0.65, 0.55) E3: (0.60, 0.50) | E1: (0.65, 0.48) E2: (0.65, 0.50) E3: (0.70, 0.45) | E1: (0.65, 0.58) E2: (0.50, 0.65) E3: (0.65, 0.45) |
| T6 | E1: (0.65, 0.45) E2: (0.60, 0.48) E3: (0.55, 0.50) | E1: (0.62, 0.50) E2: (0.60, 0.52) E3: (0.58, 0.65) | E1: (0.58, 0.49) E2: (0.55, 0.50) E3: (0.68, 0.48) | E1: (0.65, 0.45) E2: (0.57, 0.48) E3: (0.60, 0.50) | E1: (0.62, 0.55) E2: (0.60, 0.55) E3: (0.58, 0.55) |
| T7 | E1: (0.50, 0.58) E2: (0.55, 0.50) E3: (0.52, 0.57) | E1: (0.58, 0.60) E2: (0.50, 0.60) E3: (0.45, 0.60) | E1: (0.55, 0.65) E2: (0.53, 0.64) E3: (0.50, 0.60) | E1: (0.45, 0.55) E2: (0.60, 0.50) E3: (0.65, 0.53) | E1: (0.48, 0.70) E2: (0.50, 0.60) E3: (0.55, 0.60) |
| T8 | E1: (0.67, 0.46) E2: (0.65, 0.45) E3: (0.60, 0.50) | E1: (0.57, 0.68) E2: (0.52, 0.57) E3: (0.50, 0.60) | E1: (0.58, 0.65) E2: (0.55, 0.60) E3: (0.50, 0.62) | E1: (0.60, 0.50) E2: (0.65, 0.55) E3: (0.68, 0.53) | E1: (0.57, 0.58) E2: (0.52, 0.60) E3: (0.45, 0.65) |
| R1 | R2 | R3 | R4 | R5 | |
|---|---|---|---|---|---|
| T1 | Y (0.381,0.702, 0.601) | Y (0.691,0.480, 0.541) | Y (0.579,0.564, 0.589) | Y (0.559,0.618, 0.552) | Y (0.648,0.504, 0.572) |
| T2 | Y (0.628,0.430, 0.649) | Y (0.598,0.509, 0.620) | Y (0.609,0.460, 0.646) | Y (0.556,0.588, 0.587) | Y (0.571,0.526, 0.630) |
| T3 | Y (0.551,0.680, 0.484) | Y (0.680,0.483, 0.551) | Y (0.604,0.556, 0.571) | Y (0.648,0.535, 0.542) | Y (0.680,0.500, 0.536) |
| T4 | Y (0.578,0.521, 0.649) | Y (0.537,0.633, 0.620) | Y (0.500,0.616, 0.646) | Y (0.591,0.528, 0.587) | Y (0.538,0.544, 0.630) |
| T5 | Y (0.568,0.535, 0.625) | Y (0.640,0.495, 0.587) | Y (0.615,0.493, 0.615) | Y (0.667,0.476, 0.573) | Y (0.615,0.552, 0.563) |
| T6 | Y (0.607,0.474, 0.638) | Y (0.602,0.550, 0.579) | Y (0.609,0.490, 0.624) | Y (0.613,0.474, 0.632) | Y (0.602,0.550, 0.579) |
| T7 | Y (0.521,0.553, 0.650) | Y (0.520,0.600, 0.608) | Y (0.529,0.631, 0.568) | Y (0.570,0.529, 0.629) | Y (0.510,0.638, 0.578) |
| T8 | Y (0.643,0.470, 0.605) | Y (0.535,0.621, 0.573) | Y (0.548,0.626, 0.556) | Y (0.642,0.523, 0.560) | Y (0.521,0.608, 0.599) |
| R1 | R2 | R3 | R4 | R5 | |
|---|---|---|---|---|---|
| T1 | Y(0.381, 0.702, 0.601) | Y (0.691, 0.480, 0.541) | Y (0.579, 0.564, 0.589) | Y (0.559, 0.618, 0.552) | Y (0.648, 0.504, 0.572) |
| T2 | Y (0.628, 0.430, 0.649) | Y (0.598, 0.509, 0.620) | Y (0.609, 0.460, 0.646) | Y (0.556, 0.588, 0.587) | Y (0.571, 0.526, 0.630) |
| T3 | Y (0.551, 0.680, 0.484) | Y (0.680, 0.483, 0.551) | Y (0.604, 0.556, 0.571) | Y (0.648, 0.535, 0.542) | Y (0.680, 0.500, 0.536) |
| T4 | Y (0.578, 0.521, 0.649) | Y (0.537, 0.633, 0.620) | Y (0.500, 0.616, 0.646) | Y (0.591, 0.528, 0.587) | Y (0.538, 0.544, 0.630) |
| T5 | Y (0.535, 0.568, 0.625) | Y (0.495, 0.640, 0.587) | Y (0.493, 0.615, 0.615) | Y (0.476, 0.667, 0.573) | Y (0.552, 0.615, 0.563) |
| T6 | Y (0.474, 0.607, 0.638) | Y (0.550, 0.602, 0.579) | Y (0.490, 0.609, 0.624) | Y (0.474, 0.613, 0.632) | Y (0.550, 0.602, 0.579) |
| T7 | Y (0.521, 0.553, 0.650) | Y (0.520, 0.600, 0.608) | Y (0.529, 0.631, 0.568) | Y (0.570, 0.529, 0.629) | Y (0.510, 0.638, 0.578) |
| T8 | Y (0.643, 0.470, 0.605) | Y (0.535, 0.621, 0.573) | Y (0.548, 0.626, 0.556) | Y (0.642, 0.523, 0.560) | Y (0.521, 0.608, 0.599) |
| Linguistic Values | PFNs |
|---|---|
| Extremely Low (EL) | Y(0.1500, 0.9500) |
| Very Low (VL) | Y(0.2500, 0.9000) |
| Low (L) | Y(0.3000, 0.8500) |
| Medium Low (ML) | Y(0.3500, 0.7500) |
| Medium (M) | Y(0.4500, 0.6500) |
| Medium High (MH) | Y(0.6000, 0.5000) |
| High (H) | Y(0.7000, 0.3500) |
| Very High (VH) | Y(0.8000, 0.3000) |
| Criteria | E1 | E2 | E3 | Aggregated PFNs | Score Values |
|---|---|---|---|---|---|
| T1 | H | VH | VVH | Y(0.788, 0.300, 0.538) | 0.765 |
| T2 | MH | ML | H | Y(0.592, 0.500, 0.633) | 0.550 |
| T3 | M | M | MH | Y(0.507, 0.597, 0.621) | 0.450 |
| T4 | ML | ML | MH | Y(0.456, 0.658, 0.633) | 0.388 |
| T5 | MH | H | ML | Y(0.579, 0.515, 0.632) | 0.535 |
| T6 | H | M | MH | Y(0.614, 0.468, 0.635) | 0.579 |
| T7 | VH | H | VH | Y(0.776, 0.313, 0.547) | 0.752 |
| T8 | VH | H | H | Y(0.745, 0.329, 0.580) | 0.723 |
| Criteria | Crisp Values | ||||
|---|---|---|---|---|---|
| T1 | 0.765 | - | 1.000 | 1.000 | 0.1463 |
| T7 | 0.752 | 0.013 | 1.013 | 0.987 | 0.1444 |
| T8 | 0.723 | 0.029 | 1.029 | 0.959 | 0.1403 |
| T6 | 0.579 | 0.144 | 1.144 | 0.838 | 0.1226 |
| T2 | 0.550 | 0.029 | 1.029 | 0.814 | 0.1191 |
| T5 | 0.535 | 0.015 | 1.015 | 0.802 | 0.1173 |
| T3 | 0.450 | 0.085 | 1.085 | 0.739 | 0.1081 |
| T4 | 0.388 | 0.062 | 1.062 | 0.696 | 0.1019 |
| Si | Ii | Qi | |
|---|---|---|---|
| R1 | 0.547 | 0.183 | 0.857 |
| R2 | 0.545 | 0.140 | 0.519 |
| R3 | 0.634 | 0.145 | 0.669 |
| R4 | 0.262 | 0.119 | 0.000 |
| R5 | 0.661 | 0.144 | 0.695 |
| Ranking order |
| R1 | R2 | R3 | R4 | R5 | |
|---|---|---|---|---|---|
| 0.0 | 1.000 | 0.328 | 0.406 | 0.000 | 0.391 |
| 0.1 | 0.971 | 0.366 | 0.459 | 0.000 | 0.452 |
| 0.2 | 0.943 | 0.404 | 0.511 | 0.000 | 0.512 |
| 0.3 | 0.914 | 0.442 | 0.564 | 0.000 | 0.573 |
| 0.4 | 0.886 | 0.481 | 0.617 | 0.000 | 0.634 |
| 0.5 | 0.857 | 0.519 | 0.669 | 0.000 | 0.695 |
| 0.6 | 0.829 | 0.557 | 0.722 | 0.000 | 0.756 |
| 0.7 | 0.800 | 0.595 | 0.775 | 0.000 | 0.817 |
| 0.8 | 0.771 | 0.633 | 0.827 | 0.000 | 0.878 |
| 0.9 | 0.743 | 0.671 | 0.880 | 0.000 | 0.939 |
| 1.0 | 0.714 | 0.709 | 0.932 | 0.000 | 1.000 |
| Alternative | Ranking | Ranking | ||||
|---|---|---|---|---|---|---|
| R1 | 0.101 | 0.085 | 0.457 | 4 | −1.0446 | 4 |
| R2 | 0.068 | 0.102 | 0.598 | 2 | −0.3036 | 2 |
| R3 | 0.099 | 0.081 | 0.449 | 5 | −1.0446 | 4 |
| R4 | 0.056 | 0.112 | 0.665 | 1 | 0.0000 | 1 |
| R5 | 0.086 | 0.083 | 0.491 | 3 | −0.7946 | 3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rani, P.; Mishra, A.R.; Mardani, A.; Cavallaro, F.; Štreimikienė, D.; Khan, S.A.R. Pythagorean Fuzzy SWARA–VIKOR Framework for Performance Evaluation of Solar Panel Selection. Sustainability 2020, 12, 4278. https://doi.org/10.3390/su12104278
Rani P, Mishra AR, Mardani A, Cavallaro F, Štreimikienė D, Khan SAR. Pythagorean Fuzzy SWARA–VIKOR Framework for Performance Evaluation of Solar Panel Selection. Sustainability. 2020; 12(10):4278. https://doi.org/10.3390/su12104278
Chicago/Turabian StyleRani, Pratibha, Arunodaya Raj Mishra, Abbas Mardani, Fausto Cavallaro, Dalia Štreimikienė, and Syed Abdul Rehman Khan. 2020. "Pythagorean Fuzzy SWARA–VIKOR Framework for Performance Evaluation of Solar Panel Selection" Sustainability 12, no. 10: 4278. https://doi.org/10.3390/su12104278
APA StyleRani, P., Mishra, A. R., Mardani, A., Cavallaro, F., Štreimikienė, D., & Khan, S. A. R. (2020). Pythagorean Fuzzy SWARA–VIKOR Framework for Performance Evaluation of Solar Panel Selection. Sustainability, 12(10), 4278. https://doi.org/10.3390/su12104278










