Effect of Gamma Irradiation on Structural Features and Dissolution of Nuclear Waste Na–Al–P Glasses in Water
Abstract
1. Introduction
2. Materials and Methods
3. Structural Properties of the Glasses before and after Irradiation
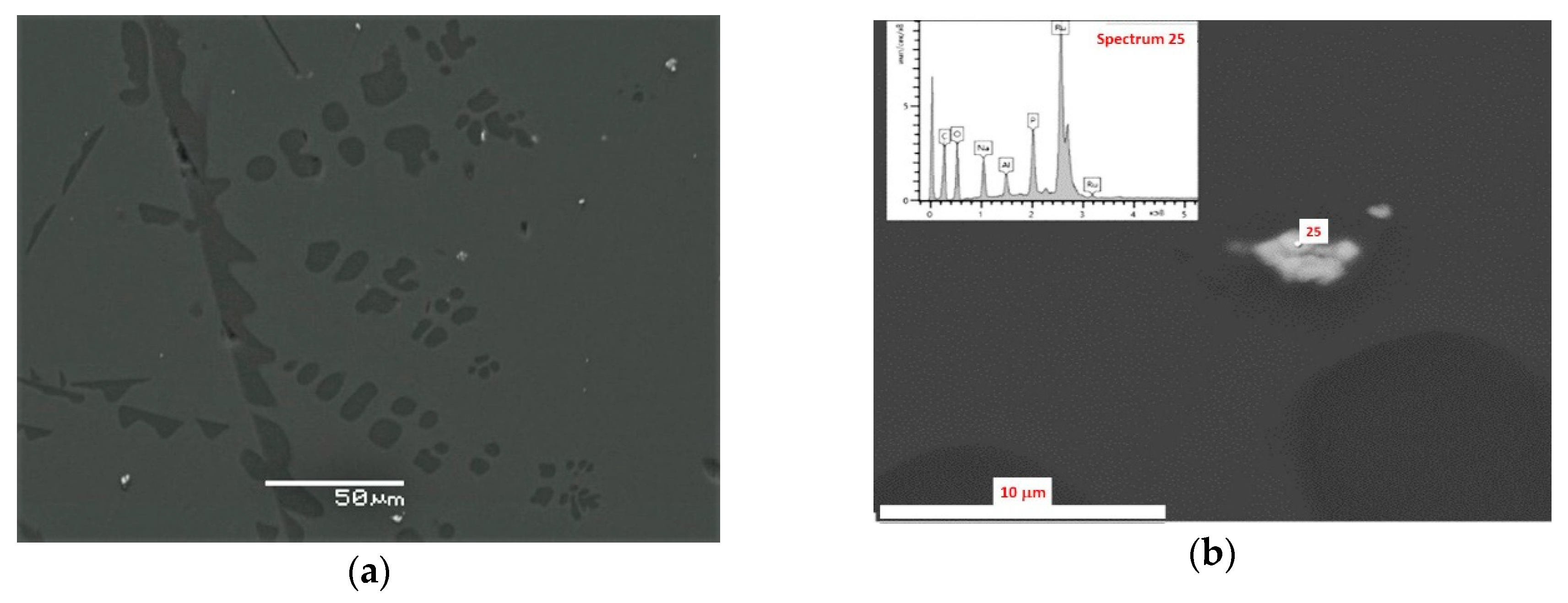
3.1. SEM/EDS Data
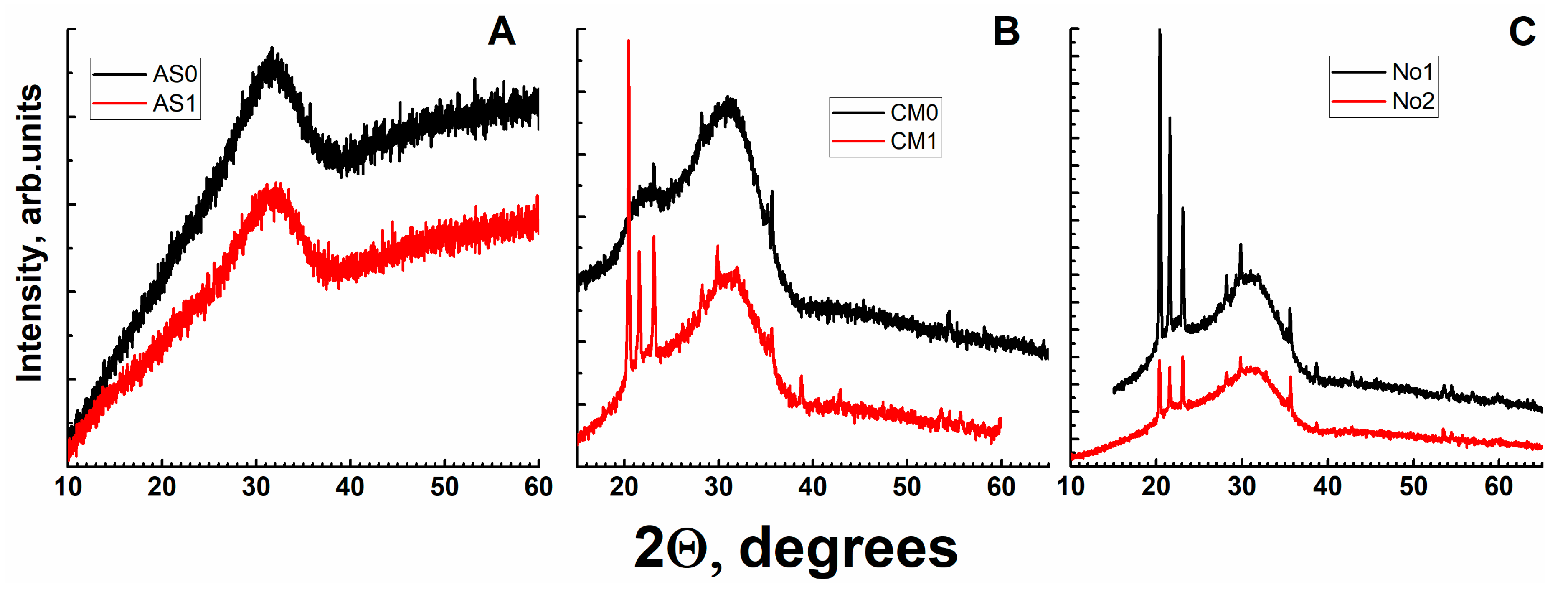
3.2. X-ray Diffraction
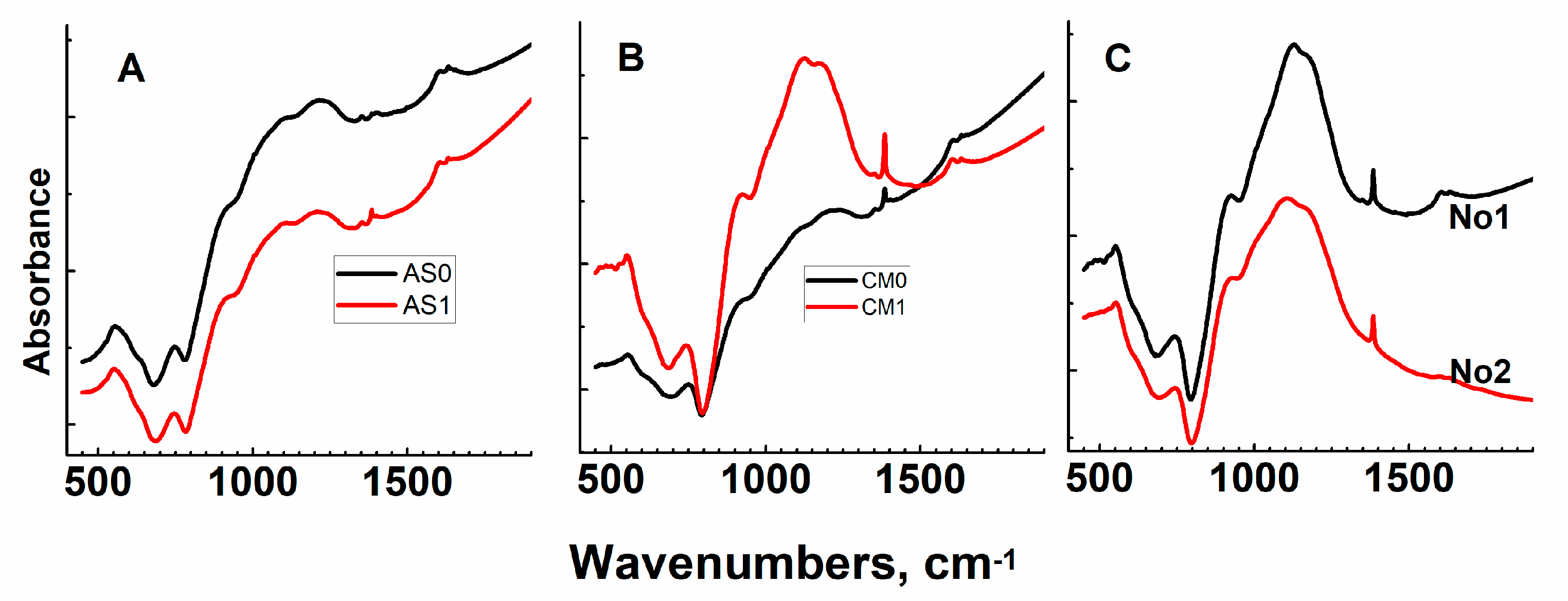
3.3. Raman and Infrared Spectroscopy
4. Leaching and Dissolution
4.1. Hydrolytic Durability
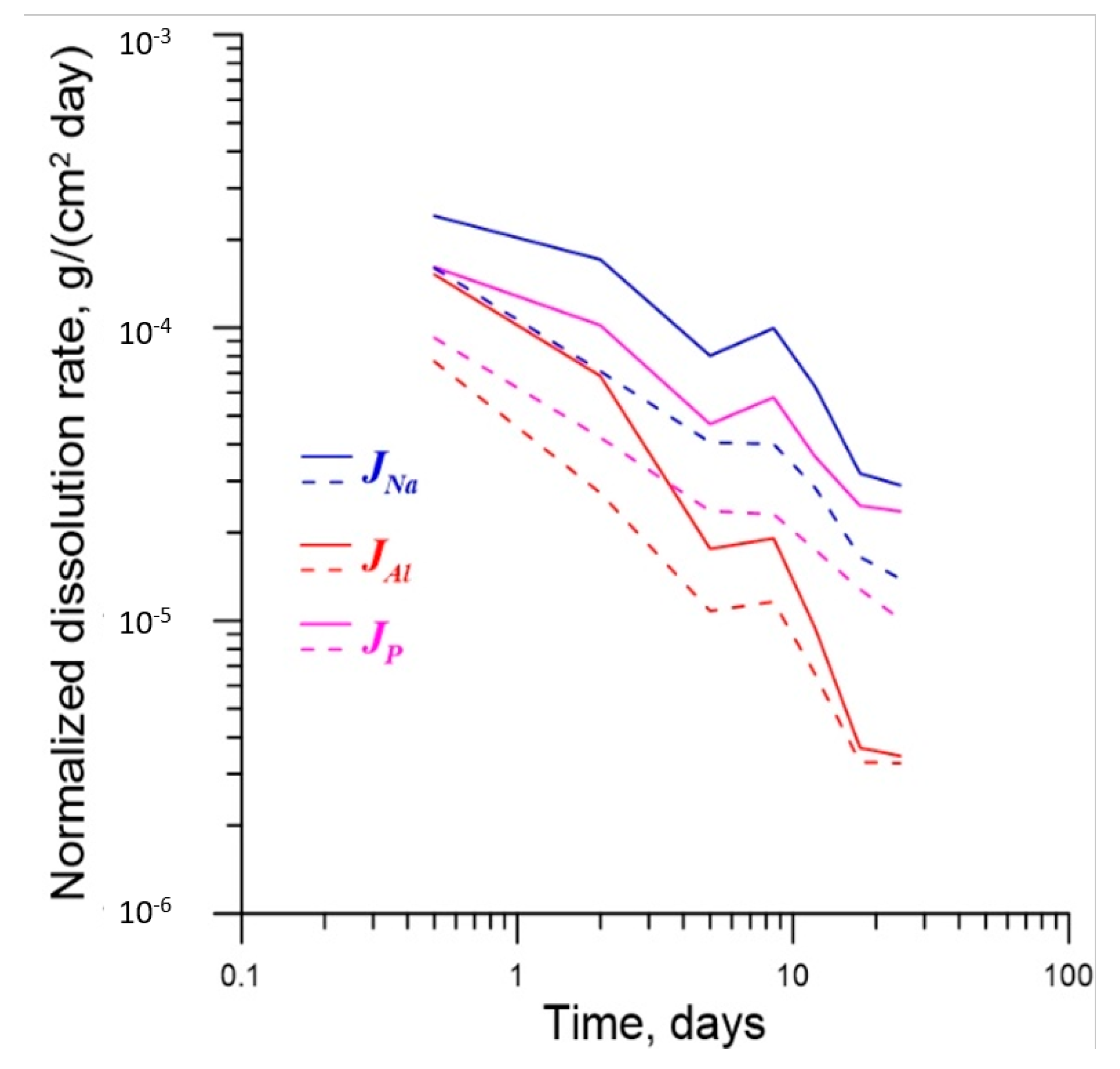
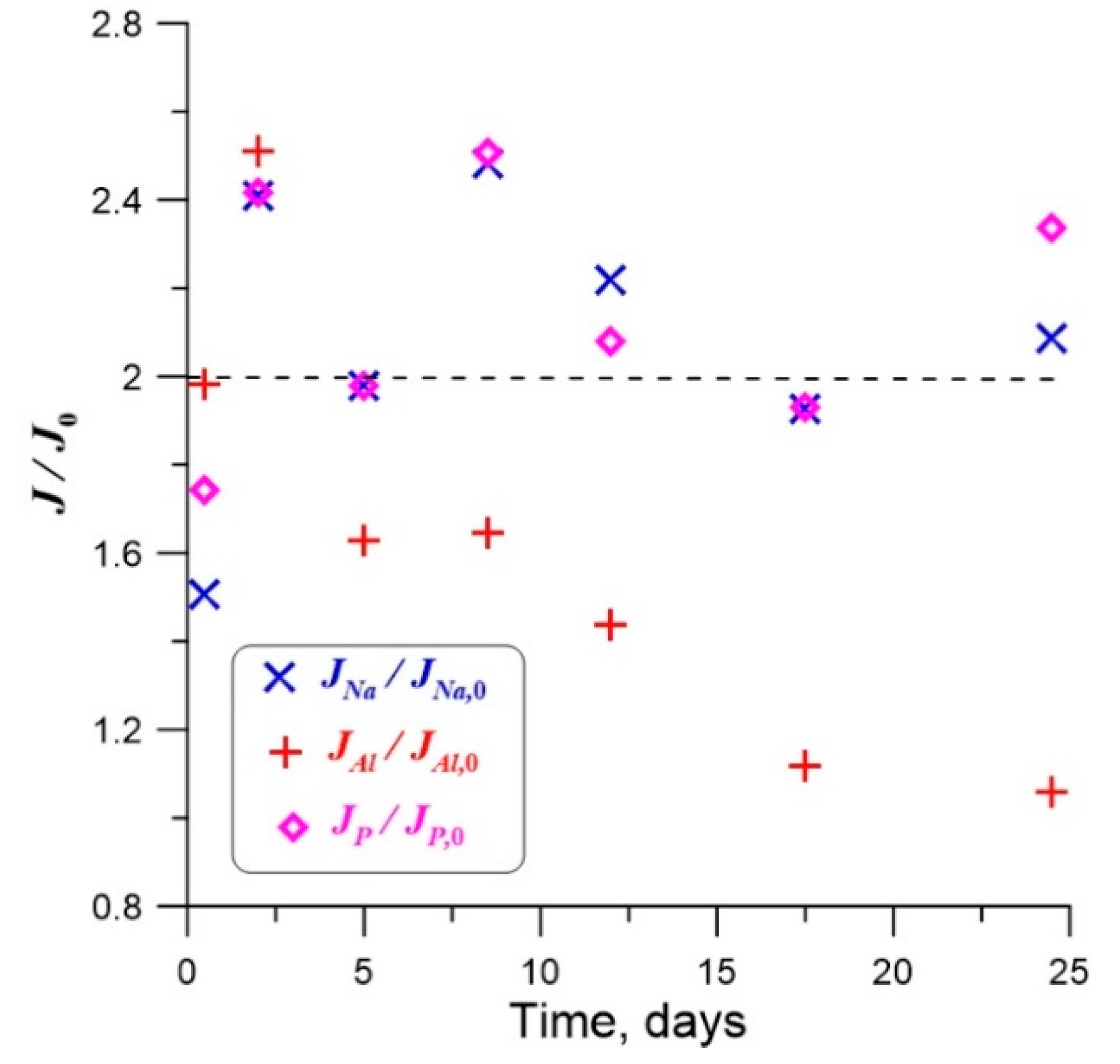
4.2. Effect of γ-Radiation on Dissolution of Glass
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Raman and Infrared Spectra of Sodium–Aluminum–Phosphate Glasses Investigated
Appendix A1. Raman Spectroscopy

Appendix A2. Infrared Spectroscopy
Appendix B. Integral Dissolution Rates of Sodium–Aluminum–Phosphate Glasses Investigated
| Sample | Time, d | Na | Al | Fe | P | Ca | Cr | Mn | Ni | La | U |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NAPas0 (90°С) | 1 | 2.41 × 10−4 | 1.52 × 10−4 | 1.75 × 10−6 | 1.61 × 10−4 | ||||||
| 3 | 1.94 × 10−4 | 9.64 × 10−5 | 7.09 × 10−7 | 1.22 × 10−4 | |||||||
| 7 | 1.29 × 10−4 | 5.14 × 10−5 | 3.49 × 10−7 | 7.91 × 10−5 | |||||||
| 10 | 1.20 × 10−4 | 4.17 × 10−5 | 2.89 × 10−7 | 7.28 × 10−5 | |||||||
| 14 | 1.04 × 10−4 | 3.25 × 10−5 | 2.83 × 10−7 | 6.24 × 10−5 | |||||||
| 21 | 7.99 × 10−5 | 2.29 × 10−5 | 2.05 × 10−7 | 4.98 × 10−5 | |||||||
| 28 | 6.72 × 10−5 | 1.80 × 10−5 | 1.55 × 10−7 | 4.32 × 10−5 | |||||||
| NAPas1 (90°С) | 1 | 1.60 × 10−4 | 7.67 × 10−5 | 1.34 × 10−5 | 9.24 × 10−5 | ||||||
| 3 | 1.01 × 10−4 | 4.37 × 10−5 | 6.12 × 10−6 | 5.89 × 10−5 | |||||||
| 7 | 6.63 × 10−5 | 2.49 × 10−5 | 3.03 × 10−6 | 3.88 × 10−5 | |||||||
| 10 | 5.84 × 10−5 | 2.09 × 10−5 | 2.40 × 10−6 | 3.41 × 10−5 | |||||||
| 14 | 4.99 × 10−5 | 1.68 × 10−5 | 1.83 × 10−6 | 2.93 × 10−5 | |||||||
| 21 | 3.88 × 10−5 | 1.23 × 10−5 | 1.32 × 10−6 | 2.38 × 10−5 | |||||||
| 28 | 3.25 × 10−5 | 1.01 × 10−5 | 1.13 × 10−6 | 2.04 × 10−5 | |||||||
| NAPcm0 (90°С) | 1 | 1.57 × 10−4 | 6.28 × 10−5 | 4.53 × 10−5 | 7.98 × 10−5 | 5.90 × 10−5 | 6.30 × 10−5 | 6.98 × 10−5 | 5.40 × 10−5 | 2.50 × 10−5 | 8.07 × 10−5 |
| 3 | 9.93 × 10−5 | 3.86 × 10−5 | 2.43 × 10−5 | 5.17 × 10−5 | 2.31 × 10−5 | 3.83 × 10−5 | 3.13 × 10−5 | 3.37 × 10−5 | 1.42 × 10−5 | 5.11 × 10−5 | |
| 7 | 6.04 × 10−5 | 2.29 × 10−5 | 1.36 × 10−5 | 3.16 × 10−5 | 2.88 × 10−5 | 2.25 × 10−5 | 1.50 × 10−5 | 1.99 × 10−5 | 7.57 × 10−6 | 3.15 × 10−5 | |
| 10 | 5.47 × 10−5 | 1.93 × 10−5 | 1.02 × 10−5 | 2.78 × 10−5 | 6.81 × 10−5 | 1.74 × 10−5 | 1.24 × 10−5 | 1.84 × 10−5 | 6.10 × 10−6 | 2.74 × 10−5 | |
| 14 | 3.94 × 10−5 | 1.39 × 10−5 | 7.44 × 10−6 | 2.01 × 10−5 | 6.42 × 10−5 | 1.25 × 10−5 | 9.02 × 10−6 | 1.32 × 10−5 | 4.42 × 10−6 | 2.04 × 10−5 | |
| 21 | 3.20 × 10−5 | 1.05 × 10−5 | 5.23 × 10−6 | 1.81 × 10−5 | 4.28 × 10−5 | 8.40 × 10−6 | 6.10 × 10−6 | 9.43 × 10−6 | 2.99 × 10−6 | 1.52 × 10−5 | |
| 28 | 2.76 × 10−5 | 8.67 × 10−6 | 4.21 × 10−6 | 1.62 × 10−5 | 3.21 × 10−5 | 6.34 × 10−6 | 4.64 × 10−6 | 7.51 × 10−6 | 2.41 × 10−6 | 1.25 × 10−5 | |
| NAPcm0 (25°С) | 1 | 2.23 × 10−5 | 8.16 × 10−6 | 7.37 × 10−6 | 1.31 × 10−5 | 9.72 × 10−5 | 1.14 × 10−6 | 7.86 × 10−6 | 7.03 × 10−6 | 6.25 × 10−6 | 1.19 × 10−5 |
| 3 | 1.34 × 10−5 | 4.64 × 10−6 | 3.96 × 10−6 | 7.67 × 10−6 | 5.09 × 10−5 | 7.58 × 10−7 | 4.82 × 10−6 | 4.21 × 10−6 | 2.40 × 10−6 | 7.94 × 10−6 | |
| 7 | 1.08 × 10−5 | 3.56 × 10−6 | 2.93 × 10−6 | 6.30 × 10−6 | 2.83 × 10−5 | 4.87 × 10−7 | 4.90 × 10−6 | 4.40 × 10−6 | 1.17 × 10−6 | 5.10 × 10−6 | |
| 10 | 1.04 × 10−5 | 3.46 × 10−6 | 2.86 × 10−6 | 6.16 × 10−6 | 2.67 × 10−5 | 4.55 × 10−7 | 6.34 × 10−6 | 5.20 × 10−6 | 1.48 × 10−6 | 4.76 × 10−6 | |
| 14 | 9.24 × 10−6 | 3.13 × 10−6 | 2.56 × 10−6 | 5.63 × 10−6 | 2.75 × 10−5 | 4.06 × 10−7 | 6.14 × 10−6 | 4.91 × 10−6 | 1.41 × 10−6 | 4.25 × 10−6 | |
| 21 | 7.78 × 10−6 | 2.67 × 10−6 | 2.08 × 10−6 | 5.13 × 10−6 | 1.85 × 10−5 | 3.25 × 10−7 | 5.84 × 10−6 | 4.50 × 10−6 | 9.84 × 10−7 | 3.40 × 10−6 | |
| 28 | 6.93 × 10−6 | 2.38 × 10−6 | 1.80 × 10−6 | 4.73 × 10−6 | 1.40 × 10−5 | 2.84 × 10−7 | 5.77 × 10−6 | 4.24 × 10−6 | 7.73 × 10−7 | 2.98 × 10−6 | |
| NAPcm (90°С) | 1 | 1.40 × 10−4 | 6.96 × 10−5 | 3.85 × 10−5 | 7.67 × 10−5 | 4.31 × 10−6 | 6.26 × 10−5 | 3.40 × 10−5 | 8.89 × 10−5 | 2.89 × 10−5 | 6.01 × 10−5 |
| 3 | 8.68 × 10−5 | 4.21 × 10−5 | 2.05 × 10−5 | 4.76 × 10−5 | 3.36 × 10−4 | 3.79 × 10−5 | 1.67 × 10−5 | 5.49 × 10−5 | 1.49 × 10−5 | 3.89 × 10−5 | |
| 7 | 5.26 × 10−5 | 2.48 × 10−5 | 1.10 × 10−5 | 2.88 × 10−5 | 1.48 × 10−4 | 2.16 × 10−5 | 8.14 × 10−6 | 3.20 × 10−5 | 8.14 × 10−6 | 2.38 × 10−5 | |
| 10 | 4.55 × 10−5 | 2.13 × 10−5 | 8.70 × 10−6 | 2.48 × 10−5 | 1.04 × 10−4 | 1.83 × 10−5 | 6.17 × 10−6 | 2.74 × 10−5 | 6.61 × 10−6 | 2.06 × 10−5 | |
| 14 | 3.87 × 10−5 | 1.77 × 10−5 | 6.78 × 10−6 | 2.09 × 10−5 | 1.01 × 10−4 | 1.51 × 10−5 | 4.40 × 10−6 | 2.26 × 10−5 | 5.13 × 10−6 | 1.73 × 10−5 | |
| 21 | 2.95 × 10−5 | 1.32 × 10−5 | 4.73 × 10−6 | 1.65 × 10−5 | 6.73 × 10−5 | 1.09 × 10−5 | 3.04 × 10−6 | 1.63 × 10−5 | 3.48 × 10−6 | 1.25 × 10−5 | |
| 28 | 2.48 × 10−5 | 1.09 × 10−5 | 3.82 × 10−6 | 1.43 × 10−5 | 5.06 × 10−5 | 8.96 × 10−6 | 2.31 × 10−6 | 1.34 × 10−5 | 3.03 × 10−6 | 1.02 × 10−5 | |
| NAPcm1 (25°С) | 1 | 2.13 × 10−5 | 8.53 × 10−6 | 7.96 × 10−6 | 1.26 × 10−5 | 5.56 × 10−5 | 1.09 × 10−6 | 6.06 × 10−6 | 1.04 × 10−5 | 2.76 × 10−6 | 9.92 × 10−6 |
| 3 | 1.29 × 10−5 | 5.02 × 10−6 | 4.63 × 10−6 | 7.75 × 10−6 | 5.29 × 10−5 | 7.25 × 10−7 | 3.88 × 10−6 | 5.98 × 10−6 | 1.09 × 10−6 | 6.61 × 10−6 | |
| 7 | 9.57 × 10−6 | 3.55 × 10−6 | 3.13 × 10−6 | 5.83 × 10−6 | 2.38 × 10−5 | 4.66 × 10−7 | 2.73 × 10−6 | 4.60 × 10−6 | 5.43 × 10−7 | 4.25 × 10−6 | |
| 10 | 9.02 × 10−6 | 3.29 × 10−6 | 2.82 × 10−6 | 5.57 × 10−6 | 1.71 × 10−5 | 4.35 × 10−7 | 2.85 × 10−6 | 5.08 × 10−6 | 4.32 × 10−7 | 3.97 × 10−6 | |
| 14 | 8.32 × 10−6 | 2.86 × 10−6 | 2.38 × 10−6 | 4.95 × 10−6 | 1.73 × 10−5 | 3.88 × 10−7 | 3.03 × 10−6 | 5.13 × 10−6 | 3.46 × 10−7 | 3.54 × 10−6 | |
| 21 | 6.62 × 10−6 | 2.21 × 10−6 | 1.79 × 10−6 | 4.19 × 10−6 | 1.17 × 10−5 | 3.11 × 10−7 | 2.55 × 10−6 | 4.12 × 10−6 | 2.55 × 10−7 | 2.83 × 10−6 | |
| 28 | 5.74 × 10−6 | 1.87 × 10−6 | 1.35 × 10−6 | 3.80 × 10−6 | 8.93 × 10−6 | 2.72 × 10−7 | 2.31 × 10−6 | 3.65 × 10−6 | 2.10 × 10−7 | 2.48 × 10−6 | |
| NAP1 | 1 | 1.67 × 10−4 | 7.31 × 10−5 | 5.49 × 10−5 | 9.11 × 10−5 | 4.17 × 10−6 | 9.61 × 10−5 | 5.40 × 10−5 | 7.45 × 10−5 | 3.34 × 10−5 | 1.13 × 10−4 |
| 3 | 1.01 × 10−4 | 4.25 × 10−5 | 2.90 × 10−5 | 5.58 × 10−5 | 2.78 × 10−6 | 5.73 × 10−5 | 2.54 × 10−5 | 4.42 × 10−5 | 1.44 × 10−5 | 6.40 × 10−5 | |
| 7 | 6.02 × 10−5 | 2.43 × 10−5 | 1.58 × 10−5 | 3.33 × 10−5 | 3.75 × 10−5 | 3.35 × 10−5 | 1.22 × 10−5 | 2.52 × 10−5 | 7.11 × 10−6 | 3.72 × 10−5 | |
| 10 | 5.31 × 10−5 | 2.10 × 10−5 | 1.25 × 10−5 | 2.92 × 10−5 | 3.28 × 10−5 | 2.85 × 10−5 | 8.95 × 10−6 | 2.08 × 10−5 | 5.42 × 10−6 | 3.21 × 10−5 | |
| 14 | 4.53 × 10−5 | 1.76 × 10−5 | 1.05 × 10−5 | 2.52 × 10−5 | 3.21 × 10−5 | 2.42 × 10−5 | 7.34 × 10−6 | 1.67 × 10−5 | 4.93 × 10−6 | 2.66 × 10−5 | |
| 21 | 3.44 × 10−5 | 1.26 × 10−5 | 7.20 × 10−6 | 2.02 × 10−5 | 2.16 × 10−5 | 1.72 × 10−5 | 4.95 × 10−6 | 1.17 × 10−5 | 3.31 × 10−6 | 1.90 × 10−5 | |
| 28 | 2.91 × 10−5 | 1.00 × 10−5 | 5.41 × 10−6 | 1.78 × 10−5 | 1.64 × 10−5 | 1.35 × 10−5 | 3.75 × 10−6 | 9.10 × 10−6 | 2.51 × 10−6 | 1.50 × 10−5 | |
| NAP2 (90°С) | 1 | 1.78 × 10−4 | 8.75 × 10−5 | 5.01 × 10−5 | 9.77 × 10−5 | 1.21 × 10−5 | 7.95 × 10−5 | 4.58 × 10−5 | 6.98 × 10−5 | 1.68 × 10−5 | 7.76 × 10−5 |
| 3 | 1.12 × 10−4 | 5.59 × 10−5 | 3.12 × 10−5 | 6.34 × 10−5 | 4.03 × 10−6 | 5.18 × 10−5 | 2.90 × 10−5 | 4.69 × 10−5 | 1.56 × 10−5 | 5.05 × 10−5 | |
| 7 | 6.51 × 10−5 | 3.15 × 10−5 | 1.60 × 10−5 | 3.68 × 10−5 | 1.73 × 10−6 | 2.85 × 10−5 | 1.44 × 10−5 | 2.64 × 10−5 | 7.78 × 10−6 | 2.94 × 10−5 | |
| 10 | 5.59 × 10−5 | 2.67 × 10−5 | 1.27 × 10−5 | 3.15 × 10−5 | 1.69 × 10−5 | 2.40 × 10−5 | 1.10 × 10−5 | 2.24 × 10−5 | 6.01 × 10−6 | 2.55 × 10−5 | |
| 14 | 4.77 × 10−5 | 2.25 × 10−5 | 9.82 × 10−6 | 2.67 × 10−5 | 2.13 × 10−5 | 1.97 × 10−5 | 8.38 × 10−6 | 1.85 × 10−5 | 4.69 × 10−6 | 2.14 × 10−5 | |
| 21 | 3.55 × 10−5 | 1.63 × 10−5 | 6.81 × 10−6 | 2.04 × 10−5 | 1.48 × 10−5 | 1.41 × 10−5 | 5.64 × 10−6 | 1.33 × 10−5 | 3.16 × 10−6 | 1.54 × 10−5 | |
| 28 | 2.93 × 10−5 | 1.33 × 10−5 | 5.37 × 10−6 | 1.72 × 10−5 | 1.12 × 10−5 | 1.12 × 10−5 | 4.27 × 10−6 | 1.06 × 10−5 | 2.55 × 10−6 | 1.23 × 10−5 |
| Al | Ca | Cr | Fe | La | Mn | Na | Ni | P | Ru | U |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.01 | 0.01 | 0.001 | 0.01 | 0.001 | 0.001 | 0.01 | 0.001 | 0.02 | 0.05 | 0.05 |
References
- IAEA. Energy, Electricity and Nuclear Power Estimates for the Period. up to 2050, 2019th ed.; IAEA: Vienna, Austria, 2019; p. 139. [Google Scholar]
- NEA. Nuclear Energy Data; OECD, NEA: Paris, France, 2019; p. 117. [Google Scholar]
- Batorshin, G.S.; Kirillov, S.N.; Smirnov, I.V.; Sarychev, G.A.; Tananaev, I.G.; Fedorova, O.V.; Myasoedov, B.F. Integrated separation of valuable components from technogenic radioactive waste as an option to create a cost-effective nuclear fuel cycle. Radiat. Saf. Issues 2015, 3, 30–36. (in Russian). [Google Scholar]
- IAEA PRIS. The Power Reactor Information System. Available online: https://pris.iaea.org/PRIS/home.aspx (accessed on 6 April 2020).
- IAEA. Status and Trends in Spent Fuel and Radioactive Waste Management; IAEA: Vienna, Austria, 2018; p. 59. [Google Scholar]
- Ojovan, M.I.; Lee, W.E.; Kalmykov, S.N. An. Introduction to Nuclear Waste Immobilisation, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2005; p. 497. [Google Scholar]
- Phillips, J.R.; Korinny, A.; Depisch, F.; Drace, Z. Update of the INPRO methodology in the area of waste management. Sustainability 2018, 10, 9. [Google Scholar] [CrossRef]
- Diaz-Maurin, F.; Ewing, R.C. Mission Impossible? Socio-technical integration of nuclear waste geological disposal systems. Sustainability 2018, 10, 39. [Google Scholar] [CrossRef]
- Fedorov, Y.S.; Zil’berman, B.Y.; Aloi, A.S.; Puzikov, E.A.; Shadrin, A.Y.; Alyapyshev, M.Y. Problems of modernization of spent nuclear fuel extraction processing. Russ. J. Gen. Chem. 2011, 81, 1932–1948. [Google Scholar] [CrossRef]
- Kopyrin, A.A.; Karelin, A.I.; Karelin, V.A. Technology for the Production and Radio-Chemical Processing of Nuclear Fuel; Atomizdat Publishing House CJSC: Moscow, Russia, 2008; p. 576. [Google Scholar]
- Vashman, A.A.; Demine, A.V.; Krylova, N.V.; Kushnikov, V.V.; Matyunin, Y.I.; Poluektov, P.P.; Polyakov, A.S.; Teterin, E.G. Phosphate Glasses with Radioactive Waste; CNIIatominform: Moscow, Russia, 1997; p. 172. [Google Scholar]
- Remizov, M.B.; Kozlov, P.V.; Logunov, M.V.; Koltyshev, V.K.; Korchenkin, K.K. Conceptual and technical solutions for the creation of Mayak plants for vitrification of current and accumulated liquid HLW. Radiat. Saf. Issues 2014, 3, 17–25. [Google Scholar]
- Kozlov, P.V.; Remizov, M.B.; Belanova, E.A.; Vlasova, N.V.; Orlova, V.A.; Martynov, K.V. Modification of the composition of aluminophosphate glasses with HLW simulators to increase their stability. 1. The effect of modifiers on the viscosity and crystallization ability of melts. Probl. Radiat. Saf. 2019, 1, 3–15. (in Russian). [Google Scholar]
- Laverov, N.P.; Yudintsev, S.V.; Kochkin, B.T.; Malkovsky, V.I. The Russian strategy of using crystalline rock as a repository for nuclear waste. Elements 2016, 12, 253–256. [Google Scholar] [CrossRef]
- Kochkin, B.T.; Malkovsky, V.I.; Yudintsev, S.V. Scientific Basis for Assessing the Safety of the Geological Isolation of Long-Lived Radioactive Waste (Yenisei Project); IGEM RAS: Moscow, Russia, 2017; p. 384. [Google Scholar]
- Lutze, W. Radioactive Waste Forms for the Future; Elsevier Science Publishers, B.V.: Amsterdam, The Netherlands, 1988; pp. 1–160. [Google Scholar]
- Donald, I.W. Waste Immobilisation in Glass and Ceramic Based Hosts; Wiley: Chichester, UK, 2010. [Google Scholar]
- Jantzen, C.M. Development of glass matrices for HLW radioactive wastes. In Handbook of Advanced Radioactive Waste Conditioning Technologies; Woodhead: Cambridge, UK, 2011; pp. 230–292. [Google Scholar]
- Sobolev, I.A.; Ojovan, M.I.; Scherbatova, T.D.; Batyukhnova, O.G. Glasses for Radioactive Waste; Energoatomizdat: Moscow, Russia, 1999. [Google Scholar]
- Gin, S.; Jollivet, P.; Tribet, M.; Peuget, S.; Schuller, S. Radionuclides containment in nuclear glasses: An overview. Radiochim. Acta 2017, 105, 927–959. [Google Scholar] [CrossRef]
- Laverov, N.P.; Velichkin, V.I.; Omelyanenko, B.I.; Yudintsev, S.V.; Petrov, V.A.; Bychkov, A.V. Isolation of Spent Nuclear Materials: Geological and Geochemical Foundations; IFZ RAS: Moscow, Russia, 2008; p. 280. [Google Scholar]
- Ojovan, M.I.; Lee, W.E. New Developments in Glassy Nuclear Wasteforms; Nova: New York, NY, USA, 2007; p. 131. [Google Scholar]
- Caurant, D.; Loiseau, P.; Majérus, O.; Aubin-Cheval-donnet, V.; Bardez, I.; Quintas, A. Glasses, Glass-Ceramics and Ceramics for Immobilization of Highly Radioactive Nuclear Wastes; Nova: New York, NY, USA, 2009; p. 445. [Google Scholar]
- Jantzen, C.M.; Ojovan, M.I. On selection of matrix (wasteform) material for higher activity nuclear waste immobilization (Review). Russ. J. Inorg. Chem. 2019, 64, 1611–1624. [Google Scholar] [CrossRef]
- Gin, S.; Abdelouas, A.; Criscenti, L.J.; Ebert, W.L.; Ferrand, K.; Geisler, T.; Harrison, M.T.; Inagaki, Y.; Mitsui, S.; Mueller, K.T.; et al. An international initiative on long-term behavior of high-level nuclear waste glass. Mater. Today 2013, 16, 243–248. [Google Scholar] [CrossRef]
- Ojovan, M.I. On alteration rate renewal stage of nuclear waste glass corrosion. MRS Adv. 2020, 5, 111–120. [Google Scholar] [CrossRef]
- The Fifth National Report of the Russian Federation on the Fulfillment of Obligations Arising from the Joint Convention on the Safety of Spent Fuel Management and on the Safety of Radioactive Waste Management. Moscow. 2017. Available online: http://www.gosnadzor.ru/activity/international/national%20reports/Russian_Federation_rus.pdf (accessed on 6 April 2020). (In Russian).
- Dorogov, V.I.; Ponizov, A.V.; Khaperskaya, A.V. On the preparation of the fifth national report of the Russian Federation on the fulfillment of obligations arising from the Joint Convention on the Safety of Spent Fuel Management and on the Safety of Radioactive Waste Management. Radioact. Waste 2017, 1, 100–107. (In Russian) [Google Scholar]
- Kryukov, O.V.; Khaperskaya, A.V.; Dorofeev, A.N.; Ferapontov, A.V.; Kudryavtsev, E.G.; Linge, I.I.; Utkin, S.S.; Dorogov, V.I.; Sharafutdinov, R.B.; Ponizov, A.V.; et al. Fulfillment of Russia’s obligations under the Joint Convention on the Safety of Spent Fuel Management and on the Safety of Radioactive Waste Management. Radioact. Waste 2019, 1, 25–36. (In Russian) [Google Scholar]
- Kenneth, L.N.; Gregg, J.L. Advanced Separation Techniques for Nuclear Fuel Reprocessing and Radioactive Waste Treatment; Woodhead Publishing Limited: Cambridge, UK, 2011; p. 492. [Google Scholar]
- State Standard of Russian Federation. Waste Highly Radioactive Solidified. General Technical Requirements; GOST Р 50926-96; Standards Publishing: Moscow, Russia, 2013; p. 5. Available online: http://docs.cntd.ru/document/gost-r-50926-96 (accessed on 6 April 2020).
- State Standard of Russian Federation. Radioactive Waste. Determination of Chemical Resistance of Solidified High-Level Waste by Continuous Leaching; GOST Р 52126-2003; Standards Publishing: Moscow, Russia, 2003; p. 6. Available online: http://docs.cntd.ru/document/gost-r-52126-2003 (accessed on 6 April 2020).
- American Society for Testing and Materials. Standard Test. Method for Static Leaching of Monolithic Waste Forms for Disposal of Radioactive Waste; ASTM C 1220—98; ASTM International: West Conshohocken, PA, USA, 2004; p. 16. [Google Scholar]
- Martynov, K.V.; Nekrasov, A.N.; Kotelnikov, A.R.; Shiryaev, A.A.; Stefanovsky, S.V. Subliquidus phase relations in the low-alumina section of the Na2O–Al2O3–P2O5 system and the radioactive waste vitrification. Glas. Phys. Chem. 2018, 44, 591–600. [Google Scholar] [CrossRef]
- Remizov, M.B.; Myasoedov, B.F.; Nikonov, B.S.; Stefanovsky, S.V.; Belanova, E.A. Phase composition and structure of molybdenum-, copper- and cesium-containing sodium-aluminum-phosphate glass materials for immobilization of highly active waste from nuclear reactors. Phys. Chem. Glass 2014, 40, 707–717. [Google Scholar] [CrossRef]
- Yudintsev, S.V.; Malkovsky, V.I.; Mokhov, A.V. Hydrothermal transformations in an aluminophosphate glass matrix containing simulators of high-level radioactive wastes. Dokl. Earth Sci. 2016, 468, 503–506. [Google Scholar] [CrossRef]
- Stefanovsky, S.V.; Stefanovsky, O.; Remizov, M.; Kozlov, P.V.; Belanova, E.; Makarovsky, R.; Myasoedov, B. Sodium–aluminum–iron phosphate glasses as legacy high level waste forms. Prog. Nucl. Energy 2017, 94, 229–234. [Google Scholar] [CrossRef]
- Stefanovsky, S.V.; Stefanovsky, O.; Myasoedov, B.; Vinikurov, S.; Danilov, S.S.; Nikonov, B.; Maslakov, K.I.; Teterin, Y.A. The phase composition, structure, and hydrolytic durability of sodium-aluminum-(iron)-phosphate glassy materials doped with lanthanum, cerium, europium, and gadolinium oxides. J. Non-Cryst. Solids 2017, 471, 421–428. [Google Scholar] [CrossRef]
- Malkovsky, V.I.; Yudintsev, S.V.; Mokhov, A.V.; Pervukhina, A.M. Leaching of degraded matrices—Preservatives of highly radioactive waste based on Na-Al-P-glasses. At. Energy 2018, 123, 3–177. [Google Scholar]
- Malkovsky, V.I.; Yudintsev, S.V.; Aleksandrova, E.V. Influence of Na-Al-Fe-P glass alteration in hot non-saturated vapor on leaching of vitrified radioactive wastes in water. J. Nucl. Mater. 2018, 508, 212–218. [Google Scholar] [CrossRef]
- Stefanovsky, S.V.; Prusakov, I.L.; Stefanovsky, O.I.; Kadyko, M.I.; Averin, A.A.; Makarenkov, V.I.; Trigub, A.L.; Nikonov, B.S. The structure of rhenium-containing sodium alumino (iron) phosphate glasses. Int. J. Appl. Glass Sci. 2019, 10, 479–487. [Google Scholar] [CrossRef]
- Stefanovsky, S.V.; Stefanovsky, O.I.; Danilov, S.S.; Kadyko, M.I. Phosphate-based glasses and glass ceramics for immobilization of lanthanides and actinides. Ceram. Int. 2019, 45, 9331–9338. [Google Scholar] [CrossRef]
- Matyunin, Y.I. The Dissertation for the Degree of Candidate of Chemical Sciences; VNIINM: Moscow, Russia, 2000. [Google Scholar]
- Stefanovsky, S.V.; Stefanovskaya, O.I.; Vinokurov, S.E.; Danilov, S.S.; Myasoedov, B.F. Phase composition, structure, and hydrolytic durability of glasses in the Na2O-Al2O3-(Fe2O3)-P2O5 system at replacement of Al2O3 by Fe2O3. Radiochemistry 2015, 57, 348–355. [Google Scholar] [CrossRef]
- Danilov, S.S.; Vinokurov, S.E.; Stefanovsky, S.V.; Myasoedov, B.F. Hydrolytic stability of uranium-containing sodium aluminum (iron) phosphate glasses. Radiochemistry 2017, 59, 259–263. [Google Scholar] [CrossRef]
- Poluektov, P.P.; Schmidt, O.V.; Kascheev, V.A.; Ojovan, M.I. Modelling aqueous corrosion of nuclear waste phosphate glass. J. Nucl. Mater. 2017, 484, 357–366. [Google Scholar] [CrossRef]
- Boldyrev, K.A.; Martynov, K.V.; Kryuchkov, D.V.; Zakharova, E.V.; Ermolaev, V.M. Numerical modeling of leaching of aluminophosphate glass in the batch mode in the presence of bentonite. Radiochemistry 2019, 61, 612–618. [Google Scholar] [CrossRef]
- Van Iseghem, P.; Grambow, B. The long-term corrosion and modeling of two simulated Belgian reference high-level waste glasses. Res. Soc. Symp. Proc. 1988, 176, 631–639. [Google Scholar]
- Frugier, P.; Chave, T.; Gin, S.; Lartigue, J.-E. Application of the GRAAL model to leaching experiments with SON68 nuclear glass in initially pure water. J. Nucl. Mater. 2009, 392, 552–567. [Google Scholar] [CrossRef]
- Ojovan, M.I. Mass spectrometric evidencing on modified random network microstructure and medium range order in silicate glasses. J. Non-Cryst. Solids 2016, 434, 71–78. [Google Scholar] [CrossRef]
- Gin, S.; Ribet, I.; Peuget, S.; Delaye, J.-M. Long-term behavior of glasses. In Nuclear Waste Conditioning; CEA: Paris, France, 2009; pp. 51–64. [Google Scholar]
- Fournier, M.; Gin, S.; Frugier, P. Resumption of nuclear glass alteration: State of the art. J. Nucl. Mater. 2014, 448, 348–363. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Wright, M.H. Practical Optimization; Academic Press Inc.: London, UK, 1981; p. 401. [Google Scholar]
- Zotov, A.V.; Levin, K.A.; Magazina, L.O.; Mukhamet-Galeev, A.P.; Omelianenko, B.I.; Samotoin, N.D.; Shapovalov, Y.B. Interaction of aluminophosphate glass with water at elevated temperatures. Geochem. Int. 1996, 34, 805–817. [Google Scholar]
- Charnes, A.; Frome, E.L.; Yu, P.L. The equivalence of generalized least squares and maximum likelihood estimates in the exponential family. J. Am. Stat. Assoc. 1976, 71, 169–171. [Google Scholar] [CrossRef]
- Ojovan, M.I.; Pankov, A.S.; Lee, W.E. The ion exchange phase in corrosion of nuclear waste glasses. J. Nucl. Mater. 2006, 358, 57–68. [Google Scholar] [CrossRef]
- Peuget, S.; Tribet, M.; Mougnaud, S.; Miro, S.; Jégou, C. Radiations effects in ISG glass: From structural changes to long-term aqueous behavior. NPJ Mater. Degrad. 2018, 2, 23. [Google Scholar] [CrossRef]
- Sun, K.; Wang, L.M.; Ewing, R.C. Microstructure and chemistry of an aluminophosphate glass waste form under electron beam irradiation. Mater. Res. Soc. Symp. Proc. 2004, 807, 121–126. [Google Scholar] [CrossRef]




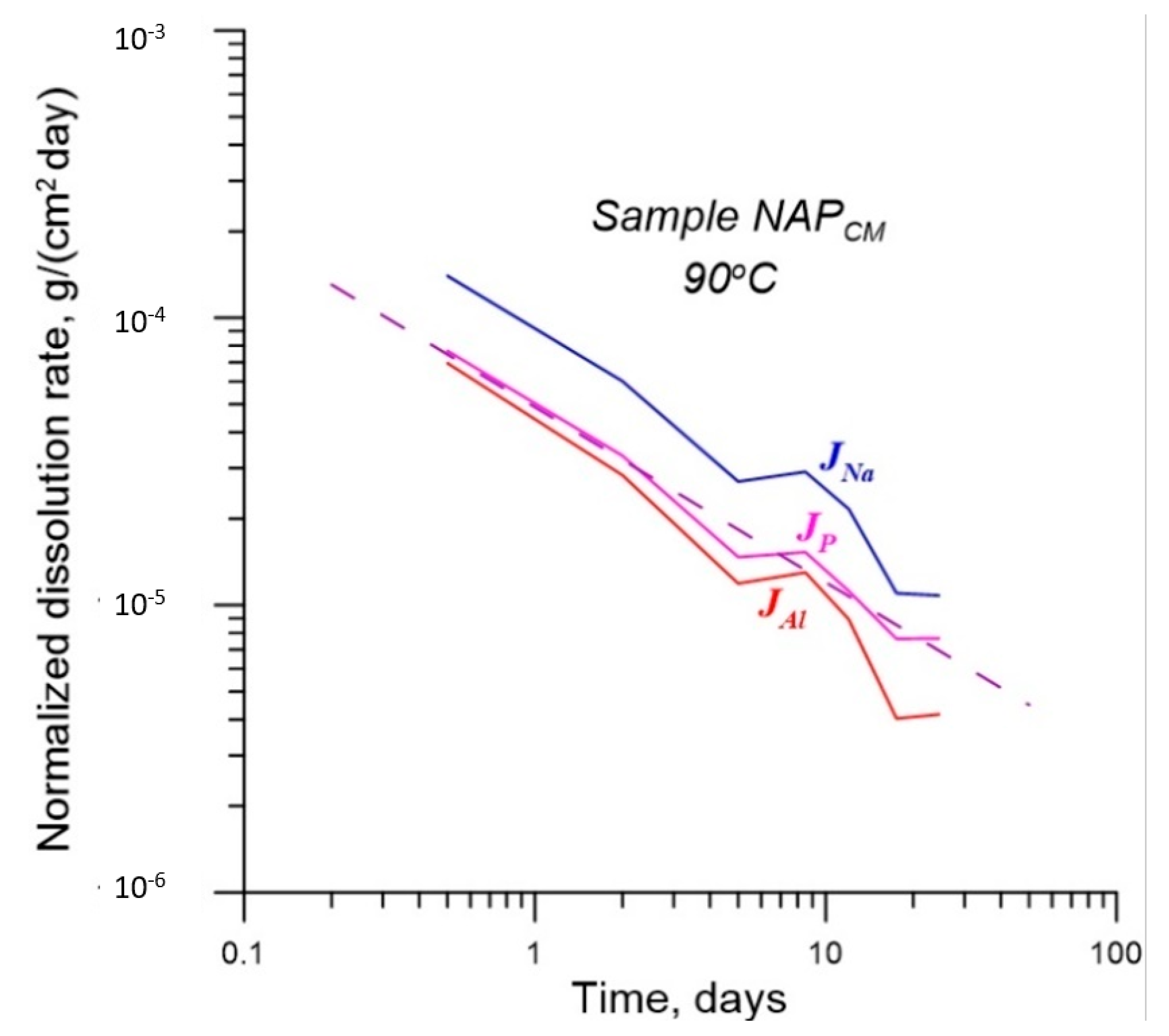
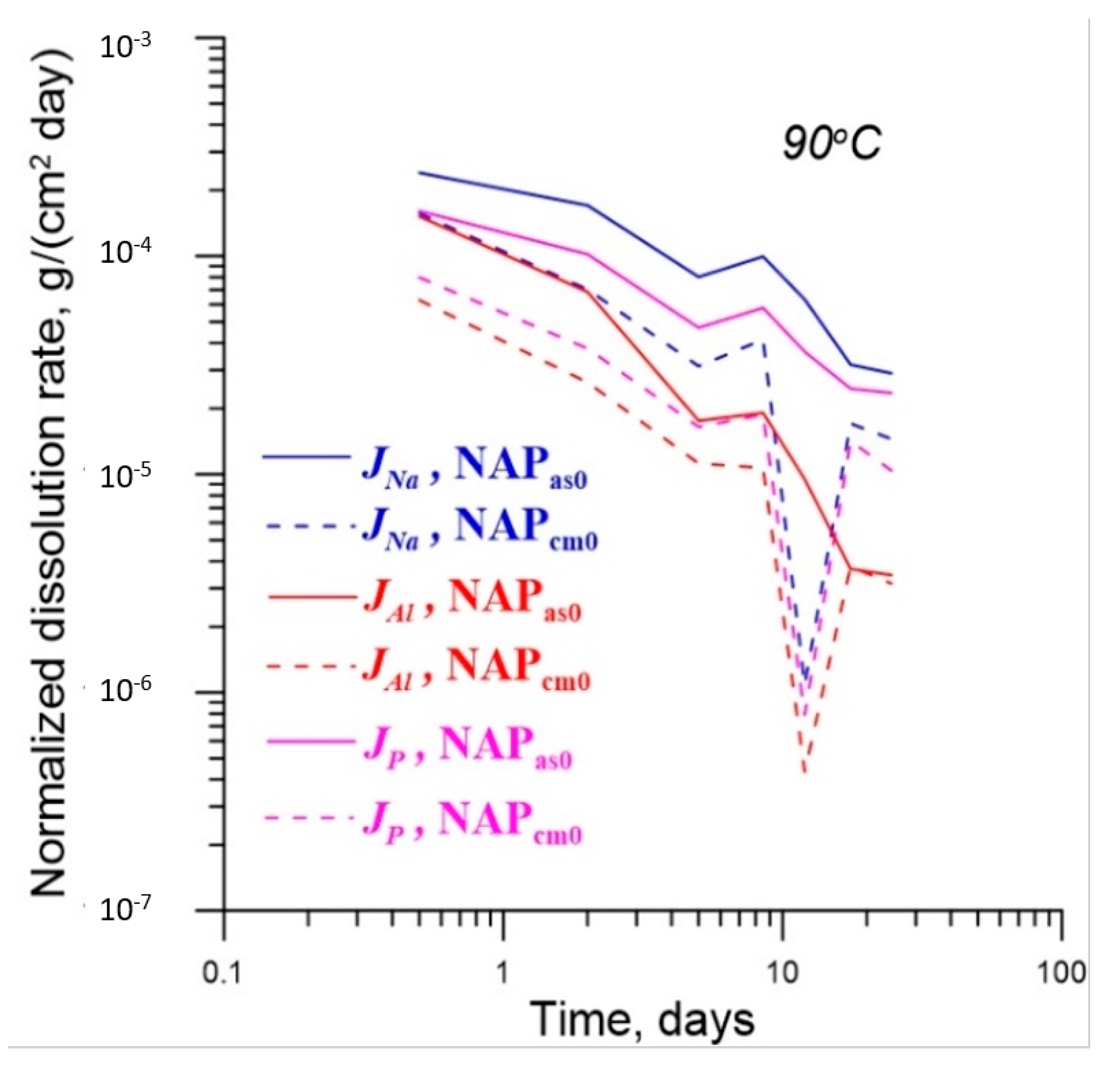
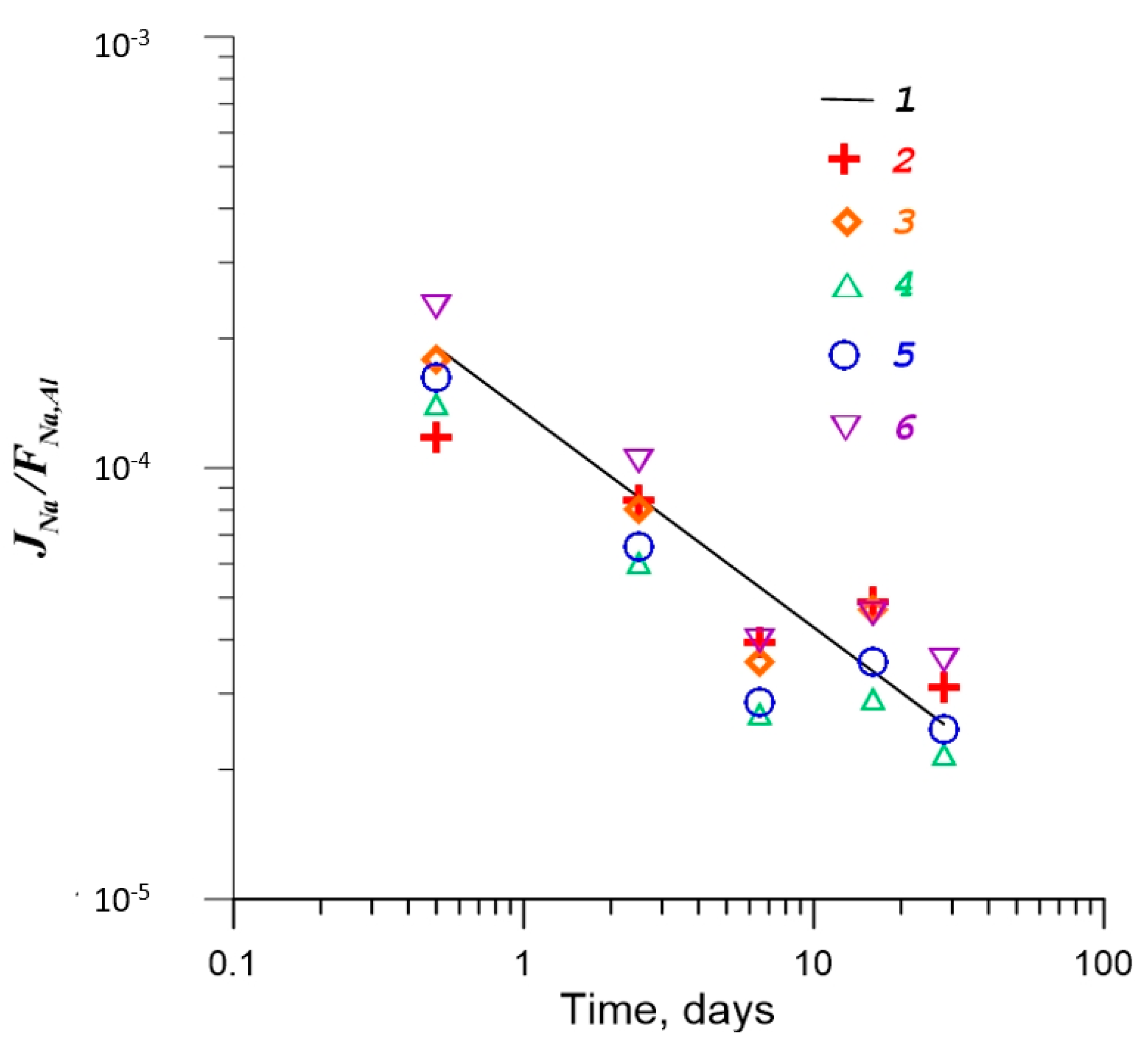
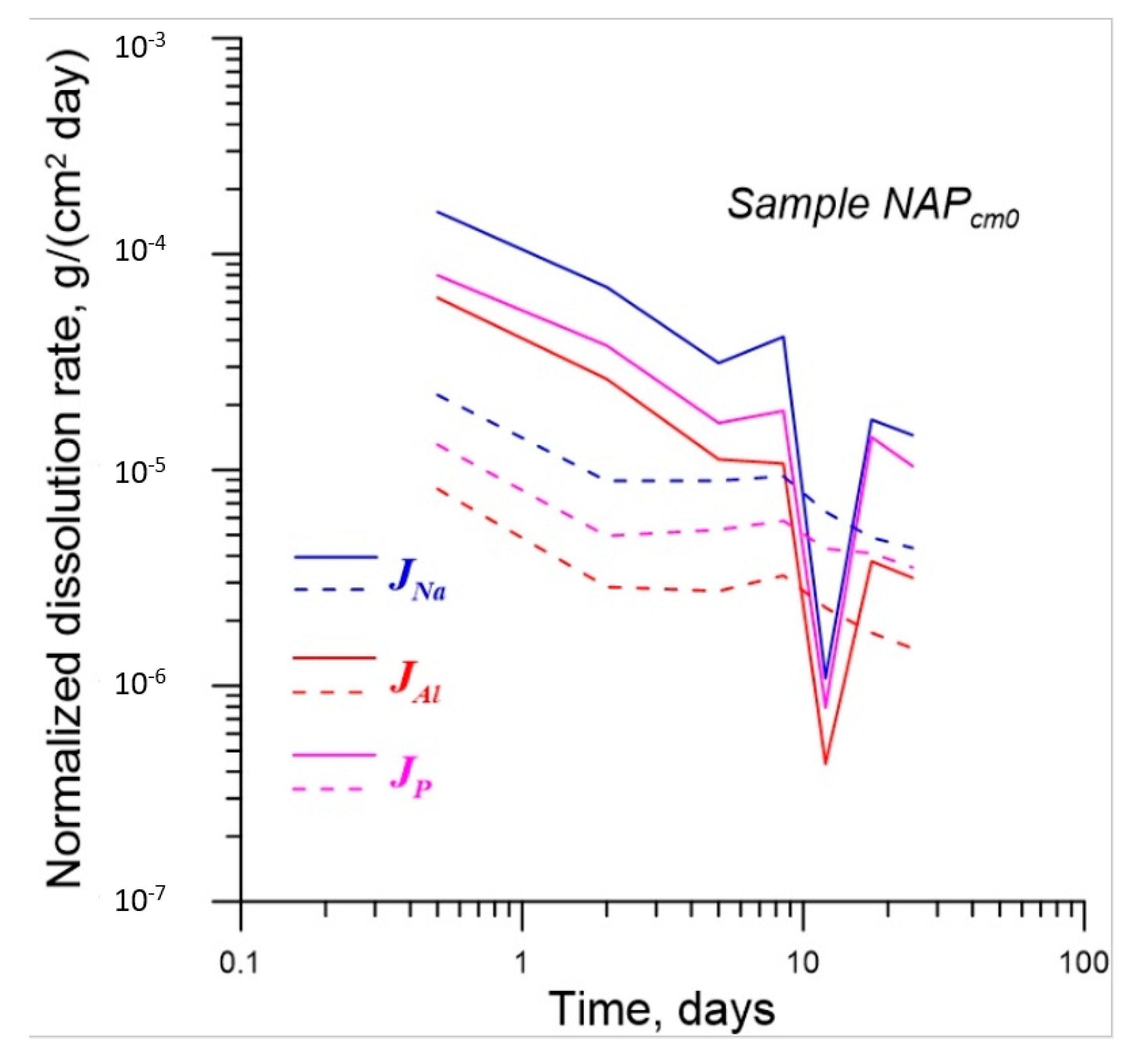
| No. | Na2O | Al2O3 | Fe2O3 | P2O5 | CaO | NiO | La2O3 | Cr2O3 | MnO | RuO2 | UO2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| NAPas0 | 22.3 | 9.2 | 15.6 | 52.1 | - | - | - | - | - | - | - |
| NAPas1 | 22.1 | 9.2 | 15.2 | 52.4 | - | - | - | - | - | - | - |
| NAPcm0 | 26.2 | 15.6 | 1.3 | 53.4 | 0.9 | 0.4 | 0.3 | 0.3 | 0.3 | 0.5 * | 1.4 |
| NAPcm | 26.4 | 14.4 | 1.3 | 54.2 | 0.9 | 0.3 | 0.5 | 0.4 | 0.2 | 0.5 * | 1.3 |
| NAP1 | 26.7 | 14.7 | 1.4 | 53.8 | 0.9 | 0.3 | 0.4 | 0.2 | 0.3 | 0.5 * | 1.3 |
| NAP2 | 24.9 | 16.2 | 1.5 | 53.6 | 0.9 | 0.4 | 0.4 | 0.4 | 0.4 | 0.5 * | 1.2 |
| Mayak 1 | 23.5 | 15.8 | 1.6 | 53.3 | 1.0 | 0.3 | 0.1 | 0.4 | - | - | - |
| Oxide, wt.% | Spectrum 9 | Spectrum 10 | Spectrum 11 | Spectrum 12 | Spectrum 13 |
|---|---|---|---|---|---|
| Na2O | 22.3 | 22.4 | 22.4 | 22.3 | 22.6 |
| Al2O3 | 9.2 | 9.5 | 9.2 | 9.4 | 9.2 |
| SiO2 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
| P2O5 | 52.1 | 51.8 | 51.7 | 51.9 | 51.7 |
| K2O | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| Fe2O3 | 15.6 | 15.4 | 15.8 | 15.5 | 15.7 |
| Oxide, wt.% | Spectrum 1 | Spectrum 2 | Spectrum 3 | Spectrum 5 | Spectrum 6 |
|---|---|---|---|---|---|
| Na2O | 22.1 | 22.4 | 22.4 | 22.3 | 22.8 |
| Al2O3 | 9.2 | 9.4 | 9.3 | 9.3 | 9.3 |
| SiO2 | 0.7 | 1.2 | 0.3 | 0.4 | 0.2 |
| P2O5 | 52.4 | 51.8 | 51.8 | 51.9 | 51.5 |
| K2O | 0.5 | 0.4 | 0.5 | 0.5 | 0.6 |
| Fe2O3 | 15.2 | 14.8 | 15.7 | 15.7 | 15.6 |
| Oxide, wt.% | Spectrum 15 | Spectrum 16 | Spectrum 17 | Spectrum 18 | Spectrum 19 |
|---|---|---|---|---|---|
| Na2O | 26.2 | 26.7 | 26.1 | 26.7 | 26.7 |
| Al2O3 | 15.6 | 15.0 | 15.2 | 15.1 | 14.9 |
| SiO2 | bdl * | bdl | bdl | 0.3 | bdl |
| P2O5 | 53.4 | 53.7 | 53.9 | 53.4 | 53.2 |
| CaO | 0.9 | 0.9 | 0.8 | 1.0 | 1.1 |
| Cr2O3 | 0.3 | 0.2 | 0.3 | 0.4 | 0.3 |
| MnO | 0.3 | 0.4 | 0.3 | 0.4 | 0.3 |
| Fe2O3 | 1.3 | 1.2 | 1.2 | 1.2 | 1.4 |
| NiO | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
| La2O3 | 0.3 | 0.3 | 0.5 | 0.3 | 0.6 |
| UO2 | 1.4 | 1.2 | 1.3 | 1.0 | 1.1 |
| Oxide, wt.% | Spectrum 20 | Spectrum 21 | Spectrum 22 | Spectrum 23 | Spectrum 24 |
|---|---|---|---|---|---|
| Na2O | 0.4 | 0.3 | 0.2 | 0.2 | 0.4 |
| Al2O3 | 41.8 | 41.4 | 42.1 | 42.0 | 41.5 |
| P2O5 | 57.4 | 58.2 | 57.5 | 57.8 | 57.8 |
| Fe2O3 | 0.3 | 0.2 | 0.2 | 0.0 | 0.3 |
| Oxide, wt.% | Sp. 27 | Sp. 28 | Sp. 29 | Sp. 30 | Sp. 31 | Sp. 55 | Sp. 56 | Sp. 57 | Sp. 58 |
|---|---|---|---|---|---|---|---|---|---|
| Na2O | 26.7 | 26.8 | 26.7 | 26.9 | 26.5 | 24.9 | 25.2 | 25.0 | 24.9 |
| Al2O3 | 14.7 | 14.8 | 14.9 | 14.6 | 14.9 | 16.2 | 16.7 | 16.0 | 16.5 |
| P2O5 | 53.8 | 53.7 | 53.9 | 53.4 | 53.2 | 53.2 | 53.2 | 53.2 | 53.2 |
| CaO | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 1.0 |
| Cr2O3 | 0.2 | 0.4 | 0.4 | 0.3 | 0.3 | 0.4 | 0.3 | 0.4 | 0.3 |
| MnO | 0.3 | 0.3 | 0.3 | 0.2 | 0.3 | 0.4 | 0.3 | 0.3 | 0.3 |
| Fe2O3 | 1.4 | 1.3 | 1.2 | 1.5 | 1.2 | 1.5 | 1.4 | 1.5 | 1.2 |
| NiO | 0.3 | 0.3 | 0.3 | 0.5 | 0.4 | 0.4 | 0.4 | 0.4 | 0.5 |
| La2O3 | 0.4 | 0.7 | 0.6 | 0.5 | 0.5 | 0.4 | 0.5 | 0.2 | 0.5 |
| UO2 | 1.3 | 1.3 | 1.3 | 0.9 | 1.4 | 1.2 | 1.4 | 1.3 | 1.2 |
| Element | t = 5 Days | t = 8.5 Days |
|---|---|---|
| Al | 4.07 | 3.30 |
| Na | 3.51 | 4.50 |
| P | 3.12 | 3.23 |
| Element | t = 5 Days | t = 8.5 Days | t = 12 Days |
|---|---|---|---|
| Al | 4.83 | 4.85 | 5.04 |
| Na | 3.80 | 3.75 | 3.28 |
| P | 3.35 | 3.06 | 3.30 |
| Element | t = 0.5 Days | t =2 Days | t = 5 Days | t = 8.5 Days | t = 12 Days |
|---|---|---|---|---|---|
| Al | 1.98 | 2.51 | 1.63 | 1.64 | 1.44 |
| Na | 1.51 | 2.41 | 1.98 | 2.48 | 2.22 |
| P | 1.74 | 2.41 | 1.98 | 2.51 | 2.08 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luzhetsky, A.V.; Petrov, V.A.; Yudintsev, S.V.; Malkovsky, V.I.; Ojovan, M.I.; Nickolsky, M.S.; Shiryaev, A.A.; Danilov, S.S.; Ostashkina, E.E. Effect of Gamma Irradiation on Structural Features and Dissolution of Nuclear Waste Na–Al–P Glasses in Water. Sustainability 2020, 12, 4137. https://doi.org/10.3390/su12104137
Luzhetsky AV, Petrov VA, Yudintsev SV, Malkovsky VI, Ojovan MI, Nickolsky MS, Shiryaev AA, Danilov SS, Ostashkina EE. Effect of Gamma Irradiation on Structural Features and Dissolution of Nuclear Waste Na–Al–P Glasses in Water. Sustainability. 2020; 12(10):4137. https://doi.org/10.3390/su12104137
Chicago/Turabian StyleLuzhetsky, Alexey V., Vladislav A. Petrov, Sergey V. Yudintsev, Viktor I. Malkovsky, Michael I. Ojovan, Maximilian S. Nickolsky, Andrey A. Shiryaev, Sergey S. Danilov, and Elizaveta E. Ostashkina. 2020. "Effect of Gamma Irradiation on Structural Features and Dissolution of Nuclear Waste Na–Al–P Glasses in Water" Sustainability 12, no. 10: 4137. https://doi.org/10.3390/su12104137
APA StyleLuzhetsky, A. V., Petrov, V. A., Yudintsev, S. V., Malkovsky, V. I., Ojovan, M. I., Nickolsky, M. S., Shiryaev, A. A., Danilov, S. S., & Ostashkina, E. E. (2020). Effect of Gamma Irradiation on Structural Features and Dissolution of Nuclear Waste Na–Al–P Glasses in Water. Sustainability, 12(10), 4137. https://doi.org/10.3390/su12104137






